2018届江苏省扬州、泰州、淮安、南通、徐州、宿迁、连云港市高三第三次调研测试英语试题
江苏省扬州、泰州、淮安、南通、徐州、宿迁、连云港市2018届高三第三次调研测试物理试题 含解析

2018届高三年级第三次模拟考试物理一、单项选择题:本题共5小题,每小题3分,共计15分.每小题只有一个....选项符合题意.1. 春秋末年齐国人的著作《考工记》中有“马力既竭,辀犹能一取焉”,意思是马对车不施加拉力了,车还能继续向前运动.这是关于惯性的最早记述.下列关于惯性的说法中正确的是( )A. 车只在运动时才具有惯性B. 撤去拉力后车的惯性大小不变C. 拉力可以改变车的惯性D. 车运动越快惯性越大【答案】B【解析】惯性指物体保持原来运动状态不变的性质,惯性是物体本身固有的属性,任何物体任何状态下都有惯性;质量是物体惯性大小的唯一的量度,故B正确,ACD错误。
2. 如图所示,带有孔的小球A套在粗糙的倾斜直杆上,与正下方的小球B通过轻绳连接,处于静止状态.给小球B施加水平力F使其缓慢上升,直到小球A刚要滑动.在此过程中( )A. 水平力F的大小不变B. 杆对小球A的支持力不变C. 轻绳对小球B的拉力先变大后变小D. 杆对小球A的摩擦力先变小后变大【答案】D【解析】对球受拉力F、重力和细线的拉力T,合力为零如图所示:由此可知,随着θ的增加,拉力F和细线张力T均增加,故A错误,C错误;再对A、B球整体分析,受重力、拉力F、支持力N和静摩擦力f,如图所示:设杆与水平方向的夹角为θ,根据平衡条件,在垂直杆方向有,随着F的增加,支持力N增加;在平行杆方向,有:,可得:,可知随着F的增加,静摩擦力逐渐减小,当时,摩擦力为零,此后静摩擦力反向增加;故B错误,D正确。
所以D正确,ABC错误。
3. 磁流体发电机原理如图所示,等离子体高速喷射到加有强磁场的管道内,正、负离子在洛伦兹力作用下分别向A、B两金属板偏转,形成直流电源对外供电.则( )A. 仅减小两板间的距离,发电机的电动势将增大B. 仅增强磁感应强度,发电机的电动势将减小C. 仅增加负载的阻值,发电机的输出功率将增大D. 仅增大磁流体的喷射速度,发电机的总功率将增大【答案】D【解析】电荷处于平衡有:,解得:E电=Bdv,由此可知仅减小两板间的距离,发电机的电动势将减小,仅增强磁感应强度,发电机的电动势将增大,故AB错误;根据欧姆定律定律和功率公式可知,当外阻和内阻相等时,输出功率最大,所以增加负载的阻值,发电机的输出功率不一定增大,故C错误;由E电=Bdv,可知仅增大磁流体的喷射速度,电动势将增大,因为总电阻不变,所以输出功率将增大,故D正确。
冲刺压轴题 专题难点突破三角函数

< ϕ < ) 的图象关于直线 x = 对称,则 ϕ 的值是上 a , b , c ,已知 tan A 满足 a cos B - b cos A = 3 (得图象过点 ⎛ π 1 ⎫, ⎪ ,则 ϕ 的最小值是江苏省 高三数学一轮复习典型题专题训练三角函数一、填空题1、(2018 江苏高考)已知函数 y = sin(2 x + ϕ)(-▲ .π π π2 2 32、(2017 江苏高考)若 tan (α﹣ π 1)= .则 tan α=4 63、(2016 江苏高考)定义在区间[0,3π]的函数 y =sin2x 的图象与 y =cos x 的图象的交点个数是 ▲4、(南京市 2018 高三 9 月学情调研)若函数 f (x )=A sin(ωx +ϕ)(A >0,ω>0,|ϕ|<π)的部分图象如图所示,则 f (-π)的值为▲ .π 5π5 、(前黄高级中学、姜堰中学等五校 2018 高三上第一次学情监测)已知 α ∈ ( ,) ,且3 6π 3cos(α - ) = ,则 sin α 的值是▲.3 56、(苏锡常镇 2018 高三 3 月教学情况调研(一))设三角形 ABC 的内角 A , B , C 的对边分别为 3c - b= tan B b,则 cos A = .7、(苏锡常镇 2018 高三 5 月调研(二模))已知函数 f ( x ) = sin(π x + ϕ)(0 < x < 2π ) 在 x = 2 时取 得最大值,则 ϕ =8、(苏锡常镇 2018 高三 5 月调研(二模))设△ ABC 的内角 A , B , C 的对边分别是 a ,b ,c 且tan A c ,则 =.5 tan B9、(苏州市 2018 高三上期初调研)将函数 y = sin (2x + ϕ )(0 < ϕ < π ) )的图象沿 x 轴向左平移 π8个单位,得到函数 y = f (x ) 的图象,若函数 y = f (x ) 的图象过原点,则 ϕ 的值是.10、 无锡市 2018 高三上期中考试)将函数 y = sin 2 x 的图象向右平移 ϕ (ϕ > 0) 个单位长度,若所⎝ 3 2 ⎭.(θ ⎡ π π ⎤ ,16、 镇江市 2018 届高三第一次模拟(期末)考试)函数 y = cos x - x tan x 的定义域为 ⎢-4 4 ⎥⎦, cos(α + β ) = - .π 111、(徐州市 2018 高三上期中考试)函数 f ( x ) = 2sin( x + ) 的周期为▲3 412、(扬州、泰州、淮安、南通、徐州、宿迁、连云港市 2018 高三第三次调研)在△ ABC 中,若 sin A :sin B :sin C = 4:5:6 ,则 cosC 的值为 ▲13、 镇江市 2018 届高三第一次模拟(期末)考试)函数 y = 3sin(2x + π4) 图像两对称轴的距离为14 、( 无 锡 市 2018 高 三 上 期 中 考 试 ) 已 知 sin 2 x + 2sin x cos x - 3cos 2 x = 0 , 则cos2 x =.15 、(镇江市 2018 届高三第一次模拟(期末)考试)已知锐角 θ 满足 tan θ= 6 cos,则s in θ + c os θs in θ - c os θ=( , ⎣其值域为二、解答题1、(2018 江苏高考)已知 α , β 为锐角, tan α = 4 355(1)求 cos2 α 的值;(2)求 tan(α - β ) 的值.2、(2018 江苏高考)某农场有一块农田,如图所示,它的边界由圆 O 的一段圆弧 MPN (P 为此圆弧的中点)和线段 MN 构成.已知圆 O 的半径为 40 米,点 P 到 MN 的距离为 50 米.现规划在此农田上修建两个温室大棚,大棚Ⅰ内的地块形状为矩形ABCD ,大棚Ⅱ内的地块形状为△CDP ,要求 A, B 均在线段 MN 上, C, D 均在圆弧上.设 OC 与 MN 所成的角为 θ .(1)用 θ 分别表示矩形 ABCD 和 △CDP 的面积,并确定 sin θ 的取值范围;(2)若大棚Ⅰ内种植甲种蔬菜,大棚Ⅱ内种植乙种蔬菜,且甲、乙两种蔬菜的单位面积年产值之比为 4 ∶3 .求当 θ 为何值时,能使甲、乙两种蔬菜的年总产值最大.,C = . cos B = .(1)若 c =2a ,求 的值;(2)若 C -B = ,求 sin A 的值.点 O ,始边为 x 轴的正半轴,终边与单位圆 O 的交点分别为 P ,Q .已知点 P 的横坐标为 ,点 Q 的纵坐标为 .3、(2016 江苏高考)在 △ABC 中,AC =6, cos B = (1)求 AB 的长; 4 π 5 4(2)求 cos( A - π 6)的值.4、(南京市 2018 高三 9 月学情调研)在△ABC 中,内角 A ,B ,C 所对的边分别为 a ,b ,c ,4 5sin Bsin Cπ45、(南京市 2018 高三第三次(5 月)模拟)在平面直角坐标系 xOy 中,锐角 α,β 的顶点为坐标原2 773 314(1)求 cos2α 的值;(2)求 2α- β 的值.( 3 时,求 ∠OPQ 的大小;(sin A = , tan (A - B ) = ,角 C 为钝角, b = 5.6、(前黄高级中学、姜堰中学等五校 2018 高三上第一次学情监测)已知 ∆ABC 的内角 A, B, C 所对 的边分别为 a, b , c ,已知 asinB + 3b cosA = 3c .(1)求角 B 的大小;(2)若 ∆ABC 的面积为 7 3 4, b = 43, a > c ,求 a, c .7、 苏锡常镇 2018 高三 3 月教学情况调研(一))如图,某景区内有一半圆形花圃,其直径 AB 为 6 ,O 是圆心,且 O C ⊥ AB .在 OC 上有一座观赏亭 Q ,其中 ∠AQC =π赏亭 P ,记 ∠POB = θ (0 < θ <2 ) .2π 3.计划在 BC 上再建一座观(1)当 θ =π(2)当 ∠OPQ 越大,游客在观赏亭 P 处的观赏效果越佳,求游客在观赏亭 P 处的观赏效果最佳时,角 θ 的正弦值.8、 苏锡常镇 2018 高三 5 月调研(二模) 在ABC 中,内角 A , B ,C 的对边分别是 a ,b ,c ,设△ ABC 的面积为 S ,且 4S =3( a 2 + c 2 - b 2 ) .(1)求 ∠B 的大小;(2)设向量 m = (sin 2 A,3cos A) , n = (3, -2cos A) ,求 m ⋅ n 的取值范围.9、(无锡市 2018 高三上期中考试) 在三角形 ABC 中,角 A,B,C 的对边分别为 a,b,c ,若 3 1 53(1)求 sin B 的值; (2)求边 c 的长.10、(无锡市 2018 高三上期中考试)在一块杂草地上有一条小路 AB,现在小路的一边围出一个三角形(如图)区域,在三角形 ABC 内种植花卉.已知 AB 长为 1 千米,设角 C = θ , AC 边长为 BC 边长的 a (a > 1)倍,三角形 ABC 的面积为 S (千米 2).(1)试用 θ 和 a 表示 S ;(2)若恰好当θ=60时,S取得最大值,求a的值.11、(徐州市2018高三上期中考试)已知△ABC的内角A,B,C所对的边分别为a,b,c,且a+2c=2b cosA.(1)求角B的大小;(2)若b=23,a+c=4,求△ABC的面积.12、(扬州、泰州、淮安、南通、徐州、宿迁、连云港市2018高三第三次调研)如图是函数πf(x)=A sin(ωx+ϕ)(A>0,ω>0,ϕ≤)在一个周期内的图象.已知2点P(-6,0),Q(-2,-3)是图象上的最低点,R是图象上的最高点.(1)求函数f(x)的解析式;(2)记∠RPO=α,∠Q PO=β(α,β均为锐角),求tan(2α+β)的值.13、(镇江市2018届高三第一次模拟(期末)考试)在∆ABC中,角A,B,C所对的边分别为a, b,c,若b cos A+a cos B=-2c cos C.(1)求C的大小;(2)若b=2a,且∆ABC的面积为23,求c.14、(苏北四市(徐州、淮安、连云港、宿迁)2017届高三上学期期末)在∆ABC中,角A,B,C的对边分别为a,b,c.已知2cos A(b cos C+c cos B)=a.(1)求角A的值;(2)若cos B=35,求sin(B-C)的值.2,求函数f(x)的值域;411、612、13、14、0或15、3+228516、[2-,1]1、解:(1)因为tanα=4,tanα=,所以sinα=cosα.15、(苏州市2017届高三上学期期中调研)已知函数f(x)=2sin(x+π(1)若0≤x≤π3)⋅c os x.(2)设∆ABC的三个内角A,B,C所对的边分别为a,b,c,若A为锐角且f(A)=32,b=2,c=3,求cos(A-B)的值.16、(盐城市2017届高三上学期期中)设函数f(x)=A s in(ωx+ϕ)(A,ω,ϕ为常数,且A>0,ω>0,0<ϕ<π)的部分图象如图所示.(1)求A,ω,ϕ的值;3π(2)设θ为锐角,且f(θ)=-3,求f(θ-)的值.56参考答案一、填空题π4+331、-2、1.43、74、-15、6106、1π3ππ7、8、49、10、3241π42π24二、解答题sinα43cosα3因为sin2α+cos2α=1,所以cos2α=9 25,又因为cos(α+β)=-5,所以sin(α+β)=1-cos2(α+β)=,,所以tan2α==-,因此,tan(α-β)=tan[2α-(α+β)]==-.,θ∈(0,).(θ(θ当θ∈(θ0,π(θ因此,cos2α=2cos2α-1=-7.25(2)因为α,β为锐角,所以α+β∈(0,π).2555因此tan(α+β)=-2.因为tanα=42tanα2431-tan2α7tan2α-tan(α+β)21+tan2αtan(α+β)112、解:(1)连结PO并延长交MN于H,则PH⊥MN,所以OH=10.过O作OE⊥BC于E,则OE∥MN,所以∠COE=θ,故OE=40cosθ,EC=40sinθ,则矩形ABCD的面积为2×40cosθ(40sinθ+10)=800(4sinθcosθ+cosθ),△CDP的面积为1×2×40cosθ(40–40sinθ)=1600(cosθ–sinθcosθ).2过N作GN⊥MN,分别交圆弧和OE的延长线于G和K,则GK=KN=10.令∠GOK=θ0,则sinθ=1π46当θ∈[θ0,π2)时,才能作出满足条件的矩形ABCD,所以sinθ的取值范围是[14,1).答:矩形ABCD的面积为800(4sinθcosθ+cos△θ)平方米,CDP的面积为1600(cosθ–sinθcosθ),sinθ的取值范围是[1,1).4(2)因为甲、乙两种蔬菜的单位面积年产值之比为4∶3,设甲的单位面积的年产值为4k,乙的单位面积的年产值为3k(k>0),则年总产值为4k×800(4sinθcosθ+cosθ)+3k×1600(cosθ–sinθcosθ)=8000k(sinθcosθ+cosθ),θ∈[θ,设f(θ)=sinθcosθ+cosθ,θ∈[θ0,π2π2).),则f′)=cos2θ-sin2θ-sinθ=-(2sin2θ+sinθ-1)=-(2sinθ-1)(sinθ+1).令f′)=0,得θ=π6,6)时,f′)>0,所以f(θ)为增函数;当 θ∈( π , )时, f ′θ )<0 ,所以 f (θ)为减函数,在△ABC 中,因为 cos B = ,所以 = . ………………………2 分( )2+c 2-b 2 因为 c =2a ,所以 = ,即 2= , 2 所以 = .……………………………4 分sin C c所以 = .……………………………6 分因为 cos B = ,B ∈(0,π),所以 sin B = 1-cos 2B = .………………………2 分π( 6 2因此,当 θ= π 6 时,f (θ)取到最大值.答:当 θ= π 6 时,能使甲、乙两种蔬菜的年总产值最大3、4、解:(1)解法 14a 2+c 2-b 2 4 5 2ac 5c 2 4 b 2 9 c 5 c 20 2c ×b 3 5c 10sin B b又由正弦定理得 = ,sin B 3 5sin C 10解法 24 35 5因为 c =2a ,由正弦定理得 sin C =2sin A ,所以 sin C =2sin(B +C )= cos C + sin C ,又因为 sin 2C +cos 2C =1,sin C >0,解得 sin C =2 5 所以 = .………………………6 分 (2)因为 cos B = ,所以 cos2B =2cos 2B -1= .…………………………8 分又 0<B <π,所以 sin B = 1-cos 2B = ,所以 sin2B =2sin B cos B =2× × = .…………………………10 分因为 C -B = ,即 C =B + ,所以 A =π-(B +C )= -2B ,所以 sin A =sin( -2B )=sin cos2B -cos sin2B………………………………12 分× -(- )×. …………………………………14 分(6 85 5即-sin C =2cos C .………………………4 分5,sin B 3 5sin C 104 75 25353 4 245 5 25π π 3π4 4 43π43π 3π4 4= 27 2 24 2 25 2 25=31 2502 75、解: 1)因为点 P 的横坐标为 7 ,P 在单位圆上,α 为锐角,2 7所以 cos α= 7 ,………………………2 分1 所以cos2α=2cos 2α-1=7.……………………………4 分3 3 3 3(2)因为点 Q 的纵坐标为 14 ,所以 sin β= 14 .………………………6 分13又因为 β 为锐角,所以 cos β=14.……………………………8 分2 7 21因为 cos α= 7 ,且 α 为锐角,所以 sin α= 7 ,4 3 因此 sin2α=2sin αcos α= 7 ,………………………10 分所以 sin(2α-β) =4 3 13 1 3 3 37 ×14-7× 14 = 2 . …………………12 分因为 α 为锐角,所以 0<2α<π.π又 cos2α>0,所以 0<2α<2,π π π 又 β 为锐角,所以-2<2α-β<2,所以 2α-β=3.…………………14 分ac=,即ac=7,(43)=(a+c)-2ac-ac,2(2-θ=由正弦定理得OQπ,所以2-θ=由正弦定理得OQ=6、【解】(1)由已知asinB+3b cosA=3sinC,结合正弦定理得sinAsinB+3sinBcosA=3sinC,所以sinAsinB+3sinBcosA=3sin(A+B)=3(sinAcosB+sinBcosA),即sinAsinB=3sinAcosB,即tanB=3,因为B∈(0,π),所以B=π3.………………7分(2)由S∆ABC =1πacsinB,B=,得2337344又b2=(a+c)2-2ac-2accosB,得2所以{ac=7a=7,又a>c,∴{.………………14分a+c=8c=17、解:1)设∠OPQ=α,由题,Rt∆OAQ中,OA=3,∠AQO=π-∠AQC=π-2ππ=,33所以OQ=3,在∆OPQ中,OP=3,∠POQ=ππ2-π3=π6,OP=,sin∠OPQ sin∠OQP即3sinα=3π5π3sinα=sin(π-α-)=sin(-α),sin(π-α-)666则3sinα=sin 5π5π13cosα-cos sinα=cosα+6622sinα,所以3sinα=cosα,3π因为α为锐角,所以cosα≠0,所以tanα=,得α=;36(2)设∠OPQ=α,在∆OPQ中,OP=3,∠POQ=ππ2-π3=π6,OP33=,即,sin∠OPQ sin∠OQP sinαπsin(π-α-(-θ))2ππ所以3sinα=sin(π-α-(-θ))=sin(-(α-θ))=cos(α-θ)=cosαcosθ+sinαsinθ,22从而(3-sinθ)sinα=cosαcosθ,其中3-sinθ≠0,cosα≠0,记 f (θ ) = cos θ 2所以 tan α =cos θ 3 - sin θ ,1 - 3 sin θ π , f '(θ ) = ,θ ∈ (0, ) ; 3 - sin θ( 3 - sin θ )2 2令 f '(θ ) = 0 , sin θ = 3 3π 3 ,存在唯一θ ∈ (0, ) 使得 sin θ = , 0 0 3 当 θ ∈ (0,θ ) 时 f '(θ ) > 0 , f (θ ) 单调增,当θ ∈ (θ , 0 0 所以当 θ = θ 时, f (θ ) 最大,即 tan ∠OPQ 最大, 0π2 ) 时 f '(θ ) < 0 , f (θ ) 单调减,又 ∠OPQ 为锐角,从而 ∠OPQ 最大,此时 sin θ = 3 3.答:观赏效果达到最佳时,θ 的正弦值为8、3 3.9、10、ac sin B=2⨯4⨯11、(1)因为a+2c=2b cosA,由正弦定理,得sinA+2sin C=2sinBcosA.···························································2分因为C=π-(A+B),所以sinA+2sin(A+B)=2sinBcosA.即sinA+2sin AcosB+2cos Asin B=2sinBcosA,所以sinA⋅(1+2cosB)=0.····························································································4分1因为sinA≠0,所以cosB=-.················································································6分2又因为0<B<π,所以B=2π3.···················································································································7分(2)由余弦定理a2+c2-2ac cos B=b2及b=23得,a2+c2+ac=12,即(a+c)2-ac=12.··································································································10分又因为a+c=4,所以ac=4,···············································································································12分所以S 113△ABC =22=3.·································································14分12、sin A sin B sin C所以 cos C =- ,(6 分) 所以 ab sin C =2 3.(8 分) 13、解析:(1) 由正弦定理 a 所以 C =2π .(7 分)b c = = , 且 b cos A +a cos B =-2c cos C 得(2 分)sin B cos A +sin A cos B =-2sin C cos C ,所以 sin (B +A)=-2sin C cos C.(3 分)因为 A ,B ,C 为三角形的内角,所以 B +A =π -C ,所以 sin C =-2sin C cos C.(4 分)因为 C ∈(0,π ),所以 sin C>0.(5 分)1 23(2) 因为△ABC 的面积为 2 3, 1 2由(1)知 C =2π ,所以 sin C = ,所以 ab =8.(9 分) 所以 c 2=a 2+b 2-2ab cos C =22+42-2×2×4×⎝-2⎭=28,(13 分) 由 0 ≤ x ≤ 得, ≤ 2x + ≤ , - ≤ sin(2 x + ) ≤1 , .........4 分 ,即函数 f ( x ) 的值域为 [0,1 + ∴ 0 ≤ sin(2 x + ) + ≤1 + ] . .....6 分 3 3 2因为 b =2a ,所以 a =2,b =4,(11 分)⎛ 1⎫所以 c =2 7.(14 分)14、(1)由正弦定理可知, 2cos A(sin B cos C + sin C cos B) = sin A , ………………2 分即 2cos Asin A = sin A ,因为 A ∈ (0, π) ,所以 sin A ≠ 0 ,所以 2cos A = 1 ,即 cos A = 1 2, ………………………………………………4 分 又 A ∈ (0, π) ,所以 A = π 3. ……………………………………………………6 分 (2)因为 cos B = 3 4 , B ∈ (0, π) ,所以 sin B = 1 - cos 2 B = ,…………………8 分 5 5 24 7 所以 sin 2B = 2sin B cos B = , cos2 B = 1 - 2sin 2 B = - , ……………10 分 25 25 2π 2π 所以 sin(B - C) = sin[B - ( - B)] = sin(2B - ) 3 3 2π 2π = sin 2B cos - cos2 B s in 3 324 1 7 3 =- ⨯ - (- ) ⨯ 25 2 25 2………………………………12 分 = 7 3 - 24 50.…………………………………………………14 分 15、解:(1) f ( x ) = (sin x + 3 cos x)cos x = sin x cos x + 3 cos 2 x 1 3 3 π 3 = sin 2 x + cos2 x + = sin(2 x + ) + 2 2 2 3 2. .........2 分 π π π 4π 2 3 3 33 π 2 3π 3 3 3 3 2 2 2π 3 3 π (2)由 f ( A ) = sin(2 A + ) + = 得 sin(2 A + ) = 0 , 3 2 2 3π π π 4π π π 又由 0 < A < ,∴ < 2 A + < ,∴ 2 A + = π , A = . ........8 分 2 3 3 3 3 3在 ∆ABC 中,由余弦定理 a 2 = b 2 + c 2 - 2bc cos A =7 ,得 a = 7 . .......10 分 由正弦定理 a b = sin A sin B,得 sin B = b s in A 21 = a 7 , ......12 分 2 7 ∵ b < a ,∴ B < A ,∴ cos B = , 71 2 7 3 21 5 7 ∴ cos( A - B) = cos A c os B + sin Asin B = ⨯ + ⨯ = 2 7 2 7 14. ....15 分= 2 , ……………4分⎪ = π ,∴ω = 由 f = - 3 ,得 2 ⎪ ⎝ 12 ⎭ ⎝ 12 ⎭ θ ∈ (0, ) ,∴ 2θ + ∈ , ⎪ ,又 sin(2θ + ) < 0 ,所以 2θ + ∈ π , ⎪ , ∴ f (θ - ) = 3 sin 2θ = 3 sin ⎢(2θ + ) - = 3 ⎢sin(2θ + )cos - cos(2θ + )sin = 3 - ⨯ + ⨯ 10 . ……………14分 2 ⎪⎭ 5 2 5 π ⎛ π 4π ⎫ 3 ⎝ 3 3 ⎭ ⎦⎦16、解:(1)由图像,得 A = 3 , ……………2分最小正周期 T = 4 ⎛ 7π π ⎫ 2π + 3 ⎝ 12 6 ⎭ T ∴ f ( x ) = 3 sin(2 x + ϕ ) , ⎛ 7π ⎫ ⎛ 7π ⎫ ⎪ π + ϕ = - + 2k π , k ∈ Z , 2 5π π ∴ϕ = - + 2k π , k ∈ Z , 0 < ϕ < π ,∴ϕ = . ……………7分 3 3π 3 π 3 (2)由 f (θ ) = 3 sin(2θ + ) = - 3 ,得 sin(2θ + ) = - , 3 5 3 5π π π ⎛ 4π ⎫ 2 3 3 ⎝ 3 ⎭π π 4 ∴ c os(2θ + ) = - 1 - sin 2(2θ + ) = - , ……………10分 3 3 5π ⎡ π π ⎤ 6 ⎣3 3 ⎥ ⎡ π π π π ⎤ ⎣ 3 3 3 3 ⎥⎛ 3 1 4 3 ⎫ 12 - 3 3 = ⎝。
江苏省徐州市、宿迁市、连云港市2022届高三第三次模拟考试(三模) 英语 图片版含答案

高三班级第三次模拟考试英语试题参考答案第一部分听力(共两节,满分20分)1-5 CCBAB 6-10 ABAAC 11-15 BBCBB 16-20 ABCAB其次部分英语学问运用(共两节,满分35分)第一节单项填空(共15题;每小题1分,满分15分)21 – 25 DCBDA 26 – 30 ABDAB 31 – 35BCBCB其次节完型填空(共20小题;每小题1分,满分20分)36-40 ABDAB 41-45 ABCDA 46-50 CACDB 51-55 CABDB第三部分阅读理解(共15小题;每小题2分,满分30分)56 – 57 DB 58 – 60 ADC 61-64BADD 65 – 70 BDCCDC第四部分任务型阅读(共10小题;每小题l分,满分l0分)71. Finding 72. possibility/probability 73. participating 74. Factors 75. emotionally76. confidence/willingness 77. stronger 78. access 79. leaving/quitting80. instead第五部分:书面表达(满分 25分)这篇小短文有204个字。
本篇小文章是选自《美国语文经典读本》其次册第八课。
[Sample]To have her kittens stay in the proper place—attic, Puss tried several times but was always stopped by the servant. Thanks for a strange and kind cat’s help, she made it. (32words)I’m deeply moved by what the strange cat did. He helped Puss selflessly asking for nothing in return, which made me think of what happened to me recently. It was on Monday morning, when several teachers attended our English lesson. Among them, a middle-aged teacher sat beside me, leaving her wallet on my desk. But she forgot to take it after class. So I rushed out, gave it back to her and ran away.As far as I am concerned, the spirit of being ready to help others should be advocated. Helping others is a traditional virtue in China. If you help others today, maybe others will help you in the future. In this way, we can construct a harmonious society. (121words)听力原文Text1M: Welcome home, Mary! Have you had any problems at university since last September?W: Merry Christmas, Uncle! Well, nothing to speak of.M: No more worries? No complaints? Great!Text2M: Excuse me. Can you tell me where the Shanghai Grand Theater is? I’m completely lost.W: Oh, just walk along this street and turn right at the corner. You will see the Shanghai Museum on People’s Avenue. The Shanghai Grand Theater is opposite that.Text3W: I heard you got full marks in the math exam. Congratulations!M: Thanks! I’m sure you also did a good job.Text4M: I don’t know why people are just mad about David Beckham. Is there really anything so fascinating with him? W: He appeals to the fans thanks to two things, his bending kicks and his good looks.Text5 W: Rod, I hear you’ll be leaving at the end of this month. Is it true?M: Yeah. I’ve been offered a much better position with another firm. I’d be a fool to turn it down.Text6W: What do you plan to do during the holiday?M: I want to visit China. Can you recommend any interesting places I should visit there?W: I think Shanghai will interest you. It is a big city.M: Good idea. Where are you going to spend your holiday?W: I will stay at home. I want to spend my time studying French. It is said that French is a very popular language because it is the most beautiful language in the world. I think it’s a very useful language, even though it isn’t very easy.M: You really work hard all the time. You should really do some sports. For example, you can play basketball or football.W: That’s a good idea, but I think I’d rather play table tennis better. That’s a fun sport.Text7W: Hi, Tom! What are you doing?M: Oh, I’m studying for an English test.W: Have you made any progress?M: No, as a matter of fact, v ery little. I really don’t know how to study all this stuff! How is your English? How do you study?W: Well, you might try using the Internet to help you, you can listen to English songs Online, watch films in English, and find lots of other things that can increase your interest and help you learn English. That really worked. Many of my classmates also made great progress. The Internet helps you not only learn English but also expand your knowledge of Western cultures.M: That’s really wonderful. I never t hought English language learning could be so much fun.W: Yes, in fact, learning English is not as difficult as you think.M: Next time, can you show me how to practice English online?W: Sure. Well, I have to return some books. Good luck in your examination!M: Thank you! Bye.Text8W: Doctor, I’ve got a little pain and numbness in my ears.M: Let me see. Well, do you often listen to loud music with earphones?W: Yes. I usually listen to music or practice English listening two or three hours per day.M: That’s the very problem. Listening to loud music more than 90 minutes a day can damage your hearing according to a new study.W: How can I improve my hearing, doctor?M: Well, stop listening to loud music with earphones immediately.W: Can’t I listen to music with earphones in the future?M: Oh, yes, but later. Try to reduce the time you use earphones and never use your ears too much.W: By the way, are there any user-friendly earphones to protect my ears?M: No, in the future we may get some. From now on you should concern yourself about your hearing loss, or it may cause a terrible result.W: I see. Thank you, doctor.Text9W: Good afternoon. I’d like some information about the train, please.M: Yes, Madam. Where are you going?W: To London. You see, I have a sister there and she studies in…M: So your question is“When is the next train to London?”. Is that right?W: Yes, that’s right. When’s the next train to London?M: At half past four. That’s in about six minutes.W: Thank you very much. Oh! Can I get something to eat on the train? I always have something to eat when I travel. I find that a cup of tea and a cake always calm me down.M: Yes, Madam. You can get what you want on the train.W: Oh, good! Err, how much does a cup of tea cost?M: I’m not s ure, Madam. Fifty pence, I think.W: Oh, dear! Things are getting so expensive.M: Yes, Madam. Your train is going to leave in five minutes from Platform 13.W: Platform 13! Oh, dear! I never travel on trains that leave from Platform 13! 13 is an unlucky n umber. When’s the next train after the 4:30 one?Text10M: Attention please! Thank you. Now, welcome to the Spring Hotel. We hope you have a wonderful holiday. Let me tell you about some of the services we have here. On the ground floor, you will find reception. Here we can answer your questions and help you with any general problems. Please leave your room key here whenever you go out. On the sixth floor is a restaurant where you can have breakfast from half past seven to half past nine each morning. The bedrooms are on the fourth and fifth floors. If you want to use a phone, there are telephones available on the second floor. Any questions? No? Fine. You can go shopping on the first floor. For people who like sports, if you want to swim, there’s a nice n ew pool on the seventh floor, where you can swim and enjoy the warm sunshine. We also have some tennis courts behind the hotel. Oh, and if you want to watch your favorite program, the televisions are on the third floor. Any questions? No? Well, good. Have a nice holiday.My office is on the sixth floor, just next to the pub. lf you’re in need of any help, please don’t hesitate to come and ask.。
2020年江苏省徐州市、淮安市、南通市、泰州市、扬州市、连云港市、宿迁市高考数学三模试卷 (解析版)
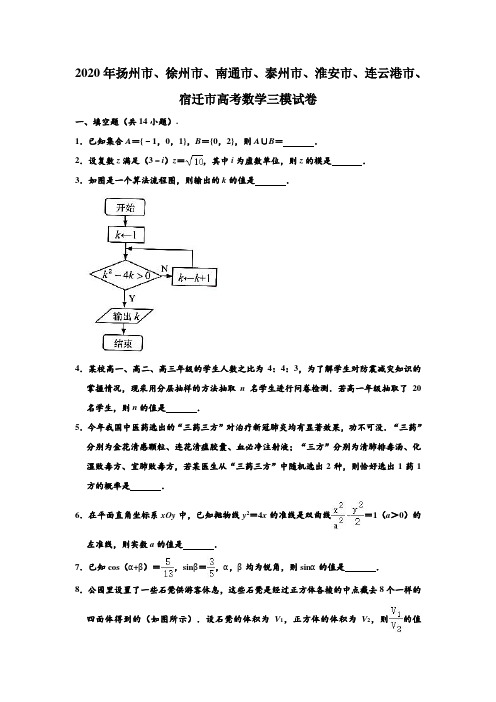
2020年扬州市、徐州市、南通市、泰州市、淮安市、连云港市、宿迁市高考数学三模试卷一、填空题(共14小题).1.已知集合A={﹣1,0,1},B={0,2},则A∪B=.2.设复数z满足(3﹣i)z=,其中i为虚数单位,则z的模是.3.如图是一个算法流程图,则输出的k的值是.4.某校高一、高二、高三年级的学生人数之比为4:4:3,为了解学生对防震减灾知识的掌握情况,现采用分层抽样的方法抽取n名学生进行问卷检测.若高一年级抽取了20名学生,则n的值是.5.今年我国中医药选出的“三药三方”对治疗新冠肺炎均有显著效果,功不可没.“三药”分别为金花清感颗粒、连花清瘟胶囊、血必净注射液;“三方”分别为清肺排毒汤、化湿败毒方、宜肺败毒方,若某医生从“三药三方”中随机选出2种,则恰好选出1药1方的概率是.6.在平面直角坐标系xOy中,已知抛物线y2=4x的准线是双曲线=1(a>0)的左准线,则实数a的值是.7.已知cos(α+β)=,sinβ=,α,β均为锐角,则sinα的值是.8.公园里设置了一些石凳供游客休息,这些石凳是经过正方体各棱的中点截去8个一样的四面体得到的(如图所示).设石凳的体积为V1,正方体的体积为V2,则的值是.9.已知x>1,y>1,xy=10,则的最小值是.10.已知等比数列{a n}的前n项和为S n,若4S2,S4,﹣2S3成等差数列,且a2+a3=2,则a6的值是.11.海伦(Heron,约公元1世纪)是古希腊亚历山大时期的数学家,以他的名字命名的“海伦公式”是几何学中的著名公式,它给出了利用三角形的三边长a,b,c计算其面积的公式S△ABC=,其中p=,若a=5,b=6,c=7,则借助“海伦公式”可求得△ABC的内切圆的半径r的值是.12.如图,△ABC为等边三角形,分别延长BA,CB,AC到点D,E,F,使得AD=BE =CF.若,且DE=,则的值是.13.已知函数f(x)=,若函数g(x)=f(﹣x)+f(x)有且仅有四个不同的零点,则实数k的取值范围是.14.在平面直角坐标系xOy中,过点P(2,﹣6)作直线交圆O:x2+y2=16于A,B两点,C(x0,y0)为弦AB的中点,则的取值范围是.二、解答题(本大题共6小题,共计90分.请在答题纸指定区域内作答,解答应写出文字说明,证明过程或演算步骤.)15.△ABC中,角A,B,C所对的边分别为a,b,c.若.(1)求cos C的值;(2)若A=C,求sin B的值.16.如图,在直三棱柱ABC﹣A1B1C1中,AC⏊BC,D,E分别是A1B1,BC的中点.求证:(1)平面ACD⊥平面BCC1B1;(2)B1E∥平面ACD.17.某单位科技活动纪念章的结构如图所示,O是半径分别为1cm,2cm的两个同心圆的圆心,等腰△ABC的顶点A在外圆上,底边BC的两个端点都在内圆上,点O,A在直线BC的同侧.若线段BC与劣弧所围成的弓形面积为S1,△OAB与△OAC的面积之和为S2,设∠BOC=2θ.(1)当θ=时,求S2﹣S1的值;(2)经研究发现当S2﹣S1的值最大时,纪念章最美观,求当纪念章最美观时,cosθ的值.(求导参考公式:(sin2x)'=2cos2x,(cos2x)'=﹣2sin2x)18.(16分)如图,在平面直角坐标系xOy中,已知椭圆=1(a>b>0)的左、右焦点分别为F1,F2,过点F2的直线交椭圆于M,N两点.已知椭圆的短轴长为2,离心率为.(1)求椭圆的标准方程;(2)当直线MN的斜率为时,求F1M+F1N的值;(3)若以MN为直径的圆与x轴相交的右交点为P(t,0),求实数t的取值范围.19.(16分)已知{a n}是各项均为正数的无穷数列,数列{b n}满足b n=a n•a n+k(n∈N*),其中常数k为正整数.(1)设数列{a n}前n项的积,当k=2时,求数列{b n}的通项公式;(2)若{a n}是首项为1,公差d为整数的等差数列,且b2﹣b1=4,求数列的前2020项的和;(3)若{b n}是等比数列,且对任意的n∈N*,a n•a n+2k=a n+k2,其中k≥2,试问:{a n}是等比数列吗?请证明你的结论.20.(16分)已知函数f(x)=,g(x)=,其中e是自然对数的底数.(1)若函数f(x)的极大值为,求实数a的值;(2)当a=e时,若曲线y=f(x)与y=g(x)在x=x0处的切线互相垂直,求x0的值;(3)设函数h(x)=g(x)﹣f(x),若h(x)>0对任意的x∈(0,1)恒成立,求实数a的取值范围.【选做题】本题包括21,22,23三小题,请选定其中两题作答,每小题10分,共计20分,解答时应写出文字说明,证明过程或演算步骤.[选修4-2:矩阵与变换]21.已知m∈R,=是矩阵M=的一个特征向量,求M的逆矩阵M﹣1.[选修4-4:坐标系与参数方程]22.在极坐标系中,圆C的方程为ρ=2r sinθ(r>0).以极点为坐标原点,极轴为x轴正半轴建立平面直角坐标系,直线l的参数方程为(t为参数).若直线l与圆C恒有公共点,求r的取值范围.[选修4-5:不等式选讲]23.已知x>1,y>1,且x+y=4,求证:≥8.【必做题】第24题、第25题,每题10分,共计20分,解答时应写出文字说明,证明过程或演算步骤.24.某“芝麻开门”娱乐活动中,共有5扇门,游戏者根据规则开门,并根据打开门的数量获取相应奖励.已知开每扇门相互独立,且规则相同,开每扇门的规则是:从给定的6把钥匙(其中有且只有1把钥匙能打开门)中,随机地逐把抽取钥匙进行试开,钥匙使用后不放回.若门被打开,则转为开下一扇门;若连续4次未能打开,则放弃这扇门,转为开下一扇门;直至5扇门都进行了试开,活动结束.(1)设随机变量X为试开第一扇门所用的钥匙数,求X的分布列及数学期望E(X);(2)求恰好成功打开4扇门的概率.25.如图,在平面直角坐标系xOy中,已知抛物线y2=2px(p>0)的焦点为F,准线与x 轴的交点为E.过点F的直线与抛物线相交于A,B两点,EA,EB分别与y轴相交于M,N两点,当AB⊥x轴时,EA=2.(1)求抛物线的方程;(2)设△EAB的面积为S1,△EMN面积为S2,求的取值范围.参考答案一、填空题(本大题共14小题,每小题5分,共计70分.不需要写出解答过程,请将答案填写在答题卡相应的位置上.)1.已知集合A={﹣1,0,1},B={0,2},则A∪B={﹣1,0,1,2}.【分析】进行并集的运算即可.解:∵A={﹣1,0,1},B={0,2},∴A∪B={﹣1,0,1,2}.故答案为:{﹣1,0,1,2}.2.设复数z满足(3﹣i)z=,其中i为虚数单位,则z的模是1.【分析】把已知等式变形,再由商的模等于模的商求解.解:由(3﹣i)z=,得z=,∴|z|=||=.故答案为:1.3.如图是一个算法流程图,则输出的k的值是5.【分析】由已知中的程序语句可知:该程序的功能是利用循环结构计算并输出变量k的值,模拟程序的运行过程,分析循环中各变量值的变化情况,可得答案.解:模拟程序的运行,可得k=1不满足条件k2﹣4k>0,执行循环体,k=2不满足条件k2﹣4k>0,执行循环体,k=3不满足条件k2﹣4k>0,执行循环体,k=4不满足条件k2﹣4k>0,执行循环体,k=5此时,满足条件k2﹣4k>0,退出循环,输出k的值为5.故答案为:5.4.某校高一、高二、高三年级的学生人数之比为4:4:3,为了解学生对防震减灾知识的掌握情况,现采用分层抽样的方法抽取n名学生进行问卷检测.若高一年级抽取了20名学生,则n的值是55.【分析】先求出高一年级学生占的比例,再根据比例即可求解结论.解:高一年级学生占的比例为=,故应满足:=⇒n=55人,故答案为:55.5.今年我国中医药选出的“三药三方”对治疗新冠肺炎均有显著效果,功不可没.“三药”分别为金花清感颗粒、连花清瘟胶囊、血必净注射液;“三方”分别为清肺排毒汤、化湿败毒方、宜肺败毒方,若某医生从“三药三方”中随机选出2种,则恰好选出1药1方的概率是.【分析】某医生从“三药三方”中随机选出2种,基本事件总数n==15,恰好选出1药1方包含的基本事件个数m==9.由此能求出恰好选出1药1方的概率.解:“三药三方”对治疗新冠肺炎均有显著效果,功不可没.“三药”分别为金花清感颗粒、连花清瘟胶囊、血必净注射液,“三方”分别为清肺排毒汤、化湿败毒方、宜肺败毒方,若某医生从“三药三方”中随机选出2种,基本事件总数n==15,恰好选出1药1方包含的基本事件个数m==9.∴恰好选出1药1方的概率是p===.故答案为:.6.在平面直角坐标系xOy中,已知抛物线y2=4x的准线是双曲线=1(a>0)的左准线,则实数a的值是.【分析】求出抛物线的准线方程,求出双曲线的左准线方程,得到关系式,求解即可.解:抛物线y2=4x的准线是双曲线=1(a>0)的左准线,可得:﹣1=﹣=﹣,解得a=.故答案为:.7.已知cos(α+β)=,sinβ=,α,β均为锐角,则sinα的值是.【分析】由α,β的范围得出α+β的范围,然后利用同角三角函数间的基本关系,由cos (α+β)和sinβ的值,求出sin(α+β)和cosβ的值,然后由α=(α+β)﹣β,把所求的式子利用两角差的正弦函数公式化简后,将各自的值代入即可求出值.解:解:由cos(α+β)=,sinβ=,根据α,β∈(0,),得到α+β∈(0,π),所以sin(α+β)==,cosβ==,则sinα=sin[(α+β)﹣β]=sin(α+β)cosβ﹣cos(α+β)sinβ=×﹣×=.故答案为:.8.公园里设置了一些石凳供游客休息,这些石凳是经过正方体各棱的中点截去8个一样的四面体得到的(如图所示).设石凳的体积为V1,正方体的体积为V2,则的值是.【分析】设正方体的棱长为2a,求出正方体的体积,再由正方体的体积减去8个三棱锥的体积得石凳的体积,则答案可求.解:设正方体的棱长为2a,则正方体的体积.由题意可得,石凳的体积为V1=8a3﹣=.∴=.故答案为:.9.已知x>1,y>1,xy=10,则的最小值是9.【分析】利用“乘1法”与基本不等式的性质即可得出.解:因为x>1,y>1,xy=10,所以lgx+lgy=1,则=()(lgx+lgy)=5+=9,当且仅当时即lgy=2lgx且xy=10即x=,y=时取等号,故答案为:9.10.已知等比数列{a n}的前n项和为S n,若4S2,S4,﹣2S3成等差数列,且a2+a3=2,则a6的值是﹣32.【分析】等比数列{a n}的公比设为q,运用等差数列的中项性质和等比数列的通项公式,解方程可得首项和公比,进而得到所求值.解:等比数列{a n}的公比设为q,前n项和为S n,若4S2,S4,﹣2S3成等差数列,则2S4=4S2﹣2S3,可得2(a1+a1q+a1q2+a1q3)=4(a1+a1q)﹣2(a1+a1q+a1q2),化为2+q=0,可得q=﹣2,由a2+a3=2,可得﹣2a1+4a1=2,解得a1=1,则a6=1•(﹣2)5=﹣32,故答案为:﹣32.11.海伦(Heron,约公元1世纪)是古希腊亚历山大时期的数学家,以他的名字命名的“海伦公式”是几何学中的著名公式,它给出了利用三角形的三边长a,b,c计算其面积的公式S△ABC=,其中p=,若a=5,b=6,c=7,则借助“海伦公式”可求得△ABC的内切圆的半径r的值是.【分析】利用S△ABC==pr,代入即可得出.解:∵a=5,b=6,c=7,∴p===9.则S△ABC==r×(5+6+7),可得:r=.故答案为:.12.如图,△ABC为等边三角形,分别延长BA,CB,AC到点D,E,F,使得AD=BE =CF.若,且DE=,则的值是.【分析】设AD=BE=CF=x,由于,所以BA=2AD=2x=AC=BC,BD=3x.在△BDE中,由余弦定理知,,代入数据可解得x=1,从而有AF=3,CE=3,然后结合平面向量数量积的运算即可得解.解:设AD=BE=CF=x,∵,∴BA=2AD=2x=AC=BC,∴BD=BA+AD=3x,在△BDE中,由余弦定理知,,即,解得x=1.∴AF=3,CE=3,∴=.故答案为:.13.已知函数f(x)=,若函数g(x)=f(﹣x)+f(x)有且仅有四个不同的零点,则实数k的取值范围是(27,+∞).【分析】表示出函数g(x),分k=0,k<0及k=0讨论,易知当k=0及k<0时均不合题意,而观察解析式可知,问题可化为有且仅有两个不同的零点,故利用导数研究函数g(x)在(0,+∞)上的最小值小于0即可.解:依题意,,当k=0时,原函数有且只有一个零点,不合题意,故k≠0;观察解析式,易知函数g(x)为偶函数,则函数g(x)有且仅有四个不同的零点,可转化为有且仅有两个不同的零点,当k<0时,函数g(x)在(0,+∞)上递增,最多一个零点,不合题意;当k>0时,,令g′(x)>0,解得,令g′(x)<0,解得,故函数g(x)在上递减,在上递增,要使g(x)在(0,+∞)上有且仅有两个不同的零点,则,解得k>27.故答案为:(27,+∞).14.在平面直角坐标系xOy中,过点P(2,﹣6)作直线交圆O:x2+y2=16于A,B两点,C(x0,y0)为弦AB的中点,则的取值范围是[,).【分析】作出图象,根据条件可求得点C的运动轨迹为x2+y2﹣2x+6y=0,的取值范围可转化为求点C与点Q(﹣1,3)的距离范围,数形结合即可解:如图所示,由圆的性质知:PC⊥OC,∴•=0,又∵=(x0﹣2,y0+6),=(x0,y0),则•=x0(x0﹣2)+y0(y0+6)=x02+y02﹣2x0+6y0=0∴点C的轨迹方程为圆:x2+y2﹣2x+6y=0即(x﹣1)2+(y+3)2=10,圆心(1,﹣3),半径r=则的取值范围可转化为求点C与点Q(﹣1,3)的距离范围如图所示,因为点C在圆O内,故只需求出OQ和QM或QN的长度即可,易得OQ==,联立,整理得2x﹣6y﹣16=0即直线MN方程为x﹣3y﹣8=0,再联立,解得,,即M(,),N(,),故QM==QN==,因为C取不到M或N点,故的取值范围是[,).故答案为:[,).二、解答题(本大题共6小题,共计90分.请在答题纸指定区域内作答,解答应写出文字说明,证明过程或演算步骤.)15.△ABC中,角A,B,C所对的边分别为a,b,c.若.(1)求cos C的值;(2)若A=C,求sin B的值.【分析】(1)利用正弦定理转化条件,利用余弦定理求得cos C的值;(2)利用三角函数的内角和定理与三角恒等变换,即可求出sin B的值.解:(1)△ABC中,,由正弦定理得=,整理得5(a2+b2﹣c2)=8ab,由余弦定理得cos C===;(2)由(1)知cos C=,C是△ABC的内角,所以sin C==;又A=C,所以sin B=sin(π﹣A﹣C)=sin(A+C)=sin2C=2sin C cos C=2××=.16.如图,在直三棱柱ABC﹣A1B1C1中,AC⏊BC,D,E分别是A1B1,BC的中点.求证:(1)平面ACD⊥平面BCC1B1;(2)B1E∥平面ACD.【分析】(1)推导出AC⊥CC1,AC⊥平面BCC1B1,由此能证明平面ACD⊥平面BCC1B1.(2)取AC中点F,连结EF,DF,推导出四边形B1DFE为平行四边形,从而B1E∥DF,由此能证明B1E∥平面ACD.【解答】证明:(1)直三棱柱ABC﹣A1B1C1中,CC1⊥底面ABC,又AC⊂底面ABC,∴AC⊥CC1,∵AC⊥BC1,CC1∩BC=C,∴AC⊥平面BCC1B1,∵AC⊂平面ACD,∴平面ACD⊥平面BCC1B1.(2)取AC中点F,连结EF,DF,∵E,F分别为BC,AC中点,∴EF∥AB,EF=,直三棱柱ABC﹣A1B1C1中,AB A1B1,∵D为A1B1中点,∴B1D∥AB,B1D=,∴EF B1D,∴四边形B1DFE为平行四边形,∴B1E∥DF,∵DF⊂平面ACD,B1E⊄平面ACD,∴B1E∥平面ACD.17.某单位科技活动纪念章的结构如图所示,O是半径分别为1cm,2cm的两个同心圆的圆心,等腰△ABC的顶点A在外圆上,底边BC的两个端点都在内圆上,点O,A在直线BC的同侧.若线段BC与劣弧所围成的弓形面积为S1,△OAB与△OAC的面积之和为S2,设∠BOC=2θ.(1)当θ=时,求S2﹣S1的值;(2)经研究发现当S2﹣S1的值最大时,纪念章最美观,求当纪念章最美观时,cosθ的值.(求导参考公式:(sin2x)'=2cos2x,(cos2x)'=﹣2sin2x)【分析】(1)结合弓形面积公式及三角形的面积公式分别求出S2,S1,然后结合三角函数的性质即可求解;(2)结合(1)的面积表示,结合导数与单调性的关系可求.解:(1)由题意可知,∠BOC=2θ∈(0,π),故,S1==θ﹣sinθcosθ=,S2=﹣sin2θ=﹣sin2θ=2sinθ,当时,S1=,S2=,故S2﹣S1=(cm2),(2)S2﹣S1=2sinθ+sin2θ﹣θ,,令f(θ)=2sinθ+sin2θ﹣θ,,则f′(θ)=2cosθ+cos2θ﹣1=2cos2θ+2cosθ﹣2,令f′(θ)=0可得,cosθ=(舍负),记cosθ0=,,当θ∈(0,θ0)时,f′(θ)>0,函数单调递增,当时,f′(θ)<0,函数单调递减,故当θ=θ0时,即cosθ=时,f(θ)取得最大值,即S2﹣S1取得最大值.18.(16分)如图,在平面直角坐标系xOy中,已知椭圆=1(a>b>0)的左、右焦点分别为F1,F2,过点F2的直线交椭圆于M,N两点.已知椭圆的短轴长为2,离心率为.(1)求椭圆的标准方程;(2)当直线MN的斜率为时,求F1M+F1N的值;(3)若以MN为直径的圆与x轴相交的右交点为P(t,0),求实数t的取值范围.【分析】(1)设焦距为2c,运用离心率公式,可得a,b,c的方程,解方程可得a,b,进而得到椭圆方程;(2)由(1)可得c=2,即F1(﹣2,0),F2(2,0),联立直线方程和椭圆方程,求得M,N,即可得到所求和;(3)方法一、讨论直线MN的斜率不存在,求得|MN|,可得t的值;MN的斜率存在时,设MN:y=k(x﹣2),M(x1,y1),N(x2,y2),联立椭圆方程,运用韦达定理和中点坐标公式,弦长公式,结合圆的方程和换元,运用函数的单调性可得所求范围;方法二、运用直径所对的圆周角为直角,结合向量的数量积的性质和坐标表示,化简整理,可得t的不等式组,解得t的范围.解:(1)设焦距为2c,则2b=2,b2=a2﹣c2,e==,解得a=,b=,则椭圆的方程为+=1;(2)由(1)可得c=2,即F1(﹣2,0),F2(2,0),由可得或,即M(,),N(,﹣)或N(,),M(,﹣),因此|F1M|+|F1N|=+=;(3)方法一、①MN的斜率不存在时,MN:x=2,|MN|=,以MN为直径的圆的方程为(x﹣2)2+y2=,其与x轴相交的右交点为P(2+,0),即t=2+;②MN的斜率存在时,设MN:y=k(x﹣2),M(x1,y1),N(x2,y2),由,可得(1+3k2)x2﹣12k2x+12k2﹣6=0,△=(12k2)2﹣4(1+3k2)(12k2﹣6)=24(k2+1)>0恒成立,x1+x2=,x1x2=,|x1﹣x2|===,y1+y2=k(x1+x2)﹣4k=k•﹣4k=﹣,则MN的中点为(,﹣),|MN|=•|x1﹣x2|=•=,故以MN为直径的圆的方程为(x﹣)2+(y+)2=,令y=0,可得x=,由题意可得t=,可令1+3k2=m(m≥1),则k2=,t=2﹣+,可令x=,x∈(0,2],可得t=2﹣x+,可令f(x)=2﹣x+,x∈(0,2),由于(x+)2<x2+x+,则f′(x)=<0,故f(x)在(0,2)递减,f(0)=2+,f(2)=,因此f(x)∈[,2+),综上可得t∈[,2+].方法二、x1x2=,则y1y2=k2(x1﹣2)(x2﹣2)=k2[x1x2﹣2(x1+x2)+4]=k2[﹣2•+4]=﹣,P在以MN为直径的圆上,则•=0,(x1﹣t)(x2﹣t)+y1y2=0,x1x2﹣t(x1+x2)+t2+y1y2=0,即﹣+t2﹣=0,化为(3t2﹣12t+10)k2=6﹣t2,由于P为右交点,故t>2,因此,解得t∈[,2+].19.(16分)已知{a n}是各项均为正数的无穷数列,数列{b n}满足b n=a n•a n+k(n∈N*),其中常数k为正整数.(1)设数列{a n}前n项的积,当k=2时,求数列{b n}的通项公式;(2)若{a n}是首项为1,公差d为整数的等差数列,且b2﹣b1=4,求数列的前2020项的和;(3)若{b n}是等比数列,且对任意的n∈N*,a n•a n+2k=a n+k2,其中k≥2,试问:{a n}是等比数列吗?请证明你的结论.【分析】(1)直接利用关系式的变换的应用求出数列通项公式.(2)首先求出数列的通项公式,进一步利用裂项相消法在数列求和中的应用求出结果.(3)利用等比数列的的定义的应用求出结果.解:(1)因为,所以(n≥2),两式相除得:=2n﹣1(n≥2),当n=1时,,符号上式,∴(n∈N*),当k=2时,b n=a n•a n+2=2n﹣1•2n+1=4n;(2)由于b n=a n a n+1,且a1=1,所以b1=a1a k+1=a k+1,b2=a2a k+2=(d+1)(a k+1+d).所以=4,由于d和k都为正整数,所以d≥1,所以a k+1≥a2=1+d≥2,所以d2+d(a k+1+1)=4≥d2+3d.解得d≤1,所以d=1,即a n=n.所以d2+d(a k+1+1)=4=a k+1+2,即a k+1=2,解得k=1.所以b n=a n+1a n=n(n+1),所以.则:,所以.(3){b n}是等比数列,公比为,且对任意的n∈N*,所以=q2k.a n•a n+2k=a n+k2,所以,所以,所以=,则,所以.故数列{a n}是等比数列.20.(16分)已知函数f(x)=,g(x)=,其中e是自然对数的底数.(1)若函数f(x)的极大值为,求实数a的值;(2)当a=e时,若曲线y=f(x)与y=g(x)在x=x0处的切线互相垂直,求x0的值;(3)设函数h(x)=g(x)﹣f(x),若h(x)>0对任意的x∈(0,1)恒成立,求实数a的取值范围.【分析】(1)由题意可知a>0,先对f(x)求导,分析单调性,得到极大值,让其等于,即可解得a的值.(2)分别求出f(x),g(x)在x=x0处切线的斜率,让它们乘积等于1,即可解得x0的值.(3)问题可以转化为,对任意x∈(0,1)恒成立,设H(x)=,由(1)可知,H(x)在(0,1)上单调递增,且当x∈(1,+∞)时,H(x)>0,当x∈(0,1)时,H(x)<0,可得ae x>x,也就是ae x>x对任意x∈(0,1)恒成立,即,设G(x)=(x∈(0,1)),只要G(x)max≤a,即可得出答案.解:(1)因为f(x)=,则f′(x)==,因为g(x)=,所以a>0,则当x∈(0,e)时,f′(x)>0,f(x)单调递增,当x∈(e,+∞)时,f′(x)<0,f(x)单调递减,所以当x=e时,f(x)的极大值f(e)==,解得a=1.(2)当a=e时,f(x)=,g(x)=,则f′(x)=,g′(x)=,由题意可知,f′(x0)g′(x0)=•=﹣1,整理得x0e+elnx0=e,设φ(x)=xe x+elnx,则φ′(x)=(x+1)e x+>0,所以φ(x)单调递增,因为φ(1)=e,所以x0=1.(3)由题意可知,>0,对任意x∈(0,1)恒成立,整理得,对任意x∈(0,1)恒成立,设H(x)=,由(1)可知,H(x)在(0,1)上单调递增,且当x∈(1,+∞)时,H(x)>0,当x∈(0,1)时,H(x)<0,若ae x≥1>x,则H(ae x)≥0>H(x),若0<ae x<1,则H(ae x)>H(x),且H(x)在(0,1)上单调递增,所以ae x>x,综上可知,ae x>x对任意x∈(0,1)恒成立,即,设G(x)=(x∈(0,1)),则G′(x)=>0,所以G(x)单调递增,所以G(x)<G(1)=≤a,即a的取值范围为[,+∞).【选做题】本题包括21,22,23三小题,请选定其中两题作答,每小题10分,共计20分,解答时应写出文字说明,证明过程或演算步骤.[选修4-2:矩阵与变换]21.已知m∈R,=是矩阵M=的一个特征向量,求M的逆矩阵M﹣1.【分析】由=是属于特征值n的一个特征向量,得M=n,然后求出m,得到矩阵M,再设矩阵的逆矩阵M﹣1=,由MM﹣1=,求出M的逆矩阵M﹣1.解:由=是属于特征值n的一个特征向量,得M=n,∵M==,=n=,∴1+m=3=n,解得m=2,∴矩阵M=,设矩阵的逆矩阵M﹣1=,则MM﹣1===,∴,解得a=﹣,b=,c=,d=﹣,解得M﹣1=.[选修4-4:坐标系与参数方程]22.在极坐标系中,圆C的方程为ρ=2r sinθ(r>0).以极点为坐标原点,极轴为x轴正半轴建立平面直角坐标系,直线l的参数方程为(t为参数).若直线l与圆C恒有公共点,求r的取值范围.【分析】求出圆的直角坐标方程,把直线的参数方程化为普通方程,利用点到直线的距离与半径列出不等式求解即可.解:由ρ=2r sinθ得ρ2=2rρsinθ,∴圆C的方程为x2+y2﹣2ry=0,把参数方程为(t为参数),消去参数t,可得:普通方程:x﹣y﹣2=0,直线与圆有公共点,可得:d=≤r,解得r≥2.∴实数r的取值范围为[2,+∞).[选修4-5:不等式选讲]23.已知x>1,y>1,且x+y=4,求证:≥8.【分析】设x﹣1=m,y﹣1=n,则m>0,n>0,且m+n=2,再利用基本不等式即可得证.【解答】证明:设x﹣1=m,y﹣1=n,又x>1,y>1,则m>0,n>0,且m+n=x+y ﹣2=2,∴=,当且仅当m=n=1,即x=y=2时,等号成立,故原命题得证.【必做题】第24题、第25题,每题10分,共计20分,解答时应写出文字说明,证明过程或演算步骤.24.某“芝麻开门”娱乐活动中,共有5扇门,游戏者根据规则开门,并根据打开门的数量获取相应奖励.已知开每扇门相互独立,且规则相同,开每扇门的规则是:从给定的6把钥匙(其中有且只有1把钥匙能打开门)中,随机地逐把抽取钥匙进行试开,钥匙使用后不放回.若门被打开,则转为开下一扇门;若连续4次未能打开,则放弃这扇门,转为开下一扇门;直至5扇门都进行了试开,活动结束.(1)设随机变量X为试开第一扇门所用的钥匙数,求X的分布列及数学期望E(X);(2)求恰好成功打开4扇门的概率.【分析】(1)根据互斥事件概率公式计算X的可能取值对应的概率,得出分布列和数学期望;(2)根据二项分布的概率公式计算概率.解:(1)X的可能取值为1,2,3,4,P(X=1)=,P(X=2)==,P(X=3)==,P(X=4)==,∴X的分布列是:X1234PE(X)=1×+2×+3×+4×=3.(2)每扇门被打开的概率为=,设被打开的门的数量为ξ,则ξ~B(5,),∴恰好成功打开4扇门的概率为:P(ξ=4)=•()4•=.25.如图,在平面直角坐标系xOy中,已知抛物线y2=2px(p>0)的焦点为F,准线与x 轴的交点为E.过点F的直线与抛物线相交于A,B两点,EA,EB分别与y轴相交于M,N两点,当AB⊥x轴时,EA=2.(1)求抛物线的方程;(2)设△EAB的面积为S1,△EMN面积为S2,求的取值范围.【分析】(1)求得抛物线的焦点坐标,以及E的坐标,运用两点间的距离公式,解得p,进而得到抛物线的方程;(2)设AB:x=my+,A(x1,y1),B(x2,y2),联立抛物线的方程,运用韦达定理,以及直线方程,求得M,N的坐标,化简整理,运用三角形的面积公式,化简整理,结合韦达定理,即可得到所求范围..解:(1)抛物线y2=2px(p>0)的焦点为F(,0),准线与x轴的交点为E(﹣,0),当AB⊥x轴时,A的横坐标为,所以y A2=2px A=P2,所以|EA|===2,解得p=,所以抛物线的方程为y2=2x;(2)设AB:x=my+,A(x1,y1),B(x2,y2),联立抛物线的方程y2=2x,消去x,可得y2﹣2my﹣2=0,则y1+y2=2m,y1y2=﹣2,直线AE的斜率为k AE=,则AE的方程为y=(x+),令x=0,可得y=•,即M(0,•),同理可得N(0,•),===2(x1+)(x2+)=2[x1x2+(x1+x2)+]=2x1x2+(x1+x2)+1=+(+)+1=1+[(y1+y2)2﹣2y1y2]+1=(y1+y2)2+4=4m2+4≥4.(当m=0时,取得等号).即的取值范围为[4,+∞).。
高中化学离子方程式试题.docx

离子方程式1.( 2018 届天津市河西区高三第三次模拟考试)下列各组离子能大量共存,且当加入试剂后反应的离子方程式书写正确的是()选项离子组加入试剂发生反应的离子方程式A3+-、 Cl-NaOH 溶液3++ 3OH-=Fe(OH) 3↓Fe、 I FeB K +、 ClO -、 SO42-盐酸H+ +ClO - =HClOC K +、 OH -、 Cl -过量 SO2SO2+ OH -=HSO 3-DH+、 Fe2+、 SO42-3 2 溶液SO42-+ Ba 2+ =BaSO4↓Ba(NO )2.( 2018 届江苏省盐城市高三第三次模拟考试)下列指定反应的离子方程式正确的是()A. MnO 2与浓盐酸混合加热:MnO 2+4H ++4Cl -MnCl 2+Cl 2↑O+2H--B. NaAlO 2溶液中通入过量 CO2: AlO 2 +CO 2+2H 2O=Al(OH) 3↓+HCO3C. FeSO4溶液中加入盐酸酸化的H 2O2:Fe2++H 2O2+2H +=Fe3++2H 2OD. Ca(HCO 3)2溶液中加入过量氨水: Ca2+-↓ +H++HCO 3 +NH 3·H2O=CaCO 32O+NH 43.( 2018 届江苏省苏锡常镇四市高三调研)下列指定反应的离子方程式正确的是A. 氯气通入水中+--: Cl 2+H 2O2H +Cl +ClOB. 向苯酚浊液中滴加Na2CO3溶液 :2C6H5OH+CO 32- =2C6H 5O-+H 2O+CO 2↑C. 向偏铝酸钠溶液中加入--2-NaHCO 3溶液 : AlO 2+HCO 3 +H 2O=Al(OH) 3↓ +CO3D. 碳酸氢铵溶液中加入足量NaOH 溶液共热 : NH 4+ +OH -NH 3↑ +H2O4.( 2018 届江苏省南通市高三第三次调研测试)下列指定反应的离子方程式正确的是A. 电解熔融NaCl : 2Cl-+2H 2O2OH -+ Cl 2↑+ H 2↑B.用氨水溶解 AgCl 沉淀: Ag ++ 2NH 3·H 2O= [Ag(NH 3 )2] ++ 2H 2OC.Na2CO3溶液吸收溴蒸气: 3CO32-+ Br 2=Br -+ BrO 3-+ 3CO2D.金属钠与水反应: 2Na+ 2H 2O= 2Na++ 2OH -+ H2↑5.(江苏省南京市2018 届高三第三次模拟考试)常温下,下列各组离子在指定溶被中一定能大量共存的是3+2+--A. 澄清透明的溶液中: Fe ,Ba、 NO 3、 ClB. 使酚酞变红色的溶液中:Na+、 NH 4+、 C1-、 SO42-C. c(Al 3+)=0.1mol/L的溶液中 :K +、 Mg 2+、 SO42-、 AlO 2-D. 由水电商产生的c(H + )=10-13mol/L 的溶被中 :K +、 Na+、CH 3COO -、 NO 3-6.( 2018 届江苏省南京市高三第三次模拟考试)下列指定反应的离子方程式正确的是A. 将饱和 FeCl3溶液滴入沸水中制备3++ Fe(OH) 3胶体: Fe +3H2O=Fe(OH) 3↓+3HB. 向硫酸铝溶液中滴加过量氨水:2Al3++6NH 3·H 2O=2Al(OH)↓ +6NH+34C. 向 Na ClO 溶液中通入过量的 SO2: SO2+ClO -+H 2O=HSO 3- +HClOD. 向 (NH 4)2Fe(SO4 )2溶液中滴加过量2+-NaOH 溶液: Fe +2OH =Fe(OH) 2↓7.( 2018 届山东省泰安市高三第二次模拟考试)下列有关离子方程式或离子共存的叙述正确的是A. 用肥皂 (主要成份C17H 35COONa) 水检验含有较多钙离子的硬水:2C17H 35COO -+Ca2+===(C 17H35COO)2Ca↓B.将磁性氧化铁溶于氢碘酸: Fe3O4 +8H +=2Fe3++Fe2++4H 2OC.常温下,在=0.1 的溶液中: Na+、 K +、 SO42-、 HCO 3-能大量共存D.在 NaC1O 溶液中: SO32-、 OH -、 C1-、 K +能大量共存8.( 2018 届江苏省泰州中学高三下学期学业水平测试模拟三)下列反应的离子方程式书写正确的是A. 过量 SO2通入氢氧化钙溶液中:﹣﹣OH+SO 2═ HSO3+2+B.碳酸钙与足量醋酸反应: CaCO3+2H ═ Ca +H 2O+CO 2↑C.氯化铝溶液与过量氨水反应: Al 3++4NH 3?H2 O═ AlO2﹣ +4NH 4++2H 2O+3+D.铁与稀硫酸溶液反应: 2Fe+6H ═ 2Fe +3H 2↑9.( 2018 届湖北省荆州中学高三 4 月月考)下列解释事实的方程式正确的是()A. 电解饱和食盐水,产生黄绿色气体:2NaCl + 2H 2O2NaOH + H 2↑ + Cl2↑B. 用 Na2CO3溶液将水垢中的CaSO4转化为 CaCO3: CO32- + Ca2+ ==== CaCO 3↓C. 浓氨水检验泄露的氯气,产生白烟:2NH 3 + 3Cl 2 === 6HCl + N 2D. 铜丝溶于浓硝酸生成绿色溶液:3Cu + 8H + + 2NO 3-3Cu2+ + 2NO↑ + 4H2O10.( 2018 届福建省厦门市双十中学高三第八次能力考试)工业碳酸钠 (纯度约为 98%)中含有 Mg 2+2+、、FeCl-和 SO42-等杂质,提纯工艺流程如下:下列说法不正确的是...A.步骤①,通入热空气可加快溶解速率2+3+-↓ + Fe(OH)↓B. 步骤②,产生滤渣的离子反应为:Mg+ Fe+ 5OH == Mg(OH) 23C.步骤③,趁热过滤时温度控制不当会使Na2CO3?H2O 中混有 Na2CO3?10H2O 等杂质D.步骤④,灼烧时用到的主要仪器有铁坩埚、泥三角、三脚架、酒精灯11.( 2018 届湖南省衡阳市第八中学高三第三次质检)向FeCl3、Al2(SO4)3的混和溶液中逐滴加入Ba(OH) 2(aq),形成沉淀的情况如下图所示。
江苏省泰州、南通、扬州、宿迁、淮安五市2013届高三第三次调研测试数学试卷

(第3题)(第5题)江苏省(泰州、南通、扬州、宿迁、淮安)五市2013届高三第三次调研测试 数学试卷一、填空题:本大题共14小题,每小题5分,共70分. 1. 已知集合(]2 1A=-,,[)1 2B =-,,则A B =U ▲ .【答案】(2 2)-,2. 设复数z 满足(34i)50z ++=(i 是虚数单位),则复数z 的模为 ▲ . 【答案】13. 右图是一个算法流程图,则输出的S 的值是 ▲ .【答案】2400 4. “MN>”是“22log log M N>”成立的 ▲ 条件.(从“充要”,“充分不必要”,“必要不充分”中选择一个正确的填写) 【答案】必要不充分5. 根据某固定测速点测得的某时段内过往的100辆 机动车的行驶速度(单位:km/h)绘制的频率分布 直方图如右图所示.该路段限速标志牌提示机动车辆正常行驶速度为60 km/h~120 km/h ,则该时 段内非正常行驶的机动车辆数为 ▲ . 【答案】156. 在平面直角坐标系xO y 中,抛物线22(0)x py p =>上纵坐标为1的一点到焦点的距离为3,则焦点到准线的距离为 ▲ .【答案】4(第9题)7. 从集合{}1 2 3 4 5 6 7 8 9,,,,,,,,中任取两个不同的数,则其中一个数恰是另一个数的3倍的概率为 ▲ .【答案】1128. 在平面直角坐标系xO y 中,设点P 为圆C :22(1)4x y -+=上的任意一点,点Q (2a ,3a-)(a ∈R ),则线段P Q 长度的最小值为 ▲ .【答案29. 函数()sin()f x A x ωϕ=+(0A >,0ω>,02)ϕ<π≤在R 上的部分图象如图所示,则(2013)f 的值为 ▲ .【答案】-10.各项均为正数的等比数列{}n a 中,211a a -=.当3a 取最小值时,数列{}n a 的通项公式a n = ▲ .【答案】12n - 11.已知函数2221 0 () 0a x x x f x x b x c x ⎧--⎪=⎨++<⎪⎩,≥,,是偶函数,直线y t=与函数()yf x =的图象自左向右依次交于四个不同点A ,B ,C ,D .若A B B C=,则实数t 的值为 ▲ .【答案】74-12.过点(1 0)P -,作曲线C :exy =的切线,切点为1T ,设1T 在x 轴上的投影是点1H ,过点1H 再作曲线C 的切线,切点为2T ,设2T 在x 轴上的投影是点2H ,…,依次下去,得到第1n +()n ∈N 个切点1n T +.则点1n T +的坐标为 ▲ .【答案】() e nn ,13.在平面四边形ABCD中,点E ,F 分别是边AD ,BC 的中点,且AB 1=,E F=CD =.若15A DB C⋅=uuu r uuu r,则A CB D⋅uuu r uuu r的值为 ▲ .【答案】1314.已知实数a 1,a 2,a 3,a 4满足a 1+a 2+a 30=,a 1a 42+a 2a 4-a 20=,且a 1>a 2>a 3,则a 4的取值范围是 ▲ . 【答案】二、解答题15.如图,在四棱锥P A B C D-中,底面A B C D 是矩形,四条侧棱长均相等.(1)求证:A B//平面P C D ;(2)求证:平面P A C ⊥平面A B C D .证明:(1)在矩形A B C D 中,//A B C D , 又A B ⊄平面P C D ,C D ⊂平面P C D ,所以A B //平面P C D . ………6分(2)如图,连结B D ,交A C 于点O ,连结P O ,在矩形A B C D 中,点O 为 A C B D ,的中点, 又P A P B P C P D ===,故P O A C⊥,P OB D⊥, ………9分又A C B D O=I ,A CB D ,⊂平面A B C D ,所以P O ⊥平面A B C D , ………12分又P O⊂平面P A C ,所以平面P A C ⊥平面A B C D . ………14分16.在△ABC 中,角A ,B ,C 所对的边分别为a ,b ,c .已知222222sin 2sin sin C b a cA C c a b--=---.(1)求角B 的大小;(2)设222sin sin sin TA B C=++,求T 的取值范围.解:(1)在△ABC 中,AB(第15题)PDO222222sin 2co s co sB sin co s 2sin sin 2co s co s sin co s C b a c a c B c C BA C a b C b CBC c a b---====----, ………3分因为sin 0C ≠,所以sin cos 2sin cos sin cos B CA B C B=-,所以2sin cos sin cos sin cos sin()sin A B B C C B B C A=+=+=, ………5分因为sin 0A ≠,所以1co s 2B =,因为0πB <<,所以π3B=. ………7分(2)222131sin sin sin (1co s 2)(1co s 2)242T A B C A C =++=-++-()71714π(co s 2co s 2)co s 2co s 242423A C A A -⎡⎤=⎢⎥⎣+=--⎦+()()71171πco s 22co s 2422423A A A =--=-+ ………11分因为2π03A <<,所以4π023A <<,故ππ5π2333A <+<,因此()π11co s 232A -+<≤,所以3924T <≤. ………14分17.某单位设计的两种密封玻璃窗如图所示:图1是单层玻璃,厚度为8 mm ;图2是双层中空玻璃,厚度均为4 mm ,中间留有厚度为x 的空气隔层.根据热传导知识,对于厚度为d 的均匀介质, 两侧的温度差为T ∆,单位时间内,在单位面积上通过的热量T Qk d∆=⋅,其中k 为热传导系数.假定单位时间内,在单位面积上通过每一层玻璃及空气隔层的热量相等.(注:玻璃的热传导系 数为3410 J m m /C -⨯⋅ ,空气的热传导系数为42.510 J m m /C -⨯⋅ .)(1)设室内,室外温度均分别为1T ,2T ,内层玻璃外侧温度为1T ',外层玻璃内侧温度为2T ', 且1122T T T T ''>>>.试分别求出单层玻璃和双层中空玻璃单位时间内,在单位面积上通过的热量(结果用1T ,2T 及x 表示);(2)为使双层中空玻璃单位时间内,在单位面积上通过的热量只有单层玻璃的4%,应如何设计x的大小?解:(1)设单层玻璃和双层中空玻璃单位时间内,在单位面积上通过的热量分别为1Q ,2Q , 则31212141082 000T T T T Q ---=⨯⋅=, ………2分34311122224102.51041044T T T T T T Q x---''''---=⨯⋅=⨯⋅=⨯⋅………6分111222343444102.510410T T T T T T x---''''---===⨯⨯⨯11122234344410 2.510410T T T T T T x ---''''-+-+-=++⨯⨯⨯124 0002 000T T x -=+. ………9分 (2)由(1)知21121Q Q x =+,当121x =+4%时,解得12x =(mm ).答:当12x =mm 时,双层中空玻璃通过的热量只有单层玻璃的4%. ………14分. 18.如图,在平面直角坐标系xO y 中,椭圆22221(y x a b ab+=>分别过O ,F 的两条弦A B ,C D 相交于点E (异于A ,O EE F=.图1图2(第17题)(1)求椭圆的方程;(2)求证:直线A C ,B D 的斜率之和为定值.(1)解:由题意,得1c =,c e a ==,故a=从而2221b a c =-=,所以椭圆的方程为2212xy +=. ① ………5分(2)证明:设直线A B 的方程为ykx=,②直线C D 的方程为(1)yk x =--, ③ ………7分由①②得,点A ,B的横坐标为由①③得,点C ,D21k+ ………9分记11( )A x kx ,,22( )B x kx ,,33( (1))C x k x -,,44( (1))D x k x -,,则直线A C ,B D 的斜率之和为 13241324(1)(1)kx k x kx k x x x x x ----+--132413241324(1)()()(1)()()x x x x x x x x k x x x x +--+-+-=⋅--1234123413242()()()()()x x x x x x x x k x x x x --+++=⋅-- ………13分2222213242(1)2420212121()()k kk k k k x x x x -⎛⎫---+ ⎪+++⎝⎭=⋅--=. ………16分19.已知数列{}n a 是首项为1,公差为d 的等差数列,数列{}n b 是首项为1,公比为(1)q q>的等比数列. (1)若55a b =,3q=,求数列{}n n a b ⋅的前n项和;(2)若存在正整数(2)k k ≥,使得k ka b =.试比较n a 与n b 的大小,并说明理由.解:(1)依题意,5145511381a b b q -===⨯=,故5181120514a a d--===-,所以120(1)2019na n n =+-=-, ………3分令2111213413(2019)3n nS n -=⨯+⨯+⨯+⋅⋅⋅+-⋅, ①则213 13213(2039)3(2019)3n nnS n n -=⨯+⨯+⋅⋅⋅+-⋅+-⋅, ②①-②得,()2121+20333(2019)3n nnS n --=⨯++⋅⋅⋅+--⋅,13(13)1+20(2019)313n nn --=⨯--⋅-(2920)329nn =-⋅-,所以(2029)3292nnn S -⋅+=. ………7分(2)因为kka b =,所以11(1)k k d q-+-=,即111k qd k --=-,故111(1)1k nqa n k --=+--,又1n nb q-=, ………9分所以1111(1)1k n nn q b a qn k --⎡⎤--=-+-⎢⎥-⎣⎦()()111(1)1(1)11n k k q n q k --⎡⎤=-----⎣⎦-()()23231(1)1(1)11n n k k q k q q q n q q q k -----⎡⎤=-++⋅⋅⋅++--++⋅⋅⋅++⎣⎦-………11分(ⅰ)当1n k<<时,由1q >知()()232311()1(1)1n n k k n nn q b a k n q q q n q q q k ------⎡⎤-=-++⋅⋅⋅++--++⋅⋅⋅+⎣⎦-211()(1)(1)()1n n q k n n q n k n qk ---⎡⎤<-----⎣⎦-22(1)()(1)1n q qk n n k ----=--<, ………13分(ⅱ)当nk>时,由1q>知()()231231(1)()11n n k k k n n q b a k q q q n k q q q k ------⎡⎤-=-++⋅⋅⋅+--++⋅⋅⋅++⎣⎦-121(1)()()(1)1k k q k n k qn k k qk ---⎡⎤>-----⎣⎦-22(1)()k q q n k -=-->, 综上所述,当1n k<<时,nna b >;当nk>时,nna b <;当1 nk=,时,nna b =.………16分(注:仅给出“1n k<<时,nna b >;nk>时,nna b <”得2分.)20.设()f x 是定义在(0 )+∞,的可导函数,且不恒为0,记()()()n nf xg x n x=∈*N .若对定义域内的每一个x ,总有()0n g x <,则称()f x 为“n 阶负函数”;若对定义域内的每一个x ,总有[]()0ng x '≥,则称()f x 为“n 阶不减函数”([]()ng x '为函数()n g x 的导函数).(1)若31()(0)a f x x x xx=-->既是“1阶负函数”,又是“1阶不减函数”,求实数a 的取值范围;(2)对任给的“2阶不减函数”()f x ,如果存在常数c ,使得()f x c<恒成立,试判断()f x 是否为“2阶负函数”?并说明理由. 解:(1)依题意,142()1()1f x ag x x xx==--在(0 )+∞,上单调递增,故15342[()]0a g x xx'=-+≥ 恒成立,得212a x≤, ………2分因为0x>,所以0a ≤. ………4分而当0a ≤时,1421()10a g x xx=--<显然在(0 )+∞,恒成立,所以0a ≤. ………6分(2)①先证()0f x ≤:若不存在正实数0x ,使得20()0g x >,则2()0g x ≤恒成立. ………8分 假设存在正实数0x ,使得20()0g x >,则有0()0f x >,由题意,当0x >时,2()0g x '≥,可得2()g x 在(0 )+∞,上单调递增, 当0xx >时,022()()f x f x xx >恒成立,即202()()f x f x xx >⋅恒成立,故必存在10x x >,使得20112()()f x f x x mx >⋅>(其中m 为任意常数),这与()f x c<恒成立(即()f x 有上界)矛盾,故假设不成立,所以当0x >时,2()0g x ≤,即()0f x ≤; ………13分②再证()0f x =无解:假设存在正实数2x ,使得2()0f x =,则对于任意320x x >>,有322232()()0f x f x x x >=,即有3()0f x >,这与①矛盾,故假设不成立, 所以()0f x =无解,综上得()0f x <,即2()0g x <,故所有满足题设的()f x 都是“2阶负函数”. ………16分。
【扬州、泰州、淮安、南通、徐州、宿迁、连云港】2018届高三年级三模英语试卷及答案

南通等七市 2017-2018 学年度高三第三次调研测试英语科目第一部分听力(略)第二部分英语知识运用(共两节,满分35分)第一节单项填空(共15小题;每小题1分,满分15分)21.Elizabeth shows great _______ in her choice of friends, so she has a lot of trustworthy companions.prehensionB. discriminationC.determinationD. consideration22.Our school holds seminars for students at regular intervals ________ the potential of their future is explored.A. whenB.whereC. thatD.who23.-May I speak to Alan, please?-Sorry, wrong number. There isn’t Alan ________ h ere.A.somethingB.anythingC.everythingD.nothing24. Trans to NanTong now only come to the outer city limits, because building the railway tracks into the city _______ many old buildings.A.would have damagedB.damagedC.should have damagedD.has damaged25 ________ J ack gets home after school is calculated so that Mum can ensure him warm means.A.ThatB.WhenC.WhetherD.How26.-What did the teacher recommend for appreciating the classic yesterday?- _______ the movie before reading the book.A.To seeB.Having seenC.To have seenD. Seeing27.Sue was greatly inspired though she made ________improvements in her English writing.A.modestB.brilliantC.tremendousD.considerable28.Senior 3 students in our school are motivated to study harder and evaluated on a monthly basis to find out how they _____ _ .A. have been learningB.will learnC. had learntD. learnt29 ________ to pension and free medical care,senior citizens in our village are properly looked after and live happy lives.A. EntitlingB.Being entitledC.EntitledD.Having entitled30.Varieties of magazines and research papers are _______ with the aim of feeding readers’ appetite for specific knowledge.A.put outB.made outid outD.taken out31.China is sure to further reduce the poor rural population by over 10 million ________ we Chinese work hard together.A.if onlyB.even ifC.as long asD.for fear that32.-What’s the weather forecast for tomorrow?-Sorry, I was on the phone and ________ most of it.A.had missedB.missedC.would missD.was missing33.The new system introduced last month is not working very effectively ________ professional training.A.in place ofB. in case ofC.in terms ofD.in defense of34.-Did your boss adopt your idea?-No, he just laughed and ________it as impossible.A. reservedB.advocatedC.anticipatedD.dismissed35.-What’s the matter with you, Jennifer?-Just a bad dream ______ _.A.that’s OKB. that’s itC.that’s rightD.that’s all第二节完形填空(共20 小题;每小题 1 分,满分20 分)请认真阅读下面短文,从短文后各题所给的A、B、C、D 四个选项中,选出最佳选项,并在答题卡上将该选项涂黑。
2019年高考语文一轮复习专题17:语言运用之得体准确测案含答案

(时间:40分钟,分值:80分)班级学号得分1.【2018届河北唐山市高三四月份五校联考】下列各句中,表达得体的一句是()(4分)A.今天惠临贵公司参观学习,确实学到了不少新的知识,为此特向你们表示诚挚谢意。
B.你们家现在几口人?你的内人现在哪里工作?经济收入情况怎么样?有需要帮助的吗?C.您老不在府上不要紧,只要您的舍亲在就行,我们此行,就是一瞻您的府第的风貌。
D.施老先生台鉴:值此先生荣获2017年生命科学大奖之际,谨致此函,以示诚挚祝贺。
【答案】D2.【2018届河南省天一大联考高三阶段性测试(五)】下列各句中,表达得体的一句是()(4分)A.暑假期间,我回到了久违的高中母校,熟悉的一草一木不禁让我陷入对往昔的回忆之中。
B.刚刚杨教授对于大气污染问题的演讲可谓真知灼见,现在该轮到小王谈谈他的拙见了。
C.王强大学毕业后,偶然遇见多年没见的辅导员,激动地说:“久仰了!一切还好吧?”D.看了你新出的大作,欣喜之余内心又觉惶恐,本想写篇序文,可惜只有八斗之才,恐难胜任。
【答案】A【解析】本题考查语言表达得体的能力。
解答时要注意结合对象、场合、语体来分析。
A项,久违:一般用作久别重逢的客套。
使用正确。
B项,拙见:对自己的见解的谦称。
此处用于别人,谦敬欠当。
C项,久仰:客套话,用于与人初次见面时。
此处用于多年不见的熟人,不得体。
D项,八斗之才:比喻才高。
与“内心又觉惶恐”“恐难胜任”不符。
可改为谦辞“才疏学浅”。
3.【2018届辽宁省部分重点中学协作体高三模拟考试】下列各句中,表达得体的一项是()(4分)A.今天是你们喜结良缘的日子,我代表我家人祝贺你们的弄瓦之喜,祝你俩幸福美满,水寿偕老!B.王老师,身体好点了么?班级的事情也不用您太留恋,您的课由别的老师代上了,同学们都很听话,都等着您早日回到我们身边。
C.惊悉令堂仙逝,无比震惊悲痛!析祷安息,敬请节衰顺变!D.尽管只是绵薄之力,但他费了很大的动,我们应该感谢。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2018届江苏省扬州、泰州、淮安、南通、徐州、宿迁、连云港市高三第三次调研测试英语试题第一部分听力 (共两节,满分20分)第一节 (共5小题;每小题1分,满分5分)听下面5段对话。
每段对话后有一个小题,从题中所给的A、B、C三个选项中选出最佳选项,并标在试卷的相应位置。
听完每段对话后,你都有10秒钟的时间来回答有关小题和阅读下一小题。
每段对话仅读一遍。
1. What did the woman leave in the taxi?A. A hat.B. A T-shirt.C. A sweater.2. How much did the woman pay for the dress?A. 10 dollars.B. 30 dollars.C. 40 dollars.3. What does the man often put on a Christmas tree?A. A doll.B. A star.C. An angel.4. What does Gina tell Sam to do?A. Scratch his arm even more.B. Buy some special medicine.C. Sleep with the windows shut.5. What does the man imply about the woman in the end?A. She always buys new clothes.B. She should do the laundry herself.C. She needs a new washing machine.第二节(共15小题;每小题1分,满分15分)听下面5段对话或独白。
每段对话或独白后有几个小题,从题中所给的A、B、C三个选项中选出最佳选项,并标在试卷的相应位置。
听每段对话或独白前,你将有时间阅读各个小题,每小题5秒钟;听完后,各小题将给出5秒钟的作答时间。
每段对话或独白读两遍。
听第6段材料,回答第6、7题。
6. What does the woman want the man to do?A. Put off spring break.B. See some western art.C. Drive her to the exhibit.7. What is the relationship between the speakers?A. Mother and son.B. Brother and sister.C. Taxi driver and passenger.听第7段材料,回答第8至10题。
8. Why did Teresa raise her hand the first time?A. She had a question.B. She needed to relax her arm.C. She wanted to use the bathroom.9. What did Mr. Johnson ask the class to do?A. Turn to page 55.B. Copy a famous painting.C. Ask questions later on.10. When will the film be shown?A. At the end of class.B. In less than one minute.C. After Teresa gets back.听第8段材料,回答第11至13题。
11. What did the man start doing two years ago?A. Teaching.B. Raising money.C. Saving wild animals.12. Why is the man tired?A. He took care of a bear all night.B. He stayed up sending emails.C. He graded a lot of homework.13. What does the man say about the bears at the end of the conversation?A. They are dirty.B. They are cool.C. They are lovely.听第9段材料,回答第14至16题。
14. Why isn’t Cindy studying for the test?A. She is too tired.B. She has a headache.C. She can’t find her book.15. What does Bob offer to do for Cindy in the end?A. Call her a taxi.B. Cover her head.C. Give her some hot water.16. Where does the conversation take place?A. At home.B. At a doctor’s.C. In a classroom.听第10段材料,回答第17至20题。
17. What are Christmas crackers?A. Paper tubes with a gift inside.B. A kind of Christmas food.C. Toys with loud sound.18. What do all three British Christmas desserts have in common?A. They all look and taste about the same.B. They are all made out of nuts and dried fruit.C. They are all similar to the American fruitcake.19. What is American fruitcake similar to?A. Christmas cake.B. Christmas pudding.C. Sweet pie.20. What is the speaker mainly talking about?A. Christmas traditions in England.B. A special Christmas dinner.C. Interesting plays.第二部分英语知识运用(共两节, 满分35分)第一节单项填空(共15小题;每小题1分,满分15分)请认真阅读下面各题,从题中所给的A、B、C、D四个选项中,选出最佳选项,并在答题卡上将该项涂黑。
21. Elizabeth shows great ______ in her choice of friends, so she has a lot of trustworthycompanions.A. comprehensionB. discriminationC. determinationD. consideration22. Our school holds seminars for students at regular intervals ______ the potential of their futureis explored.A. whenB. whereC. thatD. who23. —May I speak to Alan, please?—Sorry, wrong number. There isn’t Alan ______ here.A. somethingB. anythingC. everythingD. nothing24. Trains to Nantong now only come to the outer city limits, because building the railway tracksinto the city ______ many old buildings.A. would have damagedB. damagedC. should have damagedD. has damaged25. ______ Jack gets home after school is calculated so that Mum can ensure him warm meals.A. ThatB. WhenC. WhetherD. How26. —What did the teacher recommend for appreciating the classic yesterday?—______ the movie before reading the book.A. To seeB. Having seenC. To have seenD. Seeing27.Sue was greatly inspired though she made ______improvements in her English writing.A. modestB. brilliantC. tremendousD.considerable28. Senior 3 students in our school are motivated to study harder and evaluated on a monthly basisto find out how they ______.A. have been learningB. will learnC. had learntD. learned29. ______ to pension and free medical care, senior citizens in our village are properly lookedafter and live happy lives.A. EntitlingB. Being entitledC. EntitledD. Having entitled30.V arieties of magazines and research papers are ______ with the aim o f feeding readers’appetite for specific knowledge.A. put outB. made outC. laid outD. taken out31.China is sure to further reduce the poor rural population by over 10 million ______ weChinese work hard together.A. if onlyB. even ifC. as long asD. for fear that32. —What’s the weather forecast for tomorrow?—Sorry, I was on the phone and ______ most of it.A. had missedB. missedC. would missD. was missing33.The new system introduced last month is not working very effectively ______ professionaltraining.A. in place ofB. in case ofC. in terms ofD. in defense of34. —Did your boss adopt your idea?—No, he just laughed and ______ it as impossible.A. reservedB. advocatedC. anticipatedD.dismissed35. —What’s the matter with you, Jennifer?—Just a bad dream, ______.A. that’s OKB. that’s itC. that’s rightD. that’s all第二节完形填空 (共20小题;每小题1分,满分20分)请认真阅读下面短文,从短文后各题所给的A、B、C、D四个选项中,选出最佳选项,并在答题卡上将该项涂黑。
