定积分定义
《定积分的定义》课件

总结词:定积分具有线性性质、可加性、可减性、可 乘性和可除性。
详细描述:定积分具有一系列的性质,其中最重要的是 线性性质,即两个函数的和或差的积分等于它们各自积 分的和或差;其次,定积分具有可加性和可减性,即函 数在一个区间上的积分等于该区间左端点处的函数值与 区间长度乘积的一半减去右端点处的函数值与区间长度 乘积的一半;此外,定积分还具有可乘性和可除性,即 函数与常数的乘积的积分等于该常数乘以函数的积分, 函数除以常数的积分等于函数乘以该常数的倒数。这些 性质在求解定积分时非常有用。
功的计算
定积分可用于计算力在空间上所做的功,通过将力在空间上进行积 分得到总功。
电磁学中的应用
在电磁学中,电场强度和磁场强度是空间的函数,通过定积分可以 计算电场强度和磁场强度在空间上的分布。
THANKS
感谢观看
微积分基本定理的应用
总结词
微积分基本定理的应用非常广泛,它 为解决各种实际问题提供了重要的数 学工具。
详细描述
通过微积分基本定理,我们可以计算 各种函数的定积分,从而解决诸如面 积、体积、长度、平均值、极值等问 题。此外,它也是微分方程求解的重 要基础。
微积分基本定理的证明
总结词
微积分基本定理的证明涉及到了极限理论、实数性质等深奥的数学知识,是数学严谨性的一个典范。
详细描述
证明微积分基本定理需要利用极限的运算性质和实数完备性等数学知识。其证明过程体现了数学的严 谨性和逻辑性,是数学教学中的重要内容。同时,对于理解微积分的本质和深化数学素养具有重要意 义。
03
定积分的计算方法
直接法
总结词
直接计算定积分的基本方法
详细描述
直接法是计算定积分最基本的方法,它基于定积分的定义,通过将被积函数进行微分和 积分,然后进行计算。这种方法适用于一些简单的定积分计算,但对于一些复杂的定积
高数定积分定义

高数定积分定义
定积分是微积分中的一个重要概念,它是对函数在一定区间上的
积分结果的确定。
在数学中,积分是微积分中的一种基本概念,定义
了一种反向操作,即由导数得到原函数。
定积分的定义是指在函数y=f(x)的x轴某一区间[a,b]上,将其分割成许多小的矩形,并将这些矩形的面积分别求出。
当分割的小矩形
数趋向于无穷大时,这些小矩形组成的面积总和即为该函数在区间[a, b]上的定积分,用符号∫abf(x)dx表示。
其中dx代表自变量的微元,f(x)代表被积函数,而a和b是积分
的上下限。
上述式子也可以看作是在曲线y=f(x)与x轴之间的面积之
积分。
为了方便计算,往往将上述区间分割成等分的若干小区间,其中
小区间的个数记作n,区间长为Δx。
于是有Δx=(b-a)/n,而小矩形
面积为f(xi)Δx,其中xi为小区间的中点。
将这些面积相加,即可得到该函数在区间[a, b]上的近似定积分。
在极限n趋向于无穷大的情况下,上述近似定积分将趋近于函数
在区间[a, b]上的定积分,即∫abf(x)dx。
因此,定积分又可以描述为曲线y=f(x)在区间[a, b]上与x轴之
间面积大小的确定。
而由于定积分的值只与积分区间及被积函数有关,因此在定积分的计算中,被积函数函数的表达式及积分区间的范围就
成为了最为重要的关键。
定积分在实际问题中的应用非常广泛,例如可以用于求曲线与坐标轴的面积,求函数在某个区间上的平均值,以及求物体在某一时间间隔内的位移等问题。
同时,定积分也是微积分中重要的积分概念之一,有较高的理论和实际应用价值。
定积分的性质

定积分可以表示为黎曼和的形式,即将区间[a,b]分成若干小区间,每个小区间的长度为$\Delta x$,并取小区间 的左端点$x_{i-1}$和右端点$x_i$作为积分的下限和上限,然后对每个小区间上的函数值$f(x_i)$进行求和,最后 将所有小区间的和再乘以$\Delta x$得到定积分的值。
对于任意实数$k_1, k_2$,有$\int (k_1f(x) + k_2g(x)) dx = k_1 \int f(x) dx + k_2 \int g(x) dx$
常数倍
对于任意实数$k$,有$\int kf(x) dx = k \int f(x) dx$
区间可加性
区间可加
对于任意分割$a = x_0 < x_1 < \ldots < x_n = b$,有$\int_{a}^{b}f(x) dx = \sum_{i=0}^{n-1} \int_{x_{i}}^{x_{i+1}}f(x) dx$
利用定积分的性质
如果$f(x) \geq g(x)$,则 $\int_{a}^{b}f(x)dx \geq
\int_{a}^{b}g(x)dx$。
利用定积分的性质
如果$f(x) = g(x)$,则$\int_{a}^{b}f(x)dx = \int_{a}^{b}g(x)dx$。
04
定积分的极限性质
定积分的性质
线性性质
定积分具有线性性质,即对于常数$c$和$d$,有$\int_{a}^{b} (c\varphi_1(x) + d\varphi_2(x)) dx = c\int_{a}^{b} \varphi_1(x) dx + d\int_{a}^{b} \varphi_2(x) dx$。
解释定积分的概念

解释定积分的概念
定积分是积分的一种,是函数f(x)在区间[a,b]上积分和的极限。
具体来说,定积分定义如下:设函数f(x) 在区间[a,b]上连续,将区间[a,b]分成n个子
区间[x₀,x₁], (x₁,x₂], (x₂,x₃], …, (xₙ-1,xₙ],其中x₀=a,xₙ=b。
a叫做积分下限,b叫做积分上限,区间[a, b]叫做积分区间,函数f(x)叫做被积函数,x
叫做积分变量,f(x)dx 叫做被积表达式,∫ 叫做积分号。
同时,应注意定积分与不定积分之间的关系:若定积分存在,则它是一个具体的数值,而不定积分是一个函数表达式,它们仅仅在数学上有一个计算关系(牛顿-莱布尼茨公式)。
一个函数,可以存在不定积分,而不存在定积分;也可以存在定积分,而不存在不定积分。
一个连续函数,一定存在定积分和不定积分;若只有有限个间断点,则定积分存在;若有跳跃间断点,则原函数一定不存在,即不定积分一定不存在。
以上内容仅供参考,如需更多信息,建议查阅相关文献或咨询数学专业人士。
定积分的概念及性质

定积分的概念、微积分基本定理及其简单应用一. 定积分的定义A )定义: 设函数f(x)在[a,b]上有界,在[a,b]中任意插入若干个分点,把区间[a,b]分成n 个小区间,记},......,,max{,,......2,1,211n i i i x x x n i x x x ∆∆∆==-=∆-λ在[i i x x ,1-]上任意取一点i ξ,作和式:)1.......()(1ini ix f ∆∑=ξ 如果无论[a,b]作怎样分割,也无论i ξ在[i i x x ,1-]怎样选取,只要0→λ有→∆∑=ini ixf 1)(ξI (I 为一个确定的常数),则称极限I 是f(x)在[a,b]上的定积分,简称积分,记做⎰b adx x f )(即I=⎰badx x f )(其中f(x)为被积函数,f(x)dx 为积分表达式,a 为积分下限,b 为积分上限,x 称为积分变量,[a,b]称为积分区间。
例:求曲边图形面积:3x y =的图像在[]1,0∈x 间与1=x 及x 轴围成的图形面积。
注:1、有定义知道⎰ba dx x f )(表示一个具体的数,与函数f(x)以及区间[a,b]有关,而与积分变量x 无关,即⎰badx x f )(=⎰badu u f )(=⎰badt t f )(2、定义中的0→λ不能用∞→n 代替3、如果ini ix f Lim∆∑=→1)(ξλ存在,则它就是f(x)在[a,b]上的定积分,那么f(x)必须在[a,b]上满足什么条件f(x)在[a,b]上才可积分呢?经典反例:⎩⎨⎧=中的无理点,为,中的有理点,为]10[0]10[,1)(x x x f 在[0,1]上不可积。
可见函数f(x)在什么情况下可积分并不是一件容易的事情。
以下给出两个充分条件。
定理1 设f(x)在区间[a,b]上连续,则f(x)在[a,b]上可积。
定理2 设f(x)在区间[a,b]上有界,且只有有限个间断点,则f(x)在[a,b]上可积。
定积分的定义
误差更小
定积分的定义
v 右图是正弦在一个周 期上的积分示意。为 20等分情形,取左端 点处的函数值
左端点型
定积分的定义
v 右图是正弦在一个周 期上的积分示意。为 20等分情形,取右端 点处的函数值
右端点型
定积分的定义
v 右图是正弦在一个周 期上积分梯形公式的 示意。为8个分点情形。
梯形公式
定积分的定义
v 右图是正弦在一个周 期上积分梯形公式的 示意。为15个分点情 形。
v 可以看到,梯形公式 比矩形公式精确度高。
梯形,15个分点
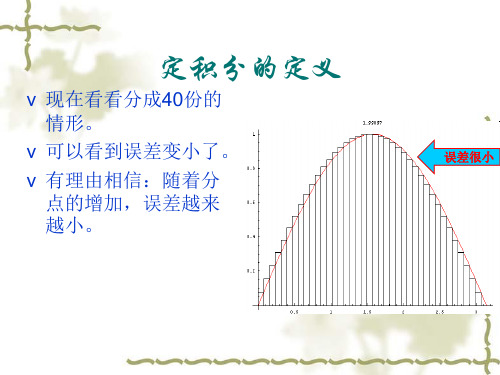
定积分的定义
v 现在看看分成40份的 情形。
v 可以看到误差变小了。
v 有理由相信:随着分 点的增加,的定义
v 当然,小区间上的面 积也可以用其他容易 求出面积的图形的面 积来表示,比如梯形。
v 这就是定积分的梯形 算法。
v 右图是取5等分的情形, 就已经非常精确了。
《定积分定义》课件

定积分的计算涉及到将被积函数与区间长度进行乘积,并 对所有这些乘积求和。
定积分的几何意义
面积
定积分可以用来计算平面图形在 某个区间上的面积,特别是当这 些图形由直线、抛物线、圆等基
本图形组成时。
体积
在三维空间中,定积分可以用来计 算旋转体等复杂几何体的体积。
物理意义
在物理学中,定积分常用于计算变 力在某个区间上做的功、曲线运动 的位移等。
物理中的定积分应用
总结词
在物理学中,定积分常用于解决与速度、加 速度、功等相关的物理问题。
详细描述
在物理学中,定积分的应用非常广泛。例如 ,在分析质点的运动时,可以利用定积分计 算质点的速度、加速度和位移;在分析弹性 体的应力分布时,可以利用定积分计算弹性 体内各点的应力值。此外,定积分还在电磁
学、光学等领域有着广泛的应用。
分部积分法
总结词
分部积分法是通过将被积函数分解为两个函数的乘积,然后分别积分,最后求和得到结 果的方法。
详细描述
分部积分法需要掌握分部积分的公式和计算技巧,如u和v的选取、分部积分的步骤等 。通过分部积分,可以将复杂的积分转化为容易计算的积分,或者将不易找到原函数的
积分转化为容易找到原函数的积分。
体积的计算
总结词
定积分在计算三维空间中物体的体积时发挥 了重要作用,可以应用于旋转体体积的计算 。
详细描述
定积分在计算旋转体的体积时非常有用。例 如,利用定积分可以计算圆柱、圆锥、球等 旋转体的体积。这些体积的计算公式都是通 过将旋转体划分为若干个小薄片,然后利用 定积分的性质计算这些小薄片的体积总和得 到的。
04
定积分的应用
平面图形面积的计算
总结词
定积分与不定积分定义

定积分与不定积分定义
定积分和不定积分是高数中的重要概念,它们均有其特定的定义。
定积分是指将复杂函数拆分成一系列简单函数,然后将其求和计算出函数在某一区间上的总和。
它可以用来计算曲线下的面积、曲线的位移以及函数的变化等。
定积分是求取函数积分的一种方法,其定义为:若f(x)是定义在区间[a,b]上的连续
函数,则把[a,b]上f(x)的积分称为定积分,记作:∫abf(x)dx不
定积分是指在求取函数的积分时,没有给定区间,即没有给定函数的定义域,而是由求积分的过程中求出区间。
不定积分是求取函数积分的一种方法,其定义为:若f(x)是定义在实数集
上的连续函数,则把f(x)的不定积分称为不定积分,记作:
∫f(x)dx定积分和不定积分的应用十分广泛,它们在数学、物理、经济学等领域都有着重要的作用。
在求解复杂函数的积分问题时,定积分和不定积分可以通过求取函数的定积分和不定积分等方法来解决。
定积分和不定积分是高数中的重要概念,它们的定义和应用都十分广泛,可以用来解决多种复杂函数的积分问题。
在研究高数中,要深入研究定积分和不定积分的定义和应用,以便更好地理解复杂函数的求积分问题。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
∀ξi ∈ [ x i −1, x i ],
作和式
∑ f( ξ i )∆x i ,其中 ∆x i = x i − x i−1 ,
i =1
1≤ i ≤ n
n
令 λ = max ∆x i
ξ 如果不论 [a, b] 怎样分法及 i 如何选取,当λ → 0 时,
和式的极限存在,则称此极限为函数f (x) 在 [a, b] 上的
y
y=x
2
-1
o
1
x
x 2 + y2 = 2
(3)解: A = ∫
1 −1
2 − x dx − ∫
2
1 x 2 dx −1
二、定积分的性质
k 性质 1 若 f (x) 在 [a, b] 上可积, 是任意常数,则kf ( x)
在 [a, b] 上也可积,且 ∫ kf ( x )dx = k ∫ f ( x )dx 。
y
y =1
b
b
b
则 ∫ a 1 ⋅ dx = ∫ a dx = b − a 。
b
b
∫a kdx = k (b − a ).
b
a
o
b
x
性质 4(定积分对区间的可加性) (定积分对区间的可加性)
设 f (x) 在一个闭区间上可积,则f (x) 在该区间的任何子
b 区间上也可积并且对该区间上的任意三点 a , , c 都有
∵当 ∆x i → 0 时, M i − m i → 0 ,
∆A i − f ( ξ i ) ∆x i = 0, ∴ lim ∆x i → 0 ∆x i
∴近似值 f( ξ i )∆x i 的误差 ∆A i − f (ξ i )∆x i 是比
∆x i 高阶的无穷小,即
∆A i = f ( ξ i ) ∆x i + o ( ∆x i )
b
A1
a
A3
d b x
A2
∫ a f (x )dx = A1 − A 2 + A3
例 2、利用定积分表示图中的面积。
y
y = a2
y
y = x2
−π
y = sin x
π
o
x
o
a
3
x
a 2 x dx 0
π 0
(1)解: A = a − ∫
0 −π
(2)解: A = − ∫ sin xdx + ∫ sin xdx
变速直线运动的物体所经过的路程 S 是速度函数
v = v( t ) 在时间区间[a, b] 上的定积分: S = ∫ v( t )dt 。
a b
2.定积分定义的剖析
(1)积分 ∫
b f ( x )dx a
仅与被积函数f (x) 和积分区间[a,b]
有关,而与区间 [a,b]的分法与点ξ i 的取法无关。
(2)取近似
∀ξi ∈ [ x i −1, x i ],
∆A i ≈ f(ξi )∆x i
( i = 1, 2, ⋯ , n ).
设 m i 和 M i 分别是 f (x) 在 [ x i−1 , x i ] 上的最小值和最大值,则 −
m i ∆x i ≤ ∆A i ≤ M i ∆x i ,
∆A i − f (ξi )∆x i ∆x i ≤ M i − mi .
3.1.2 3.1.2 定积分的定义
1.定义 1.定义 设 f (x) 是定义在 [a, b] 上的有界函数,任取一组分点
a = x < x1 < x 2 < ⋯ < x i −1 < x i < ⋯ < x n −1 < x n = b,
把[a,b]分成 n 个小区间[ x i−1 , x i ] ( i = 1, 2, ⋯ n ) ,
定积分,记作 ∫
b
b f ( x )dx a
,即
∫ a f (x )dx = λlimo ∑ f(ξi )∆x i →
i =1
n
.
∫
b f ( x )dx a
读作“函数f (x) 从 a 到 b 的定积分。 ”
f ( x)dx —被积表达式 被积表达式, 被积表达式
f ( x) —被积函数 被积函数, 被积函数
∫0
∑ λ →0
i =1
i
i
n →∞
1 e n −1
定积分的性质和几何意义 3.1.3 定积分的性质和几何意义
一、定积分的几何意义
1.若 f (x) 在 [a, b] 上连续,且 f ( x) ≥ 0 ,则 ∫
表示以 y = f ( x ) 为曲边的曲边梯形面积 A。
y y = f ( x)
b f ( x )dx a
o
a
b
x
y M
C N D
o
M1
N1
x
A MCND = A MCNN1M1 − A MDNN1M1
2、设 y = f ( x ) 在 [a, b] 上连续,且 f ( x) ≥ 0 ,求以曲线
y = f (x ) 为曲边,底为[a,b]的曲边梯形的面积 A。
计算步骤如下:
y y = f (x)
o
a=x
b f ( x )dx a
。
3、若 f (x) 在 [a, b] 上连续,且有正有负时,则 ∫
b f ( x )dx a
就等于由连续曲线 y = f ( x ) ,直线 x=a,x=b 及 x 轴所
围成的几个曲边梯形面积的代数和,在 x 轴上方的面积
取正号,在 x 轴下方的面积取负号。 y
y = f (x) o c
x —积分变量 积分变量, 积分变量
a —积分下限 积分下限, 积分下限
积分区间, [a,b]—积分区间 积分区间
积分上限。 b —积分上限 积分上限
若定积分 ∫
b f ( x )dx a
存在,则称f (x) 在[a, b] 上可积。
曲边梯形的面积 A 是曲边函数y = f ( x ) 在区间
= ∫ abf ( x )dx 。 [a,b]上的定积分: A
这说明 ∆x i 越小, f( ξ i )∆x i 的近似程度越高。
(3)求和
A ≈ f(ξ1 )∆x1 + f(ξ 2 )∆x 2 + ⋯ + f(ξi )∆x i + ⋯ + f(ξ n )∆x n
即 A ≈ ∑ f( ξ i )∆x i 。
i =1 n
把 n 个小矩形面积相加(即台阶形面积) ,得到曲边梯形 的面积 A 的近似值。
t 的连续函数,且 v( t ) ≥ 0 ,求在时间间隔 [a, b] 上物体
所经过的路程 S。
(1)分割
任取分点: a = t < t 1 < t 2 < ⋯ < t i −1 < t i < ⋯ < t n −1 < t n = b ,
把时间区间 [a, b] 分成 n 个小区间:
[ t , t 1 ] ,[ t 1 , t 2 ] ,…,[ t i−1 , t i ] ,…, [ t n−1 , t n ] 。
∴ f (ξ i )∆x i ≤ 0 , ∑ f (ξ i ) ∆x i ≤ 0 ,
i =1 n
故 ∫
b f ( x )dx a
= lim
∑ f( ξ i )∆x i λ →o
i =1
n
≤0 。
y = f (x)
而 f (ξ i )∆x i 表示小矩形面积,
∴∫
b f ( x )dx a
= −A 或 A = − ∫
A = ∫ f ( x )dx
a
b
o
a
b
x
2.若 f (x) 在 [a, b] 上连续,且 f ( x) ≤ 0 ,则 ∫
或 A = − ∫ a f ( x )dx 。
b
b f ( x )dx a
= −A
∵在 [a, b] 上 f ( x) ≤ 0 ,
y a o
b x
∴ f (ξ i ) ≤ 0 ,而 ∆x i > 0 ,
(4)取极限
设 λ = max ∆x i ,
1≤ i ≤ n
A = lim ∑ f( ξ i )∆x i
λ →o i =1
n
以上四个步骤可以概括为一句话: 分割取近似,求和取极限。 “分割取近似,求和取极限 ” 分割取近似
(二)变速直线运动的路程
设一物体作变速直线运动,已知速度 v = v(t ) 是时间
(3)求和 n S ≈ v(ξ1 )∆t1 + v(ξ 2 ) ∆t 2 + ⋯ + v(ξ n ) ∆t n = ∑ v(ξi )∆t i
(4)取极限
i =1
λ = max ∆t i ,
1≤ i ≤ n
n
S = lim
∑ v(ξi )∆t i . λ →o
i =1
上述两个实例,一个是几何学中的面积问题, 一个是物理学中的路程问题,尽管它们的实际意 义完全不同,但是从抽象的数量关系来看,它们 的分析结构形式完全一样,都是函数在区间上具 函数在区间上具 有特殊结构的和式的极限,对于这种和式的极限, 有特殊结构的和式的极限 可以抽象出新的数学概念—定积分 定积分。 定积分
故
∑ f (ξ i )∆x i = ∑ e
i =1 i =1
n
n
i −1 n
1 1 ⋅ = (1 + e n n
1 n
+e
2 n
+⋯+ e
n −1 n )
1 1 1 − (e n ) n = ⋅ = (e − 1) ⋅ 1 n 1− e n e
