电磁场与电磁波低频电子电路3章(20120314)
电磁场与电磁波:第三章作业答案
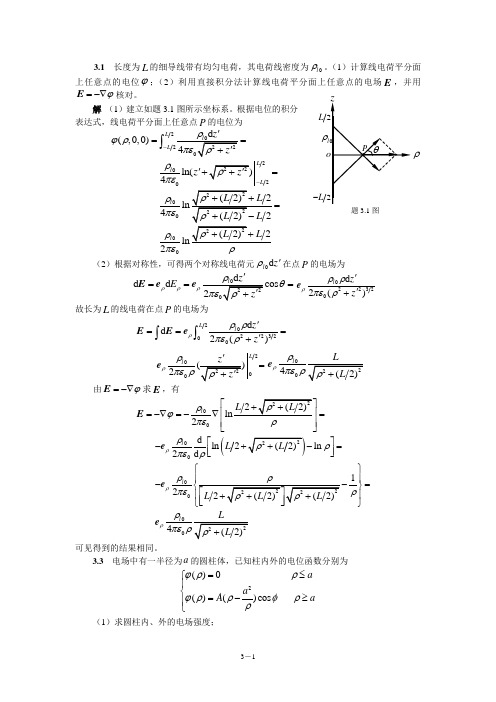
3.1 长度为L 的细导线带有均匀电荷,其电荷线密度为0l ρ。
(1)计算线电荷平分面上任意点的电位ϕ;(2)利用直接积分法计算线电荷平分面上任意点的电场E ,并用ϕ=-∇E 核对。
解 (1)建立如题3.1图所示坐标系。
根据电位的积分表达式,线电荷平分面上任意点P 的电位为2(,0,0)L L ϕρ-==⎰2ln(4L l L z ρπε-'+=04l ρπε=02l ρπε (2)根据对称性,可得两个对称线电荷元z l 'd 0ρ在点P 的电场为d d E ρρρθ'===Ee e 022320d 2()l z z ρρρπερ''+e故长为L 的线电荷在点P 的电场为2022320d d 2()L l z z ρρρπερ'==='+⎰⎰E E e20002L l ρρπερ'=e ρe 由ϕ=-∇E 求E ,有002l ρϕπε⎡⎢=-∇=-∇=⎢⎥⎣⎦E(00d ln 2ln 2d l L ρρρπερ⎡⎤-+-=⎢⎥⎣⎦e0012l ρρπερ⎧⎫⎪--=⎬⎪⎭e ρe可见得到的结果相同。
3.3 电场中有一半径为a 的圆柱体,已知柱内外的电位函数分别为2()0()()cos a a A aϕρρϕρρφρρ=≤⎧⎪⎨=-≥⎪⎩(1)求圆柱内、外的电场强度;L L -ρρ题3.1图(2)这个圆柱是什么材料制成的?表面有电荷分布吗?试求之。
解 (1)由ϕ=-∇E ,可得到a ρ<时, 0ϕ=-∇=Ea ρ>时, ϕ=-∇=E 22[()cos ][()cos ]a a A A ρφρφρφρρρφρ∂∂----=∂∂e e 2222(1)cos (1)sin a a A A ρφφφρρ-++-e e(2)该圆柱体为等位体,所以是由导体制成的,其表面有电荷分布,电荷面密度为0002cos S n a a A ρρρρεεεφ=====-e E e E3.4 已知0>y的空间中没有电荷,下列几个函数中哪些是可能的电位的解? (1)cosh y e x -; (2)x e y cos -;(3)cos sin e x x (4)z y x sin sin sin 。
电磁场与电磁波 PPT

合成波得平均能流密度矢量
S1av
1 2
Re[E1(r )
H1 (r )]
1 2
Re[ex E1y (r )H1z (r )
பைடு நூலகம்
ez E1y (r )H1x (r )]
eexx
24EEimim
11
ssinini isisnin2 (2k(1kz1czocsosi) i
)
例6、4、1 当垂直极化得平面波以角度i 由空气向无限大得理
电磁场与电磁波
因此得到,产生全反射得条件为:
电磁波由稠密媒质入射到稀疏媒质中,即ε1 >ε2
入射角不小于c arcsin 2 1 , c 称为全反射的临界角。
对全反射得进一步讨论
θ i <θc 时,不产生全反射
θ i =θc 时, sint
1 2
sin c
1
t 90o
// 1
2
1 c
arcsin
0 4 0
6
可见入射角θi=π/ 3大于临界角θc=π/ 6 ,此时发生全反射。
入射得圆极化波可以分解成平行极化与垂直极化得两个线极 化波,虽然两个线极化波得反射系数得大小此时都为1,但它们得相 位差不等于±π/ 2,因此反射波就是椭圆极化波。
例6、3、1 下图为光纤得剖面示意图,如果要求光波从空气进 入光纤芯线后,在芯线与包层得分界面上发生全反射,从一端传至另 一端,确定入射角得最大值。
透射波沿分界面方向传播,没有沿z方向传播得功率,并且反射功 率密度将等于入射功率密度。
θ i >θc 时,
sint
1 2
sin i
1
// 1
ktz k2 cost k2 1 sin 2 t
电磁场与电磁波(第4版)第3章部分习题参考解答
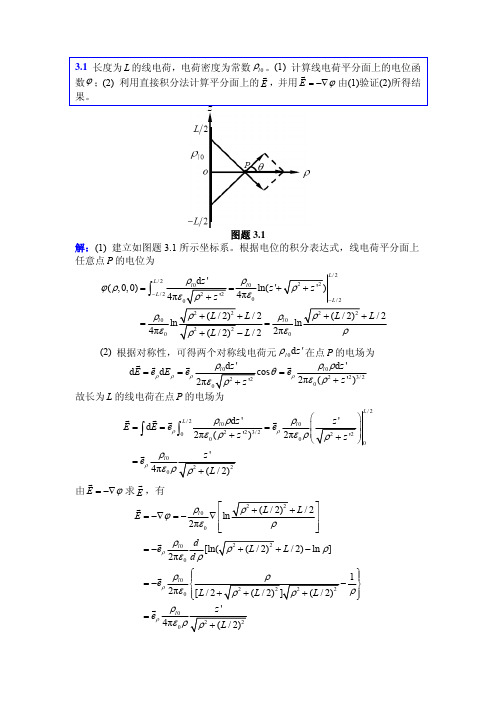
ρ ≥ a 时, E = −∇ϕ = −eρ
G
G ∂ ∂ρ
3.4 已知 y > 0 的空间中没有电荷,试判断下列函数中哪些是可能的电位解? (1) e− y cosh x ;(2) e− y cos x ;(3) e− 2 sin x cos x ;(4) sin x sin y sin z 。 解:在电荷体密度 ρ = 0 的空间,电位函数应满足拉普拉斯方程 ∇ 2ϕ = 0 。
∂2 − y ∂2 − y ∂2 − y (e cosh x) + 2 (e cosh x) + 2 (e cosh x) = 2e− y cosh x ≠ 0 (1) ∂x 2 ∂y ∂z −y 所以函数 e cosh x 不是 y > 0 空间中的电位解; ∂2 − y ∂2 − y ∂2 − y (e cos x) + 2 (e cos x) + 2 (e cos x) = −e− y cos x + e− y cos x = 0 (2) ∂x 2 ∂y ∂z −y 所以函数 e cos x 是 y > 0 空间中可能的电位解; ∂ − 2 ∂ ∂ (e sin x cos x) + 2 (e− 2 sin x cos x) + 2 (e − 2 sin x cos x) (3) 2 ∂x ∂y ∂z
G ρ = −eρ l 0 2πε 0 G = eρ
ρl 0 4πε 0 ρ
⎧ ρ 1⎫ ⎪ ⎪ − ⎬ ⎨ 2 2 2 2 ρ⎪ ⎪[ L / 2 + ρ + ( L / 2) ] ρ + ( L / 2) ⎩ ⎭ z'
ρ 2 + ( L / 2) 2
3.2 点电荷 q1 = q 位于 P 1 ( − a, 0, 0) ,另一点电荷 q2 = −2q 位于 P 2 ( a, 0, 0) ,求空间的 零电位面。 解:两个点电荷 + q 和 −2q 在空间产生的电位 ⎤ q 1 ⎡ 2q ϕ ( x, y , z ) = − ⎢ ⎥ 2 2 2 2 2 2 4 πε 0 ⎢ ( ) ( ) ⎥ x a y z x a y z + + + − + + ⎣ ⎦ 1 2 − =0 令 ϕ ( x, y, z ) = 0 ,则有 2 2 2 2 ( x + a) + y + z ( x − a) + y 2 + z 2
电子科大电磁场与波课件第三章

电子科技大学编写
高等教育出版社 & 高等教育电子音像出版社 出版
电磁场与电磁波
第3章 静态电磁场及其边值问题的解
8
本章内容安排
3.1 静电场分析
3.2 导电媒质中的恒定电场分析
3.3 恒定磁场分析 3.4 静态场的边值问题及解的惟一性定理
3.5 镜像法
3.6 分离变量法
电子科技大学编写
高等教育出版社 & 高等教育电子音像出版社 出版
2
(r )
q C 4π R
E
2 0
介质
z
r
r
q(r)
y
R r r
o
x
电子科技大学编写
高等教育出版社 & 高等教育电子音像出版社 出版
电磁场与电磁波
第3章 静态电磁场及其边值问题的解
20
4. 利用电位求无限大均匀媒质空间中的问题
2.
边界条件(一般性问题)
en ( D1 D2 ) S en ( E1 E 2 ) 0
或
D1n D2 n S E1t E2t 0
3.
按媒质分类的两类问题(特殊性问题) 理想介质:
电子科技大学编写
0
电磁场与电磁波
第3章 静态电磁场及其边值问题的解
17
2. 电场强度与电位函数的关系
已知 E 求
E dl
d dl E dl
已知
求 E
E
如何求出电位函数?
电子科技大学编写
高等教育出版社 & 高等教育电子音像出版社 出版
北京交通大学《电磁场和电磁兼容(闻映红编著)》闻映红课件第3章_电磁波

1
E a y 37.7e
j 2z
H a x 0.1e
S平均
j 2z
* 1 2 Re E H a z 1.885 W/m 2
五、波的极化
1. 极化——电磁波的电场矢量E在空间的取向。
电磁波的发送与接收——极化匹配
2. 极化的类型:
线极化 圆极化 椭圆极化
第3章
电磁波
第1节 波动方程
一、波动方程
在无源均匀媒质中
E H t
H E t
B H 0
D E 0
H E t ( E ) E H t
k E y ( z) 0
2
E y Emy e jkz
E z Emz e jkz
Ez ( z) 2 k Ez ( z) 0 2 z
E (a x Emx a y Emy a z Emz )e
E 0
jkz
E0e
jkz
( E0 e
Em sin(t k z )
则合成电场的振幅是不变的
2 2 E Em Em Em
合成电场取向与x轴的夹角
tan Ey Ex tan(t k z )
椭圆极化——时变电磁场电场矢量E的端点 在空间随时间变化的轨迹为一椭圆
椭圆极化波的E矢量的两个分量 之间有一任意相位差, 振幅也不相同
0 0 120 377 0
Ω
⒋ 电场和磁场在空间任意点的能量密度相等
1 2 we E x 2
电磁场与电磁波

电磁场与电磁波电磁场和电磁波是物理学中非常重要的概念,它们在我们的日常生活中扮演着重要的角色。
本文将会探讨电磁场与电磁波的定义、特性以及应用。
首先,我们来了解什么是电磁场。
电磁场是由电荷和电流产生的一种物理场,在空间中具有能量和动量。
电磁场包含了电场和磁场两个要素。
电场是由电荷产生的力场,而磁场则是由电流产生的力场。
当电荷或电流存在时,它们会在周围产生电场和磁场,这些场相互作用并相互影响,形成电磁场。
电磁场的特性非常丰富。
首先,电磁场是无形的,即我们无法直接感知电磁场的存在。
然而,我们可以通过观察电场和磁场的效应来间接感知电磁场。
例如,当我们将一个带有电荷的物体靠近另一个带有电荷的物体时,它们会相互排斥或吸引,这是由于它们之间相互作用的电场产生的效应。
其次,电磁场具有传播性。
当电荷或电流发生变化时,电磁场会随之变化,并以一种特定的形式传播出去,形成电磁波。
电磁波是电磁场的一种特殊表现形式,它可以在真空中传播,并以光速传播。
电磁波包括了不同频率和波长的波,例如无线电波、微波、可见光、紫外线、X射线和γ射线等。
电磁场和电磁波在许多领域有广泛的应用。
其中一个重要的应用是通信。
无线电波被广泛用于无线电通信、电视和手机等设备中。
电磁波还被应用于医疗诊断和治疗领域。
例如,X射线被用于检查骨骼和器官,而核磁共振成像(MRI)则被用于观察人体内部的结构和病变。
此外,电磁场和电磁波还被用于能源和工业领域。
例如,电力是通过电磁场的作用而传输的。
发电厂中的发电机通过生成电流产生电磁场,并将电能输送到我们的家庭和工厂。
另外,激光器利用强大的电磁场来产生一束高强度的激光光束,广泛用于切割、焊接和激光打印等工业应用。
除了以上的应用外,电磁场和电磁波还在科学研究中扮演着重要角色。
电磁波可以用于研究星际空间和宇宙中的天体。
天文学家通过收集来自外太空的电磁波,并分析其中的信息,来研究宇宙的演化和构成。
此外,科学家们还利用电磁波来研究物质的微观结构和性质,以及探索量子力学等领域。
电磁场课件-第三章微带传输线

在微带线中,导波速度受到介质和导 体材料的影响,不同材料的微带线具 有不同的导波速度。
传播常数与衰减
传播常数
传播常数是描述电磁波在传输线中传播特性的参数,包括相位常数和衰减常数。
衰减
在微带线中,电磁波会因为介质和导体材料的损耗而发生衰减,衰减的大小与传输线的长度和频率有 关。
04 微带线的传输模式
降低介质损耗的方法包括选择低损耗的介质材料、降低介质温度和减小电场强度 等。
色散特性
色散是指不同频率的信号在传输过程中具有不同的相速度和 群速度的现象。在微带线中,色散主要与介质的介电常数和 电导率等因素有关。
了解色散特性对于设计高性能的微带线系统和避免信号失真 非常重要。通过优化微带线的结构和参数,可以减小色散效 应,提高信号传输质量。
03 微带传输线的电气特性
电场分布
电场分布特点
在微带线中,电场主要分布在导体和介质之间,而导体内部 电场强度较小。
电场分布与传输模式
电场的分布与传输模式有关,例如在准TEM模式下,电场主 要分布在导体两侧,而在其他模式下,电场分布可能更加复 杂。
阻抗与导波速度
阻抗计算
微带线的阻抗可以通过其几何尺寸和 介质参数计算得出,阻抗值与传输线 的特性阻抗有关。
微带线的宽度通常在几毫米到几十毫 米之间,根据传输信号的频率和介质 基片的电气性能来选择合适的宽度。
厚度
微带线的厚度通常在几微米到几百微 米之间,较薄的介质基片可以减小线 路的介质损耗,提高传输效率。
介质基片
种类
常用的介质基片有氧化铝、陶瓷、聚四氟乙烯等,根据应用场景和性能要求选 择合适的介质基片。
响。
应用场景
01
02
03
电磁场与电磁波第三版之

l
◇ 实验证明,导电媒质中电流密度与电场 强度成正比J, 即 E
◇ 称为导电媒质的电导率。
要想在导电媒质中维持恒定电流,必须依靠非静电力将B
极板的正电荷q抵抗电场力搬到A极板。这种提供非静电力将其
它形设式局的外能场量强转E为e为 电fqe 能装,置则称电为源电电源动。 Ee dl (V)
q 1 1 q 40 R Rp 40R C
若取RP 处的电位为零,
则 q
4 0 R
◇ 体电荷d 、面电荷dS 、线电ldl产生的电位分别
荷
为
1 d C
40 R
, 1 dS C
40 s R
, 1 ldl C
40 l R
例3.3.1 求电偶极p 子qdl 的电r位 (教材例3.3.
引入极化电荷后,介质的极化效应由极化电荷表征,即空间
的电场由自由电荷和极化电荷产生。而极化电荷和自由电荷的
实质相S D0同dS,则q qp , l E dl 0
而
qp
pd
ppd
p dS
s
由实验证明,P 和 E 之间有一定的线性关系,
得 s D0 P dS q
即
p e0E
产生E的电41场0 qR强R3 度
◇
任意电荷分布产生的电场E r强 度1
40
r '
R3
R d
'
◇ 定义任意电荷分布产生的电位
D0
r
0
E
r
1 4
r '
R3
Rd
'
移矢量
◇ 关系式D0 0E 称为真空的电特性方程或本 构关系
3.2 真空中静电场的基本方程
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
iD vUS
|
Q点
gm
η 0.1 ~0.2
第三章 半导体受控器件的分析
按结构精细化小信号模型说明
第三章 半导体受控器件的分析
3.3
直流工作点分析
要点:直流电源作用下的计算问题。
3.3.1 工作点的建立及近似计算
具体步骤:(1)直流通路 (2)近似计算法或作图法的选择
第三章 半导体受控器件的分析
普通高等教育“十一五”国家级规划教材
21世纪高等院校信息与通信工程规划教材
《低频电子电路》
《低频电子电路》
第三章 半导体受控器件的分析
总论:
• 因半导体PN结的复杂性,导致非线性导电 具有区域特性,区域特性是分析的关键点。
---------具体包含: 区域条件 区域模型与表达方式
《低频电子电路》
3.3.1 工作点的建立及近似计算
双电源供电方案
具体步骤:(1)画出直流通路(c) ,其中 E<0
(2)近似计算法或作图法的选择
第三章 半导体受控器件的分析
ቤተ መጻሕፍቲ ባይዱ
采用近似计算方法
(1)假设晶体管处于放大区 (2)晶体管特性描述
VBE(on) 、β、 ICBO ≈0
(3)设其它元器件参数已知
I BQ E VBE(on) RB 0
I CQ I BQ (1 ) I CBO 0
VCEQ 5 I CQ RC 5V
晶体管PN结必然均处于反偏状态。即 VCEQ 5 I BQ 0 I CQ 0
第三章 半导体受控器件的分析
采用近似计算方法的要点
首先,假设晶体管处于放大区,并按放大区计算。 判断计算结论与之前“放大区”假设是否矛盾, 若不矛盾,则计算结果可信。 若矛盾,则应结合计算结果,正确判断晶体管所 处区域,再根据该区域的情况另行计算。
第三章 半导体受控器件的分析
作图法与采用作图法对前述计算的说明
(1)假设晶体管在任何情况下均处于处于放大区, 则晶体管特性可描述为如下图所示的实线直线。
第三章 半导体受控器件的分析
(2)输入回路
晶体管B、E之外的线性电路特性
vBE E iB RB ----输入直流负载线
将输入直流负载线与晶体管特性画在同一图上, 所得交点,即为所求工作点。
第三章 半导体受控器件的分析
3.2.2 晶体管微变等效电路分析法及条件
管子处于放大区,在信号作用下的小范围变 化时的近似线性等效电路。
第三章 半导体受控器件的分析
放大情况-小信号基础电路模型
(1)输入与二极管相似 (2)输出 c 受 b 的控制
i
i
说明如下:
第三章 半导体受控器件的分析
按结构精细化模型
其中,( 1 )参数 re 的为放大情况下 的发射结交流小信号等效电阻; ( 2 ) 低频晶体管 rbb 为 200 300 ,高频 晶体管约几十欧姆。
第三章 半导体受控器件的分析
参数的数学表达
vCE (2) rce iC
Q
|VA | VCEQ |VA | I CQ I CQ
I CQ I BQ (1 ) I CBO 0
VCEQ 5 I CQ RC 5V
结论分析:计算结果 显然与放大区假设矛 盾,计算结果不可信。
第三章 半导体受控器件的分析
采用近似计算方法
在 E<0条件下,晶体管 发射极反偏,基极电流不可 能小于0。结合上述计算
I BQ E VBE(on) RB 0
3.2.1 晶体管非门基础电路
要点:发射结反偏, 集 电 结 反 偏 。 --管子截止,输出高 电位5V。
要点:管子导通(放大、饱 和或击穿)---电阻参数合理 情况下,管子可以处于饱和, 输出低电位(约等于0V)。
第三章 半导体受控器件的分析
要点:管子导通 (放大、饱和)。
在电阻 RB2 或 RC 较大情况下,管子均可以 处于饱和状态,输出低电位约等于0V。
发射极E
N+
P
N 基极B
集电极C
发射结
集电结
第三章 半导体受控器件的分析
参数的数学表达
(1)
vBE rbe rbb rbe rbb iB
vBE rbb (1 ) iE
Q
VT rbb (1 ) I EQ
Q
rbb (1 )re
第三章 半导体受控器件的分析
电路模型
注:各种场效 应管的小信号 特性相同。
第三章 半导体受控器件的分析
参 数 的 数 学 表 达
(1) (2)
饱和时,输入电阻极大
iD gm vGS
|
Q点
(3)
iD 1 rds vDS
|
Q点
I DQ VA
(4)
场效应管衬底(或背栅)跨导
g mu
第三章 半导体受控器件的分析
3.1 非线性半导体元器件的分析概述
回顾第一章例题 1.3.2 或门电路
(二极管上电压在 大范围的内确定)
第三章 半导体受控器件的分析
回顾第一章例题
1.4.3
全波整流电路
(二极管上电压 在大范围内变化)
第三章 半导体受控器件的分析
回顾第一章例题 1.3.2 电位平移电路
第三章 半导体受控器件的分析
参数的数学表达
(3)
放大倍数与跨导的关系
iC gm vBE
即:
Q
ic ic vbe ib rbe rbe
gmrb'e
第三章 半导体受控器件的分析
3.2.3 场效应管微变等效电路
条件:管子处于饱和区,在信号作用下的小范 围变化时的近似线性等效电路。
工作点
(二极管上电压在导通 区内的较小范围变化)
.
第三章 半导体受控器件的分析
3.2 非线性受控电流器件的求解分析
3.2.1 晶体管非门基础电路
已知:输入只有 5V 和 0V两种情况。
要点:输出应属高低 电位情况,即是在非 线性大范围内求点。
具体步骤:分别以两种 输入电平出发来分析。
第三章 半导体受控器件的分析
第三章
3.1
半导体受控器件的分析
非线性半导体元器件的分析概述
回顾第一章分析 3.2 非线性受控器件的求解分析与应用 具体方法 3.3 直流工作点分析 大范围锁定工作点
3.4 应用目标、非线性元器件的区域特性 和分析方法的选取
第三章 半导体受控器件的分析
3.1 非线性半导体元器件的分析概述
1. 明确非线性元器件工作区域 2. 明确非线性元器件是否需要工作点平台
