ch7一阶电路和二阶电路的时域分析(2)2013
第七章 一阶电路和二阶电路的时域分析

等效初始值:
等效初始值:
难点 1. 初始值的求解; 2. 时间常数的求解; 3. 阶跃响应与冲激响应。 §7.1 动态电路的方程及其初始条件 动态电路 含有动态元件电容和电感的电路。 特点: 当动态电路状态发生改变时(换路)需要经历一个变化过程才能达 到新的稳定状态。这个变化过程称为电路的过渡过程。 2. 换路 电路结构或电路参数发生突变而引起电路变化统称为换路。 意义:能量不能发生突变。 产生原因:电路内部含有储能元件 L、C,电路在换路时能量发生变 化,而能量的储存和释放都需要一定的时间来完成。
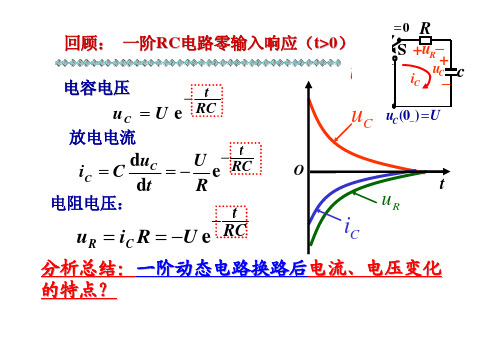
3 同一电路中所有响应具有相同的时间常数。 4 一阶电路的零输入响应和初始值成正比,称为零输入线性。 §7.3 一阶电路的零状态响应 零状态响应:动态元件初始能量为零,由t >0电路中外加激励作用所产 生的响应。
1. RC电路: t<0,K在1,电路稳定, 有 t=0,K从1打到2,有 t>0,K在2, 有 解答形式为:
换路定律: 在换路前后电容电流和电感电压为有限值的条件下,换路前后瞬间电容 电压和电感电流不能跃变。 (1)若iC 有限,则: uC ( 0+ )= uC ( 0- ) (2)若uL 有限,则: iL( 0+ )=iL( 0- )
3. 电路初始值的确定
电路初始值 独立初始值:uC (0+)、 iL(0+); 非独立初始值:其余电量在t= 0+时的值;
应用条件:一阶电路;开关激励 时间常数计算:RC电路:;
RL电路:; 实际现象讨论:
(1) 当负载端接有大电容时,电源合闸可能会产生冲击电流。
(1)
(2)
(2) 当负载端接有大电感时,开关断开可能会产生冲击电压。
电路课件 电路07 一阶电路和二阶电路的时域分析

2019年3月29日星期五
经典法
5
• 线性电容在任意时刻t,其电荷、电压与电流关系:
q(t ) q(t0 ) iC ( )d
t0 t
线性电容换路瞬间情况
uC (t ) uC (t0 )
• q、uc和ic分别为电容电荷、电压和电流。令t0=0-, t=0+得: 0 0
第7章一阶电路和二阶电路的时域分析
2019年3月29日星期五
3
• 动态电路:含动态元件电容和电感电路。 • 动态电路方程:以电流和电压为变量的微分方程或微 分-积分方程。 • 一阶电路:电路仅一个动态元件,可把动态元件以外 电阻电路用戴维宁或诺顿定理置换,建立一阶常微分 方程。 • 含2或n个动态元件,方程为2或n阶微分方程。 • 动态电路一个特征是当电路结构或元件参数发生变化 时(如电路中电源或无源元件断开或接入,信号突然 注入等),可能使电路改变原来工作状态,转变到另 一工作状态,需经历一个过程,工程上称过渡过程。 • 电路结构或参数变化统称“换路”,t=0时刻进行。 • 换路前最终时刻记为t=0-,换路后最初时刻记为t=0+, 换路经历时间为0-到0+。
第7章一阶电路和二阶电路的时域分析 7-2一阶电路的零输入响应
2019年3月29日星期五
RC电路零输入响应-1
12
• 电路中电流 • 电阻上电压
RC电路零输入响应-2
1
t t duC U 0 RC t d 1 RC RC i C C (U 0e ) C ( )U 0e e dt dt 1 RC R
R
13
RC电路零输入响应-3
第七章 一阶电路和二阶电路的时域分析(part-2)
解
u C ( ∞ ) = 4i1 + 2i1 = 6i1 = 12 V u = 10 i1 → Req = u / i1 = 10 Ω
7.4.1 一阶RL电路的零输入响应
US iL ( 0 + ) = iL ( 0 − ) = = I0 R1 + Rห้องสมุดไป่ตู้应用KVL得:
d iL L + Ri L = 0 dt
iC = iC (∞) + [iC (0 + ) − iC (∞)] e
−
t RC
计算电流能否套用 公式?
套用全响应电压公式
R
C
uC (t ) = Ue − t / RC t ≥ 0
S(t = 0)
−
+
uC
duC iC = C dt
i
t U =− e RC t ≥ 0 −
R
(a= ) U uC (0 -)
(2) 确定稳态值 u c ( ∞ ) 由换路后电路求稳态值 u c ( ∞ ) 9mA
6× 3 3 uC ( ∞ ) = 9 × 10 × × 10 6+ 3 = 18 V
−3
+ R ) 6kΩ uC ( 0 −t=0-等效电路
(3) 由换路后电路求 时间常数 τ
τ = R0C 6× 3 −6 3 = × 10 × 2 × 10 6+ 3 −3 = 4 × 10 s
−
t L/ R
t ≥0
t − L/ R
L uL
–
d iL u L (t ) = L = − RI 0 e dt
τ时间常数
①电压、电流是随时间按同一指数规律衰减的函数; I0 iL 连续 函数 t 0 -RI0 uL t 跃变
第7章_一阶电路和二阶电路的时域分析

②测量方法: a.对任意时刻而言,
t 0 t 0
uC (t0 ) = U 0 e
b.次切距长:
AB BC = tan
= U0e
e 1 = 0.368 uC (t0 )
t 0
U0
uC
uC ( t 0 )
A
uC ( t 0 ) U 0e = = = t 0 1 duC U 0e dt t =t0
uC (t ) 4e 0.5t = = e 0.5t A ③求i(t):i (t ) = 4 4
(t 0)
19
习题: 7-2、7-4、7-5。
20
三、RL电路的零输入响应:
求i(t),uR(t), uL(t),(t≧0) 1、物理过程:
U0 i (0 ) = i (0 ) = R0
R
t=0 + iL uL L -
解: 根据换路定则:
i L 不能突变
i L (0 ) = i L (0 ) = 0 A
+ *** t =0K 时的等效电路: R
换路后的电压方程 :
+ U -
t=0
+ + iL uL (0+) uL L L - - iL(0+)
U = iL (0+ ) R + u L (0+ )
uC (0+ ) = uC (0- ) = U 0
uC (0+ ) → 0
U0 i (0 + ) = → 0 为放电过程。 R
13
2、数学分析: ①列微分方程:由KVL, +u U0 _ C
C
S
t=0
电路第七章一阶电路和二阶电路的时域分析.

当动态电路状态发生改变时(换路)需要经历 一个变化过程才能达到新的稳定状态。这个变化过 程称为电路的过渡过程。 过渡过程产生的原因: 电路内部含有储能元件L,C。电路在换路时能量发生变 化,而能量的储存和释放都需要一定的时间来完成。
0
ic(t)
c
2 3
0.0184u t (s) 0 4
t RC
uc(0)= u0 2 3 4
t RC
RR u
t
(s)
du C t d u0 e C iC t C dt dt
u0 e R
2.时间常数
uc不能跃变, 结论: ic可以跃变。
解得 :
R 0 L
A I0
I0
iL(t)
iL t I 0e
R t L
t 0
0
R R t t diL t d L L u L t L L I e RI e 0 0 dt dt
2 3 4
t
(s)
t0
t 0 =RC
t0
f(0)
f(t) t
iL t iL 0e
=LG
0
4
(s)
C.零输入响应都是按指数规律衰减的,衰减的快慢由 决定,越小, uc(t),iL(t)衰减的越快。
D.时间常数的求法:
在换路后(即 t 0 )的电路中求。 R是从动态元件两端看进去的戴维宁等效电阻。
(3) 只有当电容器两端电压变化时,才有电流。
六.电感的伏安关系
1 . 电感中的电压 现象: a .开关合上: us + _ b .开关打开: us +
第7章一阶电路和二阶电路的时域分析

①
S
②
2 3
6
解 iL (0 ) iL (0 )
24 6 2A 4 2 3 // 6 3 6
24V 4
i1
4
iL
换路后电路为零输入响应: L 6 1s Req 6
uL 6H
2Ω
Req 3 (2 4) // 6 6
iL (0+) = iL (0-)=3A
(3) 由0+等效电路求 iC(0+) , uL(0+)
uL(0+)
3 i2 (0 ) 3 1 A 3 6
uL (0 ) 6i2 (0 ) 6V
返回本节
0+等效电路
上 页
下 页
5.电路初始值的确定 例2 求 uC(0+) 、iL(0+) 、
返回本节
上 页
下 页
5.电路初始值的确定 例1 求 i2(0+) 和 uL(0+) 。
iL S(t=0) 3 1 + i 2 2 + u 6 9V 1H L – – 3 i2(0+) 6 3A + –
(1) 由0-电路求 iL(0-)
+ 9V – 3 iL
iL (0 ) 3 A (2) 由换路定律
电路如下图
R0
S(t=0)
1 2
i
U0 L
R
uL R
i
L
uL
(a)
(b)
换路前电路处于稳态,电感电流I0=U0/R0 = i(0-) , 电感中储存一定的磁场能量,在 t=0 时开关由1→2, 换路后的电路如图(b)所示。 (b)
CH7 一阶电路和二阶电路的时域分析2

端电压。
5
2A + –
10
10 +
解
Req 10 10 20
u
K
2H
U S 2 10 20V L / Req 2 / 20 0.1s i L ( ) U S / Req 1 A
iL
t>0
uL
–
i L ( t ) (1 e
uL ( t ) U S e
i L (t ) 6 ( 2 6)e
i2 (t ) 4 ( 2 4)e
5 t
5 t
6 4e
5 t
5 t
t0
i1 ( t ) 2 (0 2)e 5 t 2 2e 5 t A 4 2e A
例
解
已知:t=0时开关闭合,求换路后的电流i(t) 。
0
t
uc ( t ) uc ( ) [uc (0 ) uc ( )]e
t
uC 0.667 ( 2 0.667)e 0.5 t 0.667 1.33e 0.5 t t 0
例
解
t=0时,开关闭合,求t>0后的iL、i1、i2
i1 5 5
i L (0 ) i L (0 ) 10 / 5 2 A
f (t ) (t ) (t t0 )
f(t) 1 t O t0 O t O -1 t0 t
(t) 1
( t- t0 )
激励
响应
(t )
R
+ uS(t) _ + uC(t ) _
u C (t ) (1 e )(t )
例 t=0时 , 开关K闭合,已知 uC(0-)=0,
一阶电路和二阶电路的时域分析

一阶电路和二阶电路的时域分析一、一阶电路的时域分析:一阶电路指的是由一个电感或电容与线性电阻串联或并联而成的电路。
对于串联的一阶电路,其特征方程为:L di(t)/dt + Ri(t) = V(t) ---------- (1)其中,L是电感的感值,R是电阻的电阻值,i(t)是电路中的电流,V(t)是电路中的输入电压。
通过对上述方程进行求解可以得到电路中电流与时间的关系。
对于并联的一阶电路,其特征方程为:1/R C dq(t)/dt + q(t) = V(t) ---------- (2)其中,C是电容的电容值,q(t)是电路中电荷的变化,V(t)是电路中的输入电压。
同样,通过对上述方程进行求解可以得到电路中电荷与时间的关系。
一阶电路的响应可以分为自由响应和强迫响应两部分。
自由响应指的是由于电路中初始条件的存在,电流或电荷在没有外部输入电压的情况下的变化。
强迫响应指的是由于外部输入电压作用而产生的电流或电荷的变化。
对于一个初始处于稳定状态的电路,在有外部输入电压作用时,电路中电流或电荷会从初始值开始发生变化,最终趋于一个新的稳定状态。
这一过程可以由电流或电荷的指数递减或递增的形式表示。
在分析一阶电路的时域特性时,可以利用巴塞尔函数法或拉普拉斯变换法。
巴塞尔函数法主要是通过巴塞尔函数的表达式计算电压或电流的变化情况;拉普拉斯变换法则通过将时域的微分方程转化为复频域的代数方程,然后求解代数方程,最后再对求得的结果进行逆变换获得电流或电压的表达式。
二、二阶电路的时域分析:二阶电路是指由两个电感或电容与线性电阻串联或并联而成的电路。
对于串联的二阶电路,其特征方程为:L₁L₂ d²i(t)/dt² + (L₁R₁+L₂R₂+L₁R₂+L₂R₁) di(t)/dt + R₁R₂i(t) = V(t) ---------- (3)其中,L₁和L₂分别是两个电感的感值,R₁和R₂分别是两个电阻的电阻值,i(t)是电路中的电流,V(t)是电路中的输入电压。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
Chapter 7 一阶电路和 二阶电路的时域分析续Time domain analysis of first-order circuit and second-order circuit1主要内容阶跃函数和冲激函数 一阶电路的阶跃响应 一阶电路的冲激响应 二阶电路的零输入响应 二阶电路的零状态响应2Chapter7 一阶电路和二阶电路的时域分析7.7 阶跃函数和冲激函数7.7 阶跃函数和冲激函数 (Step function and Impulse function)在动态电路的分析中常引用阶跃函数和冲激函数来 描述电路中的激励和响应。
阶跃函数和冲激函数具有不连续点(跃变点)或其导数 与积分有不连续点。
3Chapter7 一阶电路和二阶电路的时域分析7.7 阶跃函数和冲激函数 z z7.7.1 阶跃函数 1. 单位阶跃函数 用 ε(t)表示,定义为⎧0 ε (t ) = ⎨ ⎩1 t<0 t >01 oε(t)t将ε(t) 乘以常数k,可构成幅值为k的阶跃函数 kε ( t ) 阶跃函数又称开关函数,其实际意义为:4Chapter7 一阶电路和二阶电路的时域分析7.7 阶跃函数和冲激函数2.延时阶跃函数 如果把单位阶跃函数延迟, 则有:ε(t − t0) 1 0 t0 t⎧0 ε (t − t0 ) = ⎨ ⎩13. 脉冲函数t < t0 t > t0f (t) = ε(t − t1) − ε(t − t2) 其中脉冲幅度为1, 脉宽为(t2 − t1)。
f (t) 1 0 t1 t2 t5Chapter7 一阶电路和二阶电路的时域分析7.7 阶跃函数和冲激函数单位阶跃函数可用来“起始”任意一个函数f (t)。
设f (t)对所有t 都有定义,则⎧0 f ( t )ε ( t − t 0 ) = ⎨ ⎩ f (t ) t < t0 t > t0f (t)ε(t− t0)波形为f (t)0t0t0t0t单位阶跃函数可组成许多复杂信号。
6 Chapter7 一阶电路和二阶电路的时域分析7.7 阶跃函数和冲激函数 z z7.7.2 冲激函数强度为1 10δ(t)1. 单位冲激函数 单位冲激函数δ(t),其数学定义为:∞ ⎧ ⎪ ∫ δ ( t )dt = 1 ⎨ −∞ ⎪ ( t ≠ 0) ⎩δ ( t ) = 0t p(t)1 Δδ(t)函数是单位脉冲函数的极限。
δ ( t) = lim p( t )Δ →0−Δ 0 2Δ 2tδ(t)用一种集中(离散的)瞬时作用的效应来代替一种平均持续作用的效应,反映“强度”的概念。
习惯上将7∫∞−∞δ ( t )dt 称为冲激强度。
Chapter7 一阶电路和二阶电路的时域分析7.7 阶跃函数和冲激函数2. 延时冲激函数 定义在 t =t0处、强度为k的延时冲激 函数kδ(t − t0)为:∞ ⎧ ⎪ ∫ δ ( t − t 0 )dt = 1 ⎨ −∞ ⎪ (t ≠ t0 ) ⎩δ ( t − t 0 ) = 0kδ(t− t0) 0 t0 t3. 冲激函数的一些性质 n冲激函数是阶跃函数的导数⎧0 t < 0 ∫−∞ δ (ξ )dξ = ⎨ ⎩1 t > 0t⎧0 t < 0 ε (t ) = ⎨ ⎩1 t > 0t∫−∞δ (ξ )dξ = ε ( t )从而可得:8d ε (t ) = δ (t ) dtChapter7 一阶电路和二阶电路的时域分析7.7 阶跃函数和冲激函数o筛分性(采样性) 设函数f (t)在t =0时连续,当t ≠0, δ(t) =0, 所以有: f (t)δ(t)= f (0)δ(t) 因此∞ ∞∫−∞f ( t )δ ( t )dt = f (0)∫ δ ( t )dt = f (0)−∞同理,对于在t =τ 连续的函数f (t),有∫∞−∞f ( t )δ ( t − τ )dt = f (τ )上式表明:单位冲激函数能把f (t)在冲激出现时刻的函 数值筛选出来,这一性质称为冲激函数的筛分性质。
9Chapter7 一阶电路和二阶电路的时域分析7.8 一阶电路的阶跃响应7.8 一阶电路的阶跃响应若电路初始状态为零,输入为单位阶跃信号,则相应的 响应为单位阶跃响应。
用s(t)表示。
R εt i C uC t ut R i C uC相当于t= 0时接入一个1V电压源的零状态响应。
s(t) = uC =(1− e-t/τ)ε (t) 若输入是任意的阶跃信号,其响应等于同一电路的单位阶 跃响应乘上相应的倍数。
10Chapter7 一阶电路和二阶电路的时域分析电压源的波形如图所示,u C (0−) = 0,求u C =?t (ms)u s (t )这是矩形脉冲通过电路的零状态响应。
V)2()1(10)1()1(10)2()1(−−−−−=∴−−−−t et eu t t C εε1210V在图示电路中,例7.8解:电路的时间常数:单位阶跃响应为:τ= RC =1ms (1)()tC u e t τε−=−()10(1)10(2)s u t t t εε=−−−Q u C t (ms )(V)0106.3217.9 一阶电路的冲激(Impulse)响应zh(t)=ds(t)/dtz 7.9.1利用h(t )=ds(t)/dt 求解单位冲激响应在信号间有⎪⎩⎪⎨⎧==∫∞−td t t dt d t ξξδεεδ)()()()(存在可证明,在响应之间亦有关系dtt ds t h )()(=在单位冲激信号δ(t )激励下电路的零状态响应称为单位冲激响应,用h (t )表示。
成立。
当i s =ε(t )时,u C =s (t ))()(t s dtdt h =在δ(t )激励下的响应h (t ),可用一个具有相应初始条件的零输入响应来等效。
在图示电路中求u C 。
s (t )=R (1−e -t /τ)ε(t )当i s =δ(t )时,u C =h (t ))(1)()1(t e C t e R t t εδττ−−+−=)]()1([t e R dt d t ετ−−=)(1t e Ct ετ−=)(1)(t e Ct h t ετ−=——u C (0+)=1/C 引起的零输入响应Cu u C C 1)0()0(+=−+即为:若某初始电压为零的电容C ,在一个单位冲激电流源δ(t )作用下(并联),有zh(t)z 7.9.2 用δ(t)引起的相应初始值求解单位冲激响应h(t )δtu CC u Cu CC1(0)C u C+=⎪⎩⎪⎨⎧==+−0)0()(1C C C u t u R dt du C δ将时间分成[0−,0+],[ 0+,t )。
∫∫∫+−+−+−=+000000)(1dt t dt u R dt dtdu C C Cδ0Cu C (0+)1Cu C 1)0(=+分析:在[0−,0+]内:在[0+,t )内,则有⎪⎩⎪⎨⎧==++C u u R dt du C C C C 1)0(01其解(零输入响应)为:)(1)(t e Ct h t ετ−=同理,若某个初始电流为零的电感,当与一个单位冲激电压源δ(t )串联时,有1(0)(0)L L i i L+−=+即δtLi Li LLi L1(0)L i L+=u C (0−)=0 ,电流源i s (t )的波形如图所示,R =1Ω,C =2F ,求t ≥0时的u C 。
1234t (s)0i s (A)1082个冲激信号可分别用2个初始值等效。
C u C 10)0(=+将问题变换成零输入响应的情况,电路方程为:例7.9在图示电路中,解:i s (t ) =10δ(t ) −8δ(t −2)ACu C 8)2(−=+⎪⎩⎪⎨⎧−===+++C u C u u R dt du C C C C C 8)2(,10)0(01⎪⎩⎪⎨⎧−===+++C u C u u R dt du C C C C C 8)2(,10)0(01当第一个冲激δ(t )单独作用时:)(10)1(t e Cut Cετ−=当第二个冲激δ(t −2)单独作用时:)2(8)(10)2()2()1(−−+=+=−−−t e Ct e C uuu t t CCC εεττ当2个冲激共同作用时,总响应为:)2(8)2()2(−−=−−t e Cut Cετ1234t (s)i s (A)108代入参数,上述结果为:)2(4)(5)2(5.05.0−−=−−−t e t e u t t C εε或⎩⎨⎧≥−=−=≤≤=−−−−−−S t e e e u St e u t t Ct C 216.2)45(205)2(5.0)2(5.015.0其波形如图21345t (S)u C (V)51.84−2.16)2(8)(10)2()2()1(−−+=+=−−−t e Ct e C uuu t t CCC εεττh含有2个独立的动态元件称二阶电路,需要用二阶微分方程描述。
h线性电路的零输入响应是初始状态的线性函数;零状态响应是输入信号的线性函数;完全响应等于零输入响应和零状态响应的叠加等概念对二阶电路仍适用。
7.10 二阶电路的零输入响应z RLC串联电路的零输入响应z二阶电路响应特点的复平面表示zz 7.10.1 RLC 串联电路的零输入响应根据KVL :u R + u L + u C =0由元件伏安关系:22dtu d LC dt diL u C L ==dtdu Ci C=dt du RCRi u CR ==022=++C C C u dt du RC dtu d LC 电路方程为:已知:U C (0–)=U 0I L (0–)=I 0求:t ≥0时的u C (t ) 和i (t )。
000(0);C C t du I u U dt C++===⎪⎪⎩⎪⎪⎨⎧===+++=+C I dt du U u u LC dt du L R dt u d t C C C C C 00022;)0(01定义:LC10=ωLR 2=α阻尼系数:谐振角频率:022022=++C C C u dtdu dt u d ωα特征方程为:2022,1ωαα−±−=p 或LC L R L R p 12222,1−⎟⎠⎞⎜⎝⎛±−=p 2 + 2αp + ω02 = 0电路的零输入响应形式与α,ω0的相对数值有关。
1. 当α>ω0,即2LR C>时,电路为过阻尼情况p 1,p 2为2个不相等的负实数,响应为:tp tp C ek ek u 2121+=2. 当α=ω0,即时,电路为临界阻尼情况2LR C=p 1= p 2= −α为2个相等的负实数,响应为tC et k k u α−+=)(212022,1ωαα−±−=p LC L R L R p 12222,1−⎟⎠⎞⎜⎝⎛±−=二阶电路的零输入响应形式与α,ω0数值的关系:3. 当α<ω0,即时,电路为欠阻尼情况p 1= −α+ j ωd ;p 2= −α−j ωd 为一对共轭复数。
