2012江苏高考数学卷
2012江苏高考数学试卷(含答案)

2012江苏高考数学试卷注意事项:考生在答题前请认真阅读本注意事项及各题答题要求1.本试卷共4页,均为非选择题(第1题-第20题,共20题)。
本卷满分为160分。
考试时间为120分钟。
考试结束后,请将本试卷和答题卡一并交回。
2.答题前请务必将自己的姓名、准考证号用0.5毫米黑色墨水签字笔填写在试卷及答题卡的规定位置。
3.请认真核对监考员在答题卡上所粘贴的条形码上的姓名、准考证号与您本人是否相符。
4.作答试题,必须用0.5毫米黑色墨水签字笔在答题卡上的指定位置作答,在其他位置作答一律无效。
5.如需作图,须用2B 铅笔绘,写清楚,线条,符号等须加黑加粗。
参考公式:(1)样本数据x 1 ,x 2 ,…,x n 的方差s 2=n i=11n ∑(x i -x )2,其中n i i=11x n ∑.(2)(2)直棱柱的侧面积S=ch ,其中c 为底面积,h 为高.(3)棱柱的体积V= Sh ,其中S 为底面积,h 为高.一.填空题:本大题共14小题,每小题5分,共计70分,请把答案填写在答题卡的相应位置........上。
..1、已知集合},2,0,1{},4,2,2,1{-=-=B A 则_______,=⋂B A2、函数)12(log )(5+=x x f 的单调增区间是__________3、设复数i 满足i z i 23)1(+-=+(i 是虚数单位),则z 的实部是_________4、根据如图所示的伪代码,当输入b a ,分别为2,3时,最后输出的m 的值是________ Read a ,b If a >b Then m ←a Else m ←bEnd If Print m 5、从1,2,3,4这四个数中一次随机取两个数,则其中一个数是另一个的两倍的概率是______ 6、某老师从星期一到星期五收到信件数分别是10,6,8,5,6,则该组数据的方差___2=s 7、已知,2)4tan(=+πx 则xx2tan tan 的值为__________8、在平面直角坐标系xOy 中,过坐标原点的一条直线与函数xx f 2)(=的图象交于P 、Q 两点,则线段PQ 长的最小值是________9、函数ϕϕ,,(),sin()(w A wx A x f +=是常数,)0,0>>w A 的部分图象如图所示,则____)0(=f3ππ12710、已知→→21,e e 是夹角为π3的两个单位向量,,,22121→→→→→→+=-=e e k b e e a 若0=⋅→→b a ,则k的值为11、已知实数0≠a ,函数⎩⎨⎧≥--<+=1,21,2)(x a x x a x x f ,若)1()1(a f a f +=-,则a 的值为________12、在平面直角坐标系xOy 中,已知点P 是函数)0()(>=x e x f x的图象上的动点,该图象在P 处的切线l 交y 轴于点M ,过点P 作l 的垂线交y 轴于点N ,设线段MN 的中点的纵坐标为t ,则t 的最大值是_____________13、设7211a a a ≤≤≤≤ ,其中7531,,,a a a a 成公比为q 的等比数列,642,,a a a 成公差为1的等差数列,则q 的最小值是________ 14、设集合},,)2(2|),{(222R y x m y x my x A ∈≤+-≤=, },,122|),{(R y x m y x m y x B ∈+≤+≤=, 若,φ≠⋂B A 则实数m 的取值范围是______________二、解答题:本大题共6小题,共计90分,请在答题卡指定区域内作答,解答时应写出文字说明、证明过程活盐酸步骤。
2012年江苏省高考数学试卷答案与解析

2012年江苏省高考数学试卷参考答案与试题解析一、填空题:本大题共14小题.每小题5分.共计70分.请把答案填写在答题卡相应位置上.1.(5分)(2012•江苏)已知集合A={1。
2.4}。
B={2.4。
6}。
则A∪B={1.2.4.6}.考点:并集及其运算.专题: 集合.分析:由题意.A.B两个集合的元素已经给出。
故由并集的运算规则直接得到两个集合的并集即可解答:解:∵A={1.2。
4}。
B={2.4.6}。
∴A∪B={1。
2.4。
6}故答案为{1.2.4.6}点评:本题考查并集运算。
属于集合中的简单计算题。
解题的关键是理解并的运算定义2.(5分)(2012•江苏)某学校高一、高二、高三年级的学生人数之比为3:3:4。
现用分层抽样的方法从该校高中三个年级的学生中抽取容量为50的样本.则应从高二年级抽取15 名学生.考点: 分层抽样方法.专题: 概率与统计.分析:根据三个年级的人数比。
做出高二所占的比例。
用要抽取得样本容量乘以高二所占的比例。
得到要抽取的高二的人数.解答:解:∵高一、高二、高三年级的学生人数之比为3:3:4。
∴高二在总体中所占的比例是=。
∵用分层抽样的方法从该校高中三个年级的学生中抽取容量为50的样本.∴要从高二抽取.故答案为:15点评:本题考查分层抽样方法。
本题解题的关键是看出三个年级中各个年级所占的比例。
这就是在抽样过程中被抽到的概率.本题是一个基础题.3.(5分)(2012•江苏)设a。
b∈R。
a+bi=(i为虚数单位)。
则a+b的值为8 .考点:复数代数形式的乘除运算;复数相等的充要条件.专题: 数系的扩充和复数.分析:由题意.可对复数代数式分子与分母都乘以1+2i。
再由进行计算即可得到a+bi=5+3i。
再由复数相等的充分条件即可得到a.b的值.从而得到所求的答案解答:解:由题.a。
b∈R。
a+bi=所以a=5。
b=3。
故a+b=8故答案为8点评:本题考查复数代数形式的乘除运算.解题的关键是分子分母都乘以分母的共轭。
2012年江苏省高考数学试卷含答案

2012江苏高考数学试卷注意事项:考生在答题前请认真阅读本注意事项及各题答题要求1.本试卷共4页,均为非选择题(第1题-第20题,共20题)。
本卷满分为160分。
考试时间为120分钟。
考试结束后,请将本试卷和答题卡一并交回。
2.答题前请务必将自己的姓名、准考证号用0.5毫米黑色墨水签字笔填写在试卷及答题卡的规定位置。
3.请认真核对监考员在答题卡上所粘贴的条形码上的姓名、准考证号与您本人是否相符。
4.作答试题,必须用0.5毫米黑色墨水签字笔在答题卡上的指定位置作答,在其他位置作答一律无效。
5.如需作图,须用2B 铅笔绘,写清楚,线条,符号等须加黑加粗。
参考公式:(1)样本数据x 1 ,x 2 ,…,x n 的方差s 2=n i=11n ∑(x i -x )2,其中n i i=11x n ∑.(2)(2)直棱柱的侧面积S=ch ,其中c 为底面积,h 为高. (3)棱柱的体积V= Sh ,其中S 为底面积,h 为高.一.填空题:本大题共14小题,每小题5分,共计70分,请把答案填写在答题卡的相应位置上。
..........1、已知集合},2,0,1{},4,2,2,1{-=-=B A 则_______,=⋂B A2、函数)12(log )(5+=x x f 的单调增区间是__________3、设复数i 满足i z i 23)1(+-=+(i 是虚数单位),则z 的实部是_________4、根据如图所示的伪代码,当输入b a ,分别为2,3时,最后输出的m 的值是________ Read a ,b If a >b Then m ←a Else m ←b End If Print m5、从1,2,3,4这四个数中一次随机取两个数,则其中一个数是另一个的两倍的概率是______6、某老师从星期一到星期五收到信件数分别是10,6,8,5,6,则该组数据的方差___2=s7、已知,2)4tan(=+πx 则xx2tan tan 的值为__________ 8、在平面直角坐标系xOy 中,过坐标原点的一条直线与函数xx f 2)(=的图象交于P 、Q 两点,则线段PQ 长的最小值是________9、函数ϕϕ,,(),sin()(w A wx A x f +=是常数,)0,0>>w A 的部分图象如图所示,则____)0(=f3π210、已知→→21,e e 是夹角为π32的两个单位向量,,,22121→→→→→→+=-=e e k b e e a 若0=⋅→→b a ,则k 的值为11、已知实数0≠a ,函数⎩⎨⎧≥--<+=1,21,2)(x a x x a x x f ,若)1()1(a f a f +=-,则a 的值为________12、在平面直角坐标系xOy 中,已知点P 是函数)0()(>=x e x f x 的图象上的动点,该图象在P 处的切线l 交y 轴于点M ,过点P 作l 的垂线交y 轴于点N ,设线段MN 的中点的纵坐标为t ,则t 的最大值是_____________13、设7211a a a ≤≤≤≤ ,其中7531,,,a a a a 成公比为q 的等比数列,642,,a a a 成公差为1的等差数列,则q 的最小值是________14、设集合},,)2(2|),{(222R y x m y x my x A ∈≤+-≤=, },,122|),{(R y x m y x m y x B ∈+≤+≤=, 若,φ≠⋂B A 则实数m 的取值范围是______________二、解答题:本大题共6小题,共计90分,请在答题卡指定区域内15、在△ABC 中,角A 、B 、C 所对应的边为a ,(1)若,cos 2)6sin(A A =+π求A 的值;(2)若c b A 3,31cos ==,求C sin 的值.A16、如图,在四棱锥ABCDP 中,平面PAD⊥平面ABCD,AB=AD,∠BAD=60°,E、F分别是AP、AD的中点求证:(1)直线E F‖平面PCD;(2)平面BEF⊥平面PAD17、请你设计一个包装盒,如图所示,ABCD是边长为60cm的正方形硬纸片,切去阴影部分所示的四个全等的等腰直角三角形,再沿虚线折起,使得ABCD四个点重合于图中的点P,正好形成一个正四棱柱形状的包装盒,E、F在AB上是被切去的等腰直角三角形斜边的两个端点,设AE=FB=xcm(1)若广告商要求包装盒侧面积S(cm2)最大,试问x应取何值?(2)若广告商要求包装盒容积V(cm3)最大,试问x应取何值?并求出此时包装盒的高与底面边长的比值。
2012江苏高考数学试卷答案及其解析

2012江苏高考数学试卷答案及其解析一.填空题:1.已知集合{124}A =,,,{246}B =,,,则AB = .【答案】 {}6,4,2,1 【解析】根据集合的并集运算,两个集合的并集就是所有属于集合A 和集合B 的元素组成的集合,从所给的两个集合的元素可知,它们的元素是1 ,2,4,6,所以答案为{}6,4,2,1. 【点评】本题重点考查集合的运算.容易出错的地方是审错题目,把并集运算看成交集运算.属于基本题,难度系数较小.2. 某学校高一、高二、高三年级的学生人数之比为334::,现用分层抽样的方法从该校高中三个年级的学生中抽取容量为50的样本,则应从高二年级抽取 名学生. 【答案】15【解析】根据分层抽样的方法步骤,按照一定比例抽取,样本容量为50,那么根据题意得:从高三一共可以抽取人数为:1510350=⨯人,答案 15 . 【点评】本题主要考查统计部分知识:抽样方法问题,分层抽样的具体实施步骤.分层抽样也叫做“按比例抽样”,也就是说,要根据每一层的个体数的多少抽取,这样才能够保证样本的科学性与普遍性,这样得到的数据才更有价值、才能够较精确地反映总体水平,本题属于容易题,也是高考热点问题,希望引起重视. 3. 设a b ∈R ,,117ii 12ia b -+=-(i 为虚数单位),则a b +的值为 . 【答案】8【解析】据题i ii i i i i i bi a 3551525)21)(21()21)(711(21711+=+=+-+-=--=+,所以 ,3,5==b a 从而 8=+b a .【点评】本题主要考查复数的基本运算和复数相等的条件运用,属于基本题,一定要注意审题,对于复数的除法运算,要切实掌握其运算技巧和常规思路,再者,需要注意分母实数化的实质.4. 右图是一个算法流程图,则输出的k 的值是 . 【答案】5【解析】根据循环结构的流程图,当1=k 时,此时0452=+-k k ;不满足条件,继续执行循环体,当2=k 时,6452-=+-k k ;不满足条件,继续执行循环,当3=k 时,2452-=+-k k 不满足条件,然后依次出现同样的结果,当5=k 时,此时4452=+-k k ,此时满足条件跳出循环,输出k 的值为5.【点评】本题主要考查算法的定义、流程图及其构成,考查循环结构的流程图.注意循环条件的设置,以及循环体的构成,特别是注意最后一次循环的k 的值.这是新课标的新增内容,也是近几年的常考题目,要准确理解循环结构流程图的执行过程.5. 函数()f x =的定义域为 .【答案】(【解析】根据题意得到 0log 216≥-x ,同时,x >0 ,解得21log 6≤x ,解得6≤x ,又x >0,所以函数的定义域为:(.【点评】本题主要考查函数基本性质、对数函数的单调性和图象的运用.本题容易忽略x >0这个条件,因此,要切实对基本初等函数的图象与性质有清晰的认识,在复习中应引起高度重视.本题属于基本题,难度适中.6. 现有10个数,它们能构成一个以1为首项,3-为公比的等比数列,若从这10个数中随机抽取一个数,则它小于8的概率是 . 【答案】53 【解析】组成满足条件的数列为:.19683,6561,2187,729,243,81,27.9,3,1-----从中随机取出一个数共有取法10种,其中小于8的取法共有6种,因此取出的这个数小于8的概率为C1AC53. 【点评】本题主要考查古典概型.在利用古典概型解决问题时,关键弄清基本事件数和基本事件总数,本题要注意审题,“一次随机取两个数”,意味着这两个数不能重复,这一点要特别注意.7.如图,在长方体1111ABCD A B C D -中,3cm AB AD ==,12cm AA =,则四棱锥D D BB A 11-的体积为 cm 3.【答案】36cm【解析】如图所示,连结AC 交BD 于点O ,因为 平面D D BB ABCD 11⊥,又因为BD AC ⊥,所以,D D BB AC 11平面⊥,所以四棱锥D D BB A 11-的高为AO ,根据题意3cm AB AD ==,所以223=AO ,又因为BD =,12cm AA =,故矩形D D BB 11的面积为2,从而四棱锥D D BB A 11-的体积316cm 3V =⨯=. 【点评】本题重点考查空间几何体的体积公式的运用.本题综合性较强,结合空间中点线面的位置关系、平面与平面垂直的性质定理考查.重点找到四棱锥D D BB A 11-的高为AO ,这是解决该类问题的关键.在复习中,要对空间几何体的表面积和体积公式记准、记牢,并且会灵活运用.本题属于中档题,难度适中.8. 在平面直角坐标系xOy 中,若双曲线22214x y m m -=+,则m 的值为 . 【答案】2DABC1C 1D 1A1B【解析】根据题目条件双曲线的焦点位置在x 轴上(否则不成立),因此m >0,由离心率公式得到542=++mm m ,解得 2=m . 【点评】本题考查双曲线的概念、标准方程和简单的几何性质.这是大纲中明确要求的,在对本部分复习时要注意:侧重于基本关系和基本理论性质的考查,从近几年的高考命题趋势看,几乎年年都有所涉及,要引起足够的重视.本题属于中档题,难度适中.9. 如图,在矩形ABCD中,2AB BC ==,点E 为BC 的中点,点F 在边CD 上,若2AB AF =,则AE BF 的值是 .【答案】2【解析】根据题意,→→→+=DF BC AF 所以()cos 0AB AF AB BC DF AB BC AB DF AB DF AB DF →→→→→→→→→→→→→→•=•+=•+•=•=⋅︒==从而得到1=→DF ,又因为→→→→→→+=+=CF BC BF DF AD AE ,,所以2180cos 00)()(2=⋅+++=+•+=•︒→→→→→→→→→CF DF BC CF BC DF AD BF AE .【点评】本题主要考查平面向量的基本运算,同时,结合平面向量的数量积运算解决.设法找到1=→DF ,这是本题的解题关键,本题属于中等偏难题目.10. 设()f x 是定义在R 上且周期为2的函数,在区间[11]-,上,0111()201x x ax f x bx x <+-⎧⎪=+⎨⎪+⎩≤≤≤,,,,其中a b ∈R ,.若1322f f ⎛⎫⎛⎫= ⎪ ⎪⎝⎭⎝⎭,则3a b +的值为 .【答案】10- .【解析】因为1322f f ⎛⎫⎛⎫= ⎪ ⎪⎝⎭⎝⎭,函数()f x 的周期为2,所以)21()223()21(-=-=f f f ,根据0111()201x x ax f x bx x <+-⎧⎪=+⎨⎪+⎩≤≤≤,,,,得到223-=+b a , 又)1()1(-=f f ,得到02,221=++=+-b a b a 即,结合上面的式子解得4,2-==b a ,所以103-=+b a .【点评】本题重点考查函数的性质、分段函数的理解和函数周期性的应用.利用函数的周期性将式子化简为)21()223()21(-=-=f f f 然后借助于分段函数的解析式解决.属于中档题,难度适中.11. 设α为锐角,若4cos 65απ⎛⎫+= ⎪⎝⎭,则)122sin(πα+的值为 .【答案】50217 【解析】根据4cos 65απ⎛⎫+= ⎪⎝⎭,2571251621)6(cos 2)32cos(2=-⨯=-+=+παπα, 因为0)32cos( πα+,所以25242571)32sin(2=⎪⎭⎫⎝⎛-=+πα,因为502174sin)32cos(4cos)32sin(]4)32sin[()122sin(=+-+=-+=+ππαππαππαπα. 【点评】本题重点考查两角和与差的三角公式、角的灵活拆分、二倍角公式的运用.在求解三角函数值时,要注意角的取值情况,切勿出现增根情况.本题属于中档题,运算量较大,难度稍高.12. 在平面直角坐标系xOy 中,圆C 的方程为228150x y x +-+=,若直线2y kx =-上至少存在一点,使得以该点为圆心,1为半径的圆与圆C 有公共点,则k 的最大值是 . 【答案】34 【解析】根据题意228150x y x +-+=将此化成标准形式为:()1422=+-y x ,得到,该圆的圆心为M ()0,4半径为1 ,若直线2y kx =-上至少存在一点,使得以该点为圆心,1为半径的圆与圆C 有公共点,只需要圆心M ()0,4到直线2y kx =-的距离11+≤d ,即可,所以有21242≤+-=k k d ,化简得0)43(≤-k k 解得340≤≤k ,所以k 的最大值是34 .【点评】本题主要考查直线与圆的位置关系、点到直线的距离公式、圆的一般式方程和标准方程的互化,考查知识较综合,考查转化思想在求解参数范围中的运用.本题的解题关键就是对若直线2y kx =-上至少存在一点,使得以该点为圆心,1为半径的圆与圆C 有公共点,这句话的理解,只需要圆心M ()0,4到直线2y kx =-的距离11+≤d 即可,从而将问题得以转化.本题属于中档题,难度适中.13. 已知函数2()()f x x ax b a b =++∈R ,的值域为[0)+∞,,若关于x 的不等式()f x c <的解集为(6)m m +,,则实数c 的值为 . 【答案】9【解析】根据函数0)(2≥++=b ax x x f ,得到042=-b a ,又因为关于x 的不等式()f x c <,可化为:20x ax b c ++-<,它的解集为()6,+m m ,设函数c b ax x x f -++=2)(图象与x 轴的交点的横坐标分别为21,x x ,则6612=-+=-m m x x ,从而,36)(212=-x x ,即364)(21221=-+x x x x ,又因为a x x cb x x -=+-=2121,,代入得到 9=c .【点评】本题重点考查二次函数、一元二次不等式和一元二次方程的关系,根与系数的关系.二次函数的图象与二次不等式的解集的对应关系要理清.属于中档题,难度不大. 14. 已知正数a b c ,,满足:4ln 53ln b c a a c c c a c b -+-≤≤≥,,则ba的取值范围是 . 【答案】[]7,e【解析】根据条件4ln 53ln b c a a c c c a c b -+-≤≤≥,,()cbc c b c a lnln ln =-≤,得到 ln ,1ac b a b e c c c ≥≥>,得到c b <.又因为b a c ≤-35,所以35a b c +<,由已知a c b -≤4,得到4a b c +>.从而b b a ≤+4,解得31≥a b .【点评】本题主要考查不等式的基本性质、对数的基本运算.关键是注意不等式的等价变形,做到每一步都要等价.本题属于中高档题,难度较大. 二、解答题15. (本小题满分14分)在ABC ∆中,已知3AB AC BA BC =. (1)求证:tan 3tan B A =;(2)若cos C =求A 的值. 【答案及解析】【点评】本题主要考查向量的数量积的定义与数量积运算、两角和与差的三角公式、三角恒等变形以及向量共线成立的条件.本题综合性较强,转化思想在解题中灵活运用,注意两角和与差的三角公式的运用,考查分析问题和解决问题的能力,从今年的高考命题趋势看,几乎年年都命制该类型的试题,因此平时练习时加强该题型的训练.本题属于中档题,难度适中.16. (本小题满分14分)如图,在直三棱柱111ABC A B C -中,1111A B AC =,D E ,分别是棱1BC CC ,上的点(点D 不同于点C ),且AD DE F ⊥,为11B C 的中点. 求证:(1)平面ADE ⊥平面11BCC B ; (2)直线1//A F 平面ADE . 【答案及解析】【点评】本题主要考查空间中点、线、面的位置关系,考查线面垂直、面面垂直的性质与判定,线面平行的判定.解题过程中注意中点这一条件的应用,做题规律就是“无中点、取中点,相连得到中位线”.本题属于中档题,难度不大,考查基础为主,注意问题的等价转化. 17. (本小题满分14分) 【答案及解析】【点评】本题主要考查二次函数的图象与性质以及求解函数最值问题.在利用导数求解函数的最值问题时,要注意增根的取舍,通过平面几何图形考查函数问题时,首先审清题目,然后建立数学模型,接着求解数学模型,最后,还原为实际问题.本题属于中档题,难度适中. 18.(【答案及解析】【点评】本题综合考查导数的定义、计算及其在求解函数极值和最值中的运用.考查较全面系统,要注意变形的等价性和函数零点的认识、极值和极值点的理解.本题主要考查数形结合思想和分类讨论思想,属于中高档试题,难度中等偏上,考查知识比较综合,全方位考查分析问题和解决问题的能力,运算量比较大. 19. (本小题满分16分)(i )若12AF BF -=1AF 的斜率; (ii )求证:12PF PF +是定值. 【答案及解析】【点评】本题主要考查椭圆的定义、几何性质以及直线与椭圆的关系.本题注意解题中,待。
2012年江苏省高考数学真题(解析版)

2012 年普通高等学校招生全国统一考试(江苏卷)
数学Ⅰ
注 意 事 项
考生在答题前请认真阅读本注意事项及各题答题要求: 1.本试卷共 4 页,均为非选择题(第 1 题~第 20 题,共 20 题) 。本卷满分为 160 分。考试 时间为 120 分钟。考试结束后,请将本试卷和答题卡一并交回。 2.答题前,请您务必将自己的姓名、考试证号用 0.5 毫米黑色墨水的签字笔填写在试卷及 答题卡的规定位置。 3.请认真核对监考员在答题卡上所粘贴的条形码上的姓名、准考证号与您本人是否相符。 4.作答试题必须用 0.5 毫米黑色墨水的签字笔在答题卡的指定位置作答,在其它位置 作答一律无效。 5.如需作图,须用 2B 铅笔绘、写清楚,线条、符号等须加黑、加粗。
2 1 2
1≤ x 0 , ax 1, 其中 a , 若 f ( x) bx 2 bR . , 0 ≤ x ≤ 1, x 1
【答案】 10 。 【考点】周期函数的性质。
1 f 2
3 则 a 3b 的值为 f , 2
【答案】2。 【考点】双曲线的性质。 【解析】由
.
x2 y2 2 1 得 a = m,b = m 2 4,c = m m 2 4 。 m m 4
c m m2 4 ∴ e= = = 5 ,即 m 2 4m 4=0 ,解得 m =2 பைடு நூலகம் a m
9.如图,在矩形 ABCD 中, AB 2 , BC 2 ,点 E 为 BC 的中点,
【答案】 0, 6 。 【解析】根据二次根式和对数函数有意义的条件,得
x > 0 x > 0 x > 0 0< x 6 。 1 1 2= 6 1 2log 6 x 0 log 6 x x 6 2
2012江苏高考数学试卷 完整试卷附加标准答案 纯Word版.doc

14.已知正数 满足: 则 的取值范围是▲.
二、解答题:本大题共6小题,共计90分.请在答题卡指定区域内作答,解答时应写出文字说明、证明过程或演算步骤.
15.(本小题满分14分)
在 中,已知 .
(1)求证: ;
(2)若 求A的值.
绝密★启用前
2012年普通高等学校招生全国统一考试(江苏卷)
数学Ⅰ
参考公式:
棱锥的体积 ,其中 为底面积, 为高.
一、填空题:本大题共14小题,每小题5分,共计70分.请把答案填写在答题卡相应位置上.
1.已知集合 , ,则 ▲.
2.某学校高一、高二、高三年级的学生人数之比为 ,现用分层抽样的方法从该校高中三个年级的学生中抽取容量为50的样本,则应从高二年级抽取▲名学生.
3.设 , (i为虚数单位),则 的值
为▲.
4.右图是一个算法流程图,则输出的k的值是▲.
5.函数 的定义域为▲.
6.现有10个数,它们能构成一个以1为首项, 为公比的
等比数列,若从这10个数中随机抽取一个数,则它小于8
的概率是▲.
7.如图,在长方体 中, , ,
则四棱锥 的体积为▲cm3.
8.在平面直角坐标系 中,若双曲线 的离心率
(1)求炮的最大射程;
(2)设在第一象限有一飞行物(忽略其大小),其飞行高度为3.2千米,试问它的横坐标a不超过多少时,炮弹可以击中它?请说明理由.
18.(本小题满分16分)
若函数 在x=x0取得极大值或者极小值则x=x0是 的极值点
16.(本小题满分14分)
如图,在直三棱柱 中, , 分别是棱 上的点(点D不同于点C),且 为 的中点.
2012年江苏高考数学试卷(高清版含详细答案)

2012年江苏高考数学试卷(高清版含详细答案)参考公式:(1)样本数据x 1 ,x 2 ,…,x n 的方差s 2=n i=11n ∑(x i -x )2,其中n i i=11x n ∑.(2)(2)直棱柱的侧面积S=ch ,其中c 为底面积,h 为高.(3)棱柱的体积V= Sh ,其中S 为底面积,h 为高.一.填空题:本大题共14小题,每小题5分,共计70分,请把答案填写在答题卡的相应位置上。
.......... 1、已知集合},2,0,1{},4,2,2,1{-=-=B A 则_______,=⋂B A 2、函数)12(log )(5+=x x f 的单调增区间是__________3、设复数i 满足i z i 23)1(+-=+(i 是虚数单位),则z 的实部是_________4、根据如图所示的伪代码,当输入b a ,分别为2,3时,最后输出的m 的值是________ Read a ,b If a >b Then m ←a Else m ←b End If Print m5、从1,2,3,4这四个数中一次随机取两个数,则其中一个数是另一个的两倍的概率是______6、某老师从星期一到星期五收到信件数分别是10,6,8,5,6,则该组数据的方差___2=s7、已知,2)4tan(=+πx 则xx2tan tan 的值为__________8、在平面直角坐标系xOy 中,过坐标原点的一条直线与函数xx f 2)(=的图象交于P 、Q 两点,则线段PQ 长的最小值是________9、函数ϕϕ,,(),sin()(w A wx A x f +=是常数,)0,0>>w A 的部分图象如图所示,则____)0(=f3ππ12710、已知→→21,e e 是夹角为π32的两个单位向量,,,22121→→→→→→+=-=e e k b e e a 若0=⋅→→b a ,则k 的值为11、已知实数0≠a ,函数⎩⎨⎧≥--<+=1,21,2)(x a x x a x x f ,若)1()1(a f a f +=-,则a 的值为________12、在平面直角坐标系xOy 中,已知点P 是函数)0()(>=x e x f x 的图象上的动点,该图象在P 处的切线l 交y 轴于点M ,过点P 作l 的垂线交y 轴于点N ,设线段MN 的中点的纵坐标为t ,则t 的最大值是_____________ 13、设7211a a a ≤≤≤≤ ,其中7531,,,a a a a 成公比为q 的等比数列,642,,a a a 成公差为1的等差数列,则q 的最小值是________ 14、设集合},,)2(2|),{(222R y x m y x my x A ∈≤+-≤=, },,122|),{(R y x m y x m y x B ∈+≤+≤=, 若,φ≠⋂B A 则实数m 的取值范围是______________二、解答题:本大题共6小题,共计90分,请在答题卡指定区域内作答,解答时应写出文字说明、证明过程活盐酸步骤。
2012江苏高考数学试题及答案
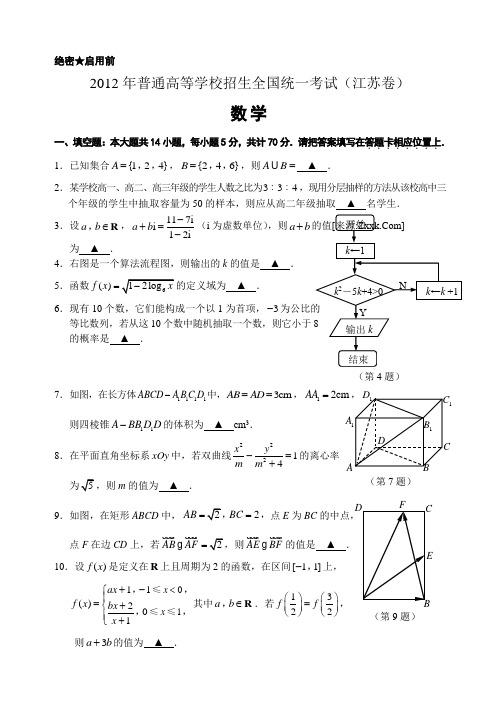
绝密★启用前2012年普通高等学校招生全国统一考试(江苏卷)数学一、填空题:本大题共14小题,每小题5分,共计70分.请把答案填写在答题卡相应位置上......... 1.已知集合{124}A =,,,{246}B =,,,则A B = ▲ .2.某学校高一、高二、高三年级的学生人数之比为334::,现用分层抽样的方法从该校高中三个年级的学生中抽取容量为50的样本,则应从高二年级抽取 ▲ 名学生. 3.设a b ∈R ,,117i i 12ia b -+=-(i 为虚数单位),则a b +为 ▲ .4.右图是一个算法流程图,则输出的k 的值是 ▲ . 5.函数()f x 的定义域为 ▲ .6.现有10个数,它们能构成一个以1为首项,3-等比数列,若从这10个数中随机抽取一个数,则它小于的概率是 ▲ .7.如图,在长方体1111ABCD A B C D -中,3cm AB AD ==,12cm AA =, 则四棱锥11A BB D D -的体积为 ▲ cm 3.8.在平面直角坐标系xOy 中,若双曲线22214x y m m -=+的离心率 m 的值为 ▲ .9.如图,在矩形ABCD 中,2AB BC =,点E 为BC 的中点,点F 在边CD 上,若AB AF AE BF的值是 ▲ .10.设()f x 是定义在R 上且周期为2的函数,在区间[11]-,上,0111()201x x ax f x bx x <+-⎧⎪=+⎨⎪+⎩≤≤≤,,,,其中a b ∈R ,.若1322f f ⎛⎫⎛⎫= ⎪ ⎪⎝⎭⎝⎭, 则3a b +的值为 ▲ .(第4题)DABC1 1D 1A1B(第7题)(第9题)11.设α为锐角,若4cos 65απ⎛⎫+= ⎪⎝⎭,则sin 212απ⎛⎫+ ⎪⎝⎭的值为 ▲ .12.在平面直角坐标系xOy 中,圆C 的方程为228150x y x +-+=,若直线2y kx =-上至少存在一点,使得以该点为圆心,1为半径的圆与圆C 有公共点,则k 的最大值是 ▲ .[来源:学科网ZXXK]13.已知函数2()()f x x ax b a b =++∈R ,的值域为[0)+∞,,若关于x 的不等式()f x c <的解集为(6)m m +,,则实数c 的值为 ▲ .14.已知正数a b c ,,满足:4ln 53ln b c a a c c c a c b -+-≤≤≥,,则ba的取值范围是 ▲ .二、解答题:本大题共6小题,共计90分.请在答题卡指定区域.......内作答,解答时应写出文字说明、证明过程或演算步骤. 15.(本小题满分14分)在ABC ∆中,已知3AB AC BA BC =.(1)求证:tan 3tan B A =;(2)若cos C =求A 的值. 16.(本小题满分14分)如图,在直三棱柱111ABC A B C -中,1111A B AC =,D E ,分别是棱1BC CC ,上的点(点D 不同于点C ),且AD DE F ⊥,为11B C 的中点. 求证:(1)平面ADE ⊥平面11BCC B ; (2)直线1//A F 平面ADE .17.(本小题满分14分)如图,建立平面直角坐标系xOy ,x 轴在地平面上,y 轴垂直于地平面,单位长度为1千米.某炮位于坐标原点.已知炮弹发射后的轨迹在方程221(1)(0)20y kx k x k =-+>表示的1A1C(第16题)FDCABE1B曲线上,其中k 与发射方向有关.炮的射程是指炮弹落地点的横坐标. (1)求炮的最大射程;(2)设在第一象限有一飞行物(忽略其大小),其飞行高度为3.2千米,试问它的横坐标a不超过多少时,炮弹可以击中它?请说明理由.18.(本小题满分16分)已知a ,b 是实数,1和1-是函数32()f x x ax bx =++的两个极值点. (1)求a 和b 的值;(2)设函数()g x 的导函数()()2g x f x '=+,求()g x 的极值点;(3)设()(())h x f f x c =-,其中[22]c ∈-,,求函数()y h x =的零点个数.19.(本小题满分16分)如图,在平面直角坐标系xOy 中,椭圆22221(0)x y a b a b +=>>的左、右焦点分别为1(0)F c -,,2(0)F c ,.已知(1)e ,和e ⎛ ⎝⎭都在椭圆上,其中e 为椭圆的离心率. (1)求椭圆的离心率;(2)设A ,B 是椭圆上位于x 轴上方的两点,且直线与直线2BF 平行,2AF 与1BF 交于点P .(i )若12AF BF -=,求直线1AF 的斜率; (ii )求证:12PF PF +是定值.(第19题)20.(本小题满分16分)已知各项均为正数的两个数列{}n a 和{}n b满足:1n a n *+=∈N .(1)设11n n nb b n a *+=+∈N ,,求证:数列2nn b a ⎧⎫⎛⎫⎪⎪⎨⎬ ⎪⎝⎭⎪⎪⎩⎭是等差数列;(2)设1nn nb b n a *+=∈N ,,且{}n a 是等比数列,求1a 和1b 的值.21.[选做题]本题包括A 、B 、C 、D 四小题,请选定其中两题,并在相应的答题区域内作...................答...若多做,则按作答的前两题评分. 解答时应写出文字说明、证明过程或演算步骤.A .[选修4 - 1:几何证明选讲](本小题满分10分)如图,AB 是圆O 的直径,D ,E 为圆上位于AB 异侧的两点,连结BD 并延长至点C ,使BD = DC ,连结AC ,AE ,DE . 求证:E C ∠=∠.B .[选修4 - 2:矩阵与变换](本小题满分10分)已知矩阵A 的逆矩阵113441122-⎡⎤-⎢⎥=⎢⎥⎢⎥-⎢⎥⎣⎦A ,求矩阵A 的特征值.(第21-A 题)C .[选修4 - 4:坐标系与参数方程](本小题满分10分)在极坐标中,已知圆C 经过点()4P π,,圆心为直线()sin 3ρθπ-=与极轴的交点,求圆C 的极坐标方程.D .[选修4 - 5:不等式选讲](本小题满分10分) 已知实数x ,y 满足:11|||2|36x y x y +<-<,,求证:5||18y <.【必做题】第22题、第23题,每题10分,共计20分.请在答题卡指定区域内........作答,解答时应写出文字说明、证明过程或演算步骤.[来源:Z&xx&]22.(本小题满分10分)设ξ为随机变量,从棱长为1的正方体的12条棱中任取两条,当两条棱相交时,0ξ=;当两条棱平行时,ξ的值为两条棱之间的距离;当两条棱异面时,1ξ=. (1)求概率(0)P ξ=;(2)求ξ的分布列,并求其数学期望()E ξ.23.(本小题满分10分)设集合{12}n P n =,,,…,n *∈N .记()f n 为同时满足下列条件的集合A 的个数: ①n A P ⊆;②若x A ∈,则2x A ∉;③若n P x A ∈ð,则2n P x A ∉ð. (1)求(4)f ;(2)求()f n 的解析式(用n 表示).2012年普通高等学校招生全国统一考试(江苏卷)(重点详解)1.{1246},,, 2.15 3.8 4.5 5.(0 6.357.详解:连接AC 交BD 于点O ,则四棱锥11A BB D D -的体积为11163BB D D S AO ⋅=.[来源:学*科*网Z*X*X*K]8.详解:222222221c a b b e aa -===- ,24510m m m +∴=->,.2m =. 9.详解:由AB AF 得()AB AD DF += AB DF ∴AE BF ()()AB BE BC CF AB CF BE BC =++=+()22AB CD DF AB CD AB DF =++=++= 法二:建立直角坐标系,利用坐标运算求解10.详解:由题11()()22f f =-,(1)(1)f f -=,解得3122b a b a ⎧=--⎪⎨⎪=-⎩,,24a b =⎧⎨=-⎩,, 则310a b +=-.11.详解:由α为锐角及4cos 65απ⎛⎫+= ⎪⎝⎭知360ππα<+<,252454532)6cos()6sin(2)32sin(=⨯⨯=++=+παπαπα ,2571)6(cos 2)32cos(2=-+=+παπα[来源:学§科§网Z §X §X §K]]4)32sin[()122sin(ππαπα-+=+∴50217)]32cos()32[sin(22=+-+=παπα. 12.详解:由题圆C:22(4)1x y -+=,(40)C ,,1r =,设(2)M t k t -,为另一圆的圆心,所以[02]CM =,,则22(1)(84)160k t k t +-++≤关于t ∈R 有解,故222(84)64(1)0k t k ∆=+-+≥,则403k ≤≤, ∴k 的最大值是43.13.详解:由题240a b ∆=-=(1),20x ax b c ++-=的根为 6m m +,,6m m a ++=- (2) ,(6)m m b c +=-(3),由(1) (3)得2222(6)(3)944a a c m m m =-+=-++,由(2) 32a m -+=,故9c =.14.详解:由题a b c ,,>0,534ln ln c a b c a c b a c c --+≤≤≥,,5341c b ca a a∴--≤≤, ln b c a c ≥,令b cx y a a ==,,则5341y x y --≤≤且ln 100x y x y y >>≥,,, ln 1x y y ≥化为1e yx y ≥,令1t y =,则e t x t ≥,令e t u t =,则2e (1)t t u t -'=,10t u '>>,,010t u '<<<,,所以1()t u t >,增,01()t u t <<,减,则min e u =,结合图形[e 7]bx a=∈,.17.18.19.20.23.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2012高考数学江苏卷
注意事项:
考生在答题前请认真阅读本注意事项及各题答题要求
本试卷共4页,均为非选择题(第1题-第20题,共20题)。
本卷满分为160分。
考试时间为120分钟。
考试结束后,请将本试卷和答题卡一并交回。
答题前请务必将自己的姓名、准考证号用0.5毫米黑色墨水签字笔填写在试卷及答题卡的规定位置。
请认真核对监考员在答题卡上所粘贴的条形码上的姓名、准考证号与您本人是否相符。
作答试题,必须用0.5毫米黑色墨水签字笔在答题卡上的指定位置作答,在其他位置作答一律无效。
如需作图,须用2B铅笔绘,写清楚,线条,符号等须加黑加粗。
参考公式:
样本数据x1 ,x2 ,…,xn的方差s2=
n
i=1
1
n
∑
(xi -x)2,其中
n
i
i=1
1
x
n
∑
.
(2)直棱柱的侧面积S=ch ,其中c为底面积,h 为高.
(3)棱柱的体积V= Sh ,其中S为底面积,h 为高.
一.填空题:本大题共14小题,每小题5分,共计70分,请把答案填写在答题卡的相应位置上。
1、已知集合
},
2,0,1
{
},
4,2,2,1
{-
=
-
=B
A则_______,
=
⋂B
A
2、函数
)1
2(
log
)
(
5
+
=x
x
f
的单调增区间是__________
3、设复数i满足
i
z
i2
3
)1
(+
-
=
+(i是虚数单位),则z的实部是_________
4、根据如图所示的伪代码,当输入
b
a,分别为2,3时,最后输出的m的值是________
Read a,b
If a>b Then
m←a
Else
m←b
End If
Print m
5、从1,2,3,4这四个数中一次随机取两个数,则其中一个数是另一个的两倍的概率是______
6、某老师从星期一到星期五收到信件数分别是10,6,8,5,6,则该组数据的方差
___ 2=
s
7、已知
,2
)
4
tan(=
+
π
x
则x
x
2
tan
tan
的值为__________
8、在平面直角坐标系xOy 中,过坐标原点的一条直线与函数
x x f 2)(=的图象交于P 、Q 两
点,则线段PQ 长的最小值是________ 9、函数ϕϕ,,(),sin()(w A wx A x f +=是常数,)0,0>>w A 的部分图象如图所示,则____)0(=f
3ππ127
10、已知→→21,e e 是夹角为π
32的两个单位向量,,,22121→→→→→→+=-=e e k b e e a 若0=⋅→→b a ,则k 的值为
11、已知实数0≠a ,函数
⎩⎨⎧≥--<+=1,21,2)(x a x x a x x f ,若)1()1(a f a f +=-,则a 的值为________
12、在平面直角坐标系xOy 中,已知点P 是函数
)0()(>=x e x f x 的图象上的动点,该图象在P 处的切线l 交y 轴于点M ,过点P 作l 的垂线交y 轴于点N ,设线段MN 的中点的纵坐标为t ,则t 的最大值是_____________
13、设7211a a a ≤≤≤≤Λ,其中7531,,,a a a a 成公比为q 的等比数列,642,,a a a 成公差为1的等差数列,则q 的最小值是________
14、设集合},,)2(2|
),{(222R y x m y x m y x A ∈≤+-≤=,
},,122|),{(R y x m y x m y x B ∈+≤+≤=, 若,φ≠⋂B A 则实数m 的取值范围是______________
二、解答题:本大题共6小题,共计90分,请在答题卡指定区域内作答,解答时应写出文字说明、证明过程活盐酸步骤.
15、在△ABC 中,角A 、B 、C 所对应的边为c b a ,, (1)若
,cos 2)6sin(A A =+
π 求A 的值;
2-。
