26.1.3二次函数的图像(第3课时)课件
二次函数的图象与性质(第3课时)精选教学PPT课件

湖南教育出版社
把二次函数
y 1 x2 2
的图象E向左平移1个单位,得到图形F,如图.
-3 - -1O'
5
FE
4
3
2 1
1234
由于平移不改变图形的形状和大小,因此在向左平移1个单位后;
原象
象
抛物线E:
y 1 x2 2
图形F也是抛物线
E的顶点O(0,0) 点O'(-1,0)是F的顶点
感谢父母给了我生命和无私的爱; 感谢老师给了我知识和看世界的眼睛;
感谢朋友给了我友谊和支持; 感谢完美给了我信任和展示自己能力的机会;
感谢邻家的小女孩给我以纯真无邪的笑脸; 感谢周围所有的人给了我与他人交流勾通时的快乐; 感谢生活所给予我的一切,虽然并不全都是美满和幸福;
感谢天空,给我提供了一个施展的舞台 感谢大地,给我无穷的支持与力量; 感谢太阳,给我提供光和热;
感谢伤痛,让我学会了坚忍,也练就了我释怀生命之起落的本能; 感谢生活,让我在漫长岁月的季节里拈起生命的美丽;
感谢有你,尽管远隔千里,可你寒冬里也给我温暖的心怀; 感谢关怀,生命因你而多了充实与清新;
感谢所有的一切~ ~ ~ ~ ~ ~ 感谢我身边每一位好友,为你祝福,为的敲起祈祷钟!伴你走过每一天。他是一个劫匪,坐过牢,之后又杀了人,穷途末路之际他又去抢银行。 是一个很小的储蓄所。抢劫遇到了从来没有过的不顺利,两个女子拼命反抗,他把其中一个杀了,另一个被劫持上了车。因为有人报了警,警车越来越近了,他劫持着这个女子狂逃,把车都开飞了,撞了很多人,轧了很多小摊。 这个刚刚21岁的女孩子才参加工作,为了这份工作,她拼命读书,毕业后又托了很多人,没钱送礼,是她哥卖了血供她上学为她送礼,她父母双亡,只有这一个哥哥。
26.1.3二次函数 的图象(三)

26.1.3二次函数()k h x a y +-=2的图象(三)九年级下册 编号05【学习目标】1.会画二次函数的顶点式()k h x a y +-=2的图象;2.掌握二次函数()k h x a y +-=2的性质;【学习过程】 一、知识链接: 1.将二次函数2-5y x =的图象向上平移2个单位,所得图象的解析式为 。
2.将抛物线2y x =-的图象向左平移3个单位后的抛物线的解析式为 。
二、自主学习 在右图中做出()212y x =--的图象:观察:1. 抛物线()212y x =--开口向 ;顶点坐标是 ;对称轴是直线 。
2. 抛物线()212y x =--和2y x =的形状 ,位置 。
(填“相同”或“不同”) 3. 抛物线()212y x =--是由2y x=如何平移得到的?答:。
三、合作交流平移前后的两条抛物线a 值变化吗?为什么?答: 。
四、知识梳理结合上图和课本第9页例3归纳: (一)抛物线2()+y a x h k =-的特点:1.当0a>时,开口向 ;当0a <时,开口 ;2. 顶点坐标是 ;3. 对称轴是直线 。
(二)抛物线2()+y a x h k =-与2y ax =形状 ,位置不同,2()+y a x h k =-是由2y ax =平移得到的。
二次函数图象的平移规律:左 右 ,上 下 。
(三)平移前后的两条抛物线a 值 。
五、跟踪训练 1.二次函数2)1(212+-=x y 的图象可由221x y =的图象( ) A.向左平移1个单位,再向下平移2个单位得到xyy = x 2-1-2-3-412345-1-2-312345678910OB.向左平移1个单位,再向上平移2个单位得到C.向右平移1个单位,再向下平移2个单位得到D.向右平移1个单位,再向上平移2个单位得到 2.抛物线()21653y x =--+开口 ,顶点坐标是 ,对称轴是 ,当x = 时,y 有最 值为 。
二次函数的图像课件

二次函数可以描述物体在自由落体中的运动和抛体的轨迹。
经济学
二次函数用来建模成本、收益和市场需求曲线等经济现象。
工程学
二次函数可以应用于建筑设计、电子电路和机械运动等领域。
1
顶点坐标
顶点坐标(h, k)是二次函数图像的最低或最高点。
2
开口方向
二次函数的a值决定了图像是开口向上还是向下。
3
对称轴
对称轴是通过顶点的一条垂直线,它将图像分成两个对称部分。
二次函数的图像特点
平滑曲线
二次函数图像是一条光滑的 曲线,没有突变或间断。
变化率
图像的斜率反映了函数在不 同点上的变化速度。
极值点
通过移动顶点,我们可以使 二次函数图像的最低点或最 高点达到所需的位置。
二次函数的平移变换
1
垂直平移
2
通过添加或减去一个常数,我们可以上
下移动二次函数图像。
3
水平平移
通过添加或减去一个常数,我们可以左 右移动二次函数图像。
变化顶点
平移可以使图像的顶点移动到新的位置, 改变函数的最低或最高点。
二次函数的图像课件
欢迎来到本课件!在这里,我们将深入探讨二次函数的有趣且迷人的图像特 性,帮助您了解这个重要的数学概念。
二次函数的定义
二次函数是一个形如f(x) = ax^2 + bx + c的函数,其中a、b、c是常数,且a不 等于0。
二次函数的标准形式
二次函数的标准形式是f(x) = a(x-h)^2 + k,其中(h, k)是顶点坐标。
二次函数的缩放变换
水平缩放
通过改变a的值,我们可以拉伸或压缩二次函数图像 的水平方向。
二次函数图像和性质(第3课时)ppt课件

图象
1
画出二次函数 对称轴和顶点.
y1x12,y的图 象1 ,并x考 虑1 它2 们的开口方向、
2
2
x
··· -3 -2 -1
0
1
2
3
···
y 1x12 ··· -2
1
0
1
-2 -4.5 -8
···
2
2
2
y 1x12 ··· -8 -4.5 -2
1
2
2
(1)当a>0时, 开口向上,当a<0时,开口向下;
(2)对称轴是y轴;
(3)顶点是(0,k).
抛物线y=a(x-h)2有如下特点: (1)当a>0时, 开口向上,当a<0时,开口向上;
(2)对称轴是x=h;
(3)顶点是(h,0).
19
–2
–3
–4
y 1 x2 2
12345
x
12
二次函数y=a(x±h)2的图象和性质.
h>0
y=ax2
当向右平移h时 当向左平移h时
y=a(x-h)2 y=a(x+h)2
y=a(x+h)2的图象
a>0时,开口_____, 最 ____ 点向是上顶点;
低
a<0时,开口_____, 最 ____ 点是顶点;
的
开口向_________,对称轴是________________,顶点是_________________.
y 1x12
下
2
x=1
(1,0)
7
指出下列函数图象的开口方向,对称轴和顶点坐标. 开口 对称轴 顶点坐标
1y2x32
26.1 二次函数及其图像 课件3(数学人教版九年级下册)

例3:若x∈ x 1 x 1,求函数
y =x2+ax+3的
-1
O
y的最小值为f(-1) =4-a
1 x
图像分析
题型3:轴变区间定问题
例3:若x∈ x 1 x 1,求函数 y =x2+ax+3的最小值:
y
a (2)当 1 0 2 即0≤ a<2时
-1 O
2
x
题型2:恒成立问题
例2(变):已知x2+2x+a≥4在x∈ [0,2]上恒 成立,求a的值。
体会最值与恒成立的关系
y
解:令f(x)=x2+2x+a它的 对称轴为x=-1, ∴f(x)在[0,2]上单调 递增, ∴f(x)的最小值为f(0)=a, 即 a≥ 4
-1 O
2
x
题型3:轴变区间定问题
5.当 x (1,2) 时,不等式 x mx 4 0 。 恒成立,则 m 的取值范围是
2
-1
O 1
x
a y的最小值为f( ) 2 2 a 3 4
题型3:轴变区间定问题
例3:若x∈ x 1 x 1,求函数
y =x2+ax+3的最值:
a 1 即a<-2时 (3) 当 评注:例3属于“轴动区间定”的问题,看作 y 2
对称轴沿x轴移动的过程中,函数最值的变化, 函数在 [-1,1] 上是减函数 即对称轴在定区间的左、右两侧及对称轴在定 y 的最小值为 f(1) 区间上变化情况 , 要注意开口方向及端点情况。 O -1 1 x =4+a y的最大值为f(-1)
2.2二次函数性质与应用(1)
---区间上的最值
26.1.3.二次函数y=a(x-h)2+k的图象(第3课时)

(B)2个
【解析】选A.∵2>0,∴图象的开口向上,故①错误;
图象的对称轴为直线x=3,故②错误;
图象顶点坐标为(3,1),故③错误;
当x<3时,y随x的增大而减小,故④正确. 综上所述,说法正确的只有④,共1个.
3.抛物线y=-
1 (x+3)2-1有最________点,其坐标是________. 2
答案:y=-8x2+16x-3
5.已知二次函数的图象的对称轴为x=2,函数的最小值为3,且图 象经过点(-1,5),求此二次函数图象的函数关系式. 【解析】∵二次函数图象的对称轴为x=2,y最小值=3, ∴顶点坐标(2,3), 则设所求函数关系式为y=a(x-2)2+3. 把(-1,5)代入上式,得5=a(-1-2)2+3,
【跟踪训练】
1.(2012·郴州中考)抛物线y=(x-1)2+2的顶点坐标是( (A)(-1,2) (C)(1,-2) (B)(-1,-2) (D)(1,2) )
【解析】选D.∵顶点式y=a(x-h)2+k,顶点坐标是(h,k),∴抛 物线y=(x-1)2+2的顶点坐标是(1,2).
2.(2012·扬州中考)将抛物线y=x2+1先向左平移2个单位,再
例4、要修建一个圆形喷水池,在池中心竖直安装 一根水管,在水管的顶端安一个喷水头,使喷出的 抛物线形水柱在与池中心的水平距离为1m处达到最 高,高度为3m,水柱落地处离池中心3m,水管应多 长?
1.(2012·兰州中考)已知二次函数y=a(x+1)2-b(a≠0)有最小 值1,则a,b的大小关系为( )
)
(A)y=-(x-
【解析】选C.抛物线的顶点坐标为( 1 ,3),设抛物线的解析
《二次函数图象》PPT课件

-2
-3 -4
-5
-6 -7
y=-x2
-8 -9
-10
5
从图像可以看出,二次函数y=x2和y=-x2的图像都
是一条曲线,它的形状类似于投篮球或投掷铅球时球在
空中所经过的路线. 这样的曲线叫做抛物线.
y=x2的图像叫做抛物线y=x2.
y y=x2
y
o
x
y=-x2的图像叫做抛物线y=-
x2. 实际上,二次函数的图像 o
(2)当a>0时,抛物线的开口向上,顶点是 抛物线的最低点;
y
a>0
当a<0时,抛物线的开口向下,顶点是
抛物线的最高点;
o
x
|a|越大,抛物线的开口越小;
.
a<0
16
请同学们把所学的二次函数图象的知识归纳小结。
(0,0) 最低点 y轴 向上
(0,0) 最高点 y轴 向下
.
增 减增增 大 小大大
增 增增减 大 大大小
17
8
y=x2
7
6
5
4
3
2
接各点,就得到y=x2的
1 -5 -4 -3 -2 -1 o 1 2 3 4 5
x
图像.
.
4
请画函数y=-x2的图像 解:(1) 列表
(2) 描点
(3) 连线
y 1
根据表中x,y的数值在 坐标平面中描点(x,y),
再用平滑曲线顺次连接 各点,就得到y=-x2的图 像.
.
-5 -4 -3 -2 -1-1 o 1 2 3 4 5 x
x
都是抛物线.
它们的开口向上或者向下.
一般地,二次函数y=ax2+bx+c
26.1.3 实际问题与二次函数课件3 (新人教版九年级下)
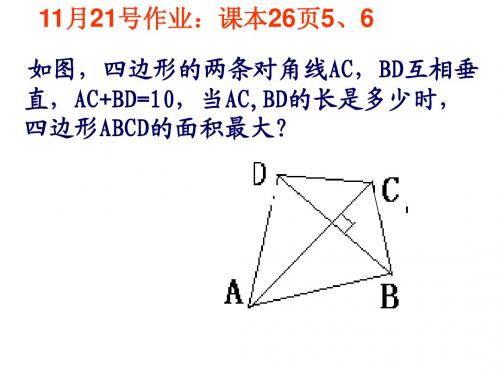
26.3 实际问题与二次函数(3)
图中是抛物线形拱桥,当水面在 l 时, 拱顶离水面2m,水面宽4m,建立适当坐 标系,求出抛物线解析式。(看谁的方法 简单) 水面下降1m时,水面宽度增加了多少? 解一
1 0.5( x 2 )2 2
例:某工厂大门是一抛物线形的水泥建筑物,大门底部宽 AB=4m,顶部C离地面的高度为4.m,,建立适当坐标系,求 抛物线解析式。 现有载满货物的汽车欲通过大门,货物顶部距地面2.5m,装 货宽度为2.4m.这辆汽车能否顺利通过大门?若能,请你通过 计算加以说明;若不能,请简要说明理由.
+2.25
.B(1,2.25)
(0体体状集装箱的货车要想通过洞拱横 截面为抛物线的隧道,如图1,已知沿底部宽AB为4m,高 OC为3.2m;集装箱的宽与车的宽相同都是2.4m;集装箱 顶部离地面2.1m。该车能通过隧道吗?请说明理由.
2.一场篮球赛中,球员甲跳起投篮,如图2,已知球在A处出手 时离地面20/9 m,与篮筐中心C的水平距离是7m,当球运行的水 平距离是4 m时,达到最大高度4m(B处),设篮球运行的路线 为抛物线.篮筐距地面3m. ①问此球能否投中? (选做)②此时对方球员乙前来盖帽,已知乙跳起后摸到的 最大高度为3.19m,他如何做才能盖帽成功?
你还有其他建立坐标系的方法吗?试一试,看 解二 谁的方法多。 一艘长宽为2米,3米的小船,装货物高度1.45 解三 米,小船能通过拱桥吗?
继续
解一 以抛物线的顶点为原点,以抛物线的对称轴为 y轴,建立平 面直角坐标系,如图所示. ∴可设这条抛物线所表示 的二次函数的解析式为:
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
例4.要修建一个圆形喷水池,在池中 心竖直安装一根水管.在水管的顶端 安装一个喷水头,使喷出的抛物线形 水柱在与池中心的水平距离为1m处 达到最高,高度为3m,水柱落地处离 池中心3m,水管应多长? 解:如图建立直角坐标系, 点(1,3) y B(1,3) 是图中这段抛物线的顶点.因此可 3 设这段抛物线对应的函数是 A 2 y=a(x-1)2+3 (0≤x≤3) ∵这段抛物线经过点(3,0) 3 1 2 a= - ∴ 0=a(3-1) +3 解得: 4 因此抛物线的解析式为: 2 1 O 3 2 y=-4 (x-1) +3 (0≤x≤3) 当x=0时,y=2.25 答:水管长应为2.25m.
( 1 )y ( 2 x 3) 5;(2)y ( 3 x 1 ) 2;
2 2
开口向上 对称轴是x=-3 顶点是(-3,5) 开口向上 对称轴是x=3 顶点是(3,7)
开口向下 对称轴是x=1 顶点是(1,-2) 开口向下 对称轴是x=-2 顶点是(-2,-6)
2 2 (3)y ( 4 x 3) 7;(4)y ( 5 x 2) 6.
2
再描点、连线
1 (1)抛物线 y ( x 1) 2 1 2
的开口方向、对称轴、顶点? 1 2 抛物线 y ( x 1) 1 2 的开口向下,
对称轴是直线x=-1,
顶点是(-1, -1).
观察二次函数 在同一直角坐标系中的图象,思考这三条抛物线 有什么关系?
1 1 2 1 2 2 y ( x 1 ) 1 y x , y x 1, 2 2 2
2 向下平移 y ( x 1 ) 1 y x y ( x 1) 2 2 1个单位 2 1个单位
一般地,抛物线y=a(x-h)2+k 与y=ax2形状相同,位置不同.把抛物线 y=ax2向上(下)向右(左)平移,可以得到 抛物线y=a(x -h)2+k.平移的方向、距 离要根据h、k的值来决定.
你认为今天这节课最需要 掌握的是 ________________ 。
作业:P14 5、(3)
驶向胜利的 彼岸
课后做练习册26.1.3 p9
再描点画图.
解: 先列表
x … -4 -3 -2 -1 0 1 2 …
1 y ( x 1) 2 1 … 2
-5.5 -3 -1.5 -1 -1.5 -3 -5.5 … 直线x=-1
1
y -5 -4 -3 -2 -1 o 1 2 3 4 5 x -1 -2 -3 -4 -5 -6 -7 -8 -9 1 -10 y ( x 1) 2 1
有什么关系?
1
y x
-5 -4 -3 -2 -1 o 1 2 3 4 5 -1 1 2 -2 y ( x 1 ) 1 平移方法1: 2 -3 -4 1 2向下平移 1 2 y x y x 1 -5 2 1个单位 2 -6 -7 向左平移 y 1 ( x 1) 2 1 -8 2 1个单位 -9 -10
在对称轴的左侧,y随着x的增大而减小. 在对称轴的右侧, y随着x的增大而增大.
向下
在对称轴的左侧,y随着x的增大而增大. 在对称轴的右侧, y随着x的增大而减小.
增减性 最值
当x=h时,最小值为k.
当x=h时,最大值为k.
1 (2)抛物线 y ( x 1) 2 1 2 1 y x2 2
二次函数y=a(x-h)2+k的图象和性质
1.顶点坐标与对称轴 2.位置与开口方向
3.增减性与最值 根据图形填表: 抛物线
y=a(x-h)2+k(a>0)
(h ,k)
直线x=h
由h和k的符号确定
y=a(x-h)2+k(a<0)
(h,k)
顶点坐标
对称轴 位置 开口方向
直线x=h
由h和k的符号确定
向上
平移,可以得到抛物线y a( x h) 2 k。
、k 的值来决定。 平移的方向、距离要根据h _____
抛物线y a ( x h) 2 k有如下特点: (1)当a 0时,开口向上 ____;当a 0,开口向下 ___; x=h ; (2)对称轴是直线____ (3)顶点坐标是 ______ 。 ( h,k)
26.1.3
2 二次函数y=a(x-h) +k的图象
1 2 y ( x 1 ) 1的图像.指出它的开口 例3.画出函数 2
方向、顶点与对称轴、 解: 先列表
x … -4 -3 -2 -1 0 1 2 …
1 y ( x 1) 2 1 … 2
-5.5 -3 -1.5 -1 -1.5 -3 -5.5 …
形状相同, 开口方向相同. 顶点不同, 对称轴不同.
1 y ( x 1) 2 1 2
1 2 y x , 2
1 2 y x 1, 2
1 1 2 2 y ( x 1 ) 1 ? y x 抛物线 怎样移动就可以得到抛物线 2 2
归纳小结
相同 一般地,抛物线y a( x h) 2 k与y ax 2形状 _____ , 不同 位置 ____ 。把抛物线y ax 2向上(下)向左(右)
C(3,0) x 3
1.完成下列表格: 二次函数 y=2(x+3)2+5 开口方向 向上 对称轴 顶点坐标
直线x=-3 (-3,5) 直线x=1 (1,-2)
y=-3(x-1)2-2
y = 4(x-3)2+7
向下
向上 向下
直线x=3
直线x=2
(3,7)
(2,-6)
y=-5(2-x)2-6
2.请回答抛物线y = 4(x-3)2+7由抛物线y=4x2怎 样平移得到? 3.抛物线y =-4(x-3)2+7能够由抛物线y=4x2平移 得到吗?
4、抛物线y=a(x+2)2-3经过点(0,0), 则a= 。 5、设抛物线的顶点为(1,-2),且经过 点(2,3),求它的解析式。 6、抛物线y=3x2向右平移3个单位再向下平移 2个单位得到的抛物线是 。 7、抛物线y=2(x+m)2+n的顶点是 。
练习
8、说出下列抛物线的开口方向、对称轴及顶点:
