九年级数学下册24.3第2课时圆内接四边形习题课件(新版)沪科版
合集下载
HK沪科版 九年级数学 下册第二学期春 部优公开课堂教学课件 第二十四章 圆 24.3 第2课时 圆内接四边形

A
O
B
D
C
解法1:∵∠CBD=30°,∠BDC=20°
∴∠C=180°-∠CBD-∠BDC=130°
∴∠A=180°-∠C=50°(圆内接四边形对角互补)
首页
变式:已知∠OAB等于40°,求∠C 的度数.
D
O
A
C
B
))
2.如图,BC为半圆O的直径,AB=AF,AC与BF交于点M. (1)若∠FBC=α,求∠ACB(用α表示) (2)过A作AD⊥BC于D,交BF于E,求证:BE=EM.
第24章 圆
24.3 圆周角
第2课时 圆内接四边形
复习 导入
自主 学习
合作 探究
课堂 小结
随堂 训练
复习导入
什么是圆周角?
圆周角概念: 顶点在圆上,并且两边都和圆相交的角叫圆
周角.
特征: ① 角的顶点在圆上.
D
B E
●O
② 角的两边都与圆相交.
A
C
首页
圆周角定理
圆周角定理:一条弧所对的圆周角等于它所对的圆心角的一半.
D
A
O
B
C
首页
如图:圆内接四边形ABCD中,
∵ 弧BCD和弧BAD所对的圆心角的和是周角 D
∴∠A+∠C=180°
同理∠B+∠D=180°
A
延长BC到点E,有
O
∠BCD+∠DCE=180°
B
∴∠A=∠DCE
CE
归纳:
由于∠A是∠DCE的补角∠BCD的对角(简称∠DCE的内对 角),于是我们得到圆内接四边形的性质:
C
∴AO=BO=CO.
∴点C在⊙O上. 又∵AB为直径,
A
O
B
D
C
解法1:∵∠CBD=30°,∠BDC=20°
∴∠C=180°-∠CBD-∠BDC=130°
∴∠A=180°-∠C=50°(圆内接四边形对角互补)
首页
变式:已知∠OAB等于40°,求∠C 的度数.
D
O
A
C
B
))
2.如图,BC为半圆O的直径,AB=AF,AC与BF交于点M. (1)若∠FBC=α,求∠ACB(用α表示) (2)过A作AD⊥BC于D,交BF于E,求证:BE=EM.
第24章 圆
24.3 圆周角
第2课时 圆内接四边形
复习 导入
自主 学习
合作 探究
课堂 小结
随堂 训练
复习导入
什么是圆周角?
圆周角概念: 顶点在圆上,并且两边都和圆相交的角叫圆
周角.
特征: ① 角的顶点在圆上.
D
B E
●O
② 角的两边都与圆相交.
A
C
首页
圆周角定理
圆周角定理:一条弧所对的圆周角等于它所对的圆心角的一半.
D
A
O
B
C
首页
如图:圆内接四边形ABCD中,
∵ 弧BCD和弧BAD所对的圆心角的和是周角 D
∴∠A+∠C=180°
同理∠B+∠D=180°
A
延长BC到点E,有
O
∠BCD+∠DCE=180°
B
∴∠A=∠DCE
CE
归纳:
由于∠A是∠DCE的补角∠BCD的对角(简称∠DCE的内对 角),于是我们得到圆内接四边形的性质:
C
∴AO=BO=CO.
∴点C在⊙O上. 又∵AB为直径,
A
台江区二中九年级数学下册第24章圆24.3圆周角第2课时圆内接四边形课件新版沪科版3

看看远处,要保护好眼睛哦~站起来 动一动,久坐对身体不好哦~
结束语
九年级数学下册第24章圆24.3圆周角第2课时圆 内接四边形课件新版沪科版3
视图〔3〕
温故知新 1、一个物体的三视图指的是什么 ?
2、说出下面一些基本几何体的三视图 :
3、你能画出以下图的三视图吗 ?
主
左
视
视
图
图
俯
导入
前面我们讨论了由立体图形〔实物〕画出 三视图 , 下面我们讨论由三视图想象出立体 图形〔实物〕.
例2 在圆内接四边形ABCD中 , ∠A、∠B、 ∠C的度数之比是2:3:6 , 求这个四边形各角的度数.
解 : 设∠A、∠B、∠C的度数分别等于2x°、 3x°、 6x°. ∵四边形ABCD内接与圆 , ∴∠A+∠C=∠B+∠D=180° ∵2x+6x=180° , ∴x=22.5 ∴∠A=45° , ∠B=67.5° , ∠C=135° , ∠D=180°-67.5°=112.5°
自主学习
例1 : 根据三视图说出立体图形的名称.
分析 : 由三视图想象立体图形时 , 要先分别根据主视 图、俯视图和左视图想象立体图形的前面、上面和左侧 面 , 然后再综合起来考虑整体图形.
练一练
1、由三视图想象实物形状 :
(1)
(2)
(3) 实
(4) 实
2、下面所给的三视图表示什么几何体?
C
圆内接四边形的对角 互补 .
D O
A
B
如下图 , 四边形ABCD内接于
E
⊙O , 试说明∠A与∠DCE的关系.
解:由于 BAD 与 B C D 所对的
C
圆心角之和是周角为360°,则 ∠A+∠BCD=180°.
结束语
九年级数学下册第24章圆24.3圆周角第2课时圆 内接四边形课件新版沪科版3
视图〔3〕
温故知新 1、一个物体的三视图指的是什么 ?
2、说出下面一些基本几何体的三视图 :
3、你能画出以下图的三视图吗 ?
主
左
视
视
图
图
俯
导入
前面我们讨论了由立体图形〔实物〕画出 三视图 , 下面我们讨论由三视图想象出立体 图形〔实物〕.
例2 在圆内接四边形ABCD中 , ∠A、∠B、 ∠C的度数之比是2:3:6 , 求这个四边形各角的度数.
解 : 设∠A、∠B、∠C的度数分别等于2x°、 3x°、 6x°. ∵四边形ABCD内接与圆 , ∴∠A+∠C=∠B+∠D=180° ∵2x+6x=180° , ∴x=22.5 ∴∠A=45° , ∠B=67.5° , ∠C=135° , ∠D=180°-67.5°=112.5°
自主学习
例1 : 根据三视图说出立体图形的名称.
分析 : 由三视图想象立体图形时 , 要先分别根据主视 图、俯视图和左视图想象立体图形的前面、上面和左侧 面 , 然后再综合起来考虑整体图形.
练一练
1、由三视图想象实物形状 :
(1)
(2)
(3) 实
(4) 实
2、下面所给的三视图表示什么几何体?
C
圆内接四边形的对角 互补 .
D O
A
B
如下图 , 四边形ABCD内接于
E
⊙O , 试说明∠A与∠DCE的关系.
解:由于 BAD 与 B C D 所对的
C
圆心角之和是周角为360°,则 ∠A+∠BCD=180°.
沪科版九年级数学下册课件:24.3《圆周角(3)圆内接四边形》ppt
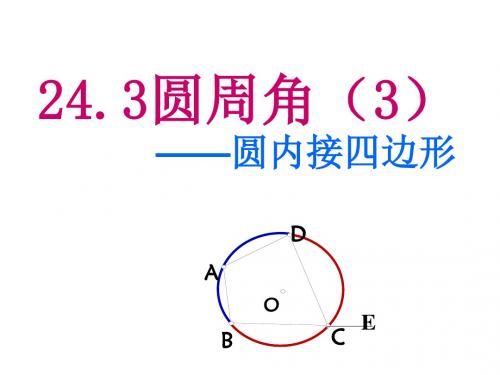
A D
O2
BF
注意:相交两圆的公共弦是常用的辅助线.
五、巩固练习 1.四边形ABCD内接于圆,AC平分∠BAD, 延长DC交AB的延长线于点E,若AC=EC, 求证:AD=EB
A
OB
DC
E
2.课本30页练习1、2.
六、小结 本节课你有什么收获? 到现在,我们学习的与圆有关的辅助线
有哪些?
七、作业 课堂作业: 1,必做题:书本上第32页第9题 2,选做题:书本上第32页第11题 家庭作业:一张试卷
2.这个圆叫做这个多边形的外接圆。
B
A
A
DC
B OO
F CD
3.如图:⊙O内接四边形ABCD,
(1)∠ A+∠1=?, ∠ B+∠D=?
(2)在∠ A ,∠ B ,∠ D ,∠ 1中,
D
哪个角与∠ 2相等?
A
其中,∠A是∠BCD的对角
(简称为∠DCE的内对角)
O
12E
B
C
圆内接四边形的性质:
圆内接四边形的对角互补,每一个外角都等于它的
三、自学提纲 看书本上第29-30页,解决以下问题 1.什么叫圆内接多边形?什么叫多边形的
外接圆? 2.圆内接四边形的对角有什么关系? 3.圆内接四边形的外角等于什么? 4.自学例2. 5.做课后32页第10题.
四、合作探究
1.圆内接多边形定义: 如果一个多边形的各个顶点都在同一个圆上, 那么这个多边形叫做这个圆的内接多边形.
24.3圆周角(3)
——圆内接四边形
D
A
O
B
CE
一、复习引入 1.什么叫圆内接三角形? 2.什么叫做圆内接四边形?
圆内接四边形-九年级数学下册同步教学课件(沪科版)

定理
圆内接四边形的对角互补,且任何 一个外角都等于它的内对角.
24.3.2 圆内接四边形
“ THANKS ”
A
圆上一条弧所对的圆周角等于它
所接四边形 讲授新课 圆内接四边形及其性质
如果一个多边形的所有顶点都在同一个圆上,这个多边 形叫做圆的内接多边形,这个圆叫做这个多边形的外接圆.
C
D O
A
B
如图所示,四边形ABCD是⊙O的内接四边形, ⊙O是
四边形ABCD的外接圆.
∵ 2x+6x=180°, ∴ x = 22.5°.
∴ ∠A = 45°, ∠B = 67.5°, ∠C =135°, ∠D =180°-67.5°=112.5°.
24.3.2 圆内接四边形
例2 如图,点 A,B,C,D 在⊙O 上,点 O 在∠D 的内部, 四边形 OABC 为平行四边形,
则∠OAD+∠OCD = _6__0__度.
24.3.2 圆内接四边形
例3 如图,已知 A,B,C,D 是 ⊙O 上的四点,延长 DC,AB 相交于点E. 若BC=BE. 求证:△ADE是等腰 三角形.
证明:∵BC=BE,∴∠BCE=∠E. ∵四边形ABCD是圆内接四边形, ∴∠A+∠DCB=180°. ∵∠BCE+∠DCB=180°, ∴∠A=∠BCE,∴∠A=∠E, ∴AD=DE, ∴△ADE是等腰三角形.
则∠APB = 120°.
C P
B A
24.3.2 圆内接四边形
5. 在⊙O 中,∠CBD =30°,∠BDC =20°,求∠A.
解:∵∠CBD = 30°,∠BDC = 20°,
A
∴∠C = 180°-∠CBD-∠BDC = 130°.
+24.3圆周角第2课时圆内接四边形+练习课件++2023—2024学年沪科版数学九年级下册+

∴∠BCE=∠E,
∴∠A=∠E,
∴DA=DE.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
9.[2023·合肥模拟]如图,AC是圆内接四边形ABCD的一条对
角 线 , 点 D关 于 AC 的 对 称 点 E在 边 BC 上 , 连 接 AE, 若
∠ABC=64°,则∠BAE的度数为( C )
A.64°
B.40°
第24章
24.3
第2课时
圆
圆周角
圆内接四边形
1.一个多边形的所有顶点都在同一个圆上,这个多边形叫做
圆的内接多边形,这个圆叫做这个多边形的外接圆.
2.圆内接四边形的对角
于
它的内对角.
互补
,且任何一个外角都
等
圆内接多边形的概念
1.【知识初练】如图,七边形ABCDEFG的七个顶点都在☉O
上,所以七边形ABCDEFG是☉O的
∴∠1+∠2+∠3+∠4+2∠5=180°.
∵∠1+∠2=64°,
∴∠3+∠4=180°-64°-2∠5=116°-2∠5.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
∵∠1+∠2+∠B=180°,∠B+∠D=180°,
∴∠D=∠1+∠2=64°,∴∠O=2∠D=128°.
在等腰三角形AOC中,
2∠5=180°-∠O=180°-128°=52°,
10
11
12
13
14
圆内接四边形的性质
3.【知识初练】 [2023·绍兴中考]如图,四边形ABCD内接于
∴∠A=∠E,
∴DA=DE.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
9.[2023·合肥模拟]如图,AC是圆内接四边形ABCD的一条对
角 线 , 点 D关 于 AC 的 对 称 点 E在 边 BC 上 , 连 接 AE, 若
∠ABC=64°,则∠BAE的度数为( C )
A.64°
B.40°
第24章
24.3
第2课时
圆
圆周角
圆内接四边形
1.一个多边形的所有顶点都在同一个圆上,这个多边形叫做
圆的内接多边形,这个圆叫做这个多边形的外接圆.
2.圆内接四边形的对角
于
它的内对角.
互补
,且任何一个外角都
等
圆内接多边形的概念
1.【知识初练】如图,七边形ABCDEFG的七个顶点都在☉O
上,所以七边形ABCDEFG是☉O的
∴∠1+∠2+∠3+∠4+2∠5=180°.
∵∠1+∠2=64°,
∴∠3+∠4=180°-64°-2∠5=116°-2∠5.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
∵∠1+∠2+∠B=180°,∠B+∠D=180°,
∴∠D=∠1+∠2=64°,∴∠O=2∠D=128°.
在等腰三角形AOC中,
2∠5=180°-∠O=180°-128°=52°,
10
11
12
13
14
圆内接四边形的性质
3.【知识初练】 [2023·绍兴中考]如图,四边形ABCD内接于
24.3 圆周角+第2课时 圆内接四边形+++课件+2024-2025学年+沪科版数学九年级下册

B.70°
C.110°
D.140°
4.如图,已知 AB 是半圆 O 的直径,∠BAC=20°,D 是 A︵C上任意一点, 则∠D 的度数为__111100°°__.
5.如图,在圆内接四边形 ABCD 中,若∠A,∠B,∠C 的度数之比为 4∶ 3∶5,则∠D 的度数为__112200°°__.
6.如图,已知 A,B,C,D 是⊙O 上的四点,延长 DC,AB 相交于点 E, 若 BC=BE.求证:△ADE 是等腰三角形.
10.如图,四边形 ABCD 的四个顶点都在⊙O 上,且 AB=AD,∠CBD=30°, ∠BDC=20°,试求∠ABD 的度数.
解:∵∠CBD=30°,∠BDC=20°,∴∠C=180°-30°-20°=130°,
又∵四边形 ABCD 内接于⊙O,∴∠A=180°-∠C=50°,
又∵AB=AD,
求证:AD 平分∠EAC.
【思路分析】由圆内接四边形的性质可得∠EAD=∠DCB.又由同圆中等弧 所对的圆周角相等,可得∠DCB=∠DAC.从而证明 AD 平分∠EAC.
【自主解答】
∵四边形 ABCD 是圆内接四边形,∴∠EAD=∠DCB. 又∵︵BD=D︵C,∴∠DAC=∠DCB. ∴∠EAD=∠DAC.∴AD 平分∠EAC.
证明:∵四边形 ABCD 是⊙O 的内接四边形, ∴∠ECB=∠A.又∵BC=BE, ∴∠E=∠ECB, ∴∠E=∠A,∴DA=DE, ∴△ADE 是等腰三角形.
7.如图,⊙C 过原点,且与两坐标轴分别交于点 A,点 B,点 A 的坐标为 (0,3),M 是第三象限内 O︵B 上一点,∠BMO=120°,则⊙C 的半径为
第 2 课时 圆内接四边形
要点感知 1.一个多边形的所有顶点都在_同_同一一个个圆圆__上,这个多边形叫做圆的内 接多边形,这个圆叫做这个多边形的_外_外接接圆圆__. 2.圆内接四边形的对角_互_互补补__,且任何一个外角都等于它的_内_内对对角角.
上海沪科版初中数学九年级下册24.3 第2课时 圆内接四边形

上海沪科版初中数学
上海沪科版初中数学 重点知识精选
掌握知识点,多做练习题,基础知识很重要! 上海沪科版初中数学 和你一起共同进步学业有成!
TB:小初高题库
上海沪科版初中数学
24.3 圆周角
第 2 课时 圆内接四边形
1.圆内接四边形 ABCD,∠A,∠B,∠C 的度数之比为 3:4:6,则∠D 的度数为 ( )
∠ADC 的度数是________.A来自DOB
C
第 5 题图
第 6 题图
6.已知如图,四边形 ABCD 内接于⊙O,若∠A=60°,则∠DCE=
.
7.如图,四边形 ABCD 内接于⊙O,AD∥BC,求证:AB=CD.
TB:小初高题库
上海沪科版初中数学
8.如图,在⊙O 的内接四边形 ABCD 中,DB=DC,∠DAE 是四边形 ABCD 的一个外 角.∠DAE 与∠DAC 相等吗?为什么?
9.(1)已知:如图 1,四边形 ABCD 内接于⊙O,延长 BC 至 E.求证: ∠A+∠BCD=180°,∠DCE=∠A. (2)依已知条件和(1)中的结论: ①如图 2,若点 C 在⊙O 外,且 A、C 两点分别在直线 BD 的两侧.试确定∠A+∠BCD 与 180°的大小关系; ②如图 3,若点 C 在⊙O 内,且 A、C 两点分别在直线 BD 的两侧.试确定∠A+∠BCD 与 180°的大小关系.
A.60 B.80 C.100 D.120 2.如 图 , 在 △ ABC 中 , AB 为 ⊙ O 的 直 径 , ∠ B=60°, ∠ BOD=100°, 则 ∠ C 的 度 数 为 ( )
A.50° B.60° C.70° D.80°
第 2 题图
第 3 题图
上海沪科版初中数学 重点知识精选
掌握知识点,多做练习题,基础知识很重要! 上海沪科版初中数学 和你一起共同进步学业有成!
TB:小初高题库
上海沪科版初中数学
24.3 圆周角
第 2 课时 圆内接四边形
1.圆内接四边形 ABCD,∠A,∠B,∠C 的度数之比为 3:4:6,则∠D 的度数为 ( )
∠ADC 的度数是________.A来自DOB
C
第 5 题图
第 6 题图
6.已知如图,四边形 ABCD 内接于⊙O,若∠A=60°,则∠DCE=
.
7.如图,四边形 ABCD 内接于⊙O,AD∥BC,求证:AB=CD.
TB:小初高题库
上海沪科版初中数学
8.如图,在⊙O 的内接四边形 ABCD 中,DB=DC,∠DAE 是四边形 ABCD 的一个外 角.∠DAE 与∠DAC 相等吗?为什么?
9.(1)已知:如图 1,四边形 ABCD 内接于⊙O,延长 BC 至 E.求证: ∠A+∠BCD=180°,∠DCE=∠A. (2)依已知条件和(1)中的结论: ①如图 2,若点 C 在⊙O 外,且 A、C 两点分别在直线 BD 的两侧.试确定∠A+∠BCD 与 180°的大小关系; ②如图 3,若点 C 在⊙O 内,且 A、C 两点分别在直线 BD 的两侧.试确定∠A+∠BCD 与 180°的大小关系.
A.60 B.80 C.100 D.120 2.如 图 , 在 △ ABC 中 , AB 为 ⊙ O 的 直 径 , ∠ B=60°, ∠ BOD=100°, 则 ∠ C 的 度 数 为 ( )
A.50° B.60° C.70° D.80°
第 2 题图
第 3 题图
2023九年级数学下册第24章圆24.3圆周角第2课时圆内接四边形教案(新版)沪科版
3.课后拓展应用
教师活动:
-布置作业:根据课堂内容,布置适量的习题,包括基础题、提高题和拓展题,以巩固学习效果。
-提供拓展资源:向学生推荐一些拓展阅读材料,如数学期刊、在线教育资源,以供学生深入学习。
-反馈作业情况:及时批改作业,给予学生个性化的反馈和指导。
学生活动:
-完成作业:认真完成作业,巩固课堂所学知识。
4.教室布置:
a.将教室分成几个小组讨论区,每个讨论区配备一台电脑或投影设备,方便学生观看多媒体资源。
b.在教室前方设置讲台,用于教师讲解和演示教学内容。
c.预留一片实验操作区域,放置画图工具和实验器材,便于学生进行实际操作。
d.教室内张贴与圆内接四边形相关的挂图和提示性标语,营造良好的学习氛围。
5.其他:
本节课使用沪科版2023九年级数学下册教材,确保每位学生都有教材。提前布置学生预习第24章圆的相关内容,特别是24.3节圆周角的知识,为学习圆内接四边形打下基础。
2.辅助材料:
a.准备与圆内接四边形相关的图片,展示不同形状和大小的圆内接四边形,帮助学生建立直观认识。
b.制作动态PPT或视频,演示圆内接四边形的性质,如对角互补、对边相等等,以便学生更好地理解和记忆。
重点题型整理
题型1:证明圆内接四边形的对角互补。
题目:证明圆内接四边形的对角互补。
解答:设ABCD是圆内接四边形,延长AB和CD相交于点E,延长AD和BC相交于点F。根据圆周角定理,得∠AED=∠BFC。又因为ABCD是圆内接四边形,所以∠AED+∠BFC=180°。因此,∠AEB+∠BFC=180°,即∠AEB和∠BFC互补。同理,可证明∠BEC和∠BFC互补,∠CED和∠DFA互补,∠CFA和∠DFA互补。因此,圆内接四边形的对角互补。
教师活动:
-布置作业:根据课堂内容,布置适量的习题,包括基础题、提高题和拓展题,以巩固学习效果。
-提供拓展资源:向学生推荐一些拓展阅读材料,如数学期刊、在线教育资源,以供学生深入学习。
-反馈作业情况:及时批改作业,给予学生个性化的反馈和指导。
学生活动:
-完成作业:认真完成作业,巩固课堂所学知识。
4.教室布置:
a.将教室分成几个小组讨论区,每个讨论区配备一台电脑或投影设备,方便学生观看多媒体资源。
b.在教室前方设置讲台,用于教师讲解和演示教学内容。
c.预留一片实验操作区域,放置画图工具和实验器材,便于学生进行实际操作。
d.教室内张贴与圆内接四边形相关的挂图和提示性标语,营造良好的学习氛围。
5.其他:
本节课使用沪科版2023九年级数学下册教材,确保每位学生都有教材。提前布置学生预习第24章圆的相关内容,特别是24.3节圆周角的知识,为学习圆内接四边形打下基础。
2.辅助材料:
a.准备与圆内接四边形相关的图片,展示不同形状和大小的圆内接四边形,帮助学生建立直观认识。
b.制作动态PPT或视频,演示圆内接四边形的性质,如对角互补、对边相等等,以便学生更好地理解和记忆。
重点题型整理
题型1:证明圆内接四边形的对角互补。
题目:证明圆内接四边形的对角互补。
解答:设ABCD是圆内接四边形,延长AB和CD相交于点E,延长AD和BC相交于点F。根据圆周角定理,得∠AED=∠BFC。又因为ABCD是圆内接四边形,所以∠AED+∠BFC=180°。因此,∠AEB+∠BFC=180°,即∠AEB和∠BFC互补。同理,可证明∠BEC和∠BFC互补,∠CED和∠DFA互补,∠CFA和∠DFA互补。因此,圆内接四边形的对角互补。
