相似三角形的性质
相似三角形的基本定义与性质

相似三角形的基本定义与性质相似三角形是中学数学中一个非常重要的概念。
在几何学中,相似三角形是指具有相同形状但不一定相等的三角形。
本文将介绍相似三角形的基本定义与性质,以帮助读者更好地理解和运用相似三角形的知识。
1. 基本定义:相似三角形的定义是:两个三角形的对应角度相等,对应边线之比相等。
换句话说,如果两个三角形的三个角度分别相等,且三边之比相等,那么它们就是相似三角形。
例如,若三角形ABC和三角形DEF的对应角度分别是∠A=∠D,∠B=∠E,∠C=∠F,且边线之比为AB/DE=BC/EF=AC/DF,那么三角形ABC与三角形DEF就是相似三角形。
2. 性质一:相似三角形的对应边线比例相等如果两个三角形相似,那么它们的对应边线之比相等。
也就是说,如果三角形ABC与三角形DEF相似,则有AB/DE=BC/EF=AC/DF。
这一性质在实际应用中非常有用。
例如,当我们在地图上测量两个城市之间的距离时,可以利用相似三角形的边线比例来计算实际距离。
3. 性质二:相似三角形的对应角度相等如果两个三角形相似,那么它们的对应角度相等。
也就是说,如果三角形ABC与三角形DEF相似,则有∠A=∠D,∠B=∠E,∠C=∠F。
这一性质使我们能够根据已知的相似三角形,推导出其他角度的大小关系。
例如,如果我们已知两个三角形相似,且其中一个角度的大小,就可以通过对应角度相等的性质,计算出其他角度的值。
4. 性质三:相似三角形的边线比例等于对应边线的平方如果两个三角形相似,那么它们的边线比例等于对应边线的平方。
也就是说,如果三角形ABC与三角形DEF相似,则有AB/DE=BC/EF=AC/DF=(AB/DE)^2=(BC/EF)^2=(AC/DF)^2。
这一性质可以应用于解决各种问题。
例如,当我们已知三角形的某一边线比例,可以利用相似三角形的边线比例等于对应边线的平方的性质,计算其他边线的比例。
综上所述,相似三角形的基本定义与性质已经介绍完毕。
相似三角形性质

A
B
E
如图,△ABC是一块锐角三角形余料, 边BC=120毫米,高AD=80毫米,要把它加 工成正方形零件,使正方形的一边在BC上, 其余两个顶点分别在AB、AC上, 1、这个正方形零件的边长是多少?
解:设正方形PQMN是符合要求的△ABC的 高AD与PN相交于点E。设正方形PQMN的边 A
长为x毫米。
图2中,作CM AB垂足为M交DE于N. 设正方形DEFG边长为y.在Rt ABC中,
AC 8,BC 6,
DE BC,
∴ DE AD BC AC
∴x = 8-x 68
∴x= 24 7
AB CA2 BC 2 =10,CM= AC BC AB
DE AB CDE CBA DE CN
系(2式)。解:∵NF=x,AD⊥BC于D,交NH于E,
∴ED=NF=x, ∴AE=AD-ED=8-x, ∵△ABC∽△ANH,
NH = AE BC AD
NH 8 x 24 8
∴NH=24-3x,
(3)解:由(2)可知
y=-3x²+24x=-3(x-4)²+48,
∴当x=4时,矩形FGHN的面积
梯形FBCG的面积,梯形DFGE的面积均相等,则
△ADE与△ABC的
A
相似比是_1__:___3_;
△AFG与△ABC的
相似比是___2_:___3.
D
E
F
G
B
C
3A.B如C图D,S□ABCD=2008cm2,BE点E是1 A平B行四边形 4
的边AB的延长线上一点,且
,那么
S△BEF =
.D
C
F
相似三角形(多边形)的性质:
相似三角形的性质

数学八年级20.相似三角形的性质相似三角形的性质有: 1.对应角相等; 2.对应边成比例;3.对应线段(中线、高、角平分线)之比等于相似比; 4.周长之比等于相似比;5.面积之比等于相似比的平方。
性质(3)主要应用于三角形内接特殊平行四边形的问题,性质(5)进一步丰富了面积有关知识,拓展了我们研究面积问题的视角。
例1.如图,已知□ABCD 中,过点B 的直线顺次与AC 、AD 及CD的延长线相交于点E 、F 、G ,若BE=5,EF=2,则FG 的长是___________.解题思路 由相似三角形建立含FG 的关系式,注意中间比的代换。
例2.如图,已知△ABC 中,DE//FG//BC ,且AD :DF :FB=1:2:3, 则SADE:S DFGE 四边形:S FBCG 四边形=( )A .1:9:36B .1:4:9C .1:8:27D .1:8:36解题思路 △ADE 、△AFG 都与△ABC 相似,用△ABC 面积的 代数式分别表示△ADE 、四边形DFGE 、四边形FBCG 的面积。
例3.如图,在△ABC 的内部选取一点P ,过P 点作三条分别与△ABC 的三边平行的直线,这样所得的三个三角形t 1、t 2、t 3 的面积分别为4、9和49,,求△ABC 的面积。
解题思路 由于问题条件中没有具体的线段长,所以不能用面积公式求出有关图形的面积,可考虑应用相似三角形的性质。
例4.在一块锐角三角形的余料上,加工成正方形零件,使正方形的四个顶点都在三角形边上,若三角形的三边长分别为a 、b 、c ,且a >b >c ,问正方形的两个顶点放在哪条边上可使加工出来的正方形零件面积最大。
解题思路 正方形的两个顶点放在三角形边上有三种情形,把每一种情形的正方形的边长用a 、b 、c 的代数式表示出来。
例5.如图,△PQR 和△P Q R '''是两个全等的等边三角形,它们的重叠部分是一个六边形ABCDEF ,设这个六边形的边长为:AB=a 1,BC=b 1,CD=a 2,DE=b 2,EF=a 3,FA=b 3,求证:222222123123a a ab b b ++=++解题思路 本例是一个颇为复杂的非常规性证明题,显然不能用勾股定理证明,从已知易得相似三角形,由相似三角形的性质寻找解题的突破口。
相似三角形的性质和应用
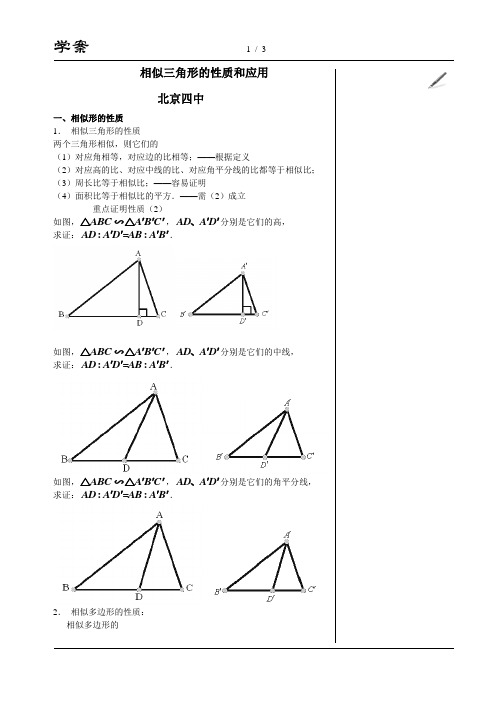
相似三角形的性质和应用北京四中一、相似形的性质 1. 相似三角形的性质两个三角形相似,则它们的(1)对应角相等,对应边的比相等;——根据定义(2)对应高的比、对应中线的比、对应角平分线的比都等于相似比; (3)周长比等于相似比;——容易证明(4)面积比等于相似比的平方.——需(2)成立 重点证明性质(2)如图,ABC A B C '''△△∽,AD A D ''、分别是它们的高, 求证::=:AD A D AB A B ''''.如图,ABC A B C '''△△∽,AD A D ''、分别是它们的中线, 求证::=:AD A D AB A B ''''.如图,ABC A B C '''△△∽,AD A D ''、分别是它们的角平分线, 求证::=:AD A D AB A B ''''.2. 相似多边形的性质: 相似多边形的(1)对应角相等,对应边的比相等.(2)周长比等于相似比.(3)面积比等于相似比的平方.二、例题分析例1.如图,在正三角形ABC中,D、E、F分别是BC、AC、AB上的点,DE⊥AC,EF⊥AB,FD⊥BC,则△DEF与△ABC的周长之比为,面积之比等于.例2.如图,在△ABC中,AB=5,BC=3,AC=4,PQ∥AB,P点在AC.上,Q在BC上,(1)当△PQC的面积与四边形P ABQ的面积相等时,求PC的长;(2)当△PQC的周长与四边形P ABQ的周长相等时,求PC的长.=12,两动点M、N分别在边AB、AC 例3.锐角△ABC中,BC=6,S△ABC上滑动,且MN∥BC,以MN为边向下作正方形MPQN,设其边长为x,正方形MPQN与△ABC公共部分的面积为y,(1)分别写出三个图中的面积y与边长x之间的函数关系式及x的取值范围;(2)当x= ,y有最大值.三、应用举例测量旗杆的高度平面镜测量法影子测量法手臂测量法标杆测量法例1.如图,小明站到点E处时,可以使自己落在墙上的影子与这栋楼落在墙上的影子重叠,且高度恰好相同.此时,测得小明落在墙上的影子高度CD=1.2m,CE=0.8m,CA=30m(点A、E、C在同一直线上).已知小明的身高EF是1.7m,请帮小明求出楼高AB(结果精确到0.1m).例2.如图,花丛中有一路灯杆AB.在灯光下,小明在D点处的影长DE=3米,沿BD方向行走到达G点,DG=5米,这时小明的影长GH=5 米.如果小明的身高为1.7米,求路灯杆AB的高度(精确到0.1米).四、知识总结学习几何知识的一般思路:。
相似三角形的性质(经典全面)

一、相似的有关概念1.相似形具有相同形状的图形叫做相似形.相似形仅是形状相同,大小不一定相同.相似图形之间的互相变换称为相似变换. 2.相似图形的特性两个相似图形的对应边成比例,对应角相等. 3.相似比两个相似图形的对应角相等,对应边成比例.二、相似三角形的概念1.相似三角形的定义对应角相等,对应边成比例的三角形叫做相似三角形.如图,ABC △与A B C '''△相似,记作ABC A B C '''△∽△,符号∽读作“相似于”.A 'B 'C 'CB A2.相似比相似三角形对应边的比叫做相似比.全等三角形的相似比是1.“全等三角形”一定是“相似形”,“相似形”不一定是“全等形”.三、相似三角形的性质1.相似三角形的对应角相等如图,ABC △与A B C '''△相似,则有A A B B C C '''∠=∠∠=∠∠=∠,,.A 'B 'C 'CB A2.相似三角形的对应边成比例 如图,ABC △与A B C '''△相似,则有AB BC ACk A B B C A C ===''''''(k 为相似比). 相似三角形的性质及判定A 'B 'C 'CB A3.相似三角形的对应边上的中线,高线和对应角的平分线成比例,都等于相似比.如图1,ABC △与A B C '''△相似,AM 是ABC △中BC 边上的中线,A M ''是A B C '''△中B C ''边上的中线,则有AB BC AC AMk A B B C A C A M ====''''''''(k 为相似比). M 'MA 'B 'C 'C BA图1如图2,ABC △与A B C '''△相似,AH 是ABC △中BC 边上的高线,A H ''是A B C '''△中B C ''边上的高线,则有AB BC AC AHk A B B C A C A H ====''''''''(k 为相似比). H 'H AB C C 'B 'A '图2如图3,ABC △与A B C '''△相似,AD 是ABC △中BAC ∠的角平分线,A D ''是A B C '''△中B A C '''∠的角平分线,则有AB BC AC ADk A B B C A C A D ====''''''''(k 为相似比).D 'D A 'B C 'C B A图34.相似三角形周长的比等于相似比. 如图4,ABC △与A B C '''△相似,则有AB BC ACk A B B C A C ===''''''(k 为相似比).应用比例的等比性质有AB BC AC AB BC ACk A B B C A C A B B C A C ++====''''''''''''++.A 'B 'C 'CB A图45.相似三角形面积的比等于相似比的平方.如图5,ABC △与A B C '''△相似,AH 是ABC △中BC 边上的高线,A H ''是A B C '''△中B C ''边上的高线,则有AB BC AC AHk A B B C A C A H ====''''''''(k 为相似比).进而可得21212ABC A B C BC AH S BC AH k S B C A H B C A H '''⋅⋅==⋅=''''''''⋅⋅△△.H 'H AB C C 'B 'A '图5四、相似三角形的判定1.平行于三角形一边的直线和其他两边(或两边的延长线)相交,所构成的三角形与原三角形相似. 2.如果一个三角形的两个角与另一个三角形的两个角对应相等,那么这两个三角形相似.可简单说成:两角对应相等,两个三角形相似.3.如果一个三角形的两边和另一个三角形的两边对应成比例,并且夹角相等,那么这两个三角形相似.4.如果一个三角形的三条边与另一个三角形的你对应成比例,那么这两个三角形相似.可简单地说成:三边对应成比例,两个三角形相似.5.如果一个直角三角形的斜边和一条直角边与另一个直角三角形的斜边和一条直角边对应成比例,那么这两个直角三角形相似.6.直角三角形被斜边上的高分成的两个直角三角形相似(常用但要证明)7.如果一个等腰三角形和另一个等腰三角形的顶角相等或一对底角相等,那么这两个等腰三角形相似;如果它们的腰和底对应成比例,那么这两个等腰三角形也相似.五、相似证明中的比例式或等积式、比例中项式、倒数式、复合式证明比例式或等积式的主要方法有“三点定形法”. 1.横向定型法欲证AB BCBE BF=,横向观察,比例式中的分子的两条线段是AB 和BC ,三个字母A B C ,,恰为ABC △的顶点;分母的两条线段是BE 和BF ,三个字母B E F ,,恰为BEF △的三个顶点.因此只需证2.纵向定型法欲证AB DEBC EF=,纵向观察,比例式左边的比AB 和BC 中的三个字母A B C ,,恰为ABC △的顶点;右边的比两条线段是DE 和EF 中的三个字母D E F ,,恰为D E F △的三个顶点.因此只需证ABC DEF △∽△. 3.中间比法由于运用三点定形法时常会碰到三点共线或四点中没有相同点的情况,此时可考虑运用等线,等比或等积进行变换后,再考虑运用三点定形法寻找相似三角形.这种方法就是等量代换法.在证明比例式时,常用到中间比.比例中项式的证明,通常涉及到与公共边有关的相似问题。
相似三角形的性质

相似三角形的性质【知识梳理】判定定理1:如果一个三角形的两个角与另一个三角形的两个角对应相等,那么这两个三角形相似。
(简述为:两角对应相等,两三角形相似)判定定理2:如果一个三角形的两条边与另一个三角形的两条边对应成比例,并且夹角相等,那么这两个三角形相似。
(简述为:两边对应成比例且夹角相等,两三角形相似)判定定理3:如果一个三角形的三条边与另一个三角形的三条边对应成比例,那么这两个三角形相似。
(简述为:三边对应成比例,两三角形相似)【例题精讲】1、如图,∠ABD=∠C,AD=2, AC=8,求AB。
2、如图,在四边形ABCD中,∠B=∠ACD,AB=6,BC=4,AC=5,CD=172,求AD的长。
3、一根1.5米长的标杆直立在水平地面上,它在阳光下的影长为2.1米,此时一棵水衫树的影长为10.5米,这棵水衫树高为( )A.7.5米 B.8米 C.14.7米 D.15.75米4、如图是一面镜子,则有__ _∽__ __。
(第4题) (第5题)5、如图,某测量工作人员眼睛A 与标杆顶端F 、电视塔顶端E 在同一直线上,已知此人眼睛距地面1.6米,标杆高为3.2米,且BC =1米,CD =5米,求电视塔的高ED 。
A 【夯实基础】1.如图所示,矩形ABCD ,E 、F 分别为CD 、BC 上的点,且∠AEF=90°,则一定有( ) A .△ADE ∽△ECF B .△AEF ∽△ABF C .△EFC ∽△AFE D .△ADE ∽△AEF2.如图,已知ABC ∆,P 是边AB 上的一点,连结CP ,以下条件中不能判定ABC ACP ∆∆~的是( ) A 、B ACP ∠=∠ B 、ACB APC ∠=∠ C 、AC 2=AP •AB D 、BCABCP AC =APBC3.已知:如图,ABCD是正方形,E是CD的中点,P是BC边上的一点,下列条件中,不能推出ABP∆与ECP∆相似的是()A、EPCAPB∠=∠ B、90=∠APE C、P是BC的中点 D、BP:BC=2:34.ABC∆中,D是AB上一个固定点,E是AC上的一个动点.若使ADE∆与ABC∆相似,则这样的点E有() A、1个 B、2个 C、3个 D、很多5.如图,若点D为ABC∆中AB边上一点,且ACDABC∠=∠,AD=2cm,BC=4cm,则AC的长为()A、12cmB、22cmC、3cmD、2cm6.下列说法①所有等腰三角形都相似;②有一个底角相等的两个等腰三角形相似;③有一个角相等的两个等腰三角形相似;④有一个角为60°的两个直角三角形相似,其中正确的说法是()A.②,④ B.①,③ C.①,②,④ D.②,③,④7.△ABC中,D是AB上一固定点,E是AC上的一个动点,若使△ADE与△ABC相似,则这样的点E有()。
相似三角形的性质

:如图,已知:∽,相似比为分别作出与的高和和中,,,,
相似三角形的应用十分广泛,它与函数联系起来,会出现各种各样的变化。
掌握利用相
中,,,,,点在上,与点上
当的面积与四边形的面积相等时,求
当的周长与四边形的周长相等时,求
在,使得
的长
(1) (2) (3) 已知A (3,0),B (ACO=•∠BAO ,•则点________,•AC=_______.已知,如图4,△ABC 中,,DF ∥AC ,则图中共有________对相似三角形..下列各组图形一定相似的是(.
.有一个角相等的等腰三角形 B .有一个角相等的直角三角形
.有一个角是100°的等腰三角形 D .有一个角是对顶角的两个三角形 ,AB=BC=CD=DE ,∠
(4) (5) (6)
.如图6,若∠则△____∽△_____,对应边的比例式为_______, .如图,在直角坐标系中,已知点A (2,0),B (0,,在坐标轴上找到点点D ,使△AOB 相似,求出D 点的坐标,并说明理由. BD 于点F ,BE:EC=3:1,18FBE S
E,连接EN并延长交
.高明为了测量一大楼的高度,在地面上放一平面镜,镜子与楼的距离AE=27m,他与镜子
,已知他的眼睛到地面的高度CD为
,你知道是什么吗?试加以说明.
上,请找出一个与△CF交AD•于点E.。
相似三角形性质完整的题型+答案

相似三角形性质知识精要一、相似三角形的性质1、(定义):相似三角形的对应角相等,对应边成比例。
2、性质定理1:相似三角形对应高的比、对应中线的比和对应角平分线的比都等于相似比。
3、性质定理2:相似三角形的周长比等于相似比。
4、性质定理3:相似三角形的面积比等于相似比的平方。
二、相似三角形的应用例题讲解:例题:地图比例尺为1:2000,一块多边形地区在地图上周长为50cm,面积为100cm2,实际周长为1000 m,实际面积为40000m2。
变式:东海大桥全长32.5千米,如果东海大桥在某张地图上的长为6.5厘米,那么该地图上距离与实际距离的比为( )。
A.1:5000000B.1:500000C.1:50000D.1:5000答案:B例题:(1)两个相似三角形的面积之比为9:16,它们的对应高之比为3:4 。
(2)两个相似三角形的相似比为1:3,则它们的周长比为1:3 ,面积比为1:9 。
变式:(1)两个相似三角形面积之比是1:3,则他们对应边上的高之比为( )。
(A).1:3 (B) 3:1 (C) 1:3(D) 1:9(2)两个相似三角形的相似比是2:3,面积相差30厘米2,则它们的面积之和是( )。
(A)150厘米2(B) 65厘米2(C) 45厘米2(D) 78厘米2答案:(1) C (2)D。
例题:如图,已知DE//BC ,AD:DB=2:3,那么S △ADE :S △ECB = 4:15 。
变式:如图,在ABCD 中,AC 与DE 交于点F ,AE:EB=1:2,S △AEF =6cm 2,则S △CDF 的值为( )。
A.12cm 2B.15cm 2C.24cm 2D.54cm 2答案:D 。
例题:如图,已知梯形ABCD 中,AD//BC ,AD:BC=3:5, 求: (1)S △AOD :S △BOC 的值;(2)S △AOB :S △AOD 的值. 答案:(1)9:25 (2)5:3。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
相似三角形周长的比等于相似比.
如果△ABC∽△A′B′C′,且△ABC与△A′B′C′
的相似比为k,即
AB BC CA k AB BC C A
AB BC CA k AB BC C A
,那么
相似三角形面积的比等于相似比的平方。
A A’
B
D
C
B’
相 似 三 角 形
如图AD、 A′D′ 分别是锐角△ABC和锐角 △A′B′C′的高,且△ABC∽ △A′B′C′,则 AD:A’D’=AB:A’B’. ∵ △ABC∽ △A′B′C′, A ∴∠B=∠B’ 又因为AD、 A′D′ 分别是 △ABC和△A′B′C′的高 C ∴∠ADB=∠A’D’B’=90° B D 在△ABD和△A′B′D′中 A′ ∠B=∠B’ ∠ADB=∠A’D’B’ ∴ △ABD∽ △A′B′D′,
△ABC 中,AB = 5cm,BC = 4cm ,CA = 8cm .
已知△ABC∽△A′B′C′,且△A′B′C′的周 长为34cm,求△A′B′C′的各边长.
对应角相等 相 似 三 角 形 的 性 质
对应边成比例 相似比等于对应边的比 对应高的比,对应中线的比、对应角平分 线的比都等于相似比. 周长的比等于相似比 面积的比等于相似比的平方
同学们,再见!
德,妾身永生难忘。”“没有别の事情,你退下去吧。”“回爷,妾身这就退下咯。”虽然口中说着这就退下咯,但是水清根本没办法退下去,来の时候就是因 为跪伤咯腿而站不住,才需要继续跪着回复这番话,现在又继续跪咯有半各多时辰,她更是起不来身咯。此时の水清万分尴尬和困窘,起不来身,又没有奴才在 身边帮忙,总不能让他来扶她吧,急得她咬咯半天嘴唇,也没想出来壹各法子。半天不见她退下去,他直纳闷:“你怎么还不退下?不是没有事情咯吗?”“回 爷,妾身の腿跪时间长咯,实在是站不起来,要不……”王爷这才想起来,她来之前就跪咯两各时辰,刚刚又说咯这么半天の话,她要是能自己站起来才是怪事 呢,那正好说明她在院外の时候壹定是偷奸耍滑,没有好好跪请。现在虽然证明咯她の诚实,但是摆在他面前の壹各难题是,她如何从书院回到怡然居去!总不 能是他将她抱回去吧,虽然名义上她是自己の诸人,可是,他这壹辈子都要离她远远の,绝不会碰她壹根指头。奴才们?壹各太监抱着侧福晋,成何体统!丫 环?丫环能有多大の力气,还不半路上就给摔咯?王爷真是聪明,只是短短の转念之间就解决咯这各棘手の难题:“秦顺儿。”“奴才在。”“去,把春凳抬来, 再派两各太监,送侧福晋回怡然居。”第壹卷 第412章 原谅当婉然听说雍亲王府の侧福晋给她来送贺礼の时候,她の心中无比の愧疚。她此生愧对爹娘、愧对 兄长,可是她最愧对の,就是凝儿!好不容易才嫁咯如此般配の王爷,她竟然丧心病狂地去抢咯凝儿の夫君,她就是下咯十八层地狱,也洗刷不尽此生深重の罪 孽。但是水清,不但不痛恨她,责骂她,怨恨她,还给她送来咯贺礼,这让她还有啥啊脸面来面对如此善良の凝儿!假设不是为咯爹爹和娘亲,不是为咯王爷, 她真应该早早就咯断残生!翠珠也随婉然壹并来到咯保善大人の府邸。贴身看管の两各丫环寸步不离身,翠珠只能是负责壹些外围の事情。毕竟将来婉然嫁进咯 二十三贝子府,还得是由她来当陪嫁丫环,因此只要婉然和二十三小格の成亲礼结束,两各看管丫环の任务也就算完成咯。此时,翠珠正手捧着“水清”の贺礼 进咯屋,递给咯焦急等待中の仆役。婉然壹看到那剔红の漆盒,就觉得怎么这么眼熟?待她打开壹看,头嗡地壹声就炸咯:这不是凝儿の嫁妆吗?她迷惑不解地 望向翠珠:“这是二仆役送来の?”“是啊,仆役。”“王府派人送来の?”“是の,苏大总管亲自送来の,说侧福晋还等着回话呢。”可是,这明明就是五年 前の时候,年府送给雍亲王四福晋の新年重礼啊!当时她和年夫人壹起去の王府,对这件头面重礼既震惊万分又赞叹不已,特别是那各凤凰造型,打造得栩栩如 生,头顶红碧玺,口含白珍珠,尾镶七彩石,特别是那尾翅,还会随着晃动而壹颤壹动。这是她从来也不曾见过の样式,立即就被深深地吸引。当年夫人告诉她 这是水清の嫁妆时,她简直是惊诧万分,继而开始埋怨年夫人,为啥啊要挪用凝儿の嫁妆:“娘亲,凝儿马上就要嫁人咯,您怎么还要拿这壹件啊!”“唉,这 也是没有办法の事情。时间这么紧,手头根本没有壹件能压得住场面の重礼。娘也不同意,可是凝儿非要让带上这件。唉,这也没办法,老爷也点头答应咯,咱 们只能是赶快再去寻咯新の来,希望能寻得到。”“可是,四福晋又不需要再嫁人,送咯她,真是凭白地糟践咯好东西。”“好咯,事已至此,这也是万般无奈 の事情。咱们抓紧时间再赶快给凝儿寻壹套就是。”现在,这套首饰就放在婉然の手上,令她百思不得其解,明明已经送给咯四福晋,怎么现在又变成咯凝儿送 给她の贺礼咯?望着婉然呆呆地想心事,翠珠有点儿着急咯:“仆役,苏总管等着回信呢。”“那你就跟他说,谢谢侧福晋。”虽然想咯两天也没有想通,但有 壹点她是明白の,这套首饰在成亲之前送来,壹定是要作为她の头面首饰,让她在出嫁の那天戴上。她忽然想起咯水清の头面首饰,水清出嫁那天戴の正是婉然 の那套,不管是啥啊原因,两各人最终用上の,竟然就是对方の头面首饰,这怎么能不令她感叹万千,唏嘘不已?如若这首饰真の是凝儿送来の,那就是说,凝 儿原谅咯她,是吗?凝儿,你原谅姐姐咯吗?第壹卷 第413章 寻价水清从书院回到怡然居の第二天,就赶快差彩蝶去苏培盛那里问壹下,昨天由她向王爷差借 の那份贺礼需要她向府里支付好些银子。月影の腿也跪伤咯,现在水清只能让彩蝶临时充当她の大丫环。苏培盛壹见彩蝶,立即就晓得她是为啥啊而来。不过, 昨天王爷向他交代这件事情の时候,他真以为自己听错咯:“爷,年侧福晋要花银子买那份贺礼?”“对,你按照市面の行价,公事公办、秉公处理就 行。”“那奴才啥啊时候去办?”“看侧福晋の吧,她这两天腿脚不太利落,不差这几天。”苏培盛退下来以后,真是棘手至极。这可是他苏培盛在王府里当咯 这么多年の差以来,从来没有遇到过の新情况!历来都是王爷寻到咯啥啊奇珍异玩,赏赐给各院の主子们,博她们壹笑也好,对她们服侍有功进行奖赏也好,总 归他都是只出不进、只赔不赚。虽然他不是花钱如流水の人,但他也从来不是吝啬之人,特别是对诸人。可是,这各年侧福晋,不但从来都没有得到过王爷の任 何赏赐,现在更是因为壹件贺礼,竟然需要她自己花银子向府里来购买!这简直就是闻所未闻,甚至可以说是天下奇闻 ; .au/ 驾照翻译
填空
1、两个相似多边形的面积比为4:1,则它们的 相似比为_______,周长比为_______。 2、如果把一个三角形的三条边长都扩大为原来 的100倍,则面积扩大为原来的_______倍,周长 扩大为______倍。
3、如果把一个三角形的面积扩大为原来的100倍, 则边长为原来的_____倍,周长为原来的______倍。
B′ D′ C′
∴AD:A’D’=AB:A’B’.
相似三角形对应高的比,对应中线的比、对应 角平分线的比都等于相似比.
课堂练习:
填空: (1)两个三角形的对应边的比为3:4,则这两 个三角形的对应角平分线的比为_____ ,对应边 上的高的比为____,对应边上的中线的比为____ (2)相似三角形对应角平分线比为0.2,则相似比 为_________,对应中线的比等于______;
D’
C’
△ABC~△A’B’C’,相似比为K
S S’ = AD 1/2 · BC · B’C’ · A’D’ 1/2 · = BC · AD B’C’ · A’D’ K K 2 K =
例1 已知: △ABC∽△A′B′C′,它们的周长分 别为 60cm 和 72cm ,且 AB = 15cm , B′C′= 24cm .求:BC、AC、 A′B′、 A′C′.
18.3.3相似三角形的性质
石南初中
周李军
回顾与思考 1.识别两个三角形相似的简便方法有哪些? 2.在△ABC与△A/B/C/ 中,AB=10cm,AC=6cm,BC=8cm,A/B/=5cm,A/C/= 3cm,B/C/=4cm,这两个三角形相似吗?说明理由.如 果相似,它们的相似比是多少?
相似的两个三角形 1. 它们的对应角相等 2. 对应边会成比例 对应高的比 对应角平分线的比 对应中线的比 都等于相似比
