【全国百强校】黑龙江省大庆铁人中学2017-2018学年高二下学期开学考试(3月)地理试题(解析版)
2017-2018学年黑龙江省大庆市铁人中学高三(下)开学数学试卷(理科)(解析版)

2017-2018学年黑龙江省大庆市铁人中学高三(下)开学数学试卷(理科)一、选择题(本大题共12小题,每小题只有一个选项正确,每小题5分,共60分.)1.(5分)已知全集U=R,集合A={x|y=lg(x﹣1)},集合,则A∩B=()A.∅B.(1,2]C.[2,+∞)D.(1,+∞)2.(5分)已知复数,则下列说法正确的是()A.z的虚部为4iB.z的共轭复数为1﹣4iC.|z|=5D.z在复平面内对应的点在第二象限3.(5分)设m,n是两条不同的直线,α,β是两个不同的平面,且m⊂α,n⊂β,下列命题中正确的是()A.若α⊥β,则m⊥n B.若α∥β,则m∥nC.若m⊥n,则α⊥βD.若n⊥α,则α⊥β4.(5分)设m∈R,则“m=0”是“直线l1:(m+1)x+(1﹣m)y﹣1=0与直线l2:(m﹣1)x+(2m+1)y+4=0垂直”的()A.充分不必要条件B.必要不充分条件C.充分必要条件D.既不充分也不必要条件5.(5分)甲、乙、丙三人参加某公司的面试,最终只有一人能够被该公司录用,得到面试结果以后,甲说:丙被录用了;乙说:甲被录用了;丙说:我没被录用.若这三人中仅有一人说法错误,则下列结论正确的是()A.丙被录用了B.乙被录用了C.甲被录用了D.无法确定谁被录用了6.(5分)(x﹣y)(x+y)5的展开式中,x2y4的系数为()A.﹣10B.﹣5C.5D.107.(5分)设{a n}是等比数列,则下列结论中正确的是()A.若a1=1,a5=4,则a3=﹣2B.若a1+a3>0,则a2+a4>0C.若a2>a1,则a3>a2D.若a2>a1>0,则a1+a3>2a28.(5分)某四面体的三视图如图所示,正视图、俯视图都是腰长为2的等腰直角三角形,侧视图是边长为2的正方形,则此四面体的四个面中面积最大的为()A.2B.4C.2D.29.(5分)如图,在长方形OABC内任取一点P(x,y),则点P落在阴影部分BCD内的概率为()A.B.C.D.10.(5分)若将函数的图象向左平移个单位长度,则平移后图象的对称轴方程为()A.B.C.D.11.(5分)已知椭圆的左焦点为F1,y轴上的点P在椭圆外,且线段PF1与椭圆E交于点M,若,则E椭圆的离心率为()A.B.C.D.12.(5分)已知函数f(x)=(ax+lnx)(x﹣lnx)﹣x2有三个不同的零点x1,x2,x3(其中x1<x2<x3),则的值为()A.1﹣a B.a﹣1C.﹣1D.1二、填空题(本大题4小题,每小题5分,共20分.)13.(5分)已知实数x,y满足约束条件,则z=2x+y的最小值为.14.(5分)某学校需要把6名同学安排到A,B,C三个兴趣小组学习,每个兴趣小组安排2名同学,已知甲不能安排到A组,乙和丙不能安排到同一小组,则安排方案的种数有.15.(5分)函数y=ln|x﹣1|的图象与函数y=﹣2cosπx,(﹣2≤x≤4)的图象所有交点的横坐标之和等于.16.(5分)在△ABC中,AB=2AC=6,=2,点P是△ABC所在平面内一点,则当222取得最小值时,.三、解答题(本大题7小题,共70分.其中17至21题为必做题,22、23题为选做题.解答过程应写出文字说明、证明过程或演算步骤.)17.(12分)设数列{a n}满足a1+2a2+4a3+…+2n﹣1a n=n.(Ⅰ)求数列{a n}的通项公式;(Ⅱ)求数列{a n+log2a n}的前n项和.18.(12分)在△ABC中,内角A,B,C所对的边分别为a,b,c,已知△ABC的面积为.(1)求a;(2)求sin B+sin C的值.19.(12分)如图,在四棱锥P﹣ABCD中,PC⊥底面ABCD,AD∥BC,AD=2BC=2,PC =2,△ABC是以AC为斜边的等腰直角三角形,E是PD的中点.(I)求证:平面EAC⊥平面PCD;(II)求直线P A与平面EAC所成角的余弦值.20.(12分)已知椭圆C:的离心率为,且以两焦点为直径的圆的内接正方形面积为2.(1)求椭圆C的标准方程;(2)若直线l:y=kx+2与椭圆C相交于A,B两点,在y轴上是否存在点D,使直线AD与BD的斜率之和k AD+k BD为定值?若存在,求出点D坐标及该定值,若不存在,试说明理由.21.(12分)已知函数.(1)当a≥0时,求函数f(x)的极值;(2)若函数f(x)有两个零点x1,x2,求a的取值范围,并证明x1+x2>2.请考生在第22、23两题中任选一题作答,如果多做,则按所做的第一题计分,作答时,请用2B铅笔在答题卡上把所选题目对应的题号涂黑.(选修4-4:坐标系与参数方程选讲)22.(10分)已知圆锥曲线和定点,F1,F2是此圆锥曲线的左、右焦点,以原点O为极点,以x轴的正半轴为极轴建立极坐标系.(Ⅰ)求直线AF2的极坐标方程;(Ⅱ)经过点F1且与直线AF2垂直的直线l交此圆锥曲线于M,N两点,求||MF1|﹣|NF1||的值.[选修4-5:不等式选讲]23.设函数f(x)=|3x+1|﹣|2x+2|.(1)求不等式f(x)≥0的解集;(2)若f(x)﹣|x+1|≤|a+1|对任意x∈R恒成立,求实数a的取值范围.2017-2018学年黑龙江省大庆市铁人中学高三(下)开学数学试卷(理科)参考答案与试题解析一、选择题(本大题共12小题,每小题只有一个选项正确,每小题5分,共60分.)1.【解答】解:由A中y=lg(x﹣1),得到x﹣1>0,即x>1,∴A=(1,+∞),由B中y==≥=2,得到B=[2,+∞),则A∩B=[2,+∞),故选:C.2.【解答】解:∵=,∴z的共轭复数为1﹣4i.故选:B.3.【解答】解:对于A,若α⊥β,则m、n位置关系不定,不正确;对于B,若α∥β,则m∥n或m,n异面,不正确;对于C,若m⊥n,则α、β位置关系不定,不正确;对于D,根据平面与平面垂直的判定可知正确.故选:D.4.【解答】解:“直线l1:(m+1)x+(1﹣m)y﹣1=0与直线l2:(m﹣1)x+(2m+1)y+4=0垂直”⇔(m+1)(m﹣1)+(1﹣m)(2m+1)=0,⇔“m=0,或m=1“,故“m=0”是“直线l1:(m+1)x+(1﹣m)y﹣1=0与直线l2:(m﹣1)x+(2m+1)y+4=0垂直”的充分不必要条件,故选:A.5.【解答】解:假设甲说的是真话,即丙被录用,则乙说的是假话,丙说的是假话,不成立;假设甲说的是假话,即丙没有被录用,则丙说的是真话,若乙说的是真话,即甲被录用,成立,故甲被录用;若乙被录用,则甲和乙的说法都错误,不成立.故选:C.6.【解答】解:(x+y)5的通项公式为:T r+1=•x5﹣r•y r,令5﹣r=1,得r=4;令5﹣r=2,得r=3;∴(x﹣y)(x+y)5的展开式中x2y4的系数为:×1+(﹣1)×=﹣5.故选:B.7.【解答】解:A.由等比数列的性质可得:=a1•a5=4,由于奇数项的符号相同,可得a3=2,因此不正确.B.a1+a3>0,则a2+a4=q(a1+a3),其正负由q确定,因此不正确;C.若a2>a1,则a1(q﹣1)>0,于是a3﹣a2=a1q(q﹣1),其正负由q确定,因此不正确;D.若a2>a1>0,则a1q>a1>0,可得a1>0,q>1,∴1+q2>2q,则a1(1+q2)>2a1q,即a1+a3>2a2,因此正确.故选:D.8.【解答】解:由三视图知该几何体为棱锥S﹣ABD,其中SC⊥平面ABCD;四面体S﹣ABD 的四个面中SBD面的面积最大,三角形SBD是边长为2的等边三角形,所以此四面体的四个面中面积最大的为=2.故选:C.9.【解答】解:根据题意,利用定积分计算e x dx=e x=e﹣1;∴阴影部分BCD的面积为1×e﹣(e﹣1)=1,∴所求的概率为P==.故选:D.10.【解答】解:将函数=2sin(2x+)的图象向左平移个单位长度,可得y=2sin(2x++)=2sin(2x+)的图象,令2x+=kπ+,可得x=﹣,k∈Z,则平移后图象的对称轴方程为x=﹣,k∈Z,故选:A.11.【解答】解:如图所示|OM|=|MF1|=|OP|,不妨设|OP|=,则|OM|=|MF1|=1,设∠MF1O=θ,在△MOF1中由余弦定理可得cosθ===,∴sinθ==,∴tanθ===,∵tanθ==,∴=,解得c=1,∴△MOF1为等边三角形,∴M(﹣,),∴+=1,①∵a2﹣b2=c2=1,②,由①②可得4a4﹣8a2+1=0,解得a2=<1(舍去),a2=,∴a2===()2,∴a==,∴e===﹣1,故选:C.12.【解答】解:令f(x)=0,分离参数得a=,令h(x)=,由h′(x)==0,得x=1或x=e.当x∈(0,1)时,h′(x)<0;当x∈(1,e)时,h′(x)>0;当x∈(e,+∞)时,h′(x)<0.即h(x)在(0,1),(e,+∞)上为减函数,在(1,e)上为增函数.∴0<x1<1<x2<e<x3,a==,令μ=,则a=﹣μ,即μ2+(a﹣1)μ+1﹣a=0,μ1+μ2=1﹣a<0,μ1μ2=1﹣a<0,对于μ=,μ′=则当0<x<e时,μ′>0;当x>e时,μ′<0.而当x>e时,μ恒大于0.画其简图,不妨设μ1<μ2,则μ1=,μ2==μ3=,=(1﹣μ1)2(1﹣μ2)(1﹣μ3)=[(1﹣μ1)(1﹣μ2)]2=[1﹣(1﹣a)+(1﹣a)]2=1.故选:D.二、填空题(本大题4小题,每小题5分,共20分.)13.【解答】解:由z=2x+y,得y=﹣2x+z作出不等式组对应的平面区域如图:由图象可知当直线y=﹣2x+z过点A时,直线y=﹣2x+z的在y轴的截距最小,此时z 最小,由得,即A(1,﹣1),此时z=2﹣1=1,故答案为:1.14.【解答】解:根据题意,分2步进行分析,①,将6人平均分成3组,每组2人,其中乙和丙不能安排到同一小组,将6人平均分成3组,每组2人,有=15种分组方法,其中乙丙在同一组的分法有=3种,则符合题意的分法有15﹣3=12种;②,将分好的3组对应A,B,C三个兴趣小组,甲不能安排到A组,则甲所在组的分法有3种,剩下的2组全排列,有A22=2种情况,则有2×2=4种对应方法,则有12×4=48种不同的安排方案;故答案为:48.15.【解答】解:将偶函数y=ln|x|的图象向右平移一个单位得到y=ln|x﹣1|,则函数关于x =1对称,函数y=﹣2cosπx,(﹣2≤x≤4)的图象也关于x=1对称,作出两个函数的图象,则两个图象共有6个交点,两两关于x=1对称,设对称的两个交点的横坐标为a,b,则=1,即a+b=2,则所有交点的横坐标为3×2=6,故答案为:616.【解答】解:∵=2,||•||•cos B=||2,∴||•cos B=||=6,∴⊥,即∠A=,以A为坐标原点建立如图所示的坐标系,则B(6,0),C(0,3),设P(x,y),则222=x2+y2+(x﹣6)2+y2+x2+(y﹣3)2,=3x2﹣12x+3y2﹣6y+45,=3[(x﹣2)2+(y﹣1)2+10],∴当x=2,y=1时取的最小值,此时•=(2,1)•(﹣6,3)=﹣12+3=﹣9,故答案为:﹣9.三、解答题(本大题7小题,共70分.其中17至21题为必做题,22、23题为选做题.解答过程应写出文字说明、证明过程或演算步骤.)17.【解答】解:(Ⅰ)∵数列{a n}满足∴当n≥2时,…(2分)∴当n≥2时,2n﹣1a n=1,即…(4分)当n=1时,a n=1满足上式∴数列{a n}的通项公式…(6分)(Ⅱ)由(Ⅰ)知,…(7分)∴(a1+log2a1)+(a2+log2a2)+(a3+log2a3)+…+(a n+log2a n),=…(9分)=…(12分)18.【解答】解:(1)由△ABC的面积为,得.因,所以,所以,得bc=35,又b﹣c=2,由余弦定理得:,=,所以a=8.(2)法一:由(1)中b﹣c=2,bc=35.解得b=7,c=5,由正弦定理得:,所以,法二:由(1)有(b+c)2=(b﹣c)2+4bc=22+4×35=144,所以b+c=12.由正弦定理得,所以.19.【解答】证明:(Ⅰ)∵在四棱锥P﹣ABCD中,PC⊥底面ABCD,AC⊂平面ABCD,∴AC⊥PC,∵AD∥BC,AD=2BC=2,PC=2,△ABC是以AC为斜边的等腰直角三角形,∴CD=AC=,∴CD2+AC2=AD2,∴AC⊥DC,∵PC∩CD=C,∴AC⊥平面PCD,∵AC⊂平面ABCD,∴平面EAC⊥平面PCD.解:(II)以C为原点,CD为x轴,CA为y轴,CP为z轴,建立空间直角坐标系,A(0,,0),P(0,0,2),D(,0,0),E(,0,1),C(0,0,0),=(0,﹣,2),=(0,,0),=(,0,1),设平面EAC的法向量=(x,y,z),则,取x=2,得=(2,0,﹣),设直线P A与平面EAC所成角为θ,则sinθ===,cosθ==.∴直线P A与平面EAC所成角的余弦值为.20.【解答】解:(1)由已知可得解得a2=2,b2=c2=1,所求椭圆方程为.(2)由得(1+2k2)x2+8kx+6=0,则△=64k2﹣24(1+2k2)=16k2﹣24>0,解得或.设A(x1,y1),B(x2,y2),则,,设存在点D(0,m),则,,所以==.要使k AD+k BD为定值,只需6k﹣4k(2﹣m)=6k﹣8k+4mk=2(2m﹣1),k与参数k无关,故2m﹣1=0,解得,当时,k AD+k BD=0.综上所述,存在点,使得k AD+k BD为定值,且定值为0.21.【解答】解:(1)由,得,当a≥0时,ax+1>0,若0<x<1,f'(x)>0;若x>1,f'(x)<0,故当a≥0时,f(x)在x=1处取得的极大值;函数f(x)无极小值.(2)当a≥0时,由(1)知f(x)在x=1处取得极大值,且当x趋向于0时,f(x)趋向于负无穷大,又f(2)=ln2﹣2<0,f(x)有两个零点,则,解得a>2.当﹣1<a<0时,若0<x<1,f'(x)>0;若;若,则f(x)在x=1处取得极大值,在处取得极小值,由于,则f(x)仅有一个零点.当a=﹣1时,,则f(x)仅有一个零点.当a<﹣1时,若;若;若x>1,f'(x)>0,则f(x)在x=1处取得极小值,在处取得极大值,由于,则f(x)仅有一个零点.综上,f(x)有两个零点时,a的取值范围是(2,+∞).两零点分别在区间(0,1)和(1,+∞)内,不妨设0<x1<1,x2>1.欲证x1+x2>2,需证明x2>2﹣x1,又由(1)知f(x)在(1,+∞)单调递减,故只需证明f(2﹣x1)>f(x2)=0即可.,又,所以f(2﹣x1)=ln(2﹣x1)﹣ln(x1)+2x1﹣2,令h(x)=ln(2﹣x)﹣lnx+2x﹣2(0<x<1),则,则h(x)在(0,1)上单调递减,所以h(x)>h(1)=0,即f(2﹣x1)>0,所以x1+x2>2.请考生在第22、23两题中任选一题作答,如果多做,则按所做的第一题计分,作答时,请用2B铅笔在答题卡上把所选题目对应的题号涂黑.(选修4-4:坐标系与参数方程选讲)22.【解答】解:(Ⅰ)消去参数α可得曲线C的方程为+y2=1,可得F1(﹣,0),F2(,0),∴直线AF2的斜率为k==﹣1,故直线方程为y﹣=﹣(x﹣0),即x+y=,∴极坐标方程为ρcosθ+ρsinθ=;(Ⅱ)经过点F1(﹣,0)且与直线AF2垂直的直线l斜率为1,故l的方程为y﹣0=x+,即y=x+,联立可解得M(,),N(,),∴由两点间的距离公式可得||MF1|﹣|NF1||=.[选修4-5:不等式选讲]23.【解答】解:(1)f(x)≥0,即|3x+1|﹣|2x+2|≥0,即①或②或③,解①可得x<﹣1;解②可得;解③可得x≥1.综上,不等式f(x)≥0的解集为.(2)f(x)﹣|x+1|≤|a+1|等价于|3x+1|﹣|2x+2|﹣|x+1|≤|a+1|恒成立,等价于|3x+1|﹣|3x+3|≤|a+1|恒成立,而|3x+1|﹣|3x+3|≤|(3x+1)﹣(3x+3)|=2,所以2≤|a+1|,得a+1≥2或a+1≤﹣2,解得a≥1或a≤﹣3,即实数a的取值范围是(﹣∞,﹣3]∪[1,+∞).。
铁人中学2017级高二学年下学期开学考试英语试题

铁人中学2017级高二学年下学期开学考试英语试题试题说明:1、本试题满分150分,答题时间120分钟。
2、请将答案填写在答题卡上,考试结束后只交答题卡。
第Ⅰ卷选择题部分第一部分:单项填空(共20小题,每小题1.5分,满分30分)从A、B、C、D四个选项中,选出可以填入空白处的最佳选项。
1.It was______of Michael to inform us of his delay in case we got worried.A.carelessB.considerateC.patientD.generous2.Tom had to______the invitation to the party last weekend because he was too busy.A.turn inB.turn downC.turn overD.turn to3.He always______other’s help______.His colleagues don’t want to cooperate with him.A.considers;seriouslyB.respects;thankfullyC.takes;for grantedD.takes;into account4.—Do you have enough to______all your daily expenses?—Oh yes,enough and to spare.A.coverB.spendC.fillD.offer5.We’ll send you a copy as soon as it becomes_______.We are working on it day and night.A.presentB.qualifiedC.availableD.renewable6.His parents decided that,with two children______,they would open a restaurant.A.to be educatedcatedC.to educatecating7.Mike claims______all his homework,but no one believes him.A.to have finishedB.to be finishingC.having finishedD.that to finish.8.There is a board by the road,which______“Parking______.”A.writes,forbiddingB.reading,forbiddingC.says,forbiddenD.saying,forbidden9.Look at the black clouds!They______that it will rain soon.A.indicateB.adviseC.say D think10.—Sorry,Mum!I failed the job interview again.—Oh,it’s too bad.You______have made full preparations.A.mustB.canC.wouldD.should11.The______look on the manager's face suggested that he______to overcome the difficulty.A.determined;be determinedB.determined;was determinedC.determining;determineD.determining;determined12.______I always felt I would pass the exam,I never thought I would get an A.A.OnceB.WhileC.IfD.Until13.It is the most instructive lecture that I______since I came to this school.A.attendedB.had attendedC.am attendingD.have attended14.Look at the trouble we are in.If only we______our teacher’s advice!A.tookB.would takeC.had takenD.would have taken15.—Where is Mother?—She is in the kitchen.She______the housework all morning.A.has been doingB.was doingC.has doneD.is doing16.Whenever I met her,______was fairly often,she greeted me with a sweet smile.A.whoB.whichC.whenD.that17.—Our country is developing at an amazing speed!—Yes.This is______makes me feel so proud.A.whichB.whyC.whereD.what18.Recently a survey______prices of the same goods in two different supermarkets has caused aheated discussion among citizens.paringparedparesD.being compared19.It was in the park,______stands an old temple,______we asked our guide to take a photo forthe two of us.A.which;thatB.that;whichC.where;thatD.that;where20.______of the danger in the street,she had to go home with a friend______her.A.Warning;followingB.Having warned;followingC.Having been warned;followingD.Warned;followed第二部分阅读理解(共两节20小题;每小题2分,满分40分)第一节:阅读下列短文,从每题所给的四个选项(A、B、C和D)中,选出最佳选项,并在答题卡上将该项涂黑。
黑龙江省大庆铁人中学2018_2019学年高二数学下学期开学考试试题文

铁人中学2017级高二学年下学期开学考试数学(文)试题试题说明:1、本试题满分150分,答题时间120分钟2、请将答案填写在答题卡上,考试结束后只交答题卡第Ⅰ卷 选择题部分一、选择题(每小题只有一个选项正确,每小题5分,共60分) 1.已知条件p :301+>-xx ,条件q :2560-+<x x ,则q ⌝是p ⌝的( ) A .充分不必要条件 B .必要不充分条件 C .充要条件 D .既不充分也不必要条件2. 命题“存在实数x ,x x 212<+”的否定为( )A .存在实数x ,x x 212≥+B .对所有的实数x ,x x 212<+C .不存在实数x ,x x 212≥+ D .对所有的实数x ,x x 212≥+3.从3个红球、2个白球中随机取出2个球,则取出的2个球不全是红球的概率是( ) A .101 B .103 C .107D .534.阅读下面的程序框图,运行相应的程序,则输出i 的值为( )A. 3B. 4C. 5D. 65. 用秦九韶算法计算多项式()31082365223456-+-+++=x x x x x x x f ,当2=x 时,3V 的值为( ) A .9B .24C .71D .1346.已知一个k 进制的数123与十进制的数38相等,那么k =( ) A .7或5 B .7- C .5 D .都不对7.设双曲线12222=-by a x (0>>a b )的半焦距为c ,直线过()0,a ,()b ,0两点,已知原点到直线l 的距离为c 43,则双曲线的离心率为( ) A.2 B.3 C.2 D.332 8.在棱长为2的正方体1111D C B A ABCD -中,点O 为底面ABCD 的中心,在正方体1111D C B A ABCD -内随机取一点P ,则点P 到点O 的距离大于1的概率为( ) A.12π B .121π- C.6π D .61π- 9.现有10名工人某天生产同一零件,生产的件数是15,17,14,10,15,17,17,16,14,12,设其平均数为a ,中位数为b ,众数为c ,则有( )A.c b a >> B .a c b >> C.b a c >> D .a b c >>10.“纹样”是中国艺术宝库的瑰宝,“火纹”是常见的一种传统纹样.为了测算某火纹纹样(如图阴影部分所示)的面积,作一个边长为5的正方形将其包含在内,并向该正方形内随机投掷1000个点,已知恰有400个点落在阴影部分,据此可估计阴影部分的面积是( )A .2B .3C .10D .1511.如图,设抛物线x y 42=的焦点为F ,不经过焦点的直线上有三个不同的点A ,B ,C ,其中点A ,B 在抛物线上,点C 在y 轴上,则BCF ∆与ACF ∆的面积之比是( )A.11--AF BF B.1122--AF BF C.11++AF BF D.1122++AF BF 12. 已知椭圆12222=+by a x (0>>b a )的左、右焦点分别为1F (0,c -),2F (0,c ),若椭圆上存在点P ,使1221sin sin F PF cF PF a ∠=∠成立,则该椭圆的离心率的取值范围是( )A.()10,B.()11-2, C.()11-3, D.()1-20,第Ⅱ卷 非选择题部分二、填空题(每小题5分,共20分) 13. 1785与840的最大公约数为 .14.设中心在原点的椭圆与双曲线12222=-y x 有公共的焦点,且它们的离心率互为倒数,则该椭圆的方程是__________.15. 已知双曲线C :12222=-b y a x (0>a ,0>b )的左右顶点分别为A ,B ,点P 是双曲线C 上与A ,B ,不重合的动点,若2=⋅PB PA k k ,求双曲线的离心率 ________.16. 给出下列4个命题: ①函数()⎪⎭⎫⎝⎛-=32sin πx x f 的图像关于125π=x 对称 . ②命题p ,q 都是假命题,则命题“q p ∧⌝”为真命题.③在空间中,m ,n 是两条不重合的直线,α,β是两个不重合的平面,如果βα⊥,n =βα ,n m ⊥,那么β⊥m .④将函数x y cos =的图象向右平移3π个单位,得到函数⎪⎭⎫ ⎝⎛-=3cos πx y 的图象. 其中正确命题的序号是________.三、解答题(共6小题,共70分)17. (本小题满分10分)设甲、乙、丙三个乒乓球协会的运动员人数分别为27、9、18.现采用分层抽样的方法从这三个协会中抽取6名运动员组队参加比赛. (1)求应从这三个协会中分别抽取的运动员的人数;(2)将抽取的6名运动员进行编号,编号分别为1A 、2A 、3A 、4A 、5A 、6A .现从这6名运动员中随机抽取2人参加双打比赛. ①用所给编号列出所有可能的结果;②设A 为事件“编号为5A 和6A 的两名运动员中至少有1人被抽到”,求事件A 发生的概率.18. (本小题满分12分)我国是世界上严重缺水的国家,某市政府为了鼓励居民节约用水,计划调整居民生活用水收费方案,拟确定一个合理的月用水量标准x (吨),一位居民的月用水量不超过x 的部分按平价收费,超出x 的部分按议价收费.为了了解居民用水情况,通过抽样,获得了某年100位居民每人的月均用水量(单位:吨),将数据按照[)5.0,0,[)1,5.0, ,[]5.4,4分成9组,制成了如图所示的频率分布直方图.(1)求直方图中a 的值;(2)设该市有30万居民,估计全市居民中月均用水量不低于3吨的人数,并说明理由; (3)若该市政府希望使85%的居民每月的用水量不超过标准x (吨),估计x 的值,并说明理由.19. (本小题满分12分)如图所示,茎叶图记录了甲、乙两组各四名同学完成某道数学题(此数学题满分为12分)的得分情况.乙组某个数据的个位数模糊,记为x ,已知甲、乙两组的平均成绩相同.(1)求x 的值,并判断哪组学生成绩更稳定; (2)在甲、乙两组中各抽出一名同学,求这两名同学的得分之和低于20分的概率.20. (本小题满分12分)已知直线2-=kx y 交抛物线x y 82=于A ,B 两点,且AB 的中点的横坐标为2.求弦AB 的长.21. (本小题满分12分)假设关于某设备的使用年限x (年)和所支出的年平均维修费用y (万元)(即维修费用之和除以使用年限),有如下的统计资料:(1)求回归方程.(2)估计使用年限为10年时所支出的年平均维修费用是多少? 参考公式:2121ˆxn x yx n y x bni i ni ii --=∑∑==;x b y aˆˆ-=.22. (本小题满分12分)已知中心在原点,焦点在x 轴上的椭圆,离心率22=e ,是经过抛物线y x 42=的焦点. (1)求椭圆的标准方程;(2)如图,若过点()0,2B 的直线l (斜率不等于零)与 椭圆交于不同的两点E ,F (E 在B ,F 之间), 试求OBE ∆与OBF ∆面积之比的取值范围.铁人中学2017级高二学年下学期开学考试数学(文)试题(答案) 第Ⅰ卷 选择题、填空题部分一、选择题(每小题只有一个选项正确,每小题5分,共60分)三、填空题(每小题5分,共20分)13、 105 . 14、 1222=+y x .15 16、 ①④________. 1.答案:B 2. 答案:D解析:命题“存在实数x ,x x 212<+”为特称命题,其否定为全称命题,注意否定量词的同时否定结论.故选D. 3.答案:C 4. 答案:B 5. 答案:C 6. 答案:C解析:()()3232112322++=+⨯+⨯=k k k k k ,所以38322=++k k ,即03522=-+k k ,解得5=k 或7-=k (舍去). 7. 答案:A 解析:l 的方程为1=+bya x ,原点到直线的距离cb a ab d 4322=+=, 整理得()()04342222=--c aca ,所以c a 23=或c a =2.所以2==a c e 或332. 因为0>>a b ,所以332=e (舍去).故2=e ,故选A. 8. 答案:B 9. 答案:D解析:总和为147,7.14=a ;样本数据17分布最广,即频率最大,为众数,17=c ;中位数为15. 10. 答案:C 11. 答案: A解析:由图形可知,BCF ∆与ACF ∆有公共的顶点F ,且A ,B ,C ,三点共线,易知BCF ∆与ACF ∆的面积之比就等于ACBC.由抛物线方程知焦点()0,1F ,作准线l ,则l 的方程为1-=x .因为点A ,B 在抛物线上,过A ,B 分别作AK ,BH 与准线垂直,垂足分别为点K ,H ,且与y 轴分别交于点N ,M .由抛物线定义,得1-=BF BM ,1-=AF AN .在CAN ∆中,AN BM //,所以11--==AF BF AN BM AC BC . 12. 答案:B 解析:由正弦定理及1221sin sin F PF c F PF a ∠=∠,得212112sin sin PF PF F PF F PF a c =∠∠=. 在21F PF ∆中,设x PF =2,则x a PF -=21,则xx a a c -=2,即22a ax cx =+, 得c a a x +=22.又c a x c a +<<-,所以c a c a a c a +<+<-22. 由ca a c a +<-22,得22c a ->,显然恒成立;由c a ca a +<+22,得0222>-+a ac c ,即0122>-+e e ,解得21+->e 或21--<e (舍去).又10<<e ,所以e 的取值范围是()11-2,,故选B.13.答案:10514.答案:1222=+y x 解析:设椭圆方程为12222=+by a x ,焦点为()0,c -,()0,c .双曲线1212122=-y x 的焦点为()0,1-,()0,1,2=e ,所以椭圆的离心率为22,据题意得221==a a c ,所以2=a ,而122=-b a ,所以12=b .椭圆方程为1222=+y x .15.答案:3 16.答案:①④第Ⅱ卷 解答题部分17. (本小题满分10分)答案:(1)甲、乙、丙三个乒乓球协会的运动员人数分别为27、9、18,则共有5418927=++人,分层抽样的方法从这三个协会中抽取6名运动员,则抽样比为91546=,则39127=⨯人、1919=⨯人、29118=⨯人, 所以应从甲、乙、丙三个协会中抽取的运动员人数分别为3、1、2.(2)①从6名运动员中随机抽取2人参加双打比赛的所有可能结果为{A 1,A 2},{A 1,A 3},{A 1,A 4},{A 1,A 5},{A 1,A 6},{A 2,A 3},{A 2,A 4},{A 2,A 5},{A 2,A 6},{A 3,A 4},{A 3,A 5},{A 3,A 6},{A 4,A 5},{A 4,A 6},{A 5,A 6},共15种.②编号为A 5和A 6的两名运动员中至少有1人被抽到的所有可能结果为{A 1,A 5},{A 1,A 6},{A 2,A 5},{A 2,A 6},{A 3,A 5},{A 3,A 6},{A 4,A 5},{A 4,A 6},{A 5,A 6},共9种. 因此,事件A 发生的概率P (A )=915=35.18. (本小题满分12分)答案:(1)由频率分布直方图知,月均用水量在[0,0.5)中的频率为0.08×0.5=0.04,同理,在[0.5,1),[1.5,2),[2,2.5),[2,5.3),[3,3.5),[3.5,4),[4,4.5]中的频率分别为0.08,0.20,0.26,0.06,0.04,0.02.由0.04+0.08+0.5×a +0.20+0.26+0.5×a +0.06+0.04+0.02=1, 解得a =0. 30.(2)由(1)可知,100位居民每人月均用水量不低于3吨的频率为0.06+0.04+0.02=0.12. 由以上样本的频率,可以估计全市30万居民中月均用水量不低于3吨的人数为 300 000×0.12=36 000.(3)因为前6组的频率之和为0.04+0.08+0.15+0.20+0.26+0.15=0.88>0.85, 而前5组的频率之和为0.04+0.08+0.15+0.20+0.26=0.73<0.85, 所以35.2<≤x .由()73.085.05.23.0-=-⨯x ,解得9.2=x .所以,估计月用水量标准为9.2吨时,85%的居民每月的用水量不超过标准.19. 答案:(1)104111199=+++=甲x ,104101298=++++=xx 乙,所以1=x ,又()()()()[]1101110111091094122222=-+-+-+-=甲s , ()()()()[]25101210111091084122222=-+-+-+-=乙s , 所以22乙甲s s <,所以甲组成绩比乙组稳定.(2)记甲组4名同学为:1A ,2A ,3A ,4A ;乙组4名同学为:1B ,2B ,3B ,4B .分别从甲、乙两组中各抽取一名同学所有可能的结果为:(1A ,1B ),(1A ,2B ),(1A ,3B ),(1A ,4B ),(2A ,1B ),(2A ,2B ),(2A ,3B ),(2A ,4B ),(3A ,1B ),(3A ,2B ),(3A ,3B ),(3A ,4B ),(4A ,1B ),(4A ,2B ),(4A ,3B ),(4A ,4B ),共16种,其中得分之和低于20分的共6种,所以得分之和低于20分的概率83166==P . 20.答案:设A ,B 两点的坐标分别为()11,y x ,()22,y x ,AB 的中点C 的坐标为()0,2y . 将2-=kx y 代入x y 82=中,得方程()042422=++-x k x k , 当()0164>+=∆k ,即1->k 且0≠k 时,方程有两实根1x ,2x . 根据韦达定理知()22124k k x x +=+.又2221=+x x ,故()4242=+k k ,解得2=k 或1-=k (舍) 从而()()1521212212212=-+=-+-=x x k y y x x AB .21. 答案:(1)从散点图可以看出,这些点大致分布在一条直线的附近,因此,两变量呈线性相关关系.()0.46543251=++++⨯=x ,()0.50.75.65.58.32.251=++++⨯=y ;3.11251=∑=i ii yx ,1005=y x ,90512=∑=i i x ,8052=x ,所以23.1ˆ=b,08.0ˆ=a 可求回归方程是08.023.1ˆ+=x y(2)由(1)知,当10=x 时, 38.1208.01023.1ˆ=+⨯=y(万元). 故估计使用年限为10年时所支出的年平均维修费用是38.12万元.22. 答案:(1)设椭圆方程为12222=+b y a x (0>>b a ),则22==a c e ①因为抛物线y x 42=的焦点为()1,0,所以1102222=+ba ②由①②解得22=a ,12=b .所以椭圆的标准方程为1222=+y x . (2)如下图所示,由题意知直线l 的斜率存在且不为零, 设l 的方程为()2-=x k y (0≠k )③将③代入1222=+y x ,整理得()()028*******=-+-+k x k x k . 由0>∆得2102<<k .设()11,y x E ,()22,y x F ,则⎪⎪⎩⎪⎪⎨⎧+-=⋅+=+122812822212221k k x x k k x x ④ 令OBF OBES S ∆∆=λ,则BFBE =λ. 由此得λ=,2221--=x x λ,且10<<λ.由④得()()12422221+-=-+-k x x , ()()()12242222212121+=++-=-⋅-k x x x x x x ,所以()812122+=+k λλ,即()211422-+=λλk .因为2102<<k ,所以()21211402<-+<λλ 解得223223+<<-λ.又因为10<<λ,所以1223<<-λ. 所以OBE ∆和OBF ∆面积之比的取值范围是(223-,1).。
黑龙江省大庆铁人中学2018_2019学年高二化学下学期开学考试试题

铁人中学2017级高二学年下学期开学考试化学试题试题说明:1、本试题满分分,答题时间分钟。
2、请将答案填写在答题卡上,考试结束后只交答题卡。
3、可能用到的相对原子质量:H:1 C:12 N:14 O:16 S:32 Na:23 Fe:56 Cu:64 K:39第Ⅰ卷选择题部分(共42分)选择题(每小题只有一个选项正确,每小题2分,共42分。
)1.对于可逆反应 A(g)+2B(g)⇌2C(g)H<0,达到平衡时,要使正反应速率增大,且A的转化率增大,以下采取的措施可行的是()A.升高温度 B.增大 A的浓度 C.减小 C 的浓度 D.增大压强2.下列不能用勒夏特列原理解释的事实是( )A.棕红色的NO2加压后颜色先变深后变浅B.氢气、碘蒸气、碘化氢气体组成的平衡体系加压后颜色变深C.黄绿色的氯水光照后颜色变浅D.合成氨工业使用高压以提高氨的产量3.对于可逆反应N2(g)+3H2(g)2NH3(g) ΔH<0,下列各项对示意图的解释与图象相符的是( )A.①压强对反应的影响(p2>p1)B.②温度对反应的影响C.③平衡体系增加N2对反应的影响D.④催化剂对反应的影响4.N2O5是一种新型硝化剂。
在一定温度下可发生以下反应:2N 2O5(g)4NO2(g)+O2(g) ΔH>0,T1温度下的部分实验数据见下表500 1 000 1 500A.500 s内N2O5分解速率为2.96×10-3mol·(L·s)-1B.T1温度下的平衡常数为K1=125,1 000 s时转化率为50%C.T1温度下的平衡常数为K1,T3温度下的平衡常数为K3,若K1>K3,则T1>T3D.其他条件不变时,T2温度下反应到1 000 s时测得N2O5(g)浓度为2.98 mol·L-1,则T1<T25.常温时,下列三种溶液:①0.001 mol·L-1氨水与0.001 mol·L-1HCl溶液等体积混合液②pH=3的HCl与pH=11的NaOH溶液等体积混合液③pH=11的氨水与pH=3的HCl溶液等体积混合液。
黑龙江省大庆铁人中学2017-2018学年高二下学期开学考试(3月)生物Word版含答案

大庆铁人中学高二学年下学期开学验收考试生物试题命题人:刘佳菊审题人:郑红梅试题说明:1、本试题满分100 分,答题时间90分钟。
2、请将答案填写在答题卡上,考试结束后只交答题卡。
第Ⅰ卷选择题部分一、选择题(每小题只有一个选项正确,每小题2分,共60分。
)1.下列有关稳态的叙述中,正确的是()A. 稳态是机体通过消化、呼吸、循环、排泄这四个系统的协调活动来维持B. 内环境稳态就是机体在神经﹣体液﹣免疫调节网络的调节下,通过各器官、系统的协调配合共同维持内环境各种成分相对稳定的状态C. 在正常情况下,内环境的各项理化性质是保持不变的D. 在正常情况下,内环境中各成分的含量是经常处于变动之中,但保持在适宜的范围内2.在刚刚过去的校运动会上,某同学由于长时间运动引起机体缺氧时,血液pH的变化趋势、引起pH变化的物质、能起缓冲作用的物质分别为()A. 降低、CO2、Na2CO3B. 降低、乳酸、NaHCO3C. 升高、CO2、H2CO3D. 升高、乳酸、NaHCO33.下列说法正确的是()A. 激素、ATP合成酶和氨基酸都属于人体内环境的组成成分B. 肾上腺、甲状腺、唾液腺产生的分泌物,均直接排放到内环境中C. 外界环境的变化和体内细胞代谢活动均可影响内环境的稳态D. 血糖浓度、尿液浓度、体内温度、细胞外液渗透压的相对稳定都属于内环境的稳态4.下图是细胞直接与内环境进行物质交换的示意图,⑤处箭头表示血液流动的方向。
下列说法正确的是()A. ①是人体内新陈代谢的主要场所B. ③生活的内环境中的水可来自于①和④C. ①中的葡萄糖至少需穿过3层生物膜才能被③利用D. 若③为肺泡细胞,则①处的氧气浓度低于⑤处5.如图为测定A、B为两个神经元之间电流传递的实验装置,图中ab=cd。
用微电极分别刺激b、c处,电流表的变化是()A. 刺激b点,B神经元上电位由“外负内正”迅速变为“外正内负”B. 刺激c点,A神经元上电位由“外正内负”迅速变为“外负内正”C. 刺激b点,灵敏电流针发生2次方向相反的偏转D. 刺激c点,灵敏电流计发生2次方向相同的偏转6.肉毒杆菌毒素是从肉毒杆菌提取的一种细菌毒素蛋白,它能阻遏乙酰胆碱释放,从而起到麻痹肌肉的作用。
黑龙江省大庆铁人中学2017-2018学年高二英语下学期开学考试(3月)试题答案

答案第I卷第一部分:基础知识考查(每小题1.5分,共20小题,满分 30 分)1-4 ACBD 5-8 DABC 9-12 ADBC 13-16 CADB 17-20 CABD第二部分:阅读理解(每小题2分,共20小题,满分40分)21-24 BBAD 25-28 DCBB 29-31ACD 32-35 DADB 36-40 AFDGC.第三部分完形填空(共20小题;每小题1.5分,满分30分)41-45ACBDC 46-50BCAAB 51-55CCBDB 56-60 ABADC第Ⅱ卷第一节:语法填空(共10题,每题1.5分,共15分)61. strangely 62. until 63. mine 64. why 65. a66. fearing 67. than 68. preparations 69. like 70.needs第二节:短文改错(满分10分)71.... join in our ... 去掉in72.... as more time as ... more →much73.... who likes playing ... likes→like74.... the important rule ... rule→rules75.And I was ... was→am76.... a strongly basketball ... strongly→strong77.... help me improved ... improved→improve78.... one of best ... best 前加the79.If I make ... I→they80.... they will won. won→win第三节:书面表达(满分25分)Hi,Sharon,This is Li Xia.I learned from your post that you want to improve your Mandarin. I am willing to help you with your Mandarin.As a native Chinese speaker,I can speak Chinese clearly and fluently,and my teachers think highly of my spoken Chinese.I have taught some foreigners Mandarin, which makes me have much experience in teaching.As for speaking Mandarin, it’s better to pay much attention to the pronunciation.Besides,you must take notice of the handwriting. And you also should keep it in mind that comparing notes with your classmates frequently is a good way to improve your study.In return I hope you can help me with my spoken English.When I speak English,I often feel a little nervous. Can you give me some advice on how to overcome that?Looking forward to hearing from you.Li Xia1。
黑龙江省大庆市2017_2018学年高二物理下学期开学考试3月试题_含答案 师生通用

大庆铁人中学高二学年下学期开学考试物理试题试题说明:1、本试题满分110分,答题时间90分钟。
2、请将答案填写在答题卡上,考试结束后只交答题卡。
一、选择题(每小题5分,共60分.1-8题单选,9-12多选,全部选对得5分,选对但不全得3分,有错选得0分)1.下列装置中没有用到带电粒子在磁场中发生偏转的原理的是( ) A .磁流体发电机 B .回旋加速器 C .示波管 D .电视显像管2.如图所示,A 和B 是两个完全相同的灯泡,C 和D 都是理想二极管,两二极管的正向电阻为零,反向电阻无穷大,L 是带铁芯的线圈,其自感系数很大,直流电阻忽略不计。
下列说法正确的是( ) A .开关S 闭合,A 先亮B .开关S 闭合,A 、B 同时亮C .开关S 断开,B 逐渐熄灭D .开关S 断开,A 闪亮一下,然后逐渐熄灭3.1922年英国物理学家阿斯顿因质谱仪的发明、同位素和质谱的研究荣获了诺贝尔化学奖。
若速度相同的一束粒子由左端射入质谱仪后的运动轨迹如图所示,则下列说法正确的是( ) A .该束带电粒子带负电B .速度选择器的P 1极板带正电C .在B 2磁场中运动半径越大的粒子,质量越大D .在B 2磁场中运动半径越大的粒子,比荷q/m 越大4.如图所示,把一个装有导电溶液的圆形玻璃器皿放入磁场中,玻璃器皿的中心放一个圆柱形电极B ,与电池的正极相连;沿器皿边缘内壁放一个圆环形电极A ,与电池的负极相连。
从器皿上方往下看(俯视),对于导电溶液和溶液中正、负离子的运动,下列说法中正确的是( ) A .溶液做逆时针方向运动 B .溶液做顺时针方向运动C .正离子沿圆形玻璃器皿的半径向边缘移动D .负离子沿圆形玻璃器皿的半径向中心移动5.现将电池组、滑线变阻器、带铁芯的线圈A 、线圈B 、电流计及开关如下图连接。
在开关闭合、线圈A 放在线圈B 中的情况下,某同学发现当他将滑线变阻器的滑动端P 向左加速滑动时,电流计指针向右偏转。
2017-2018学年黑龙江省大庆市铁人中学高二(下)段考数学试卷(文科) Word版含解析
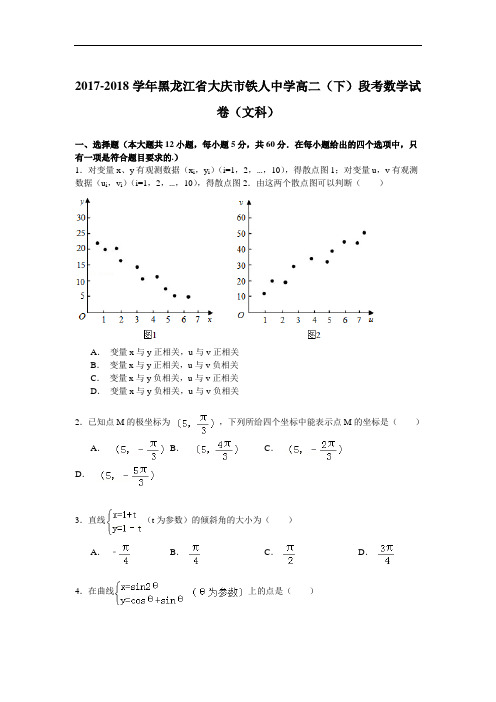
2017-2018学年黑龙江省大庆市铁人中学高二(下)段考数学试卷(文科)一、选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.)1.对变量x、y有观测数据(x i,y i)(i=1,2,…,10),得散点图1;对变量u,v有观测数据(u i,v i)(i=1,2,…,10),得散点图2.由这两个散点图可以判断()A.变量x与y正相关,u与v正相关B.变量x与y正相关,u与v负相关C.变量x与y负相关,u与v正相关D.变量x与y负相关,u与v负相关2.已知点M的极坐标为,下列所给四个坐标中能表示点M的坐标是()A. B.C.D.3.直线(t为参数)的倾斜角的大小为()A.﹣B.C.D.4.在曲线上的点是()A.B.C.D.5.将曲线c按伸缩变换公式变换得到曲线方程为x/2+y/2=1,则曲线c的方程为()A.B.C.4x2+9y2=1 D.4x2+9y2=366.化极坐标方程ρ2cosθ﹣ρ=0为直角坐标方程为()A.x2+y2=0或y=1 B.x=1 C.x2+y2=0或x=1 D.y=17.已知点P的极坐标是(1,π),则过点P且垂直极轴所在直线的直线方程是()A.ρ=1 B.ρ=cosθC.D.8.直线:3x﹣4y﹣9=0与圆:,(θ为参数)的位置关系是()A.相切B.相离C.直线过圆心D.相交但直线不过圆心9.椭圆(φ是参数)的离心率是()A.B.C.D.10.在吸烟与患肺病这两个分类变量的计算中,下列说法正确的是()①若k2的观测值满足k2≥6.635,我们有99%的把握认为吸烟与患肺病有关系,那么在100个吸烟的人中必有99人患有肺病;②从独立性检验可知有99%的把握认为吸烟与患病有关系时,我们说某人吸烟,那么他有99%的可能患有肺病;③从统计量中得知在犯错误的概率不超过0.05的前提下认为吸烟与患肺病有关系.A.①B.①③C.③D.②12.面直角坐标系中,直线l的参数方程是(t为参数),以坐标原点为极点,x轴的正半轴为极轴,建立极坐标系,已知曲线C的极坐标方程为ρ2cos2θ+ρ2sin2θ﹣2ρsinθ﹣3=0.若直线l与曲线C相交于A、B两点,则|AB|=()A.B.C.3 D.13.直角坐标系xoy中,以原点为极点,x轴的正半轴为极轴建立极坐标系,设点A,B分别在曲线C1:(θ为参数)和曲线C2:ρ=1上,则|AB|的最小值为()A.3 B.C.D.二、填空题(本大题共4小题,每小题5分,共20分)14.已知x、y的取值如下表:x 0 1 3 4y 2.2 4.3 4.8 6.7从散点图分析,y与x线性相关,且回归方程为=0.95x+a,则a=.15.极点到直线的距离为.16.已知M为双曲线﹣y2=1(a>0)上任意一点,O为原点,过点M做双曲线两渐近线的平行线,分别与两渐近线交于A,B两点.若平行四边形MAOB的面积为2,则a=.17.(坐标系与参数方程选做题)已知曲线C的参数方程为(θ为参数),则曲线C上的点到直线x+y+2=0的距离的最大值为.三、解答题(本大题共6小题,共70分.解答应写出必要的文字说明、证明过程或演算步骤)18.设直线l经过点M0(1,5)、倾斜角为.(1)求直线l的参数方程;(2)若直线l和圆x2+y2=16的两个交点为A、B,求|MA|•|MB|.19.已知点P(x,y)是圆x2+y2=2y上的动点,(1)求2x+y的取值范围;(2)若x+y+a≥0恒成立,求实数a的取值范围.20.某企业有两个分厂生产某种零件,按规定内径尺寸(单位:mm)的值落在(29.94,30.06)的零件为优质品.从两个分厂生产的零件中抽出500件,量其内径尺寸的结果如表:甲厂分组[29.86,29.90)[29.90,29.94)[29.94,29.98)[29.98,30.02)[30.02,30.06)[30.06,30.10)[30.10,30.14)频数12 63 86 182 92 61 4 乙厂分组[29.86,29.90)[29.90,29.94)[29.94,29.98)[29.98,30.02)[30.02,30.06)[30.06,30.10)[3 0.10,30.14)频数29 71 85 159 76 62 18 (1)试分别估计两个分厂生产的零件的优质品率;(2)由于以上统计数据填下面2×2列联表,并问是否有99%的把握认为“两个分厂生产的零件的质量有差异”.甲厂乙厂合计优质品非优质品合计下面的临界值表供参考:(参考公式:K2=,其中n=a+b+c+d)P=(K2≥k0)0.15 0.10 0.05[ 0.025 0.010 0.005 0.001k0 2.072 2.706 3.841 5.024 6.635 7.879 10.82821.平面直角坐标系中,将曲线(a为参数)上的每一点横坐标不变,纵坐标变为原来的2倍得到曲线C1,以坐标原点为极点,x轴的非负半轴为极轴,建立的极坐标系中,曲线C2的方程为ρ=4sinθ.(1)求曲线C1的普通方程和曲线C2的直角坐标方程;(2)求C1和C2公共弦的垂直平分线的极坐标方程.22.为了解七班学生喜爱打篮球是否与性别有关,对本班50人进行了问卷调查得到了如下的列联表:已知在全部50人中随机抽取1人抽到喜爱打篮球的学生的概率为.喜爱打篮球不喜爱打篮球合计男生 5女生10合计50(1)请将上面的列联表补充完整(不用写计算过程);(2)能否在犯错误的概率不超过0.005的前提下认为喜爱打篮球与性别有关?说明你的理由.23.在直角坐标系xOy中,直线l的参数方程为(t为参数,0≤α<π).以原点为极点,x轴的正半轴为极轴建立极坐标系.已知曲线C的极坐标方程为ρcos2θ=4sinθ.(1)求直线l与曲线C的平面直角坐标方程;(2)设直线l与曲线C交于不同的两点A、B,若|AB|=8,求α的值.2017-2018学年黑龙江省大庆市铁人中学高二(下)段考数学试卷(文科)参考答案与试题解析一、选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.)1.对变量x、y有观测数据(x i,y i)(i=1,2,…,10),得散点图1;对变量u,v有观测数据(u i,v i)(i=1,2,…,10),得散点图2.由这两个散点图可以判断()A.变量x与y正相关,u与v正相关B.变量x与y正相关,u与v负相关C.变量x与y负相关,u与v正相关D.变量x与y负相关,u与v负相关考点:散点图.专题:数形结合法.分析:通过观察散点图可以知道,y随x的增大而减小,各点整体呈下降趋势,x与y负相关,u随v的增大而增大,各点整体呈上升趋势,u与v正相关.解答:解:由题图1可知,y随x的增大而减小,各点整体呈下降趋势,x与y负相关,由题图2可知,u随v的增大而增大,各点整体呈上升趋势,u与v正相关.故选C点评:本题考查散点图,是通过读图来解决问题,考查读图能力,是一个基础题,本题可以粗略的反应两个变量之间的关系,是不是线性相关,是正相关还是负相关.2.已知点M的极坐标为,下列所给四个坐标中能表示点M的坐标是()A. B.C.D.考点:点的极坐标和直角坐标的互化.专题:计算题.分析:由于和是终边相同的角,故点M的极坐标也可表示为.解答:解:点M的极坐标为,由于和是终边相同的角,故点M 的坐标也可表示为,故选D.点评:本题考查点的极坐标、终边相同的角的表示方法,是一道基础题.3.直线(t为参数)的倾斜角的大小为()A.﹣B.C.D.考点:直线的倾斜角;直线的参数方程.专题:计算题;直线与圆.分析:化参数方程为普通方程,求出斜率,即可求得倾斜角.解答:解:化参数方程为普通方程,两方程相加可得x+y=2,则直线的斜率为﹣1,故倾斜角为故选D.点评:本题考查直线的斜率与倾斜角的关系,解题的关键是化参数方程为普通方程.4.在曲线上的点是()A.B.C.D.考点:参数方程化成普通方程.专题:计算题.分析:先找曲线的普通方程y2=1+x,结合选项可找出符合条件的点.解答:解:曲线的普通方程为y2=1+xx=sin2θ≤1结合选项可得时,满足条件故选:B点评:本题目主要考查了参数方程化为普通方程,解题的关键是灵活利用三角函数的二倍角公式及同角平方关系,属于基础试题.5.将曲线c按伸缩变换公式变换得到曲线方程为x/2+y/2=1,则曲线c的方程为()A.B.C.4x2+9y2=1 D.4x2+9y2=36考点:伸缩变换.专题:计算题.分析:只要把伸缩变换公式代入曲线方程为x/2+y/2=1,即可得原曲线c的方程.解答:解:由题意,把伸缩变换公式代入曲线方程为x/2+y/2=1,得(2x)2+(3y)2=1,即4x2+9y2=1.∴曲线c的方程为4x2+9y2=1.故选C.点评:本题考查了伸缩变换,弄清变化公式的意义和求解的方程即可.6.化极坐标方程ρ2cosθ﹣ρ=0为直角坐标方程为()A.x2+y2=0或y=1 B.x=1 C.x2+y2=0或x=1 D.y=1考点:点的极坐标和直角坐标的互化.专题:计算题.分析:利用直角坐标与极坐标间的关系,即利用ρcosθ=x,ρsinθ=y,ρ2=x2+y2,进行代换即得.解答:解:∵ρ2cosθ﹣ρ=0,∴ρcosθ﹣1=0或ρ=0,∵,∴x2+y2=0或x=1,故选C.点评:本题考查点的极坐标和直角坐标的互化,能在极坐标系中用极坐标刻画点的位置,体会在极坐标系和平面直角坐标系中刻画点的位置的区别,能进行极坐标和直角坐标的互化.7.已知点P的极坐标是(1,π),则过点P且垂直极轴所在直线的直线方程是()A.ρ=1 B.ρ=cosθC.D.考点:简单曲线的极坐标方程.专题:计算题.分析:利用点P的直角坐标是(﹣1,0),过点P且垂直极轴所在直线的直线方程是x=﹣1,化为极坐标方程,得到答案.解答:解:点P的直角坐标是(﹣1,0),则过点P且垂直极轴所在直线的直线方程是x=﹣1,化为极坐标方程为ρcosθ=﹣1,即,故选C.点评:本题考查参数方程与普通方程之间的转化,得到过点P且垂直极轴所在直线的直线方程是x=﹣1,是解题的关键.8.直线:3x﹣4y﹣9=0与圆:,(θ为参数)的位置关系是()A.相切B.相离C.直线过圆心D.相交但直线不过圆心考点:直线与圆的位置关系.专题:计算题.分析:根据圆的参数方程变化成圆的标准方程,看出圆心和半径,计算圆心到直线的距离,比较距离与半径的大小关系,得到位置关系.解答:解:∵圆:,(θ为参数)∴圆的标准方程是x2+y2=4圆心是(0,0),半径是2,∴圆心到直线的距离是d==<r∴直线与圆相交,且不过圆心,故选D.点评:本题考查直线与圆的位置关系,本题解题的关键是求出圆的标准方程,算出圆心到直线的距离,本题是一个基础题.9.椭圆(φ是参数)的离心率是()A.B.C.D.考点:参数方程化成普通方程;椭圆的简单性质.专题:圆锥曲线的定义、性质与方程.分析:把椭圆的参数化为普通方程为+=1,求出a、b、c 的值,再根据离心率等于e=求得结果.解答:解:椭圆(φ是参数)消去参数化为普通方程为+=1,∴a=5,b=3,∴c=4,∴e==,故选B.点评:本题主要考查把参数方程化为普通方程的方法,本题主要考查椭圆的标准方程,以及简单性质的应用,属于基础题.10.在吸烟与患肺病这两个分类变量的计算中,下列说法正确的是()①若k2的观测值满足k2≥6.635,我们有99%的把握认为吸烟与患肺病有关系,那么在100个吸烟的人中必有99人患有肺病;②从独立性检验可知有99%的把握认为吸烟与患病有关系时,我们说某人吸烟,那么他有99%的可能患有肺病;③从统计量中得知在犯错误的概率不超过0.05的前提下认为吸烟与患肺病有关系.A.①B.①③C.③D.②考点:独立性检验的应用.专题:应用题;概率与统计.分析:本题的考察点是独立性检验的应用,根据独立性检测考察两个变量是否有关系的方法进行判断,准确的理解判断方法及K2的含义是解决本题的关键.解答:解:①若k2的观测值为k=6.635,我们有99%的把握认为吸烟与患肺病有关系,但不表示在100个吸烟的人中必有99人患有肺病,故不正确.②从独立性检验可知有99%的把握认为吸烟与患病有关系时,也不表示某人吸烟,那么他有99%的可能患有肺病,故不正确.③若从统计量中求出有95%的是吸烟与患肺病的比例,表示在犯错误的概率不超过0.05的前提下认为吸烟与患肺病有关系,故正确.故选:C.点评:若要推断的论述为H:“X与Y有关系”,可以利用独立性检验来考查两个变量是否有关系,并且能较精确地给出这种判断的可靠程度.12.面直角坐标系中,直线l的参数方程是(t为参数),以坐标原点为极点,x轴的正半轴为极轴,建立极坐标系,已知曲线C的极坐标方程为ρ2cos2θ+ρ2sin2θ﹣2ρsinθ﹣3=0.若直线l与曲线C相交于A、B两点,则|AB|=()A.B.C.3 D.考点:简单曲线的极坐标方程;参数方程化成普通方程.专题:坐标系和参数方程.分析:化极坐标方程为直角坐标方程,化参数方程为普通方程,联立后利用弦长公式得答案.解答:解:由,得y=,由ρ2cos2θ+ρ2sin2θ﹣2ρsinθ﹣3=0,得x2+y2﹣2y﹣3=0,联立,得.设A(x1,y1),B(x2,y2),则.∴|AB|=.故选:B.点评:本题考查简单曲线的极坐标方程,考查了参数方程化普通方程,训练了弦长公式的应用,是基础题.13.直角坐标系xoy中,以原点为极点,x轴的正半轴为极轴建立极坐标系,设点A,B分别在曲线C1:(θ为参数)和曲线C2:ρ=1上,则|AB|的最小值为()A.3 B.C.D.考点:参数方程化成普通方程.专题:坐标系和参数方程.分析:把极坐标与参数方程分别化为直角坐标方程、普通方程,利用两点之间的距离公式求出圆心之间的距离,即可得出.解答:解:曲线C1:(θ为参数),化为(x﹣3)2+(y﹣4)2=1,可得圆心C1(3,4),半径R=1;曲线C2:ρ=1,化为x2+y2=1,可得圆心C2(0,0),半径r=1.|C1C2|==5.∴|AB|的最小值=5﹣R﹣r=3.故选:A.点评:本题考查了参数方程化为普通方程、极坐标方程化为直角坐标方程、两点之间的距离公式,考查了推理能力与计算能力,属于中档题.二、填空题(本大题共4小题,每小题5分,共20分)14.已知x、y的取值如下表:x 0 1 3 4y 2.2 4.3 4.8 6.7从散点图分析,y与x线性相关,且回归方程为=0.95x+a,则a= 2.6.考点:最小二乘法;线性回归方程.专题:计算题.分析:本题考查的知识点是线性回归直线的性质,由线性回归直线方程中系数的求法,我们可知在回归直线上,满足回归直线的方程,我们根据已知表中数据计算出,再将点的坐标代入回归直线方程,即可求出对应的a值.解答:解:点在回归直线上,计算得;代入得a=2.6;故答案为2.6.点评:统计也是高考新增的考点,回归直线方程的求法,又是统计中的一个重要知识点,其系数公式及性质要求大家要熟练掌握并应用.15.极点到直线的距离为.考点:简单曲线的极坐标方程.专题:计算题.分析:将直线的极坐标方程化为普通方程,利用点到直线间的距离公式即可解决.解答:解;∵ρ=(ρ∈R),∴sin(θ+)=1,∴•(sinθ+cosθ)=1,∴ρsinθ+ρcosθ=1,而ρcosθ=x,ρsinθ=y,∴x+y=1.∴极点到直线的距离转化为原点到直线x+y=1的距离,设为d,则d==.故答案为:.点评:本题考查直线的极坐标方程,化为普通方程是关键,属于基础题.16.已知M为双曲线﹣y2=1(a>0)上任意一点,O为原点,过点M做双曲线两渐近线的平行线,分别与两渐近线交于A,B两点.若平行四边形MAOB的面积为2,则a=16.考点:双曲线的简单性质.专题:计算题;圆锥曲线的定义、性质与方程.分析:求出|OA|,M点到OA的距离,利用平行四边形MAOB的面积为2,求出a.解答:解:双曲线的渐近线方程是:x±y=0,设M(m,n)是双曲线上任一点,过M平行于OB:x+y=0的方程是:x+y﹣m﹣n=0,联立x﹣y=0,得两直线交点A(,),|OA|=(),M点到OA的距离是:d=,∵|OA|•d=2,∴()•=2,∴m2﹣an2=4,∵m2﹣an2=a,∴a=16.故答案为:16.点评:本题考查双曲线的方程与性质,考查学生的计算能力,是中档题.17.(坐标系与参数方程选做题)已知曲线C的参数方程为(θ为参数),则曲线C上的点到直线x+y+2=0的距离的最大值为+1.考点:圆的参数方程;点到直线的距离公式.专题:计算题.分析:把曲线C的参数方程化为普通方程为(x﹣1)2+y2=1,表示以(1,0)为圆心,半径等于1的圆.求出圆心到直线的距离,将此距离再加上半径,即得所求.解答:解:∵曲线C的参数方程为(θ为参数),消去参数化为普通方程为(x ﹣1)2+y2=1,表示以(1,0)为圆心,半径等于1的圆.圆心到直线x+y+2=0的距离为=,故曲线C上的点到直线x+y+2=0的距离的最大值为+1,故答案为+1.点评:本题主要考查把参数方程化为普通方程的方法,点到直线的距离公式的应用,直线和圆的位置关系,属于基础题.三、解答题(本大题共6小题,共70分.解答应写出必要的文字说明、证明过程或演算步骤)18.设直线l经过点M0(1,5)、倾斜角为.(1)求直线l的参数方程;(2)若直线l和圆x2+y2=16的两个交点为A、B,求|MA|•|MB|.考点:参数方程化成普通方程.专题:坐标系和参数方程.分析:(1)由=,经过点M0(1,5),即可得出直线l的参数方程.(2)把直线l的参数方程代入圆x2+y2=16可得+10=0.利用|MA|•|MB|=|t1t2|即可得出.解答:解:(1)∵=,经过点M0(1,5),∴直线l的参数方程为.(2)把直线l的参数方程代入圆x2+y2=16可得+10=0.∴t1t2=10.∴|MA|•|MB|=|t1t2|=10.点评:本题考查了直线的参数方程及其应用、直线与曲线相交弦长问题,考查了推理能力与计算能力,属于中档题.19.已知点P(x,y)是圆x2+y2=2y上的动点,(1)求2x+y的取值范围;(2)若x+y+a≥0恒成立,求实数a的取值范围.考点:圆的参数方程;函数恒成立问题;正弦函数的单调性.专题:计算题.分析:(1)先将圆的一般式方程转化成参数方程,然后代入所求的表达式中,利用辅助角公式求出取值范围即可;(2)将圆的参数方程代入所求的关系式,将参数a分离出来,研究不等式另一侧的最值确保恒成立即可.解答:解:(1)设圆的参数方程为,∴.(2)x+y+a=cosθ+sinθ+1+a≥0恒成立,∴,∴.点评:本题主要考查了圆的参数方程,以及恒成立问题和正弦函数的值域问题,属于基础题.20.某企业有两个分厂生产某种零件,按规定内径尺寸(单位:mm)的值落在(29.94,30.06)的零件为优质品.从两个分厂生产的零件中抽出500件,量其内径尺寸的结果如表:甲厂分组[29.86,29.90)[29.90,29.94)[29.94,29.98)[29.98,30.02)[30.02,30.06)[30.06,30.10)[30.10,30.14)频数12 63 86 182 92 61 4 乙厂分组[29.86,29.90)[29.90,29.94)[29.94,29.98)[29.98,30.02)[30.02,30.06)[30.06,30.10)[3 0.10,30.14)频数29 71 85 159 76 62 18 (1)试分别估计两个分厂生产的零件的优质品率;(2)由于以上统计数据填下面2×2列联表,并问是否有99%的把握认为“两个分厂生产的零件的质量有差异”.甲厂乙厂合计优质品非优质品合计下面的临界值表供参考:(参考公式:K2=,其中n=a+b+c+d)P=(K2≥k0)0.15 0.10 0.05[ 0.025 0.010 0.005 0.001k0 2.072 2.706 3.841 5.024 6.635 7.879 10.828考点:独立性检验的应用.分析:(1)利用优质品数除以样本容量,即可估计零件的优质品率;(2)利用统计数据可填写2×2列联表,再利用公式,求出k2,利用给出的临界值表,即可得出结论.解答:解:(1)甲厂抽查的产品中有360件优质品,从而甲厂生产的零件的优质品率估计为=72%;乙厂抽查的产品中有320件优质品,从而乙厂生产的零件的优质品率估计为=64%.(2)甲厂乙厂合计优质品360 320 680非优质品140 180 320合计500 500 1000k2=≈7.35>6.635,所以有99%的把握认为“两个分厂生产的零件的质量质量有差异”.点评:本题重点考查独立性检验的应用,解题的关键是正确统计,运用好公式,属于基础题.21.平面直角坐标系中,将曲线(a为参数)上的每一点横坐标不变,纵坐标变为原来的2倍得到曲线C1,以坐标原点为极点,x轴的非负半轴为极轴,建立的极坐标系中,曲线C2的方程为ρ=4sinθ.(1)求曲线C1的普通方程和曲线C2的直角坐标方程;(2)求C1和C2公共弦的垂直平分线的极坐标方程.考点:参数方程化成普通方程.专题:坐标系和参数方程.分析:(1)消去参数以及利用极坐标方程和普通坐标之间的关系进行化简即可求曲线C1的普通方程和曲线C2的直角坐标方程;(2)C1和C2公共弦的垂直平分线实质是两圆圆心对应的直线,然后转化为极坐标即可.解答:解:(Ⅰ)横坐标不变,纵坐标变为原来的2倍得到(α为参数)∴消去参数α得C1:(x﹣2)2+y2=4,由ρ=4sinθ.得ρ2=4ρsinθ.即x2+y2=4y,即x2+y2﹣4y=0,即C2:x2+y2﹣4y=0.(Ⅱ)由(Ⅰ)知C1:(x﹣2)2+y2=4的圆心为C1:(2,0),C2:x2+y2﹣4y=0,即:x2+(y﹣2)2=4,圆心为C2:(0,2),则C1和C2公共弦的垂直平分线即为直线的C1C2:,即x+y=2,∵x=ρcosθ,y=ρsinθ,∴ρcosθ+ρsinθ=2,即ρcos(θ﹣)=,即极坐标方程是ρcos(θ﹣)=.点评:本题主要考查参数方程,极坐标方程和直角坐标方程之间的转化,要求熟练掌握相应的转化公式.22.为了解七班学生喜爱打篮球是否与性别有关,对本班50人进行了问卷调查得到了如下的列联表:已知在全部50人中随机抽取1人抽到喜爱打篮球的学生的概率为.喜爱打篮球不喜爱打篮球合计男生 5女生10合计50(1)请将上面的列联表补充完整(不用写计算过程);(2)能否在犯错误的概率不超过0.005的前提下认为喜爱打篮球与性别有关?说明你的理由.考点:独立性检验的应用.专题:计算题;概率与统计.分析:(1)由在全部50人中随机抽取1人抽到喜爱打篮球的学生的概率为,我们可以计算出喜爱打篮球的学生人数为30,我们易得到表中各项数据的值.(2)我们可以根据列联表中的数据,代入公式,计算出K2值,然后代入离散系数表,比较即可得到答案.解答:解:(1)列联表补充如下:﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣(6分)喜爱打篮球不喜爱打篮球合计男生20 5 25女生10 15 25合计30 20 50(2)∵K2=≈8.333>7.879,∴在犯错误的概率不超过0.005的前提下,认为喜爱打篮球与性别有关.点评:独立性检验的应用的步骤为:根据已知条件将数据归结到一个表格内,列出列联表,再根据列联表中的数据,代入公式,计算出K2值,然后代入离散系数表,比较即可得到答案.23.在直角坐标系xOy中,直线l的参数方程为(t为参数,0≤α<π).以原点为极点,x轴的正半轴为极轴建立极坐标系.已知曲线C的极坐标方程为ρcos2θ=4sinθ.(1)求直线l与曲线C的平面直角坐标方程;(2)设直线l与曲线C交于不同的两点A、B,若|AB|=8,求α的值.考点:直线的参数方程;简单曲线的极坐标方程.专题:直线与圆.分析:(1)先利用消去参数t得到曲线C的直角坐标方程.再将原极坐标方程ρcos2θ=4sinθ两边同时乘以ρ,利用极坐标与直角坐标之间的关系即可得出其直角坐标方程;(2)将代入曲线C的标准方程:x2=4y得:t2cos2α﹣4tsinα﹣4=0,利用直线的参数方程中t的几何意义结合根与系数的关系建立关于α的方程即可求出求出α的值.解答:解:(1)消去参数t,得直线l的直角坐标方程为:sinαx﹣cosαy+cosα=0.曲线C的极坐标方程为ρcos2θ=4sinθ,即ρ2cos2θ=4ρsinθ,曲线C的标准方程:x2=4y.(2)将代入曲线C的标准方程:x2=4y得:t2cos2α﹣4tsinα﹣4=0,∴|AB|=|t1﹣t2|==8,∴cosα=.∴或.点评:本题考查点的极坐标和直角坐标的互化,以及利用平面几何知识解决最值问题.利用直角坐标与极坐标间的关系,即利用ρcosθ=x,ρsinθ=y,ρ2=x2+y2,进行代换即得.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
大庆铁人中学高二下学期开学验收考试地理试题第Ⅰ卷一、选择题(每小题只有一个选项正确,每小题2分,共56分。
)读下图,完成下列小题。
1. 图中①②③区域面积相比A. ①>②B. ②>③C. ①=③D. 无法比较2. 下列相关说法,正确的是A. ③区域海面距地心距离比①稍长B. ③区域位于①区域的西北方向C. ③区域位于北半球、东半球D. 东北航向是②区域向③区域飞行的最近航线【答案】1. B 2. B【解析】试题分析:1. 在经纬网图中。
所跨的经纬度数相同,所在纬度越低,代表的实际面积越大。
三地都跨了20个经度和20个纬度,其中①②两地处在赤道和纬度20°之间,面积相等,而③地所处纬度较高,面积比其他两地小。
2. 该题主要考查经纬网的应用。
由于地球是赤道略鼓,两级稍扁的椭球体,所以,③区域海面地心距离比①略短,A错误。
①地位于南半球,经度范围在20°W与40°W之间,所以。
③位于①区域的西北方向,B 正确;③区域位于160°E以东,属于西半球,C错误;②区域到③区域的最短走法是先向东北,后向东南,D错误。
故答案选B项。
【考点定位】经纬网地图的判读。
【名师点睛】经纬网的应用1.定“位置”地球仪上,经纬线相互交织,构成经纬网,利用经纬网可确定任何一点的地理位置(地理坐标——纬度、经度)。
2.定“对称点”⑴关于赤道对称的两点:经度相同;纬度相反,数值相等,如图A(40°N,20°W)与B(40°S,20°W)。
⑵关于地轴对称的两点:经线相对,和为180°;纬度相同,如图A(40°N,20°W)与C(40°N,160°E)。
⑶关于地心对称的两点:经线相对,和为180°;纬度相反,数值相等,如图A(40°N,20°W)与D(40°S,160°E)。
3.定“方向”⑴方格状经纬网图①确定南北方向在南北半球的两点,北半球在北,南半球在南;同在北半球,纬度值大者在北;同在南半球,纬度值大者在南。
②确定东西方向同在东经度,经度值大者在东;同在西经度,经度值大者在西。
若分别在东西经,如下图所示:⑵弧线式经纬网图(以极点经纬网图为例)①如图中A、B两点位于同一纬线上,根据自转方向判断B在A的东方。
②B、C位于同一经线上,根据极点位置判断C位于B的南方。
③C、A既不在同一经线上,也不在同一纬线上,根据以上原理分别判断东西、南北方向,可确定C在A 的东南方。
4.定“距离”⑴根据纬度差定经线长度:纬度1°的实际经线弧长处处相等,大约是111千米,如图中AB。
若两地在同一条经线上,只要知道两地的纬度差,就可以计算出两地之间的距离。
⑵根据经度差定纬线长度:经度1°的纬线弧长由低纬向高纬递减,大约是111×cosφ千米(φ表示该纬线的纬度数值),如图中AC。
5.定“最短航向”地球上两点间最短航线为球面最短距离,即经过两点的大圆劣弧长度。
(注:所谓大圆指过地心的平面与球面的交线),常见的大圆如下图所示:⑴同一经线上的两点,其最短距离的劣弧线就在经线上。
如下图中弧AB长即为AB两点间的最短距离,A 在B的正南方。
⑵若两点的经度差为180°,过这两点的大圆便是经线圈,最短距离经过极点。
如上图中从B到C的最短航线经过北极点,从B到N是向正北方,从N到C是向正南方。
⑶出发地与目的地不在同一经线圈上,过两点的大圆不是与经线圈重合,两点之间的最短距离是这个大圆的劣弧段长,分析方向变化要看劣弧的走向。
如上图中EF之间的最短航线是弧EPF的长,从E到P是向西北方向,从P到F是向西南方向。
6.定“范围”⑴相同纬度且跨经度数相同的两幅图,其所示地区的面积相等。
⑵跨经纬度数相同的地图,纬度越高,表示的实际范围越小。
⑶图幅相同的两幅图,中心点纬度数相同,则跨经纬度越广,所表示的实际范围越大,比例尺越小。
下图是某水库大坝位置示意图。
据此回答下列小题。
3. 若水库大坝再加高100米,该地区的四个村庄可能会发生什么情况A. ①号村庄会被淹没B. ②号村庄会被淹没C. ③号村庄会被淹没D. ④号村庄会被淹没4. 关于下图的叙述,正确的是A. 乙河水流向西北B. 村庄②的气温明显高于①村C. 支流甲河画错了D. 村庄③比④要高出100米【答案】3. C 4. C【解析】3. 若水库大坝再加高100米,即达到200米等高线处,位于200米等高线内的库区会被淹没,该地区的四个村庄可能会③号村庄会被淹没,C对。
①号村庄、②号村庄位于库区外,不会被淹没,A、B错。
④号村庄海拔在200米以上,不会被淹没,D错。
4. 河流流向与等高线凸出方向相反,乙河水流向东南,A错。
村庄②的海拔较高,气温明显低于①村,B错。
支流甲河位于山脊上,画错了,C对。
村庄③比④要低出100米,D错。
点睛:大坝高度是200米,位于200米等高线内的库区会被淹没。
河流流向与等高线凸出方向相反。
海拔高,气温低。
河流出现在山谷中,山脊地形没有河流。
读下列四幅图,回答下面小题。
5. 上图中,坡度最陡的一幅是A. ①B. ②C. ③D. ④6. 表示实地范围最大,内容最简略的是A. ①B. ②C. ③D. ④【答案】5. B 6. A【解析】6. 表示实地范围最大,内容最简略的是比例尺最小图。
比例尺可以写成分数形式,比例尺最小的是①,A 对。
②、③、④比例尺较大,B、C、D错。
一个旅游团从广州出发飞越浩瀚的太平洋到美国观光,判断以下行程中发生的地理事件,回答下列各题。
7. 飞机在飞越太平洋中部时,由于时差的缘故,空姐要求旅客把自己的手表A. 调快1小时B. 调慢1小时C. 调快24小时D. 调慢24小时8. 到达美国后,酒店大堂悬挂着三个大钟(如下图所示),这时北京时间可能为A. 5时B. 8时C. 16时D. 21时【答案】7. D 8. B【解析】试题分析:7. 从广州出发飞越浩瀚的太平洋到美国观光,飞越太平洋时为从东12区进入西12区,日期晚一天,因此应当调慢24小时,故选D。
8. 读图可知,到达美国后,格林尼治时间为0点或者12点,广州为北京时间,比格林尼治时间早8小时,应为8点或者20点,故选B。
【考点定位】时间计算读“地球表面受热过程示意图”,回答下列各题。
9. 图中箭头②比①细的主要原因是A. 大气逆辐射B. 地面反射C. 大气削弱作用D. 地面削弱10. 利用人造烟雾可以防御霜冻,因为人造烟雾能使A. ①减弱B. ②增强C. ③减弱D. ④增强【答案】9. C 10. D【解析】试题分析:9. 当太阳辐射通过大气层到达地面的过程中,由于大气对它有一定的吸收、散射和反射作用,使到达地面的总辐射有明显削弱,特别是波长短的辐射能削弱显著,这种现象称为大气削弱作用或衰减作用,所以形成图中箭头②比①细。
10. 农民点燃田地里的秸秆,烟雾弥漫,就相当于增厚了云层,加大了对地面辐射的吸收,从而增强了大气逆辐射,对地面起着保温作用,从而防止霜冻。
考点:大气受热过程下图示意地球上局部气压带和风带分布。
读图完成下列各题:11. 甲气压带表示A. 赤道低气压带B. 副热带高气压带C. 副极地低气压带D. 极地高气压带12. 乙风带表示A. 东南信风带B. 极地东风带C. 中纬西风带D. 东北信风带【答案】11. A 12. C【解析】11. 根据纬度,甲气压带位于赤道附近,表示赤道低气压带,A对。
副热带高气压带位于30°纬线附近,B 错。
副极地低气压带位于60°纬线附近,C错。
极地高气压带位于极点附近,D错。
12. 乙风带位于北半球,副高北侧,表示中纬西风带,吹西南风,C对。
东南信风带位于南半球,A错。
极地东风带位于副极地低气压带和极地高气压带之间,C错。
东北信风带位于赤道低气压带北侧,D错。
读气温和降水统计图,完成下列各题。
A. B. C. D.13. 其中代表热带雨林气候的是A. 图AB. 图BC. 图CD. 图D【答案】A【解析】其中代表热带雨林气候的是A图,终年高温多雨,A对。
图B夏季高温干燥,冬季温和多雨,是地中海气候,B错。
图C是热带草原或热带季风气候,C错。
图D是温带大陆性气候,D错。
点睛:热带雨林气候的是终年高温多雨。
夏季高温干燥,冬季温和多雨,是地中海气候。
热带草原或热带季风气候,位于热带,干湿季节分明。
温带大陆性气候全年少雨,最冷月气温小于0度。
14. 下列关于世界气候地区差异的叙述,错误的是A. 北纬40°~60°大陆内部,深居内陆距海远,全年降水少B. 热带地区既有多雨区,也有少雨区C. 副热带大陆东岸,雨热同期;副热带大陆西岸,主要受季风影响D. 南北纬40°~60°大陆西岸,受西风影响,降水丰富【答案】C【解析】北纬40°~60°大陆内部,深居内陆,距海远,全年降水少,A正确。
热带地区既有多雨区,也有少雨区,B正确。
副热带大陆东岸,雨热同期。
副热带大陆西岸,主要受气压带、风带影响,C错误。
南北纬40°~60°大陆西岸,受西风影响,降水丰富,D正确。
读“长江中游某地连续六天的天气情况统计图”,分析回答下题。
15. 如图所示天气变化的原因可能是A. 冷锋过境B. 反气旋过境C. 气旋过境D. 暖锋过境16. 有关该地区这几日的叙述,正确的是A. 气温日较差不断缩小B. 空气的湿度不断增大C. 7、8日大气的保温作用最强D. 7日河水水位最高【答案】15. D 16. C【解析】15. 根据图中所示天气变化,连续几天中,有阴雨天气,天气系统过境后,气温升高,可能是暖锋过境,D 对。
冷锋过境后,气温下降,A错。
反气旋过境无降雨天气,B错。
气旋过境前后气温变化不大,C错。
16. 该地区这几日气温日较差先缩小,后增大,A错。
空气的湿度先增大,后减小,B错。
7、8日阴天,大气的保温作用最强,C对。
7日、8日都有降水,7日河水水位没达到最高,D错。
读“我国某区域1月和7月等温线分布图”(下图)(冬夏季等值距相同),完成下面各题。
17. 对该区域1月份等温线走向影响最大的是A. 地形B. 纬度C. 海陆D. 洋流18. A地7月气温可能是A. 29℃B. 27℃C. 25℃D. 23℃【答案】17. B 18. B【解析】试题分析:17. 根据等温线的特征可知,1月等温线大致与纬线平行,说明纬度不同的地区,接受的太阳辐射不同,等温线走向受纬度因素影响大,B对。
地形影响等温线是闭合曲线,A错。
海陆影响等温线与海岸线延伸方面一致,C错。
