成都市历年真题———几何证明(B卷大题)
最新成都八年级上数学B卷练习:几何、一次函数(含解析)

成都八年级上数学B卷:几何、一次函数1.(2017秋•金堂县期末)已知△ABC中,AB=AC=BC=6.点P射线BA上一点,点Q是AC的延长线上一点,且BP=CQ,连接PQ,与直线BC相交于点D.(1)如图①,当点P为AB的中点时,求CD的长;(2)如图②,过点P作直线BC的垂线,垂足为E,当点P,Q分别在射线BA和AC的延长线上任意地移动过程中,线段BE,DE,CD中是否存在长度保持不变的线段?请说明理由.2.(2017秋•金堂县期末)如图,在平面直角坐标系xOy中,直线y=2x+2与y 轴交于点A,与x轴交于点B.直线l⊥x轴负半轴于点C,点D是直线l上一点且位于x轴上方.已知CO=CD=4.(1)求经过A,D两点的直线的函数关系式和点B的坐标;(2)在直线l上是否存在点P使得△BDP为等腰三角形,若存在,直接写出P 点坐标,若不存在,请说明理由.3.(2010•宁德)如图,四边形ABCD是正方形,△ABE是等边三角形,M为对角线BD(不含B点)上任意一点,将BM绕点B逆时针旋转60°得到BN,连接EN、AM、CM.(1)求证:△AMB≌△ENB;(2)①当M点在何处时,AM+CM的值最小;②当M点在何处时,AM+BM+CM的值最小,并说明理由;(3)当AM+BM+CM的最小值为时,求正方形的边长.4.(2017秋•金牛区校级期中)在学完勾股定理的证明后发现运用“不同方式表示同一图形的面积”可以证明一类含有线段的等式,这种方法称之为面积法.学有所用:在等腰△ABC中,AB=AC,其一腰上的高为h,M是底边BC上的任意一点,M到腰AB、AC的距离分别为h1、h2.(1)结合图1,(1)结合图1,写出h1、h2、h之间有什么样的结论.(不证明)(2)如图2,当点M在BC延长线上时,直接写出h1、h2、h之间又有什么样的结论;(3)利用以上结论解答,如图3在平面直角坐标系中有两条直线l1:y=x+3,l 2:y=﹣3x+3,若l2上的一点M到l1的距离是.求点M的坐标.5.(2018春•信丰县期末)如图,在平面直角坐标系中,已知A(a,0),B(b,0),其中a,b满足|a+1|+(b﹣3)2=0.(1)填空:a= ,b= ;(2)如果在第三象限内有一点M(﹣2,m),请用含m的式子表示△ABM的面积;(3)在(2)条件下,当m=﹣时,在y轴上有一点P,使得△BMP的面积与△ABM的面积相等,请求出点P的坐标.6.(2014秋•凌河区校级期末)如图,△ABC是直角三角形,∠BAC=90°,D是斜边BC的中点,E、F分别是AB、AC边上的点,且DE⊥DF.(1)如图1,试说明BE2+CF2=EF2;(2)如图2,若AB=AC,BE=12,CF=5,求△DEF的面积.7.(2015秋•连云港期末)如图1,已知直线y=2x+2与y轴、x轴分别交于A、B 两点,以B为直角顶点在第二象限作等腰Rt△ABC(1)求点C的坐标,并求出直线AC的关系式.(2)如图2,直线CB交y轴于E,在直线CB上取一点D,连接AD,若AD=AC,求证:BE=DE.(3)如图3,在(1)的条件下,直线AC交x轴于M,P(,k)是线段BC 上一点,在线段BM上是否存在一点N,使直线PN平分△BCM的面积?若存在,请求出点N的坐标;若不存在,请说明理由.8.(2018•潮南区模拟)如图①,等腰直角三角形ABC的顶点A的坐标为(0,﹣1),C的坐标为(4,3),直角顶点B在第四象限,线段AC与x轴交于点D.将线段DC绕点D逆时针旋转90°至DE.(1)直接写出点B、D、E的坐标并求出直线DE的解析式.(2)如图②,点P以每秒1个单位的速度沿线段AC从点A运动到点C的过程中,过点P作与x轴平行的直线PG,交直线DE于点G,求与△DPG的面积S与运动时间t的函数关系式,并求出自变量t的取值范围.(3)如图③,设点F为直线DE上的点,连接AF,一动点M从点A出发,沿线段AF以每秒1个单位的速度运动到F,再沿线段FE以每秒个单位的速度运动到E后停止.当点F的坐标是多少时,是否存在点M在整个运动过程中用时最少?若存在,请求出点F的坐标;若不存在,请说明理由.9.(2016秋•金牛区期末)如图1,在平面直角坐标系中,点A坐标为(﹣4,4),点B的坐标为(4,0).(1)求直线AB的解析式;(2)点M是坐标轴上的一个点,若AB为直角边构造直角三角形△ABM,请求出满足条件的所有点M的坐标;(3)如图2,以点A为直角顶点作∠CAD=90°,射线AC交x轴的负半轴与点C,射线AD交y轴的负半轴与点D,当∠CAD绕点A旋转时,OC﹣OD的值是否发生变化?若不变,直接写出它的值;若变化,直接写出它的变化范围(不要解题过程).10.(2007•金华)如图1,在平面直角坐标系中,已知点A(0,4),点B在x 正半轴上,且∠ABO=30度.动点P在线段AB上从点A向点B以每秒个单位的速度运动,设运动时间为t秒.在x轴上取两点M,N作等边△PMN.(1)求直线AB的解析式;(2)求等边△PMN的边长(用t的代数式表示),并求出当等边△PMN的顶点M 运动到与原点O重合时t的值;(3)如果取OB的中点D,以OD为边在Rt△AOB内部作如图2所示的矩形ODCE,点C在线段AB上.设等边△PMN和矩形ODCE重叠部分的面积为S,请求出当0≤t≤2秒时S与t的函数关系式,并求出S的最大值.11.(2015秋•锦江区校级期中)如图Rt△ABC,AB=AC=6,D为AC上一点,连接BD,AF⊥BD交BD于H,交BC于F,CE⊥AC交AF的延长线于E,(1)求证:△ABD≌△CAE;(2)当D为AC上离A点最近的三等分点时,连接DE,求DE的长;(3)当D为AC上离A点最近的n等分点时,连接BE,求S△BDC :S△BEC(用含n的代数式表示,直接写出答案)12.(2015秋•锦江区校级期中)如图,以长方形OABC的顶点O为原点,OA所在直线为x轴,OC所在直线为y轴,建立平面直角坐标系.已知OA=3,OC=2,点E是AB的中点,在OA上取一点D,连结BD,点A关于BD的对称点恰好落在线段BC边上的点F处.(1)直接写出点E,F的坐标;(2)在线段CB上是否存在一点P,使△OEP为等腰三角形?若存在,求出所有满足条件的P点坐标;若不存在,请说明理由.(3)在x轴、y轴上是否分别存在点M、N,使四边形MNFE的周长最小?如果存在,求出周长的最小值;如果不存在,请说明理由.13.(2013秋•惠山区校级期末)如图,在平面直角坐标系中,A(a,0),B(0,b),且a、b满足(a﹣2)2+=0.(1)求直线AB的解析式;(2)若点M为直线y=mx上一点,且△ABM是等腰直角三角形,求m值;(3)过A点的直线y=kx﹣2k交y轴于负半轴于P,N点的横坐标为﹣1,过N 点的直线y=x﹣交AP于点M,试证明的值为定值.14.(2016秋•武侯区期末)如图,已知直线l1:y=x+2与直线l2:y=﹣kx+4(k≠0)相交于点F,直线l1,l2分别交x轴于点E,G.长方形ABCD的顶点C,D分别在l2和y轴上,顶点A,B都在x轴上,且点B与点E重合,点A与点O重合,长方形ABCD的面积是12.(1)求k的值;(2)求证:△EFG是等腰直角三角形;(3)若长方形ABCD从原地出发,沿x轴正方向以每秒1个单位长度的速度平移,设移动时间为t秒,长方形ABCD与△EFG重叠部分的面积为S.①当0≤t≤1时,求S的最大值;②当1<t≤4时,直接写出S与t之间的函数关系式(要求写出自变量t的取值范围).15.(2016秋•武侯区期末)如图,已知直线y=x过点A,AB⊥y轴于点B,AC⊥x 轴于点C,点P是y轴上的一动点,连接AP交直线BC于点E.点N在直线BC 上,连接AN且∠PAN=90°,在射线AN上截取AD=AE,连接DE.(1)求证:BE2+EC2=2AE2;(2)若点A的坐标是(6,m),点P的坐标是(0,m),求线段AD的长;(3)当=时,求的值.16.(2016秋•武侯区期末)如图,已知Rt△ABC中,∠ACB=90°,∠BAC=30°,延长BC至D使CD=BC,连接AD.(1)求证:△ABD是等边三角形;(2)若E为线段CD的中点,且AD=4,点P为线段AC上一动点,连接EP,BP.①求EP+AP的最小值;②求2BP+AP的最小值.17.(2017秋•金牛区校级月考)如图,在矩形纸片ABCD中,ABCD中,AB=6,BC=8.把△BCD沿对角线BD折叠,使点C落在C′处,BC′交AD于点G;E、F分别是C′D 和BD上的点,线段EF交AD于点H,把△FDE沿EF折叠,使点D落在D′处,点D′恰好与点A重合.(1)求证:△ABG≌△C′DG;(2)求GH的长.18.(2017春•芙蓉区校级期中)已知点A(﹣2,3),B(4,3),C(﹣1,﹣3),求(1)A,B两点之间的距离及点C到x轴的距离.(2)三角形ABC的面积.(3)若点P在y轴上,当△ABP的面积为6时,求点P的坐标.19.(2017秋•成都期中)定义:如图①,点M、N把线段AB分割成AM、MN和BN,若以AM、MN、BN为边的三角形是一个直角三角形,则称点M,N是线段AB的勾股分割点.(1)已知点M、N是线段AB的勾股分割点,若AM=2,MN=3,求BN的长;(2)如图②,在等腰直角△ABC中,AC=BC,∠ACB=90°,点M、N为边AB上两点,满足∠MCN=45°,求证:点M、N是线段AB的勾股分割点;阳阳同学在解决第(2)小题时遇到了困难,陈老师对阳阳说:要证明勾股分割点,则需设法构造直角三角形,你可以把△CBN绕点C逆时针旋转90°试一试.请根据陈老师的提示完成第(2)小题的证明过程;(3)在(2)的问题中,若∠ACM=15°,AM=1,CM=+1.求BM的长.(提示:在直角三角形中,30°角所对的直角边等于斜边的一半.)20.(2017秋•成都期中)如图,在平面直角坐标系中,直线L是第一、三象限的角平分线.(1)由图观察易知A(0,2)关于直线l的对称点A′的坐标为(2,0),请在图中分别标明B(5,3)、C(﹣2,5)关于直线l的对称点B′、C′的位置,并写出他们的坐标:B′、C′;(2)结合图形观察以上三组点的坐标,直接写出坐标面内任一点P(a,b)关于第一、三象限的角平分线l的对称点P′的坐标为;(3)已知两点D(1,﹣3)、E(﹣1,﹣4),试在直线L上画出点Q,使△QDE 的周长最小,并求△QDE周长的最小值.21.(2017秋•成都月考)在等腰Rt△ABC中,∠ABC=90°,AB=BC,(1)如图1,D为线段BC的延长线上一点,连接AD,过点B作BE⊥AD,已知AB=6,AD=10,则CD= ,BE= ;(2)如图2,点F是线段AC上一点,连接BF,过点C作CG⊥BF于点G,过点B 作BH⊥AC于点H,连接GH,①若=,S=5,求AC的长;②求证:CG﹣BG=GH.△BCG22.(2016秋•金牛区期末)通过类比联想,引申拓展研究典型题目,可达到解一题知一类的目的,下面是一个案例,请补充完整.原题:如图1,点E、F分别在正方形ABCD的边BC、CD上,∠EAF=45°,连结EF,试猜想EF、BE、DF之间的数量关系.(1)思路梳理把△ABE绕点A逆时针旋转90°至△ADG,可使AB与AD重合,由∠ADG=∠B=90°,得∠FDG=180°,即点F、D、G共线,易证△AFG≌,故EF、BE、DF之间的数量关系为.(2)类比引申如图2,点E、F分别在正方形ABCD的边CB、DC的延长线上,∠EAF=45°,连结EF,试猜想EF、BE、DF之间的数量关系为,并给出证明.(3)联想拓展如图3,在△ABC中,∠BAC=90°,AB=AC,点D、E均在边BC上,且∠BAD+∠EAC=45°,若BD=3,EC=6,求DE的长.参考答案与试题解析1.(2017秋•金堂县期末)已知△ABC中,AB=AC=BC=6.点P射线BA上一点,点Q是AC的延长线上一点,且BP=CQ,连接PQ,与直线BC相交于点D.(1)如图①,当点P为AB的中点时,求CD的长;(2)如图②,过点P作直线BC的垂线,垂足为E,当点P,Q分别在射线BA和AC的延长线上任意地移动过程中,线段BE,DE,CD中是否存在长度保持不变的线段?请说明理由.【解答】解:(1)过P点作PF∥AC交BC于F∵点P为AB的中点,∴BP=AB=3,∵AB=AC=BC,∴∠B=∠ACB=∠BAC=60°,∵PF∥AC,∴∠PFB=∠ACB=60°,∠BPF=∠BAC=60°,∴△PBF是等边三角形,∴BF=FP=BP=3,∴FC=BC﹣BF=3,由题意,BP=CQ,∴FP=CQ,∵PF∥AC,∴∠DPF=∠DQC又∠PDF=∠QDC,∴△PFD≌△QCD∴CD=DF=FC=(2)当点P,Q在移动的过程中,线段DE的长度保持不变分两种情况讨论:①当点P在线段AB上时,过点P作PF∥AC交BC于F,由(1)知PB=PF,∵PE⊥BC,∴BE=EF,由(1)知△PFD≌△QCD,CD=DF,∴DE=EF+DF=BC=3,②得点P在BA的延长线上时,同理可得DE=3,∴当点P、Q在移动的过程中,线段DE的长度保持不变.2.(2017秋•金堂县期末)如图,在平面直角坐标系xOy中,直线y=2x+2与y 轴交于点A,与x轴交于点B.直线l⊥x轴负半轴于点C,点D是直线l上一点且位于x轴上方.已知CO=CD=4.(1)求经过A,D两点的直线的函数关系式和点B的坐标;(2)在直线l上是否存在点P使得△BDP为等腰三角形,若存在,直接写出P 点坐标,若不存在,请说明理由.【解答】解:(1)对于直线y=2x+2,当x=0时,y=2;当y=0时,x=﹣1, ∴点A 的坐标为(0,2),点B 的坐标为(﹣1,0),又∵CO=CD=4,∴点D 的坐标为(﹣4,4),设直线AD 的函数表达式为y=kx+b ,则有,解得:,∴直线AD 的函数表达式为y=﹣x+2;(2)存在,设P (﹣4,p ),分三种情况考虑:当BD=P 1D 时,可得(﹣1+4)2+(0﹣4)2=(p ﹣4)2,解得:p=9或p=﹣1,此时P 1(﹣4,9),P 2(﹣4,﹣1);当BP 3=BD 时,则有(﹣1+4)2+(0﹣p )2=(﹣1+4)2+(0﹣4)2,解得:p=﹣4,此时P 3(﹣4,﹣4);当BP 4=DP 4时,(﹣1+4)2+(0﹣p )2=(p ﹣4)2,解得:p=,此时P 4(﹣4,),综上,共有四个点满足要求.分别是P 1(﹣4,9),P 2(﹣4,﹣4),P 3(﹣4,﹣1),P 4(﹣4,).3.(2010•宁德)如图,四边形ABCD是正方形,△ABE是等边三角形,M为对角线BD(不含B点)上任意一点,将BM绕点B逆时针旋转60°得到BN,连接EN、AM、CM.(1)求证:△AMB≌△ENB;(2)①当M点在何处时,AM+CM的值最小;②当M点在何处时,AM+BM+CM的值最小,并说明理由;(3)当AM+BM+CM的最小值为时,求正方形的边长.【解答】(1)证明:∵△ABE是等边三角形,∴BA=BE,∠ABE=60°.∵∠MBN=60°,∴∠MBN﹣∠ABN=∠ABE﹣∠ABN.即∠MBA=∠NBE.又∵MB=NB,∴△AMB≌△ENB(SAS).(2)解:①当M点落在BD的中点时,A、M、C三点共线,AM+CM的值最小.②如图,连接CE,当M点位于BD与CE的交点处时,AM+BM+CM的值最小.理由如下:连接MN,由(1)知,△AMB≌△ENB,∴AM=EN,∵∠MBN=60°,MB=NB,∴△BMN是等边三角形.∴BM=MN.∴AM+BM+CM=EN+MN+CM.根据“两点之间线段最短”可知,若E、N、M、C在同一条直线上时,EN+MN+CM 取得最小值,最小值为EC.在△ABM和△CBM中,,∴△ABM≌△CBM,∴∠BAM=∠BCM,∴∠BCM=∠BEN,∵EB=CB,∴若连接EC,则∠BEC=∠BCE,∵∠BCM=∠BCE,∠BEN=∠BEC,∴M、N可以同时在直线EC上.∴当M点位于BD与CE的交点处时,AM+BM+CM的值最小,即等于EC的长.(3)解:过E点作EF⊥BC交CB的延长线于F,∴∠EBF=∠ABF﹣∠ABE=90°﹣60°=30°.设正方形的边长为x,则BF=x,EF=.在Rt△EFC中,∵EF2+FC2=EC2,∴()2+(x+x)2=.解得x1=,x2=﹣(舍去负值).∴正方形的边长为.4.(2017秋•金牛区校级期中)在学完勾股定理的证明后发现运用“不同方式表示同一图形的面积”可以证明一类含有线段的等式,这种方法称之为面积法.学有所用:在等腰△ABC中,AB=AC,其一腰上的高为h,M是底边BC上的任意一点,M到腰AB、AC的距离分别为h1、h2.(1)结合图1,(1)结合图1,写出h1、h2、h之间有什么样的结论.(不证明)(2)如图2,当点M在BC延长线上时,直接写出h1、h2、h之间又有什么样的结论;(3)利用以上结论解答,如图3在平面直角坐标系中有两条直线l1:y=x+3,l 2:y=﹣3x+3,若l2上的一点M到l1的距离是.求点M的坐标.【解答】解:(1)h1+h2=h;如图1,连接AM,∵S△ABC=AC•BD=AC•h,S△ABM =AB•ME=AB•h1,S△ACM =AC•MF=AC•h2,.又∵S△ABC =S△ABM﹣S△ACM,∴AC•h=AB•h1+AC•h2.∵AB=AC,∴h=h1+h2.(2)结论:h=h1﹣h2.理由:如图,连接MA,∵S△ABC=AC•BD=AC•h,S△ABM =AB•ME=AB•h1,S△ACM =AC•MF=AC•h2,.又∵S△ABC =S△ABM﹣S△ACM,∴AC•h=AB•h1﹣AC•h2.∵AB=AC,∴h=h1﹣h2.(3)解:在y=x+3中,令x=0得y=3;令y=0得x=﹣4,所以A(﹣4,0),B (0,3)同理得C(1,0).AB=5,AC=5,所以AB=AC,即△ABC为等腰三角形.(ⅰ)当点M在BC边上时,由h1+h2=h得:+My=OB=3,My=3﹣=把它代入y=﹣3x+3中求得:Mx=,所以此时M(,).(ⅱ)当点M在CB延长线上时,由h1﹣h2=h得:My﹣=OB=3,My=3+=,把它代入y=﹣3x+3中求得:Mx=﹣,所以此时M(﹣,).综合(ⅰ)、(ⅱ)知:点M的坐标为M(,)或(﹣,).5.(2018春•信丰县期末)如图,在平面直角坐标系中,已知A(a,0),B(b,0),其中a,b满足|a+1|+(b﹣3)2=0.(1)填空:a= ﹣1 ,b= 3 ;(2)如果在第三象限内有一点M(﹣2,m),请用含m的式子表示△ABM的面积;(3)在(2)条件下,当m=﹣时,在y轴上有一点P,使得△BMP的面积与△ABM的面积相等,请求出点P的坐标.【解答】解:(1)∵|a+1|+(b﹣3)2=0,∴a+1=0且b﹣3=0,解得:a=﹣1,b=3,故答案为:﹣1,3;(2)过点M作MN⊥x轴于点N,∵A(﹣1,0)B(3,0)∴AB=1+3=4,又∵点M(﹣2,m)在第三象限∴MN=|m|=﹣m∴S△ABM=AB•MN=×4×(﹣m)=﹣2m;(3)当m=﹣时,M(﹣2,﹣)∴S△ABM=﹣2×(﹣)=3,点P有两种情况:①当点P在y轴正半轴上时,设点p(0,k)S△BMP=5×(+k)﹣×2×(+k)﹣×5×﹣×3×k=k+,∵S△BMP =S△ABM,∴k+=3,解得:k=0.3,∴点P坐标为(0,0.3);②当点P在y轴负半轴上时,设点p(0,n),S△BMP=﹣5n﹣×2×(﹣n﹣)﹣×5×﹣×3×(﹣n)=﹣n﹣,∵S△BMP =S△ABM,∴﹣n﹣=3,解得:n=﹣2.1∴点P坐标为(0,﹣2.1),故点P的坐标为(0,0.3)或(0,﹣2.1).6.(2014秋•凌河区校级期末)如图,△ABC是直角三角形,∠BAC=90°,D是斜边BC的中点,E、F分别是AB、AC边上的点,且DE⊥DF.(1)如图1,试说明BE2+CF2=EF2;(2)如图2,若AB=AC,BE=12,CF=5,求△DEF的面积.【解答】(1)证明:延长ED至点G,使得DG=DE,连接FG,CG,∵DE=DG,DF⊥DE,∴DF垂直平分DE,∴EF=FG,∵D是BC中点,∴BD=CD,在△BDE和△CDG中,,∴△BDE≌△CDG(SAS),∴BE=CG,∠DCG=∠DBE,∵∠ACB+∠DBE=90°,∴∠ACB+∠DCG=90°,即∠FCG=90°,∵CG2+CF2=FG2,∴BE2+CF2=EF2;(2)解:连接AD,∵AB=AC,D是BC中点,∴∠BAD=∠C=45°,AD=BD=CD,∵∠ADE+∠ADF=90°,∠ADF+∠CDF=90°,∴∠ADE=∠CDF,在△ADE和△CDF中,,∴△ADE≌△CDF(ASA),∴AE=CF,BE=AF,AB=AC=17,∴S四边形AEDF =S△ABC,∴S△AEF=×5×12=30,∴△DEF的面积=S△ABC ﹣S△AEF=.7.(2015秋•连云港期末)如图1,已知直线y=2x+2与y轴、x轴分别交于A、B 两点,以B为直角顶点在第二象限作等腰Rt△ABC(1)求点C的坐标,并求出直线AC的关系式.(2)如图2,直线CB交y轴于E,在直线CB上取一点D,连接AD,若AD=AC,求证:BE=DE.(3)如图3,在(1)的条件下,直线AC交x轴于M,P(,k)是线段BC 上一点,在线段BM上是否存在一点N,使直线PN平分△BCM的面积?若存在,请求出点N的坐标;若不存在,请说明理由.【解答】解:(1)如图1,作CQ⊥x轴,垂足为Q,∵∠OBA+∠OAB=90°,∠OBA+∠QBC=90°,∴∠OAB=∠QBC,又∵AB=BC,∠AOB=∠Q=90°,∴△ABO≌△BCQ,∴BQ=AO=2,OQ=BQ+BO=3,CQ=OB=1,∴C(﹣3,1),由A(0,2),C(﹣3,1)可知,直线AC:y=x+2;(2)如图2,作CH⊥x轴于H,DF⊥x轴于F,DG⊥y轴于G,∵AC=AD,AB⊥CB,∴BC=BD,∴△BCH≌△BDF,∴BF=BH=2,∴OF=OB=1,∴DG=OB,∴△BOE≌△DGE,∴BE=DE;(3)如图3,直线BC:y=﹣x﹣,P(,k)是线段BC上一点,∴P(﹣,),由y=x+2知M(﹣6,0),=.∴BM=5,则S△BCM假设存在点N使直线PN平分△BCM的面积,则BN•=×,∴BN=,ON=,∵BN<BM,∴点N在线段BM上,∴N(﹣,0).8.(2018•潮南区模拟)如图①,等腰直角三角形ABC的顶点A的坐标为(0,﹣1),C的坐标为(4,3),直角顶点B在第四象限,线段AC与x轴交于点D.将线段DC绕点D逆时针旋转90°至DE.(1)直接写出点B、D、E的坐标并求出直线DE的解析式.(2)如图②,点P以每秒1个单位的速度沿线段AC从点A运动到点C的过程中,过点P作与x轴平行的直线PG,交直线DE于点G,求与△DPG的面积S与运动时间t的函数关系式,并求出自变量t的取值范围.(3)如图③,设点F为直线DE上的点,连接AF,一动点M从点A出发,沿线段AF以每秒1个单位的速度运动到F,再沿线段FE以每秒个单位的速度运动到E后停止.当点F的坐标是多少时,是否存在点M在整个运动过程中用时最少?若存在,请求出点F的坐标;若不存在,请说明理由.【解答】解:(1)如图①中,由题意得:B(4,﹣1),D(1,0).E(﹣2,3).设直线DE为y=kx+b(k≠0)把D(1,0).E(﹣2,3)代入得解之得:∴直线DE为:y=﹣x+1.(2)在Rt△ABC中,由BA=BC=4,∴AC==4,由AP=t (0≤t≤4),同理可得:AD==,由题意可知:ED⊥AC,∠DPG=∠DAB=45°∴△DPG为等腰直角三角形S=DP2,如图②中,①当0≤t<时,PD=﹣t,∴S=PD2=(﹣t)2=t2﹣t+1.②当时,易得DP=t﹣,∴S=PD2=(t﹣)2=t2﹣t+1.综上:S=t2﹣t+1.(0≤t)(3)如图③,易得∠EDO=45°.过点E作EK∥x轴交y轴于H,则∠KEF=∠EDO=45°.过点F作FG⊥EK于点G,则FG=EG=EF,由题意,动点M运动的路径为折线AF+EF,运动时间:t=AF+EF,∴t=AF+FG,即运动时间等于折线AF+FG的长度,由垂线段最短可知,折线AF+FG的长度的最小值为EK与线段AB之间的垂线段.=AH,直线DE与y轴的交点即为所求之F点,则t最小∵直线DE解析式为:y=﹣x+1∴F(0,1),综上所述,当点F(0,1)坐标为时,点M在整个运动过程中用时最少.9.(2016秋•金牛区期末)如图1,在平面直角坐标系中,点A坐标为(﹣4,4),点B的坐标为(4,0).(1)求直线AB的解析式;(2)点M是坐标轴上的一个点,若AB为直角边构造直角三角形△ABM,请求出满足条件的所有点M的坐标;(3)如图2,以点A为直角顶点作∠CAD=90°,射线AC交x轴的负半轴与点C,射线AD交y轴的负半轴与点D,当∠CAD绕点A旋转时,OC﹣OD的值是否发生变化?若不变,直接写出它的值;若变化,直接写出它的变化范围(不要解题过程).【解答】解:(1)设直线AB的解析式为:y=kx+b(k≠0).∵点A(﹣4,4),点B(0,2)在直线AB上,∴,解得,∴直线AB的解析式为:y=﹣x+2;(2)∵△ABM是以AB为直角边的直角三角形,∴有∠BAM=90°或∠ABM=90°,①当∠BAM=90°时,如图1,过A作AB的垂线,交x轴于点M1,交y轴于点M2,则可知△AEM1∽△BEA,∴=,由(1)可知OE=OB=AE=4,∴=,解得M1E=2,∴OM1=2+4=6,∴M1(﹣6,0),∵AE∥y轴,∴=,即=,解得OM2=12,∴M2(0,12);②当∠ABM=90°时,如图2,过B作AB的垂线,交y轴于点M3,设直线AB交y轴于点E,则由(1)可知E(0,2),∴OE=2,OB=4,OB,由题意可知△BOE∽△M3∴=,即=,解得OM=8,3(0,﹣8),∴M3综上可知点M的坐标为(﹣6,0)或(0,12)或(0,﹣8);(3)不变.理由如下:过点A分别作x轴、y轴的垂线,垂足分别为G、H,如图3.则∠AGC=∠AHD=90°,又∵∠HOC=90°,∴∠GAH=90°,∴∠DAG+∠DAH=90°,∵∠CAD=90°,∴∠DAG+∠CAG=90°,∴∠CAG=∠DAH.∵A(﹣4,4),∴OG=AH=AG=OH=4.在△AGC和△AHD中∴△AGC≌△AHD(ASA),∴GC=HD.∴OC﹣OD=(OG+GC)﹣(HD﹣OH)=OG+OH=8.故OC﹣OD的值不发生变化,值为8.10.(2007•金华)如图1,在平面直角坐标系中,已知点A(0,4),点B在x 正半轴上,且∠ABO=30度.动点P在线段AB上从点A向点B以每秒个单位的速度运动,设运动时间为t秒.在x轴上取两点M,N作等边△PMN.(1)求直线AB的解析式;(2)求等边△PMN的边长(用t的代数式表示),并求出当等边△PMN的顶点M 运动到与原点O重合时t的值;(3)如果取OB的中点D,以OD为边在Rt△AOB内部作如图2所示的矩形ODCE,点C在线段AB上.设等边△PMN和矩形ODCE重叠部分的面积为S,请求出当0≤t≤2秒时S与t的函数关系式,并求出S的最大值.【解答】解:(1)由OA=4,∠ABO=30°,得到OB=12,∴B(12,0),设直线AB解析式为y=kx+b,把A和B坐标代入得:,解得:,则直线AB的解析式为:y=﹣x+4.(2)∵∠AOB=90°,∠ABO=30°,∴AB=2OA=8,∵AP=t,∴BP=AB﹣AP=8t,∵△PMN是等边三角形,∴∠MPB=90°,∵tan∠PBM=,∴PM=(8﹣t)×=8﹣t.如图1,过P分别作PQ⊥y轴于Q,PS⊥x轴于S,可求得AQ=AP=t,PS=QO=4﹣t,∴PM=(4﹣)÷=8﹣t,当点M与点O重合时,∵∠BAO=60°,∴AO=2AP.∴4=2t,∴t=2.(3)①当0≤t≤1时,见图2.设PN交EC于点G,重叠部分为直角梯形EONG,作GH⊥OB于H.∵∠GNH=60°,,∴HN=2,∵PM=8﹣t,∴BM=16﹣2t,∵OB=12,∴ON=(8﹣t)﹣(16﹣2t﹣12)=4+t,∴OH=ON﹣HN=4+t﹣2=2+t=EG,∴S=(2+t+4+t)×2=2t+6.∵S随t的增大而增大,∴当t=1时,Smax=8.②当1<t<2时,见图3.设PM交EC于点I,交EO于点F,PN交EC于点G,重叠部分为五边形OFIGN.作GH⊥OB于H,∵FO=4﹣2t,∴EF=2﹣(4﹣2t)=2t﹣2,∴EI=2t﹣2.∴S=S梯形ONGE ﹣S△FEI=2t+6﹣(2t﹣2)(2t﹣2)=﹣2t2+6t+4由题意可得MO=4﹣2t,OF=(4﹣2t)×,PC=4﹣t,PI=4﹣t,再计算S△FMO=(4﹣2t)2×S△PMN =(8﹣t)2,S△PIG=(4﹣t)2,∴S=S△PMN ﹣S△PIG﹣S△FMO=(8﹣t)2﹣(4﹣t)2﹣(4﹣2t)2×=﹣2t2+6t+4∵﹣2<0,∴当时,S有最大值,Smax=.③当t=2时,MP=MN=6,即N与D重合,设PM交EC于点I,PD交EC于点G,重叠部分为等腰梯形IMNG,见图4.S=×62﹣×22=8,综上所述:当0≤t≤1时,S=2t+6;当1<t<2时,S=﹣2t2+6t+4;当t=2时,S=8.∵,∴S的最大值是.11.(2015秋•锦江区校级期中)如图Rt△ABC,AB=AC=6,D为AC上一点,连接BD,AF⊥BD交BD于H,交BC于F,CE⊥AC交AF的延长线于E,(1)求证:△ABD≌△CAE;(2)当D为AC上离A点最近的三等分点时,连接DE,求DE的长;(3)当D为AC上离A点最近的n等分点时,连接BE,求S△BDC :S△BEC(用含n的代数式表示,直接写出答案)【解答】解:(1)如图1,Rt△ABC中,∠BAD=90°,AH⊥BD,∴∠1+∠2=∠1+∠3=90°,∴∠2=∠3,又∵CE⊥AC,∴∠ACE=∠BAD=90°,在△ABD和△CAE中,,∴△ABD≌△CAE(ASA);(2)如图2,∵△ABD≌△CAE,∴CE=AD,∵D为AC上离A点最近的三等分点,AC=6,∴AD=2,CD=4,∴CE=2,∵∠DCE=90°,∴Rt△CDE中,DE===2;(3)如图3,∵△ABD≌△CAE,∴CE=AD,∵D为AC上离A点最近的n等分点,AC=6,∴AD=,CD=6﹣=,∴CE=,∴S△BDC=×CD×AB=××6=,S△BEC=×CE×AC=××6=,∴S△BDC :S△BEC=:=n﹣1.12.(2015秋•锦江区校级期中)如图,以长方形OABC的顶点O为原点,OA所在直线为x轴,OC所在直线为y轴,建立平面直角坐标系.已知OA=3,OC=2,点E是AB的中点,在OA上取一点D,连结BD,点A关于BD的对称点恰好落在线段BC边上的点F处.(1)直接写出点E,F的坐标;(2)在线段CB上是否存在一点P,使△OEP为等腰三角形?若存在,求出所有满足条件的P点坐标;若不存在,请说明理由.(3)在x轴、y轴上是否分别存在点M、N,使四边形MNFE的周长最小?如果存在,求出周长的最小值;如果不存在,请说明理由.【解答】解:(1)∵OC=2,四边形OABC是矩形,∴AB=OC=2,∵点E是AB的中点,∴AE=1,∵AO=3,∴E(3,1),根据折叠可得DA=DF,∴DF=CO=2,∴AD=2,∴DO=3﹣2=1,∴F(1,2),(2)存在,理由:由(1)知,E(3,1),O(0,0)设P(a,2)(0≤a≤3),∴PE=,PO=,EO=,∵△OEP为等腰三角形,∴①当PE=PO时,∴=,∴a=1,∴P(1,2);②当PE=EO时,∴=,∴a=0或a=6(舍),∴P(0,2),③当PO=EO时,∴=,∴a=或a=﹣(舍),∴P(,2),即:满足条件的点P的坐标为(1,2)或(0,2)或(,2).(3)如图2,作点E关于x轴的对称点E′,作点F关于y轴的对称点F′,连接E′F′,分别与x轴、y轴交于点M、N,连接FN、NM、ME,此时四边形MNFE的周长最小.∴E′(3,﹣1),F′(﹣1,2),设直线E′F′的解析式为y=kx+b,有,解这个方程组,得,∴直线E′F′的解析式为y=﹣x+.当y=0时,x=,∴M点的坐标为(,0).当x=0时,y=,∴N点的坐标为(0,).∵E与E′关于x轴对称,F与F′关于y轴对称,∴NF=NF′,ME=ME′.F′B=4,E′B=3.在Rt△BE′F′中,F'E'==5.∴FN+NM+ME=F′N+NM+ME′=F′E′=5.在Rt△BEF中,EF==.∴FN+NM+ME+EF=F'E'+EF=5+,即四边形MNFE的周长最小值是5+.13.(2013秋•惠山区校级期末)如图,在平面直角坐标系中,A(a,0),B(0,b),且a、b满足(a﹣2)2+=0.(1)求直线AB的解析式;(2)若点M为直线y=mx上一点,且△ABM是等腰直角三角形,求m值;(3)过A点的直线y=kx﹣2k交y轴于负半轴于P,N点的横坐标为﹣1,过N 点的直线y=x﹣交AP于点M,试证明的值为定值.【解答】解:(1)∵(a﹣2)2+=0,∴a=2,b=4,∴A(2,0),B(0,4),设直线AB的解析式是y=kx+b,代入得:,解得:k=﹣2,b=4,则函数解析式为:y=﹣2x+4;(2)如图2,分三种情况:①如图1,当BM⊥BA,且BM=BA时,过M作MN⊥y轴于N,∵BM⊥BA,MN⊥y轴,OB⊥OA,∴∠MBA=∠MNB=∠BOA=90°,∴∠NBM+∠NMB=90°,∠ABO+∠NBM=90°,∴∠ABO=∠NMB,在△BMN和△ABO中,,∴△BMN≌△ABO(AAS),MN=OB=4,BN=OA=2,∴ON=2+4=6,∴M的坐标为(4,6),代入y=mx得:m=,②如图2,当AM⊥BA,且AM=BA时,过M作MN⊥x轴于N,△BOA≌△ANM(AAS),同理求出M的坐标为(6,2),m=,③如图4,当AM⊥BM,且AM=BM时,过M作MN⊥X轴于N,MH⊥Y轴于H,则△BHM≌△AMN,∴MN=MH,设M(x,x)代入y=mx得:x=mx,∴m=1,答:m的值是或或1.(3)解:如图3,结论2是正确的且定值为2,设NM与x轴的交点为H,过M作MG⊥x轴于G,过H作HD⊥x轴,HD交MP于D 点,连接ND,由y=与x轴交于H点,∴H(1,0),由y=与y=kx﹣2k交于M点,∴M(3,k),而A(2,0),∴A为HG的中点,∴△AMG≌△ADH(ASA),又因为N点的横坐标为﹣1,且在y=上,∴可得N 的纵坐标为﹣k,同理P的纵坐标为﹣2k,∴ND平行于x轴且N、D的横坐标分别为﹣1、1∴N与D关于y轴对称,∵△AMG≌△ADH≌△DPC≌△NPC,∴PN=PD=AD=AM,∴=2.14.(2016秋•武侯区期末)如图,已知直线l1:y=x+2与直线l2:y=﹣kx+4(k≠0)相交于点F,直线l1,l2分别交x轴于点E,G.长方形ABCD的顶点C,D分别在l2和y轴上,顶点A,B都在x轴上,且点B与点E重合,点A与点O重合,长方形ABCD的面积是12.(1)求k的值;(2)求证:△EFG是等腰直角三角形;(3)若长方形ABCD从原地出发,沿x轴正方向以每秒1个单位长度的速度平移,设移动时间为t秒,长方形ABCD与△EFG重叠部分的面积为S.①当0≤t≤1时,求S的最大值;②当1<t≤4时,直接写出S与t之间的函数关系式(要求写出自变量t的取值范围).【解答】解:(1)∵直线l1:y=x+2,∴B(﹣2,0),∴AB=OB=2,∵长方形ABCD的面积是12,∴AB×BC=12,∴OD=6,∴C(﹣2,6),∵直线l2:y=﹣kx+4(k≠0),∴2k+4=6,∴k=1;(2)如图1,记直线l1与y轴的交点为M,直线l2:与y轴的交点为N,∵直线l1:y=x+2与直线l2:y=﹣x+4(k≠0),∴M(0,2),N(0,4),G(4,0)∴OM=2=OE,ON=4=OG,∴∠OEM=45°,∠OGN=45°,∴∠EFG=90°,EF=GF,∴△EFG是等腰直角三角形;(3)∵直线l1:y=x+2与直线l2:y=﹣x+4(k≠0)相交于点F,∴F(1,3),①如图2,记长方形的边BC,AD与直线l1的交点为P,Q,由运动知,BE=t,∴BP=t,AE=t+2,∴AQ=BP=t+2,∴S=S梯形ABPQ=(t+t+2)×2=2t+2,∴当t=1时,S最大=4;②当1<t≤3时,如图3,过点F作FH⊥x轴于H,∴OH=1,FH=3,同①的方法得,BE=BI=t,AJ=AG=4﹣t,∴BH=EH﹣BE=3﹣t,AH=2﹣(3﹣t)=t﹣1,∴S=S梯形BIFH +S梯形AJFH=(t+3)×(3﹣t)+(4﹣t+3)×(t﹣1)=﹣t2+4t+1,当3<t≤4时,如图4,记长方形ABCD的边BC,AD与直线l2的交点为Q',P',由运动知,BE=t,∴BQ'=BG=6﹣t,AP'=AG=6﹣(t+2)=4﹣t,∴S=S梯形ABQ'P'=(6﹣t+4﹣t)×2=﹣2t+10.即:S=.15.(2016秋•武侯区期末)如图,已知直线y=x过点A,AB⊥y轴于点B,AC⊥x 轴于点C,点P是y轴上的一动点,连接AP交直线BC于点E.点N在直线BC 上,连接AN且∠PAN=90°,在射线AN上截取AD=AE,连接DE.(1)求证:BE2+EC2=2AE2;(2)若点A的坐标是(6,m),点P的坐标是(0,m),求线段AD的长;(3)当=时,求的值.【解答】(1)证明:如图1中,∵直线y=x过点A,AB⊥y轴,AC⊥x轴,∴AB=AC=OC=OB,四边形ABOC是正方形,∴∠ABC=∠PAD=90°,∠ABC=∠ACB=45°,∴∠BAE=∠DAC,在△BAE和△CAD中,,∴△BAE≌△CAD,∴BE=CD,∠ABE=∠ACD=45°,∴∠ECD=90°,∴EC2+CD2=ED2,∵△AED是等腰直角三角形,∵DE2=2AE2,∴EC2+BE2=2AE2.(2)解:如图2中,作EF⊥AB于F,EH⊥OB于H.则四边形BFEH是正方形.∴EF=EH,∵A(6,m),∴AB=AC=6,m=6,∵点P的坐标是(0,m),∴P(0,4),∴PB=2,∵==,∴=,∴==,∵PA==2,∴AD=AE=×2=.(3)解:如图2中,∵PB∥AC,∴===,设PB=a,则AC=AC=3a,∴PA==a,∴AD=AE=PA=a,∴DE=AE=a,∴==.(不用相似,解法如下:连接PC,设△ABE的面积为b,则△AEC的面积为3b,△PAC的面积为4b,推出△PEC的面积为b,所以△PEC的面积:△AEC的面积=1:3,推出PE:AE=1:3,就不难证明PB:AB=1:3)16.(2016秋•武侯区期末)如图,已知Rt△ABC中,∠ACB=90°,∠BAC=30°,延长BC至D使CD=BC,连接AD.(1)求证:△ABD是等边三角形;(2)若E为线段CD的中点,且AD=4,点P为线段AC上一动点,连接EP,BP.①求EP+AP的最小值;②求2BP+AP的最小值.【解答】(1)证明:∵∠ACB=90°,∠BAC=30°∴AC⊥BD,∠B=60°∵DC=CB,∴AD=AB,∵∠B=60°,∴△ABD是等边三角形.(2)①如图1中,作PF⊥AB于F,EF′⊥AB于F′,交AC于P′.∵∠PAF=30°,∠PFA=90°,。
真题汇总2022年四川省成都市中考数学历年真题练习 (B)卷(含答案及解析)
2022年四川省成都市中考数学历年真题练习 (B )卷 考试时间:90分钟;命题人:数学教研组 考生注意:1、本卷分第I 卷(选择题)和第Ⅱ卷(非选择题)两部分,满分100分,考试时间90分钟2、答卷前,考生务必用0.5毫米黑色签字笔将自己的姓名、班级填写在试卷规定位置上3、答案必须写在试卷各个题目指定区域内相应的位置,如需改动,先划掉原来的答案,然后再写上新的答案;不准使用涂改液、胶带纸、修正带,不按以上要求作答的答案无效。
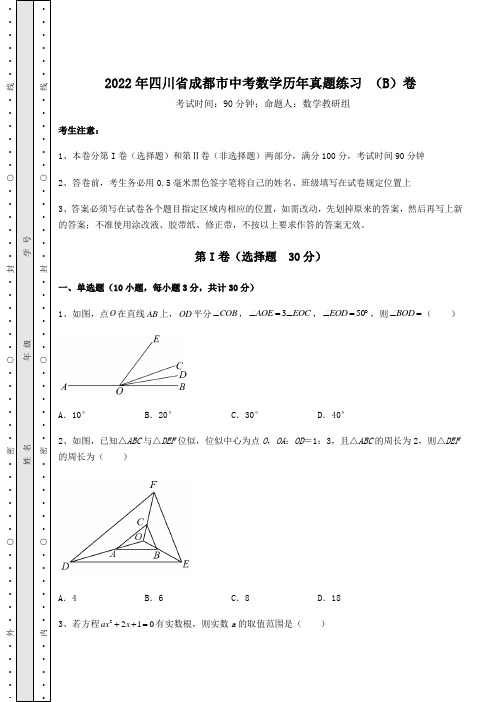
第I 卷(选择题 30分) 一、单选题(10小题,每小题3分,共计30分) 1、如图,点O 在直线AB 上,OD 平分COB ∠,3AOE EOC ∠=∠,50EOD ∠=︒,则BOD ∠=( ) A .10° B .20° C .30° D .40°2、如图,已知△ABC 与△DEF 位似,位似中心为点O ,OA :OD =1:3,且△ABC 的周长为2,则△DEF 的周长为( ) A .4B .6C .8D .18 3、若方程2210ax x ++=有实数根,则实数a 的取值范围是( )·线○封○密○外A .1a <B .1a ≤C .1a ≤且0a ≠D .1a <且0a ≠4、已知2250x x --=的两个根为1x 、2x ,则12x x +的值为( )A .-2B .2C .-5D .55、将抛物线y =x 2先向右平移3个单位长度,再向上平移5个单位长度,所得抛物线的解析式为( )A .y =(x +3)2+5B .y =(x ﹣3)2+5C .y =(x +5)2+3D .y =(x ﹣5)2+36、几个同学打算合买一副球拍,每人出7元,则还少4元;每人出8元,就多出3元.他们一共有( )个人.A .6B .7C .8D .97、对于新能源汽车企业来说,2021年是不平凡的一年,无论是特斯拉还是中国的蔚来、小鹏、理想都实现了销量的成倍增长,下图是四家车企的标志,其中既是轴对称图形,又是中心对称图形的是( )A .B .C .D .8、若反比例函数k y x =的图象经过点()2,2P -,则该函数图象不经过的点是( ) A .(1,4) B .(2,-2) C .(4,-1) D .(1,-4)9、已知点(2,3)A m +与点(4,)B n -关于y 轴对称,则m n +的值为( )A .5B .1-C .3-D .9-10、如图,点C 是以点O 为圆心,AB 为直径的半圆上的动点(点C 不与点A ,B 重合),4AB =.设弦AC 的长为x ,ABC ∆的面积为y ,则下列图象中,能表示y 与x 的函数关系的图象大致是( ) A . B . C . D . 第Ⅱ卷(非选择题 70分)二、填空题(5小题,每小题4分,共计20分)1、在⊙O 中,圆心角∠AOC =120°,则⊙O 内接四边形ABCD 的内角∠ABC =_____.2、如图,直线AA ∥AA ∥AA ,如果AA AA =13,AA =2,AA =6,那么线段BE 的长是_____________.3、给出下列程序:若输入的A 值为1时,输出值为1;若输入的A 值为1-时,输出值为−3;则当输·线○封○密·○外入的A 值为8时,输出值为______.4、写出一个比1大且比2小的无理数______.5、底面圆的半径为3,高为4的圆锥的全面积是______.三、解答题(5小题,每小题10分,共计50分)1、(1)()2322114()82x y xyz xy ⎛⎫-⋅-÷ ⎪⎝⎭. (2)22[(1)(2)22()]ab ab a b ab +--+÷-.2、如图,在四边形ABCD 中,对角线BD 平分∠ABC ,∠A =120°,∠C =60°,AB =17,AD =12.(1)求证:AD =DC ;(2)求四边形ABCD 的周长.3、如图,在AOB ∠内部作射线OC 和COB ∠的平分线OD .(1)请补全图形;(2)若100AOB ∠=︒,60AOC ∠=︒,求BOD ∠的度数;(3)若OC 是AOB ∠的角平分线,7BOD COA ︒∠+∠=,求BOD ∠的度数.4、在平面直角坐标系xOy 中,对于点(,)P x y 和(,)Q x y ',给出如下定义:若()0'(0)y x y y x ⎧=⎨-<⎩,则称点Q 为点P 的“可控变点” 例如:点(1,2)的“可控变点”为点(1,2),点(1,3)-的“可控变点”为点(1,3)--. (1)点(5,2)--的“可控变点”坐标为 ; (2)若点P 在函数216y x =-+的图象上,其“可控变点” Q 的纵坐标y '是7,求“可控变点” Q 的横坐标: (3)若点P 在函数()2165y x x a =-+-的图象上,其“可控变点” Q 的纵坐标y '的取值范围是1616y '-,求a 的值.5、阅读材料:在合并同类项中,()535313a a a a a -+=-+=,类似地,我们把()x y +看成一个整体,则()()()()()()535313x y x y x y x y x y +-+++=-++=+.“整体思想”是中学数学解题中的一种重要的思想,它在多项式的化简与求值中应用极为广泛. (1)把()2x y -看成一个整体,合并()()()222362x y x y x y ---+-的结果是 . (2)已知221a b -=,求2324a b -+的值: (3)已知21a b -=,21b c -=-,2c d -=,求653a b c d -+-的值.-参考答案- 一、单选题 1、A 【分析】 设∠BOD =x ,分别表示出∠COD ,∠COE ,根据∠EOD =50°得出方程,解之即可. 【详解】 ·线○封○密○外解:设∠BOD=x,∵OD平分∠COB,∴∠BOD=∠COD=x,∴∠AOC=180°-2x,∵∠AOE=3∠EOC,∴∠EOC=14∠AOC=18024x︒-=902x︒-,∵∠EOD=50°,∴90502xx︒-+=︒,解得:x=10,故选A.【点睛】本题考查角平分线的意义,通过图形表示出各个角,是正确计算的前提.2、B【分析】由ABC与DEF是位似图形,且:1:3OA OD=知ABC与DEF的位似比是1:3,从而得出ABC周长:DEF周长1:3=,由此即可解答.【详解】解:∵ABC与DEF是位似图形,且:1:3OA OD=,ABC∴与DEF的位似比是1:3.则ABC周长:DEF周长1:3=,∵△ABC的周长为2,∴DEF周长236=⨯=故选:B .【点睛】本题考查了位似变换:位似图形的任意一对对应点与位似中心在同一直线上,它们到位似中心的距离之比等于相似比,位似是相似的特殊形式,位似比等于相似比,其对应的周长比等于相似比. 3、B【分析】若方程为一元二次方程,则有0a ≠,24440b ac a =-=-≥,求解;若0a =,方程为一元一次方程,判断210x +=有实数根,进而求解取值范围即可. 【详解】 解:若方程为一元二次方程,则有0a ≠,24440b ac a =-=-≥ 解得1a ≤且0a ≠ 若0a =,方程为一元一次方程,210x +=有实数根 故选B .【点睛】本题考查了一元二次方程根的判别,一元一次方程的根.解题的关键在于全面考虑00a a =≠,的情况. 4、B 【分析】 直接运用一元二次方程根与系数的关系求解即可. 【详解】 解:∵2250x x --=的两个根为1x 、2x , ∴122=()21x x -+-= 故选:B·线○封○密·○外【点睛】本题主要考查了一元二次方程根与系数的关系,若1x 、2x 为一元二次方程20ax bx c ++=的两个实数根,则有12=b x x a +-,12=c x x a. 5、B【分析】根据二次函数图象左加右减,上加下减的平移规律进行求解.【详解】解:将抛物线y =x 2先向右平移3个单位长度,得:y =(x ﹣3)2;再向上平移5个单位长度,得:y =(x ﹣3)2+5,故选:B .【点睛】本题考察了二次函数抛物线的平移问题,解题的关键是根据左加右减,上加下减的平移规律进行求解.6、B【分析】依题意,按照一元一次方程定义和实际应用,列方程计算,即可;【详解】由题知,设合买球拍同学的人数为x ;∴ 7483x x +=-,可得:7x =∴故选B【点睛】本题主要考查一元一次方程的实际应用,关键在熟练审题和列方程计算;7、C【分析】根据轴对称图形与中心对称图形的概念结合所给图形的特点即可得出答案.【详解】解:A 、是轴对称图形,不是中心对称图形,故错误;B 、是轴对称图形,不是中心对称图形,故错误;C 、既是轴对称图形,又是中心对称图形,故正确;D 、既不是轴对称图形,也不是中心对称图形,故错误.故选:C . 【点睛】 本题考查了中心对称图形及轴对称图形的特点,轴对称图形的关键是寻找对称轴,图形两部分折叠后可重合;中心对称图形是要寻找对称中心,旋转180°后与原图重合.8、A【分析】 由题意可求反比例函数解析式4y x =-,将点的坐标一一打入求出xy 的值,即可求函数的图象不经过的点. 【详解】 解:因为反比例函数k y x =的图象经过点(2,2)P -, 所以4k =-,选项A 1444xy =⨯=≠-,该函数图象不经过的点(1,4),故选项A 符合题意; 选项B ()224xy =⨯-=-,该函数图象经过的点(2,-2),故选项B 不符合题意; 选项C ()414xy =⨯-=-,该函数图象经过的点(4,-1),故选项C 不符合题意;·线○封○密○外选项B ()144xy =⨯-=-,该函数图象经过的点(1,-4),故选项D 不符合题意;故选A.【点睛】考查了反比例函数图象上点的坐标特征,熟练运用反比例函数图象上点的坐标满足其解析式是本题的关键.9、A【分析】点坐标关于y 轴对称,横坐标互为相反数,纵坐标相等,可求得m n ,的值,进而可求m n +的值.【详解】解:由题意知:()2403m n ⎧++-=⎨=⎩解得23m n =⎧⎨=⎩∴235m n +=+=故选A .【点睛】本题考查了关于y 轴对称的点坐标的关系,代数式求值等知识.解题的关键在于理解关于y 轴对称的点坐标,横坐标互为相反数,纵坐标相等.10、B【分析】由AB 为圆的直径,得到∠C =90°,在Rt △ABC 中,由勾股定理得到BC =而列出△ABC 面积的表达式即可求解.【详解】解:∵AB 为圆的直径, ∴∠C =90°,4AB =,AC x =,由勾股定理可知:∴BC ==∴1122∆=⋅=⋅ABC S BC AC x 此函数不是二次函数,也不是一次函数,∴排除选项A 和选项C , AB 为定值,当OC AB ⊥时,ABC ∆面积最大,此时AC =即x =y 最大,故排除D ,选B . 故选:B . 【点睛】 本题考查了动点问题的函数图象,根据题意列出函数表达式是解决问题的关键. 二、填空题 1、120° 【分析】 先根据圆周角定理求出∠D ,然后根据圆内接四边形的性质求解即可. 【详解】解:∵∠AOC =120°∴∠D =12∠AOC =60°∵⊙O 内接四边形ABCD ·线○封○密○外∴∠ABC=180°-∠D=120°.故答案是120°.【点睛】本题主要考查了圆周角定理、圆内接四边形的性质等知识点,掌握圆内接四边形的性质是解答本题的关键.2、3【分析】过点D作DG∥AC交CF于点G,交BE于点H,根据AA∥AA∥AA,可得AAAA =AAAA=13,四边形ABHD和四边形ACGD是平行四边形,从而得到BH=AD=CG=2,AAAA =14,进而得到FG=4,再由BE∥CF,得到△DEH∽△DFG,从而得到HE=1,即可求解.【详解】解:如图,过点D作DG∥AC交CF于点G,交BE于点H,∵AA∥AA∥AA,∴AAAA =AAAA=13,四边形ABHD和四边形ACGD是平行四边形,∴BH=AD=CG=2,AAAA =14,∵AA=6,∴FG=4,∵BE ∥CF , ∴△DEH ∽△DFG ,∴AAAA =AAAA =14 , ∴HE =1, ∴BE =BH +HE =3. 故答案为:3 【点睛】本题主要考查了平行线分线段成比例,平行四边形的判定和性质,相似三角形的性质和判定,熟练掌握平行线分线段成比例,平行四边形的判定和性质,相似三角形的性质和判定是解题的关键. 3、3【分析】设输出的值为y ,根据程序可得计算法则:A =A √A 3+A ,根据待定系数法确定k ,b 的值,再将8代入即可. 【详解】 解:设输出的值为A ,根据图示可得计算法则为A =A √A 3+A ,∵若输入的A 值为1时,输出值为1;若输入的A 值为1-时,输出值为−3, ∴{A +A =1−A +A =−3,解得{A =2A =−1, ∴A =2√A 3−1, 当A =8时,A =2×2−1=3, 4、故答案为: 【点睛】 本题以程序为背景考查了求代数式的值,关键是弄清楚图示给出的计算程序. ·线○封○密○外3.答案不唯一,如√2、√3等【分析】根据无理数的大小比较和无理数的定义写出范围内的一个数即可.【详解】解:一个比1大且比2小的无理数有√2,√3等,故答案为:答案不唯一,如√2、√3等.【点睛】本题考查了对估算无理数和无理数的定义的应用,注意:答案不唯一.5、24A【分析】首先根据底面半径和高利用勾股定理求得母线长,然后直接利用圆锥的底面积和侧面积公式代入求出即可.【详解】∵圆锥的底面半径为3,高为4,∴母线长为5,∴圆锥的底面积为:AA2=9A,圆锥的侧面积为:AAA=A×3×5=15A,∴圆锥的全面积为:9A+15A=24A故答案为:24A.【点睛】本题考查了圆锥的计算,正确理解圆锥的侧面展开图与原来的扇形之间的关系是解决本题的关键.三、解答题1、(1)2xz;(2)ab+1【分析】(1)先计算积的乘方,后自左到右依次计算即可, (2)先计算括号里的,最后计算除法. 【详解】解:(1)原式2324(4)()11(84()())x x y y z x y -÷=-⨯ 34421214x y z x y ÷==2xz ; (2)原式=22222[22()2]ab ab a b a b ab -+÷--+-=22)(()a a a b b b --÷- =ab +1.【点睛】本题考查了整式的混合运算,熟练掌握运算的顺序,运算公式和运算法则是解题的关键. 2、 (1)证明见解析; (2)70.【分析】 (1)在BC 上取一点E ,使BE =AB ,连接DE ,证得△ABD ≌△EBD ,进一步得出∠BED =∠A ,利用等腰三角形的判定与性质与等量代换解决问题; (2)首先判定△DEC 为等边三角形,求得BC ,进一步结合(1)的结论解决问题. (1) 证明:在BC 上取一点E ,使BE =AB ,连结DE . ·线○封○密○外∵BD 平分∠ABC , ∴∠ABD =∠CBD . 在△ABD 和△EBD 中,AB BE ABD EBD BD BD =⎧⎪∠=∠⎨⎪=⎩, ∴△ABD ≌△EBD (SAS );∴DE =AD =12,∠BED =∠A ,AB =BE =17. ∵∠A =120°, ∴∠DEC =60°. ∵∠C =60°, ∴∠DEC =∠C , ∴DE =DC , ∴AD =DC . (2)∵∠C =60°,DE =DC , ∴△DEC 为等边三角形, ∴EC =CD =AD . ∵AD =12,∴EC =CD =12,∴四边形ABCD 的周长=17+17+12+12+12=70. 【点睛】此题考查全等三角形的判定与性质,等腰三角形和等边三角形的判定与性质,结合图形,灵活解答. 3、(1)图见解析 (2)20BOD ∠=︒(3)(7)3BOD ∠=︒ 【分析】(1)先根据射线的画法作射线OC ,再利用量角器画COB ∠的平分线OD 即可得; (2)先根据角的和差可得40COB ∠=︒,再根据角平分线的定义即可得;(3)先根据角平分线的定义可得12COA COB AOB ∠=∠=∠,1142CO BOD B B AO ∠=∠=∠,再根据7BOD COA ︒∠+∠=可得AOB ∠的度数,由此即可得.(1)解:补全图形如下:(2) 解:100AOB ∠=︒,60AOC ∠=︒, 40AOB AO COB C ∴∠=∠=-∠︒,·线○封○密·○外OD 是COB ∠的平分线,2012CO OD B B ∠∴=∠=︒;(3)解:OC 是AOB ∠的角平分线,12COA COB AOB ∴∠=∠=∠,OD 是COB ∠的平分线,1142C BOD AOB OB ∠=∴∠=∠,7BOD COA ∠+∠=︒,17214AOB AOB ∴∠+∠=︒, 解得(28)3AOB ∠=︒, 1287))433((BOD ∴=⨯︒=∠︒.【点睛】本题考查了画射线和角平分线、与角平分线有关的计算,熟练掌握角平分线的运算是解题关键. 4、 (1)(5,2)-(2)“可控变点” Q 的横坐标为3或(3)a =【分析】(1)根据可控变点的定义,可得答案;(2)根据可控变点的定义,可得函数解析式,根据自变量与函数值得对应关系,可得答案;(3)根据可控变点的定义,可得函数解析式,根据自变量与函数值得对应关系,结合图象可得答案.(1) 50-<,2y y ∴'=-=,即点(5,2)--的“可控变点”坐标为(5,2)-; (2) 由题意,得 216y x =-+的图象上的点P 的“可控变点”必在函数()0'(0)y x y y x ⎧=⎨-<⎩的图象上,如图1,“可控变点” Q 的纵坐标y '的是7,∴当2167x -+=时,解得3x =,当2167x -=时,解得x =故答案为:3或(3) ·线○封○密·○外由题意,得y =-x 2+16的图象上的点P 的“可控变点”必在函数y ′= 2216(0)16(0)x x y x x ⎧-+-<'≥=⎨⎩的图象上,如图2,当x =-5时,x 2-16=9, ∴-16<y ′=x 2-16≤9(x <0), ∴y ′=-16在y ′=-x 2+16(x ≥0)上, ∴-16=-x 2+16,∴x∴实数a 的值为 【点睛】本题考查了新定义,二次函数的图象与性质,利用可控变点的定义得出函数解析式是解题关键,又利用了自变量与函数值的对应关系. 5、(1)()2x y -- (2)1(3)9【分析】(1)将系数相加减即可;(2)将原式变形后整体代入221a b -=,即可求出答案; (3)将原式变形后()()()2223a b b c c d =---+-,再整体代入计算. (1) 解:()()()222362x y x y x y ---+-=()2362x y -+-() =()2x y --, 故答案为:()2x y --; (2) 解:∵221a b -=∴原式()2322321a b =--=-=; (3)解:∵21a b -=,21b c -=-,2c d -=, ∴原式24233a b b c c d =--++- ()()()2223a b b c c d =---+- 126=++ 9=. 【点睛】 此题考查了整式的加减法,整式的化简求值,正确掌握整式的加减法计算法则及整体代入计算方法是解题的关键.·线○封○密·○外。
成都中考B卷填空题几何专练7套

精选文档成都中考 B 填几何专练(一)1. 如图,等边△ ABC 中,点 D、E 、F 分别在边 BC、CA 、AB 上,且 BD=2DC , CE=2EA , AF=2FB , AD 与 BE 订交于点 P,BE 与 CF 订交于点 Q,CF 与 AD 订交于点 R,则 AP:PR:RD=.若△ABC 的面积为1,则△PQR 的面积为.2.如下图,已知∠ AOB= 30°,P 是∠ AOB 内一点,且点 P 到 OA、OB 的距离分别为 1、2,以 P 点为圆心的圆分别与OA、OB 订交于点 M、 N,且 MN 恰为圆的直径,则该圆的半径为____________.3.在直角坐标系中, O 为坐标原点, A 是双曲线k( k>0)在第一象限图象上的一点,且直线OA 是y=x第一象限的角均分线,直线OA 交双曲线于另一点C.将 OA 向上平移32 个单位后与双曲线在第一象限的图象交于点 M,交 y 轴于点 N,若MN1OA=2,则 k= __________.︵4.如图,扇形 AOB 中, OA=1,∠ AOB=90°,半圆 O1的圆心 O1在 OA 上,并与 AB 内切于点 A,半圆︵O2的圆心 O2在 OB 上,并与 AB 内切于点 B,半圆 O1与半圆 O2相切.设两半圆的面积之和为S,则 S 的取值范围是 ______________________.5.如图,平行四边形 ABCD 中, AM ⊥BC 于 M,AN⊥CD 于 N,已知 AB= 10, BM = 6, MC= 3,则 MN 的长为 ____________.6.如图,在菱形 ABCD 中,对角线 AC、BD 交于点 O,以 OB 为直径作⊙ M,过 D 作⊙ M 的切线,切点为N,分别交 AC、 BC 于点 E、F.若 AE= 5,CE=3,BF =___________,DF = ___________.7.如图,正方形 ABCD 中,点 E 、F 、G、H 分别在边AB、BC、CD 、DA 上,且 EG 与 FH 的夹角为 45°.若正方形 ABCD 的边长为 1, FH 的长为5,则 EG 的长为 ____________.28.已知抛物线y=ax2+ bx+c( a≠0)与 x 轴交于 A、B 两点,极点为 C,当△ ABC 为等腰直角三角形时,b2- 4ac 的值为 __________;当△ ABC 为等边三角形时, b 2- 4ac 的值为 __________.9.如图,△ ABC 中, AB= 7,BC= 12,CA= 11,内切圆 O 分别与 AB、BC、CA 相切于点 D、 E、 F,则AD : BE : CF =_______________.成都中考 B 填几何专练(二)1.如图,△ ABC 内接于⊙ O, BC= a, AC= b,∠A-∠ B=90°,则⊙ O 的半径为 _______________.2.如图, Rt△ABC 中,∠ ACB=90°, AC=2BC,CD⊥AB 于点 D ,过 AC 的中点 E 作 AC 的垂线,交ABEN于点 F,交 CD 的延伸线于点G,M 为 CD 中点,连结AM 交 EF 于点 N,则FG = ____________.3.如图,半径为 r1的⊙ O1内切于半径为r 2的⊙ O2,切点为 P,⊙ O2的弦 AB 过⊙ O1的圆心 O1,与⊙ O1交于 C、D ,且 AC : CD : DB= 3 : 4 : 2,则r 1= ___________.r 24.(1)如图 1,在边长为 1 的正方形 ABCD 内,两个动圆⊙ O1与⊙ O2相互外切,且⊙ O1与边 AB、AD 相切,⊙ O2与边 BC、 CD 相切,设⊙ O1与⊙ O2面积之和为 S,则 S 的取值范围是 _________________;( 2)如图 2,在矩形ABCD 中, AB=32,BC= 1,两个动圆⊙ O1与⊙ O2相互外切,且⊙ O1与边 AB、AD相切,⊙ O2与边 BC、CD 相切,设⊙ O1与⊙ O2面积之和为S,则 S 的取值范围是 _________________.5.如图,等腰梯形ABCD 中, AD∥BC,∠ B=60°, AB= CD= AD= 2,M 是 BC 的中点.将△DMC 绕点M旋转,得△D ′MC′,D′M 与 AB 交于点 E, C′M 与 AD 交于点 F,连结 EF ,则△ AEF 的周长的最小值为_____________.6.如图,已知矩形ABCD的面积为2011cm2,梯形 AFGE 的极点 F 在 BC 上, D 是腰 EG 的中点,则梯形AFGE 的面积为 ____________cm2.7.如图,在边长为 1 的正方形 ABCD 中,分别以A、B、C、D 为圆心, 1 为半径画四分之一圆,交点为E、F 、G、H,则中间暗影部分的周长为_____________,面积为 _____________.8.如图,在边长为 1 的正方形 ABCD 中, E、F 分别是 BC、CD 边上的动点,知足∠EAF =45°,则△CEF 内切圆半径的最大值为_____________.9.如图,在边长为 1 的正方形ABCD 中,点 M、N 分别在 CB、DC 的延伸线上,且∠ MAN=45°.过D作DP ⊥ AN 交 AM 于点 P,连结 PC,若 C 为 DN 的中点,则PC 的长为 _____________.成都中考 B 填几何专练(三)1.如,正方形 ABCD 的 2, M 是 AB 的中点,点 P 是射 DC 上的点.若以 C 心, CP 半径的与段 DM 只有一个公共点, PD 的取范是 __________________________________.2.如,点 A、 B 分在 x 正半和 y 半上, OA=OB= 2,点 E 是 y 正半上一点,接EA, O 作 OP⊥ EA 于 P,接PB , P 作 PF⊥ PB 交 x 正半于 F,接 EF.当 OE= 1 ,S△EAF=S1;OE= 2 , S△EAF= S2;⋯; OE=n , S△EAF = S n, S1+ S2+S3+⋯+S n=___________.3.如,直=B、点 C, B、C 两点的抛物y=2+bx+ c 与 x y x-3 与 x 、 y 分订交于点ax的另一交点 A ,点 D ,且称是直 x= 1.若平行于 x 的直 y=k与△BCD的外接有公共点, k 的取范是 _____________________.4.如,在Rt△ABC 中,∠ ACB=90°,半径 4 的⊙ A 与 AB 订交于点 D,与 AC 订交于点E,DE 并延,与段 BC 的延交于点P .已知 tan∠BPD =1,CE= 2,△ABC 的周.25.如图,在平行四边形ABCD 中, AE⊥ BC 于 E,AF ⊥CD 于 F ,H 是△ AEF 的垂心.若AC =20,EF =16,则 AH = __________.6.如图, AD 均分∠ BAC,交△ABC 的外接圆于点D, DE ∥BC ,交 AC 的延伸线于点E.若 AB= 4,AD=5,CE= 1,则 DE= __________.7.将一副三角板如图搁置,∠ BAC=∠BDC = 90°,∠ ABC= 45°,∠ DBC = 30°,BC= 4 2,则△ ADC的面积为 _____________.8.已知△ABC 中, AB=6,AC =BC= 5,将△ ABC 折叠,使点 A 落在 BC 边上的点 D 处,折痕为 EF (点 E 、F 分别在边 AB、AC 上).(1)当 ED⊥ BC 时, BE 的长为 ___________ ;(2)当以 B、E、D 为极点的三角形与△ DEF 相像时, BE 的长为 ___________.成都中考 B 填几何专练(四)1.如图,将正方形沿图中虚线(此中 a <b )剪成①②③④四块图形,用这四块图形恰能拼成一个矩形(非a正方形),则b 的值为 _____________.2.如图是一块矩形钢板 ABCD , AB = 4,BC = 3.工人师傅想用它裁出两块全等的、面积最大的△ APB 和△ CP ′D 钢板,且∠ APB =∠ CP ′D = 60°,则 △ APB 的面积为 ______________,请在图中画出切合要求的点P 和 P ′.( 2 小题变练) 已知矩形 ABCD 中,AB =4 3,BC = m ,P 是矩形 ABCD 边上的一动点, 且使得∠ APB =60°,假如这样的点 P 有 4 个,则 m 的取值范围是 ______________.3.已知 △ABC 中,∠ ABC = 30°, AB = 3,BC = 4,以 AC 为边在 △ ABC 外作等边三角形 ACD ,连结 BD ,则 BD 的长为 ____________.( 3 题变练)已知 △ ABC 中,∠ ABC =45°,AB =7 2,BC = 17,以 AC 为斜边在 △ ABC 外作等腰直角三 角形 ACD ,连结 BD ,则 BD 的长为 ____________.4.已知正方形ABCD 的面积是 144,E、M 分别是边 AB、AD 上的点,分别以 BE、DM 为边在正方形ABCD 内作正方形BEFG 和正方形DMNP .若两个小正方形重叠部分的面积是1,A、F、P 三点共线,则 tan∠ DAP =__________.5.如图,矩形纸片 ABCD 中, AB= 4,折叠纸片,使极点 A 落在 CD 边上的点′A 处, EF 为折痕(点 E、′′AE 相切于点 E,且与 AD 边也相切,F 分别在边 BC 、AD 上),连结 AE、 A E.若△ ECA 的外接圆恰巧与则 AD = __________.6.已知△ABC 中,∠ ABC= 45°, AB=52, BC= 12,将线段 AC 绕点 A 逆时针旋转90°,得线段 AD ,2连结 BD,则 BD 的长为 ____________.7.如图,等腰直角三角形 OAB 和 BCD 的底边 OB、BD 都在 x 轴上,直角极点A、 C 都在反比率函数y=k图象上,若 D(- 8,0),则 k= __________.x成都中考 B 填几何专练(五)11.如图,直线y=-x+ b 与双曲线 y=x(x> 0)交于 A、B 两点,与 x 轴、y 轴分别交于 E 、F 两点, AC⊥ x 轴于 C,BD⊥ y 轴于 D,当 b= __________时,△ ACE、△ BDF 与△AOB 面积的和等于△EOF 面积的34.︵2.如图,△ABC 中,∠ ACB= 90°,AC= 6-2,BC=6+2,半圆 O 过 A、B、C 三点, M 是 AB 的中点, ME ⊥ AC 于 E ,MF ⊥BC 于 F,则图中暗影部分的面积为_______________.3.直线y=-2x- 4 与 x 轴交于点 A ,与 y 轴交于点 B,将线段 AB 绕着平面内的某个点旋转180°后,获得k点 C、 D,恰巧落在反比率函数y=的图象上,且 D 、 C 两点横坐标之比为 3 : 1,则 k= _________.x4.如图, AB、AP、PB 分别是半圆 O、O1、O2的直径,点 P 在直径 AB 上, PQ⊥AB 交半圆 O 于点 Q,圆 O3的与半圆 O、 O2及 PQ 都相切,若圆 O3的半径为 3,暗影部分的面积为 39π,则 AB= ___________ .5.如图,正方形 ABCD 的边长为 2, E 是 AB 边上一点,将 △ ADE 绕点 D 逆时针旋转至 △ CDF ,连结 EF 交 CD 于点 G .若 ED =EG ,则 AE = ___________.6.已知 Rt △ ABC 中,∠ ACB = 90°,BC = 2AC ,CD ⊥AB 于 D ,E 是 BC 边上一点,且 BE =2CE ,连结 AE ,与 CD 订交于点 G ,EF ⊥AE ,与 AB 边订交于点 F .将∠ FEG 绕点 E 顺时针旋转,旋转后 EF 边所在的直线与 AB 边订交于点 F ′,EG 边所在的直线与 AC 边订交于点 H ,与 CD 订交于点 G ′.若 AH = 3 5,且FF′CG ′2=7 ,则线段 G ′H 的长为 ____________.7.如图,在平面直角坐标系中, O 为坐标原点,张口向上的抛物线与 x 轴交于点 A (- 1,0)、B (3,0),D 为抛物线的极点,∠ DAB = 45°.过 A 作 AC ⊥AD 交抛物线于点 C ,动直线 l 过点 A ,与线段 CD 交于点 P ,设点 C 、D 到直线 l 的距离分别为d 1、d 2,则 d 1+ d 2 的最大值为 __________.8.如图,在梯形 ABCD 中, AD ∥ BC ,∠ B + ∠C = 120°, AD =3, BC =7,则梯形 ABCD 面积的最大值为 __________.成都中考 B 填几何专练(六)1.如, Rt△ABC 和 Rt△BCD 有公共斜BC, M 是 BC 的中点, E、 F 分是 AB、BD 上的点.若∠ABC= 30°,∠ BCD =45°, BC= 4,△ECF 的周的最小 _____________.2.如所示,点A1、A2、A3在 x 上,且 OA1=A 1A2=A 2A3,分点A1、A2、A3作 y 的平行,与反比率函数y=8( x>0)的象分交于点B1、B 2、 B3,分点 B 1、 B2、 B3作 x 的平行,分与y x交于点C1、 C2、 C3,接 OB1、OB2、OB3,那么中暗影部分的面之和____________.3.在反比率函数 y=10(x> 0)的象上,有一系列点 A、A 、 A 、⋯、 A、A,若 A的横坐 2,x123n n+11且此后每点的横坐与它前一个点的横坐的差都2.分点 A1、 A2、 A3、⋯、 A n、 A n+1作 x 与 y的垂段,组成若干个矩形如所示,将中暗影部分的面从左到右挨次S1,S2,S3,⋯,S n,S1+ S2+ S3+⋯+ S n= ____________(用含 n 的代数式表示).4.如,点 A(x1,y1)、B( x2,y2)都在双曲y=kx(x>0)上,且x2-x1=4,y1-y2=2;分点A、B 向 x 、 y 作垂段,垂足分 C、 D、E、 F, AC 与 BF 订交于 G 点,四形 FOCG 的面 2,五形 AEODB 的面 14,那么双曲的分析式 _______________.5.如图,△ABC 的面积是63,D 是 BC 上的一点,且BD : CD= 2 : 1,DE∥ AC 交 AB 于 E ,延伸 DE 到 F,使FE: ED = 2 : 1,则△ CDF 的面积是 _________.6.已知线段AB 的长为 20 2,点 D 在线段 AB 上,△ACD 是边长为10 的等边三角形,过点 D 作与 CD垂直的射线DP ,过 DP 上一动点E(不与 D 重合)作矩形CDEF ,记矩形 CDEF 的对角线交点为O,连结OB,则线段OB 长的最小值为 _____________.7.如图,△ABC 和△ ADE 都是等腰直角三角形,∠ACB=∠ ADE=90°,∠BAE=135°,AC=22,AD =1,F 为BE 中点,则CF 的长为 _______________.将△ADE 绕点 A 旋转一周,则点 F 运动路径的长为_______________ .。
最新四川省成都市八年级下期期末数学B卷汇编:几何典型难题(含解析)四边形

最新四川省成都市八年级下期期末数学B卷汇编:几何典型难题一.解答题(共20小题)1.如图,四边形OABC是菱形,点C在x轴上,AB交y轴于点H,AC交y轴于点M.已知点A (﹣3,4).(1)求AO的长;(2)求直线AC的解析式和点M的坐标;(3)点P从点A出发,以每秒2个单位的速度沿折线A﹣B﹣C运动,到达点C终止.设点P 的运动时间为t秒,△PMB的面积为S.①求S与t的函数关系式;②求S的最大值.2.定义:只有一组对角是直角的四边形叫做损矩形,连结它的两个非直角顶点的线段叫做这个损矩形的直径.(1)如图1,损矩形ABCD,∠ABC=∠ADC=90°,则该损矩形的直径是线段AC,同时我们还发现损矩形中有公共边的两个三角形角的特点,在公共边的同侧的两个角是相等的.如图1中:△ABC和△ABD有公共边AB,在AB同侧有∠ADB和∠ACB,此时∠ADB=∠ACB;再比如△ABC和△BCD有公共边BC,在CB同侧有∠BAC和∠BDC,此时∠BAC=∠BDC.请再找一对这样的角来.(2)如图2,△ABC中,∠ABC=90°,以AC为一边向外作菱形ACEF,D为菱形ACEF的中心,连结BD,当BD平分∠ABC时,判断四边形ACEF为何种特殊的四边形?请说明理由.(3)在第(2)题的条件下,若此时AB=3,BD=,求BC的长.3.如图1,在△ABC中,点P为BC边中点,直线a绕顶点A旋转,若点B,P在直线a的异侧,BM⊥直线a于点M.CN⊥直线a于点N,连接PM,PN.(1)延长MP交CN于点E(如图2).①求证:△BPM≌△CPE;②求证:PM=PN;(2)若直线a绕点A旋转到图3的位置时,点B,P在直线a的同侧,其它条件不变,此时PM=PN还成立吗?若成立,请给予证明;若不成立,请说明理由;(3)若直线a绕点A旋转到与BC边平行的位置时,其它条件不变,请直接判断四边形MBCN 的形状及此时PM=PN还成立吗?不必说明理由.4.在直角三角形ABC中,∠BAC=90°,(AC>AB),在边AC上取点D,使得BD=CD,点E、F 分别是线段BC、BD的中点,连接AF和EF,作∠FEM=∠FDC,交AC于点M,如图1所示,(1)请判断四边形EFDM是什么特殊的四边形,并证明你的结论;(2)将∠FEM绕点E顺时针旋转到∠GEN,交线段AF于点G,交AC于点N,如图2所示,请证明:EG=EN;(3)在第(2)条件下,若点G是AF中点,且∠C=30°,AB=2,如图3,求GE的长度.5.(1)如图1,正方形ABCD中,∠PCG=45°,且PD=BG,求证:FP=FC;(2)如图2,正方形ABCD中,∠PCG=45°,延长FG交CB的延长线于点F,(1)中的结论还成立吗?请说明理由;(3)在(2)的条件下,作FE⊥PC,垂足为点E,交CG于点N,连结DN,求∠NDC的度数.6.如图,在平面直角坐标系中,直线AB分别交x、y轴于点A、B,直线BC分别交x、y轴于点C、B,点A的坐标为(2,0),∠ABO=30°,且AB⊥BC.(1)求直线BC和AB的解析式;(2)将点B沿某条直线折叠到点0,折痕分别交BC、BA于点E、D,在x轴上是否存在点F,使得点D、E、F为顶点的三角形是以DE为斜边的直角三角形?若存在,请求出F点坐标;若不存在,请说明理由;(3)在平面直角坐标系内是否存在两个点,使得这两个点与B、C两点构成的四边形是正方形?若存在,请直接写出这两点的坐标;若不存在,请说明理由.7.如图,菱形ABCD的对角线AC,BD相交于点O,延长AC到E,使CE=CO,连接EB,ED.(1)求证:EB=ED;(2)过点A作AF⊥AD,交BC于点G,交BE于点F,若∠AEB=45°,①试判断△ABF的形状,并加以证明;②设CE=m,求EF的长(用含m的式子表示).8.如图,△ABC与△ADE都为等腰直角三角形,∠ABC=∠ADE=90°,连接BD,EC,且F为EC的中点.(1)如图1,若D、A、C三点在同一直线上时,请判DF与BF的关系,并说明理由;(2)如图2,将图1中的△ADE绕点A逆时针旋转m°(0<m<90),请判断(1)中的结论是否仍然成立?并证明你的判断;(3)在(2)下,若△DEF与△BCF的面积之和于△DBF的而积,请直接写出m的值.9.已知菱形ABCD的边长为5,其顶点都在坐标轴上,且点A坐标为(0,﹣3).(1)求点B的坐标及菱形ABCD的面积;(2)点P是菱形边上一动点,沿A→B→C→D运动(到达D点时停止)①如图1,当点P关于x轴对称的点Q恰好落在直线y=x﹣3上时,求点P的坐标.②探究:如图2,当P运动到BC,CD边时,作△ABP关于直线AP的对称图形为△AB′P,是否存在这样的P点,使点B′正好在直线y=x﹣3上?若存在,求出满足条件的点P坐标;若不存在,请说明理由.10.如图1,已知△ABC是等边三角形,点D,E分别在边BC,AC上,且CD=AE,AD与BE相交于点F.(1)求证:∠ABE=∠CAD;(2)如图2,以AD为边向左作等边△ADG,连接BG.ⅰ)试判断四边形AGBE的形状,并说明理由;ⅱ)若设BD=1,DC=k(0<k<1),求四边形AGBE与△ABC的周长比(用含k的代数式表示).11.如图1,在正方形ABCD中,E是BC边上一点,F是BA延长线上一点,AF=CE,连接BD,EF,FG平分∠BFE交BD于点G.(1)求证:△ADF≌△CDE;(2)求证:DF=DG;(3)如图2,若GH⊥EF于点H,且EH=FH,设正方形ABCD的边长为x,GH=y,求y与x 之间的关系式.12.如图,在平面直角坐标系xOy中,已知直线AB经过点A(﹣2,0),与y轴的正半轴交于点B,且OA=2OB.(1)求直线AB的函数表达式;(2)点C在直线AB上,且BC=AB,点E是y轴上的动点,直线EC交x轴于点D,设点E的坐标为(0,m)(m>2),求点D的坐标(用含m的代数式表示);(3)在(2)的条件下,若CE:CD=1:2,点F是直线AB上的动点,在直线AC上方的平面内是否存在一点G,使以C,G,F,E为顶点的四边形是菱形?若存在,请求出点G的坐标;若不存在,请说明理由.13.如图,正方形ABCD中,AB=4,点E是对角线AC上的一点,连接DE.过点E作EF⊥ED,交AB于点F,以DE、EF为邻边作矩形DEFG,连接AG.(1)求证:矩形DEFG是正方形;(2)求AG+AE的值;(3)若F恰为AB中点,连接DF交AC于点M,请直接写出ME的长.14.菱形ABCD中,∠BAD=60°,BD是对角线,点E、F分别是边AB、AD上两个点,且满足AE=DF,连接BF与DE相交于点G.(1)如图1,求∠BGD的度数;(2)如图2,作CH⊥BG于H点,求证:2GH=GB+DG;(3)在满足(2)的条件下,且点H在菱形内部,若GB=6,CH=4,求菱形ABCD的面积.15.在平面直角坐标系中,过点C(1,3)、D(3,1)分别作x轴的垂线,垂足分别为A、B.(1)求直线CD和直线OD的解析式;(2)点M为直线OD上的一个动点,过M作x轴的垂线交直线CD于点N,是否存在这样的点M,使得以A、C、M、N为顶点的四边形为平行四边形?若存在,求此时点M的横坐标;若不存在,请说明理由;(3)若△AOC沿CD方向平移(点C在线段CD上,且不与点D重合),在平移的过程中,设平移距离为t,△AOC与△OBD重叠部分的面积记为s,试求s与t的函数关系式.16.如图1,△ABC中,CD⊥AB于D,且BD:AD:CD=2:3:4,(1)试说明△ABC是等腰三角形;(2)已知S△ABC=40cm2,如图2,动点M从点B出发以每秒1cm的速度沿线段BA向点A运动,同时动点N从点A出发以相同速度沿线段AC向点C运动,当其中一点到达终点时整个运动都停止.设点M运动的时间为t(秒),①若△DMN的边与BC平行,求t的值;②若点E是边AC的中点,问在点M运动的过程中,△MDE能否成为等腰三角形?若能,求出t的值;若不能,请说明理由.17.如图,在平面直角坐标系中,直线l1的解析式为y=﹣x,直线l2与l1交于点A(a,﹣a),与y轴交于点B(0,b),其中a,b满足(a+3)2+=0.(1)求直线l2的解析式;(2)在平面直角坐标系中第二象限有一点P(m,5),使得S△AOP=S△AOB,请求出点P的坐标;(3)已知平行于y轴左侧有一动直线,分别与l1,l2交于点M、N,且点M在点N的下方,点Q为y轴上一动点,且△MNQ为等腰直角三角形,请求出满足条件的点Q的坐标.18.直线y=﹣x+3和x轴、y轴的交点分别为B、C,点A的坐标是(﹣,0),另一条直线经过点A、C.(1)求线段AC所对应的函数表达式;(2)动点M从B出发沿BC运动,速度为1秒一个单位长度.当点M运动到C点时停止运动.设M运动t秒时,△ABM的面积为S.①求S与t的函数关系式;②当t为何值时,S=S△ABC,(注:S△ABC表示△ABC的面积),求出对应的t值;③当t=4的时候,在坐标轴上是否存在点P,使得△BMP是以BM为直角边的直角三角形?若存在,请直接写出P点坐标,若不存在,请说明理由.19.在△ABC中,AB=AC,∠BAC=α(0°<α<60°),将线段BC绕点B逆时针旋转60°得到线段BD.(1)如图1,直接写出∠ABD的大小(用含α的式子表示);(2)如图2,∠BCE=150°,∠ABE=60°,判断△ABE的形状并加以证明;(3)在(2)的条件下,连接DE,若∠DEC=45°,求α的值.20.问题发现:如图1,△ACB和△DCE均为等边三角形,点A、D、E在同一直线上,连接BE (1)填空:①∠AEB的度数为;②线段BE、AD之间的数量关系是.(2)拓展探究:如图2,△ACB和△DCE均为等腰三角形,∠ACB=∠DCE=90°,点A、D、E 在同一直线上,CM为△DCE中DE边上的高,连接BE.请判断∠AEB的度数及线段CM、AE、BE之间的数量关系,并说明理由.二.填空题(共16小题)21.如图,在平面直角坐标系中,有一Rt△ABC,且A(﹣1,3),B(﹣3,﹣1),C(﹣3,3),已知△A1AC1是由△ABC旋转得到的.若点Q在x轴上,点P在直线AB上,要使以Q、P、A1、C为顶点的四边形是平行四边形,满足条件的点P的坐标为.122.如图所示,正方形ABCD的面积为12,△ABE是等边三角形,点E在正方形ABCD内,在对角线AC上有一点P,使PD+PE的和最小,则这个最小值为.23.如图,矩形ABCD中,AB=2,AD=1,点M在边CD上,若AM平分∠DMB,则DM的长是.24.如图,在矩形ABCD中,BC=AB,∠ADC的平分线交边BC于点E,AH⊥DE于点H,连接CH并延长交边AB于点F,连接AE交CF于点O,则的值是.25.如图,在平行四边形ABCD中,∠A=45°,AB=4,AD=2,M是AD边的中点,N是AB边上一动点,将线段MN绕点M逆时针旋转90至MN′,连接N′B,N′C,则N′B+N′C的最小值是.26.如图,AC,BD是四边形ABCD的对角线,AD⊥BD,点E为AB的中点,连接DE交AC于点F,AF=CF,DF=DE.若BC=12,则AB长为.27.如图,矩形ABCO的边OC在x轴上,边OA在y轴上,且点C的坐标为(8,0),点A的坐标为(0,6),点E、F分别足OC、BC的中点,点M,N分别是线段OA、AB上的动点(不与端点重合),则当四边形EFNM的周长最小时,点N的坐标为.28.如图,正方形ABCD的边长AB=3,点E、F分别是CB,DC延长线上的点,连AF交CB于点G,若BE=1,连接AE,且∠EAF=45°,则AG长为.29.如图,点E是正方形ABCD边AD的中点,连接CE,过点A作AF⊥CE交CE的延长线于点F,过点D作DG⊥CF交CE于点G,已知AD=2,则线段AF的长是.30.如图,已知等腰直角△ABC中,∠BAC=90°,AD⊥BC于点D,AB=5,点E是边AB上的动点(不与A,B点重合),连接DE,过点D作DF⊥DE交AC于点F,连接EF,点H在线段AD上,且DH=AD,连接EH,HF,记图中阴影部分的面积为S,△EHF的面积记为S2,则1S=,S2的取值范围是.131.如图,将△AOB绕点O按逆时针方向旋转45°后得到△COD,若∠AOB=15°,则∠AOD的度数是.32.已知:如图,AD、BE分别是△ABC的中线和角平分线,AD⊥BE,AD=BE=2,则AC的长等于.33.如图,矩形纸片ABCD中,AD=5,AB=3.若M为射线AD上的一个动点,将△ABM沿BM 折叠得到△NBM.若△NBC是直角三角形.则所有符合条件的M点所对应的AM长度的和为.34.如图,正方形ABCD在平面直角坐标系中,其中A、C两点的坐标为A(2,6),C(﹣1,﹣7),则点B的坐标是.35.如图,动点P从(0,3)出发,沿所示方向运动,每当碰到矩形的边时反弹,反弹时反射角等于入射角,当点P第2014次碰到矩形的边时,点P的坐标为.36.如图,已知△ABC中,∠ABC=90°,AB=BC,三角形的顶点在相互平行的三条直线l1,l,l3,上,且l1,l2之间的距离为2,l2,l3之间的距离为3,则AC的长是.2三.选择题(共4小题)37.如图,菱形ABCD的对角线AC与BD交于点O,过点C作AB垂线交AB延长线于点E,连结OE,若AB=2,BD=4,则OE的长为()A.6B.5C.2D.438.如图,已知△ABC的面积为12,点D在线段AC上,点F在线段BC的延长线上,且BC=4CF,四边形DCFE是平行四边形,则图中阴影部分的面积为()A.2B.3C.4D.639.如图,在菱形ABCD中,点E,点F为对角线BD的三等分点,过点E,点F与BD垂直的直线分别交AB,BC,AD,DC于点M,N,P,Q,MF与PE交于点R,NF与EQ交于点S,已知四边形RESF的面积为5cm2,则菱形ABCD的面积是()A.35cm2B.40cm2C.45cm2D.50cm240.如图所示的正方形网格中,网格线的交点称为格点.已知A、B是两格点,如果C也是图中的格点,且使得△ABC为等腰三角形,则点C的个数是()A.6B.7C.8D.9参考答案与试题解析一.解答题(共20小题)1.如图,四边形OABC是菱形,点C在x轴上,AB交y轴于点H,AC交y轴于点M.已知点A (﹣3,4).(1)求AO的长;(2)求直线AC的解析式和点M的坐标;(3)点P从点A出发,以每秒2个单位的速度沿折线A﹣B﹣C运动,到达点C终止.设点P 的运动时间为t秒,△PMB的面积为S.①求S与t的函数关系式;②求S的最大值.【解答】(1)解:∵A(﹣3,4),∴AH=3,OH=4,由勾股定理得:AO==5,答:OA的长是5.(2)解:∵菱形OABC,∴OA=OC=BC=AB=5,5﹣3=2,∴B(2,4),C(5,0),设直线AC的解析式是y=kx+b,把A(﹣3,4),C(5,0)代入得:,解得:,∴直线AC的解析式为,当x=0时,y=2.5∴M(0,2.5),答:直线AC的解析式是,点M的坐标是(0,2.5).(3)①解:过M作MN⊥BC于N,∵菱形OABC,∴∠BCA=∠OCA,∵MO⊥CO,MN⊥BC,∴OM=MN,当0≤t<2.5时,P在AB上,MH=4﹣2.5=,S=×BP×MH=×(5﹣2t)×=﹣t+,∴,当t=2.5时,P与B重合,△PMB不存在;当2.5<t≤5时,P在BC上,S=×PB×MN=×(2t﹣5)×=t﹣,∴,答:S与t的函数关系式是(0≤t<2.5)或(2.5<t≤5).②解:当P在AB上时,高MH一定,只有BP取最大值即可,即P与A重合,S最大是×5×=,同理在BC上时,P与C重合时,S最大是×5×=,∴S的最大值是,答:S的最大值是.2.定义:只有一组对角是直角的四边形叫做损矩形,连结它的两个非直角顶点的线段叫做这个损矩形的直径.(1)如图1,损矩形ABCD,∠ABC=∠ADC=90°,则该损矩形的直径是线段AC,同时我们还发现损矩形中有公共边的两个三角形角的特点,在公共边的同侧的两个角是相等的.如图1中:△ABC和△ABD有公共边AB,在AB同侧有∠ADB和∠ACB,此时∠ADB=∠ACB;再比如△ABC和△BCD有公共边BC,在CB同侧有∠BAC和∠BDC,此时∠BAC=∠BDC.请再找一对这样的角来.(2)如图2,△ABC中,∠ABC=90°,以AC为一边向外作菱形ACEF,D为菱形ACEF的中心,连结BD,当BD平分∠ABC时,判断四边形ACEF为何种特殊的四边形?请说明理由.(3)在第(2)题的条件下,若此时AB=3,BD=,求BC的长.【解答】解:(1)由图1得:△ABD和△ADC有公共边AD,在AD同侧有∠ABD和∠ACD,此时∠ABD=∠ACD;(2)四边形ACEF为正方形,理由是:∵∠ABC=90°,BD平分∠ABC,∴∠ABD=∠CBD=45°,∴∠DAC=∠CBD=45°,∵四边形ACEF是菱形,∴AE⊥CF,∴∠ADC=90°,∴△ADC是等腰直角三角形,∴AD=CD,∴AE=CF,∴菱形ACEF是正方形;(3)如图2,过D作DG⊥BC于G,过E作EH⊥BC,交BC的延长线于H,∵∠DBG=45°,∴△BDG是等腰直角三角形,∵BD=4,∴BG=4,∵四边形ACEF是正方形,∴AC=CE,∠ACE=90°,AD=DE,易得△ABC≌△CHE,∴CH=AB=3,∵AB∥DG∥EH,AD=DE,∴BG=GH=4,∴CG=4﹣3=1,∴BC=BG+CG=4+1=5.3.如图1,在△ABC中,点P为BC边中点,直线a绕顶点A旋转,若点B,P在直线a的异侧,BM⊥直线a于点M.CN⊥直线a于点N,连接PM,PN.(1)延长MP交CN于点E(如图2).①求证:△BPM≌△CPE;②求证:PM=PN;(2)若直线a绕点A旋转到图3的位置时,点B,P在直线a的同侧,其它条件不变,此时PM=PN还成立吗?若成立,请给予证明;若不成立,请说明理由;(3)若直线a绕点A旋转到与BC边平行的位置时,其它条件不变,请直接判断四边形MBCN 的形状及此时PM=PN还成立吗?不必说明理由.【解答】(1)证明:①如图2:∵BM⊥直线a于点M,CN⊥直线a于点N,∴∠BMA=∠CNM=90°,∴BM∥CN,∴∠MBP=∠ECP,又∵P为BC边中点,∴BP=CP,又∵∠BPM=∠CPE,∴△BPM≌△CPE,②∵△BPM≌△CPE,∴PM=PE∴PM=ME,∴在Rt△MNE中,PN=ME,∴PM=PN.(2)解:成立,如图3.证明:延长MP与NC的延长线相交于点E,∵BM⊥直线a于点M,CN⊥直线a于点N,∴∠BMN=∠CNM=90°∴∠BMN+∠CNM=180°,∴BM∥CN∴∠MBP=∠ECP,又∵P为BC中点,∴BP=CP,又∵∠BPM=∠CPE,在△BPM和△CPE中,,∴△BPM≌△CPE,∴PM=PE,∴PM=ME,则Rt△MNE中,PN=ME∴PM=PN.(3)解:如图4,四边形BMNC是矩形,理由:∵MN∥BC,BM⊥AM,CN⊥MN,∴∠AMB=∠ANC=90°,∠AMB+∠CBM=180°,∴∠CBM=∠AMB=∠CNA=90°,∴四边形BMNC是矩形.∵BM=CN,∠PBM=∠PCN,BP=CP,∴△PBM≌△PCN(SAS)∴PM=PN.4.在直角三角形ABC中,∠BAC=90°,(AC>AB),在边AC上取点D,使得BD=CD,点E、F 分别是线段BC、BD的中点,连接AF和EF,作∠FEM=∠FDC,交AC于点M,如图1所示,(1)请判断四边形EFDM是什么特殊的四边形,并证明你的结论;(2)将∠FEM绕点E顺时针旋转到∠GEN,交线段AF于点G,交AC于点N,如图2所示,请证明:EG=EN;(3)在第(2)条件下,若点G是AF中点,且∠C=30°,AB=2,如图3,求GE的长度.【解答】解:(1)∵E,F是BC,BD的中点,∴EF∥CD,∴∠BFE=∠BDC,∵∠FEM=∠FDC,∴∠BFE=∠FEM,∴DF∥EM,∵EF∥CD,∴四边形EFDM是平行四边形,∵EM∥BD,点E是BC的中点,∴点M是CD的中点,∵点F是BD中点,∴DF=BD,∵BD=CD,∴DF=DM,∵四边形DFEM是平行四边形,∴▱DFEM是菱形;(2)由旋转知,∠FEM=∠GEN,∴∠FEG=∠MEN,在Rt△ABD中,点F是BD中点,∴AF=DF,∴∠DAF=∠ADF,∵EF∥CD,∴∠ADF=∠DFE,∴∠DAF=∠DFE,∴∠AFE=∠AFD+∠EFD=∠AFD+∠ADF=∠CDF,∵EM∥BD,∴∠CDF=∠EMN,∴∠AFE=∠CME,由(1)知,四边形DFEM是菱形,∴EF=EM,∴△EFG≌△EMN(AAS),∴EG=EN;(3)在Rt△ABC中,∠C=30°,AB=2,∴BC=4,∠ABC=60°,∵点E是BC的中点,∴CE=2,∴∠CBD=∠C=30°,∴∠ABD=30°,∴BD=,∴CD=,AF=BD=,∵G是AF的中点,∴FG=AF=,∵△EFG≌△EMN(AAS),∴EG=EN,MN=FG=,∵E,F是BC,BD的中点,∴EF=CD=,∴DM=EF=,∴CN=CD﹣DM﹣MN=﹣﹣=过点N作NH⊥BC于H∴EH=CN=,CH=EH=,∴EH=CE﹣CH=,在Rt△ENH中,EN==,∴EG=.5.(1)如图1,正方形ABCD中,∠PCG=45°,且PD=BG,求证:FP=FC;(2)如图2,正方形ABCD中,∠PCG=45°,延长FG交CB的延长线于点F,(1)中的结论还成立吗?请说明理由;(3)在(2)的条件下,作FE⊥PC,垂足为点E,交CG于点N,连结DN,求∠NDC的度数.【解答】解:(1)∵四边形ABCD是正方形,∴BC=CD,∠BCD=∠CBG=∠D=90°,∵BG=DP,∴△BCG≌△DCP(SAS),∴CP=CG,∠BCG=∠DCP,∵∠PCG=45°,∴∠BCG+∠DCP=45°,∴∠DCP=∠BCG=22.5°,∴∠PCF=∠PCG+∠BCG=67.5°,在△PCG中,CP=CG,∠PCG=45°,∴∠CPG=(180°﹣45°)=67.5°=∠PCF,∴PF=CF;(2)如图2,∵四边形ABCD是正方形,∴∠CBG=∠BCD=90°,过点C作CH⊥CG交AD的延长线于H,∴∠CDH=90°=∠HCG.∴∠BCG=∠DCH,∴△BCG≌△DCH(ASA),∴CG=CH,∵∠HCG=90°,∠PCG=45°,∴∠PCH=45°=∠PCG,∵CP=CP,∴△PCH≌△PCG(SAS),∴∠CPG=∠CPH,∵∠CPD+∠DCP=90°,∴∠CPF+∠DCP=90°,∵∠PCF+∠DCP=90°,∴∠CPF=∠PCF,∴PF=CF;(3)如图3,连接PN,由(2)知,PF=CF,∵EF⊥CP,∴PE=CE,∴EF是线段CP的垂直平分线,∴PN=CN,∴∠CPN=∠PCN,∵∠PCN=45°,∴∠CPN=45°,∴∠CNP=90°,∵PE=CE,∴EN=CP,在Rt△CDP中,CE=PE,∴DE=CE=CP,∴EN=DE,∴∠DNE=∠NDE,设∠DCP=α,∴∠CED=∠DCP=α,∴∠DEP=2α,∵∠PEF=90°,∴∠DEN=90°+2α,∴∠NDE=(180°﹣∠DEN)=45°﹣α,∴∠NDC=∠NDE+∠CDE=45°﹣α+α=45°.6.如图,在平面直角坐标系中,直线AB分别交x、y轴于点A、B,直线BC分别交x、y轴于点C、B,点A的坐标为(2,0),∠ABO=30°,且AB⊥BC.(1)求直线BC和AB的解析式;(2)将点B沿某条直线折叠到点0,折痕分别交BC、BA于点E、D,在x轴上是否存在点F,使得点D、E、F为顶点的三角形是以DE为斜边的直角三角形?若存在,请求出F点坐标;若不存在,请说明理由;(3)在平面直角坐标系内是否存在两个点,使得这两个点与B、C两点构成的四边形是正方形?若存在,请直接写出这两点的坐标;若不存在,请说明理由.【解答】解:(1)在Rt△AOB中,∵OA=2,∠ABO=30°,∴OB=2,在Rt△OBC中,∵∠BCO=30°,OB=2,∴OC=6,∴B(0,2),C(6,0),设直线AB的解析式为y=kx+b,则有,解得,∴直线AB的解析式为y=﹣x+2,设直线BC的解析式为y=k′x+b′则有,解得,∴直线BC的解析式为y=x+2.(2)如图1中,根据对称性可知,当点F与O重合时,∠EF′D=∠EBD=90°,此时F′(0,0),设DE交OB于K,作FH⊥DE于H.当△EFD≌△DF′E时,∠EFD=∠DF′E=90°,易证DK=EH=1,DE=AC=4,∴KH=OF=4﹣2=2,∴F(﹣2,0),综上所述,满足条件的点F坐标为(﹣2,0)或(0,0).(3)如图2中,∵B(0,2),C((﹣6,0),∴BC=4,当BC为正方形BCMN的边时,M(﹣6﹣2,6),N(﹣2,2+6)或M′(2﹣6,﹣6),N′(2,2﹣6).当BC为正方形的对角线时,M″(﹣3﹣,3+),N″(﹣3,﹣3).7.如图,菱形ABCD的对角线AC,BD相交于点O,延长AC到E,使CE=CO,连接EB,ED.(1)求证:EB=ED;(2)过点A作AF⊥AD,交BC于点G,交BE于点F,若∠AEB=45°,①试判断△ABF的形状,并加以证明;②设CE=m,求EF的长(用含m的式子表示).【解答】(1)证明:∵四边形ABCD是菱形,∴EA⊥BD,OB=OD,∴EB=ED(2)解:①结论:△ABF是等腰三角形(AB=AF);理由:∵∠AEB=45°,EO⊥OB,∴△BOE是等腰直角三角形,∴∠OBE=∠OEB=45°,∵AG⊥BC,∴∠AGB=∠BOC=90°,∴∠GAC+∠ACB=90°,∠ACB+∠OBC=90°,∴∠CAG=∠CBO=∠ABO,∵∠ABF=∠ABO+∠OBE=∠ABO+45°,∠AFB=∠CAG+∠AEB=∠CAG+45°,∴∠AFB=∠ABF,∴AB=AF,∴△ABF是等腰三角形.②作EH⊥AF交AF的延长线于H.由题意CE=OC=OA=m,OB=AC═OD=2m,AE=3m,AB=AF=m,tan∠CBO=tan∠CAG==,∴EH=m,AH=m,∴FH=AH﹣AF=m,在Rt△EFH中,EF===m.8.如图,△ABC与△ADE都为等腰直角三角形,∠ABC=∠ADE=90°,连接BD,EC,且F为EC的中点.(1)如图1,若D、A、C三点在同一直线上时,请判DF与BF的关系,并说明理由;(2)如图2,将图1中的△ADE绕点A逆时针旋转m°(0<m<90),请判断(1)中的结论是否仍然成立?并证明你的判断;(3)在(2)下,若△DEF与△BCF的面积之和于△DBF的而积,请直接写出m的值.【解答】解:(1)如图1中,结论:DF=BF,DF⊥BF.理由:在Rt△BEC中,∵∠EBC=90°,EF=FC,∴BF=EC,在Rt△DCE中,∵∠EDC=90°,EF=FC,∴DF=EC,∴DF=BF,∵∠FCB=∠FBC,∠FED=∠FDE,∴∠BFC+∠DFE=(180°﹣2∠FCB)+(180°﹣2∠FDE)=360°﹣2(∠FCB+∠FED)=360°﹣2(45°+∠BEC+∠FCB)=360°﹣270°=90°,∴∠DFB=90°,即DF⊥BF.(2)结论成立.理由:如图2中,如图作CM∥DE交DF的延长线于M,延长DA交MC的延长线于N,DN交BC 于O.∵DE∥CM,∴∠FED=∠FCM,∵∠DFE=∠MFC,EF=CF,∴△DFE≌△MFC,∴DF=FM,DE=CM=AD,∵∠EDN+∠N=180°,∠EDN=90°,∴∠N=∠ABO=90°,∵∠AOB=∠CON,∴∠DAB=∠ACM,∵BA=BC,AD=CM,∴△BAD≌△BCM,∴BD=BM,∠DBA=∠CBM,∴∠DBM=∠ABC=90°,∴△DBM是等腰直角三角形,∵DF=FM,∴BF⊥DF,BF=DF=FM.(3)如图2中,由(2)可知:△DFE≌△MFC,△BDM是等腰直角三角形,DF=FM,∴S△DEF+S△BFC=S△FCM=S四边形BFMC,S△BDF=S△BFM,∴当B、C、M共线时,△DEF与△BCF的面积之和于△DBF的面积,此时旋转角为45°,∴m=45°.9.已知菱形ABCD的边长为5,其顶点都在坐标轴上,且点A坐标为(0,﹣3).(1)求点B的坐标及菱形ABCD的面积;(2)点P是菱形边上一动点,沿A→B→C→D运动(到达D点时停止)①如图1,当点P关于x轴对称的点Q恰好落在直线y=x﹣3上时,求点P的坐标.②探究:如图2,当P运动到BC,CD边时,作△ABP关于直线AP的对称图形为△AB′P,是否存在这样的P点,使点B′正好在直线y=x﹣3上?若存在,求出满足条件的点P坐标;若不存在,请说明理由.【解答】解:(1)如图1中,∵四边形ABCD菱形,∴AB=BC=CD=AD=5,OA=OC,OB=OD,∵A(0,﹣3),∴OA=3,在Rt△AOD中,OD==4,∴BD=8,AC=6,∴S菱形ABCD=×BD×AC=24.(2)①如图2中,由题意B(4,0),C(0,3),∴直线BC的解析式为y=﹣x+3,由解得,∴Q(,),∴当点P坐标为(,﹣)时,点P关于x轴对称的点Q恰好落在直线y=x﹣3上,当点P′与C重合时,点P′关于x轴对称的点Q′恰好落在直线y=x﹣3上,此时P′(0,3),综上所述,满足条件的点P坐标为(,﹣)或(0,3);②如图3中,当AP平分∠BAQ时,满足条件,由题意A(0,﹣3),B(4,0),Q(,),∴AQ=,BQ=,∵=(角平分线性质定理,可以用面积法证明),∴=,∴PB=×=,∴可得P(,).当AP′⊥AP时,B″在直线AQ上,此时直线AP′的解析式为y=﹣x﹣3,直线CD的解析式为y=x+3,由,解得,∴P′(﹣,),综上所述,满足条件的点P坐标为(,)或(﹣,).10.如图1,已知△ABC是等边三角形,点D,E分别在边BC,AC上,且CD=AE,AD与BE相交于点F.(1)求证:∠ABE=∠CAD;(2)如图2,以AD为边向左作等边△ADG,连接BG.ⅰ)试判断四边形AGBE的形状,并说明理由;ⅱ)若设BD=1,DC=k(0<k<1),求四边形AGBE与△ABC的周长比(用含k的代数式表示).【解答】(1)证明:如图1中,∵△ABC是等边三角形,∴AB=AC,∠BAE=∠C=60°,∵AE=CD,∴△BAE≌△ACD,∴∠ABE=∠CAD.(2)解:ⅰ)如图2中,结论:四边形AGBE是平行四边形.理由:∵△ADG,△ABC都是等边三角形,∴AG=AD,AB=AC,∴∠GAD=∠BAC=60°,∴△GAD≌△DAC,∴BG=CD,∠ABG=∠C,∵CD=AE,∠C=∠BAE,∴BG=AE,∠ABG=∠BAE,∴BG∥AE,∴四边形AGBE是平行四边形,ⅱ)如图2中,作AH⊥BC于H.∵BH=CH=(k+1),∴DH=|1﹣(k+1)|=|﹣k|,AH=BH=(k+1),∴AD==,∴四边形BGAE的周长=2k+,△ABC的周长=3(k+1),∴四边形AGBE与△ABC的周长比=.11.如图1,在正方形ABCD中,E是BC边上一点,F是BA延长线上一点,AF=CE,连接BD,EF,FG平分∠BFE交BD于点G.(1)求证:△ADF≌△CDE;(2)求证:DF=DG;(3)如图2,若GH⊥EF于点H,且EH=FH,设正方形ABCD的边长为x,GH=y,求y与x 之间的关系式.【解答】(1)证明:如图1中,∵四边形ABCD是正方形,∴∠C=∠BAD=∠DAF=90°,CD=DA,在△ADF和△CDE中,,∴△ADF≌△CDE.(2)证明:如图1中,∵四边形ABCD是正方形,∴∠FBG=45°,∵△ADF≌△CDE,∴DF=DE,∠ADF=∠CDE,∴∠EDF=∠ADC=90°,∠DFE=45°,∵∠FDG=45°+∠EFG,∠DGF=45°+∠GFB,∵∠EFG=∠BFG,∴∠DFG=∠DGF,∴DF=DG.(3)结论:=.理由:如图2中,作GM⊥AB于M,GN⊥BC于N.连接EG.∵GF平分∠BAE,DB平分∠EBF,∴G是△BEF的内心,∵GH⊥EF,∴GH=GN=GM=y,∵FG=FG,EG=EG,∴Rt△FGH≌Rt△FGM,Rt△EGH≌Rt△EGN,四边形GMBN是正方形,∴FH=FM,EH=EN,GN=GM=BM=BN=y,∵EH:FH=1:3,设EH=a,则FH=3a,∵FB=3a+y,BE=a+y,∵EC=AF,∴FB+BE=2x,∴3a+y+a+y=2x,∴y=x﹣2a,∴CN=2a,∵EN=EH=a,∴CE=a,在Rt△DEF中,DE=2a,在Rt△DCE中,CD==a,∴x=a,y=(﹣2)a,∴=.12.如图,在平面直角坐标系xOy中,已知直线AB经过点A(﹣2,0),与y轴的正半轴交于点B,且OA=2OB.(1)求直线AB的函数表达式;(2)点C在直线AB上,且BC=AB,点E是y轴上的动点,直线EC交x轴于点D,设点E的坐标为(0,m)(m>2),求点D的坐标(用含m的代数式表示);(3)在(2)的条件下,若CE:CD=1:2,点F是直线AB上的动点,在直线AC上方的平面内是否存在一点G,使以C,G,F,E为顶点的四边形是菱形?若存在,请求出点G的坐标;若不存在,请说明理由.【解答】解:(1)∵A(﹣2,0),OA=2OB,∴OA=2,OB=1,∴B(0,1),设直线AB的解析式为y=kx+b,则有,解得,∴直线AB的解析式为y=x+1.(2)∵BC=AB,A(﹣2,0),B(0,1),∴C(2,2),设直线DE的解析式为y=k′x+b′,则有,解得,∴直线DE的解析式为y=x+m,令y=0,得到x=,∴D(,0).(3)如图1中,作CF⊥OD于F.∵CE:CD=1:2,CF∥OE,∴==,∵CF=2,∴OE=3.∴m=3.∴E(0,3),D(6,0),①当EC为菱形ECFG的边时,F(4,3),G(2,4)或F′(1,0),G′(﹣2,2).②当EC为菱形EF″CG″的对角线时,F″G″垂直平分线段EC,易知直线DE的解析式为y=﹣x+3,直线G″F″的解析式为y=2x+,由,解得,∴F″(,),设G″(a,b),则有=,=,∴a=,b=,∴G″(,).13.如图,正方形ABCD中,AB=4,点E是对角线AC上的一点,连接DE.过点E作EF⊥ED,交AB于点F,以DE、EF为邻边作矩形DEFG,连接AG.(1)求证:矩形DEFG是正方形;(2)求AG+AE的值;(3)若F恰为AB中点,连接DF交AC于点M,请直接写出ME的长.【解答】解:(1)如图,作EM⊥AD于M,EN⊥AB于N.∵四边形ABCD是正方形,∴∠EAD=∠EAB,∵EM⊥AD于M,EN⊥AB于N,∴EM=EN,∵∠EMA=∠ENA=∠DAB=90°,∴四边形ANEM是矩形,∴∠MEN=∠DEF=90°,∴∠DEM=∠FEN,∵∠EMD=∠ENF=90°,∴△EMD≌△ENF,∴ED=EF,∵四边形DEFG是矩形,∴四边形DEFG是正方形.(2)∵四边形DEFG是正方形,四边形ABCD是正方形,∴DG=DE,DC=DA=AB=4,∠GDE=∠ADC=90°,∴∠ADG=∠CDE,∴△ADG≌△CDE,∴AG=CE,∴AE+AG=AE+EC=AC=AD=4.(3)如图,作EH⊥DF于H.∵四边形ABCD是正方形,∴AB=AD=4,AB∥CD,∵F是AB中点,∴AF=FB2∴DF==2,∵△DEF是等腰直角三角形,EH⊥AD,∴DH=HF,∴EH=DF=,∵AF∥CD,∴AF:CD=FM:MD=1:2,∴FM=,∴HM=HF﹣FM=,在Rt△EHM中,EM==.14.菱形ABCD中,∠BAD=60°,BD是对角线,点E、F分别是边AB、AD上两个点,且满足AE=DF,连接BF与DE相交于点G.(1)如图1,求∠BGD的度数;(2)如图2,作CH⊥BG于H点,求证:2GH=GB+DG;(3)在满足(2)的条件下,且点H在菱形内部,若GB=6,CH=4,求菱形ABCD的面积.【解答】(1)解:如图1﹣1中,∵四边形ABCD是菱形,∴AD=AB,∵∠A=60°,∴△ABD是等边三角形,∴AB=DB,∠A=∠FDB=60°,在△DAE和△BDF中,,∴△DAE≌△BDF,∴∠ADE=∠DBF,∵∠EGB=∠GDB+∠GBD=∠GDB+∠ADE=60°,∴∠BGD=180°﹣∠BGE=120°.(2)证明:如图1﹣2中,延长GE到M,使得GM=GB,连接CG.∵∠MGB=60°,GM=GB,∴△GMB是等边三角形,∴∠MBG=∠DBC=60°,∴∠MBD=∠GBC,在△MBD和△GBC中,,∴△MBD≌△GBC,∴DM=GC,∠M=∠CGB=60°,∵CH⊥BG,∴∠GCH=30°,∴CG=2GH,∵CG=DM=DG+GM=DG+GB,∴2GH=DG+GB.(3)如图1﹣2中,由(2)可知,在Rt△CGH中,CH=4,∠GCH=30°,∴tan30°=,∴GH=4,∵BG=6,∴BH=2,在Rt△BCH中,BC==2,∵△ABD,△BDC都是等边三角形,∴S四边形ABCD=2•S△BCD=2××(2)2=26.15.在平面直角坐标系中,过点C(1,3)、D(3,1)分别作x轴的垂线,垂足分别为A、B.(1)求直线CD和直线OD的解析式;(2)点M为直线OD上的一个动点,过M作x轴的垂线交直线CD于点N,是否存在这样的点M,使得以A、C、M、N为顶点的四边形为平行四边形?若存在,求此时点M的横坐标;若不存在,请说明理由;(3)若△AOC沿CD方向平移(点C在线段CD上,且不与点D重合),在平移的过程中,设平移距离为t,△AOC与△OBD重叠部分的面积记为s,试求s与t的函数关系式.【解答】解:(1)设直线CD的解析式为y=kx+b,则有,解得,∴直线CD的解析式为y=﹣x+4.设直线OD的解析式为y=mx,则有3m=1,m=,∴直线OD的解析式为y=x.(2)存在.理由:如图1中,设M(m,m),则N(m,﹣m+4).当AC=MN时,A、C、M、N为顶点的四边形为平行四边形,∴|﹣m+4﹣m|=3,解得m=或,∴满足条件的点M的横坐标或.(3)如图3中,设平移中的三角形为△A′O′C′,点C′在线段CD上.设O′C′与x轴交于点E,与直线OD交于点P;设A′C′与x轴交于点F,与直线OD交于点Q.因为平移距离为t,所以水平方向的平移距离为t(0≤t<2),则图中AF=t,F(1+t,0),Q(1+t,+t),C′(1+t,3﹣t).设直线O′C′的解析式为y=3x+b,将C′(1+t,3﹣t)代入得:b=﹣4t,∴直线O′C′的解析式为y=3x﹣4t.∴E(t,0).联立y=3x﹣4t与y=x,解得x=t,∴P(t,t).过点P作PG⊥x轴于点G,则PG=t.∴S=S△OFQ﹣S△OEP=OF•FQ﹣OE•PG=(1+t)(+t)﹣•t•t=﹣(t﹣1)2+.16.如图1,△ABC中,CD⊥AB于D,且BD:AD:CD=2:3:4,(1)试说明△ABC是等腰三角形;(2)已知S△ABC=40cm2,如图2,动点M从点B出发以每秒1cm的速度沿线段BA向点A运动,同时动点N从点A出发以相同速度沿线段AC向点C运动,当其中一点到达终点时整个运动都停止.设点M运动的时间为t(秒),①若△DMN的边与BC平行,求t的值;②若点E是边AC的中点,问在点M运动的过程中,△MDE能否成为等腰三角形?若能,求出t的值;若不能,请说明理由.【解答】(1)证明:设BD=2x,AD=3x,CD=4x,则AB=5x,在Rt△ACD中,AC==5x,∴AB=AC,∴△ABC是等腰三角形;(2)解:S△ABC=×5x×4x=40cm2,而x>0,∴x=2cm,则BD=4cm,AD=6cm,CD=8cm,AC=10cm.①当MN∥BC时,AM=AN,即10﹣t=t,∴t=5;当DN∥BC时,AD=AN,得:t=6;∴若△DMN的边与BC平行时,t值为5或6.②当点M在BD上,即0≤t<4时,△MDE为钝角三角形,但DM≠DE;当t=4时,点M运动到点D,不构成三角形当点M在DA上,即4<t≤10时,△MDE为等腰三角形,有3种可能.如果DE=DM,则t﹣4=5,∴t=9;如果ED=EM,则点M运动到点A,∴t=10;如果MD=ME=t﹣4,过点E做EF垂直AB于F,因为ED=EA,所以DF=AF=AD=3,在Rt△AEF中,EF=4;因为BM=t,BF=7,所以FM=t﹣7则在Rt△EFM中,(t﹣4)2﹣(t﹣7)2=42,∴t=.综上所述,符合要求的t值为9或10或.17.如图,在平面直角坐标系中,直线l1的解析式为y=﹣x,直线l2与l1交于点A(a,﹣a),与y轴交于点B(0,b),其中a,b满足(a+3)2+=0.(1)求直线l2的解析式;(2)在平面直角坐标系中第二象限有一点P(m,5),使得S△AOP=S△AOB,请求出点P的坐标;(3)已知平行于y轴左侧有一动直线,分别与l1,l2交于点M、N,且点M在点N的下方,点Q为y轴上一动点,且△MNQ为等腰直角三角形,请求出满足条件的点Q的坐标.【解答】解:(1)由(a+3)2+=0,得a=﹣3,b=4,即A(﹣3,3),B(0,4),设l2的解析式为y=kx+b,将A,B点坐标代入函数解析式,得,解得,。
最新成都市中考数学B卷专题突破练习(几何综合)含答案经典题目

最新成都市中考数学B卷专题突破:几何综合1.如图,已知AC为正方形ABCD的对角线,点P是平面内不与点A,B重合的任意一点,连接AP,将线段AP绕点P顺时针旋转90°得到线段PE,连接AE,BP,CE.(1)求证:△APE∽△ABC;(2)当线段BP与CE相交时,设交点为M,求的值以及∠BMC的度数;(3)若正方形ABCD的边长为3,AP=1,当点P,C,E在同一直线上时,求线段BP的长.2.(1)如图1,△ABC为等边三角形,点D、E分别为边AB、AC上的一点,将图形沿线段DE所在的直线翻折,使点A落在BC边上的点F处.求证:BF•CF=BD•CE.(2)如图2,按图1的翻折方式,若等边△ABC的边长为4,当DF:EF=3:2时,求sin∠DFB的值;(3)如图3,在Rt△ABC中,∠A=90°,∠ABC=30°,AC=2,点D是AB边上的中点,在BC 的下方作射线BE,使得∠CBE=30°,点P是射线BE上一个动点,当∠DPC=60°时,求BP的长;3.△ABC中,AB=AC,∠ABC=α,过点A作直线MN,使MN∥BC,点D在直线MN上,作射线BD,将射线BD绕点B顺时针旋转角α后交直线AC于点E.(1)如图①,当α=60°,且点D在射线AN上时,直接写出线段AB,AD,AE的数量关系.(2)如图②,当α=45°,且点D在射线AN上时,直写出线段AB、AD、AE的数量关系,并说明理由.(3)当α=30°时,若点D在射线AM上,∠ABE=15°,AD=﹣1,请直接写出线段AE的长度.4.如图,在菱形ABCD中,对角线AC、BD交于点O,已知AC=2,AB=5.(1)求BD的长;(2)点E为直线AD上的一个动点,连接CE,将线段EC绕点C顺时针旋转∠BCD的角度后得到对应的线段CF(即∠ECF=∠BCD),EF交CD于点P.①当E为AD的中点时,求EF的长;②连接AF、DF,当DF的长度最小时,求△ACF的面积.5.已知:点E是正方形ABCD中边AB的中点.(1)如图1,点T为线段DE上一点,连接BT并延长交AD于点M,连接AT并延长交CD于点N,且AM=DN.试判断线段AN与线段BM的关系,并证明;求证:点M是线段AD的黄金分割点.(2)如图2,在AD边上取一点M,满足AM2=DM•DA时,连接BM交DE于点T,连接AT并延长交DC于点N,求tan∠MTD的值.6.如图,点E是正方形ABCD的边BC延长线上一点,连接DE,过顶点B作BF⊥DE,垂足为F,BF交边DC于点G.(1)求证:DG•BC=DF•BG;(2)连接CF,求∠CFB的大小;(3)作点C关于直线DE的对称点H,连接CH,FH.猜想线段DF,BF,CH之间的数量关系并加以证明.7.如图①,在正方形ABCD中,对角线AC、BD交于点O,动点P在线段BC上(不含点B),∠BPE=∠ACB,PE交BO于点E,过点B作BF⊥PE,垂足为F,交AC于点G.(1)如图②,当点P与点C重合时,求证:△BOG≌△POE;(2)通过观察、测量、猜想:=,并结合图①证明你的猜想;(3)把正方形ABCD改为菱形,其他条件不变(如图②),若∠ACB=a,直接写出的值,为.(用含a的式子表示)8.如图,在△ABC中,∠ACB=90°,tan A=,AC=6,以BC为斜边向右侧作等腰直角△EBC,P 是BE延长线上一点,连接PC,以PC为直角边向下方作等腰直角△PCD,CD交线段BE于点F,连接BD.(1)求证:PC:CD=CE:BC;(2)若PE=n(0<n≤4),求△BDP的面积;(用含n的代数式表示)(3)当△BDF为等腰三角形时,请直接写出线段PE的长度.9.如图,将矩形ABCD沿AF折叠,使点D落在BC边的点E处,过点E作EG∥CD交AF于点G,连接DG.(1)求证:四边形EFDG是菱形;(2)试证明EG2=GF•AF.10.在Rt△ABC中,∠ACB=90°,AB=,AC=2,过点B作直线m∥AC,将△ABC绕点C顺时针旋转得到△A′B′C(点A,B的对应点分别为A',B′),射线CA′,CB′分别交直线m于点P,Q.(1)如图1,当P与A′重合时,求∠ACA′的度数;(2)如图2,设A′B′与BC的交点为M,当M为A′B′的中点时,求线段PQ的长;(3)在旋转过程中,当点P,Q分别在CA′,CB′的延长线上时,试探究四边形P A'B′Q的面积是否存在最小值.若存在,求出四边形P A′B′Q的最小面积;若不存在,请说明理由.11.在矩形ABCD中,AB=3,AD=4,点P为AB边上的动点(P与A、B不重合),将△BCP沿CP翻折,点B的对应点B1在矩形外,PB1交AD于E,CB1交AD于点F.(1)如图1,求证:△APE∽△DFC;(2)如图1,如果EF=PE,求BP的长;(3)如图2,连接BB′交AD于点Q,EQ:QF=8:5,求tan∠PCB.12.如图,点E,F分别在矩形ABCD的边AB,BC上,连接EF,将△BEF沿直线EF翻折得到△HEF,AB=8,BC=6,AE:EB=3:1.(1)如图1,当∠BEF=45°时,EH的延长线交DC于点M,求HM的长;(2)如图2,当FH的延长线经过点D时,求tan∠FEH的值;(3)如图3,连接AH,HC,当点F在线段BC上运动时,试探究四边形AHCD的面积是否存在最小值?若存在,求出四边形AHCD的面积的最小值;若不存在,请说明理由.13.已知,如图所示,在矩形ABCD中,点E在BC边上,△AEF=90°(1)如图①,已知点F在CD边上,AD=AE=5,AB=4,求DF的长;(2)如图②,已知AE=EF,G为AF的中点,试探究线段AB,BE,BG的数量关系;(3)如图③,点E在矩形ABCD的BC边的延长线上,AE与BG相交于O点,其他条件与(2)保持不变,AD=5,AB=4,CE=1,求△AOG的面积.14.如图,在等边△ABC中,点E,F分别是边AB,BC上的动点(不与端点重合),且始终保持AE=BF,连接AF,CE相交于点P.过点A作直线m∥BC,过点C作直线n∥AB,直线m,n相交于点D,连接PD交AC于点G.(1)求∠APC的大小;(2)求证:△APD∽△EAC;(3)在点E,F的运动过程中,若=,求的值.15.如果a:b=b:c,即b2=ac,则b叫a和c的比例中项,或等比中项.若一个三角形一条边是另两条边的等比中项,我们把这个三角形叫做等比三角形.(1)已知△ABC是等比三角形,AB=2,BC=3.请直接写出所有满足条件的AC的长;(2)如图,在四边形ABCD中,AD∥BC,对角线BD平分∠ABC,∠BAC=∠ADC,求证:△ABC是等比三角形;(3)如图2,在(2)的条件下,当∠ADC=90时,求的值.参考答案1.解:(1)∵AC是正方形ABCD的对角线,∴∠ABC=90°,∠BAC=∠BCA=45°,由旋转知,P A=PE,∠APE=90°=∠ABC,∴∠P AE=∠PEA=45°=∠BAC,∴△APE∽△ABC;(2)在Rt△ABC中,AB=CB,∴AC=AB,由(1)知,△APE∽△ABC,∴,∵∠BAC=∠P AE=45°,∴∠P AB=∠EAC,∴△P AB∽△EAC,∴==,∵△P AB∽△EAC,∴∠ABP=∠ACE,∴∠BCE+∠CBM=∠BCE+∠ABP+∠ABC=∠BCE+∠ACE+∠ABC=∠ACB+∠ABC=45°+90°=135°,∴∠BMC=180°﹣(∠BCE+∠CBM)=45°;(3)如图,在Rt△ABC中,AB=AC=3,∴AC=3,∵点P,C,E在同一条线上,且∠APE=90°,∴CP==,∴CE=CP﹣PE=﹣1或CE'=CP'+P'E=+1,由(2)知,=,∴BP=CE=(﹣1)=或BP'=CE'=;即:BP的长为或.2.(1)证明:∵△ABC是等边三角形,∠A=∠B=∠C=60°,∴∠BDF+∠BFD=180°﹣∠B=120°,由折叠知,∠DFE=∠A=60°,∴∠CFE+∠BFD=120°,∴∠BDF=∠CFE,∵∠B=∠C=60°,∴△BDF∽△CFE,∴,∴BF•CF=BD•CE;(2)解:如图2,设BD=3x(x>0),则AD=AB﹣BD=4﹣3x,由折叠知,DF=AD=4﹣3x,过点D作DH⊥BC于H,∴∠DHB=∠DHF=90°,∵∠B=60°,∴BH=x,DH=x,由(1)知,△BDF∽△CFE,∴=,∵DF:EF=3:2,∴=,∴CF=2x,∴BF=BC﹣CF=4﹣2x,∴HF=BF﹣BH=4﹣2x﹣x=4﹣x,在Rt△DHF中,DH2+HF2=DF2,∴(x)2+(4﹣x)2=(4﹣3x)2,∴x=0(舍)或x=,∴DH=,DF=4﹣3×=,∴sin∠DFB===;(3)如图3,在Rt△ABC中,AC=2,∠ABC=30°,∴BC=2AC=4,AB=AC=6,∵点D是AB的中点,∴BD=AB=3,过点C作BC的垂线交BP的延长线于Q,∴∠BCQ=90°,在Rt△BCQ中,∠CBE=30°,∴CQ==4,∴BQ=2CQ=8,∴∠BCQ=90°,∵∠CBE=30°,∴∠Q=90°﹣∠CBE=60°,∴∠DBP=∠ABC+∠CBE=60°=∠Q,∴∠CPQ+∠PCQ=120°,∵∠DPC=60°,∴∠BPD+∠CPQ=120°,∴∠BPD=∠PCQ,∴△BDP∽△QPC,∴=,∴,∴BP=2或BP=6.3.解:(1)∵当α=60°时,∠ABC=∠DBE=60°,∴∠ABD=∠CBE,又∵AB=AC,∴△ABC是等边三角形,∴AB=CB,∠ACB=60°,∴∠BCE=120°,∵MN∥BC,∴∠BAD=180°﹣∠ABC=120°,∴∠BAD=∠BCE,∴△BAD≌△BCE,∴AD=CE,∴AE=AC+CE=AB+AD;(2)AE=AB+AD.理由:当α=45°时,∠ABC=∠DBE=45°,∴∠ABD=∠CBE,∵AB=AC,∴∠ABC=∠ACB=45°,∠BAC=90°,∴△ABC是等腰直角三角形,∴BC=AB,∵MN∥BC,∴∠BAD=180°﹣∠ABC=135°,∵∠BCE=180°﹣∠ACB=135°,∴∠BAD=∠BCE,∴△BAD∽△BCE,∴==,∴CE=AD,∴AE=AC+CE=AB+AD;(3)线段AE的长度为﹣1或2﹣.由题可得,∠ABC=∠DBE=∠BAD=30°,分两种情况:①如图所示,当点E在线段AC上时,∵∠ABE=15°=∠ABC=∠DBE,∴∠ABD=∠ABE=15°,在BE上截取BF=BD,易得△ABD≌△ABF,∴AD=AF=﹣1,∠ABC=∠BAD=∠BAF=30°,∴∠AFE=∠ABF+∠BAF=15°+30°=45°,又∵∠AEF=∠CBE+∠C=15°+30°=45°,∴∠AFE=∠AEF,∴AE=AF=﹣1;②如图所示,当点E在CA的延长线上时,过D作DF⊥AB于F,过E作EG⊥BC于G,∵AD=﹣1,∠DAF=30°,∴DF=,AF=,∵∠DBF=15°+30°=45°,∴∠DBF=∠BDF,∴BF=DF=,AB=+=1=AC,易得△ABC中,BC=,∵∠EBG=15°+30°=45°,∴∠BEG=∠EBG,设BG=EG=x,则CG=﹣x,∵Rt△CEG中,tan C=,即=,∴x==EG,∴CE=2EG=3﹣,∴AE=CE﹣AC=3﹣﹣1=2﹣综上所述所,线段AE的长度为﹣1或2﹣.4.解:(1)∵四边形ABCD是菱形,∴AD=AB=BC=CD=5,AC⊥BD,OA=OC=AC=,OB=OD,在Rt△ABO中,由勾股定理得:OB===2,∴BD=2OB=4;(2)①过点C作CH⊥AD于H,如图1所示:∵四边形ABCD是菱形,∴∠BAC=∠DAC,∴cos∠BAC=cos∠DAC,∴==,即=,∴AH=2,∴CH==4,∵E为AD的中点,∴AE=AD=,∴HE=AE﹣AH=,在Rt△CHE中,由勾股定理得:EC==,由旋转的性质得:∠ECF=∠BCD,CF=CE,∴=,∴△BCD∽△ECF,∴,即=,解得:EF=2;②如图2所示:∵∠BCD=∠ECF,∴∠BCD﹣DCE=∠ECF﹣∠DCE,即∠BCE=∠DCF,在△BCE和△DCF中,,∴△BCE≌△DCF(SAS),∴BE=DF,当BE最小时,DF就最小,且BE⊥DE时,BE最小,此时∠EBC=∠FDC=90°,BE=DF=4,△EBC的面积=△ABC的面积=△DCF的面积,则四边形ACFD的面积=2△ABC的面积=5×4=20,过点F作FH⊥AD于H,过点C作CP⊥AD于P,则∠CPD=90°,∴∠PCD+∠PDC=90°,∵∠FDC=90°,∴∠PDC+∠HDF=90°,∴∠PCD=∠HDF,∴△PCD∽△HDF,∴==,∴HF=4×=,∴S△ADF=AD•HF=×5×=6,∴S△ACF=S四边形ACFD﹣S△ADF=20﹣6=14,即当DF的长度最小时,△ACF的面积为14.5.解:(1)AN=BM,AN⊥BM.理由如下:∵四边形ABCD是正方形,∴AB=DA,∠BAD=∠ADC=90°,又AM=DN,∴△ABM≌△DAN(SAS),∴∠ABM=∠DAN,AN=BM又∠BAD=90°即∠BAN+∠DAN=90°,∴∠BAN+∠ABM=90°∴∠ATB=90°,∴AN⊥BM﹣∴AN=BM,AN⊥BM;证明:∵∠ATB=90°,M是AB中点.∴TE=BE=AE,∴∠EBT=∠ETB,∠EAT=∠ATE,又∠ABM=∠DAN,∠ETB=∠MTD,∴∠MTD=∠DAN,又∠MDT=∠ADT,∴△MDT~△TDA,∴,∴DT2=MD•AD,由AB∥CD,可得∠TND=∠EAT,又∠EAT=∠ATE,∠ATE=∠DTN,∴∠TND=∠DTN∴DT=DN,又AM=DN,∴DT=AM,又DT2=MD•AD,∴AM2=MD•AD,∴,∴点M是线段AD的黄金分割点;(2)延长BM,CD交于点F,如图.∵四边形ABCD是正方形,AB∥CD,∴∠F=∠MBA,又∠FMD=∠AMB,∴△FMD~△BMA,∴,即DM•AB=AM•DF,∵AB=AD,AM2=DM•AD,∴AM=DF,由AB∥CF知,又AE=BE,∴DF=DN=AM,由AB=AD,∠BAM=∠ADN=90°,DN=AM,可证△ABM≌△DAN(SAS),∴∠ABM=∠DAN,∴∠ABT+∠TAB=∠TAB+∠DAN=∠BAD=90°,∴∠ATB=90°,又AE=BE,∴BE=ET,∴∠ABM=∠ETB=∠MTD,不妨设正方形的边长为1.设AM=x,由AM2=MD•AD,得x2=(1﹣x)•1,,又负值不合题意,舍去.∴,∴,在Rt△ABM中,tan,又∠ABM=∠MTD,∴.6.(1)证明:∵四边形ABCD是正方形,∴∠BCD=90°,∵BF⊥DE,∴∠GFD=90°,∴∠BCD=∠GFD,∵∠BGC=∠FGD,∴△BGC∽△DGF,∴,∴DG•BC=DF•BG;(2)解:如图1,连接BD,∵△BGC∽△DGF,∴,∴,∵∠BGD=∠CGF,∴△BGD∽△CGF,∴∠BDG=∠CFG,∵四边形ABCD是正方形,BD是对角线,∴∠BDG=∠ADC=45°,∴∠CFB=45°;(3)解:BF=CH+DF,理由如下:如图2,在线段FB上截取FM,使得FM=FD,连接DM,∵∠BFD=90°,∴∠MDF=∠DMF=45°,DM=DF,∵∠BDG=45°,∴∠BDM=∠CDF,∵△BGD∽△CGF,∴∠GBD=∠DCF,∴△BDM∽△CDF,∴,∴BM=CF,∵∠CFB=45°,BF⊥DE,点C关于直线DE的对称点H,∴∠EFG=∠EFC=45°,∴∠CFG=90°,∵CF=FG,∴CH=CF,∴BM=CH,∴BF=BM+FM=CH+DF.7.(1)证明:∵四边形ABCD是正方形,P与C重合,∴OB=OP,∠BOC=∠BOG=90°,∵PF⊥BG,∠PFB=90°,∴∠GBO=90°﹣∠BGO,∠EPO=90°﹣∠BGO,∴∠GBO=∠EPO,在△BOG和△POE中,,∴△BOG≌△POE(ASA);(2)解:猜想=.证明:如图2,过P作PM∥AC交BG于M,交BO于N,∴∠PNE=∠BOC=90°,∠BPN=∠OCB.∵∠OBC=∠OCB=45°,∴∠NBP=∠NPB.∴NB=NP.∵∠MBN=90°﹣∠BMN,∠NPE=90°﹣∠BMN,∴∠MBN=∠NPE,在△BMN和△PEN中,,∴△BMN≌△PEN(ASA),∴BM=PE.∵∠BPE=∠ACB,∠BPN=∠ACB,∴∠BPF=∠MPF.∵PF⊥BM,∴∠BFP=∠MFP=90°.在△BPF和△MPF中,,∴△BPF≌△MPF(ASA).∴BF=MF.即BF=BM.∴BF=PE.即=;故答案为;(3)解:如图3,过P作PM∥AC交BG于点M,交BO于点N,∴∠BPN=∠ACB=α,∠PNE=∠BOC=90°.由(2)同理可得BF=BM,∠MBN=∠EPN,∴△BMN∽△PEN,∴=.在Rt△BNP中,tanα=,∴=tanα.即=tanα.∴=tanα.故答案为tanα.8.(1)证明:∵△PCD,△EBC都是等腰直角三角形,∴CD=PC,BC=CE,∴==,==,∴=(2)解:如图1中,作PH⊥BD于H,∵△PCD,△EBC都是等腰直角三角形,∴∠PCD=∠BCE=45°,∠PBC=∠PDC=45°,∴B、C、P、D四点共圆,∴∠DBP=∠PCD=45°,∴∠CBD=∠DBP+∠PBC=45°+45°=90°,△PBH是等腰直角三角形,∵∠BCE=∠DCP=45°,∴∠BCD=∠ECP,∵∠CEP=∠CBD=90°,∴△CBD∽△CEP,∴==,∵PE=n,∴BD=n,∵tan A==,AC=6,∴BC=4,∴EC=BE=4,∴PB=4+n,PH=BH=(4+n),∴S△BDP=•BD•PH=×n×(4+n)=2n+n2(0<n≤4);(3)解:①如图2中,当BF=BD时,在BC上取一点G,使得BG=BD,∵∠PBD=45°,∴∠BDF=67.5°,∵∠CBD=90°,∴∠BDG=∠BGD=45°,∴∠BCD=∠GDC=22.5°,∴GC=GD,∵PE=n,BD=n,∴BG=n,CG=DG=BG=2n,∴BG+CG=BC=4,∴n+2n=4,∴n=4﹣4,∴PE=4﹣4;②如图3中,当FB=FD时,则∠FBD=∠FDB=45°,此时BD=BC=4,∵∠CDP=45°,∴∠BDP=90°,∵∠CPD=90°,∠CBD=90°,∴四边形CBDP为正方形,E、F点重合,∴PE=BE=4,综上所述,线段PE的长度为:4﹣4或4.9.(1)证明:∵GE∥DF,∴∠EGF=∠DFG.∵由翻折的性质可知:GD=GE,DF=EF,∠DGF=∠EGF,∴∠DGF=∠DFG.∴GD=DF.∴DG=GE=DF=EF.∴四边形EFDG为菱形.(2)解:如图所示:连接DE,交AF于点O.∵四边形EFDG为菱形,∴GF⊥DE,OG=OF=GF.∵∠DOF=∠ADF=90°,∠OFD=∠DF A,∴△DOF∽△ADF.∴=,即DF2=FO•AF.∵FO=GF,DF=EG,∴EG2=GF•AF.10.解:(1)由旋转可得:AC=A'C=2,∵∠ACB=90°,AB=,AC=2,∴BC=,∵∠ACB=90°,m∥AC,∴∠A'BC=90°,∴cos∠A'CB==,∴∠A'CB=30°,∴∠ACA'=60°;(2)∵M为A'B'的中点,∴∠A'CM=∠MA'C,由旋转可得,∠MA'C=∠A,∴∠A=∠A'CM,∴tan∠PCB=tan∠A=,∴PB=BC=,∵∠PCQ=∠PBC=90°,∴∠BQC+∠BPC=∠BCP+∠BPC=90°,∴∠BQC=∠BCP=∠A,∴tan∠BQC=tan∠A=,∴BQ=BC×=2,∴PQ=PB+BQ=;(3)∵S四边形P A'B′Q=S△PCQ﹣S△A'CB'=S△PCQ﹣,∴S四边形P A'B′Q最小,即S△PCQ最小,∴S△PCQ=PQ×BC=PQ,法一:(几何法)取PQ的中点G,∵∠PCQ=90°,∴CG=PQ,即PQ=2CG,当CG最小时,PQ最小,∴CG⊥PQ,即CG与CB重合时,CG最小,∴CG min=,PQ min=2,∴S△PCQ的最小值=3,S四边形P A'B′Q=3﹣;法二(代数法)设PB=x,BQ=y,由射影定理得:xy=3,∴当PQ最小时,x+y最小,∴(x+y)2=x2+2xy+y2=x2+6+y2≥2xy+6=12,当x=y=时,“=”成立,∴PQ=+=2,∴S△PCQ的最小值=3,S四边形P A'B′Q=3﹣.11.证明:(1)∵四边形ABCD是矩形∴∠A=∠D=∠ABC=∠BCD=90°∴∠APE+∠AEP=90°,∠DCF+∠DFC=90°,∵折叠∴∠ABC=∠PB1C=90°,∴∠B1EF+∠B1FE=90°,又∵∠B1EF=∠AEP,∠B1FE=∠DFC,∴∠DFC=∠APE,且∠A=∠D,∴△APE∽△DFC(2)∵PE=EF,∠A=∠B1=90°,∠AEP=∠B1EF,∴△APE≌△B1FE(AAS),∴AE=B1E,AP=B1F,∴AE+EF=PE+B1E,∴AF=B1P,设BP=a,则AP=3﹣a=B1F,∵折叠∴BP=B1P=a,BC=B1C=4,∴AF=a,CF=4﹣(3﹣a)=a+1∴DF=AD﹣AF=4﹣a,在Rt△DFC中,CF2=DF2+CD2,∴(a+1)2=(4﹣a)2+9,∴a=2.4即BP=2.4(3)∵折叠∴BC=B1C,BP=B1P,∠BCP=∠B1CP,∴CP垂直平分BB1,∴∠B1BC+∠BCP=90°,∵BC=B1C,∴∠B1BC=∠BB1C,且∠BB1C+∠PB1B=90°∴∠PB1B=∠PCB,∵四边形ABCD是矩形∴AD∥BC∴∠B1BC=∠B1QF,∴∠B1QF=∠BB1C,∴QF=B1F∵EQ:QF=8:5,∴设EQ=8k,QF=5k,∴B1F=5k,EF=EQ+QF=13k,在Rt△B1EF中,B1E==12k,如图,过点Q作HQ⊥B1E于点H,又∵∠PB1C=90°,∴HQ∥B1F∴△EHQ∽△EB1F,∴∴∴EH=,HQ=∴B1H=∴tan∠PCB=tan∠PB1B==12.解:(1)如图1中,当∠BEF=45°时,易知四边形EBFH是正方形,∵AB=8,AE:EB=3:1,∴AE=6,EB=2,∵∠C=∠EBC=∠BEM=90°,∴四边形EBCM是矩形,∴EM=BC=6,∵EH=BE=2,∴HM=6﹣2=4.(2)如图2中,连接DE.在Rt△EAD中,∵∠A=90°,AD=AB=6,∴DE=6,在Rt△EDH中,DH==2设BF=FH=x,则DF=x+2,FC=6﹣x,在Rt△DFC中,∵DF2=DC2+CF2,∴(2+x)2=82+(6﹣x)2,∴x=﹣3,∴tan∠FEH==.(3)如图3中,连接AC,作EM⊥AC于M.∵∠EAM=∠BAC,∠AME=∠B=90°,∴△AME∽△ABC,∴=,∴=,∴EM=,∵S四边形AHCD=S△ACH+S△ADC,S△ACD=×6×8=24,∴当△ACH的面积最小时,四边形AHCD的面积最小,∵当EH与EM重合时,点H到直线AC的距离最小,最小值=﹣2=,∴△ACH的面积的最小值=×10×=8,∴四边形AHCD的面积的最小值为8+24=32.13.解:(1)∵四边形ABCD是矩形,∴∠A=∠C=∠D=90°,CD=AB=4,∵AD=AE,AD=5,∴AE=5,在Rt△ABE中,由勾股定理得,BE==3,∴EC=2,在Rt△AEF和Rt△ADF中,,∴Rt△AEF≌Rt△ADF(HL),∴EF=DF,设DF=EF=x,则CF=4﹣x,在Rt△CEF中,由勾股定理得:22+(4﹣x)2=x2,解得:x=,即DF的长为;(2)AB+BE=BG.理由如下:作FM⊥BC交BC的延长线于M,作GN⊥BC于N,连接GM,如图②所示:在△ABE和△EMF中,,∴△ABE≌△EMF(AAS)∴AB=EM,BE=FM,∵AB⊥BC,FM⊥BC,GN⊥BC,∴AB∥GN∥FM,又点G为AF的中点,∴点N为BM的中点,GN=(AB+FM),∴GN=BM,∴GB=GN,∠BGM=90°,∴BM=BG,∴AB+BE=BG.(3)连接EG,作OP⊥BE于P,作OQ⊥AG于Q,如图③所示:∵四边形ABCD是矩形,∴BC=AD=5,∠ABC=90°,∴BE=BC+CE=6,∴AE===2,∵△AEF是等腰直角三角形,G是AF的中点,∴∠GAE=45°,EG⊥AF,∴△AGE是等腰直角三角形,∠AGE=90°,∴AE=AG,∴AG=,∵∠ABE=90°,∴∠ABE+∠AGE=180°,∴A、B、E、G四点共圆,∴∠GBE=∠GAE=45°,∴△OBP是等腰直角三角形,∴OP=BP,设OP=BP=x,∵tan∠AEB====,即=,∴PE=x,∵BP+PE=BE=6,∴x+x=6,解得:x=,∴OP=,PE=×=,∴OE==,∴AO=AE﹣OE=2﹣=,在Rt△AOQ中,∠OAQ=45°,∴OQ=OA=,∴△AOG的面积=AG×OQ=××=.14.(1)解:∵△ABC是等边三角形,∴AC=AB,∠B=∠CAE=60°,∵AE=BF,∴△ABF≌△CAE(SAS),∴∠BAF=∠ACE,∴∠CPF=∠ACP+∠CAP=∠BAF+∠CAP=∠CAB=60°,∴∠APC=120°.(2)证明:∵m∥BC,n∥AB,∴∠DAC=∠ACB=60°,∠ACD=∠BAC=60°,∴△ADC是等边三角形,∴∠ADC=60°,∵∠APC+∠ADC=180°,∴A,P,C,D四点共圆,∴∠ACP=∠ADP,∠APD=∠ACD=60°∵∠APD=∠CAE=60°,∠ACE=∠ADP,∴△APD∽△EAC.(3)解:作DH⊥AC于H.∵==,∴可以假设PG=k,DG=4k,∵∠ADG=∠ADP,∠DAG=∠DP A=60°,∴△DAG∽△DP A,∴DA2=DG•DP=20k2,∵DA>0,∴DA=2k,∴AH=AD=k,DH=k,在Rt△DGH中,GH==k,∴AG=AH﹣GH=k﹣k,AC=2k∴==.当点G在点H下方时,根据对称性可得:=.综上所述,的值为或.15.解:(1)∵△ABC是等比三角形,且AB=2、BC=3,①当AB2=BC•AC时,得:4=3AC,解得:AC=;②当BC2=AB•AC时,得:9=2AC,解得:AC=;③当AC2=AB•BC时,得:AC2=6,解得:AC=(负值舍去);所以当AC=或或时,△ABC是比例三角形;(2)∵AD∥BC,∴∠ACB=∠CAD,又∵∠BAC=∠ADC,∴△ABC∽△DCA,∴=,即CA2=BC•AD,∵AD∥BC,∴∠ADB=∠CBD,∵BD平分∠ABC,∴∠ABD=∠CBD,∴∠ADB=∠ABD,∴AB=AD,∴CA2=BC•AB,∴△ABC是比例三角形;(3)如图,过点A作AH⊥BD于点H,∵AB=AD,∴BH=BD,∵AD∥BC,∠ADC=90°,∴∠BCD=90°,∴∠BHA=∠BCD=90°,又∵∠ABH=∠DBC,∴△ABH∽△DBC,∴=,即AB•BC=BH•DB,∴AB•BC=BD2,又∵AB•BC=AC2,∴BD2=AC2,∴=.方法二:利用勾股定理可得:BD2=BC2+CD2=AB2+AC2+CD2=AD2+AC2+CD2AC2+AC2=2AC2,∴=.。
成都初三数学b卷试题及答案

成都初三数学b卷试题及答案一、选择题(每题3分,共30分)1. 下列哪个选项是二次函数的一般形式?A. y=ax+bB. y=ax^2+bx+cC. y=a(x-h)^2+kD. y=a(x+b)^2+c答案:B2. 一个圆的半径为3,那么它的面积是多少?A. 9πB. 18πC. 27πD. 36π答案:C3. 如果一个角的补角是它的两倍,那么这个角的度数是多少?A. 30°B. 60°C. 90°D. 120°答案:A4. 一个等腰三角形的两边长分别为4和6,那么它的周长是多少?A. 14B. 16C. 18D. 20答案:C5. 一个数的立方根等于它本身,这个数可能是?A. 1B. -1C. 0D. 以上都是答案:D6. 已知一组数据的平均数是5,中位数是4,众数是3,那么这组数据的极差是多少?A. 2B. 4C. 6D. 无法确定答案:D7. 直角三角形的两直角边长分别为3和4,那么它的斜边长是多少?A. 5B. 6C. 7D. 8答案:A8. 下列哪个选项是不等式的基本性质?A. 若a>b,则a+c>b+cB. 若a>b,c>0,则ac>bcC. 若a>b,c<0,则ac>bcD. 若a>b,则a/c>b/c答案:A9. 一个正多边形的内角和是720°,那么这个多边形的边数是多少?A. 5B. 6C. 8D. 10答案:C10. 一个数的相反数是-5,那么这个数是多少?A. 5B. -5C. 0D. 无法确定答案:A二、填空题(每题3分,共15分)11. 已知一个等腰三角形的顶角是80°,那么它的底角是多少度?________答案:50°12. 一个数的绝对值是5,那么这个数可能是________答案:±513. 一个二次函数的顶点坐标是(2,3),那么它的对称轴是________答案:x=214. 一个圆的直径是8,那么它的周长是多少?________答案:8π15. 一个三角形的三边长分别是3,4,5,那么这个三角形的面积是多少?________答案:6三、解答题(共55分)16. (10分)已知一个二次函数y=ax^2+bx+c,其中a=1,b=-2,c=1,求这个函数的顶点坐标和对称轴。
成都市中考核心考点 - 第十二讲 几何类综合压轴题(27题)(B卷)

成都中考核心考点(成都版)简介--只要抓住核心考点,就能拿到卷子上80%的分数在历年的成都中考数学试题中,核心考点虽然只占总考点的20%,却占总分值的80%。
掌握了核心考点,相当于用20%的时间来把握80%的分数,在最短的时间内实现快速提分。
本文共分两轮复习:第一轮过关核心考点聚焦常考考点,五年真题回顾,三年诊断精选。
本文分13讲,由成都市中考数学A卷和B卷难度区分度较大,A卷1-19题较基础,大部分学生都容易掌握,选题主要以中考题和诊断题为主,20题-28题有一定综合性,选题除了中考题和诊断题外,还选择了大量的模拟题和改编题。
第一讲:考点1-考点6,第二讲:考点7-考点10,第三讲:考点11-考点14,第四讲:考点15-考点19,第五讲:考点20,第六讲:考点21,………第十三讲:考点28.(从考点20开始,每个考点一讲)。
第二轮过关B卷攻略专攻B卷重难,五年考点扫描,专题考向攻略。
暂定:B填空7-8讲,应用题1讲,几何综合3讲,抛物线综合5讲考点27、几何图形综合(压轴)命题方向:主要以三角形和四边形为基架,从全等过渡到相似,从定点过渡到动点,求线段、比例、探究数量关系; 五年真题1. (18成都)在Rt ABC ∆中,90ABC ∠=︒,7AB =,2AC =,过点B 作直线//m AC ,将ABC ∆绕点C 顺时针得到A B C ∆′′(点A ,B 的对应点分别为A ′,B ′)射线CA ′,CB ′分别交直线m 于点P ,Q . (1)如图1,当P 与A ′重合时,求ACA ∠′的度数;(2)如图2,设A B ′′与BC 的交点为M ,当M 为A B ′′的中点时,求线段PQ 的长;(3)在旋转过程时,当点,P Q 分别在CA ′,CB ′的延长线上时,试探究四边形PA B Q ′′的面积是否存在最小值.若存在,求出四边形PA B Q ′′的最小面积;若不存在,请说明理由.2.(16成都)如图①,△ABC 中,∠ABC =45°,AH ⊥BC 于点H ,点D 在AH 上,且DH =CH ,连接BD . (1)求证:BD=AC ;(2)将△BHD 绕点H 旋转,得到△EHF (点B ,D 分别与点E ,F 对应),连接AE .ⅰ)如图②,当点F 落在AC 上时(F 不与C 重合),若BC =4,tanC =3,求AE 的长;ⅱ)如图③,当△EHF 是由△BHD 绕点H 逆时针旋转30°得到时,设射线CF 与AE 相交于点G ,连接GH ,试探究线段GH 与EF 之间满足的等量关系,并说明理由。
成都B卷测试卷

B 卷(共50分)一、填空题。
(每题4分,共20分)21、已知二次函数m x x y ++-=22的部分图象如图所示,则关于x 的一元二次方程022=++-m x x 的解为 ▲ .22、如图,已知梯形ABCD 中,090=∠B ,AD//BC ,沿着CE 翻折,点D 与点B 重合,AD=2,AB=4,则ECB ∠tan = ▲ ,CD= ▲.23、设1x 、2x 是一元二次方程0342=-+x x 的两个根,且()23522221=+-+a x x x ,则a = ▲ .24、如图①,在直角梯形ABCD 中,∠B=︒90,AB//CD ,动点P 从B 点出发,由B →C →D →A 沿边运动。
设点P 运动的路程为x ,ABP ∆的面积为y ,如果关于x 的函数y 的图象如图②所示,则ABC ∆的面积为 ▲ .25、如图,用火柴棍摆出一列正方形图案,若按这种方式摆下去,摆第n 个图案用 ▲ 根火柴棍(用含n 的代数式表示).26、(8分)某电脑经销商计划购进一批电脑机箱和液晶显示器,若购电脑机箱10台和液晶显示器8台,共需要资金7000元;若购进电脑机箱2台和液晶显示器5台,共需要资金4120元.(1)每台电脑机箱、液晶显示器的进价各是多少元?(2)该经销商购进这两种商品共50台,而可用于购买这两种商品的资金不超过22240元.根据市场行情,销售电脑机箱、液晶显示器一台分别可获利10元和160元.该经销商希望销售完这两种商品,所获利润不少于4100元.试问:该经销商有哪几种进货方案?哪种方案① ② ③ ……获利最大?最大利润是多少?27、(10分) 已知,矩形ABCD 中,4AB cm =,8BC cm =,AC 的垂直平分线EF 分别交AD 、BC 于点E 、F ,垂足为O .(1)如图1,连接AF 、CE .求证四边形AFCE 为菱形,并求AF 的长;(2)如图2,动点P 、Q 分别从A 、C 两点同时出发,沿AFB ∆和CDE ∆各边匀速运动一周.即点P 自A →F →B →A 停止,点Q 自C →D →E →C 停止.在运动过程中,①已知点P 的速度为每秒5cm ,点Q 的速度为每秒4cm ,运动时间为t 秒,当A 、C 、P 、Q 四点为顶点的四边形是平行四边形时,求t 的值.②若点P 、Q 的运动路程分别为a 、b (单位:cm ,0ab ≠),已知A 、C 、P 、Q 四点为顶点的四边形是平行四边形,求a 与b 满足的数量关系式.AB C D E F 图1 O 图2备用图28、(12分)如图,在平面直角坐标系中,二次函数c bx x y ++=2的图象与x 轴交于A 、B 两点, A 点在原点的左侧,B 点的坐标为(3,0),与y 轴交于C (0,3-)点,点P 是直线BC 下方的抛物线上一动点.(1)求这个二次函数的表达式.(2)连结PO 、PC ,并把△POC 沿CO 翻折,得到四边形POP’C , 那么是否存在点P ,使四边形POP’C 为菱形?若存在,请求出此时点P 的坐标;若不存在,请说明理由.(3)当点P 运动到什么位置时,四边形 ABPC 的面积最大并求出此时P 点的坐标和四边形ABPC 的最大面积.B 卷(共50分)第25题 A B C A 1 A 2 A 3 B 1 B 2 B 3 一、 填空题:(每小题4分,共20分)21.等腰三角形ABC 腰长为34,底角为030,则△ABC 的面积为 .22.某幢建筑物,从10米高的窗口A 用水管和向外喷水,喷的水流呈抛物线(抛物线所在平面与墙面垂直,(如图)如果抛物线的最高点M 离墙1米,离地面403米,则水流下落点B 离墙距离OB 是__________米 23.因为33cos30cos 21022︒=︒=-,,所以)30180cos(210cos 000+= =2330cos 0-=-;因为22cos 45cos 22522︒=︒=-,, 所以2cos 225cos(18045)cos 452︒=︒+︒=-︒=-; 猜想:一般地,当a 为锐角时,有cos(180)cos a a ︒+=-,由此可知cos 240︒的值等于___________.24.如图矩形纸片ABCD ,AB =5cm ,BC =10cm ,CD 上有一点E ,ED =2cm ,AD 上有一点P ,PD =3cm ,过P 作PF ⊥AD 交BC 于F ,将纸片折叠,使P 点与E 点重合,折痕与PF 交于Q 点,则PQ 的长是____________cm.25.如图,△ABC 的面积为1,分别取AC 、BC 两边的中点A 1、B 1,则四边形A 1ABB 1的面积为3 4,再分别取A 1C 、B 1C 的中点A 2、B 2,A 2C 、B 2C 的中点A 3、B 3,依次取下去….利用这一图形,能直观地计算出3 4+3 42+3 43+…+3 4n =_____. 二、(共8分)26.如图,已知二次函数c bx x y ++-=221的图象经过A (2,0)、B (0,-6) 两点。
