同济大学木结构第六章 木结构力学性能
中国古建筑论文:中国古建筑木结构力学研究

中国古建筑木结构力学研究前言中国文化博大精深,流传至今的文化当中包含了大量我国古人的智慧,古建筑可以说是当今世界上最伟大的创造发明之一,从古代起就以其舒适、优美和实用等特点流传至日韩等国。
在当今世界经济飞速发展的背景下,中国古建筑已经成为人类世界最宝贵的文化遗产之一。
而古建筑中的古木结构是最具特色的一种,中国古代的佛寺及观音阁等都以古木结构为主。
现阶段加强对该结构的研究对于保护人类文化遗产具有重要的意义。
近年来我国涌现出越来越多的学者从不同的角度对其展开研究,本文将从力学角度对其研究进展进行描述。
一、中国古建筑木材力学性能青铜和石器时期,我国的木材资源相当丰富,当时的生产力和环境条件下,人们通过智慧运用木材来搭建房屋。
经过古人不断的努力,他们意识到了木材搭建房屋的种种优点,并逐渐将木结构搭建房屋的技术和经验流传了下来。
但是值得注意的是,木结构同其他结构的建筑相同,在建造建筑时同样也存在着许多问题。
(一)材性劣化我国的木结构古建筑经过上千年的洗礼,至今为止已经受到了各种不同的虫蛀及腐蚀,其材性受环境的影响较大,劣化现象严重。
在现阶段的古建筑木结构力学研究过程中,专家们最为关心的问题就是古建筑中的材性劣化问题。
近年来我国相关方面的专家针对木结构的古建筑材性的变化进行了仔细的对比和研究,其中有对大概拥有九百年历史的北岳庙大殿的研究和约有二百年历史的易昌陵碑楼的研究。
经对比,专家们总结出木结构古建筑受到环境和时间的影响比较严重,经历时间越久的建筑,它们的材质更加脆弱,力学性能更加低下,虽然不同的树木种类会使其产生不同的腐蚀程度,但是其变化的整体趋势是相同的。
最初我国对材性劣化的研究方法是应用接种腐朽菌的方式,这种方法能够促使木材腐朽速度加快,从而进行对比,得到想要的实验结果,其结果表明不同的木材,其物理及化学性质是按照一定规律进行衰变的。
(二)木材的各向异性木质材料最大的特点就是它的各向异性,我国在对木结构的精细化有限元进行研究的过程中,专家陈志勇提出了本构模型,该模型能够充分反映出木材各项异性中的抗压能力、弹性及二次应变的硬化在横纹承压下的反应等,以编制的方式在ABAQUS当中融入木材本构模型,同时专家还将这一方式在易昌陵碑楼的受力性能研究中进行了充分的应用,加强分析了对斗栱等受力性能的有限元。
同济大学结构力学

金茂大厦421m
西尔斯大厦 442m
同济大学结构力学
学习方法 1、采用课堂讲课和自学教材相结合的方法,以讲课为主,有部分内容给大家自学,目的是培养大家自学的能 力。在自学过程中,不能理解的内容,大家可以相互讨论,当然也可将看不懂的问题和我一起探讨。 2、希望同学们应以讲课内容为主,作简单笔记,在学习理论、概念的同时,一定要作相当数量的习题,通过 手算的方法和技巧来掌握力学的概念以及分析和计算的方法。
几何特征:其横截面上两个方向的尺寸远小于长度。 典型形式:梁、刚架、拱和珩架。 (b)板壳结构——也称薄壁结构。 几何特征:其厚度远小于其余两个方向上的尺度。 典型形式:房屋建筑中的楼板、壳体屋盖及飞机和轮船的外 壳等。 (c)实体结构——也称三维连续体结构。 几何特征:结构的长、宽、高三个方向的尺寸大小相仿。 典型形式:重力式挡土墙、水工建筑中的重力坝等。
人类建筑师总想将摩天大楼越盖越高,美国有527米高的芝加哥西尔斯大厦,加拿大有553米高的多 伦多CN电视塔,阿联酋迪拜市正在建造一座高达807米的世界最高楼。然而这些摩天大楼和日本大成 建筑公司蓝图中的“X-Seed 4000”摩天巨塔相比,却全都是“小巫见大巫”。
美国“高层建筑及城市居住委员会”设定了4个衡量标准:最高一层地板的高度、最高一层屋顶的高度、 大厦尖顶的高度及大厦最高点的高度。
吉隆坡的双子塔452m
台北市的101大楼508m
芝加哥“螺旋之尖”摩天大楼的建设方案获得了政府批 准,“螺旋之尖”摩天大楼全高610米,建成后将是全 美最高的大楼,它也将是世界各大城市里高楼建筑的一 个典范。
同济大学钢结构基本原理PPT课件

应力幅:由于存在残余应力,r不能代表实际应力变化情况
Dmaxmin
最大拉应力
疲劳强度曲线:
最小拉应力或压应力 拉(+)压(-)
42
匀质材料疲劳强度与应力比的关系:
K 0 1 , 1
0 max K , 0 max K ,
min
r max
应力幅与应力循环次数关系:
max
断裂韧性KIC: KIC a0
KI<KIC 稳定,裂纹不扩散 KI=KIc 临界 KI>KIC 失稳,裂纹扩展
弹性断裂力学公式(张开位移理论):
dI
2a
Ef y
d IC
稳定
d I d IC
不稳定
位移临界值 KIC EfydIC
40
影响脆性断裂的因素:裂纹尺寸、作用应力、材料韧性
提高抗脆断措施: 焊接施工管理,避免焊接裂纹、杂质 避免焊缝集中、采取措施避免或消除焊接残余应力 优化细部构造措施、避免应力集中 选择合理钢材,低温动力下工作时选用高等级钢
脆性破坏: 脆性断裂,应力<fy,无明显变形、无预兆,端口平直 拉应力超过晶粒抗拉能力。 强度理论 应力>fy破坏 ?不适用于脆性断裂 断裂力学理论 ! I型裂纹:张开型 II型裂纹:滑移型 III型裂纹:撕开型
39
弹性断裂力学公式:
系数 裂纹宽度一半 应力
应力强度因子:KI a
临界应力0:裂纹失稳扩展时应力
涂料 底层处理(抛丸除锈等) + 底漆 + 面漆 耐侯钢材 Cu-P-Ti-Re: 09CuPCrNi,16CuCr, 12MnCuCr
Cu-P-Ni-Cr: SMA400AW, AP, SMA490AW
38
同济大学 木结构

Leff
Δ
Axial load P (kN)
P
Displacement Δ (mm)
Compression members
(1) Strength
N An
≤
fc
N
where N —— compression
An —— net area
fc —— compression strength
(2) Stability
and modulus of elasticity
If log applied have not been cut out the checking parts, the design
values of compressive resistance strength and bending resistance strength parallel to grain and modulus of elasticity will be increased by 15%.
Strength For some import dimension lumber, there are design values of strength in our timber code.
Strength For some import dimension lumber, there are design values of strength in our timber code.
Technical Specification for Light Wood-Frame Constructions, DG/TJ08-2059-2009
Leff
Δ
buckling and material failure)
第六章-力法(二) ,同济大学结构力学课件,朱慈勉版教材,吕凤悟老师课件
半结构选取的关键在于正确判别另外半结构对选取半结构的约束作用。 判别方法有两种:
根据对称轴上的杆件和截面的变形(或位移)特征判别。(适用于所有结构)
根据对称轴上的杆件和截面的内力特征判别。 (一般只适用于奇数跨结构)
【例】试用力法求作图示刚架的弯矩图。 各杆 EI C 。
Strucural Analysis
School of Civil Engineering, Tongji Univ.
§6-5 对称性的利用—力法简化计算
【例】试用力法求作图示刚架的弯矩图。各杆 EI C 。
【解】利用对称性简化为一次超静定。
11X1 1p 0
11
144 EI
,
1 p
1800 EI
X1 12.5kN
M M1X1 M p
Strucural Analysis
School of Civil Engineering, Tongji Univ.
§6-5 对称性的利用—力法简化计算
取半结构计算
§6-5 对称性的利用—力法简化计算
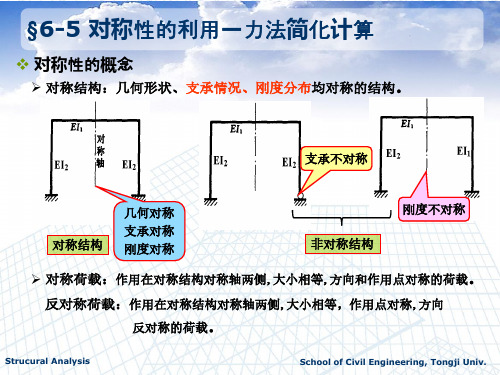
对称性的概念
对称结构:几何形状、支承情况、刚度分布均对称的结构。
支承不对称
对称结构
几何对称 支承对称 刚度对称
非对称结构
刚度不对称
对称荷载:作用在对称结构对称轴两侧,大小相等,方向和作用点对称的荷载。 反对称荷载:作用在对称结构对称轴两侧,大小相等,作用点对称,方向
13X 3 23X 3
1 p 2p
0 0
31X1 32 X 2 33 X 3 3 p 0
第一章绪论木结构

第一章绪论木结构
目录 退出
11
1.3.1 胶合板定义和特点
1.3.1.1定义:把由原木旋切或刨切成的单板按一定规则 胶和起来形成的板材。 1.3.1.1 特点:﹙与木板相比﹚ ①强重比高 ②幅面大 ③外观美观 ④各向异性减少 ⑤ 保留了天然材的优点,隐蔽了一部分缺陷.
第一章绪论木结构
目录 退出
12
6
1.2.4集成材用途 集成材没有改变木材的结构和特点,它仍和木材一样是一种天 然基材,但从物理力学性能来看,在抗拉和抗压强度方面都优于实 体木材,在材料质量的均匀化方面也优于实体木材。因此,集成材 可以代替实体木材应用于各种相应的领域。
结构用集成材
集成材是随着建筑业对长大结构构件的需求量大增而发展起来 的,主要用于体育馆、音乐厅、厂房、仓库等建筑物的木结构梁, 其中三铰拱梁应用最为普遍,这是在以前的木结构中无法实现的
第一章绪论木结构
目录 退出
7
非结构集成材
非结构用集成材主要作为家具和室内装修用材。
在家具方面,集成材以集成板材、集成方材和集成弯曲材的形
式应用到家具的制造业。
集成板材应用于桌类的面板、柜类的旁板、顶底板等大幅面部
件,柜类隔板、底板和抽屉底板等不外露的部件及抽屉面板、侧板、
底板、柜类小门等小幅面部件。
第一章绪论木结构
目录 退出
5
12.3集成材 分类
(1)按使用环境,集成材可分为室内用集成材和室外用集成材。 室内用集成材在室内干燥状态下使用,只要满足室内使用环境下的 耐久性,即可达到使用者要求。室外用集成材在室外使用,经常遭 受雨、雪的浸蚀以及太阳光线照射,故要求具有较高的耐久性。
(2)按产品的形状,集成材可分为板状集成材、通直集成材和弯 曲集成材。也可以把集成材制成异形截面,如工字形截面集成材和 箱型截面集成材或叫做中空截面集成材。
同济大学高等结构动力学课件(全)

车辆振动作用 地震振动作用 风致振动作用
同济大学土木工程防灾国家重点实验室、 同济大学土木工程防灾国家重点实验室、桥梁工程系
主要内容
第一讲 单自由度系统自由振动 第二讲 单自由度系统强迫振动 第三讲 广义单自由度叠加方法 第四讲 广义单自由度分步方法 第五讲 多自由度系统动力问题 第六讲 特征值问题求解方法 第七讲 随机振动基础 第八讲 结构随机振动分析 第九讲 结构动力可靠性分析 第十讲 桥梁车辆振动作用 第十一讲 桥梁地震振动作用 第十二讲 桥梁风致振动作用
阻尼比计算:
2πξω vn = exp vn +1 ωD
Hale Waihona Puke 两边取对数: δ ≡ ln vn = 2πξ ≈ 2πξ = c
ξ≈
vn +1 1−ξ v n − v n +1
2mf
2πv n +1
ξ≈
vn − vn+m 2mπv n + m
振幅衰减值:振幅减小50%的振动次数
1. 1结构重力影响(续)
&&(t ) + cv &(t ) + k∆ st + kv (t ) = p (t ) + W mv
∵ k∆ st = W ∴ ∵ ∴
&&(t ) + cv &(t ) + kv (t ) = p (t ) mv
&&(t ) , v & (t ) &&(t ) = v ν &(t ) = v
A = 0,
B=− p0 β k 1 1 − β 2
无阻尼系统通解:
p v(t ) = 0 k 1 1 − β 2 (sin ω t − β sin ωt )
note 7.木结构

7.1.2 木材主要力学性能指标 根据外力种类划分有 压缩强度(包括顺 根据外力种类划分有:压缩强度(包括顺 纹抗压强度,横纹抗压强度,局部抗压强度)、 拉伸强度(包括顺纹抗拉强度,横纹抗拉强 拉伸强度(包括顺纹抗拉强度 横纹抗拉强 度)、抗弯强度、抗剪强度、扭曲强度、冲击 韧性、硬度、抗劈力等。 韧性 硬度 抗劈力等 按加载速度和作用方法划分有:静态强度、 冲击强度、疲劳强度、蠕变强度。
子周围产生应力集中,与同一比重的无节木材相 比,表示出小的弹性模量。 •
7.1.3 木结构用材的分类 7 1 3 木结构用材的分类
7.2木结构的连接 7 2木结构的连接
• 7.2.1齿连接 齿连接 • 7 2 2螺栓连接和钉连接 7.2.2螺栓连接和钉连接
7.2.1齿连接
7.2.2螺栓连接和钉连接 7 2 2螺栓连接和钉连接
7.3 木结构的防火和防护 7 3 木结构的防火和防护
7.4 其பைடு நூலகம்规定 7 4 其他规定
7.1.1.3 7 1 1 3 顺纹拉伸 木材顺纹拉伸破坏主要是纵向撕裂和微纤丝之间的剪 切。微纤丝纵向结合非常牢固,所以顺纹拉伸时的变形不 切 微纤丝纵向结合非常牢固 所以顺纹拉伸时的变形不 大,通常应变值小于1%~3%,强度值却很高。即使在这 种情况下,微纤丝本身的拉伸强度也未能充分发挥,因为 木材的纤维会在微纤丝之间撕开。木材顺纹剪切强度特别 低,通常只有顺纹抗拉强度的6%~10%。顺纹拉伸时,微 纤丝之间产生滑移使微纤丝撕裂破坏,其破坏断面通常呈 锯齿状、细裂片状或针状撕裂。其断面形状的不规则程度, 取决于木材顺拉强度和顺剪强度之比值。一般健全材该比 取决于木材顺拉强度和顺剪强度之比值 一般健全材该比 值较大,破坏常在强度较弱的部位剪切开,破坏断面不平 整 整,呈锯齿状木茬。 锯齿状木茬
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
tension of fibres along the edges
compression perpendicular to grain
notch bearing plate
glulam beams
bearing plate on steel column
I joists
3.5 Bending combined with tension member
3.6 Bending combined with compression member
① strength
N + M ≤1 An f c Wn f m
② Stability in the bending plane
N ϕϕm A0
≤
fc
where ϕ ——stability factor for compression ϕm —— load combination factor
Combination of tension and shear, although tension fracture is the initiating mode
Bending failure
M Wn
≤
fm
where
M —— bending moment Wn —— net elastic section modulus
4
Bending combined with compression member
③ Stability out the bending plane
N ϕ y A0
fc
+
⎜⎜⎝⎛
ϕ
M LWf
m
⎟⎟⎠⎞ 2
≤1
where ϕ y —— stability factor for compression out the bending plane
flexure, determined based on
the ratio of the height to width of section,
lateral brace and timber strength grade etc.
2
Prevention of lateral torsional
buckling
but,
Direct compression transfer of loads in the end zones reduces the total shear force to be carried.
This part of the load transferred in direct compression
decking or joists
< 610 mm
top edge < 8d plus bridging
<9
both edges
Bridging for floor joists
Shear failures
One of the very weak properties of wood,and
Shrinkage cracks often occur at the ends of beams in the zone of maximum shear stress.
N + M ≤1 An f t Wn f m
where
N —— tension M —— bending moment An —— net area Wn —— net elastic section modulus ft —— tension strength fm —— bending strength
f m —— bending resistance strength
Lateral torsional buckling of deep I-joists
Lateral torsional buckling
Elastic buckling: Mcr = π / Le (G J E Iy )0.5
Torsional stiffness
ϕl = 1.0
when lateral support is provided as shown
h/b h
b
<4
Lateral support at spacing:
no support
<5 < 6.5 < 7.5
purlins or tie rods
< 610 mm compression edge held by
w —— calculating deflection based on
standard load effects
3
Notch
Bearing failure
The “soft” property of wood
Not only compression perpendicular to grain but also tension of the fibres along edges
1
Bending failure in compression
Only likely for very high grade material Bending failure mode
Bending failure in tension
Most likely failure mode
Bral section
Shear failure
VS Ib
≤
fv
where V —— shear force, without consideration within h S —— area modulus I —— moment of inertia b —— width f v —— shear resistance strength parallel to grain
Notch failure
3V 2bhn
⎜⎜⎝⎛
h hn
⎟⎟⎠⎞ ≤
fv
where h —— depth
hn —— net depth of the section not including the notch depth
Excessive deflections
w ≤ [w]
[ ] where w —— deflection limit of a bending member
Lateral bending stiffness
Le
y x
y
y
Δx
Δy x
θ
x
y
Lateral torsional
buckling
M ϕlW
≤
fm
where M —— bending moment W —— section modulus
f m —— bending resistance strength ϕl —— lateral stability factor of member in
3.4 Bending Members
Bending Test
Parallel Strand Lumber girders
Bending Test
Bending Test
What can go wrong ?
Bending failure Lateral torsional buckling Shear failure Notch failure Bearing failure Excessive deflections
ϕL —— lateral stability factor for bending
Reading Materials
《木结构设计》(Timber Engineering)
(中国建筑工业出版社) 《木结构设计规范》(GB 50005-2003)
5
