高数下(同济六)知识点知识分享
高数下期末总复习大全(同济六版)(2020年整理).pptx

学海无 涯
xy
(t), (t),
z (t),
空
间 ( t )
曲
线
:
zy
(x) (x)
切向量
T ((t0 ) , (t0 ) , (t0 ))
切向量
T (1 , (x) , (x))
法向量
F(x, y, z) 0
空 间 曲 面 :
n ( Fx (x0 , y0 , z0 ) , Fy (x0 , y0 , z0 ) , Fz (x0 , y0 , z0 ) )
x x0 y y0 z z0 fx (x0 , y0 ) f y (x0 ,y0 ) 1
学海无 涯
第十章 重积分
积分类型
二重积分
I f x, yd
D
重积分
计算方法
(1)
利用直角坐标系
X—型 Y—型
b
2 ( x)
f (x, y)dxdy dx f (x, y)dy a (x)
a ax2 a 2 a 2
y
z
和差
c a b ax bx , ay by , az bz
单位向量
方向余弦
点乘(数量积 ) 叉乘(向量积 )
c ab
垂直 平行
交角余弦
投影
c a b c a-b a 0 ,则 e a
aa
设 a 与 x, y, z 轴的夹角分别为,, , 则方向余弦分别为cos,cos,cos
学海无 涯
高数下期末总复习大全(同济六版)
第八章 向量与解析几何
定义 向量
模
向量代数 定义与运算的几何表达
有大小、有方向. 记作a 或 AB
向量a 的模记作 a
在直角坐标系下的表示
最好的高数下册(同济六版)复习提纲
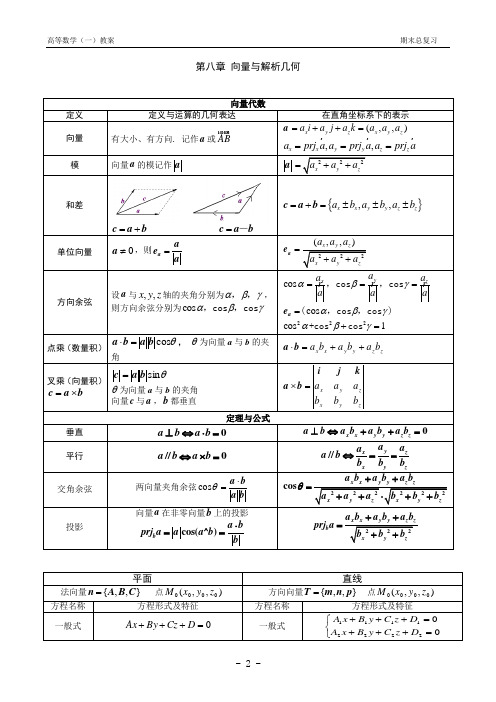
第八章 向量与解析几何向量代数定义 定义与运算的几何表达在直角坐标系下的表示向量 有大小、有方向. 记作a 或AB a (,,)x y z x y z a i a j a k a a a =++=,,x x y y z z a prj a a prj a a prj a ===模向量a 的模记作aa 222x y z a a a =++和差c a b =+ c a b =-=+c a b {},,=±±±x x y y z z a b a b a b单位向量0a ≠,则a ae a=a e 222(,,)=++x y z x y z a a a a a a方向余弦设a 与,,x y z 轴的夹角分别为αβγ,,,则方向余弦分别为cos αβγ,cos ,coscos y x z a a a aaaαβγ===,cos ,coscos a e αβγ=(,cos ,cos ) 222cos 1αβγ+=+cos cos 点乘(数量积)θcos b a b a =⋅, θ为向量a 与b 的夹角z z y y x x b a b a b a ++=⋅b a叉乘(向量积)b ac ⨯=θsin b a c = θ为向量a 与b 的夹角 向量c 与a ,b 都垂直zy xz y xb b b a a a k j ib a =⨯ 定理与公式垂直 0a b a b ⊥⇔⋅= 0x x y y z z a b a b a b a b ⊥⇔++=平行//0a b a b ⇔⨯=//y zx x y za a a ab b b b ⇔==交角余弦两向量夹角余弦ba ba ⋅=θcos222222cos x x y y z zx y z x y z a b a b a b a a a b b b θ++=++⋅++投影向量a 在非零向量b 上的投影cos()b a bprj a a a b b∧⋅==222x x y y z zb x y za b a b a b prj a b b b ++=++平面直线法向量{,,}n A B C = 点),,(0000z y x M方向向量{,,}T m n p = 点),,(0000z y x M方程名称 方程形式及特征方程名称 方程形式及特征一般式0=+++D Cz By Ax一般式⎩⎨⎧=+++=+++0022221111D z C y B x A D z C y B x A点法式0)()()(000=-+-+-z z C y y B x x A点向式pz z n y y m x x 000-=-=- 三点式1112121213131310x x y y z z x x y y z z x x y y z z ------=--- 参数式⎪⎩⎪⎨⎧+=+=+=ptz z nt y y mt x x 000 截距式 1x y za b c++= 两点式 000101010---==---x x y y z z x x y y z z面面垂直 0212121=++C C B B A A线线垂直 0212121=++p p n n m m面面平行 212121C C B B A A == 线线平行 212121p p n n m m == 线面垂直pC n B m A == 线面平行 0=++Cp Bn Am点面距离),,(0000z y x M 0=+++D Cz By Ax 面面距离10Ax By Cz D +++= 20+++=Ax By Cz D222000CB A DCz By Ax d +++++=12222D D d A B C-=++面面夹角线线夹角线面夹角},,{1111C B A n =},,{2222C B A n = },,{1111p n m =s },,{2222p n m =s},,{p n m =s },,{C B A =n222222212121212121||cos C B A C B A C C B B A A ++⋅++++=θ 222222212121212121cos p n m p n m p p n n m m ++⋅++++=ϕ 222222sin p n m C B A Cp Bn Am ++⋅++++=ϕ空间曲线Γ:()() ()x t y t z t ϕψω=⎧⎪=⎨⎪=⎩,,,)(βα≤≤t 切向量))(,)(,)((000t t t T ωψϕ'''=切“线”方程:)()()(000000t z z t y y t x x ωψϕ'-='-='-法平“面”方程:0))(()()()()(000000=-'+-'+-'z z t y y t x x t ωψϕ()()y x z x ϕψ=⎧⎨=⎩ 切向量))(,)(,1(x x T ψϕ''= 切“线”方程:)()(100000x z z x y y x x ψϕ'-='-=- 法平“面”方程:0))(()()()(00000=-'+-'+-z z x y y x x x ψϕ空间曲面 ∑:0),,(=z y x F法向量000000000((,,),(,,),(,,))x y z n F x y z F x y z F x y z = 切平“面”方程:000000000000(,,)()(,,)()(,,)()0x x x F x y z x x F x y z y y F x y z z z -+-+-=法“线“方程:),,(),,(),,(000000000000z y x F z z z y x F y y z y x F x x z y x -=-=- ),(y x f z =0000((,),(,),1)x y n f x y f x y =--切平“面”方程:0)())(,())(,(0000000=---+-z z y y y x f x x y x f y x或0000((,),(,),1)x y n f x y f x y =-法“线“方程:1),(),(0000000--=-=-z z y x f y y y x f x x y x第十章 重积分重积分 积分类型计算方法典型例题二重积分()σd ,⎰⎰=Dy x f I平面薄片的质量质量=面密度⨯面积(1) 利用直角坐标系X —型 ⎰⎰⎰⎰=Dbax x dy y x f dx dxdy y x f )()(21),(),(φφY —型⎰⎰⎰⎰=dcy y Ddx y x f dy dxdy y x f )()(21),(),(ϕϕP141—例1、例3(2)利用极坐标系 使用原则(1) 积分区域的边界曲线易于用极坐标方程表示( 含圆弧,直线段 );(2) 被积函数用极坐标变量表示较简单( 含22()x y α+, α为实数 )21()()(cos ,sin )(cos ,sin )Df d d d f d βϕθαϕθρθρθρρθθρθρθρρ=⎰⎰⎰⎰02θπ≤≤ 0θπ≤≤ 2πθπ≤≤P147—例5(3)利用积分区域的对称性与被积函数的奇偶性当D 关于y 轴对称时,(关于x 轴对称时,有类似结论)110(,)(,)(,)2(,)(,)(,)(,)D f x y x f x y f x y I f x y dxdyf x y x f x y f x y D D ⎧⎪⎪-=-⎪⎪=⎨⎪⎪-=⎪⎪⎩⎰⎰对于是奇函数,即对于是偶函数,即是的右半部分P141—例2应用该性质更方便计算步骤及注意事项1. 画出积分区域2. 选择坐标系 标准:域边界应尽量多为坐标轴,被积函数关于坐标变量易分离3. 确定积分次序 原则:积分区域分块少,累次积分好算为妙4. 确定积分限 方法:图示法 先积一条线,后扫积分域 5. 计算要简便 注意:充分利用对称性,奇偶性三重积分⎰⎰⎰Ω=dvz y x f I ),,(空间立体物的质量质量=密度⨯面积(1) 利用直角坐标⎩⎨⎧截面法投影法投影⎰⎰⎰⎰⎰⎰=Ωbay x z y x z x y x y z z y x f y x V z y x f ),(),()()(2121d ),,(d d d ),,(P159—例1P160—例2(2) 利用柱面坐标 cos sin x r y r z z θθ=⎧⎪=⎨⎪=⎩相当于在投影法的基础上直角坐标转换成极坐标 适用范围:○1积分区域表面用柱面坐标表示时方程简单;如 旋转体 ○2被积函数用柱面坐标表示时变量易分离.如2222()()f x y f x z ++ 21()()(,,)d d d (cos ,sin ,)d b r ar f x y z V z f z βθαθθρθρθρρΩ=⎰⎰⎰⎰⎰⎰P161—例3(3)利用球面坐标 cos sin cos sin sin sin cos x r y r z r ρθϕθρθϕθϕ==⎧⎪==⎨⎪=⎩dv r drd d =2sin ϕϕθ适用范围:○1积分域表面用球面坐标表示时方程简单;如,球体,锥体. ○2被积函数用球面坐标表示时变量易分离. 如,222()f x y z ++ 222111(,)2(,)d d (sin cos ,sin sin ,cos )sin d I f αβρθϕαβρθϕϕθρϕθρϕθρϕρϕρ=⎰⎰⎰P165—10-(1)(4)利用积分区域的对称性与被积函数的奇偶性第十一章曲线积分与曲面积分曲线积分与曲面积分积分类型 计算方法典型例题第一类曲线积分 ⎰=Lds y x f I ),(曲形构件的质量 质量=线密度⨯弧长参数法(转化为定积分)(1):()L y x ϕ= dt t t t t f I ⎰+=βαψϕϕϕ)(')('))(),((22(2)():()()x t L t y t ϕαβφ=⎧≤≤⎨=⎩ dx x y x y x f I b a⎰+=)('1))(,(2(3)()()r r θαθβ=≤≤()cos :()sin x r L y r θθθθ=⎧⎨=⎩θθθθθθθβαd r r r r f I ⎰+=)(')()sin )(,cos )((22P189-例1 P190-3平面第二类曲线积分⎰+=LQdy Pdx I变力沿曲线所做的功(1) 参数法(转化为定积分)():()()x t L t y t ϕαβφ=⎧⎨=⎩单调地从到t t t t Q t t t P y Q x P Ld )}()](),([)()](),([{d d ψψϕϕψϕβα'+'=+⎰⎰P196-例1、例2、例3、例4(2)利用格林公式(转化为二重积分)条件:①L 封闭,分段光滑,有向(左手法则围成平面区域D ) ②P ,Q 具有一阶连续偏导数 结论:dy dx yPx Q Qdy Pdx DL⎰⎰⎰∂∂-∂∂=+)(应用:⎪⎩⎪⎨⎧助线不是封闭曲线,添加辅有瑕点,挖洞满足条件直接应用P205-例4P214-5(1)(4)(3)利用路径无关定理(特殊路径法)等价条件:①yP x Q ∂∂=∂∂ ②0=+⎰LQdy Pdx③⎰+LQdy Pdx 与路径无关,与起点、终点有关④Qdy Pdx +具有原函数),(y x u(特殊路径法,偏积分法,凑微分法)P211-例5、例6、例7(4)两类曲线积分的联系⎰⎰+=+=LLds Q P Qdy Pdx I )cos cos (βα空间第二类曲线积分LI Pdx Qdy Rdz =++⎰(1)参数法(转化为定积分)dt t t t t R t t t t Q t t t t P Rdz Qdy Pdx )}()](),(),([ )()](),(),([ )()](),(),([{ωωψϕψωψϕϕωψϕβα'+'+'=++⎰⎰Γ(2)利用斯托克斯公式(转化第二类曲面积分) 条件:①L 封闭,分段光滑,有向②P ,Q ,R 具有一阶连续偏导数P240-例1变力沿曲线所做的功结论:dxdyy p x Q dzdx x Rz P dydz z Q y R RdzQdy Pdx L)()()(∂∂-∂∂+∂∂-∂∂+∂∂-∂∂=++⎰⎰⎰∑应用:⎩⎨⎧助线不是封闭曲线,添加辅满足条件直接应用第一类曲面积分 dvz y x f I ⎰⎰∑=),,(曲面薄片的质量 质量=面密度⨯面积 投影法∑:),(y x z z = 投影到xoy 面dxdy z z y x z y x f dv z y x f I xyD y x ⎰⎰⎰⎰++==∑221)),(,,(),,(类似的还有投影到yoz 面和zox 面的公式P217-例1、例2第二类曲面积分I Pdydz Qdzdx R∑=++⎰⎰流体流向曲面一侧的流量(1)投影法○1dydz z y z y x p Pdydz yzD ⎰⎰⎰⎰±=∑),),,(( ∑:),(y x z z =,γ为∑的法向量与x 轴的夹角 前侧取“+”,cos 0γ>;后侧取“-”,cos 0γ<○2dzdx z z x y x p Qdzdx yzD ⎰⎰⎰⎰±=∑)),,(,( ∑:),(z x y y =,β为∑的法向量与y 轴的夹角 右侧取“+”,cos 0β>;左侧取“-”,cos 0β<○3dxdy y x z y x Q Qdxdy yzD ⎰⎰⎰⎰±=∑)),(,,( ∑:),(z y x x =,α为∑的法向量与x 轴的夹角 上侧取“+”, cos 0α>;下侧取“-”,cos 0α< P226-例2(2)高斯公式 右手法则取定∑的侧条件:①∑封闭,分片光滑,是所围空间闭区域Ω的外侧②P ,Q ,R 具有一阶连续偏导数 结论:⎰⎰⎰⎰⎰Ω∑∂∂+∂∂+∂∂=++)(zR y Q x P Rdxdy Qdzdz Pdydz 应用:⎩⎨⎧助面不是封闭曲面,添加辅满足条件直接应用P231-例1、例2(3)两类曲面积分之间的联系(cos cos cos )Pdydz Qdzdx Rdxd y P Q R dS αβγ∑∑++=++⎰⎰⎰⎰转换投影法:()()zzdydz dxdy dzdx dxdy xy∂∂=-=-∂∂ P228-例3所有类型的积分:○1定义:四步法——分割、代替、求和、取极限; ○2性质:对积分的范围具有可加性,具有线性性; ○3对坐标的积分,积分区域对称与被积函数的奇偶性。
高数(同济第六版)第八章总结

第八章空间解析几何与向量代数第一节向量及其线性运算
1、右手定则方向角
2、记Prju r或(r)u :向量r在u轴上的投影
第二节数量积向量积混合积
1、a*b
=
大小——a·b·sin
方向——右手定则确定
2、a*b=a=(a1,a2,a3)b=(b1,b2,b3)
3、混合积为(a*b)·c记作[abc]的作用:
①平行六面体的体积
②[abc]=0时说明三向量共面
③满足轮换对称性:[abc]= [bca] = [cab]
第三节曲面及其方程
①椭圆锥面
③单叶双曲面④双叶双曲面
⑤椭圆抛物面⑥双曲抛物面
第四节空间曲线及其方程
1、一般方程:F(x,y,z)=0
G(x,y,z)=0
x=x(t)
2、参数方程:y=y(t)
z=z(t)
第五节平面及其方程
1、点法式方程:A(x-x0)+B(y-y0)+C(z-z0)=0
[其中法向量n=(A,B,C) M0为(x0,y0,z0)]
2、一般方程:Ax+By+Cz+D=0(一般需要四个平面上的点求出)第六节空间直线及其方程
1、一般方程:A1x+B1y+C1z+D1=0
A2x+B2y+C2z+D2=0
2、点向式:
[其中方向向量为s=(p,m,n) 已知点为M0(x0,y0,z0)] 3、平面束方程的重要应用:P48。
高数(同济第六版)下册多元函数的积分学及其应用知识点

第十章多元函数的积分学及其应用一、二重积分1.二重积分的概念�定义:设(,)f x y 是有界闭区域D 上的有界函数,“分割、近似、求和、取极限”:01(,)lim (,)n i iii D f x y d f λσξησ→==∆∑∫∫其中:D 为积分区域,(,)f x y 称为被积函数,d σ为面积元素。
�几何意义:当(,)0f x y ≥,(,)D f x y d σ∫∫表示以区域D 为底、以曲面(,)z f x y =为顶的曲顶柱体的体积。
�非均匀平面薄片的质量:(,)DM x y d µσ=∫∫。
2.二重积分的性质�性质1(线性性质).),(),()],(),([∫∫∫∫∫∫±=±DD D d y x g d y x f d y x g y x f σβσασβα�性质2(区域具有可加性)如果闭区域D 可被曲线分为两个没有公共内点的闭子区域1D 和2D ,则.),(),(),(21∫∫∫∫∫∫+=D D Dd y x f d y x f d y x f σσσ�性质3如果在闭区域D 上,σ,1),(=y x f 为D 的面积,则.1σσσ==⋅∫∫∫∫DD d d 几何意义:以D 为底、高为1的平顶柱体的体积在数值上等于柱体的底面积。
�性质4(单调性)如果在闭区域D 上,有),,(),(y x g y x f ≤则.),(),(∫∫∫∫≤DD d y x g d y x f σσ推论1.|),(|),(∫∫∫∫≤DD d y x f d y x f σσ推论2设m M ,分别是),(y x f 在闭区域D 上的最大值和最小值,σ为D 的面积,则.),(σσσM d y x f m D≤≤∫∫这个不等式称为二重积分的估值不等式。
�性质5(积分中值定理)如果函数(,)f x y D 上连续,σ是D 的面积,那么在D 上至少存在一点(,)ξη,使得(,)(,)Df x y d f σξησ=⋅∫∫。
高数下册总结(同济第六版)

高数同济版下高数(下)小结一、微分方程复习要点解微分方程时,先要判断一下方程是属于什么类型,然后按所属类型的相应解法求出其通解. 一阶微分方程的解法小结:高数同济版下二阶微分方程的解法小结:非齐次方程的特解的形式为:高数同济版下主要一阶1、可分离变量方程、线性微分方程的求解; 2、二阶常系数齐次线性微分方程的求解; 3、二阶常系数非齐次线性微分方程的特解二、多元函数微分学复习要点一、偏导数的求法 1、显函数的偏导数的求法时,应将看作常量,对求导,在求时,应将看作常量,对求导,所运用的是一元函数的求导法则与求导公式2、复合函数的偏导数的求法设,,,则,几种特殊情况: 1),,,则2),,则 3),则3、隐函数求偏导数的求法 1)一个方程的情况,设是由方程唯一确定的隐函数,则,高数同济版下或者视,由方程两边同时对 2)方程组的情况由方程组 . 两边同时对求导解出即可二、全微分的求法方法1:利用公式方法2:直接两边同时求微分,解出即可.其中要注意应用微分形式的不变性:三、空间曲线的切线及空间曲面的法平面的求法 1)设空间曲线Г的参数方程为,则当时,在曲线上对应处的切线方向向量为,切线方程为法平面方程为2)若曲面的方程为,则在点处的法向,切平面方程为法线方程为高数同济版下若曲面的方程为,则在点处的法向,切平面方程为法线方程为四、多元函数极值(最值)的求法 1 无条件极值的求法设函数在点的某邻域内具有二阶连续偏导数,由,解出驻点,记, 1)若时有极小值 2)若,则在点处无极值 3)若,不能判定在点处是否取得极值,则在点处取得极值,且当时有极大值,当2 条件极值的求法函数在满足条件下极值的方法如下: 1)化为无条件极值:若能从条件解出代入中,则使函数成为一元函数无条件的极值问题 2)拉格朗日乘数法作辅助函数,其中为参数,解方程组高数同济版下求出驻点坐标,则驻点可能是条件极值点 3 最大值与最小值的求法若多元函数在闭区域上连续,求出函数在区域内部的驻点,计算出在这些点处的函数值,并与区域的边界上的最大(最小)值比较,最大(最小)者,就是最大(最小)值. 主要1、偏导数的求法与全微分的求法;2、空间曲线的切线及空间曲面的法平面的求法3、最大值与最小值的求法三、多元函数积分学复习要点七种积分的概念、计算方法及应用如下表所示:高数同济版下高数同济版下*定积分的几何应用定积分应用的常用公式: (1)面积 (2)体积(型区域的面积)(横截面面积已知的立体体积)(所围图形绕的立体体积)(所围图形绕体体积)(所围图形绕轴的立体体积)。
【K12学习】高数下(同济六)知识点

高数下(同济六)知识点高等数学教案期末总复习高等数学下册习题常见类型题型1 求向量的坐标、模、方向角、方向余弦、数量积、向量积题型2 已知条件求平面与直线方程题型3 计算一阶偏导数及高阶偏导数题型 4 求多元复合函数的偏导数题型5 求方程所确定的隐函数的偏导数题型6 求方向导数、梯度、曲线的切线、曲面的切平面题型7 求极值、利用拉格郎日乘数法求最值题型8 利用直角坐标计算二重积分题型9 利用极坐标计算二重积分题型10 计算带绝对值的二重积分题型11 利用二重积分证明恒等式题型12 利用对称性质计算二重积分题型13 只有一种积分次序可计算的积分例1、求21dxx42sinysinydydxdyx2xyy解:dx12x42sinysinysinysinydydxdydxdydxdyx2xyyyyD1D22y2 siny2sinydxdydydx(y1)sinydycos1sin11y1yyD1D2 题型14 利用投影法计算三重积分题型15 利用柱坐标计算三重积分题型16 利用球坐标计算三重积分题型17 利用切片法计算三重积分题型18 利用三重积分计算立体的体积题型19 计算对弧长的曲线积分题型20 计算对面积的曲面积分题型21 计算对坐标的曲线积分题型22 利用格林公式计算对坐标的曲线积分题型23 曲线积分与路径无关及全微分求积题型24 计算对坐标的曲面积分- 2 -高等数学教案期末总复习题型25 利用高斯公式计算对坐标的曲面积分题型26 可分离变量的微分方程、齐次方程题型27一阶线性微分方程题型29 可降阶方程题型30二阶常系数非齐次线性方程第八章向量与解析几何定义向量模向量代数定义与运算的几何表达在直角坐标系下的表示 aaxiayjazk(ax,ay,az) 有大小、有方向. 记作a或AB 向量a的模记作a axprjxa,ayprjya,azprjza aax2ay2az2 和差cab ca-b 单位向量cabaxbx,ayby,azbz aa0,则ea a设a与x,y,z轴的夹角分别为,,,则方向余弦分别为cos,cos,cos ea(ax,ay,az)axayaz222 方向余弦 aaacosx,cosy,cosz aaaea(cos,cos,cos) cos2+cos2cos21 点乘 ababcos,为向量a与b的夹角abaxbxaybyazbz iabaxbxjaybykaz bzcabsin 叉乘为向量a与b的夹角 cab 向量c与a,b都垂直定理与公式垂直平行abab0 a//bab0 abaxbxaybyazbz0 a//bcosaxayaz bxbybz2222交角余弦 ab两向量夹角余弦cos ab向量a在非零向量b上的投影axbxaybyazbzaxayazbxbybzprjbaaxbxaybyazbzbxbybz22222 投影 ab prjbaacos(ab)b- 3 -高等数学教案期末总复习平面法向量n{A,B,C} 点M0(x0,y0,z0) 方程名称一般式点法式方程形式及特征直线方向向量T{m,n,p} 点M0(x0,y0,z0) 方程名称一般式点向式方程形式及特征A1xB1yC1zD10 A2xB2yC2zD20AxByCzD0A(xx0)B(yy0)C(zz0)0 xx1yy1y2y1y3y1zz1z2z10z3z1xx0yy0zz0 mnpxx0mtyy0nt zzpt0xx0yy0zz0x1x0y1y0z1z0三点式 x2x1x3x1参数式截距式面面垂直面面平行线面垂直xyz1 abcA1A2B1B2C1C20 A1B1C1A2B2C2ABC mnp两点式线线垂直线线平行线面平行m1m2n1n2p1p20 m1n1p1 m2n2p2AmBnCp0 点面距离M0(x0,y0,z0) AxByCzD0 面面距离AxByCzD10 AxByCzD20 dAx0By0Cz0DABC222 dD1D2ABC222 面面夹角n1{A1,B1,C1}n2{A2,B2,C2} 线线夹角s1{m1,n1,p1}s2{m2,n2,p2} 线面夹角s{m,n,p} n{A,B,C} AmBnCpA2B2C2m2n2p2cos|A1A2B1B2C1C2|A1B1C1A2B2C22222 22 cosm1m2n1n2p1p2222m12n12p12m2n2p2 sin x(t),y(t),z(t),切“线”方程:切向量 xx0yy0zz0 (t0)(t0)(t0)空间(t) 曲线:T((t0),(t0),(t0)) 法平“面”方程:(t0)(xx0)(t0)(yy0)(t0)(zz0)0 切“线”方程:y(x)切向量 z(x)T(1,(x),(x)) xx0yy0zz0 1(x0)(x0)法平“面”方程: (xx0)(x0)(yy0)(x0)(zz0)0- 4 -高等数学教案期末总复习法向量F(x,y,z)0 空间曲面:n(Fx(x0,y0,z0),Fy(x0,y0,z0),Fz(x0,y0,z0))n(fx(x0,y0),fy(x0,y0),1) 切平“面”方程:Fx(x0,y0,z0)(xx0)Fx(x0,y0,z0)(yy0)Fx(x0,y0,z0)(zz0) 0法“线“方程:xx0yy0zz0 Fx(x0,y0,z0)Fy(x0,y0,z0)Fz(x0,y0,z0)切平“面”方程:fx(x0,y0)(xx0)fy(x0,y0)(yy0)(zz0)0 法“线“方程:zf(x,y) 或n(fx(x0,y0),fy(x0,y0),1)xx0yy0zz0 fx(x0,y0)fy(x0,y0)1 重积分计算方法第十章重积分积分类型二重积分典型例题利用直角坐标系 X—型Y—型Df(x,y)dxdydxadcb2(x)1(x)2(y)f(x,y)dy P141—例1、例3 Df(x,y)dxdydy1(y)f(x,y)dx Ifx,ydD利用极坐标系使用原则 (1) 积分区域的边界曲线易于用极坐标方程表示( 含圆弧,直线段 ); (2) 被积函数用极坐标变量表示较简单( 含(xy), 22 平面薄片的质量质量=面密度面积为实数 ) P147—例 5 f(cos,sin)ddDd2 1 f(cos,sin)d02 0 2 利用积分区域的对称性与被积函数的奇偶性 P141—例2 应用该性质更方便当D关于y 轴对称时,- 5 -高等数学教案期末总复习0I2f(x,y)dxdyD1计算步骤及注意事项 f(x,y)对于x是奇函数,即f(x,y)f(x,y)f(x,y)对于x是偶函数,即f(x,y)f(x,y)D1是D的右半部分1.画出积分区域 2.选择坐标系标准:域边界应尽量多为坐标轴,被积函数关于坐标变量易分离 3.确定积分次序原则:积分区域分块少,累次积分好算为妙 4.确定积分限方法:图示法先积一条线,后扫积分域 5.计算要简便注意:充分利用对称性,奇偶性三重积分 (1) 利用直角坐标投影投影法截面法ba y2(x)f(x,y,z)dVdxy1(x)dyz2(x,y)z1(x,y)f(x,y,z)dzP159—例1 P160—例2 xrcos 利用柱面坐标yrsin zz 相当于在投影法的基础上直角坐标转换成极坐标适用范围: 1积分区域表面用柱面坐标表示时方程简单;如旋转体○2被积函数用柱面坐标表示时变量易分离.如f(xy)f(xz) ○If(x,y,z)dvP161—例 3 空间立体物的质量质量=密度面积2222f(x,y,z)dVdzdabr2 r1 f(cos,sin,z)d xcosrsincos利用球面坐标ysinrsinsin zrcosdvr2sindrdd 适用范围: 1积分域表面用球面坐标表示时方程简单;如,球体,锥体. ○2被积函数用球面坐标表示时变量易分离. 如,f(xyz) ○P165—10-(1) 222Idd11222(,)1(,)f(sincos,sinsin,cos)2sind 利用积分区域的对称性与被积函数的奇偶性- 6 -。
高数下(同济六)知识点
高等数学下册习题常见鬓型求向疑得坐标、模、方向角、方向余弦、数量积、向量积计算一阶偏导数及高阶偏导数利用直角坐标计算二重枳分利用二重积分证明恒等式例1. 求解:(将二次积分交换顺序);沁4,胡注如y+JJ 空竺畑y 才 y " y Di y 址 y= JJ sin 兀'y dxdy = J" d)j 对 n "舐=Jjy -1) sin 九•ydy = cos1 — sin 1 qua y I y y ' 题型14利用投影法讣算三重积分题型27—阶线性微分方程 题型29可降阶方程题型15 利用柱坐标计算三重积分题型16 利用球坐标讣算三重积分 题型17 利用切片法讣算三重积分 题型18 利用三重积分计算立体得体积 题型19 il 算对弧长得曲线积分 题型20 il 算对而积得曲而积分 题型21 讣算对坐标得曲线积分题型22 利用格林公式计算对坐标得曲线枳分 题型23 曲线枳分与路径无关及全微分求枳 题型24 讣算对坐标得曲而积分题型25 利用高斯公式计算对坐标得曲面积分题型26 可分离变量得微分方程、齐次方程 题型1 题型2 由已知条件求平而与直线方程题型4 求多元复合函数得偏导数 题型5 求方程所确定得隐函数得偏导数题型6 求方向导数、梯度、曲线得切线、曲而得切平而 题型7 求极值、利用拉格郎日乘数法求最值题型9 利用极坐标讣算二重积分 题型10 计算带绝对值得二重积分题型12 利用对称性质计算二重枳分 题型13只有一种积分次序可计算得积分题型30二阶常系数非齐次线性方程第八章向量与解析几何切向量切“线”方程:法平“面”方程:法向量切平“面”方程:法“线“方程:或切平“面”方程:法“线“方程:第十章重积分(1) 积分区域得边界曲线易于用极坐标方程表示(含圆弧,宜线段); (2) 被枳函数用极坐标变量表示较简单(含;为实数)积分类型 二重枳分 平面薄片得质 质量=而密度而积重积分 计算方法(1) 利用直角坐标系X-型 y —型①利用极坐标系使用原则典型例题P141-例 I 、例3PI47-例 5⑶利用积分区域得对称性与被积函数得奇偶性当D 关于y 轴对称时,(关于X 轴对称时,有类似结PI41-例 2 应用该性质更方便计算步骤及注意事项1・画出积分区域 2・选择坐标系 3.确定积分次序 t 确定枳分限 5.计算要简便标准:域边界应尽量多为坐标轴,被积函数关于坐标变量易分离原则:积分区域分块少,累次积分好算为妙 方法:图示法先积一条线,后扫枳分域 注意:充分利用对称性,奇偶性X三重积分空间立体物得质量质量=密度而积①定义:四步法一分割、代替、求与、取极限:②性质:对积分得范用具有可加性,具有线性性:③对坐标得积分,积分区域对称与被积函数得奇偶性。
高等数学第六版上下册(同济大学出版社)课件
不定积分的几何意义
不定积分表示的是一种曲线族 ,每一条曲线都有一个与之对
应的方程。
积分的应用场景
01
物理应用
积分在物理中有广泛的应用,例 如计算物体的质量、重心、转动 惯量等。
工程应用
02
03
经济应用
积分在工程中有广泛的应用,例 如计算曲线的长度、面积、体积 等。
积分在经济中有广泛的应用,例 如计算总成本、总收益、总利润 等。
05
多重积分与向量分析
二重积分的概念与性质
二重积分的定义
二重积分是定积分在二维平面上的推广,表示一个二元函数在某个区域上的累积值。
二重积分的性质
二重积分具有可加性、可减性、可交换性等性质,这些性质使得二重积分在解决实际问题中具有广泛的应用。
三重积分的概念与性质
三重积分的定义
三重积分是定积分在三维空间上的推广 ,表示一个三元函数在某个区域上的累 积值。
03
导数与微分
导数的概念与性质
导数的定义
导数描述了函数在某一点附近的变化率,是函数局部 性质的一种体现。
导数的几何意义
导数在几何上表示函数图像在某一点的切线的斜率。
导数的性质
导数具有一些基本的性质,如线性性质、乘积法则、 商的导数法则等。
微分的概念与性质
微分的定义
01
微分是函数在某一点附近的小变化量,用于近似计算函数的值
求函数的最值
导数可以用于求函数在一定区间内的最大值和最小值,这在优化问题中具有广泛的应用。
04
积分
定积分的概念与性质
01
定积分的定义
定积分是积分的一种,是函数在区间上与区间的乘积在区间的两个端点
高等数学第六版(同济版)第六章复习资料
第六章 定积分的应用引入:前面学习了定积分的理论,这一章要应用这些理论来分析和解决一些实际问题中出现的量.用定积分计算这些量,必须把它们表示成定积分,先介绍将所求量表示成定积分的方法——元素法.第一节 定积分的元素法我们先用定积分的引例——曲边梯形的面积,引出元素以及元素法的概念: 一、元素及元素法1.元素:由连续曲线)0)(()(≥=x f x f y 与直线b x a x ==、以及x 轴所围成的曲边梯形的面积为:∑==ni i A A 1∆∑=≈ni i i x f 1)(∆ξ∑==ni i i x d f 1)(ξ⎰=bax d x f )(.(由微分知识得i i x d x =∆),称x d x f )(为面积元素或面积微元,记为x d x f dA )(=.2.元素法:用元素法将所求量表示成定积分的方法,称为元素法. 由此可知,曲边梯形的面积是将面积微元累加得到的.下面我们通过曲边梯形的面积来总结出实际问题中所求的量能用定积分表示的条件: 二、用元素法将所求量能表示成定积分的条件:(设所求量为U ) 1.量U 与变量x 的所在区间],[b a 有关; 2.量U 对于区间],[b a 具有可加性;3.量U 的部分量有近似值,即i i i x f U ∆ξ∆)(≈. 三、用元素法将所求量能表示成定积分的步骤:1.由实际情况选一变量如x 为积分变量,确定该其变化区间],[b a .2.分],[b a 为n 个小区间,取其中一个小区间],[x d x x +,计算其上的部分量U ∆的近似值:x d x f U d )(=,的所求量的一个元素.3.以x d x f U d )(=为被积表达式,在],[b a 上作定积分,即得所求量的定积分表达式:⎰=bax d x f U )(.注:元素的几何形状常取为:条,带,段,环,扇,片,壳等.内容小结:本节介绍了元素法以及用元素法将所求量表示成定积分的方法与步骤.第二节 定积分在几何上的应用一、平面图形的面积1.直角坐标情形:曲线)0)((≥=x f y 与直线)(b a b x a x <==、及x 轴所围成的曲边梯形面积为x d x f A ba )(⎰=,因为面积元素为x d x f A d )(=.2.参数方程情形:若曲线],[,)0)(()(b a x x f x f y ∈≥=的参数方程为⎩⎨⎧==)()(t y t x ψϕ,且满足(1). a =)(αϕ, b =)(βϕ;(2). )(t x ϕ=在],[βα或],[αβ上具有连续导数,且)(t y ψ=连续,则由曲线)(x f y =所围成的曲边图形的面积为:x d x f A ba )(⎰=t d t t )(')(ϕψβα⎰=.3.极坐标情形:设曲线的极坐标方程为]),[,0)(()(βαθθϕθϕρ∈≥=, 且)(θϕ在],[βα上连续,则由曲线)(θϕρ=与射线αθ=以及βθ=所 围成图形的面积为θθϕβαd A ⎰=)(212. 由于当θ在],[βα上变动时,极径)(θϕρ=也随之变动,故不能直接利用扇形面积公式θ221R A =来计算. 推导: ①.取极角θ为积分变量,],[βαθ∈.②.在],[βα上任取一小区间],[θθθd +,其上的曲边扇形面积的近似值:[]θθϕd A d 2)(21=. ③.以[]θθϕd 2)(21为被积表达式,在],[βα上作定积分,得曲边扇形的面积公式: θθϕβαd A ⎰=)(212.例1. 计算两条抛物线22x y x y ==、在第一象限所围所围图形的面积.解:首先确定图形的范围,由⎪⎩⎪⎨⎧==22xy xy 得交点)0,0(、)1,1(, 取x 为积分变量,由于面积元素()x d x x A d 2-=,所以所求面积为()⎰-=102x d x x A 103233132⎪⎪⎭⎫⎝⎛+=x x 31=.注:⎰=10x d x A ⎰-12x d x ()⎰-=102x d x x .例2. 计算抛物线x y 22=与直线4-=x y 所围图形的面积.解:由⎩⎨⎧-==422x y xy 得交点)2,2(-、)4,8(,若取x 为积分变量,则有⎰⎰--+=8220)]4(2[22x d x x x d x A 822238223421322324⎪⎪⎭⎫ ⎝⎛+-+=x x x x 18=. 若取y 为积分变量,则有18642248232422=⎪⎪⎭⎫⎝⎛-+=⎪⎪⎭⎫ ⎝⎛-+=⎰-y y y y d y y A . 例3. 求椭圆12222=+by a x 所围图形的面积.解:由于椭圆关于两个坐标轴对称,设椭圆在第一象限所围成的面积 为1A ,则所求面积为x d y A A a⎰==0144.设π)20(sin cos ≤≤⎩⎨⎧==t tb y t a x ,当0=x 时,2π=t ,当a x =时,0=t ,且t d t a x d sin -=,于是t d t a t b x d y A a )sin (sin 4402/0-⋅==⎰⎰πt d t ab ⎰=2/02sin 4πt d ts ab ⎰-=2/022cos 14πb a π=. 例4.计算阿基米德螺线)0(>=a a θρ对应θ从0变到π2所围图形面积. 解:由题可知,积分变量],[βαθ∈,于是所求面积为θθπd a A ⎰=202)(211032312θ⋅=a 23π34a =.例5.计算心形线)0()cos 1(>+=a a θρ所围图形的面积.解:心形线所围成的图形关于极轴对称,设极轴上半部分图形的面积为1A , 则心形线所围成的图形面积为12A .取极角θ为积分变量,],[βαθ∈,于是⎰+=πθθ022)cos 1(212d a A ⎰++=πθθθ022)cos 2cos 1(d a ⎰⎪⎭⎫⎝⎛++=πθθθ02cos 22cos 2123d a 2π23a =.二、体积1.旋转体的体积:(1).旋转体:由一个平面图形绕这平面内一条直线旋转一周而成的立体称为旋转体,该直线称为旋转轴.注:圆柱体、圆台、球体等都是旋转体,它们都可以看做是由连续曲线)(x f y =与直线a x =、b x =以及x 轴围成的曲边梯形绕x 轴旋转一周所围成的立体.(2).旋转体的体积:①.由曲线)(x f y =与直线a x =、b x =以及x 轴所围成的曲边梯形 绕x 轴旋转而成的旋转体的体积:)()]([2b a x d x f V ba <=⎰π.推导:取x 为积分变量,],[b a x ∈,在],[b a 上任取一小区间],[x x x ∆+,其上的窄曲边梯形绕x 轴旋转而成的薄层的体积近似等于以)(x f 为底面半径、以x d 为高的扁圆柱体的体积,即体积元素为x d x f V d 2)]([π=,以x d x f 2)]([π为被积表达式,在],[b a 上作定积分即得所求旋转体的体积:)()]([2b a x d x f V ba<=⎰π.②.由曲线)(y x ϕ=与直线c y =、d y =以及y 轴所围成的曲边梯形绕y 轴旋转而成的旋转体的体积:)()]([2d c y d y V dc <=⎰ϕπ.例6.连接坐标原点O 及点),(r h P 的直线、直线h x = 及x 轴围成 一个直角三角形,将它绕x 轴旋转构成一个底半径为r 、高为h 的 圆锥体,求其体积.解:过)0,0(O 及),(r h P 的直线方程为:x hry =. 取x 为积分变量,],0[h x ∈,则所求旋转体的体积为⎰⎥⎦⎤⎢⎣⎡=hx d x h r V 02πh r 231π=.例7.计算由椭圆12222=+by a x 所围成的图形绕x 轴旋转而成的旋转体的体积.解:该旋转椭球体可看做是由半椭圆与x 轴所围成的绕x 轴旋转而成的立体,半椭圆方程为:22x a ab y -=. 取x 为积分变量,],[a a x -∈,则所求立体体积为⎰--=aa x d x a ab V )(2222π234ab π=.例8.计算由摆线)sin (t t a x -=,)cos 1(t a y -=相应于π20≤≤t 的一拱, 直线0=y 所围成的图形分别绕x 轴、y 轴旋转而成的旋转体的体积.解:记摆线绕x 轴旋转而成的旋转体的体积为x V ,取x 为积分变量,],[a a x -∈,则⎰=a x x d x y V ππ202)(⎰--=ππ2022)cos 1()cos 1(t d t a t •a⎰-+-=ππ20323)cos cos 3cos 31(t d t t t •a⎰-=ππ203)cos 31(t d t •a⎰++ππ203)12(cos 23t d t •a ⎰--ππ2023)(sin )sin 1(t d t •a 325a π=.记摆线绕y 轴旋转而成的旋转体的体积为y V ,取y 为积分变量,]2,0[a y ∈,则⎰⎰-=aay y d y x y d y x V 20212022)()(ππ⎰⎰---=πππππ022222sin )sin (sin )sin (t d t a t t a t d t a t t a⎰-=0222sin )sin (ππt d t a t t a ⎰-+ππ022sin )sin (t d t a t t a ⎰--ππ022sin )sin (t d t a t t a⎰+--=ππ203223)sin sin 2sin (t d t t t t t a⎰-=ππ2023sin t d t t a ⎰-+ππ203)2cos 1(t d t t a ⎰-+ππ2023)(cos )cos 1(t d t a336a π=.2.平行截面面积为已知的立体的体积:设一非旋转体的 立体介于过点a x =、b x =且垂直于x 轴的两个平面之间, 该立体过x 轴上的点x 且垂直于x 轴的截面面积为)(x A , 则该立体的体积为:⎰=ba dx x A V )(.推导:若)(x A 为连续函数且已知,取x 为积分变量,],[b a x ∈,在],[b a 上任取一小区间],[x d x x +,其上的薄层的体积近似等于底面积为)(x A 、高为x d 的扁圆柱体的体积,即得体积元素:x d x A V d )(=,以x d x A )(为被积表达式,在],[b a 上作定积分,得所求立体的体积公式:⎰=ba dx x A V )(.例9.一平面经过半径为R 的圆柱体的底圆的中心,并与底面交 成角α,计算着平面截圆柱体所得立体的体积.解:取该平面与圆柱体的底面的交线为x 轴,底面上过圆中心且 垂直于x 轴的直线为y 轴,则底面圆方程为:222R y x =+,该立体中过x 轴上的点x 且垂直于x 轴的截面是一个直角三角形,两直角边分别为y 和αtan y ,即22x R -和22tan x R -α,从而截面面积为αtan )(21)(22x R x A -=,于是所求体积为⎰--=R R x d x R V αtan )(2122⎰-=R x d •x R 022)(tan ααtan 223R =.例4.求以半径为R 的圆为底、以平行且等于底圆直径的线段为顶、高为h 的正劈锥体的体积.解:取底面圆所在的平面为xoy 平面,圆心o 为原点,并使x 轴 与正劈锥体的顶平行,底面圆方程为:222R y x =+,过x 轴上的点]),[(b a x x ∈作垂直于x 轴的平面截正劈锥体得等腰三角形,截面面积为22)(x R h y h x A -==,于是,所求正劈锥体的体积为⎰--=RRx d x R h V 22⎰-=R x d x R h 0222⎰=2/022cos 2πθθd h R ⎰+=2/02)2cos 1(πθθd h R 22hR π=.三、平面曲线的弧长引入:我们知道,用刘徽的割圆术可以定义圆的周长,即利用圆的内接正多边形的周长当边数无限增加时的极限来确定,现在将刘徽的割圆术加以推广,来定义平面曲线的弧长,从而应用定积分来计算平面曲线的弧长. 1.平面曲线弧长的相关概念(1).平面曲线弧长:若在曲线弧B A 上任取分点0M A =, ,,,,,121i i M M M M -,B M M n n =-,1,依次连接相邻分点得到该曲线弧的一内接折线,记|}{|max 11i i ni M M -≤≤=λ,若当分点的数目无限增加且每一个小弧段i i M M1-都缩向一点,即0→λ时,折线的长∑=-n i i i M M 11||的极限存在,则称此极限值为曲线弧B A的弧长,并称该曲线弧是可求长的,记作||lim 10i i M M s -→=λ.(2).光滑曲线:若曲线上每一点处都存在切线,且切线随切点的移动而连续转动,则称该曲线为光滑曲线.(3).定理:光滑曲线可求长. 2.光滑曲线弧长的计算(1).直角坐标情形:设曲线弧的直角坐标方程为)(x f y =,b x a ≤≤,若)(x f 在],[b a 上具有一阶连续函数,则曲线弧长为x d x f s ba ⎰'+=)(12.推导:取x 为积分变量,曲线)(x f y =上的相应于],[b a 上任意小区间],[x d x x +上的一段弧的长度近似等于曲线在点))(,(x f x 处切线上相应的一段的长度,又切线上相应小段的长度为x d x f y d x d 222))('(1)()(+=+,从而有弧长元素x d x f s d 2))('(1+=,以x d x f 2))('(1+为被积表达式,在],[b a 上作定积分,得弧长公式:x d x f s ba⎰'+=)(12.(2).参数方程情形:设曲线弧的参数方程为⎩⎨⎧==)()(t y t x ψϕ,βα≤≤t ,若)(t ϕ及)(t ψ在],[βα上具有连续导数,则曲线弧长为t d t t s ⎰'+'=βαψϕ)()(22.推导:取参数t 为积分变量,曲线上相应于],[βα上任意小区间],[t d t t +上的一段弧的长度的近似值即为弧长元素22)()(y d x d s d +=t d t t )(')('22ψϕ+=,以t d t t )(')('22ψϕ+为被积表达式,在],[βα上作定积分,得弧长公式:t d t t s ⎰+=βαψϕ)(')('22.(3).参数方程情形:设曲线弧的极坐标方程为)(θρρ=,],[βαθ∈,若)(θρ在],[βα上具有连续导数,则曲线弧长为:θθρθρβαd s ⎰+=)(')(22.推导:由直角坐标与极坐标的关系得:⎩⎨⎧==θθρθθρsin )(cos )(y x ,βθα≤≤,即为曲线的以极角θ为参数的参数方程,弧长元素为 θθρθρθθθd d y x s d )(')()]([)]([2222+='+'=, 于是曲线弧长为:θθρθρβαd s ⎰+=)(')(22.例11.计算曲线2332x y =上相应于x 从a 到b 的一段弧的长度.解:x d x x d x y s baba⎰⎰+=+=1)('12])1()1[(32)1(322323123a b x +-+=+=.例12.计算摆线⎩⎨⎧-=-=)cos 1()sin (θθθa y a x )0(>a 一拱π)20(≤≤θ的弧长.解:由于弧长元素为θθθd y x s d )(')('22+=θθθd a a 2222sin )cos 1(+-=θθd a )cos 1(2-=θθd a 2sin 2=,于是,所求弧长为a d a s 82sin2π20==⎰θθ.例13.求阿基米德螺线)0(>=a a θρ相应于π20≤≤θ一段的一拱. 解:弧长元素为θθρθρd s d )(')(22+=θθd a a 222+=θθd a 21+=,于是,所求弧长为θθd a s ⎰+=π2021⎥⎦⎤+++⎢⎣⎡+=πθθθθ20221ln 2112a )π41π2ln(2π41π22++++=a a .。
高数(同济第六版)下册无穷级数要点
若 lim S n = S ,称数列收敛, S 为级数的和,即:
n →∞
∑u
N =1
n
=S;
若 lim S n 不存在,称级数发散。
n →∞
�
性质:
(1) 若级数 � �
∑u ,∑v
n n
n
都收敛,则
∑ (u
± vn ) 也收敛,且 ∑ (un ± vn ) = ∑ un ± ∑ vn
也收敛,且
∑ cu
n =0
幂级数收敛定理——阿贝尔定理
∞
如果幂级数
∑a x
n n =0
n
当 x = x0 ( x0 ≠ 0) 时收敛, 则对满足不等式 x < x0 的一切 x , 幂级
数都收敛,并且是绝对收敛;
∞
如果幂级数 数都发散。
∑a x
n n =0
n
当 x = x0 ( x0 ≠ 0) 时发散, 则对满足不等式 x > x0 的一切 x , 幂级
∑ u ( x) = u ( x) + u ( x ) + ⋯ + u ( x ) + ⋯ 为函数项级数。
n
1 2
∞
n
n =1
∞
�
函数项的收敛点: ∀x0 ∈ I ,
∑ u ( x ) 收敛,称 x 为函数项级数的收敛点;
n
0 0
n =1
∞
函数项的发散点: ∀x0 ∈ I , � � 收敛域:收敛点的全体。
n →∞
p
∑u
n =1
n
收敛。
∞
�
比值审敛法:设
∑u
n =1
n
是正项级数,则 lim
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
高等数学下册习题常见类型题型1 求向量的坐标、模、方向角、方向余弦、数量积、向量积 题型2 由已知条件求平面与直线方程 题型3 计算一阶偏导数及高阶偏导数 题型4 求多元复合函数的偏导数 题型5 求方程所确定的隐函数的偏导数题型6 求方向导数、梯度、曲线的切线、曲面的切平面 题型7 求极值、利用拉格郎日乘数法求最值 题型8 利用直角坐标计算二重积分 题型9 利用极坐标计算二重积分 题型10 计算带绝对值的二重积分 题型11 利用二重积分证明恒等式 题型12 利用对称性质计算二重积分 题型13 只有一种积分次序可计算的积分例1、求24212xdx dx +⎰⎰解:(将二次积分交换顺序)12212242122211sin sin sin sin (1)sin cos1sin1xD D y y D D y y dx dx dxdy dxdyy y yy dxdy dy dx y ydy y y πππππ+=+===-=-⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰U题型14 利用投影法计算三重积分 题型15 利用柱坐标计算三重积分 题型16 利用球坐标计算三重积分 题型17 利用切片法计算三重积分 题型18 利用三重积分计算立体的体积 题型19 计算对弧长的曲线积分 题型20 计算对面积的曲面积分 题型21 计算对坐标的曲线积分题型22 利用格林公式计算对坐标的曲线积分 题型23 曲线积分与路径无关及全微分求积 题型24 计算对坐标的曲面积分题型25 利用高斯公式计算对坐标的曲面积分 题型26 可分离变量的微分方程、齐次方程 题型27一阶线性微分方程 题型29 可降阶方程题型30二阶常系数非齐次线性方程第八章 向量与解析几何向量代数定义 定义与运算的几何表达在直角坐标系下的表示向量 有大小、有方向. 记作a 或AB u u u ra (,,)x y z x y z a i a j a k a a a =++=,,x x y y z z a prj a a prj a a prj a ===r r r模向量a 的模记作aa 222x y z a a a =++和差c a b =+ c a b =-=+c a b {},,=±±±x x y y z z a b a b a b单位向量0a ≠,则a ae a=a e 222(,,)=++x y z x y za a a a a a方向余弦设a 与,,x y z 轴的夹角分别为αβγ,,,则方向余弦分别为cos αβγ,cos ,coscos y x z a a aa a a αβγ===r r r ,cos ,coscos a e αβγ=(,cos ,cos ) 222cos 1αβγ+=+cos cos 点乘(数量积)θcos b a b a =⋅, θ为向量a 与b 的夹角z z y y x x b a b a b a ++=⋅b a叉乘(向量积)b ac ⨯=θsin b a c =θ为向量a 与b 的夹角 向量c 与a ,b 都垂直zy xz y xb b b a a a k j ib a =⨯ 定理与公式垂直 0a b a b ⊥⇔⋅= 0x x y y z z a b a b a b a b ⊥⇔++=平行//0a b a b ⇔⨯=//y zx x y za a a ab b b b ⇔==交角余弦两向量夹角余弦ba ba ⋅=θcos 222222cos x x y y z zx y z x y z a b a b a b a a a b b b θ++=++⋅++投影向量a 在非零向量b 上的投影cos()b a bprj a a a b b∧⋅== 222x x y y z zb x y za b a b a b prj a b b b ++=++空间曲面 ∑:0),,(=z y x F法向量000000000((,,),(,,),(,,))x y z n F x y z F x y z F x y z =r切平“面”方程:000000000000(,,)()(,,)()(,,)()0x x x F x y z x x F x y z y y F x y z z z -+-+-=法“线“方程:),,(),,(),,(000000000000z y x F z z z y x F y y z y x F x x z y x -=-=- ),(y x f z = 0000((,),(,),1)x y n f x y f x y =--r或0000((,),(,),1)x y n f x y f x y =-r切平“面”方程:0)())(,())(,(0000000=---+-z z y y y x f x x y x f y x法“线“方程:1),(),(0000000--=-=-z z y x f y y y x f x x y x 重积分 积分类型计算方法典型例题二重积分()σd ,⎰⎰=Dy x f I平面薄片的质量质量=面密度⨯面积(1) 利用直角坐标系X —型 ⎰⎰⎰⎰=Dbax x dy y x f dx dxdy y x f )()(21),(),(φφY —型⎰⎰⎰⎰=dcy y Ddx y x f dy dxdy y x f )()(21),(),(ϕϕP141—例1、例3(2)利用极坐标系 使用原则(1) 积分区域的边界曲线易于用极坐标方程表示( 含圆弧,直线段 );(2) 被积函数用极坐标变量表示较简单( 含22()x y α+, α为实数 )21()()(cos ,sin )(cos ,sin )Df d d d f d βϕθαϕθρθρθρρθθρθρθρρ=⎰⎰⎰⎰02θπ≤≤ 0θπ≤≤ 2πθπ≤≤P147—例5(3)利用积分区域的对称性与被积函数的奇偶性当D 关于y 轴对称时,(关于x 轴对称时,有类似结论)P141—例2应用该性质更方便第十一章曲线积分与曲面积分所有类型的积分:○1定义:四步法——分割、代替、求和、取极限;○2性质:对积分的范围具有可加性,具有线性性;○3对坐标的积分,积分区域对称与被积函数的奇偶性。
第十章级数无穷级数常数项级数傅立叶级数幂级数一般项级数正项级数用收敛定义,nns∞→lim存在常数项级数的基本性质常数项级数的基本性质○1若级数收敛,各项同乘同一常数仍收敛.○2两个收敛级数的和差仍收敛.注:一敛、一散之和必发散;两散和、差必发散.○3去掉、加上或改变级数有限项,不改变其收敛性.○4若级数收敛,则对这级数的项任意加括号后所成的级数仍收敛,且其和不变。
推论:如果加括号后所成的级数发散,则原来级数也发散.注:收敛级数去括号后未必收敛.○5(必要条件)如果级数收敛,则0lim=→nnu莱布尼茨判别法若1+≥nnuu且0lim=∞→nnu,则∑∞=--11)1(nnn u收敛nu∑和nv∑都是正项级数,且nnvu≤.若nv∑收敛,则nu∑也收敛;若nu∑发散,则nv∑也发散.比较判别法比较判别法的极限形式nu∑和nv∑都是正项级数,且lvunnn=∞→lim,则○1若+∞<<l0,nu∑与nv∑同敛或同散;○2若0=l,nv∑收敛,nu∑也收敛;○3如果+∞=l,nv∑发散,nu∑也发散。
比值判别法根值判别法nu∑是正项级数,ρ=+∞→nnn uu1lim,ρ=∞→nnnulim,则1<ρ时收敛;1>ρ(ρ=+∞)时发散;1=ρ时可能收敛也可能发散.收敛性和函数展成幂级数nnnxa∑∞=0,ρ=+∞→nnn aa1lim,1,0;,0;0,.R R Rρρρρ=≠=+∞===+∞缺项级数用比值审敛法求收敛半径)(xs的性质○1在收敛域I上连续;○2在收敛域),(RR-内可导,且可逐项求导;○3和函数)(xs在收敛域I上可积分,且可逐项积分.(R不变,收敛域可能变化).直接展开:泰勒级数间接展开:六个常用展开式11(11)1nnx xx∞==-<<-∑11()!x nne x xn∞==-∞<<+∞∑22TT lπ==∑∞=++=10)sincos(2)(nnnnxbnxaaxf⎰-=πππdxxfa)(1⎰-=πππnxdxxfancos)(1⎰-=πππnxdxxfbnsin)(1收敛定理x是连续点,收敛于)(xf;x是间断点,收敛于)]()([21+-+xfxf周期延拓)(xf为奇函数,正弦级数,奇延拓;)(xf为偶函数,余弦级数、偶延拓.交错级数。
