河南省通许县丽星中学八年级数学上册 第14章 勾股定理复习导学案2
河南省通许县丽星中学八年级数学上册 14.1.2 直角三角形的判定导学案

14章勾股定理第三课时学习目标:1、掌握勾股定理,能运用勾股定理由已知直角三角形的两边长求出第三边的长2、用勾股定理的逆定理来判断一个三角形是否是直角三角形3、会解决圆柱、长方体的最短路线问题,如何判断一个角是直角重难点:理解掌握勾股定理与勾股定理的逆定理。
自学过程:一.(1)导入据说,古埃及人曾用下面的方法画直角:他们用13个等距的结把一根绳子分成等长的12段,一个工匠同时握住绳子的第1个结和第13个结,两个助手分别握住第4个结和第8个结,拉紧绳子,就会得到一个直角三角形,其直角在第4个结处.你知道这是什么道理吗?(2)复习1.三角形的三边关系?2.直角是三角形有哪些性质?3.勾股定理?4.一个三角形满足什么条件是直角三角形呢?二.新授1.小组探究试用小塑料棒拼出三边长度分别为如下数据的三角形,猜想它们是些什么形状的三角形?(按角分类)(1)3,4,5(2)6,9,13 (3)9,12,15(4)5,12,13请比较上述每个三角形的两条较短边的平方和与最长边的平方之间的大小关系. 并指出最长边所对的角是什么角结论:如果三角形的三边长a,b,c满足______________,那么这个三角形是直角三角形即勾股定理的逆定理(思考)反之,如果三角形的两条较短的边的平方和不等于最长边的平方,那么这个三角形还是直角三角形吗?___________试一试:学过上面的内容,你能否运用所学的知识说明一下古埃及人画直角的理论依据呢?三、典例剖析:设三角形三边长分别为下列各组数,试判断各三角形是否是直角三角形(1)7,24.,25 (2)37,12,35 (3)13,9,11分析:根据勾股定理的逆定理,判断一个三角形是否是直角三角形,只要看两条较短的边的平方和是否等于最长的边的平方★★归纳:用勾股定理逆定理判断三角形是否是直角三角形的步骤①、确定最大边(如c,c边所对的角是∠C)②、验证:2c与22ba+是否相等若2c=22ba+,则△ABC是以∠C=90°的直角三角形若2c≠22ba+,则△ABC不是直角三角形四、随堂练习:(1)设三角形的三边分别等于下列各组数,试判断各三角形是不是直角三角形?如果是请指明哪一个条边所对的角是直角?(1)12,16,20 (2)8,12,15 (3)5,6,8学以致用:1.一个零件的形状如左图所示,已知∠A=90°,按规定这个零件中∠DBC都应该为直角。
初中八年级数学《勾股定理》复习导学案设计

第十七章勾股定理学习目标:1.回顾本章知识,在回顾过程中主动构建起本章知识结构;2.思考勾股定理的发现证明和应用过程,体会出入相补思想、数形结合思想、转化思想在解决数学问题中的作用.学习重点:勾股定理的应用.教学过程:复习勾股定理:如果直角三角形两直角边分别为a,b,斜边为c,那么a2 + b2 = c2即直角三角形两直角边的平方和等于斜边的平方.一. 基础知识运用第一组练习: 勾股定理的直接应用(一)知两边或一边一角型1.如图,已知在△ABC 中,∠B =90°,一直角边为a,斜边为b,则另一直角边c满足c2 = .【思考】为什么不是c²=a²+b²?2.在Rt△ABC中,∠C=90°,∠A=30°,AC=3.求AB、BC的长。
(二)知一边及另两边关系型如图,已知在△ABC 中,∠B =90°,若BC=4 , AB=x ,AC=8-x,则AB= ,AC= .(三)分类讨论的题型1. 对三角形边的分类.已知一个直角三角形的两条边长是 3 cm和 4 cm,第三条边的长是.注意:这里并没有指明已知的两条边就是直角边,所以4 cm可以是直角边,也可以是斜边,即应分情况讨论.2. 对三角形高的分类.已知:在△ABC中,AB=15 cm,AC=13 cm,高AD=12 cm,求S△ABC.【思考】本组题,利用勾股定理解决了哪些类型题目?注意事项是什么?利用勾股定理能求三角形的边长和高等线段的长度.注意没有图形的题目,先画图,再考虑是否需分类讨论.思考:利用勾股定理解题决实际问题时,基本步骤是什么?第二组练习: 用勾股定理解决简单的实际问题1.在一块平地上,张大爷家屋前9米远处有一棵大树.在一次强风中,这棵大树从离地面6米处折断倒下,量得倒下部分的长是10米.出门在外的张大爷担心自己的房子被倒下的大树砸到.大树倒下时能砸到张大爷的房子吗?()A.一定不会B.可能会C.一定会D.以上答案都不对2. 如图,滑杆在机械槽内运动,∠ACB为直角,已知滑杆AB长2.5米,顶端A在AC上运动,量得滑杆下端B距C点的距离为1.5米,当端点B向右移动0.5米时,求滑杆顶端A下滑多少米?思考:利用勾股定理解题决实际问题时,基本步骤是什么?二、努力提高:会用勾股定理解决较综合的问题。
第14章 勾股定理全章导学案

华文学校导学案八年级数学 课题 勾股定理 课时:一 编写 :景伟华学习目标(含重难点):1.了解勾股定理的发现过程,掌握勾股定理的内容,会用面积法证明勾股定理。
2.培养在实际生活中发现问题总结规律的意识和能力。
自学导读:1、直角△ABC 的主要性质是:∠C=90°(用几何语言表示)(两锐角之间的关系: 2.23+24与25,25+212和213有什么关系?即23+24 25,25+212 213, 由此我们可以得出什么结论?可猜想:命题1:如果直角三角形的两直角边分别为a 、b ,斜边为c ,那么 。
勾股定理的证明1、已知:在△ABC 中,∠C=90°,∠A 、∠B 、∠C 的对边为a 、b 、c 。
求证: 222ab c +=证明:4S △+S 小正= S 大正=根据的等量关系:由此我们得出:勾股定理的内容是: 。
合作探究展示 1、在Rt △ABC 中,90C∠=︒ ,(1)如果a=3,b=4,则c=________;2)如果a=6,b=8,则c=________;(3)如果a=5,b=12,则c=________;(4) 如果a=15,b=20,则c=________. 2、下列说法正确的是( )A.若a 、b 、c 是△ABC 的三边,则222a b c +=B.若a 、b 、c 是Rt △ABC 的三边,则222ab c += C.若a 、b 、c 是Rt △ABC 的三边,90A ∠=︒, 则222a b c +=D.若a 、b 、c 是Rt △ABC 的三边,90C∠=︒ ,则222a b c +=3、一个直角三角形中,两直角边长分别为3和4,下列说法正确的是( )A .斜边长为25 B .三角形周长为25 C .斜边长为5 D .三角形面积为204、如图,三个正方形中的两个的面积S1=25,S2=144,则另一个的面积S3为________.5、一个直角三角形的两边长分别为5cm 和12cm,则第三边的长为 。
初中数学八年级第十四章勾股定理复习(二)导学案

AB=AC
9点D是ABC边BC上一点,且AC-CD2二AD
求证:aB-ac2二bD^cD2
三,课堂小结及作业布置
教学反思
基础训练
启发提咼
津南卷测验
教
成
学
果
过
检
程
验
学
后
记
一、小组合作
,归纳知识点
快速将本章知识点总结,组内研讨
教
自
二、习题选练
学
主
1三角形的三边a,b,c满足
关系,这个
三角形是直角三角形,他的最大边是
过
学
2已知三角形三边长为1,
1, V2,
则此三角形是三
角形
程
习
3在厶ABC中,AB=7 BC=8则当AC二时,
/C=90
4若个三角形的三边长之比为5:
12:13,周长是60,
课题
第十四章勾股定理
授课人
授课时间
周
课型
复习(二)
主备人
吴静
审核人
学习
1通过复习,使学生加深对勾股定理及逆定理的理解,提高认识。
学习
2进一步灵活准确利用所学知识解决有关问题。
目标
3通过解题提高学生用数学的意识,增强学生学习数学的积极性。
重点
巩固
集体备课内容
个案补充
则此三角形的面积为
5已知一个三角形的两边长分别为3和4,则当第三边长
是时,这个三角形是直角三角形
6如果△ABC的三边长a,b,c满足关系式"a+2b-30+
2
c-15 +(b-9)=0,是判断△ABC的形状
14章 勾股定理复习学案
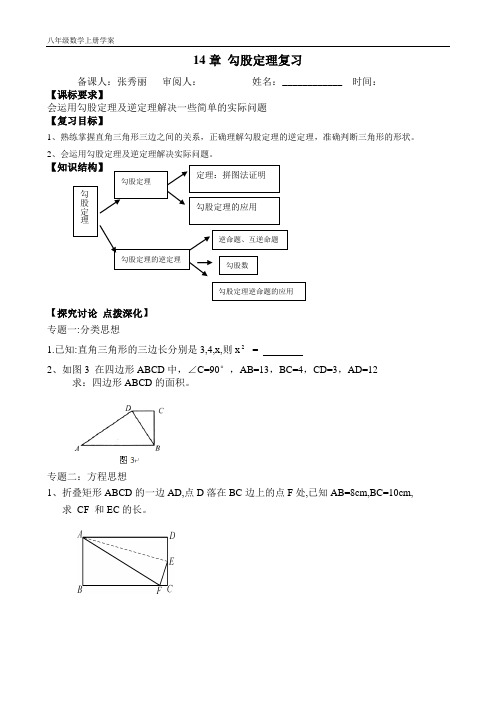
14章勾股定理复习备课人:张秀丽审阅人:姓名:____________ 时间:【课标要求】会运用勾股定理及逆定理解决一些简单的实际问题【复习目标】1、熟练掌握直角三角形三边之间的关系,正确理解勾股定理的逆定理,准确判断三角形的形状。
2、会运用勾股定理及逆定理解决实际问题。
【探究讨论点拨深化】专题一:分类思想1.已知:直角三角形的三边长分别是3,4,x,则x2=2、如图3 在四边形ABCD中,∠C=90°,AB=13,BC=4,CD=3,AD=12求:四边形ABCD的面积。
专题二:方程思想1、折叠矩形ABCD的一边AD,点D落在BC边上的点F处,已知AB=8cm,BC=10cm,求CF 和EC的长。
2、 在一棵树的10米高的D 处有两只猴子,其中一只猴子爬下树走到离树20米的池塘A 处,另一只爬到树顶后直接跃向池塘A 处,如果两只猴子所经过的距离相等,试问这棵树有多高?专题三:展开思想如图,一圆柱高8cm,底面半径2cm,一只蚂蚁从点A 爬到点B 处吃食物,要爬行的最短路程( 取3)是( )小检测(20分)(1----4题)1、在Rt △ABC 中,已知两直角边长a=1,b=3, 那么斜边 c 的长为 。
2、已知直角三角形的两边长为3,2.则另一条边长是 。
3、分别以下列四组数为一个三角形的边长(1)3,4,5 (2)5,12,13 (3)8,15,17 (4) 4,5,6 其中能组成直角三角形的有4、写出“线段垂直平分线上的点到线段两端点的距离相等”的逆命题是5、小明想知道学校旗杆的高,他发现旗杆上的绳子垂到地面还多一米,当他把绳子的下端拉开5米后,发现下端刚好接触地面,则旗杆的高为( )6、酒店在装修时,在大厅的主楼梯上铺设某种红色地毯,已知这种地毯每平方米售价30元,主楼梯宽2米,其侧面如图5所示,他购买地毯至少需要 ( )元。
【学后记】 D BC A.8。
八年级上册导学案:勾股定理(2)
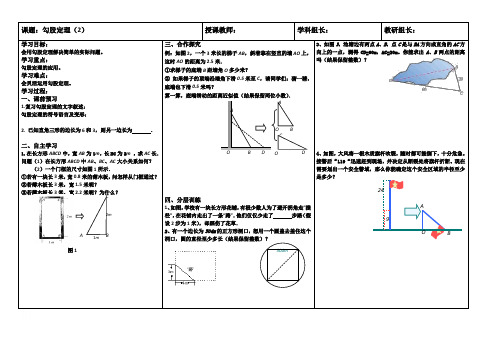
课题:勾股定理(2)授课教师: 学科组长: 教研组长: 学习目标: 会用勾股定理解决简单的实际问题。
学习重点: 勾股定理的应用。
学习难点: 会灵活运用勾股定理。
学习过程: 一、课前预习 1.复习勾股定理的文字叙述: 勾股定理的符号语言及变形: 2. 已知直角三形的边长为6和3,则另一边长为 . 二、自主学习1.在长方形ABCD 中,宽AB 为1m ,长BC 为2m ,求AC 长. 问题(1)在长方形ABCD 中AB 、BC 、AC 大小关系如何? (2)一个门框的尺寸如图1所示. ①若有一块长3米,宽0.8米的薄木板,问怎样从门框通过? ②若薄木板长3米,宽1.5米呢? ③若薄木板长3米,宽2.2米呢?为什么?图1 三、合作探究 例:如图2,一个3米长的梯子AB ,斜着靠在竖直的墙AO 上,这时AO 的距离为2.5米.①求梯子的底端B 距墙角O 多少米?② 如果梯子的顶端沿墙角下滑0.5米至C ,请同学们:猜一猜,底端也下滑0.5米吗? 算一算,底端滑动的距离近似值(结果保留两位小数). 四、分层训练 1、如图,学校有一块长方形花铺,有极少数人为了避开拐角走“捷径”,在花铺内走出了一条“路”.他们仅仅少走了 步路(假设2步为1米),却踩伤了花草. 2、有一个边长为50dm 的正方形洞口,想用一个圆盖去盖住这个洞口,圆的直径至少多长(结果保留整数)? 3、如图3,池塘边有两点A 、B ,点C 是与BA 方向成直角的AC 方向上的一点,测得CB=60m ,AC=20m 。
你能求出A 、B 两点的距离吗(结果保留整数)?4、如图,大风将一根木质旗杆吹裂,随时都可能倒下,十分危急。
接警后“119“迅速赶到现场,并决定从断裂处将旗杆折断。
现在需要划出一个安全警域,那么你能确定这个安全区域的半径至少是多少?B C 1m 2m A O B D C A C A O B O D 50dm 249O A B。
勾股定理复习导学案 (2)

勾股定理复习课导学案姓名___________ 一、学习目标1、记住勾股定理和勾股定理逆定理的内容。
2、会运用勾股定理及逆定理解决问题。
3、体会常见的数学思想—方程思想和数学建模思想。
二、学习重点:勾股定理、勾股定理逆定理学习难点:结合方程的思想并运用勾股定理及逆定理解决问题。
三、课前预习 (一)预习要求:研读导学案,完成预习内容。
用红笔在导学案上对不理解的问题进行标注,以便课堂上合作交流。
(二)预习内容:1. 自主梳理、问题导学 (1)、勾股定理: 。
(即: ) (2)、勾股定理的逆定理: .2. 课前训练 10.三个正方形的面积如图,正方形A 的面积为( ) A. 6 B.4 C. 64 D. 81.在Rt △ABC 中,若∠C=90°,BC=3,AC=4,则AB= .2.在Rt △ABC 中,若∠C=90°,BC=5,AB=13,则AB=3.在Rt △ABC 中,若其中两边分别为6,8,则第三边长为4.在Rt △ABC 中,若∠C=90°, ∠A=45°,BC=2, 则AB= AC= .5.在Rt △ABC 中,若∠C=90°, ∠A=30°,BC=2, 则AB= AC= .6.在Rt △ABC 中,若∠C=90°, ∠A=30°,AC=2, 则AB= AC= . 7.在Rt △ABC 中,∠C=90°,AC=3,AB+BC=8,则AB=8、分别以下列四组数为一个三角形的边长:(1)3、4、5(2)5、12、13(3)8、15、17(4)4、5、6,其中能够成直角三角形的有___________9.命题“对顶角相等”的逆命题为________________________,它是____命题.(填“真”或“假”)cbaCBAcbaCBA cbaCBAcbaCBAcbaC BA10.如下图,已知OA =OB ,那么数轴上点A 所表示的数是_______教学过程:知识点一、直接考察勾股定理1.要登上某建筑物,靠墙有一架梯子,底端离建筑物5,顶端离地面12,则梯子的长度为( ) A .12B .13C .14D .152.一轮船以16海里/时的速度从港口A 出发向东北方向航行,另一轮船以12海里/时的速度同时从港口A 出发向东南方向航行,离开港口2小时后,则两船相距 ( ) A 、25海里 B 、30海里 C 、35海里 D 、40海里 3.已知x 、y 为正数,且|x -2|+(y -4)2=0,如果以x 、y 的长为直角边作一个直角三角形,那么以这个直角三角形的斜边长为 .4、一种盛饮料的圆柱形杯,测得内部底面半径为2.5㎝,高为12㎝,吸管放进杯里,杯口外面至少要露出4.6㎝,问吸管要做_________cm5、如图4为某楼梯,测得楼梯的长为5米,高3米,计划在楼梯表面铺地毯,要__________米?5米3米6、如图一个圆柱,底圆周长6cm ,高4cm ,一只蚂蚁沿外壁爬行,要从A 最少要爬行 cm7、 一只蚂蚁从长、宽都是3,高是8的长方体纸箱的A 点沿纸箱爬到B 点,那么它所行的最短路线的长是_____________。
八年级数学上册第14章勾股定理14.2勾股定理的应用导学案新版华东师大版word版本

14.2勾股定理的应用【学习目标】1.正确运用勾股定理及逆定理2.经历研究勾股定理的应用过程,掌握定理的应用方法,应用“数形联合”的思想来解决。
3.培育合情推理能力,提升合作沟通意识,领会勾股定理的应用价值。
【学习重难点】1、掌握勾股定理及逆定理2、正确运用勾股定理及逆定理【学习过程】一、课前准备1、已知Rt △ ABC中,∠ C=90°,若 BC=4,AC=2,则AB=_______;若AB=4, BC=则AC=________.2、一个直角三角形的模具,量得此中两边的长分别为5cm、 3cm, ?则第三边的长是_________.3.要登上8m高的建筑物,为了安全需要,需使梯子底端离建筑建6m. ?问起码需要多长的梯子?二、学习新知自主学习:1.如图,一圆柱体的底面周长为20cm,高AB为4cm,BC是上底面的直径.一只蚂蚁从点 A 出发,沿着圆柱的侧面爬行到点C,试求出爬行的最短行程.(精准到0.01cm)( 1)自制一个圆柱,试试从 A 点到 C 点沿圆柱侧面画出几条路线,你以为哪条路线最短呢?( 2)如图,将圆柱侧面剪展开成一个长方形,从 A 点到 C 点的最短行程是什么?你画对了吗?( 3)蚂蚁从 A 点出发,想吃到 C 点上的食品,它沿圆柱侧面爬行的最短行程是多少?学习领会:我们知道勾股定理揭露了直角三角形的三边之间的数量关系,已知直角三角形中的任意两边就能够依照勾股定理求出第三边.从应用勾股定理解决实质问题中,我们进一步认22 2识到把直角三角形中三边关系“ a +b =c ”当作一个方程,只需依照问题的条件把它转变为我们会解的方程,就把解实质问题转变为解方程.实例剖析:例 1、一辆装满货物的卡车,其外形高2.5 米,宽 1.6 米,要开进厂门形状如左图的某工厂,问这辆卡车可否经过该工厂的厂门?例 2、如图,在 5× 5 的正方形网格中,每个小正方形的边长都为1,请在给定网格中按以下要求画出图形:从点 A 出发一条线段AB 使它的另一端点 B 在格点(即小正方形的极点)上,且长度为 2 2画出全部的以( 1)中的 AB为边的等腰三角形,使另一个极点在格点上,且另两边的长度都是无理数例 3:已知 CD=6 m, AD=8 m,∠ ADC=90°, BC=24m,AB=26m。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第14章勾股定理复习导学案(2)考点六:应用勾股定理解决勾股树问题
例、如右图所示的图形中,所有的四边形都是正方形,所有的三角形都是直角三角形,其中最大的正方形的边长为5,求正方形A,B,C,D的面积的和.
分析:勾股树问题中,处理好两个方面的问题,一个是正方形的边长与面积的关系,另一个是正方形的面积与直角三角形直角边与斜边的关系。
点评:请同学们自己把其内在的一般变化规律总结一下。
考点七:应用勾股定理解决数学风车问题
例、(09年安顺)图甲是我国古代著名的“赵爽弦图”的示意图,它是由四个全等的直角三角形围成的。
在Rt△ABC中,若直角边AC=6,BC=5,将四个直角三角形中边长为6的直角边分别向外延长一倍,得到图乙所示的“数学风车”,则这个风车的外围周长(图乙中的实线)是
______________。
分析:因为,直角边AC=6,BC=5,当将四个直角三角形中边长为6的直角边分别向外延长一倍后,得到四个直角边分别是12和5的直角三角形,所求的最长实边恰好是这些直角三角形的斜边长,因此,斜边长为:=13,较短的实边长是6,所以,这个风车的外围周长为:4×13+4×6=76.
解:这个风车的外围周长为76.
考点八:判别一个三角形是否是直角三角形
例1:分别以下列四组数为一个三角形的边长:(1)3、4、5(2)5、12、13(3)8、15、17(4)
4、5、6,其中能够成直角三角形的有
【强化训练】:已知△ABC中,三条边长分别为a=n2-1,b=2n,c=n2+1(n>1).试判断该三角形是否是直角三角形,若是,请指出哪一条边所对的角是直角.
考点九:其他图形与直角三角形
例:如图,一块地,已知AD=8m,CD=6m,∠D=90°,AB=26m,BC=24m,求这块地的面积
.
考点十:构造直角三角形解决实际问题
例、在某一平地上,有一棵树高8米的大树,一棵树高2米的小树,两树之间相距8
米。
今一只小
鸟在其中一棵树的树梢上,要飞到另一棵树的树梢上,问它飞行的最短距离是多少?(画出草图然后解答)
考点十一:与展开图有关的计算
例、如图,在棱长为1的正方体ABCD—A’B’C’D’的表面上,求从顶点A到顶点C’的最短距离.
【强化训练】:如图一个圆柱,底圆周长6cm,高4cm,一只蚂蚁沿外壁爬行,要从A点爬到B点,则最少要爬行 cm
四、课时作业优化设计
【驻足“双基”】
1.设直角三角形的三条边长为连续自然数,则这个直角三角形的面积是_____.
2.直角三角形的两直角边分别为5cm,12cm,其中斜边上的高为().
A.6cm B.8.5cm C.30
13
cm D.
60
13
cm
【提升“学力”】
3.如图,△ABC的三边分别为AC=5,BC=12,AB=13,将△ABC沿AD折叠,使AC•落在AB上,求DC的长.
4.如图,一只鸭子要从边长分别为16m和6m的长方形水池一角M•游到水池另一边中点N,那么这只鸭子游的最短路程应为多少米?
【聚焦“中考”】
5.(海南省中考题)如图,铁路上A、B两点相距25km,C、D为两村庄,DA•垂直AB于A,CB 垂直AB于B,已知AD=15km,BC=10km,现在要在铁路AB上建一个土特产品收购站E,使得
C、D两村到E站的距离相等,则E站建在距A站多少千米处?
A
B。
