材料力学课件复习习题
材料力学复习习题(可打印版)ppt课件

两者均小于 []=170MPa 。可见,无论采用第三或是 第四强度理论进行强度校核,该结构都是安全的。
qL 2
L=3m
qL 2
+
x
M
qL 8
2
qL 3600 3 F 540 N S max 2 2
x
2 2 qL 3600 3 M 405 N max 8 8
+
q=3.6kN/m
求最大应力并校核强度
M M 6 4050 max 6 max max 2 2 W bh 0 . 12 0 . 18 z
件,[]=40MPa,试用第一强度理论校核杆的强度。 T P A T A A P
解:危险点A的应力状态如图:
P 4 50 3 10 6 . 37 MP 2 A 0 . 1
2
2
T 16 7000 35 . 7 MPa 3 W 0 . 1 n
sin 2 cos 2 xy
2、求主应力、主平面
主应力: m ax
m in
x y
2
(
x y2
2
) xy
2
80 . 7 ( MPa ), 0 ,3 60 . 7 ( MPa ) 1 2
主平面位置:
80 . 7 ( MP ) 40 60 40 60 2 2 ( ) ( 50 ) 60 . 7 ( MP ) 2 2
F 2 F A N 1 1 1
3、根据水平杆的强度,求许可载荷 查表得水平杆AB的面积为A2=2×12.74cm2
F F cos 3 F N 2 N 1
材料力学复习题

材料力学复习题材料力学是研究材料力学性质和材料的应力、应变、变形和破坏等相关问题的学科。
通过对材料的组织结构、原子结构以及力学行为的分析和研究,可以深入了解材料的性能和性质,为材料工程和结构设计提供科学依据。
下面是一些材料力学的复习题,帮助大家回顾和巩固所学的知识。
1. 什么是应力?与应变有什么关系?请用公式表示。
应力是单位面积上的力,表示为F/A。
应变是物体长度或体积的相对变化,通常用ΔL/L或ΔV/V表示。
应力和应变的关系由胡克定律给出:应力等于弹性模量乘以应变,即σ = Eε。
2. 什么是杨氏模量?如何计算?它的单位是什么?杨氏模量是材料的刚度指标,表示为E。
计算公式为E = σ/ε,其中σ为应力,ε为应变。
杨氏模量的单位是帕斯卡(Pa)。
3. 弹性模量、剪切模量和泊松比之间有何关系?弹性模量E、剪切模量G和泊松比ν之间的关系由以下公式给出:E = 2G(1 + ν)。
4. 什么是屈服点?屈服强度是什么?如何确定材料的屈服点?屈服点是材料在加载过程中开始发生塑性变形的点。
屈服强度是材料开始发生可测量的塑性变形时所承受的最大应力。
可以通过在材料上施加加载并测量其应力-应变曲线,确定屈服点。
5. 什么是断裂韧性?如何计算断裂韧性?断裂韧性是材料抵抗断裂的能力,通常用断裂韧性K来表示。
计算断裂韧性的常用方法是通过计算材料的断裂过程中吸收的总能量来实现。
根据线弹性断裂力学理论,K可以通过以下公式计算:K = σf²πc,其中σf为断裂强度,c为断裂过程中裂纹的长度。
6. 什么是材料的疲劳强度?如何评估材料的疲劳寿命?疲劳强度是材料在循环加载或应力下能够承受的最大应力水平。
评估材料的疲劳寿命通常通过进行疲劳试验并绘制S-N曲线得出。
S-N曲线描述了应力幅与循环寿命之间的关系。
7. 什么是塑性变形?与弹性变形有何区别?塑性变形是材料在加载过程中超过其弹性极限时发生的永久性变形。
与弹性变形不同,塑性变形是不可恢复的,并伴随着局部晶体滑移和位错运动。
材料力学复习 PPT课件
M c y1 Iz
[sc ]
y1 y2
[st ] [s c ]
20 y
20
F
q=F/b
A
CB
D
b
b
b
Fb/2
C截面的强度条件由最大的拉应
力控制。
Fb/4
s t max
MC y1 Iz
( F 2) 0.134 4 5493108
30 106
F 24.6 kN
B截面
s t max
T 0.2d 3
T
1930
d 3 0.2tmax 3 0.2 66.7 106 0.053 m 5.3 cm
A空 8.5 0.303 A实 28.2
可见, 采用钢管时, 其重量只有实心圆 轴的30%, 耗费的材料要少得多。
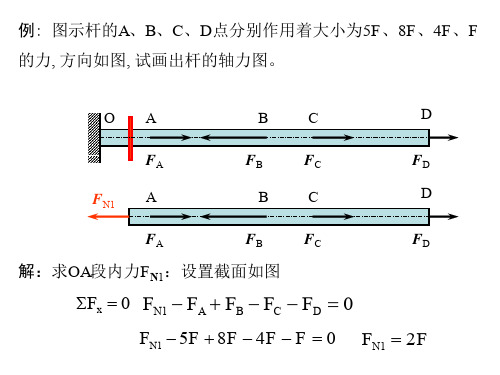
例: 作内力图。已知F1=F2=2 kN, Me=10 kN·m, q=1 kN/m。
s t max
My1 Iz
s cmax
My2 Iz
60 280
sc max
Oz
st max
s t max y1 [s t ] 1 s c max y2 [s c ] 3
y1 1 y2 3
d
60 280
y
y2
y1 y2 280 mm
由上两式确定出
Oz
y1
y
y y2 210 mm
80
120 20
y1
B截面
st
M B y1 Iz
4000 0.052 763108
27.2106 Pa 27.2 MPa [s t]
材料力学总复习-习题课4ppt课件

(a)桁架的承载能力强,因为(b) 桁架的压杆长度长,且压力大。
(a)
题4图
(b)
二、计算题
5. 作图示梁的剪力图和弯矩图,并写出
Q 和 M ,(15分)。 m ax m ax
解: FA = 7qa/6(↑), FD= qa/6(↓)
,
|Qmax|=7qa/6 |Mmax|=5qa2/6
6.已知电动机输出功率P=75kW,转速n=955rmp,输出轴直径D=50mm,输出轴 与外设轮毂采用键连接,已知键长度L=50mm,许用切应力和许用挤压应力分别 为 , ,试确定键的宽度b和高度h。(假设键各有一 60 MPa 100 MPa bs 半嵌入轴和轮毂内) (10分)
7.在xy平面内放置的直角折杆ABC,受力如图,已知F=120kN,q=8kN/m, a=2m;在yz平面内有 ,折杆ABC的直径d=150mm, =160MPa,试按第四 强度理论校核固定端A的强度。 (15分)
解:
轴力
弯矩
FN=F=120kN,
M 0 . 8 a q a 25 . 6 kN m
,
10.图示长、宽、高分别为l、b和h的矩形截面悬臂梁,在x-y平面和x-z平面内受到 两个垂直方向的力偶矩M1和M2的作用。已知该悬臂梁的弹性模量为E,泊松比为μ。 在某截面的前、后表面各粘贴了3个轴向应变片,其中应变片1和4位于前后表面的最 上端,应变片2和5位于前后表面的中间,应变片3和6位于前后表面的最下端。在不 提供额外温度补偿片的情况下,请选取若干个电阻应变片,组成两个惠斯通半桥, 分别直接测得外力偶矩M1和M2。要求:绘出惠斯通桥路接线图,并推导出外力偶矩 M1和M2和应变仪读数的显式关系式。 (15分) (1)用3,1应变片组成半桥测M1:
材料力学复习题共93页

2、要冒一次险!整个生命就是一场冒险。走得最远的人,常是愿意 去做,并愿意去冒险的人。“稳妥”之船,从未能从岸边走远。-戴尔.卡耐基。
梦 境
3、人生就像一杯没有加糖的咖啡,喝起来是苦涩的,回味起来却有 久久不会退去的余香。
材料力学复习题 4、守业的最好办法就是不断的发展。 5、当爱不能完美,我宁愿选择无悔,不管来生多么美丽,我不愿失 去今生对你的记忆,我不求天长地久的美景,我只要生生世世的轮 回里有你。
谢谢
11、越是没有本领的就越加自命不凡。——邓拓 12、越是无能的人,越喜欢挑剔别人的错儿。——爱尔兰 13、知人者智,自知者明。胜人者有力,自胜者强。——老子 14、意志坚强的人能把世界放在手中像泥块一样任意揉捏。——歌德 15、最具挑战性的挑战莫过于提升自我
材料力学习题(PPT)共17页文档
3E I
3
1
2l 1
Pll ) Pll l
2
3 GIp
fc
2Pl3 3EI
Pl3 GIp
T图
施加的单位力和P同位置、同方向, 所以M0c图、T0c图和M图、T图形 状一样
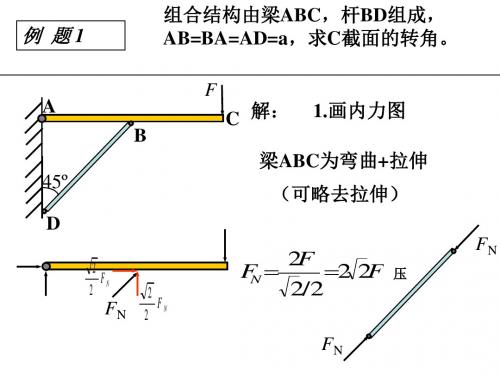
例7:图示开口刚架,EI=const。求沿P力作用线方向的相对 线位移 ΔAB 。
解:
AB2E Pa I38 11 322 12 1
2F
压
画出AC的M图,DB 的轴力图。
F
FN
FN
2 2F
A
F C 2.加单位载荷m0=1,画内力图
B
FN a
1 2/2
2 a
压
45º
D
(M)
2 2
FN
FN
2 2 FN
m0=1
1
画出AC的 M 图,DB 的FN图。
FN
2
FN
a
3.图乘法
(M)
Fa
(FN)
M
2 2F
1
2 2F 2a 2
C
例3:图示梁的抗弯刚度为EI,试求D点的铅垂位移。
vC
3 EI
Pa2 2
2a
3
Pa 3 EI
例 题4
求C处的线位移。
解: 1.画内力图
BC段为弯曲(x 轴为 中性轴)
AB段为弯曲(z 轴为 中性轴)+扭转
y
x z
Al
ql 2 2
(MT)
ql 2
qC l
B
ql 2 2
2.求 cx ,应在C处沿x方向加单位力。
qa A 2
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
例题 5.1
F A A
A
求图所示悬臂梁A端的挠度与转角。
x
B
x
l
y
例题 5.2
求图所示悬臂梁B端的挠度与转角。
B
A
x
l
x
y
例题 5.5
用积分法求图示各梁挠曲线方程时,试问下列各梁 的挠曲线近似微分方程应分几段;将分别出现几个积 分常数,并写出其确定积分常数的边界条件
q
A
B
EI z
C
x
k
l 2
(4)在弯扭组合变形圆截面杆的外边界上,各点的应力状 态都处于平面应力状态。( )
(5)在弯曲与扭转组合变形圆截面杆的外边界上,各点主 应力必然是σ1> σ2 ,σ2=0,σ3<0 。 ( )
(6)在拉伸、弯曲和扭转组合变形圆截面杆的外边界上, 各点主应力必然是σ1 >0, σ2=0, σ3<0 。( )
Me
2
1
d
D
例题 4.6
20 kN
X1
图示外伸梁,,试作剪力图和弯矩图.
10kN m
X2
40 kN m
A
35kN
B
1m
4m
25kN
例题
4.9
作图示梁的内力图
3kN
D
4.5kN m
A
2kN m
B E
C
FA 10kN 1m 2m
2m
FB 2kN 1m
kN
kNm
例题
4.10
4kN m
A
B
96.4 C
l 2
l 2
200 50
z
例题 4.30
q
A
简支梁如图所示,试求梁的最底层纤维的总伸长。
B
h
x
dx
l
b
例题 4.38
若对称弯曲直梁的弯曲刚度EI沿杆轴为 常量,其变形后梁轴_____.
A、 为圆弧线,且长度不变。 B、 为圆弧线,而长度改变。 C、 不为圆弧线,但长度不变。
D、 不为圆弧线,且长度改变。
关于低碳钢试样拉伸至屈服时,有以下结论,请判断哪一个是正确 的: (A)应力和塑性变形很快增加,因而认为材料失效; (B)应力和塑性变形虽然很快增加,但不意味着材料失效; (C)应力不增加,塑性变形很快增加,因而认为材料失效; (D)应力不增加,塑性变形很快增加,但不意味着材料失效。 正确答案是( )
B b e
A
a
c的杆系是由两根圆截面钢杆铰接而成。已知 α=300,杆长L=2m,杆的直径d=25mm,材 料的弹性模量E=2.1×105MPa,设在结点A处悬 挂一重物F=100kN,试求结点A的位移δA。
1 α α 2
B
FNAB FNAC
C
A
A
F
塑性材料冷作硬化后,材料的力学性能发生了变化。试判断以 下结论哪一个是正确的: (A)屈服应力提高,弹性模量降低; (B)屈服应力提高,塑性降低; (C)屈服应力不变,弹性模量不变; (D)屈服应力不变,塑性不变。 正确答案是( )
关于 0.2 有如下四种论述,请判断哪一个是正确的: (A)弹性应变为0.2%时的应力值; (B)总应变为0.2%时的应力值; (C)塑性应变为0.2%时的应力值; (D)塑性应变为0.2时的应力值。 正确答案是( )
低碳钢加载→卸载→ 再加载路径有以下四种,请判断哪一 个是正确的:( ) (A)OAB →BC →COAB ; (B)OAB →BD →DOAB ; (C)OAB →BAO→ODB; (D)OAB →BD →DB。 正确答案是( )
F
0 .5 m
M
试判断下列论述是否正确,正确的在括号内打 “√”,错误的打“×”
(1)杆件发生斜弯曲时,杆变形的总挠度方向一定与中性轴向垂 直。 ( )
(2)若偏心压力位于截面核心的内部,则中性轴穿越杆件 的横截面。 ( )
(3)若压力作用点离截面核心越远,则中性轴离截面越远。 ( )
试判断下列论述是否正确,正确的在括号内打 “√”,错误的打“×”
50
x
100
o
构件中某点为平面应力状态,两斜截面上的应力如图所 示。试用应力圆求主应力和最大切应力
100
50 100
A
200
o
单元体如图示,求三个主应力和最大切应力。
50MPa
80MPa
某点的应力状态如图所示,当σx,σy,σz不变,τx增大时 关于εx值的说法正确的是____.
试判断下列论述是否正确,正确的在括号内打 “√”,错误的打“×”
(7)承受斜弯曲的杆件,其中性轴必然通过横截面的形心, 而且中性轴上正应力必为零。( ) (8)承受偏心拉伸(压缩)的杆件,其中性轴仍然通过横 截面的形心。 ( ) (9)偏心拉压杆件中性轴的位置,取决于梁截面的几何尺 寸和载荷作用点的位置,而与载荷的大小无关。 ( ) (10)拉伸(压缩)与弯曲组合变形和偏心拉伸(压缩)组 合变形的中性轴位置都与载荷的大小无关。 ( )
6kN
2kN m
1m
1m
2m
kN
kNm
例题
4.11
80 kN m
A
160 kN
D E
40kN m
B
40 kN
F
C
310 kN 2m
kN
130 kN
1m 1m
2m
4m
kNm
例题 4.13
F
叠加法作弯矩图
q
B
A
l
例题 4.16
B
L L
求做图示刚架的内力图
C
q
qL/2
A
qL
qL/2
例题 4.19
q
A
L2
B
C
L2
某单元体应力如图所示,其铅垂方向和水平方向各平面 上的应力已知,互相垂直的二斜面ab和bc的外法线分别与x 轴成300和-600角,试求此二斜面ab和bc上的应力。
30MPa
n1
a
3
20MPa
10MPa
b
c
n2
对于图中所示之平面应力状态,若要求面内最大切应力 τmax<85MPa,试求τx的取值范围。图中应力的单位为 MPa。
l 2
y
例题 5.5
用积分法求图示AB梁挠曲线方程, 写出其确定积分 常数的边界条件。
L1
q
A
C EA
x
B
EIZ
L
y
例题 5.6
试用叠加原理求图示弯曲刚度为EIz的简支梁的跨中 截面挠度ωc和梁端截面的转角θAθB.
F
q
B
EI z
A
C
l 2
l 2
2.拉压超静定问题
例题 6.1
一铰接结构如图示,在水平刚性横梁的B端作用有载荷F, 垂直杆1,2的抗拉压刚度分别为E1A1,E2A2,若横梁AB的自重不计,求 两杆中的内力.
铸铁水管冬天结冰时会因冰膨胀而被胀裂, 而管内的冰却不会破坏。这是因为( )。
A.冰的强度较铸铁高; B.冰处于三向受压应力状态; C.冰的温度较铸铁高; D.冰的应力等于零。
若构件内危险点的应力状态为二向等拉,则除 ( )强度理论以外,利用其他三个强度理论得到 的相当应力是相等的。
A.第一; B.第二; C.第三; D.第四;
F
Me
C
B
A
C1 FC 1
FB
例题 6.13
等直梁受载如图所示.若从截面C截开选取基本结 构,则_____.
A. 多余约束力为FC,变形协调条件为ωC=0; B. 多余约束力为FC,变形协调条件为θC=0; C. 多余约束力为MC,变形协调条件为ωC=0; D. 多余约束力为MC,变形协调条件为θC=0;
低碳钢材料在拉伸实验过程中,不发生明显的塑性变形时,承受的最 大应力应当小于的数值,有以下4种答案,请判断哪一个是正确的: (A)比例极限; (B)屈服极限; (C)强度极限; (D)许用应力。 正确答案是( )
根据图示三种材料拉伸时的应力-应变曲线,得出如下四种结论,请判断哪一个是 正确的: (A)强度极限 σb(1)=σb(2)> σb(3); 弹性模量 E(1) > E(2) > E(3); 延伸率 δ(1)> δ(2)> δ(3) ; (B)强度极限 σb(2) > σb(1)> σb(3); 弹性模量 E(2) > E(1) > E(3); 延伸率 δ(1)> δ(2)> δ(3) ; (C)强度极限 σb(3)=σb(1)> σb(2); 弹性模量 E(3) > E(1) > E(2); 延伸率 δ(3)> δ(2)> δ(1) ; (D)强度极限 σb(1)=σb(2)> σb(3); 弹性模量 E(2) > E(1) > E(3); 延伸率 δ(2)> δ(1)> δ(3); 正确答案是( )
图示杆ABC由直杆和半圆组成,试作该杆 的内力图.
B
r
C
F
2r
A
例题 4.22
图示T形截面简支梁在中点承受集中力F=32kN,梁的长度L=2m。T形 截面的形心坐标yc=96.4mm,横截面对于z轴的惯性矩Iz=1.02×108mm4。求 弯矩最大截面上的最大拉应力和最大压应力。 y
F
150 50
A. 不变 B. 增大 C. 减小 D. 无法判定
y
x
z
2000年西安建筑科技大学
图示为某点的应力状态,其最大切应力 τmax=_____MPa.
40MPa
20MPa
2001年长安大学
一受扭圆轴,直径d=20mm,圆轴的材料为 钢,E=200GPa,ν=0.3.现测得圆轴表面上与轴线成450方 向的应变为ε=5.2×10-4,试求圆轴所承受的扭矩.
