简单回归分析计算例
SPSS教程-简单回归分析-案例及结果解释
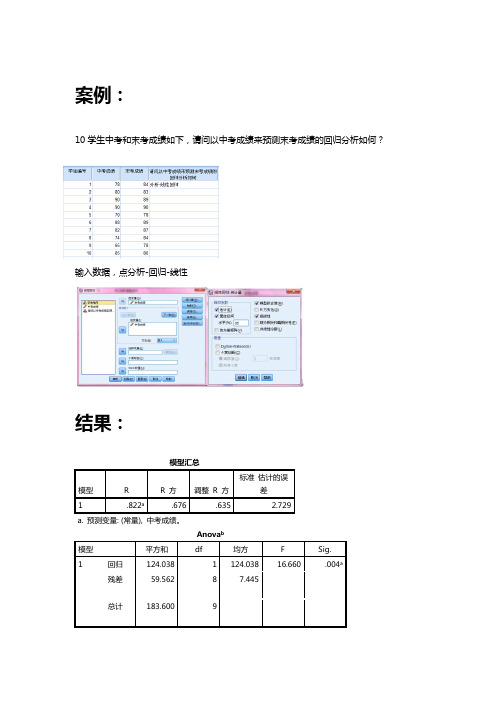
案例：
10学生中考和末考成绩如下，请问以中考成绩来预测末考成绩的回归分析如何？输入数据，点分析-回归-线性
结果：
模型汇总
模型R R 方调整R 方标准估计的误
差
1 .822a.676 .635 2.729
a. 预测变量: (常量), 中考成绩。
Anova b
模型平方和df 均方 F Sig.
1 回归124.038 1 124.038 16.660 .004a
残差59.562 8 7.445
总计183.600 9
R平方的F检验为16.660，达显著水平。
系数估计：个别变量，B，beta及显著性检验。
中考变量beta为0.822，达显著水平。
结果分析：
以中考成绩预测末考成绩，为单一回归分析，由于数学基础相同，简单回归与相关分析的主要结果相同。
Pearson相关系数、Multiple R与Beta皆为0.822，这几个系数的检验值均相同，达显著水平。
R平方则提供回归变异量，显示中考成绩预测末考成绩有63.5%的解释力，F（1，8）=16.66，p=0.004，显示该解释力具有统计上的意义。
系数估计的结果指出，中考成绩能够有效预测末考成绩，beta系数达0.822(t=4.082, p=0.004), 表示中考成绩越高，末考成绩越好。
回归计算公式举例分析
回归计算公式举例分析回归分析是一种统计方法，用于研究变量之间的关系。
它可以帮助我们了解一个或多个自变量对因变量的影响程度，以及它们之间的关联性。
在实际应用中，回归分析被广泛应用于经济学、金融学、社会学、医学等领域，用于预测、解释和控制变量之间的关系。
回归分析的基本公式如下：Y = β0 + β1X1 + β2X2 + ... + βnXn + ε。
其中，Y表示因变量，X1、X2、...、Xn表示自变量，β0表示截距，β1、β2、...、βn表示自变量的系数，ε表示误差项。
下面我们以一个简单的例子来说明回归分析的计算公式。
假设我们想研究一个人的身高（Y）与其父母的身高（X1、X2）之间的关系。
我们收集了100对父母和子女的身高数据，并进行回归分析。
首先，我们需要建立回归方程：Y = β0 + β1X1 + β2X2 + ε。
然后，我们使用最小二乘法来估计回归系数β0、β1、β2。
最小二乘法是一种常用的参数估计方法，它可以最小化误差平方和，找到最优的回归系数。
假设我们得到了如下的回归方程：Y = 60 + 0.5X1 + 0.3X2 + ε。
接下来，我们可以使用这个回归方程来进行预测。
比如，如果一个孩子的父母身高分别为170cm和165cm，那么根据回归方程，这个孩子的身高预测值为：Y = 60 + 0.5170 + 0.3165 = 60 + 85 + 49.5 = 194.5。
这个预测值可以帮助我们了解一个孩子的身高可能在哪个范围内，以及父母的身高对孩子身高的影响程度。
除了预测，回归分析还可以帮助我们了解变量之间的关系。
比如，根据回归系数，我们可以得知父母的身高对孩子的身高有正向影响，而且父亲的身高对孩子的身高影响更大。
此外，回归分析还可以帮助我们检验变量之间的关系是否显著。
通过t检验或F检验，我们可以得知回归系数是否显著不等于0，从而判断变量之间的关系是否存在。
综上所述，回归分析是一种强大的统计方法，可以帮助我们了解变量之间的关系，进行预测和解释。
回归分析案例
年人均收入 (元)x2
1250 1650 1450 1310 1310 1580 1490 1520 1620 1570
回归方程 （模型） 的显著性谁对销售 额的影响 更显著一 点？
人均 消费金额
643 690 713 803 947 1148
解：根据样本相关系数的计算公式有
r n xy x y
2
n x 2 x n y 2 y
2
2
13 9156173.99 12827.5 7457 13 16073323.77 12827.5 13 5226399 7457
回归分析案例
Spss-回归分析
【例10.1】在研究我国人均消费水平的问题中，把全国人均消费额记 为y，把人均国民收入记为x。我们收集到1981～1993年的样本数据(xi ， yi)，i =1,2,…，13，数据见表10-1，计算相关系数。
表10-1 我国人均国民收入与人均消费金额数据
年份
1981 1982 1983 1984 1985 1986 1987
单位:元
人均 国民收入
393.8 419.14 460.86 544.11 668.29 737.73 859.97
人均 消费金额
249 267 289 329 406 451 513
年份
1988 1989 1990 1991 1992 1993
人均 国民收入
1068.8 1169.2 1250.7 1429.5 1725.9 2099.5
712.5734.469
人均消费金额95%的预测区间为678.101元~747.039元之间
到2010年若国民收入到10000元，消费金额会 是多少？置信区间？
logistic回归分析案例
logistic回归分析案例Logistic回归分析案例。
Logistic回归分析是一种常用的统计分析方法，主要用于预测二分类或多分类的结果。
在实际应用中，Logistic回归分析可以帮助我们理解影响某一事件发生的因素，以及对事件发生的概率进行预测。
本文将通过一个实际的案例来介绍Logistic回归分析的应用。
案例背景。
假设我们是一家电商公司的数据分析师，现在我们需要分析用户的购买行为，并预测用户是否会购买某一产品。
我们收集了一些用户的个人信息和他们最近一次购买的产品，希望通过这些数据来预测用户是否会购买新产品。
数据准备。
首先，我们需要收集用户的个人信息和购买行为数据。
个人信息包括年龄、性别、职业等；购买行为数据包括购买的产品类型、购买时间等。
在收集完数据后，我们需要对数据进行清洗和预处理，包括缺失值处理、异常值处理等。
模型建立。
在数据准备完成后，我们可以开始建立Logistic回归模型。
首先，我们需要将数据划分为训练集和测试集，以便对模型进行验证。
然后，我们可以利用训练集来拟合Logistic回归模型，并利用测试集来评估模型的预测效果。
模型评估。
在模型建立完成后，我们需要对模型进行评估。
常用的评估指标包括准确率、精确率、召回率等。
这些指标可以帮助我们判断模型的预测效果，并对模型进行调优。
模型应用。
最后，我们可以利用建立好的Logistic回归模型来预测用户是否会购买新产品。
通过输入用户的个人信息和购买行为数据，模型可以给出用户购买新产品的概率，从而帮助我们进行精准营销和推广。
结论。
通过以上实例，我们可以看到Logistic回归分析在预测用户购买行为方面具有很好的应用价值。
通过收集用户数据、建立模型、评估模型和应用模型，我们可以更好地理解用户行为，并做出更精准的预测和决策。
总结。
Logistic回归分析是一种强大的统计工具，可以帮助我们预测二分类或多分类的结果。
在实际应用中，我们可以根据具体情况收集数据、建立模型，并利用模型进行预测和决策。
回归经典案例
回归经典案例
回归分析是一种统计学方法，用于研究变量之间的关系。
以下是一个经典的回归分析案例：
假设我们有一个数据集，其中包含一个人的身高（height）和体重（weight）信息。
我们想要研究身高和体重之间的关系，以便预测一个人
的体重。
1. 首先，我们使用散点图来可视化身高和体重之间的关系。
从散点图中可以看出，身高和体重之间存在一定的正相关关系，即随着身高的增加，体重也会增加。
2. 接下来，我们使用线性回归模型来拟合数据。
线性回归模型假设身高和体重之间的关系可以用一条直线来表示，即 y = ax + b。
其中，y 是体重，x 是身高，a 和 b 是模型参数。
3. 我们使用最小二乘法来估计模型参数 a 和 b。
最小二乘法是一种优化方法，它通过最小化预测值与实际值之间的平方误差来估计模型参数。
4. 拟合模型后，我们可以使用回归方程来预测一个人的体重。
例如，如果我们知道一个人的身高为米，我们可以使用回归方程来计算他的体重。
5. 最后，我们可以使用残差图来检查模型的拟合效果。
残差图显示了实际值与预测值之间的差异。
如果模型拟合得好，那么残差应该随机分布在零周围。
这个案例是一个简单的线性回归分析案例。
在实际应用中，回归分析可以应用于更复杂的问题，例如预测股票价格、预测疾病发病率等。
回归分析数据案例
回归分析数据案例回归分析是一种用来研究变量之间关系的统计方法，在实际情况中有很多可以应用回归分析的案例。
下面以一个销售数据案例为例，详细介绍回归分析的应用。
某电商公司想要分析广告费用与销售额之间的关系，以便确定是否需要增加广告投入来提高销售额。
公司收集了一年的数据，包括每月的广告费用和销售额。
公司使用回归分析来研究广告费用和销售额之间的关系。
首先，需要确定自变量和因变量。
在这个案例中，广告费用是自变量，销售额是因变量。
然后，利用回归模型拟合数据，得到回归方程。
假设回归方程为：销售额= β0+ β1 * 广告费用其中，β0 是截距，表示在广告费用为 0 时的销售额；β1 是斜率，表示每单位广告费用对销售额的影响。
通过计算回归方程的参数，可以得到具体的值。
接下来，用实际数据计算回归方程的参数。
假设公司收集了一年的数据，总共 12 个月的广告费用和销售额。
通过回归分析软件，可以计算得到β0 和β1 的估计值。
假设计算结果为β0= 1000，表示当广告费用为 0 时，销售额约为 1000；β1 = 2，表示每多投入 1 单位的广告费用，销售额约增加 2。
通过计算回归方程的参数，可以预测未来的销售额。
假设公司计划增加下个月的广告费用为 5000，可以利用回归方程计算出销售额的预测值。
根据回归方程：销售额 = 1000 + 2 * 5000 = 11000预测出下个月的销售额为 11000。
公司还可以利用回归方程来评估广告费用对销售额的影响。
根据回归方程的斜率β1，可以计算出每单位广告费用对销售额的影响。
在这个案例中，β1=2，说明每多投入 1 单位的广告费用，销售额平均增加 2。
通过回归分析，公司可以了解广告费用和销售额之间的关系，判断是否需要增加广告投入来提高销售额。
如果回归方程的斜率显著大于 0，说明广告费用对销售额有显著的正向影响，公司可以考虑增加广告投入。
如果回归方程的斜率接近 0 或者小于 0，说明广告费用对销售额的影响较小或者负面，公司就需要重新评估广告策略。
回归分析方法及其应用中的例子
3.1.2 虚拟变量的应用例3.1.2.1：为研究美国住房面积的需求，选用3120户家庭为建模样本，回归模型为：123log log P Y βββ++logQ=其中：Q ——3120个样本家庭的年住房面积（平方英尺） 横截面数据P ——家庭所在地的住房单位价格 Y ——家庭收入经计算：0.247log 0.96log P Y -+logy=4.17 20.371R =（）（） （）上式中2β=0.247-的价格弹性系数，3β=0.96的收入弹性系数，均符合经济学的常识，即价格上升，住房需求下降，收入上升，住房需求也上升。
但白人家庭与黑人家庭对住房的需求量是不一样的，引进虚拟变量D ：01i D ⎧=⎨⎩黑人家庭白人家庭或其他家庭模型为：112233log log log log D P D P Y D Y βαβαβα+++++logQ=例3.1.2.2：某省农业生产资料购买力和农民货币收入数据如下：（单位：十亿元）①根据上述数据建立一元线性回归方程：ˆ 1.01610.09357yx =+ 20.8821R = 0.2531y S = 67.3266F = ②带虚拟变量的回归模型，因1979年中国农村政策发生重大变化，引入虚拟变量来反映农村政策的变化。
01i D ⎧=⎨⎩19791979i i <≥年年 建立回归方程为： ˆ0.98550.06920.4945yx D =++ （）（） （）20.9498R = 0.1751y S = 75.6895F =虽然上述两个模型都可通过显着性水平检验，但可明显看出带虚拟变量的回归模型其方差解释系数更高，回归的估计误差（y S ）更小，说明模型的拟合程度更高，代表性更好。
3.5.4 岭回归的举例说明企业为用户提供的服务多种多样，那么在这些服务中哪些因素更为重要，各因素之间的重要性差异到底有多大，这些都是满意度研究需要首先解决的问题。
国际上比较流行并被实践所验证，比较科学的方法就是利用回归分析确定客户对不同服务因素的需求程度，具体方法如下：假设某电信运营商的服务界面包括了A1……Am 共M 个界面，那么各界面对总体服务满意度A 的影响可以通过以A 为因变量，以A1……Am 为自变量的回归分析，得出不同界面服务对总体A 的影响系数，从而确定各服务界面对A 的影响大小。
线性回归分析经典例题
1. “团购”已经渗透到我们每个人的生活，这离不开快递行业的发展，下表是2013-2017年全国快递业务量（x 亿件：精确到0.1）及其增长速度（y %）的数据（Ⅰ）试计算2012年的快递业务量；（Ⅱ）分别将2013年，2014年，…，2017年记成年的序号t ：1，2，3，4，5；现已知y 与t 具有线性相关关系，试建立y 关于t 的回归直线方程a x b yˆˆˆ+=； （Ⅲ）根据（Ⅱ）问中所建立的回归直线方程，估算2019年的快递业务量附：回归直线的斜率和截距地最小二乘法估计公式分别为：∑∑==--=ni ini ii x n xy x n yx b1221ˆ， x b y aˆˆ-=2.某水果种植户对某种水果进行网上销售，为了合理定价，现将该水果按事先拟定的价格进行试销，得到如下数据：单价元 7 8 9 11 12 13 销量120118112110108104已知销量与单价之间存在线性相关关系求y 关于x 的线性回归方程； 若在表格中的6种单价中任选3种单价作进一步分析，求销量恰在区间内的单价种数的分布列和期望．附：回归直线的斜率和截距的最小二乘法估计公式分别为：， ．3. (2018年全国二卷)下图是某地区2000年至2016年环境基础设施投资额y （单位：亿元）的折线图．为了预测该地区2018年的环境基础设施投资额，建立了y 与时间变量t 的两个线性回归模型．根据2000年至2016年的数据（时间变量t 的值依次为1217，，…，）建立模型①：ˆ30.413.5y t =-+；根据2010年至2016年的数据（时间变量t 的值依次为127，，…，）建立模型②：ˆ9917.5y t =+． （1）分别利用这两个模型，求该地区2018年的环境基础设施投资额的预测值； （2）你认为用哪个模型得到的预测值更可靠？并说明理由．4.(2014年全国二卷) 某地区2007年至2013年农村居民家庭纯收入y （单位：千元）的数据如下表：年份 2007 2008 2009 2010 2011 2012 2013 年份代号t 1 2 3 4 5 6 7 人均纯收入y 2.93.33.64.44.85.25.9（Ⅰ）求y 关于t 的线性回归方程；（Ⅱ）利用（Ⅰ）中的回归方程，分析2007年至2013年该地区农村居民家庭人均纯收入的变化情况，并预测该地区2015年农村居民家庭人均纯收入.附：回归直线的斜率和截距的最小二乘法估计公式分别为：()()()121niii ni i t t y y b t t ∧==--=-∑∑，ˆˆay bt =-5（2019 2卷）18．11分制乒乓球比赛，每赢一球得1分，当某局打成10∶10平后，每球交换发球权，先多得2分的一方获胜，该局比赛结束．甲、乙两位同学进行单打比赛，假设甲发球时甲得分的概率为0.5，乙发球时甲得分的概率为0.4，各球的结果相互独立．在某局双方10∶10平后，甲先发球，两人又打了X 个球该局比赛结束．(1)求P(X＝2)；(2)求事件“X＝4且甲获胜”的概率．。
回归分析实验案例数据1
实验课程案例数据1香烟消费数据：一个国家保险组织想要研究在美国所有50个州和哥伦比亚特区的香烟消费模式，表1给出了研究中所选的变量，表2给出了1970年的数据。
讨论下列问题：表1. 香烟消费数据的变量表2. 香烟消费数据（1970年）州年龄HS 收入黑人比例女性比例价格销量AL2741.3294826.251.742.789.8AK22.966.74644345.741.8121.3AZ26.358.13665350.838.5115.2AR29.139.9287818.351.538.8100.3CA28.162.64493750.839.7123CO26.263.93855350.731.1124.8CT29.1564917651.545.5120DE26.854.6452414.351.341.3155DC28.455.2507971.153.532.6200.4FL32.352.6373815.351.843.8123.6GA25.940.6335425.951.435.8109.9HI2561.9462314836.782.1ID26.459.532900.350.133.6102.4IL28.652.6450712.851.541.4124.8IN27.252.93772 6.951.332.2134.6IO28.8593751 1.251.438.5108.5KA28.759.93853 4.85138.9114KY27.538.531127.250.930.1155.8LA24.842.2309029.851.439.3115.9ME2854.733020.351.338.8128.5MD27.152.3430917.851.134.2123.5MA2958.54340 3.152.241124.3MI26.352.8418011.25139.2128.6MN26.857.638590.95140.1104.3MS25.141262636.851.637.593.4MO29.448.8378110.351.836.8121.3MT27.159.235000.35034.7111.2NB28.659.33789 2.751.234.7108.1NV27.865.24563 5.749.344189.5NH2857.637370.351.134.1265.7NJ30.152.5470110.851.641.7120.7NM23.955.23077 1.950.741.790NY30.352.7471211.952.241.7119NC26.538.5325222.25129.4172.4ND26.450.330860.449.538.993.8OH27.753.240209.151.538.1121.6OK29.451.63387 6.751.339.8108.4OR29603719 1.35129157PA30.750.2397185244.7107.3RI29.246.43959 2.750.940.2123.9SC24.837.8299030.550.934.3103.6SD27.453.331230.350.338.592.7TN28.141.8311915.851.641.699.8TX26.447.4360612.55142106.4UT23.167.332270.650.636.665.5VT26.857.134680.251.139.5122.6V A26.847.8371218.550.630.2124.3WA27.563.54053 2.150.340.396.7WV3041.63061 3.951.641.6114.5WI27.254.53812 2.950.940.2106.4WY27.262.938150.85034.4132.2(1)在销量关于6个自变量的回归模型中，检验假设“不需要女性比例这一变量”；(2)在上面的模型中，检验假设“不需要女性比例和HS这两个变量”；(3)计算收入变量回归系数的95%的置信区间；(4)去掉收入这个变量后拟合回归方程，其他变量对于销量的解释比例是多少？(5)用价格、年龄和收入作自变量拟合模型，它们对销量的解释比例是多少？(6)仅用收入作自变量拟合模型，它们对销量的解释比例是多少？(7)(8)【本文档内容可以自由复制内容或自由编辑修改内容期待你的好评和关注，我们将会做得更好】(9)(10)。
回归计算公式举例说明
回归计算公式举例说明回归分析是统计学中常用的一种分析方法，用于研究变量之间的关系。
回归分析可以帮助我们了解自变量和因变量之间的关系，并用于预测未来的结果。
在回归分析中，有许多不同的公式和方法，其中最常见的是简单线性回归和多元线性回归。
本文将以回归计算公式举例说明为标题，介绍简单线性回归和多元线性回归的计算公式，并通过具体的例子来说明其应用。
简单线性回归。
简单线性回归是回归分析中最基本的形式，用于研究一个自变量和一个因变量之间的关系。
其数学模型可以表示为：Y = β0 + β1X + ε。
其中，Y表示因变量，X表示自变量，β0和β1分别表示回归方程的截距和斜率，ε表示误差项。
简单线性回归的目标是通过最小化误差项来估计回归方程的参数β0和β1。
为了说明简单线性回归的计算公式，我们假设有一组数据，其中自变量X的取值为{1, 2, 3, 4, 5}，对应的因变量Y的取值为{2, 4, 5, 4, 5}。
我们可以通过最小二乘法来估计回归方程的参数β0和β1。
首先，我们需要计算自变量X和因变量Y的均值，分别记为X和Ȳ。
然后，我们可以计算回归方程的斜率β1和截距β0：β1 = Σ((Xi X)(Yi Ȳ)) / Σ((Xi X)²)。
β0 = Ȳβ1X。
其中，Σ表示求和符号，Xi和Yi分别表示第i个观测数据的自变量和因变量取值。
在我们的例子中，自变量X的均值为3，因变量Y的均值为4。
根据上面的公式，我们可以计算得到回归方程的斜率β1为0.6，截距β0为2。
因此，简单线性回归的回归方程可以表示为：Y = 2 + 0.6X。
通过这个回归方程，我们可以预测自变量X取不同值时对应的因变量Y的取值。
例如，当X取值为6时，根据回归方程可以预测Y的取值为6.6。
多元线性回归。
多元线性回归是回归分析中更复杂的形式，用于研究多个自变量和一个因变量之间的关系。
其数学模型可以表示为：Y = β0 + β1X1 + β2X2 + ... + βnXn + ε。
回归分析计算程序及检验
《实用回归分析》方开泰等，P58，例2.5例2.5 某病虫测报站为了能较准确地预报第三代棉铃虫的产卵期，以便能适时采取杀虫措施，保证棉花现根据这些数据建立预报方程。
首先画散点图（图2.9）。
从图看出y与x之间有线性关系。
年序6月份平均气温x（℃）7月份卵见期y（日）经计算得12023.9x平均=23.33，y平均=20.7821424.6Lxx=4.44，Lyy=171.56，Lxy=-23 31824.1由此得42722.7b=Lxy/Lxx=-23.433/4.44=-5.28 52622.3a=y平均-bx平均=20.78-(-5.28)* 61823.1回归方程为72422.9y=143.96-5.28x81623.5又计算得92422.9S回=123.726S残=47.834F=S回/S残(-)=18.107因为临界值F0.01(1,7)=12.25，所最后，求预测区间(α=5%）当x=x0时，y的预测区间为[y0-△这里y0=143.96-5.28x0验算y x2023.9n91424.6平均值23.3333320.777781824.1Lxx 4.442722.7Lxy-23.43332622.3Lyy171.55561823.1b-5.277782422.9a143.92591623.5回归方程y=143.93-5.28x2422.9r-0.84906S总171.5556S回123.6759S残47.87963F检验18.08142十分显著F0.05 5.591448F0.0112.24638σ 2.615329回归分析程序如下（双击后不是乱码）：' 回归分析C u r R o w = A c t i v e C e l l .R o w () ' 当前行号C u r C o l = A c t i v e C e l l .C o l u m n () ' 当前列号 c o l _x = C u r C o l - 2: c o l _y = C u r C o l - 3 ' 回归分析数据所在列 c o l _r e s = C u r C o l ' 分析结果所在列E l s e I f (F > F 001) T h e nF T e s t _R e s u l t = "十分显著" E n d I f ' 不同置信区间的预测范围 S i g m a _h a t 2 = S S E / (n - 2) S i g m a _h a t = S q r (S S E / (n - 2)) i m e t h o d = 2 ' 由于数据不多，使用n 不大情况下的算法 I f (i m e t h o d = 1) T h e n F o r i = 1 T o n ' 这种算法用于n 较大，x 0接近x _a v g 的情况 y _005(i , 1) = y _h a t (i ) - 2 * S i g m a _h a t y _005(i , 2) = y _h a t (i ) + 2 * S i g m a _h a t y _001(i , 1) = y _h a t (i ) - 3 * S i g m a _h a t y _001(i , 2) = y _h a t (i ) + 3 * S i g m a _h a t N e x t E l s e F o r i = 1 T o n ' 这是一种算法，用于n 不大的情况 S i g m a _h a t _y 02 = S i g m a _h a t 2 * (1 + 1 / n + (x (i ) - x _a v g ) ^ 2 / L x x ) D e l t a _005 = S q r (F 005 * S i g m a _h a t _y 02) D e l t a _001 = S q r (F 001 * S i g m a _h a t _y 02) y _005(i , 1) = y _h a t (i ) - D e l t a _005 ' 2 * S i g m a _h a t _y 0 y _005(i , 2) = y _h a t (i ) + D e l t a _005 ' 2 * S i g m a _h a t _y 0 y _001(i , 1) = y _h a t (i ) - D e l t a _001 ' 3 * S i g m a _h a t _y 0 y _001(i , 2) = y _h a t (i ) + D e l t a _001 ' 3 * S i g m a _h a t _y 0 N e x t E n d I f ' ---------------------输出到e x c e l 中 c o l _s t a t = C u r C o l i = 1 C e l l s (C u r R o w + i , c o l _s t a t - 1) = "平均值": C e l l s (C u r R o w + i , c o l _s t a t ) = x _a v g : C e l l s (C u r R o w + i , c o l _s t a t + 1) = y _a v g : i = i + 1 C e l l s (C u r R o w + i , c o l _s t a t - 1) = "L x x ": C e l l s (C u r R o w + i , c o l _s t a t ) = L x x : i = i + 1 C e l l s (C u r R o w + i , c o l _s t a t - 1) = "L x y ": C e l l s (C u r R o w + i , c o l _s t a t ) = L x y : i = i + 1 C e l l s (C u r R o w + i , c o l _s t a t - 1) = "L y y ": C e l l s (C u r R o w + i , c o l _s t a t ) = L y y : i = i + 1措施，保证棉花丰收，他们统计了近9年的当地6月份平均气温和7月份卵见期数据如表2.7..33，y平均=20.78，Lyy=171.56，Lxy=-23.433x=-23.433/4.44=-5.28bx平均=20.78-(-5.28)*23.33=143.96残(-)=18.107值F0.01(1,7)=12.25，所以回归方程高度显著。
典型例题：线性回归方程
认识线性回归方程一、线性回归方程设X与y是具有相关关系的两个变量，且相应于n个观测值的n个点大致分布在一条直线的附近，这条直线就叫做回归直线.例1.假设关于某设备的使用年限x （年）和所支出的维修费用y （万元）有如下的统计资料：若由资料知y对x呈线性相关关系，试求：（1）线性回归方程y = a+bxi（2）估计使用年限10年时，维修费用是多少？分析：因为y对x呈线性相关关系，所以可以用线性相关的方法解决问题.解：（1）制表于是有& = • =].23,。
=亍一庚= 5 — 1.23x4 = 0.08.90-5x42・•・线性回归方程为y = 1.23X+0.08 ；（2）当x = 10时，『 = 1.23x10+0.08 = 12.38 （万元）,即估计使用10年时1 / 3维修费用约是12.38万元.评注：已知y对x呈线性相关关系，无须进行相关性检验，否则应首先进行相关性检验.二、回归分析通过对有关数据的分析，作出散点图，并利用散点图直观地认识两个变量的 相关关系，也可以用相关系数r 来确定两个变量的线性相关关系.例2. —个车间为了规定工时定额，需要确定加工零件所花费的时间，为此 进行了 10次试验，测得的数据如下：零件数X （个） 10 2030 40 5060708090100加工时间y （分）62 68 75 81 89 95 102 108 115 122（1） y 与X 是否具有线性相关关系？（2） 如果y 与x 具有线性相关关系，求回归直线方程.分析：先求出r 的值，I"的值越接近于1,表明两个变量的线性相关关系越 强.解：（1）列岀下表，并用科学计算器进行计算.■11 2 3 4 5 6 7 8 9 10 xi10 20 30 40 50 60 70 80 90 100 开626875818995102108115122620 1360 2250 3240 4450 5700 71408640 10350 12200 10x = 55, y = 91.7,r-l10= 38500,=87777,/-I10工尤必=55950r-l55950-10x55x91.77(38500 -10 x 552)(87777 -10 x 91.72)•••0.9998>0・632,「.y 与x 具有线性相关关系;（2）设所求的回归直线方程为y 从，« 0.9998 o工心-10厂/-Ia = y-bx = 9\.7-0.668x55 a54.96 ,•••所求的回归直线方程为,y = 0.668x+54.96 •评注：这类问题的解决方法一般分为两步，第一步分析两个变量是否有线性 相关关系，第二步求回归直线方程.那么山上表可知 d55950-10x55x91.738500-I0x552~* 0.668,10D )l-10xy)0 _ jOx /-I。
回归分析举例
回归分析举例回归分析是一种预测性的建模技术，它研究的是因变量（目标）和自变量（预测器）之间的关系。
这种技术通常用于预测分析，时间序列模型以及发现变量之间的因果关系。
例如，司机的鲁莽驾驶与道路交通事故数量之间的关系，最好的研究方法就是回归。
回归分析是建模和分析数据的重要工具。
在这里，我们使用曲线/线来拟合这些数据点，在这种方式下，从曲线或线到数据点的距离差异最小。
我会在接下来的部分详细解释这一点。
我们为什么使用回归分析？如上所述，回归分析估计了两个或多个变量之间的关系。
下面，让我们举一个简单的例子来理解它：比如说，在当前的经济条件下，你要估计一家公司的销售额增长情况。
现在，你有公司最新的数据，这些数据显示出销售额增长大约是经济增长的2.5倍。
那么使用回归分析，我们就可以根据当前和过去的信息来预测未来公司的销售情况。
使用回归分析的好处良多。
具体如下：1.它表明自变量和因变量之间的显著关系；2.它表明多个自变量对一个因变量的影响强度。
回归分析也允许我们去比较那些衡量不同尺度的变量之间的相互影响，如价格变动与促销活动数量之间联系。
这些有利于帮助市场研究人员，数据分析人员以及数据科学家排除并估计出一组最佳的变量，用来构建预测模型。
我们有多少种回归技术？有各种各样的回归技术用于预测。
这些技术主要有三个度量（自变量的个数，因变量的类型以及回归线的形状）。
我们将在下面的部分详细讨论它们。
对于那些有创意的人，如果你觉得有必要使用上面这些参数的一个组合，你甚至可以创造出一个没有被使用过的回归模型。
但在你开始之前，先了解如下最常用的回归方法：1.Linear Regression线性回归它是最为人熟知的建模技术之一。
线性回归通常是人们在学习预测模型时首选的技术之一。
在这种技术中，因变量是连续的，自变量可以是连续的也可以是离散的，回归线的性质是线性的。
线性回归使用最佳的拟合直线（也就是回归线）在因变量（Y）和一个或多个自变量（X）之间建立一种关系。
Stata软件之回归分析
0
10
20
30
5
10 years of education Fitted values
15
20
hourly wage
三、简单回归分析的Stata软件操作实例
7、wage对edu的OLS回归，只使用年龄小于或等于30岁的样 本。命令如下： reg wage edu if age<=30 得到以下运行结果，保存该运行结果；
Variable age edu exp expsq wage lnwage Obs 1225 1225 1225 1225 1225 1225 Mean 36.79755 8.992653 21.8049 613.9776 7.1255 1.808352 Std. Dev. 10.67631 2.719068 11.77443 548.3072 4.766828 .5307399 Min 16 0 0 0 1.25 .2231435 Max 60 19 50 2500 37.5 3.624341
计量经济软件应用
——Stata软件实验之一元、 多元回归分析
内容概要
一、实验目的 二、简单回归分析的Stata基本命令 三、简单回归分析的Stata软件操作实例 四、多元回归分析的Stata基本命令 五、多元回归分析的Stata软件操作实例
一、实验目的：
掌握运用Stata软件进行简单回归分析以及 多元回归分析的操作方法和步骤，并能看懂 Stata软件运行结果。
三、简单回归分析的Stata软件操作实例
1、打开数据文件。直接双击“工资方程1.dta”文件；或者点 击Stata窗口工具栏最左侧的Open键，然后选择“工资方程 1.dta”即可；或者先复制Excel表S-2中的数据，再点击Stata 窗口工具栏右起第4个Data Editor键，将数据粘贴到打开的 数据编辑窗口中，然后关闭该数据编辑窗口，点击工具栏左 起第二个Save键保存数据，保存时需要给数据文件命名。 2、给出数据的简要描述。使用describe命令，简写为： des 得到以下运行结果；
统计学案例——相关回归分析
《统计学》案例——相关回归分析案例一质量控制中的简单线性回归分析1、问题的提出某石油炼厂的催化装置通过高温及催化剂对原料的作用进行反应，生成各种产品，其中液化气用途广泛、易于储存运输，所以，提高液化气收率，降低不凝气体产量，成为提高经济效益的关键问题。
通过因果分析图和排列图的观察，发现回流温度是影响液化气收率的主要原因，因此，只有确定二者之间的相关关系，寻找适当的回流温度，才能达到提高液化气收率的目的。
经认真分析仔细研究，确定了在保持原有轻油收率的前提下，液化气收率比去年同期增长1个百分点的目标，即达到12.24%的液化气收率。
2、数据的收集序号回流温度（℃）液化气收率（%）序号回流温度（℃）液化气收率（%）1 2 3 4 5 6 7 8 9 10 11 12 13 14 1536 39 43 43 39 38 43 44 37 40 34 39 40 41 4413.1 12.8 11.3 11.4 12.3 12.5 11.1 10.8 13.1 11.9 13.6 12.2 12.2 11.8 11.116 17 18 19 20 21 22 23 24 25 26 27 28 29 3042 43 46 44 42 41 45 40 46 47 45 38 39 44 4512.3 11.9 10.9 10.4 11.5 12.5 11.1 11.1 11.1 10.8 10.5 12.1 12.5 11.5 10.9目标值确定之后，我们收集了某年某季度的回流温度和液化气收率的30组数据（如上表），进行简单直线回归分析。
3.方法的确立设线性回归模型为εββ++=x y 10，估计回归方程为x b b y10ˆ+= 将数据输入计算机，输出散点图可见，液化气收率y 具有随着回流温度x 的提高而降低的趋势。
因此，建立描述y 和x 之间关系的模型时，首选直线型是合理的。
从线性回归的计算结果，可以知道回归系数的最小二乘估计值b 0=21.263和b 1=-0.229，于是最小二乘直线为x y229.0263.21ˆ-= 这就表明，回流温度每增加1℃，估计液化气收率将减少0.229%。
简单回归系数
简单回归系数
简单回归系数是一种用于描述自变量和因变量之间线性关系的统计指标。
在简单线性回归模型中，自变量$x$和因变量$y$之间的关系可以表示为$y=a+bx$，其中$a$是截距，$b$是回归系数。
回归系数$b$表示自变量$x$每增加一个单位时，因变量$y$的平均变化量。
具体来说，如果回归系数为正数，则表示当自变量增加时，因变量也会增加；如果回归系数为负数，则表示当自变量增加时，因变量会减少；如果回归系数为零，则表示自变量和因变量之间没有线性关系。
简单回归系数的计算通常基于最小二乘法，通过最小化残差平方和来确定回归系数的值。
具体计算公式为：
$b=\frac{\sum_{i=1}^{n}(x_i-x_0)(y_i-y_0)}{\sum_{i=1}^{n}(x_i-x_0)^2}$
其中，$x_i$和$y_i$分别表示第$i$个观测值的自变量和因变量的值，$x_0$和$y_0$分别表示自变量和因变量的平均值。
简单回归系数在统计分析和数据建模中具有重要的应用。
它可以用于预测和解释自变量和因变量之间的关系，评估变量的重要性，以及进行假设检验和推断。
通过了解回归系数的大小和正负，可以帮助我们更好地理解自变量对因变量的影响程度，并做出相应的决策和预测。
简单线性回归分析
实验报告1日期姓名班级一简单线性回归分析题目：设公司的每周广告费支出和每周销售额数据如下图所示：要求：（1）广告费与消费额之间是否存在显著的相关关系？（2）计算回归模型参数。
（3）回归模型能解释销售额变动的比例有多大？（4）计算D-W的统计量。
（5）如下周的广告费支出为6700元，试预测下周的消费额（取置信区间a=0.05）步骤：一在excel里输入数据：每周广告费每周消费额4100 12.505400 13.806300 14.255400 14.254800 14.504600 13.006200 14.006100 15.006400 15.757100 16.50根据上表数据画出散点图由图可知，所有点几乎在同一条直线上，由插入趋势线后的散点图可知，每周销售额和每周广告费间的函数关系为：y=0.0011x+8.3039 ;本例中R 2值为0.719，表明销售额的变动中有71.9%可用广告费通过线性回归模型加以解释，剩余的28.1%则由其余因素引起，两个变量间的线性关系显著，可以进行下一步的回归分析。
二 回归分析(1)斜率计算公式为∑∑∑∑∑--=∧22)(x n y x xy n b x ，在H1中输入n ，在K2输入斜率b ，在L2中输入n 截距公式=(10*D12-B12*C12)/(10*E12-(B12)*(B12))；(2) 截距计算公式为 nx b n y a ∑∑∧∧-=，在K3输入截距a ，在L3输入公式=(C12/10-I2*B12/10);(3)y 的估计值为x b a y ∧∧∧+=，在F2输入公式=$L$3+$L $2*B2，并往下复制到F11处(4)检验线性关系的显著性可决系数222)(/)(1∑∑-∧---=y y y y R i i i ,在L4输入公式=1-SUMXMY2(C2:C11,F2:F11)/DEVSQ(C2:C11)；可得719039.02=R ，在L5中输入=soqr （L4），可得相关系数R=0.847962。
回归系数的标准误计算
回归系数的标准误计算回归系数的标准误是用来衡量回归系数估计值的稳定性和精确度的重要指标。
在进行回归分析时，除了关注回归系数的估计值外，我们还需要考虑其估计的精确程度，即标准误。
本文将介绍回归系数的标准误的计算方法，希望能对您有所帮助。
回归系数的标准误计算公式为：SE(β) = √(σ² / ∑(xᵢx)²)。
其中，SE(β)表示回归系数的标准误，σ²表示误差方差，xᵢ表示自变量的取值，x表示自变量的均值。
在进行回归分析时，我们通常会使用统计软件进行计算，但了解标准误的计算方法仍然是非常重要的。
下面我们将通过一个简单的示例来说明回归系数的标准误的计算过程。
假设我们有以下线性回归模型：Y = β₀ + β₁X₁ + β₂X₂ + ε。
其中，Y表示因变量，X₁和X₂表示自变量，β₀、β₁、β₂分别为截距和回归系数，ε为误差。
首先，我们需要利用最小二乘法对回归系数进行估计。
然后，我们可以计算回归系数的标准误。
假设我们已经得到了回归系数的估计值为β̂₀、β̂₁、β̂₂，以及误差方差的估计值σ̂²。
接下来，我们可以利用上述公式来计算回归系数的标准误。
首先，我们需要计算自变量的均值x，然后计算每个观测值与均值的差值，并求平方和。
最后，将误差方差除以自变量的平方和，再开平方即可得到回归系数的标准误。
在实际应用中，我们通常会利用统计软件进行回归分析，软件会自动给出回归系数的标准误。
但了解标准误的计算方法仍然是非常有益的，可以帮助我们更好地理解回归分析的结果。
总结一下，回归系数的标准误是衡量回归系数估计值的稳定性和精确度的重要指标。
在进行回归分析时，除了关注回归系数的估计值外，我们还需要考虑其估计的精确程度，即标准误。
通过本文的介绍，希望能够帮助您更好地理解回归系数的标准误的计算方法。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
【例9-3】-【例9-8】简单回归分析计算举例
利用例9-1的表9-1中已给出我国历年城镇居民人均消费支出和人均可支配收入的数据，（1）估计我国城镇居民的边际消费倾向和基础消费水平。
（2）计算我国城镇居民消费函数的总体方差Ｓ2和回归估计标准差Ｓ。
（3）对我国城镇居民边际消费倾向进行置信度为95％的区间估计。
（4）计算样本回归方程的决定系数。
（5）以５％的显著水平检验可支配收入是否对消费支出有显著影响；对Ｈo：β2＝0.7，Ｈ1：β2＜０.7进行检验。
（6）假定已知某居民家庭的年人均可支配收入为8千元，要求利用例9-3中拟合的样本回归方程与有关数据，计算该居民家庭置信度为95％的年人均消费支出的预测区间。
解：
（1）教材中的【例9-3】
Ｙt＝β1＋β2Ｘt＋u t
将表9-1中合计栏的有关数据代入（9.19）和（9.20）式，可
得：
＝＝0.6724
＝97.228÷14-0.6724×129.009÷14＝0. 7489
样本回归方程为：
＝0.7489＋0.6724Ｘt
上式中：0.6724是边际消费倾向，表示人均可支配收入每增加1千元，人均消费支出会增加0.6724千元；0.7489是基本消费水平，即与收入无关最基本的人均消费为0.7489千元。
（2）教材中的【例9-4】
将例9-1中给出的有关数据和以上得到的回归系数估计值代入
（9.23）式，得：
＝771.9598－0.7489×97.228－0. 6724×1039.683＝0.0808
将以上结果代入（9.21）式，可得：
Ｓ2＝0.0808／(14-2)＝0.006732
进而有：Ｓ＝＝0.082047
（3）教材中的【例9-5】 将前面已求得的有关数据代入（9.34）式，可得：
＝0.082047÷=0.0056
查ｔ分布表可知：显著水平为５％，自由度为12的ｔ分布双侧临
界值是2.1788，前面已求得，将其代入（9.32）式，可得：即：
（4）教材中的【例9-6】
ｒ2＝1 - ＝ 1- ＝0.9992
上式中的ＳＳＴ是利用表9-1中给出的数据按下式计算的：
ＳＳＴ＝∑－（∑Ｙt）2／ｎ
＝771.9598－（97.228）2÷14＝96.7252
（5）教材中的【例9-7】
首先,检验收入对消费支出是否有显著影响，提出假设 Ｈo：β2＝０，Ｈ1：β2≠０。
利用（9.40）式计算ｔ值
＝0. 0.6724/0.0056＝119.82
查ｔ分布表可知：显著水平为５％，自由度为12的双侧ｔ检验的临界值是2.178。
以上计算的ｔ值远远大于此临界值,所以拒绝原假设,接受备择假设，即认为可支配收入对消费支出的影响是非常显著的。
其次，对边际消费倾向是否明显小于0.7进行检验。
利用（9.40）式计算ｔ值
＝(0. 6724-0.7)/ 0.0056＝-4.9210
查ｔ分布表可知：显著水平为５％，自由度为12的单侧ｔ检验的临界值是1.782。
因为计算的ｔ值的绝对值大于此临界值,所以否定β2＝０.7的原假设，接受备择假设，认为我国城镇居民的平均消费倾向小于0.7。
（6）教材中的【例9-8】
将有关数据代入拟合好的样本回归方程，可得：
＝0.7489＋0.6724Ｘf
＝0.7489＋0.6724×8＝6.1280（千元）
从前面几例的结果可知： S=0.0820
, n=14，
213.7673
,将其代入求预测标准误差估计值的公式（9.47）式，有
Ｓｅf＝0.0820＝0.0852 （千元)
查ｔ分布表可知：显著水平为５％，自由度为12的双侧ｔ检验的临界值是2. 178。
因此，当人均可支配收入为8千元时，置信度为95 ％的消费支出的预测区间如下：
6.1280－2.178×0.0852≤Ｙf≤6.1280＋2. 178×0.0852
5.9424(千元)≤Ｙf≤
6.3135(千元)。