抛物线焦点弦经典性质
抛物线焦点弦的性质及应用

抛物线焦点弦的性质及应用抛物线是一种具有特殊性质的二次曲线,它的焦点弦性质是指过焦点parabola. 抛物线上任意一点的切线与从焦点引出的该点的法线的交点,这些交点都在焦点所在的直线上。
抛物线焦点弦的性质和应用如下:1. 焦点弦与顶点:抛物线的焦点弦通过抛物线的顶点,且与抛物线的对称轴垂直相交。
2. 焦点弦的长度:焦点弦的长度等于抛物线焦点到对称轴的距离的两倍。
3. 焦点弦的切线方程:焦点弦的切线方程可由抛物线的切线方程推导得到,即通过抛物线上一点(x1,y1)的切线方程为y = mx + (1 - m²) a/4,其中m为切线的斜率,a为焦点到对称轴的距离。
4. 焦点弦的法线方程:焦点弦的法线方程可由切线方程得到,即过抛物线上一点(x1,y1)的法线方程为y = -x/m + (x1/m + y1)。
5. 焦点弦的性质应用:抛物线焦点弦的性质在物理学、工程学和几何学等领域有广泛的应用。
在物理学中,抛物线焦点弦的性质可以用于描述光线的反射和聚焦。
例如,在反射望远镜中,抛物面用于反射并聚焦光线,使观察者能够看到远处的物体。
在工程学中,抛物线焦点弦的性质可以用于设计抛物面反射器、喇叭等产品。
抛物面反射器可以将声音或者电磁波线聚焦在焦点处,以达到提高功率传输效果的目的。
类似地,喇叭的设计也借鉴了抛物线焦点弦的性质,使声音能够更好地聚焦并扩散。
在几何学中,抛物线焦点弦的性质可以用于求解问题。
例如,已知抛物线上一点的坐标和抛物线焦点的坐标,可以通过焦点弦性质来求解该点在抛物线上的位置。
另外,抛物线焦点弦的性质还可以进一步推广到三维空间中的抛物面。
三维空间中的抛物面也具有焦点弦的性质,可以用于描述反射、聚焦和求解问题等。
综上所述,抛物线焦点弦是抛物线特有的性质之一,它的性质和应用在物理学、工程学和几何学等领域有重要的应用。
深入理解和应用这些性质可以帮助我们更好地解决各种问题,并且进一步推广到更高维度的几何形状中。
抛物线焦点弦

44A 、B 、C 、3D 、-3、亠、P 2解析:设弦的两个端点为 A( x i,y i )、B( x 2,y 2),x i x 2=, y 1 y 24P 2 ,.OA ? OB = x 1x 2 y 1y 2P 23p 23,故答案选B 。
4抛物线焦点弦的性质及应用平面内与一个定点 F 和一条定直线I 的距离相等的点的轨迹叫做抛物线。
由于抛物线定义的特殊性, 使得它有许多其他圆锥曲线所没有的特征,特别是抛物线过焦点的弦的性质尤其突出,同时也高考中经常 要考查的内容。
p设抛物线的方程为 y 2=2px(P >0),过焦点F (2,0)作倾斜角为 的直线,交抛物线于 PQ 称抛物线的焦点弦,(如图1).抛物线的焦点弦具有以下性质:2性质 1:设 P(x i ,y i ),Q(x 2,y 2),则 y i y 2=-p 2. xm —4证明:①当=90时,PQ 方程为x=2代入y 2=2px 中有y 2=p 2,即 y i =p,y 2=-p, ... y i y 2=_p 2.②当丰90时,设直线PQ 斜率为k,则PQ 方程为y=k(x - p)与y 2=2px 联立,消x 后得到: ky 2-2py-kp 2=0, . y i y 2=-p 2. 因为 y ; 2px i , y |2px 2,所以 y ; ? y ; 4p 2X i X ?,224 2y i ?y 2 p p 4p 24p 2 4P 、Q 两点,则线段所以x i x 2例i 过抛物线焦点的一条直线与它交于两点 P 、Q 通过点P 和抛物线顶点的直线交准线于点M 求证:直线MQ 平行与抛物线的对称轴.证明:为了方便比较,可将 P 点横坐标及Q 点纵坐标均用 P 点的纵坐标 ••• P(2p,y i ),Q(x 2,y 2),但 y i y 2=-p 2.y2=- y i ,PM方程是:y 書x,当x= - 时尸-土即为M点的纵坐标, 这样M 点与Q 点的纵坐标相同,故 MQ/ Ox.Ml 7i )J\ /F (L n) r■E 32[例2]设坐标原点为 O ,抛物线y 2=2x 与过焦点的直线交于 A 、B 两点,OA ? OB =y i 表性质4:以抛物线的焦点弦为直径的圆与抛物线的准线相切证法一:如图3,设PQ 中点为R,贝U R 即为PQ 为直线圆的圆心,过 R 作RS 丄MN 于 S,性质2:抛物线焦点弦的长度: ABp (X iX 2)= 2psin证明:如图所示,分别做AA 、BB i 垂直于准线I ,由抛物线定义有 ABAF 且有AFBF于是可得 BF AA BB iAF•••AB AF故命题成立.X iAF ? cosP ,1 cosBFBF ?cos ,BFX 1 x 2P .1 cosp —+ 1 cos 1 cos 1 cosP _~2sin例3已知圆M: x 2+y 2-4x=0及一条抛物线,抛物线顶点在 为 的直线l, l 与抛物线及圆由上而下顺次交于A 、BC 、D 四点,若解:如图,方程x 2+y 2-4x=0,表示的图的圆心为(2 , 0)即为抛物线的焦点,•••抛物线的方程是 y 2=8x(其中p=4),2p 8|AD|= ^7^=1=40,但圆的直径 |BC|=4 ,Olli I5• |AB|+|CD|=|AD|-|BC|=40-4=36.性质3:三角形OAB 的面积公式:S OAB2P 2 si n证法一:当直线倾斜角 为直角时, 公式显然成立。
抛物线焦点弦的性质所有公式推导

抛物线焦点弦的性质所有公式推导
抛物线焦点弦的性质在数学中是一项十分重要的内容,它涉及抛物线的函数特性和不定积分的求值,可以用来求解空间内特定形状的抛物线面积。
那么,抛物线焦点弦的性质的基本公式有哪些,如何推导呢?
最基本的抛物线焦点弦性质的公式是:抛物线面积S=2a(∫ sin ar+cos ar dr),其中a是焦点到原点距离,r是弦距离(由焦点渐近该弦的最近点)。
其推导方法是:首先设定抛物线函数为y=ax2+bx+c,其中a,b,c均为实数。
将抛物线延长为一直线y=x则可得到对应的抛物线焦点弦的性质以及两点之间的关系:一个点在x轴上,一个点在y轴上,两点之间的垂直距离即为抛物线焦点到原点的距离a,弦距离取负值即为x-c,总之两点之间垂直距离等于x-c。
接着,抛物线两边都可以用极坐标来表示,即r=x-c,θ=arcsin(r/a),令面积s积分,即可得出抛物线焦点弦的性质的基本公式:s=2a(∫sin ar+cos ar dr)。
从上述的推导来看,抛物线焦点弦的性质公式熟练掌握,可以获得任意空间内特定形状的抛物线面积求解,可以给我们的生活和娱乐活动带来更多惊喜和乐趣,可谓是大有裨益。
抛物线焦点弦性质

抛物线焦点弦性质
抛物线焦点弦性质:焦点弦长就是两个焦半径长之和。
焦半径长可以用该点的横坐标来表示,与纵坐标无关。
由于焦点弦经过焦点,其方程式可以由其斜率唯一确定,很多问题可以转化为对其斜率范围或取值的讨论。
在抛物线y²=2px中,弦长公式为d=p+x1+x2。
若直线AB的倾斜角为α,则|AB|=2p/sin²α。
y²=2px或y²=-2px时,x1x2=p²/4,y1y2=-p²。
x²=2py或x²=-2py时,y1y2=p²/4,x1x2=-p²。
焦点弦是指椭圆、双曲线或者抛物线上经过一个焦点的弦,是指同一条圆锥曲线或同一个圆上两点连接而成的线段。
焦点弦是由两个在同一条直线上的焦半径构成的。
焦半径是由一个焦点引出的射线与椭圆或双曲线相交形成的。
而由于椭圆或双曲线上的点与焦点之间的距离(即焦半径长)可以用椭圆或双曲线离心率和该点到对应的准线之间的距离来表示。
抛物线焦点弦性质及推导过程

抛物线焦点弦性质及推导过程抛物线是一种二次曲线,具有许多重要的性质。
其中一个重要的性质是焦点弦性质。
接下来,我将介绍焦点弦性质的定义、推导过程以及将该性质应用于实际问题的例子。
1.焦点弦性质的定义:考虑一个抛物线和其焦点上的两个点A和B,连接AB,然后过抛物线上的其他点C,将CA和CB分别延长,与抛物线相交于D和E。
焦点弦性质指出,点D和E的中点M一定位于直线AB上。
2.推导过程:首先,我们需要了解抛物线的标准方程是什么。
假设抛物线的焦点位于原点上方,其焦半径为p。
那么,抛物线的标准方程为y² = 4px。
接下来,设焦点F的坐标为 (0, p),则点A的坐标为 (a, 2ap),点B的坐标为 (-a, 2ap)。
由于点C(x,y)位于抛物线上,我们可以将其坐标带入抛物线的方程中得到:y² = 4px(x,y)²=4p(x,y)x² + y² = 4px我们知道直线CA的方程为 y - 2ap = (x - a)(2ap - a)。
以此类推,直线CB的方程为 y - 2ap = (x + a)(2ap + a)。
将以上两个直线方程与抛物线方程联立,我们可以求出点D和点E的坐标。
设点D的坐标为(x₁,y₁)和点E的坐标为(x₂,y₂)。
即有:x₁² + y₁² = 4px₁x₂² + y₂² = 4px₂求解出x₁和x₂,我们可以得到点D和点E的坐标。
然后,我们将点D和点E的坐标带入直线AB的方程中:y - 2ap = (x - a)(2ap - a)y - 2ap = (x + a)(2ap + a)联立以上两个方程,我们可以求解出直线AB的方程。
最后,我们求出点M的坐标,并将其带入直线AB的方程中:y - 2ap = (x - a)(2ap - a)若点M的坐标满足该方程,则说明点M位于直线AB上,证明了焦点弦性质。
抛物线焦点弦22条结论

抛物线焦点弦22条结论1、抛物线的焦点总是在数轴上的对称轴上。
2、抛物线的无穷近点总处在顶点上。
3、抛物线的顶点的坐标总是(h,k)的形式。
4、抛物线的斜率在顶点处最大,向两侧无穷远时最小。
5、抛物线不同于椭圆,即使在斜率为零时也不会平行于y轴。
6、抛物线焦点弦中椭圆内的焦点和斜率有关。
7、抛物线焦点弦中椭圆外的焦点和斜率有关。
8、抛物线焦点弦中椭圆内的线段始末点在椭圆上。
9、抛物线焦点弦中椭圆外的线段始末点在椭圆外。
10、抛物线焦点弦中,两个焦点分别对应一条双曲直线,而外圆的直径线段是两个焦点的连线。
11、抛物线的弦一定位于双曲线的两侧且是双曲线的垂直线段。
12、抛物线的焦点弦外圆的周长是抛物线的一象限周长的二倍。
13、抛物线焦点弦的另一圆的面积等于抛物线的一象限面积的两倍。
14、抛物线的焦点弦中,双曲线内外的直线段条数是一样多的。
15、抛物线焦点弦中,双曲线外的直线段总是比双曲线内的长。
16、抛物线焦点弦中,椭圆内及其外圆的线段总是一模一样的。
17、抛物线焦点弦中,双曲线外圆的形状是矩形,两个顶点在焦点上,其他两个顶点位于y轴上。
18、抛物线焦点弦中,双曲线内的所有线段的总长比双曲线外的总长要短。
19、抛物线焦点弦中,双曲线外的直线段均贯穿原点。
20、抛物线焦点弦中,两条分别从两个焦点开始,沿着双曲线直线段向原点靠近的线段,称为弦线。
21、抛物线焦点弦中,椭圆的焦点到顶点的距离,称为长轴半径的大小等于抛物线机小数a的值。
22、抛物线焦点弦中,椭圆的焦点到其他顶点的距离,称为短轴半径的大小等于抛物线机小数b的值。
焦点弦的八大结论

焦点弦的八大结论焦点弦是一种常见的数学问题,它的研究有助于我们更深入地理解数学中的一些重要概念和定理。
在这篇文章中,我们将讨论焦点弦的八大结论,了解它们分别是什么以及它们的意义。
最后,我们还将介绍焦点弦在实际应用中的一些例子。
一、焦点弦与抛物线的关系抛物线是一种经典的二次函数图像,它的形状是一个开口朝上或朝下的U字形曲线。
而焦点弦则是经过抛物线焦点的一条线段,根据抛物线的性质,焦点弦与抛物线的顶点在同一条直线上。
二、焦点弦的长度焦点弦的长度等于抛物线顶点到焦点的距离的两倍,这个结论很容易证明,只需要利用抛物线的定义式和距离公式即可得出。
三、焦点弦的中点焦点弦的中点恰好落在抛物线的准线上,这个结论也很容易证明,只需要利用抛物线的对称性即可。
四、焦点弦的垂线焦点弦的垂线恰好与抛物线相切,并且与抛物线准线垂直,这个结论涉及到了抛物线的切线和法线的概念。
五、抛物线对称性抛物线的对称轴恰好与焦点弦重合,这个结论是由于焦点弦的中点在对称轴上。
六、焦距的作用焦点弦和焦距有着密切的关系,焦点弦的长度等于焦距的两倍,这个结论是逆向推导出来的,也就是我们通过焦距来求出焦点弦的长度。
七、焦点弦的作用焦点弦在数学中有着重要的作用,它可以用来推导一些抛物线的性质,例如抛物线的切线和法线。
此外,在工程中,焦点弦也有广泛的应用,它可以用来设计一些光学系统和声学系统。
八、应用实例我们举个例子,考虑一个天线系统,它的辐射方向呈现出一条抛物线形状,我们可以通过焦点弦来设计这个天线系统的形状和大小,以达到最优的信号接收和传输效果。
类似的应用还包括椭圆镜头和声学降噪系统等。
综上所述,焦点弦是一个重要的数学问题,它在抛物线的研究和实际应用中有着广泛的应用。
理解焦点弦的八大结论有助于我们更深入地理解抛物线的概念和性质,同时也为我们提供了一些实际应用的思路和方法。
因此,学习和掌握焦点弦的八大结论是非常有益的。
(完整版)抛物线的焦点弦_经典性质及其证明过程
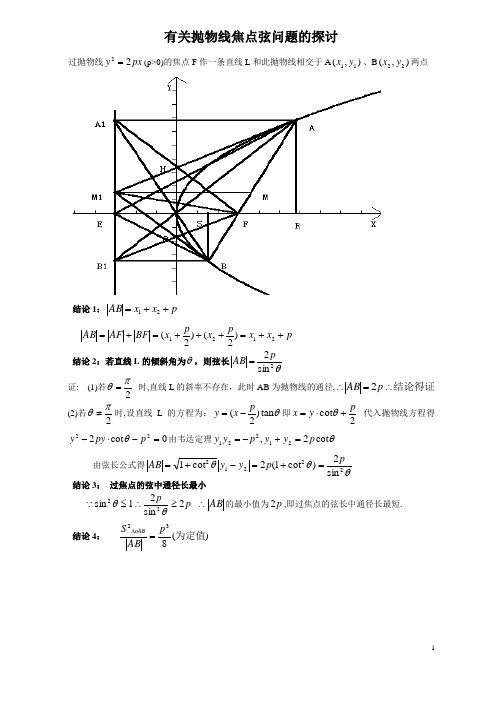
有关抛物线焦点弦问题的探讨过抛物线px y 22=(p>0)的焦点F 作一条直线L 和此抛物线相交于A ),(11y x 、B ),(22y x 两点结论1:p x x AB ++=21p x x px p x BF AF AB ++=+++=+=2121)2()2( 结论2:若直线L 的倾斜角为θ,则弦长θ2sin 2pAB =证: (1)若2πθ= 时,直线L 的斜率不存在,此时AB 为抛物线的通径,结论得证∴=∴p AB 2(2)若2πθ≠时,设直线L 的方程为:θtan )2(p x y -=即2cot py x +⋅=θ 代入抛物线方程得0cot 222=-⋅-p py y θ由韦达定理θcot 2,21221p y y p y y =+-=由弦长公式得θθθ22212sin 2)cot 1(2cot1pp y y AB =+=-+= 结论3: 过焦点的弦中通径长最小p p2sin 21sin 22≥∴≤θθ ∴AB 的最小值为p 2,即过焦点的弦长中通径长最短. 结论4: )(832为定值p AB S oAB =∆()8sin 2sin sin 2221sin 21sin 21sin 21sin 2132220P AB S p p p AB OF BF AF OF AF OF BF OF S S S OAB AF OBF OAB =∴=⋅⋅⋅=⋅⋅=+⋅=⋅⋅+⋅⋅=+=∆∆∆∆θθθθθϑθ结论5: (1) 221p y y -= (2) x 1x 2=42p证44)(,2,22222121222211P Py y x x p y x p y x ==∴== 结论6:以AB 为直径的圆与抛物线的准线相切证:设M 为AB 的中点,过A 点作准线的垂线AA 1, 过B 点作准线的垂线BB 1, 过M 点作准线的垂线MM 1,由梯形的中位线性质和抛物线的定义知 222111AB BFAF BB AA MM =+=+=故结论得证结论7:连接A 1F 、B 1 F 则 A 1F ⊥B 1FFA A FO A FO A F AA OF AA AFA F AA AF AA 11111111//,∠=∠∴∠=∠∴∠=∠∴=同理︒=∠∴∠=∠901111FB A FB B FO B ∴A 1F ⊥B 1 F 结论8:(1)AM 1⊥BM 1 (2)M 1F ⊥AB (3)BF AF FM ⋅=21(4)设AM 1 与A 1F 相交于H ,M 1B 与 FB 1相交于Q 则M 1,Q ,F ,H 四点共圆 (5)2121214M M B M AM =+证:由结论(6)知M 1 在以AB 为直径的圆上∴ AM 1⊥BM 111FB A ∆为直角三角形, M 1 是斜边A 1 B 1 的中点111111111AFA F AA F A M FA M F M M A ∠=∠∠=∠∴=∴︒=∠=∠+∠9011111M AA M FA F AA ︒=∠+∠∴90111FM A AFA∴M 1F ⊥ABBF AF F M ⋅=∴21 AM 1⊥BM 1 F B F A 90111⊥︒=∠∴ 又B AM︒=∠∴90FB A 11 所以M 1,Q ,F,H 四点共圆,22121AB B M AM =+()()()2121211242MM MM BB AABFAF ==+=+=结论9: (1)、A O 、B 1 三点共线 (2)B ,O ,A 1 三点共线(3)设直线AO 与抛物线的准线的交点为B 1,则BB 1平行于X 轴(4)设直线BO 与抛物线的准线的交点为A 1,则AA 1平行于X 轴证:因为p y p y k y p p y y x y k oB oA 2212111122,221-=-====,而221p y y -=所以122222oB oA k p y y ppk =-=-=所以三点共线。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1 1 2 性质 9: FA FB p
证明:过 A 点作 AR 垂直 X 轴于点 R,过 B 点作 BS 垂直 X 轴于点 S,
设准线与 x 轴交点为 E, 因为直线L的倾斜角为
则 ER EF FR P AF cos AF
性质 1: AB x1 x2 p
p p AB AF BF ( x1 ) ( x 2 ) x1 x 2 p 2 2
性质 2:若直线 L 的倾斜角为 , 则弦长
2p AB sin 2
证明: (1)若
2
时,直线 L 的斜率不存在,此时 AB 为抛物线的通径,
(1)证:因为 k oA
y1 y1 y2 2 y2 2p ,而 y1 y2 p 2 2 , k oB1 p x1 y1 p y1 2 2p
所以 k oA
2 y2 2p k oB1 所以三点共线。同理可证(2) 2 p p y2
p y1 2p p 2 y1 y2 (3)证: 直线OA : y , yB1 x x 令x y2 2 x1 y1 y1 y1
1 1 AB CD 1 1 1 2 2p 2 p 2 2 p 2k 2 k
ቤተ መጻሕፍቲ ባይዱ
性质 5: (1)
p y1 y2 p (2) x1x2= 4
2
2
p y p 证:设直线 L 的方程为: y k ( x ) 即 x 2 k 2 2p 2 y p2 0 代入抛物线方程得 y k 2p 2 由韦达定理 y1 y2 p , y1 y2 , k
抛物线焦点弦经典性质10条
焦点弦
通过焦点的直线,与抛物线相交
y
A ( x1 , y1 )
F
于两点,连接这两点的线段叫做
抛物线的焦点弦。
O
B ( x 2 , y2 )
x
2 y 过抛物线 2 px (p>0)的焦点 F 作一条直线 L
和此抛物线相交于 A ( x1 , y1 ) 、B ( x2 , y2 ) 两点
2 2 p 2 得x 2 -p( 2 1)x 0 设A(x1,y1 ),B(x 2 ,y2 ) 则x1 x 2 p 2 1 k 4 k
2 则 AB x1 x2 p p 2 2 ,同理 CD x3 x4 p p 2k 2 2 k
2 OAB
3
1 1 S OAB S OBF S 0 AF OF BF sin OF AF sin 2 2 1 1 1 p 2p p2 OF AF BF sin OF AB sin 2 sin 2 2 2 2 sin 2 sin 2 3 S P OAB AB 8
y
∴|AB|=|AF|+|BF| =|AD|+|BC| =2|EH|
所以EH是以AB为直径的圆E的半径,且 EH⊥l,因而圆E和准线l相切.
C H D E F A
B O
x
性质 7:连接 A1F、B1 F 则 A1F B1F
证明: AA 1 AF ,AA 1F AFA 1
AA1 / /OF AA1F A1FO A1FO A1FA
AB 2 p 结论得证
(2)若
2
时, k tan
k 0
p y p 设直线 L 的方程为: y k ( x ) 即 x 2 k 2 2p 2 y p2 0 代入抛物线方程得 y k
2p 1 由韦达定理 y1 y2 p , y1 y2 , y1 y2 2 p 1 2 k k
同理 B1 FO B1 FB A1 FB1 90
A1F B1 F
性质 8:(1). A、 O、B1 三点共线 (2).B,O,A1 三点共线 (3).设直线 AO 与抛物线的准线的交点为 B1,则 BB1 平行于 X 轴 (4).设直线 BO 与抛物线的准线的交点为 A1,则 AA1 平行于 X 轴
2
1 1 2p 由弦长公式得 AB 1 2 y1 y2 2 p(1 ) 2 2 k tan sin
性质3: 过焦点的弦中通径长最小
2p 2p 证明: sin 1 2 sin
2
AB 的最小值为 2 p ,即过焦点的弦长中通径长最短.
性质 4:
S p (定值) AB 8
P AF 1 cos
1 1 cos AF P 1 1 2 FA FB p
1 1 cos 同理可得 BF P
1 1 1 性质 10:过抛物线的焦点作两条互相垂直的弦 AB、CD,则 AB CD 2 p
p 证明: 当 时,设直线 L的方程为y k x - 将其代入方程 y 2 2px 2 2
y1 y2 ( y1 y 2 ) 2 P 2 x1 , x2 , x1 x2 2 2p 2p 4 4P
2
2
性质6:以焦点弦AB为直径的圆和抛物线的准线相切.
y
分析:运用抛物线的 定义和平面几何知识 来证比较简捷.
C H D E F A
B O
x
证明:如图,设AB的中点为E,过A,E,B分别向准 线l引垂线AD,EH,BC,垂足分别为D,H,C, 则|AF|=|AD|,|BF|=|BC|
