半导体超晶格
高等半导体物理Chapter 3 半导体超晶格物理
第三章半导体超晶格物理§3.1 超晶格的定义与分类32§3.2 超晶格的子能带§应变超晶格3.3§3.4 掺杂超晶格§3.5 超晶格结构的伏安特性§3.6 应变硅结构器件§3.7 超晶格结构的器件应用37第三章半导体超晶格物理§3.1 超晶格的定义与分类32§3.2 超晶格的子能带§应变超晶格3.3§3.4 掺杂超晶格§3.5 超晶格结构的伏安特性§3.6 应变硅结构器件§3.7 超晶格结构的器件应用37§3.1 超晶格的定义与分类3.1.1超晶格结构的提出3113.1.2超晶格结构的定义3.1.3超晶格结构的分类3.1.1超晶格结构的提出¾1970年，日本科学家江崎和华裔科学家朱兆祥在寻找具有微分电阻的新器件时，提出了一个全新的革命性概念：半导体超晶格。
他们设想，如果器件时提出了个全新的革命性概念他们设想如果用两种晶格匹配很好的半导体材料A和B交替生长周期性的半导体结构，则子沿长轴方向的连续能带将分裂成几个子带在波矢空间中子沿布电子沿生长轴方向的连续能带将分裂成几个子带，在波矢空间中电子沿布里渊区边缘运动，出现负阻。
这种运动在实空间中表现为来回振荡，这将大大提高器件的工作能力。
¾与此同时，分子束外延技术也在美国贝尔实验室和IBM公司开发成功．新Ga1-x As/GaAs 思想和新技术的巧妙结合，制成了第一类晶格匹配的组分型Alx 超晶格，标志着半导体材料的发展开始进入人工设计的新时代．分子束外延是目前薄膜生长技术中最先进的技术这种技术利用定¾分子束外延是目前薄膜生长技术中最先进的技术。
这种技术利用定向分子束流在单晶衬底上淀积，所以能够精确地控制薄层的厚度，其精度可以达到单原子层的程度。
半导体超晶格结构的优点¾半导体中的自由电子局限在一个平面内运动，成为准二维电子气。
半导体材料第10讲-超晶格
量子阱的应用
量子阱红外探测器 阱材料的子带中有两个子能带，即基态E1和第一激发态E2 ，在 材料生长过程中利用掺杂型半导体．使子带阱中基态上具有一定的二 维电子密度， 当入射辐射光子能量为hω照射到器件接收面上时，E1 上的电子将被光子激发到E2态，并隧穿势阱壁形成热电子，以致形成 与入射光强度成正比的电信号。 这种新型、快速、灵敏的红外探测器具有灵活性大、响应速度快、 量子效率高、结构简明等优点。量子阱红外探测器还具有材料均匀性 好稳定性好，重复性好及质高价廉等优点，其发展速度特别快。这种 新型量子阱探测器的问世，大大促进了大规模集成、光学逻辑电路、 红外成像技术的发展量子阱红外探测器对红外物理、红外光电子学及 其应用领域带来了革命性的发展。
半导体材料
第八章 III－V族多元合物半导体
四探针法原理 请参考 陈治明，王建农，《半导体器件的材料 物理学基础》，科学出版社，1999年5月第 一版，p: 249-268
8-1 异质结
异质结：两种不同晶体接触处所形成的结。由两种半导体单晶联
结起来构成。可分为同型(NN+，PP +)和异型(PN)两种
超晶格量子阱的一些重要现象和性质即可用二维电子气的态密度 来描述。 通过对二维电子气的态密度的计算，发现二维电子气的态 密度与能级无关。正是这种特性，给超晶格带来了许多方面的应用。
可参考：阎明，”半导体超晶格及其量子阱的原理”，上海海运 学院学报，V0l_21 No．1 Mar．2000，p=102-107
度，从而减少了复合区宽度。
异型异质结可利用改变两侧禁带宽度的相对大小来提高电子或空 穴的注入效率。
同型和异型异质结都能提供一个折射率阶跃，形成光波导的界面
半导体物理第九章2
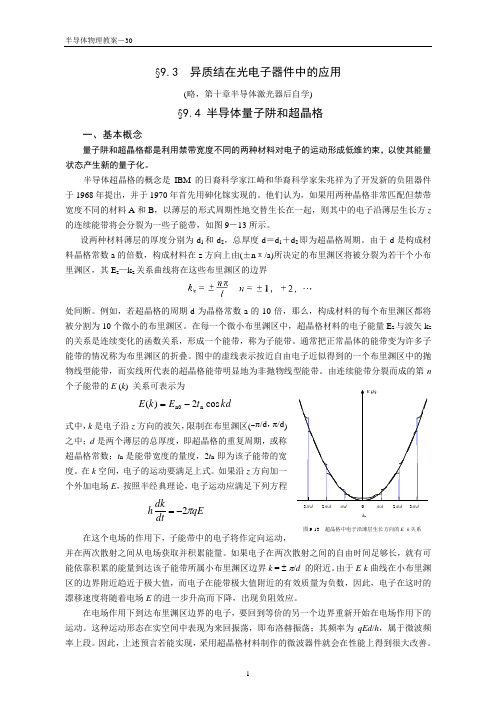
§9.3 异质结在光电子器件中的应用(略，第十章半导体激光器后自学) §9.4 半导体量子阱和超晶格一、基本概念量子阱和超晶格都是利用禁带宽度不同的两种材料对电子的运动形成低维约束，以使其能量状态产生新的量子化。
半导体超晶格的概念是IBM 的日裔科学家江崎和华裔科学家朱兆祥为了开发新的负阻器件于1968年提出，并于1970年首先用砷化镓实现的。
他们认为，如果用两种晶格非常匹配但禁带宽度不同的材料A 和B ，以薄层的形式周期性地交替生长在一起，则其中的电子沿薄层生长方z 的连续能带将会分裂为一些子能带，如图9－13所示。
设两种材料薄层的厚度分别为d 1和d 2，总厚度d ＝d 1＋d 2即为超晶格周期。
由于d 是构成材料晶格常数a 的倍数，构成材料在z 方向上由(±n π/a)所决定的布里渊区将被分裂为若干个小布里渊区，其E z —k z 关系曲线将在这些布里渊区的边界处间断。
例如，若超晶格的周期d 为晶格常数a 的10倍，那么，构成材料的每个布里渊区都将被分割为10个微小的布里渊区。
在每一个微小布里渊区中，超晶格材料的电子能量E z 与波矢k z 的关系是连续变化的函数关系，形成一个能带，称为子能带。
通常把正常晶体的能带变为许多子能带的情况称为布里渊区的折叠。
图中的虚线表示按近自由电子近似得到的一个布里渊区中的抛物线型能带，而实线所代表的超晶格能带明显地为非抛物线型能带。
由连续能带分裂而成的第n 个子能带的E (k ) 关系可表示为kd t E k E cos 2)(n n0-=式中，k 是电子沿z 方向的波矢，限制在布里渊区(-π/d ，π/d )之中；d 是两个薄层的总厚度，即超晶格的重复周期，或称超晶格常数；t n 是能带宽度的量度，2t n 即为该子能带的宽度。
在k 空间，电子的运动要满足上式。
如果沿z 方向加一个外加电场E ，按照半经典理论，电子运动应满足下列方程qE dtdkhπ2-= 在这个电场的作用下，子能带中的电子将作定向运动，并在两次散射之间从电场获取并积累能量。
1-4 电子功能与元器件半导体超晶格材料
LOGO
超晶格概念的提出
GaAs
AlGaAs GaAs AlGaAs
GaAs
超晶格定义：超晶格材料是由两种或两种以上性质不同 的薄膜相互交替生长并而形成的多层结构的晶体，在这 种超晶格材料中，由于人们可以任意改变薄膜的厚度， 控制它的周期长度。一般来说，超晶格材料的周期长度 比各薄膜单晶的晶格常数大几倍或更长，因而取名“超 晶格” 。
1.在超晶格结构中应用非晶态的理由是为了改善其结构的柔软性。 2.在非晶态的情况下，由于结构的自由度大，晶格不匹配得到缓和。 3.由于容易改变非晶态材料本身的物理性质,使器件设计上的自由度更大. 4.在较低温度上生长以及容易形成大面积.
是一种物理沉积单 晶薄膜方法。在超 高真空腔内，源材 料通过高温蒸发、 辉光放电离子化、 气体裂解，电子束 加热蒸发等方法， 产生分子束流。入 射分子束与衬底交 换能量后，经表面 吸附、迁移、成核、 生长成膜。
1-4-1 超晶格及其基本性质
分子束外延 （ MBE ： Molecular Beam Epitaxy ）
LOGO
（h1、h2为各层厚度）
利用同一种材料生长薄膜晶体时， 可以利用改变膜的厚度来控制新 的晶格常数及禁带宽度。
1-4-2 应变超晶格
2.禁带宽度
LOGO
受应变的影响，不仅 应变超晶格材料的能 带结构发生变化，同 时原成分材料的禁带 宽度也要发生变化。
能带折叠效应：间接 跃迁→直接跃迁
1-4-2 应变超晶格
LOGO
多种监控设备，可对生长过程中衬底温度，生长速度，膜厚等进行瞬时测量分 析。对表面凹凸、起伏、原子覆盖度、黏附系数、蒸发系数及表面扩散距离等 生长细节进行精确监控。由于MBE 的生长环境洁净、温度低、具有精确的原位 实时监测系统、晶体完整性好、组分与厚度均匀准确，是良好的光电薄膜，半 导体薄膜生长工具。
半导体超晶格与多量子阱
• 生长 InGaAs/InP 超晶格通常使用含有 In 、 Ga 的 金属有机物做为Ⅲ族源，PH3和AsH3为Ⅴ族源。 • InxGa1-xAs与衬底InP在x=0.53时两者晶格匹配，偏 离这一点将产生失配。偏离越大，失配越大。 x>0.53时产生压缩应变，x<0.53时产生伸张应变。 为 了 生 长 无 失 配 的 InGaAs/InP 界 面 ， 必 须 严 格 控 制 x=0.53。 • 生长速率是由反应物输入总量决定 ，一般生长 InP 和 InGaAs 分别控制在 0.1~0.3nm/s 和 0.2~0.5nm/s 为宜。
HgTe Ec1 Ev1 Λ
CdTe Ev2
EF Γ B
一、 组分超晶格的制备
制备组分超晶格时应满足如下的要求：
（1）组分超晶格是超薄层异质周期排列结构，因此制备 时生长速率应能精确地控制，以保证各层厚度的重复性；
（2）异质界面应该平坦，粗糙度低，组分变化陡峭。这 就要求生长时源的变化要快，且在保证晶体质量的条件 下，生长温度尽可能的低，以防层间组分的互扩散；
半导体超晶格与多量子阱
半导体超晶格是由两种或两种以上性质不同的超薄层材料 交替生长而成的多层结构晶体。相邻两层不同材料的厚度 的和称为超晶格的周期长度。 一般来说这个周期长度比各层单晶的晶格常数大几倍或更 长，因此这种结构获得了“超晶格”的名称。 各超薄层的厚度要与电子的de Brog1ie波长相当。设半导体 中电子的有效质量m*约为自由电子质量的l／10，能量E约 为0.1eV，则电子的de Broglie波长大致为
生长时应控制在层状生长，防止岛状生长并且采取合适 中断生长工艺，以防止界面处组分的互掺等。
界面的特性可利用PL谱和X射线双晶衍射技术来研究。
7.8 半导体超晶格
图7.8.5 横向超晶格器件
7.8.4 二维电子气的能态密度与量子霍尔效应 １. 二维电子气能态密度 如前所述，超晶格半导体附加的周期性引 起电子能谱的附加量子化，即在 z 方向形成一 系列量子能级 E1 ( z), E2 ( z), ，由式（7.8.1）可知， 由于[ 2 /(2m* )](k x2 k y2 ) 形成准连续谱，则相应 z 方 向的每一个能级 E ( z) ，电子的二维运动形成一 个子能带。子能带的态密度可由第4章的方法 求得，只不过这里是二维问题。由在 k// (kx , ky ) 空 间Ｋ标度下单位体积的态密度为1/(2π)2 可知， 以 k k k 为半径的 k// 空间圆内所包含的允许 的 k// 的数目为 :
图 7.8.3 超晶格中E-k 关系
图 7.8.4 在周期性晶体场中外加直流 电场以后电子的行为
由此可见，由于在超晶格晶体中引入了附加的一维 周期势场，其中电子的能量将呈现新的量子化现象， 原来晶格周期势场中的能带分裂成一系列子能带。
7.8.3 超晶格的负阻效应及其应用
这种附加量子化效应使得超晶格晶体产生了许许 多多新的物理现象和物理性质，如量子霍尔效应、 负阻效应等。下面简单介绍负阻效应极其应用。 研究表明，当在不同的温度下测量超晶格晶体的 电阻时，将会发现样品的电阻随外加电压变化而变 化。当外加电压增加到某一阀值时，微分电阻的数 值将会发生突变，在某些温度下会出现负阻现象。 过了突变值以后，随着外加电压的增加，电阻的数 值会出现忽大忽小的变化。电阻的这种异常变化是 块状 GaAs、AlAs 的单晶样品所没有的。关于超晶格 晶体的负阻效应可作如下的定性讨论。 图７.８.４给出了电子在直流电场中受到加速作 用以后运动的情况。假定无外电场时，电子处于Ａ
高等半导体物理Chapter 3 半导体超晶格物理
§3.1 超晶格的定义与分类 §3.2 超晶格的子能带 §3.3 应变超晶格 §3.4 掺杂超晶格 §3.5 超晶格结构的伏安特性 §3.6 应变硅结构器件 §3.7 超晶格结构的器件应用
第三章 半导体超晶格物理
§3.1 超晶格的定义与分类 §3.2 超晶格的子能带 §3.3 应变超晶格 §3.4 掺杂超晶格 §3.5 超晶格结构的伏安特性 §3.6 应变硅结构器件 §3.7 超晶格结构的器件应用
AlSb、InAs和GaSb的禁带的相对位置和组成超晶格以后的能带结构
Байду номын сангаас
3.1.3 超晶格结构的分类
¾ 不同的排列方式构成不同的异质结构，从而提供了更多地选择结构的自由度。
多元超晶格的排列方式
3.1.3 超晶格结构的分类
多维超晶格
¾ 一维超晶格与体单晶相比具有很多新奇的性质，不论在物理内涵上还是 在器件应用上都有许多令人感兴趣的问题，这些特点的来源就在于它把电子 和空穴限制在二维平面内从而产生量子力学效应的结果。 ¾ 我们发展这种思想，把载流子在维度上进一步地进行限制，可以实现二维 超晶格（即电子或空穴的运动在两个方向上被材料的尺寸所限制，电子或空 穴只能在另外的一个方向上自由运动，或称为量子线超晶格）和三维超晶格 （即电子和空穴在三个方向上的运动都被材料的尺寸所限制，或称为量子点 超晶格）。
¾ 如果窄带材料（势阱层）的宽度很小，可以和电子的德布罗意波长相比， 而宽度材料（势垒层） 的宽度也很小，即势垒的厚度也很小，从而使相邻势 阱中的电子波函数可以互相耦合，扩展成子能带，则这种结构就是超晶格结 构。 ¾ 因此，多量子阱和超晶格结构的唯一区别就是垒层的厚度的大小是否能使
相邻势阱中的波函数发生耦合。
超晶格第四章半导体超晶格
3�电学方法�C-V法�
当有外加电压Va存在时�势垒的宽度和高度的关系为�
( x0
−
x1 )
=
[
2ε1ε 2N D
qN A (ε1N A + ε 2N D
)
(VD
− Va
)]1/ 2
( x2
−
x0 )
=
[
2ε1ε 2N A
qN D (ε1N A + ε 2N D )
?异质结不同能隙材料形成的结如族族族等?主要特点能隙宽度介电常数及电子亲和势均不同?不仅是超晶格的基本组成部份其材料与结构的不同也为器件设计带来许多自由度及独特的性质21理想突变异质结能带图理想突变异质结的模型是两种材料一直到边界都保持其体内的特性在边界上才突变成另一种材料
第四章 半导体超晶格
§1 引言 §2 异质结 §3 超晶格量子阱中的新现象 §4 超晶格电子态理论 §5 超晶格晶格振动 §6 超晶格量子阱的光学性质 §7 超晶格量子阱的垂直输运性质 §8 超晶格量子阱应用例举 §9 量子Hall效应 *§10 低维超晶格和微结构
3�应变超晶格
一般认为�晶格常数的失配度<0.5%为晶格匹配� 失配度>0.5%为晶格失配。在晶格常数失配度<7% 的范围内�其中的一种或两种材料内存在应变�以 补偿晶格常数的失配�界面不产生位错与缺陷。
如�Si/Ge, GaP/InP
§2
异质结 - 超晶格的基本单元
“半导体异质结物理”, 虞丽生,科学出版社.
当势阱的宽度和载流子的有效质量已知时�可用和 实验数据相拟合的办法求出相应势阱的深度�即导 带带阶和价带带阶。
电子的跃迁满足选择定则 Δn = 0�即位于第n个重 �或轻�空图穴5 量能子级阱只中的能量跃子能迁级到和第光跃n迁个电子能级。
9.4 半导体超晶格
两种材料的禁带宽度之差为 Eg Eg2 Eg1 1.247x
bc Ec
GaAs Ga1-xAlxAs
Ev 图9-28 Ga1-xAlxAs/GaAs的能带图
其中波函数 x, y, z满足
(x, y, z) ei(kx xky y)U (z)
(9-85) (9-86)
其中U(z)代表与z有关的波函数，满足：
2
2m
d 2U (z) dz 2
V (z)U (z)
EzU (z)
（9-87）
垂直于z方向的xy平面内：电子波函数为平面波。kx、ky分别为 电子在x、y方向上的波矢，相应的能量Exy为连续谱。
图9-29中的虚线表示近自由电子的抛物线型能带，而实线所 代表的超晶格能带明显地为非抛物线型。
超晶格结构的负阻现象：如果沿z方向加一电场，则子带中的电
子可以无碰撞的达到微小布里渊区的边界，Ez~kz关系曲线的曲
率由正变负，因而电子的有效质量
m
h2
2E k 2
1
由正变负，
其导电特性将会出现负阻现象。
Ez En
n 1, 2,3,...
势阱无限深时：
En
2
2m*
n
c
2
电子的总能量E：
（9-88）
2
E
En
Exy
En
2m
(k
2 x
k
2 y
)
（9-89）
（9-89）式中，对应于一个En值，Exy可取任意正值，这时，总
能量可以取En至∞的任意正值，相当于能级En展宽成为能带，称
超晶格、光子晶体及声子
30
三、光子晶体 6
➢大量的原子按一定的空间排布结合在一起组成 晶体。在这些结构中，原子是有规则排列的， 价电子不再专属于某个原子，而是在晶体中做 共有化运动，因此原子的某些分立的能级形成 由一定能量范围内准连续分布的能级组成的能 带，相邻两个能带之间可能存在一定的能量区 间，称为能隙。电子不能在能隙中存在，只能 在能带间跳跃。
• 量子阱的结构
图4 AlGaAs/GaAs量子阱结构
18
二、超晶格材料——量子阱 12
• 负阻效应 ➢图 5 中 曲 线 BC 显示负阻效应， 即遂穿电流随 电压的升高而 降低。
图5 共振遂穿三极管的I-U曲线
19
二、超晶格材料——量子阱 13
• 应用
➢ 发光材料（LED等）
20
二、超晶格材料——量子阱 14
9
➢图 1 ( a ) 是 两 种 组 分 超 晶格结构示意图，构 成超晶格的两种材料 有不同的禁带宽度， 按它们的能带差异分 为图1（b）所示的I型 超晶格和图1（c）所 示的Ⅱ型超晶格。
10
二、超晶格材料——量子阱 4
➢组分超晶格是指在同一块单晶上生长的 大量重复相间的薄层，通常是由两种不 同材料在一个维度上层状排列的周期结 构。其中，每层的厚度都很小，可和电 子的德布罗意波长相比，因此其周期远 小于电子非弹性散射的平均自由程。
34
三、光子晶体 10
➢ 光子分子与真实分子的类比能更好地说 明光子与电子行为的相似性。图11(a)是 光子分子的扫描电镜照片，即用两个光 子原子构成一个类H+2分子。随着两个光 子原子间距的缩小，基态光子模式分裂 为两个能级，见图11(b)。
35
图 11(a) 光子分子结构的SEM照片 (b) 光子分子的光致 发光谱，从上往下光子原子间距逐渐缩小
第三章半导体超晶格
第3章 半导体超晶格3.1 半导体超晶格基本结构3.2 超晶格的应用举例3.1 半导体超晶格基本结构所谓的超晶格，是由几种成分不同或掺杂不同的超薄层周期性地堆叠起来而构成地一种特殊晶体。
超薄层堆叠地周期（称为超晶格地周期）要小于电子的平均自由程，各超薄层的宽度要与电子的德布罗意波长相当。
其特点为在晶体原来的周期性势场之上又附加了一个可以人为控制的超晶格周期势场，是一种新型的人造晶体。
超晶格的分类（一）复合超晶格利用异质结构，重复单元是由组分不同的半导体薄膜形成的超晶格称为复合超晶格，又称为组分超晶格。
按照能带不连续结构的特点可将这个类型超晶格分为四类：第Ⅰ类超晶格、第Ⅱ类错开超晶格、第Ⅱ类倒转型超晶格和第Ⅲ类超晶格。
（1） 第Ⅰ类超晶格(GaAs/AlGaAs)GaAs 材料的见地完全包含在AlGaAs 的能隙之中，电子和空穴都位于窄带隙材料的势阱中v c g E E E ∆+∆=∆x 247.1E g ＝∆，与Al 的组分x 成正比。
（2） 第Ⅱ类 —— 错开型超晶格（GaSbAs/InGaAs ）两个带隙互相错开，一个价带底在另一个价带底的下面。
电子和空穴分别处于两个不同的材料中形成了真实空间的间接带隙半导体（3） 第Ⅱ类 —— 倒转型超晶格（InAs/GaSb ）一个导带底下降到另一个价带底之下。
电子和空穴可能并存于同一个能区中，形成电子－空穴系统Ec1与Ec2能量相差一个Es ，前者的导带与后者的价带部分重叠，从而可能发生从半导体到金属的转变（4） 第Ⅲ类超晶格(HgTe/CdTe)宽带隙半导体CdTe 和零带隙半导体HgTe 构成的超晶格。
只有当超晶格的周期小于某一定值时才具有半导体特性，否则具有半金属特性。
超晶格能隙差由最低导带子能带和价带子能带的间距决定，价带能量不连续值近似为零，导带能量不连续值近似等于两种材料能隙之差。
（二）掺杂超晶格利用超薄层材料外延技术（MBE 或MOCVD ）生长具有量子尺寸效应的同一种半导体材料时，交替地改变掺杂类型的方法（即一层掺入N 型杂质，一层掺入P 型杂质），即可得到掺杂超晶格，又称为调制惨杂超晶格。
半导体超晶格中负微分电导及其非线性特性的研究共3篇
半导体超晶格中负微分电导及其非线性特性的研究共3篇半导体超晶格中负微分电导及其非线性特性的研究1半导体超晶格中负微分电导及其非线性特性的研究半导体超晶格是一种具有特殊晶体结构和性质的形式，其性能比普通半导体更为优异。
在半导体超晶格中，一些特殊的电学现象受到了研究者们的广泛关注。
其中，负微分电导现象引起了极大的兴趣。
负微分电导现象是指在某些材料中，随着电压的加大，电流并不像正常情况下那样增大，反而出现减小的现象。
这种电流随电压下降的现象被称为负微分电导（NDC），是一种负导数现象。
负微分电导的出现为新型电子器件的制备和应用提供了新的思路和可能性。
半导体超晶格材料中负微分电导现象的研究和应用也成为了当前新兴材料研究的热点。
半导体超晶格中的负微分电导现象主要是由其非线性特性引起的。
在正常情况下，电势差和电流之间的关系可以通过欧姆定律来描述，即I=U/R，其中I表示电流，U表示电势差，R表示电阻。
然而在半导体超晶格中，这种关系并不适用。
随着电压加大，电子被加速到高速运动，当电压达到一定程度后，电子将在深度周期结构中被扭曲和折射。
这些被扭曲的电子不仅导致电流的减小，还能够在结构周期内相互干涉，增强量子隧穿效应，造成电阻率的变化。
针对半导体超晶格中负微分电导现象，许多学者进行了大量的研究。
他们通过研究材料的微观结构和表征，以及研究材料的输运特性和非线性关系，加深了人们对半导体超晶格负微分电导现象的理解，为实现其应用提供了新的思路。
除了理论研究外，半导体超晶格负微分电导现象的应用也正在快速发展。
例如，该现象可用于设计新型电荷放大器、微波信号放大器、偏置稳压器件和高性能传感器等。
此外，对于新型太阳能电池和热电器件等光、热转化的能量转换领域也有广泛的应用前景。
这些应用拓展了半导体超晶格负微分电导现象的应用，提高了其应用价值和实用性。
总之，半导体超晶格中负微分电导及其非线性特性的研究，为光、电子学和信息技术领域带来了巨大的贡献。
量子阱和超晶格
量子阱和超晶格的重要性
量子阱和超晶格是现代半导体技术中的重要组成部分，对于 发展新型电子器件、光电器件和量子器件具有重要意义。
通过量子阱和超晶格的设计和制备，可以实现对电子的量子 行为和材料的物理性质的精确调控，从而优化电子器件的性 能，提高光电器件的光电转换效率，以及实现量子信息处理 和量子计算等前沿技术。
新型应用场景不断涌现
随着量子计算和超晶格技术的不断发展，将会有越来越多的新型应用场景涌现，包括量子 模拟、量子优化、量子机器学习等。
需要解决的技术挑战和伦理问题
随着量子计算和超晶格技术的不断发展，需要解决的技术挑战和伦理问题也将不断增加， 需要加强国际合作和政策引导。
THANK YOU
超晶格
超晶格主要应用于电子器件和集 成电路等领域，如高速晶体管、 集成电路、微电子器件等。
05
量子阱和超晶格的发展趋势
量子计算的发展趋势
量子计算技术不断进步
随着量子计算技术的不断发展，量子计算机的性能和稳定 性不断提升，量子算法和应用场景也在不断拓展。
硬件平台多样化
随着量子计算技术的不断发展，量子计算机的硬件平台也 在不断多样化，包括超导、离子阱、光学等多种技术路线。
热稳定性
超晶格具有较好的热稳定性，能 够在较高温度下保持稳定的性能。
超晶格的应用
电子器件
能源领域
超晶格可用于制造高速、低功耗的电 子器件。
超晶格可用于太阳能电池和热电转换 等领域，提高能源利用效率。
光电器件
超晶格在光电器件领域有广泛应用， 如激光器、探测器等。
04
半导体超晶格和多量子阱
24
10.3 垂直于超晶格方向旳电子输运
如图10. 25所示，在两端有两个高掺杂GaAs层作电极，其 中电子旳费米能级为EF。
25
10.3 垂直于超晶格方向旳电子输运
对于双势垒和三个势垒系 统旳计算成果如图10. 26所示 。伏安特征上是一系列旳峰值 ，第一种峰值旳位置相当于电 极上旳费米能级和第一种子带 底对齐旳情形。
9
10.2.1 GaAs-AlxGa1-xAs超晶格
对界面是突变异质结旳GaAs-AlxGa1-xAs超晶格旳导带和价 带都是一系列旳方形势阱。假设势垒和势阱旳宽度相同，均为 d。当势垒宽度d逐渐变小时，能级从高到低依次扩展成能带。 这种情形和原子构成晶体旳过程相同。
10
10.2.1 GaAs-AlxGa1-xAs超晶格
31
负阻振荡器
负阻振荡器：利用负阻器件抵消回路中旳正阻损耗， 产生自激振荡旳振荡器。因为负阻器件与回路仅有两端 连接，故负阻振荡器又称为“二端振荡器”。 正功率表 达能量旳消耗，负功率表达能量旳产生，即负阻器件在 一定条件下，不但不消耗交流能量，反而向外部电路提 供交流能量，当然该交流能量并不存在于负阻器件内部， 而是利用其能量变换特征，从确保电路工作旳直流能量 中取得。所以负阻振荡器一样是一种能量变换器。
18
10.2.3 HgTe-CdTe超晶格
图10.16是取d1 =2d2 , d2和d2/2时旳计算成果，纵坐标用超 晶格旳禁带宽度Eg=E1-HHl表达看得更为清楚。这两个图阐明 ，只有当超晶格旳周期不不小于某个一定旳数值时，CdTeHgTe超晶格才具有半导体特征， 当周期不小于这个数值时 超晶格将具有半金属特征。
27
半导体超晶格中的调控电子结构研究
半导体超晶格中的调控电子结构研究介绍半导体超晶格是由不同的半导体材料交替排列而成，在其中会产生许多有趣的物理现象。
利用超晶格结构，可以调节材料的基态和激发态的能级，同时有效地控制电荷的输运和激子的重组。
因此，半导体超晶格已成为材料科学和器件学中的研究热点。
我将在本文中介绍半导体超晶格中的电子结构调控研究进展，包括如何通过超晶格的设计来调整电子能级和能带的形态，以及如何通过表面修饰、缺陷工程等手段来进一步调控电子结构。
超晶格设计半导体超晶格中，周期性的电势场会影响电子的行为。
通过改变超晶格的周期、形状和组成，可以调节电子结构。
其中最为常用的手段是调节超晶格的周期。
因为超晶格的周期与材料的基本晶格有相互关系，例如将不同半导体材料堆叠成超晶格，就可以调节基本晶格中禁带宽度的大小。
另外，通过调节超晶格中元胞数目的增加或减少，可以进一步分裂或扩张电子能级，同时也能够影响材料的输运性质。
调节电子能带超晶格中的电子波函数会产生布拉格反射，对于与布拉格波矢匹配的波矢，能级出现拓扑变化。
这种拓扑结构在半导体超晶格中被称为远程布拉格反射（remote Bragg reflection）。
许多研究表明，远程布拉格反射可以有效增强材料的光电转换效率，改善器件的响应和灵敏度。
同时，超晶格结构中存在的多个布拉格点可以扩张材料的禁带宽度，使其跨越光电响应的范围，具有广阔的应用前景。
不仅可以扩展禁带宽度，超晶格的结构还可以进一步调节材料的能带结构。
例如线性超晶格结构可以改变传统材料中的能带偏移现象，线性的能带结构也是在有机太阳能电池中被广泛采用的，来调节载流子的运动。
另外，超晶格材料的电子倒转效应也被广泛研究。
这种效应意味着畸变的晶格结构可以产生倒转能带结构，从而大大提高材料的光电能量收集效率和半导体激光的效率。
调控表面态超晶格中的表面态是调节材料电子结构的强有力方法之一。
在表面密度较高的超晶格中，质子将被分布在不同的材料中，从而形成一些新的表面态。
半导体光学12应变层超晶格
式中 l x
2
Lx
1
2
sl Eym Ezn,
式中
E xl
2 2
2m*e
nx2 L2x
,l
1,2 ,3 ,
E ym与Ezn 类似.)
单个量子点的能量是量子化的.
当量子点为边长为a的正方体时,
En
2 2
2m*e
n2 a2
,n2
l2
m2
n2
● p型半导体：主要靠空穴带电. ●受主电离能 A E A Ev .
Ⅲ族原子在Ge 和Si中 A 0.02 0.2eV
与室温下 kBT 可比,因此, 室温下受主杂质 绝大部分是电离的.掺入少量受主杂质可 使空穴浓度大大增加. ③浅能级杂质
●带电中心形成附加（短程）势场,有可能
使载流使子束缚在杂质或缺陷周围,产生 局域态,其能级位于能隙中. ●●类氢模型 严格理论可以证明：只要晶体中附加势 场变化足够缓慢,导带中电子在该势场中 的运动就可以由有效质量加以描述.电子 围绕正电中心的运动与围绕氢原子核的 运动完全相似,只是库仑势场的作用大大
削弱,
F
e2 4 0 r
, r
10.
Ge r 16, Si r 12.
束缚能为
EbD ,A
me ,h H
m0
2 r
me ,h 1
m0
2 r
Ry nB2
.
其中 Ry 13.6eV 为氢原子里德堡能量，
nB 为主量子数，ε为介电常数.
5meV EbD 50meV , 20meV EbA 200meV .
▲与应变结果（压缩、拉伸）有关的能 带分裂可以增加或部分抵消因量子化产 生的能带分裂。 5. 量子阱界面的起伏
半导体超晶格
半导体超晶格材料的制造、设计是以固体能带结构的量子力学理论为基础的，也就是说，人为地改变晶体的周期势，做出具有新功能的人工超晶格结构材料。
半导体超晶格材料具有一般半导体材料不能实现的许多新现象，可以说是超薄膜晶体制备技术，量子物理和材料设计理论相结合而出现的第三种类的半导体材料。
利用这种材料，不仅可以显著提高场效应晶体管和半导体激光器等的性能，也可以制备至今还没有的功能更优异的新器件和发现更多的新物理现象，使半导体器件的设计和制造由原来的“杂质工程”发展到“能带工程”。
因此，半导体超晶格是属于高科技范畴的新型功能材料。
电子亲和势是指元素的气态原子得到一个电子时放出的能量，叫做电子亲和势。
（曾用名：电子亲和能EA）单位是kJ/mol或eV。
电子亲和势的常用符号恰好同热力学惯用符号相反。
热力学上把放出能量取为负值，例如，氟原子F（g）+e→F-（g），△H=-322kJ/mol。
而氟的电子亲和势（EA）被定义为322kJ/mol。
为此，有人建议元素的电子亲和势是指从它的气态阴离子分离出一个电子所吸收的能量。
于是，氟离子F-（g）-e→F（g），△H＝322kJ/mol。
两者所用符号就趋于统一。
可以认为，原子的电子亲和势在数值上跟它的阴离子的电离能相同。
根据电子亲和势数据可以判断原子得失电子的难易。
非金属元素一般具有较大的电子亲合势，它比金属元素容易得到电子。
电子亲和势由实验测定，但目前还不能精确地测得大多数元素的电子亲和势。
元素的电子亲和势变化的一般规律是：在同一周期中，随着原子序数的增大，元素的电子亲和势一般趋于增大，即原子结合电子的倾向增强，或它的阴离子失去电子的能力减弱。
在同一族中，元素的电子亲合势没有明显的变化规律。
当元素原子的电子排布呈现稳定的s2、p3、p6构型时，EA值趋于减小，甚至ⅡA族和零族元素的EA都是负值，这表明它们结合电子十分困难。
在常见氧化物和硫化物中含有-2价阴离子。
从O-（g）或S-（g）结合第二个电子而变成O2-（g）或S2-（g）时，要受到明显的斥力，所以这类变化是吸热的。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
半导体超晶格
材料的制造、设计是以固体能带结构的量子力学理论为基础的，也
就是说，人为地改变晶体的周期势，做出具有新功能的人工超晶格
结构材料。
半导体超晶格材料具有一般半导体材料不能实现的许
多新现象，可以说是超薄膜晶体制备技术，量子物理和材料设计理
论相结合而出现的第三种类的半导体材料。
利用这种材料，不仅可
以显著提高场效应晶体管和半导体激光器等的性能，也可以制备
至今还没有的功能更优异的新器件和发现更多的新物理现象，使
半导体器件的设计和制造由原来的“杂质工程”发展到“能带工
程”。
因此，半导体超晶格是属于高科技范畴的新型功能材料。
电子亲和势是指元素的气态原子得到一个电子时放出的能量，叫做电子亲和势。
（曾用名：电子亲和能EA）单位是kJ/mol或eV。
电子亲和势的常用符号恰好同热力学惯用符号相反。
热力学上把放出能量取为负值，例如，氟原子F（g）+e→F-（g），△H=-322kJ/mol。
而氟的电子亲和势（EA）被定义为322kJ/mol。
为此，有人建议元素的电子亲和势是指从它的气态阴离子分离出一个电子所吸收的能量。
于是，氟离子F-（g）-e→F（g），△H＝322kJ/mol。
两者所用符号就趋于统一。
可以认为，原子的电子亲和势在数值上跟它的阴离子的电离能相同。
根据电子亲和势数据可以判断原子得失电子的难易。
非金属元素一般具有较大的电子亲合势，它比金属元素容易得到电子。
电子亲和势由实验测定，但目前还不能精确地测得大多数元素的电子亲和势。
元素的电子亲和势变化的一般规律是：在同一周期中，随着原子序数的增大，元素的电子亲和势一般趋于增大，即原子结合电子的倾向增强，或它的阴离子失去电子的能力减弱。
在同一族中，元素的电子亲合势没有明显的变化规律。
当元素原子的电子排布呈现稳定的s2、p3、p6构型时，EA值趋于减小，甚至ⅡA族和零族元素的EA都是负值，这表明它们结合电子十分困难。
在常见氧化物和硫化物中含有-2价阴离子。
从O-（g）或S-（g）结合第二个电子而变成O2-（g）或S2-（g）时，要受到明显的斥力，所以这类变化是吸热的。
即O-（g）+e→O2-（g），△H＝780kJ/mol；S-（g）+e→S2-（g），△H＝590kJ/mol。
这些能量能从形成氧化物或硫化物晶体时放出的晶格能得到补偿。
电子亲和势与原子失去电子需消耗一定的能量正好相反，电子亲和势是指原子获得电子所放出的能量。
元素的一个气态原子在基态时获得一个电子成为气态的负一价离子所放出的能量，称为该元素的第一电子亲和势(First electron affinity)。
与此类推，也可得到第二、第三电子亲和
势。
第一电子亲和势用符号“E”表示，单位为kJ·mol·L，如：
Cl(g) +e → Cl(g)E= +348.7 kJ·mol·L
大多数元素的第一电子亲和势都是正值（放出能量），也有的元素为负值（吸收能量）。
这说明这种元素的原子获得电子成为负离子时比较困难，如：
O(g) +e → O(g)E= +141 kJ·mol·L
O(g) +e → O(g)E= -780 kJ·mol·L
这是因为，负离子获得电子是一个强制过程，很困难须消耗很大能量。
应该注意的是，超晶格和多量子阱都是周期排列的超薄层异
质结构，人们有时将它们混为一谈，但由于它们的势垒高度和厚度不同，其物理特性还是有区别的，当势垒足够厚(如>2}nm)和高}}};>}}* }e)时，相邻阱中的电子波函数不发生交叠，则这种结
构材料中的电子行为如同单个阱中电子行为的简单的总和，这种材料通常称之为多量子阱材料。
这种材料适于制作低阈值，窄谱线的发光器件。
如果势垒比较薄高度比较低时，由于隧道共振效应，使阱中的龟子隧穿势垒，势阱中的分立的电于能级形成了具有一定宽度的子能带，这种材料称为超晶格，它适于制备大功率的发光器件。