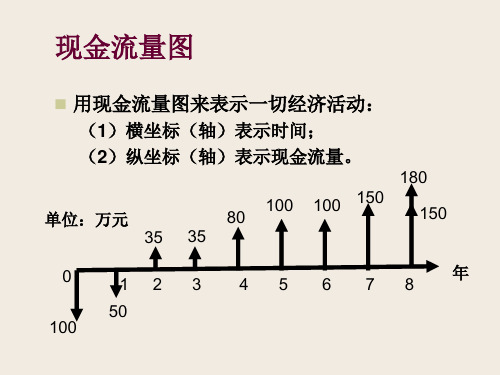
等值计算的例子
资金等值计算的实例分析

资金等值计算的实例分析在投资和财务决策中,资金等值计算是一种常用的方法,用于评估不同项目或投资方案之间的经济效益。
通过将不同项目的未来现金流量以及时间价值考虑在内,我们可以比较不同项目之间的利润率和回收期,并做出正确的决策。
本文将通过一个实例来演示资金等值计算的具体步骤和应用方式。
假设某公司正在考虑投资两个不同的项目:项目A和项目B。
为了更好地评估这两个项目的经济效益,我们需要考虑以下几个关键因素:项目的预期现金流量、投资成本以及折现率。
首先,让我们来分析项目A。
该项目的预期现金流量如下:第一年:100万元第二年:200万元第三年:300万元第四年:400万元第五年:500万元项目A的投资成本为600万元。
为了将这些现金流量的未来价值进行比较,我们需要选择适当的折现率。
在这个例子中,假设公司决定使用10%的折现率。
现在我们来计算项目A的资金等值。
根据资金等值计算的公式,我们可以得到:资金等值 = 第一年现金流量 / (1 + 折现率) ^ 第一年 + 第二年现金流量 / (1 + 折现率) ^ 第二年 + ... + 第五年现金流量 / (1 + 折现率) ^ 第五年- 投资成本将以上数据带入公式,我们可以计算出项目A的资金等值:资金等值 = 100万元 / (1 + 0.1) ^ 1 + 200万元 / (1 + 0.1) ^ 2 + 300万元 / (1 + 0.1) ^ 3 + 400万元 / (1 + 0.1) ^ 4 + 500万元 / (1 + 0.1) ^ 5 - 600万元计算得出,项目A的资金等值为181.81万元。
接下来,我们来分析项目B。
假设项目B的预期现金流量如下:第一年:150万元第二年:250万元第三年:350万元第四年:450万元第五年:550万元项目B的投资成本为500万元,折现率仍然为10%。
使用相同的公式和计算步骤,我们可以计算出项目B的资金等值:资金等值 = 150万元 / (1 + 0.1) ^ 1 + 250万元 / (1 + 0.1) ^ 2 + 350万元 / (1 + 0.1) ^ 3 + 450万元 / (1 + 0.1) ^ 4 + 550万元 / (1 + 0.1) ^ 5 - 500万元计算得出,项目B的资金等值为282.14万元。
备用:资金等值计算六个公式

资金等值计算公式
2. 等额分付复利公式 (1)等额分付终值公式 0 1 A 2 3 …
F =?
n
F A(1 i ) n 1 A(1 i ) n 2 A(1 i ) A A[1 (1 i ) (1 i ) n 2 (1 i ) n 1 ] 1[1 (1 i ) n ] A 1 (1 i ) (1 i ) n - 1 A i (1 i ) n - 1 其中 称为等额分付终值系数 ,用( F / A, i, n)表示。 i
第2章 资金等值计算/2.2资金等值计算 2.2.2 资金等值计算公式
2. 等额分付复利公式 (2)等额分付偿债基金公式 0 1 2 A=? 3 … F n
(1 i ) n 1 F A i i AF (1 i ) n 1 i 称为偿债基金系数,用 ( A / F , i , n)表示。 n (1 i ) 1
70
解:X = -100(F/P, 0.10, 3)-70(F/P, 0.10, 2) +90(P/F, 0.10, 1)+150(P/F, 0.10, 4) = -100(1.331)-70(1.21)+90(0.9091)+150(0.6830) = -133.1-84.7+81.819+102.45 = -33.531 (万元)
1. 一次支付复利公式 (2)一次支付现值公式 例:某人打算在5年后买100000元的车,已知年利率为10%,那么他现在需 在银行存多少钱? 解: F =100000,i =10%, n =5年 P = F(1+i)-n = F(P/F, i, n) = 62092 (元) 0 P=? 1 2 3 4 5 F=100000
一建工程经济公式

一建工程经济公式一建工程经济公式,这可是让很多考生头疼的一块儿!但别怕,咱们一起来捋捋。
先来说说资金等值计算的公式。
比如说,一次支付终值公式,F =P(1 + i)^n,这就像你把一笔钱存银行,利率是 i ,存了 n 年,最后能拿到的钱就是 F 。
我记得有一次,我朋友小李准备买房,东拼西凑了一笔首付款,想着把剩下的钱做个理财。
他就来问我这个公式,我给他解释,就好比他现在有 10 万块,年利率 5%,存 5 年,用这个公式就能算出 5 年后他能拿到多少钱。
再看等额支付终值公式,F = A×[(1 + i)^n - 1]/i 。
这个就像是你每个月固定存一笔钱 A ,利率是 i ,存了 n 年,最后能得到的总数。
我有个同事老张,他每个月都坚持定投基金 2000 块,年利率 8%,投了 10 年,我们就可以用这个公式算出10 年后他的这笔投资总值大概是多少。
还有等额支付现值公式,P = A×[(1 + i)^n - 1]/[i×(1 + i)^n] 。
比如说,你想买一辆车,每个月能承受的还款是A ,利率是i ,还款期限是n ,那用这个公式就能算出你最多能贷款多少钱去买车。
我家亲戚小王,想买车但又不想压力太大,每个月最多还 3000 块,贷款年利率 6%,打算还 3 年,用这个公式一算,就清楚自己能贷款的额度了。
静态投资回收期的公式也很重要,Pt = (累计净现金流量出现正值的年份数 - 1)+ 上一年累计净现金流量的绝对值 / 出现正值年份的净现金流量。
这个公式能帮咱们判断一个项目靠不靠谱,回收投资得多久。
就像之前我参与的一个小项目,前两年都在投入,第三年开始有正的现金流,我们就用这个公式算算,看看投资回收的时间是不是在预期内。
还有财务净现值的公式,FNPV = ∑(CI - CO)t(1 + ic)^(-t) 。
这个公式能衡量一个项目在财务上是不是值得做。
比如说有个新开的餐厅项目,我们预测每年的收入和支出,再给定一个基准收益率,用这个公式一算,就能知道这个餐厅未来的财务净现值是正还是负,值不值得投资。
资金的等值计算

计息期 年
一年中的计息期数 各期的有效利率 1 12.0000%
年有效利率 12.000%
半年
季度 月 周 日 连续
2
4 12 52 365
6.0000%
3.0000% 1.0000% 0.2308% 0.0329% 0.0000%
12.360%
12.551% 12.683% 12.736% 12.748% 12.750%
2.0000 1.9671 0.07 0.0017 7.17% 2.1589 1.9671
计息期与支付期相同
例2:某人要购买一处新房,一家银行提供20年期年 利率为6%的贷款30万元,该人每年要支付多少? 解:
A P A i , N 30 A 6, 20 30 0.0872 2.46 (万元) P P
FA F
A
i , N 1400 F
A
2,64 178604.53 (元)
计息期短于支付期
例7:年利率12%,每季度计息一次,每年年 末支付500元,连续支付6年,求其第0年的现 值为多少? 解:其现金流量如图
计息期短于支付期
计息期为季度,支付期为1年,计息期短于支付 期,该题不能直接套用利息公式。 需使计息期与支付期一致起来,计算方法有三种 方法一,计息期向支付期靠拢,求出支付期的有 效利率。 4 年有效利率 0.12
①当计息周期为一年时,名义利率和实际利率相等,
计息周期短于一年时,实际利率大于名义利率。
②名义利率不能是完全反映资金时间价值,实际利率 才真实地反映了资金的时间价值。 ③令i为实际利率,r为名义利率,m为复利的周期数, 则实际利率与名义利率间存在着下述关系:
资金等值计算计算题

1.一次支付终值公式例1:一次存款1万元,i =5%,存10年,则10年后连本带息可得多少?==+=)10%5(10000%)51(1000010,,P F F 10000×1.629=16290元 例2:某厂进行技术改造,2003年初贷款100万元,年利率为6%,2005年末一次偿还,问共还款多少万元?P F =()n i P F ,,=100()3%,6,P F =100×1.191=119.1万元2.一次支付现值公式例3:某工程第一期投资1500万元,第二期10年后再投资1600万元,年利率为8%,问总投资的现值是多少? P=1500+1600×()/,8%,10P F =1500+741=2241万元 例4:某项目投资情况如下,第1年年初100万,第2年年末200万,第3年年初100万,第4年年末300万,第5年年末150万,i =5%,求:①与现金流量图等值的现值?②与现金流量图等值的第10年末终值?解①P=()()()5%,5,1504%,5,3002%,5,300100F P F P F P +++=100+272.1+246.81+117.525=736.435解②F =()()()()10%,5,1008%,5,3006%,5,3005%,5,150P F P F P F P F +++=191.4+845.1+162.9=1199.43.等额支付终值公式例5:某人每年年末向银行存入8000元,连续10年,若银行年利率为8%,问10 年后共有本利和多少?解:(,,)F=8000×14.487=115896元F A i nA例6:从第1年至第5年,每年年末存入银行2000元,银行年利率为5%,求第8年年末的本利和。
4.等额分付偿债基金公式(等额分付终值公式的逆运算)例7:某厂欲积累一笔设备更新基金,用于4年后更新设备。
此项投资总额为500万元,银行利率12%,问每年末至少要存款多少?=104.62万元A=F×(,,)A i nF5.等额分付现值公式例8:某设备经济寿命为8年,预计年净收益20万元,残值为0,若投资者要求的收益率为20%,问投资者最多愿意出多少的价格购买该设备?P=A×(,,)=76.74万元P i nA例9:从第3年年末~第7年年末,每年要从银行支取5000元,i=4%,求与之等值的现值?6.等额分付资金回收公式(等额分付现值公式的逆运算)例10:某投资项目贷款200万元,银行4年内等额收回全部贷款,已知贷款利率为10%,那么项目每年的净收益不应少于多少万元?=63.09万元A=P×(,,)A i nP例11:某人第一年初存入10000元,i=4%,从第3年年末~第7年年末,每年等额提取,问每年应提取多少?四、资金等值公式的应用1.等值计算例1:某人2002年至2004年每年年末存款500元,并计划从2006年至2009年每年年末存款1000元,年利率假设为10%。
等值计算的例子讲解
1.一次支付终值公式
F=?
0
P
1
2
3
n-1
n
计算公式:
F=P (1+ i)n F=P (F/P,i,n)
课堂练习:一份遗书上规定有250000元留给未
成年的女儿,但是,暂由她的保护人保管8年。 若这笔资金的利率是 5%,问8年后这位女孩可 以得到多少钱?
F=?
0 P
1
2
3
7 n-1
8 n
解:F= P(1+ i)n =250000×(1+0.05)8 = 369250元 F= P(F/P,i,n) =250000 ×1.477 = 369250元
例: 商业住房按揭贷款
杭州商业银行按揭贷款的年名义利率 r = 5.04%,每年计息12次
年实际利率i =(1 + r/m)m
- 1
=(1 + 5.04%/12)12 – 1 = 5.158% i>r
资金等值的概念
资金等值——是指在考虑资金时间价值因素后,
不同时点上数额不等的资金在一定利率条件下具 有相等的价值。
当m =1时,i=r;m>1时,i >r;m
∞时,即 一年中无限多次计息,连续复利计算。这时的实际利 率称连续利率。
例: 从银行借入资金10万元,年名义利率r为12%,
分别按每年计息1次以及每年计息12次,求年实际利率i 和本利和F? 解:若每年计息1次 i=(1+r/m)m -1=(1+0.12/1)1 -1=12% F=P(1+i)n=10×1.12=11.2万元 若每年计息12次 i= (1+0.12/12)12 -1 =12.68% F=P(1+i)n=10×1.1268=11.268万元 即:m>1时,实际利率i大于名义利率r,计息次数 越多,实际利率i越高。
资金时间价值与等值计算例题

资金时间价值与等值计算例题2答案1、某人在第一年初存入10000元,第三年初存入20000元,存款年利率为5%,复利计息,第五年末一次性取出,问共可取出多少钱?作出现金流量图。
解:运用一次支付终值公式将这两笔存款分别折算到第年末,再相加即得。
F′=10000×(1+5%)5=12762.82 (元),F″=20000×(1+5%)3=23152.50 (元) F=F′+F″=12762.82+23152.50=35915.32(元)2、某人从第一年末开始,每年存款5000元,共存五年,利率为6%,问第五年末共可取出多少钱?取出的这笔钱相当于第一年初多少钱?作出现金流量图。
分析:已知A,i,n,运用等额支付终值公式求F,再对已经求得的F用一次支付现值公式求现值P;或者直接根据已知的A,i,n,运用等额支付现值公式求P。
解:F=5000×[(1+6%)5-1]/6%=28185.46(元)P=28185.46/(1+6%)5=21061.82 (元),或者P=5000×[(1+6%)5-1]/[6%×(1+6%)5]=21061.82 (元)3、某人准备在三年后用100000元购买一辆轿车,若从现在起每年年末存入银行等额的钱,存期三年,利率为4%,这笔等额的钱是多少?如果是在第一年初一次性存入一笔钱用于三年后买车,应存多少?作出现金流量图。
分析:已知F,i,n,运用等额支付偿债基金公式求A,运用一次支付现值公式求P。
解:A=100000×4%/[(1+4%)3-1]=32034.85(元)P=100000/(1+4%)3=88899.64 (元)。
4、某人投资1000000元,投资收益率为8%,每年等额收回本息,共六年全部收回,问每年收回多少钱?作出现金流量图。
分析:已知P,i,n,运用等额支付投资回收公式求A。
解:A=1000000×8%×(1+8%)6/[(1+8%)6-1]=216315.39(元)5、某人欲从今年起,每年末得到10000元,共二十年。
等值换算例题

等值计算公式的应用1. 预付年金的等值计算【例1】:某人每年年初存入银行5000元,年利率为10%,8年后本利和是多少?解: 查教材P.298的复利系数表知,该系数为11.4359【例2】:某公司租一仓库,租期5年,每年年初需付租金12000元,贴现率为8%,问该公司现在应筹集多少资金? 解法1:解法2:解法3:2. 延期年金的等值计算【例3】:设利率为10%,现存入多少钱,才能正好从第四年到第八年的每年年末等额提取2万元?解:45.62897%)101()8%,10,/(5000=+⋅=A F F 39.51745%)81()5%,8,/(12000=+⋅=A P P39.51745)4%,8,/(1200012000=+=A P P 39.51745)4%,8,/()5%,8,/(12000=⋅=F P A F P 7.5)3%,10,/()5%,10,/(2=⋅=F P A P P【例4】:若利率为6%,现存入多少可使今后30年每6年末提取2000元?解:P =2000(A/F ,6%,6)(P/A ,6%,30) =3947.73. 永续年金的等值计算【例5】:某地方政府一次性投入5000万元建一条地方公路,年维护费为150万元,折现率为10%,求现值。
解:该公路可按无限寿命考虑,年维护费为等额年金,可利用年金现值公式求当n →∞时的极限来解决。
i A i i i A P n n n =⎥⎦⎤⎢⎣⎡+-+⋅=∞→)1(1)1(lim4. 求解未知的i【例6】:15年前,某企业投资10000元建厂,现拟卖出该厂得25000元,这10000元的收益率是多少?解法1:F=P(F/P,i,15)(F/P,i,15)=2.5i F/P i F/P i F/P6% 2.397 2.5 8% 3.1726. 计息周期小于资金收付周期的等值计算【例7】:每半年存款1000元,年利率8%,每季计息一次,复利计息。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
(1 + i )n 1 i (1 + i )n
i (1 + i )n (1 + i )n 1
等额分 付系列
A P A F
A =F(A/F, i, n)
P= A(P/A, i, n)
A =P(A/P, i, n)
1 (1 + i )n 1 n i i
解: 单利计息法公式:F前3年=P(1+ i n) 复利计息法公式:F后4年=P(1+ i)n
F=10000(1+10%×3)(1+10%)4
=19033元
最后可收回本利和是19033元。
名义利率和实际利率
计息周期——一年内计算利息周期的次数,用m来表
示。计息周期有年、半年、季、月、周、日等。 实际利率——将计息周期实际发生的利率称为计息周 期实际利率,用 i来表示。 名义利率——计息周期的实际利率乘以每年计息周期 数就得到名义利率,用 r来表示。 实际利率 i =(1 + r/m)m -1
影响资金等值的因素有三个:
资金额大小;资金发生的时间;利率 将一个时点发生的资金金额换算成另一时点的等 值金额,这一过程叫资金等值计算。
资金等值换算的几个重要概念:
贴现与贴现率——把将来某一时点处资金金额折算成
现在时点的等值金额称为贴现或折现。贴现时所 用的利率称贴现率或折现率,用 i 表示。
练习:有一家小饭店要转让,合同期为8年,预 计年净收益20万元,若投资者要求的年收益率为 20%,问投资者最多愿意出多少价格接手小饭店?
A=20 i=20%
0
P=?
:P=A×(P/A,i ,n) =20 × (P/A,20% ,8) = 20 ×3.837 =76.74(万元)
综合的例子:一位发明者转让其专利使用权,一种收
n
F =P (1+i )n i A =F (1+i)n -1 (1+i )n i A =P (1+i)n -1
练习:某投资项目贷款200万元,银行要求在
10年内等额收回全部贷款,已知贷款利率为10 %,那么项目每年的净收益不应少于多少万元?
A=? 1 2 3 9 10
i=10%
0 P=200
例:从银行借款100元, i=10%,三年后本利和为
年初欠款 100 110 121 年末欠利息 10 11 12.1 年末欠本利和 110 121 133.1
年份 1 2 3
复利计算公式为:本利和(终值)F=P(1+ i)n (F——本利和或终值;P——现值;i——利率;n——年限)
例:
某人把10000元,按利率10%(以单利计息) 借给朋友3年。3年后,改以复利计息,朋友又使用 了4年。最后他从朋友那里收回的本利和F是多少?
练习:某人学习了工程经济学课程以后,了解到达
到富裕的最佳决策及实施这一决策的方法是利用货 币的增殖能力。如果他希望在年满59岁退休时拥有 100万元,他决定从25岁生日时就开始投资,假定 投资的年收益率为 10%,则从第 25个生日起,到 第59个生日止,每个生日必须投资多少?
i=10% F=100
25
26
27
A=?
59
解:A =F(A/F,i ,n) =100 × (A/F,10% ,35) = 100 × 0.00369=0.369(万元)
5.等额分付现值公式
A 0 1 2 3 n-1 n
P=?
(1+i )n -1 P = A i(1+i )n
P=A×(P/A,i ,n)
(1+i)n -1 F = A i F P= (1+i )n (1+i )n -1 P = A i(1+i )n
2.一次支付现值公式
F
0 P=?
1
2
3
n-1
n
P=F× (1+ i )-n
P=F×(P/F,i ,n)
课堂练习:某刚刚参加工作的大学生欲筹备未来结
婚费用,打算5年后从银行得到10万元,如果银 行利率为12%,问现在应存入银行多少钱?
F=10 0 P=?
1
2
3
4
5
解:P=F(1+ i)-n = 10×(1+12% )-5 =5.67万 元
系数代数式
(1 + i )n
1 (1 + i )n
公式
F=P(F/P, i, n)
P=F(P/F, i, n)
P
F
F
A F A P G
(P/F, i, n)
(F/A,i,n) (A/F,i, n) (P/A,i,n) (A/P,i,n) (F/G,i,n)
(1 + i )n - 1 F= A(F/A, i, n) i
A=F (A/F,i ,n)
课堂练习:一对夫妇欲积累一笔育儿基金,用于5
年后供孩子上大学用。此项基金约需要6万元,银行 利率12%,问每年末至少要存款多少?
i=12% 0 1 2 3 A=? 4 5 F=6
解:A =F(A/F,i ,n)=6×(A/F,12% ,5) = 6 × 0.15741 =0.9445(万元)
解:A = P(F/P,10%,1)(A/P,10%,5) =100×1.100×0.2638=29.018万元 A = 100(F/P,10%,6)(A/F,10%,5) = 100×1.722 ×0.1638 = 29.016万元
总结:等值计算公式
类别
一次支 付系列
求解
F
已知
P
复利系数
(F/P,i,n)
当m =1时,i=r;m>1时,i >r;m
∞时,即 一年中无限多次计息,连续复利计算。这时的实际利 率称连续利率。
例: 从银行借入资金10万元,年名义利率r为12%,
分别按每年计息1次以及每年计息12次,求年实际利率i 和本利和F? 解:若每年计息1次 i=(1+r/m)m -1=(1+0.12/1)1 -1=12% F=P(1+i)n=10×1.12=11.2万元 若每年计息12次 i= (1+0.12/12)12 -1 =12.68% F=P(1+i)n=10×1.1268=11.268万元 即:m>1时,实际利率i大于名义利率r,计息次数 越多,实际利率i越高。
2
3
解:P前5年= A1(P/A,10%,5)=45492元
P后7年=A2(P/A,10%,7)(P/F,10%,5)=18135元 P= P前5年+P后7年=63627 元
6、资金回收公式
A=? 0 1 2 3 n-1 n
P
i(1+i ) A =P (1+i )n -1
A=P×(A/P,i ,n)
例: 商业住房按揭贷款
杭州商业银行按揭贷款的年名义利率 r = 5.04%,每年计息12次
年实际利率i =(1 + r/m)m
- 1
=(1 + 5.04%/12)12 – 1 = 5.158% i>r
资金等值的概念
资金等值——是指在考虑资金时间价值因素后,
不同时点上数额不等的资金在一定利率条件下具 有相等的价值。
P =F(P/F,12%,5)= 10×0.5674=5.67 万元
3.等额分付终值公式
F=? 0 A 1 A
n
2 A
3 A
n-1 A
n
(1+i ) -1 F = A i F=A (F/A,i ,n)
课堂练习:一位工作了3年的大学生想购买一套房子,
他从 25岁起每年末向银行存入8 000元,连续存10 年,若银行年利率为8%,问10年后共有多少本利和?
6 7 100
8
9
10
年
200
第二节 资金的时间价值及其等值计算
资金时间价值——不同时间发生的等额资金在价
值上的差别称为资金的时间价值。
从两方面理解:
从投资者的角度看,资金的时间价值表现为资金 运动过程中价值的增值。
从消费者的角度看,资金一旦用于投资,就不能 用于消费。资金的时间价值体现为放弃现期消费 的损失所得到的必要补偿。
益方式是在今后5年里每年收到12000元,随后又连 续7年每年收到6000元,另一种收益方式是将前种收 益形式改为一次性付款。在不考虑税收的情况下,如要 求年收益率10%,投资者选择后一种方式,即一次性 购买专利权的价格为多少?
i=10%
A1 =12000
A2 =6000
5 6 11 12
0
P=?
1
1.一次支付终值公式
F=?
0
P
1
2
3
n-1
n
计算公式:
F=P (1+ i)n F=P (F/P,i,n)
课堂练习:一份遗书上规定有250000元留给未
成年的女儿,但是,暂由她的保护人保管8年。 若这笔资金的利率是 5%,问8年后这位女孩可 以得到多少钱?
F=?
0 P
1
2
3
7 n-1
8 n
解:F= P(1+ i)n =250000×(1+0.05)8 = 369250元 F= P(F/P,i,n) =250000 ×1.477 = 369250元
i=8% 0 1 8000 2 8000 3 8000 9 8000 F=? 10 8000
(1+i )n -1 F = A i
F=A(F/A,i ,n) = 8000×(F/A,8% ,10) =8000 ×14.487 = 115892元
