2013届高考数学第一轮专题复习测试卷 第一讲 坐标系
2013届高考数学一轮复习讲义：8.6 立体几何中的向量方法(Ⅰ) 证明平行与垂直
1 1 3 3 → → ∴AE· ＝－ × ＋ × ＝0， CD 2 4 6 4 → → ∴AE⊥CD，即 AE⊥CD.
→ 2 3 (2)方法一 ∵P(0,0,1)，∴PD＝0， ，－1. 3 3 2 3 1 → → 又AE· ＝ × PD ＋ ×(－1)＝0， 4 3 2 → → ∴PD⊥AE，即 PD⊥AE. → → → ∵AB＝(1,0,0)，∴PD· ＝0， AB
建立如图所示的空间直角坐标系 A—xyz， 则 A(0,0,0)、B(2,0,0)、C(2,2,0)、D(0,2,0)、 P(0,0,2)、E(0,0,1)、F(0,1,1)、G(1,2,0)． → → ∴PB＝(2,0，－2)，FE＝(0，－1,0)， → FG＝(1,1，－1)，
→ → → 设PB＝sFE＋tFG， 即(2,0，－2)＝s(0，－1,0)＋t(1,1，－1)， t＝2， ∴t－s＝0， －t＝－2， 解得 s＝t＝2.
(－2,1,0)． → → 因为 n⊥BA1，n⊥BD，
→ －x＋2y＋ 3z＝0， n· 1＝0， BA 故 ⇒ －2x＋y＝0， → n· ＝0 BD 令 x＝1，则 y＝2，z＝－ 3，故 n＝(1,2，－ 3)为平面 A1BD 的 → 一个法向量，而AB1＝(1,2，－ 3)， → → 所以AB1＝n，所以AB1∥n，故 AB1⊥平面 A1BD.
→ → 设平面 A1BD 的法向量为 n＝(x，y，z)，BA1＝(－1,2， 3)，BD＝
利用空间向量解决探索 性问题
例 3 如图，四棱锥 P—ABCD 中，PA⊥平 面 ABCD，PB 与底面所成的角为 45° ， 底面 ABCD 为直角梯形，∠ABC＝ 1 ∠BAD＝90° ，PA＝BC＝ AD＝1. 2 (1)求证：平面 PAC⊥平面 PCD； (2)在棱 PD 上是否存在一点 E， CE∥平面 PAB？若存在， 使 请确定 E 点的位置；若不存在，请说明理由．
2013版高考数学一轮复习精品学案选修系列(第1部分坐标系与参数方程)
2013版高考数学一轮复习精品学案：选 修 系 列第一部分：坐标系与参数方程【高考新动向】一、坐标系 1．考纲点击（1）理解坐标系的作用，了解在平面直角坐标系伸缩变换作用下平面图形的变化情况；（2）了解极坐标的基本概念，会在极坐标系中用极坐标刻画点的位置。
能进行极坐标和直角坐标的互化；（3）能在极坐标系中给出简单图形（如过极点的直线、过极点或圆心在极点的圆）表示的极坐标方程。
2．热点提示（1）根据具体问题选择适当坐标系，简捷解决问题； （2）极坐标系的应用； （3）直角坐标与极坐标的互化。
二、参数方程 1．考纲点击（1）了解参数方程，了解参数的意义；（2）能选择适当的参数写出直线、圆和椭圆的参数方程。
2．热点提示（1）参数方程和普通方程互化；（2）会利用直线参数方程中参数的几何意义解决有关线段问题； （3）会利用圆、椭圆的参数方程，解决有关的最值问题。
【考纲全景透析】1．平面直角坐标系中的坐标伸缩变换设点P(x,y)是平面直角坐标系中的任意一点,在变换(0):(0)x xy yλλϕμμ'=>⎧⎨'=>⎩的作用下,点P(x,y)对应到点(,)P x y ''',称ϕ为平面直角坐标系中的坐标伸缩变换,简称伸缩变换.2.极坐标系的概念 (1)极坐标系如图所示,在平面内取一个定点O ,叫做极点,自极点O 引一条射线Ox ,叫做极轴;再选定一个长度单位,一个角度单位(通常取弧度)及其正方向(通常取逆时针方向),这样就建立了一个极坐标系.注:极坐标系以角这一平面图形为几何背景,而平面直角坐标系以互相垂直的两条数轴为几何背景;平面直角坐标系内的点与坐标能建立一一对应的关系,而极坐标系则不可.但极坐标系和平面直角坐标系都是平面坐标系.(2)极坐标设M 是平面内一点,极点O 与点M 的距离|OM|叫做点M 的极径,记为ρ;以极轴Ox 为始边,射线OM 为终边的角xOM ∠叫做点M 的极角,记为θ.有序数对(,)ρθ叫做点M 的极坐标,记作(,)M ρθ.一般地,不作特殊说明时,我们认为0,ρ≥θ可取任意实数. 特别地,当点M 在极点时,它的极坐标为(0, θ)(θ∈R).和直角坐标不同,平面内一个点的极坐标有无数种表示.如果规定0,02ρθπ>≤<,那么除极点外,平面内的点可用唯一的极坐标(,)ρθ表示;同时,极坐标(,)ρθ表示的点也是唯一确定的.3.极坐标和直角坐标的互化(1)互化背景:把直角坐标系的原点作为极点,x 轴的正半轴作为极轴,并在两种坐标系中取相同的长度单位,如图所示:(2)互化公式:设M 是坐标平面内任意一点,它的直角坐标是(,)x y ,极坐标是(,)ρθ(0ρ≥),于是极坐标与直角坐标的互化公式如表:在一般情况下,由tan θ确定角时,可根据点M 所在的象限最小正角. 4.常见曲线的极坐标方程注:由于平面上点的极坐标的表示形式不唯一,即(,),(,2),(,),(,),ρθρπθρπθρπθ+-+--+都表示同一点的坐标,这与点的直角坐标的唯一性明显不同.所以对于曲线上的点的极坐标的多种表示形式,只要求至少有一个能满足极坐标方程即可.例如对于极坐标方程,ρθ=点(,)44M ππ可以表示为5(,2)(,2),444444ππππππππ+-或或(-)等多种形式,其中,只有(,)44ππ的极坐标满足方程ρθ=. 二、参数方程 1.参数方程的概念一般地,在平面直角坐标系中,如果曲线上任意一点的坐标,x y 都是某个变数t 的函数()()x f t y g t =⎧⎨=⎩①,并且对于t 的每一个允许值,由方程组①所确定的点(,)M x y 都在这条曲线上,那么方程①就叫做这条曲线的参数方程,联系变数,x y 的变数t 叫做参变数,简称参数,相对于参数方程而言,直接给出点的坐标间关系的方程叫做普通方程.2.参数方程和普通方程的互化(1)曲线的参数方程和普通方程是曲线方程的不同形式,一般地可以通过消去参数而从参数方程得到普通方程.(2)如果知道变数,x y 中的一个与参数t 的关系,例如()x f t =,把它代入普通方程,求出另一个变数与参数的关系()y g t =,那么()()x f t y g t =⎧⎨=⎩就是曲线的参数方程,在参数方程与普通方程的互化中,必须使,x y的取值范围保持一致.注：普通方程化为参数方程，参数方程的形式不一定唯一。
【备战】高考数学 全国统考区(甘肃、贵州、云南)精选试题分类汇编18 坐标系与参数方程 理
备战2014年高考之2013届全国统考区（甘肃、贵州、云南）精选理科试题（大部分详解）分类汇编18：坐标系与参数方程一、解答题1 ．（云南省部分名校2013届高三第一次统一考试理科数学（玉溪一中、昆明三中、楚雄一中））选修4—4：极坐标和参数方程 已知直线l 的参数方程为⎩⎨⎧=+=ty tx 32 (t 为参数)，曲线C 的极坐标方程为12cos 2=θρ(1)求曲线C 的普通方程；(2)求直线l 被曲线C 截得的弦长.【答案】从而弦长为|t 1－t 2|＝t 1＋t 22－4t 1t 2＝42－4×－62 ．（云南省玉溪一中2013届高三第五次月考理科数学）坐标系与参数方程在平面直角坐标系xOy 中，椭圆C 方程为5cos (3sin x y ϕϕϕ=⎧⎨=⎩为参数）（1）求过椭圆的右焦点，且与直线42(3x tt y t=-⎧⎨=-⎩为参数）平行的直线l 的普通方程。
（2）求椭圆C 的内接矩形ABCD 面积的最大值。
【答案】（1）由已知得椭圆的右焦点为()4,0，已知直线的参数方程可化为普通方程：220x y -+=，所以12k =,于是所求直线方程为240x y -+=。
（2）460sin cos 30sin S xy ϕϕ===2ϕ， 当22πϕ=时，面积最大为30。
3 ．（云南省昆明三中2013届高三高考适应性月考（三）理科数学）（本小题满分10分）选修4—4：坐标系与参数方程在直角坐标系xoy 中，直线l 经过点P （-1，0），其倾斜角为α，以原点O 为极点，以x 轴非负半轴为极轴，与直角坐标系xoy 取相同的长度单位，建立极坐标系.设曲线C 的极坐标方程为26cos 50.ρρθ-+=（1）若直线l 与曲线C 有公共点，求α的取值范围； （2）设()y x M ,为曲线C 上任意一点，求x y +的取值范围.【答案】解：（1）将曲线C 的极坐标方程2-6cos 50ρρθ+=化为直角坐标方程为22650x y x +-+=-----------1分 直线l 的参数方程为1cos sin x t y t αα=-+⎧⎨=⎩ （t 为参数） ----------2分将1cos sin x t y t αα=-+⎧⎨=⎩代入22650x y x +-+=整理得28c o s 120t t α-+=-------------3分直线l 与曲线C 有公共点，264cos 480α∴∆=-≥cos cos 22αα∴≥≤--------------4分[)0,,απα∈∴的取值范围是50,,66πππ⎡⎤⎡⎫⋃⎪⎢⎥⎢⎣⎦⎣⎭-----------5分(2)曲线C 的方程22650x y x +-+=可化为()2234x y -+=，其参数方程为32cos 2sin x y θθ=+⎧⎨=⎩（θ为参数）---------6分(),M x y 为曲线C上任意一点，32c o 2s i n 322s4x y πθθθ⎛⎫∴+=++=++ ⎪⎝⎭-------8分 x y∴+的取值范围是33⎡-+⎣--------------10分4 ．（【解析】贵州省四校2013届高三上学期期末联考数学（理）试题）已知点)sin ,cos 1(αα+P ，参数[]πα,0∈，点Q 在曲线C ：)4sin(29πθ+=r 上。
高三理科数学一轮复习试题选编坐标系与参数方程含答案
广东省2014届高三理科数学一轮复习试题选编25：坐标系与参数方程一、填空题1 ．（广东省茂名市2013届高三第一次模拟考试数学（理)试题）（坐标系与参数方程选做题)已知曲线C 的参数方程为2cos sin x y θθ=+⎧⎨=⎩ (θ为参数),则曲线C 上的点到直线3x —4y +4=0的距离的最大值为______________【答案】3;2 ．（广东省韶关市2013届高三第三次调研考试数学（理科）试题（word 版） )设M 、N 分别是曲线2sin 0ρθ+=和s ()4in πρθ+=上的动点,则M 、N 的最小距离是______13 ．（广东省揭阳市2013届高三3月第一次高考模拟数学(理）试题（含解析））(坐标系与参数方程选做题)已知曲线1C：ρ=和曲线2C：cos()4πρθ+=,则1C 上到2C 的距离等于的点的个数为__________。
【答案】3；将方程ρ=与cos()4πρθ+=222x y +=与20x y --=,知1C 为圆心在坐标原点，半径为的圆,2C 为直线,因圆心到直线20x y --=的距离为2,故满足条件的点的个数3n =。
4 ．（广东省揭阳一中2013届高三第三次模拟考试数学（理）试题）在极坐标系中,圆4cos ρθ=上的点到直线(sin cos )2ρθθ-=的最大距离为__________。
【答案】222+5 ．( 2013届广东省高考压轴卷数学理试题）已知曲线1C 的参数方程为（0≤θ<π)，直线l 的极坐标方程为4πθ=，()R ρ∈,则它们的交点的直角坐标为_______。
【答案】3030)66在直角坐标系中:曲线()221:105x C y y +=≥,直线:l y x =6 ．（广东省汕头市2013届高三3月教学质量测评数学(理）试题）已知直线l 方程是22x ty t =+⎧⎨=-⎩（t 为参数)，以坐标原点为极点.x 轴的正半轴为极轴建立极坐标系，圆C 的极坐标方程为ρ=2，则圆C 上的点到直线l 的距离最小值是___ 【答案】222-7 ．（广东省湛江一中等“十校"2013届高三下学期联考数学（理)试题）已知抛物线C 的参数方程为⎩⎨⎧==ty t x 882(t 为参数），若斜率为1的直线经过抛物线C 的焦点，且与圆222(4)(0)x y r r -+=>相切，则半径r =________.【答案】28 ．（广东省广州市2013届高三3月毕业班综合测试试题（一）数学（理)试题）(坐标系与参数方程选做题）在极坐标系中，定点32,2A π⎛⎫⎪⎝⎭，点B 在直线cos sin 0ρθθ=上运动，当线段AB 最短时,点B 的极坐标为_______.【答案】1116,π⎛⎫⎪⎝⎭答案可以是:11126k k ,(ππ⎛⎫+∈ ⎪⎝⎭Z )。
2013全国高考1卷理科数学试题与答案解析
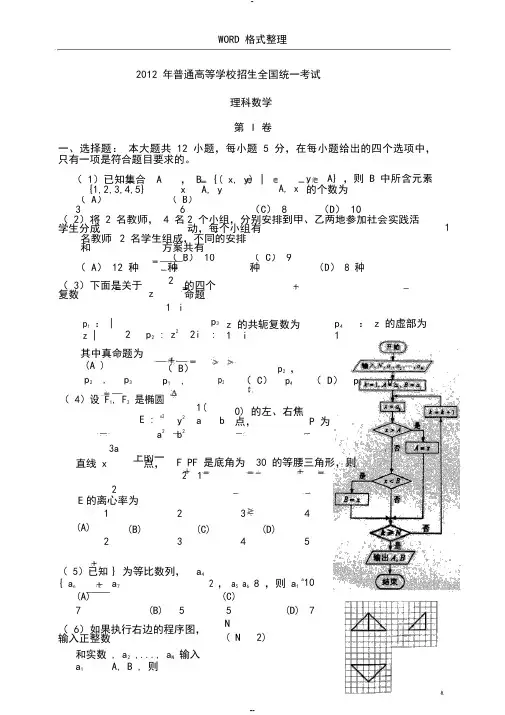
WORD 格式整理2012 年普通高等学校招生全国统一考试理科数学 第 I 卷一、选择题： 本大题共 12 小题，每小题 5 分，在每小题给出的四个选项中，只有一项是符合题目要求的。
（ 1）已知集合 A {1,2,3,4,5} ， B {( x, y) |x A, yA, x y A} ，则 B 中所含元素的个数为 （ A ） 3 （ B ）6 （C ） 8 （D ） 10（ 2）将 2 名教师， 4 名学生分成 2 个小组，分别安排到甲、乙两地参加社会实践活动，每个小组有1 名教师和2 名学生组成，不同的安排方案共有 （ A ） 12 种 （ B ） 10 种 （ C ） 9种 （D ） 8 种（ 3）下面是关于复数 z 2 的四个命题 1ip 1 ： | z | 2 p 2 : z 22i p 3 : z 的共轭复数为 1 i p 4 ： z 的虚部为1其中真命题为(A ) p 2 , p 3（ B ） p 1 ,p 2（ C ） p 2 ，p 4 （ D ） p 3 , p 4（ 4）设 F 1, F 2 是椭圆 E : x2 y 21(a b 0) 的左、右焦点， P 为a 2b 23aF PF 是底角为 30 的等腰三角形，则直线 x 上的一点，2 2 1E 的离心率为(A) 1 2 3 4 (B) 3 (C) (D) 2 4 5（ 5）已知 { a n } 为等比数列， a 4a 7 2 ， a 5 a 6 8 ，则 a 1 a10(A) 7 (B) 5 (C) 5 (D) 7（ 6）如果执行右边的程序图，输入正整数N ( N 2) 和实数 a 1 , a 2 ,..., a N 输入A, B , 则(A) A B 为 a 1 , a 2 ,..., a N 的和（ B ）AB为 a ,a ,..., a 的算式平均数 2 1 2 N（ C ） A 和 B 分别是 a 1 , a 2 ,..., a N 中最大的数和最小的数专业技术参考资料WORD 格式整理（ D ） A 和 B 分别是 a 1 , a 2 ,..., a N 中最小的数和最大的数（ 7）如图，网格纸上小正方形的边长为1，粗线画出的是某几何体的三视图，则此几何体的体积为（ A ） 6 (B)9 （ C ） 12 （ D ） 18（ 8）等轴双曲线 C 的中心在原点，焦点在 x 轴上， C 与抛物线 y 216x 的准线交于 A, B 两点，| AB | 4 3 ，则 C 的实轴长为（ A ） 2 （ B ） 2 2 （ C ） 4 （ D ） 8（ 9）已知 0 ，函数 f (x) sin( x ) 在 , 单调递减，则 的取值范围4 2(A) [ 1 ,5 ](B) [ 1 , 3] (C) (0, 1 ](D) (0, 2]2 4 2 4 2（ 10）已知函数 f ( x) 1 ，则 y f ( x) 的图像大致为1) ln(x x（ 11）已知三棱锥 S ABC 的所有顶点都在球 O 的球面上，ABC 是边长为 1 SC 为 O的正三角形， 的直径，且 SC 2 ，则此棱锥的体积为(A)2(B)3 (C)2(D)2 6 63 2（ 12）设点 P 在曲线 y 1 e x上，点 Q 在曲线 yln(2 x) 上，则 | PQ |的最小值为2(A) 1 ln 2 (B)2(1 ln2) (C) 1 ln 2 (D)2(1 ln 2) 专业技术参考资料WORD 格式整理第Ⅱ卷本卷包括必考题和选考题两部分。
2013届高三数学第一轮总复习课件46
共 74 页
16
(2)球坐标 设M(x,y,z)为空间一点,点M可用这样三个有次序的数r,φ,θ来 确定,其中r为原点O到点M间的距离,φ为有向线段OM与z轴正 方向所夹的角,θ为从z轴正半轴看,x轴正半轴按逆时针方向旋 转到有向线段OP的角,这里P为点M在xOy平面上的投影,这样 的三个数r,φ,θ构成的有序数组(r,φ,θ)叫做点M的球坐标,这里
选修4-4
坐标系与参数方程
共 74 页
1
第一讲 坐标系 走进高考第一关 考点关 回归教材 1.平面直角坐标系 (1)曲线与方程 在平面直角坐标系中,如果某曲线C上的点与一个二元方程
f(x,y)=0的实数解建立了如下的关系:
①曲线C上的点的坐标都是方程f(x,y)=0的解; ②以方程f(x,y)=0的解为坐标的点都在曲线C上.
φ(ρ,θ)=0;
共 74 页
7
②极坐标满足方程φ(ρ,θ)=0的点都在曲线C上. 那么方程φ(ρ,θ)=0叫作曲线C的极坐标方程,曲线C叫作极坐 标方程φ(ρ,θ)=0的曲线. 极坐标系中曲线与方程的关系和直角坐标系中曲线与方程的 关系是一致的.
共 74 页
8
(2)直线的极坐标方程 若直线经过点M(ρ0,θ0),且极轴到此直线的角为α,则直线l的极 坐标方程为ρsin(θ-α)=ρ0sin(θ0-α). 特殊情况: ①当直线l过极点,即ρ0=0时,方程为θ=α.
ρ=rcosθ.
③圆心位于M (r, ), 半径为r的圆的极坐标方程为 2rsin . 2
共 74 页 12
(4)圆锥曲线的极坐标方程 圆锥曲线的统一定义:与一个定点的距离和一条定直线(定点 不在定直线上)的距离的比等于常数e的点轨迹. 若以定点F为极点,过定点F作定直线l的垂线,垂足为K,FK的反 向延长线Fx为极轴,建立极坐标系,其中|KF|=p,|MF|=ρ得圆锥 曲线统一的极坐标方程.
2012届高考数学第一轮专题复习测试卷 第一讲 坐标系 2含答案
第一讲 坐标系一､选择题:（本大题共6小题,每小题6分,共36分,将正确答案的代号填在题后的括号内。
）1。
点M 的直角坐标为（—1,—，则它的球坐标为( ） 5.2,,.2,,444453.2,,.2,,4444A B C D ππππππππ⎛⎫⎛⎫ ⎪ ⎪⎝⎭⎝⎭⎛⎫⎛⎫ ⎪ ⎪⎝⎭⎝⎭解析：2,1,tan 0,tan 02,x 0.411,,15.4r y x ϕϕθϕθπθππθ======<-=-=<==由≤≤得又≤所以 答案:B2.在平面直角坐标系中，以（1,1)角坐标系的原点为极点，以Ox 为极轴的极坐标系中对应的极坐标方程为( ）()B..C.os(1)D.4in 14A ρθρθππρθρθ⎛⎫=- ⎪⎝⎭⎛⎫- ⎪⎝=-=⎭=-解析:由题意知圆的直角坐标方程为(x-1）2+（y —1)2=2.化为极坐标方程为（ρcosθ-1)2+（ρsinθ-1)2=2。
∴0.42042,04044 ..cos ρρθρθρρππππθρθρπθ⎡⎤⎛⎫--= ⎪⎢⎥⎝⎭⎣⎦⎛⎫-= ⎪⎝⎭⎡⎤⎛-∴-∴⎫--= ⎪⎢⎥⎝⎭⎣⎦⎛⎫-= ⎪⎝⎭⎛⎫- ⎪⎝⎭=也过极点与等价对应的极坐标方程为答案:A3.在极坐标系中,点(ρ,θ）与(—ρ，π—θ)的位置关系为( ）A.关于极轴所在直线对称B 。
关于极点对称C 。
重合D.关于直线θ=2π （ρ∈R）对称 解析：点(ρ,θ)也可以表示为（—ρ，π+θ),而（-ρ，π+θ)与（—ρ,π—θ)关于极轴所在直线对称,故选A 。
答案:A4.在柱坐标系中，两点24,,04,,333M N ππ⎛⎫⎛⎫ ⎪ ⎪⎝⎭⎝⎭与的距离为（ ） A.3 B.4C 。
5D 。
8解析:解法一：由柱坐标可知M 在Oxy 平面上,N 在Oxy 平面上的射影坐标为N |MN |4,24,,0MN 5.3.,C π'∴'==⎛⎫ ⎪⎝⎭再由勾股定理得故选解法二:可将M ､N 化为直角坐标,N(MN 5..C =-∴=故选答案：C5.两直线θ=α和ρcos（θ—α）=a 的位置关系是（ ）A.平行 B 。
2013年理科全国各省市高考真题——坐标系与参数方程(解答题带答案)
2013年全国各省市理科数学—坐标系与参数方程 1、2013重庆理T15.在直角坐标系xOy 中，以原点O 为极点，x 轴的正半轴为极轴建立极坐标系。
若极坐标方程为cos 4ρθ=的直线与曲线23x t y t⎧=⎪⎨=⎪⎩（t 为参数）相交于,A B 两点，则______AB =2、2013天津理T11.已知圆的极坐标方程为4cos ρθ=, 圆心为C , 点P 的极坐标为4,3π⎛⎫ ⎪⎝⎭, 则|CP | = .3、2013广东理14.(坐标系与参数方程选讲选做题)已知曲线C的参数方程为x t y t⎧=⎪⎨=⎪⎩(t 为参数),C 在点()1,1处的切线为l ,以坐标原点为极点,x 轴的正半轴为极轴建立极坐标系,则l 的极坐标方程为_____________.4、2013陕西理T15.C. (坐标系与参数方程选做题)如图, 以过原点的直线的倾斜角θ为参数, 则圆220y x x +-=的参数方程为 R y x ∈⎩⎨⎧⋅==θθθθ,sin cos cos 2 .x5、2013湖南理T9.在平面直角坐标系xoy 中，若,3cos ,:(t )C :2sin x t x l y t a y ϕϕ==⎧⎧⎨⎨=-=⎩⎩为参数过椭圆()ϕ为参数的右顶点，则常数a 的值为 .6、2013湖北理16、在直角坐标系xOy 中，椭圆C 的参数方程为cos sin x a y b θθ=⎧⎨=⎩()0a b ϕ>>为参数，。
在极坐标系（与直角坐标系xOy 取相同的长度单位，且以原点O 为极点，以x 轴正半轴为极轴）中，直线l 与圆O 的极坐标方程分别为sin 4πρθ⎛⎫+= ⎪⎝⎭()m 为非零常数与b ρ=。
若直线l 经过椭圆C 的焦点，且与圆O 相切，则椭圆C 的离心率为 。
7、2013新课标I 理T23.（本小题满分10分）选修4—4：坐标系与参数方程 已知曲线1C 的参数方程式⎩⎨⎧+=+=ty t x sin 55cos 54（t 为参数），以坐标原点为极点，以坐标原点为极点，x 轴的正半轴为极轴建立极坐标系，曲线2C 的极坐标方程为θρsin 2=.（Ⅰ）把1C 的参数方程化为极坐标方程；（Ⅱ）求1C 与2C 交点的极坐标（0≥ρ,π20<≤θ）8、2013新课标Ⅱ理T23.（本小题满分10分）选修4——4；坐标系与参数方程 已知动点P Q 、都在曲线2cos ,:2sin x t C y t =⎧⎨=⎩（t 为参数）上，对应参数分别为=t α与=2t α（02απ<<），M 为PQ 的中点。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
第一讲 坐标系
一､选择题:(本大题共6小题,每小题6分,共36分,将正确答案的代号填在题后的括号内.)
1.点M 的直角坐标为
),则它的球坐标为( )
5.2,,.2,,444453.2,,.2,,4444A B C D ππππππππ⎛⎫⎛⎫ ⎪ ⎪⎝⎭⎝⎭
⎛⎫⎛⎫ ⎪ ⎪⎝⎭⎝⎭
解析
:2,1,tan 0,tan 02,x 0.
4
11,,1
5.4
r y x ϕϕθϕθπθππ
θ===
===
<-=-=
<=
=由≤≤得又≤所以
答案:B
2.在平面直角坐标系中,以(1,1)为圆心
为半径的圆在以直角坐标系的原点为极点,以Ox 为极轴的极坐标系中对应的极坐标方程为
( )
()
B..
C.
D.44A ρθρθππρθρθ⎛
⎫=- ⎪
⎝
⎭⎛
⎫- ⎪⎝
=-
=⎭=-
解析:由题意知圆的直角坐标方程为 (x-1)2
+(y-1)2
=2.
化为极坐标方程为(ρcos θ-1)2
+(ρsin θ-1)2
=2.
∴0.40
4,04044 .
.
ρρθρθρρππππθρθρπθ⎡
⎤
⎛⎫--
= ⎪⎢⎥⎝
⎭⎣
⎦
⎛
⎫-= ⎪⎝
⎭⎡⎤
⎛
-∴-∴⎫--
= ⎪⎢⎥⎝
⎭⎣⎦
⎛
⎫-= ⎪⎝
⎭⎛
⎫- ⎪⎝
⎭= 也过极点与等价对应的极坐标方程为
答案:A
3.在极坐标系中,点(ρ,θ)与(-ρ,π-θ)的位置关系为( ) A.关于极轴所在直线对称 B.关于极点对称 C.重合 D.关于直线θ=
2
π
(ρ∈R)对称 解析:点(ρ,θ)也可以表示为(-ρ,π+θ),而(-ρ,π+θ)与(-ρ,π-θ)关于极轴所在直线对称,故选A.
答案:A
4.在柱坐标系中,两点24,,04,,333M N π
π⎛⎫⎛⎫ ⎪ ⎪⎝
⎭⎝⎭
与的距离为( ) A.3 B.4 C.5 D.8
解析:解法一:由柱坐标可知M 在Oxy 平面上,N 在Oxy 平面上的射影坐标为
N |MN |4,24,,0MN 5.3.
,
C π'∴'===⎛⎫
⎪⎝⎭
再由勾股定理得故选
解法二:可将M ､N 化为直角坐标
,N(MN 5..
C =-∴=故选
答案:C
5.两直线θ=α和ρcos(θ-α)=a 的位置关系是( ) A.平行 B.相交但不垂直 C.垂直 D.重合
解析:θ=α表示过极点且极角为α的一条直线,ρcos(θ-α)=a 表示与极点距离为a 并且垂直于上述直线的直线,选C.
答案:C
6.在极坐标方程中,曲线C 的方程是ρ=4sin θ,过点4,6π⎛⎫
⎪⎝
⎭
作曲线C 的切线,则切线长为
( )
A.4.C D 解析:ρ=4sin θ化为普通方程为x 2+(y-2)2
=4,
点4,2),6π⎛⎫
⎪⎝
⎭
化为直角坐标为切线长､圆心到定点的距离及半径构成直角三角形.
由勾股定理:
= 答案:C
二､填空题:(本大题共4小题,每小题6分,共24分,把正确答案填在题后的横线上.) 7.圆ρ=5cos θ
sin θ的圆心坐标是________.
解析:
圆的普通方程是2
2
525.22x y ⎛⎫⎛
⎫-++= ⎪ ⎪ ⎪⎝⎭⎝⎭
∴圆心为5,,2⎛
⎝转化为极坐标为5,.3π⎛
⎫
-
⎪⎝
⎭
答案:5,3π⎛⎫
-
⎪⎝
⎭
8.设直线过极坐标系中的点M(2,0),且垂直于极轴,则它的极坐标方程为________. 解析:设所求直线的任一点的极坐标为(ρ,θ),由题意可得ρcos θ=2. 答案:ρcos θ=2
9.极坐标方程分别为ρ=cosθ与ρ=sinθ的两个圆的圆心距为________.
解析:ρ=cosθ表示圆心为
1
,0,
2
⎛⎫
⎪
⎝⎭
半径为 的圆.
ρ=sinθ表示圆心为
1
,,
22
π
⎛⎫
⎪
⎝⎭
半径为 的圆.
∴圆心距d==
答案:
2
10.(2010·广东)在极坐标系(ρ,θ)(0≤θ<2π)中,曲线ρ=2sinθ与ρcosθ=-1的交点的极坐标为________.
解析:曲线ρ=2sinθ化为直角坐标方程为
x2+y2=2y,即x2+(y-1)2=1,
而ρcosθ=-1化为直角坐标方程为x=-1.
直线x=-1与圆x2+(y-1)2=1的交点坐标为(-1,1),化为极坐标为3
. 4π⎫
⎪
⎭
答案:3
4π⎫
⎪
⎭
三､解答题:(本大题共3小题,11､12题13分,13题14分,写出证明过程或推演步骤.)
11.(2010·江苏)在极坐标系中,圆ρ=2cosθ与直线3ρcosθ+4ρsinθ+a=0相切,求实数a的值.
解:化为平面直角坐标系:圆:x2-2x+y2=0,
即:(x-1)2+y2=1.直线:3x+4y+a=0.
1
=,
∴a=2或a=-8.
12.(2010·浙江自选模块卷)如图,在极坐标系(ρ,θ)中,已知曲线
213,
4
23:4422C :4sin 2C .
2:40C cos π
ρθθρθθθπρπθππππ=⎛⎛⎫ ⎪⎝⎭⎫
< ⎪⎝⎭==⎛
⎫ ⎪⎝
⎭≤≤≤≤或≤，≤≤
(1)求由曲线C 1,C 2,C 3围成的区域的面积; (2)设M 4,
2π⎛
⎫
⎪⎝
⎭
,N(2,0),射线θ=α0,
4
2π
πρα⎛⎫
<<
⎪⎝
⎭
≥与曲线C 1,C 2分别交于A,B(不同于极点O)两点.若线段AB 的中点恰好落在直线MN 上,求tan α的值.
解:(1)由已知,如图弓形OSP 的面积= ×π×22
- ×22
=π
-2,
从而,如图阴影部分的面积= ×π×22
-2(π-2)=4,
故所求面积= π×42+ ×π×22
-4=6π-4. (2)设AB 的中点为G(ρ,α),∠ONG=φ. 由题意ρ
=
2sin 2cos ,sin 2
A B
ααϕϕρρ+=
+== 在△OGN 中,
222,.
()2
.
()2sin cos ON OG sin cos sin OGN sin ONG sin sin sin sin sin cos αα
παφφ
φααα
φαα+==--==++∠∠+即所以
化简得sin 2
α-3sin αcos α=0, 又因为sin α≠0,所以tan α=3.
13.从极点O 作直线与另一直线l:ρcos θ=4相交于点M,在OM 上取一点P,使OM·OP=12. (1)求点P 的轨迹方程;
(2)设R 为l 上的任意一点,试求|RP|的最小值.
解:(1)设动点P 的极坐标为(ρ,θ),M 的极坐标为(ρ0,θ),则ρρ0=12. ∵ρ0cos θ=4,
∴ρ=3cos θ即为所求的轨迹方程.
(2)将ρ=3cos θ化为直角坐标方程是x 2
+y 2
=3x, 即(x- )2
+y 2
=( )2
,
知P 的轨迹是以( ,0)为圆心,半径为 的圆.直线l 的直角坐标方程是x=4.结合图形易得|RP|的最小值为1.。