高考数学第一轮复习立体几何专题题库
高三数学一轮复习【立体几何】练习题
高三数学一轮复习【立体几何】练习题1.空间中，用a，b，c表示三条不同的直线，γ表示平面，则下列说法正确的有()A.若a∥b，b∥c，则a∥cB.若a⊥γ，b⊥γ，则a∥bC.若a∥γ，b∥γ，则a∥bD.若a⊥b，b⊥c，则a⊥c答案AB解析根据空间平行直线的传递性可知A正确；由直线与平面垂直的性质定理知B正确；若a∥γ，b∥γ，则a，b可能平行、相交或异面，故C错误；若a⊥b，b⊥c，则a，c可能相交、平行或异面，故D错误.2.对于两条不同直线m，n和两个不同平面α，β，下列选项正确的为()A.若m⊥α，n⊥β，α⊥β，则m⊥nB.若m∥α，n∥β，α⊥β，则m⊥n或m∥nC.若m∥α，α∥β，则m∥β或m⊂βD.若m⊥α，m⊥n，则n∥α或n⊂α答案ACD解析对A，令m，n分别为直线m，n的方向向量，因为m⊥α，n⊥β，所以m⊥α，n⊥β，又α⊥β，所以m⊥n，即m⊥n，所以选项A正确；对B，如图所示，在正方体ABCD-A1B1C1D1中，令平面ABCD为平面α，平面ABB1A1为平面β，直线A1C1为m，直线C1D为n，满足α⊥β，m∥α，n∥β，但m与n既不平行也不垂直，所以选项B错误；对C，若m⊄β，过m作一平面γ分别与平面α和平面β相交，且交线分别为a，b，则m∥a，a∥b，所以m∥b，所以m∥β；若m⊂β，符合题意，所以选项C 正确；对D，若n⊂α，符合题意；若n⊄α，过直线n作一平面β与平面α相交，设交线为b，因为b⊂α，m⊥α，所以m⊥b，又m⊥n，且n，b在同一平面内，所以n∥b，所以n∥α，所以选项D正确.综上，选ACD.3.如图是一个正方体的平面展开图，则在该正方体中()A.AE∥CDB.CH∥BEC.DG⊥BHD.BG⊥DE答案BCD解析由正方体的平面展开图还原正方体如图，连接AH，DE，BG，BH，DG，HC.由图形可知，AE⊥CD，故A错误；因为HE∥BC，HE＝BC，所以四边形BCHE为平行四边形，所以CH∥BE，故B正确；因为DG⊥HC，DG⊥BC，HC∩BC＝C，HC，BC⊂平面BHC，所以DG⊥平面BHC，又BH⊂平面BHC，所以DG⊥BH，故C正确；因为BG∥AH，而DE⊥AH，所以BG⊥DE，故D正确.故选BCD.4.用一个平面截正方体，所得的截面不可能是()A.锐角三角形B.直角梯形C.有一个内角为75°的菱形D.正五边形答案BCD解析对于A，如图1，截面的形状可能是正三角形，故A可能；图1图2对于B，首先考虑平面截正方体得到的截面为梯形，且QR与AA1不平行，如图2所示，不妨假设PQ⊥QR，因为AA1⊥平面A1B1C1D1，PQ⊂平面A1B1C1D1，所以AA1⊥PQ，从而有PQ⊥平面A1ABB1，这是不可能的，故B不可能；对于C，当平面截正方体得到的截面为菱形(非正方形)时，只有如下情形，如图3，其中P，R为所在棱的中点，易知当菱形为PBRD1时，菱形中的锐角取得最小值，即∠PD1R最小.设正方体的棱长为2，则PD1＝RD1＝5，PR＝22，则由余弦定理，得cos∠PD1R＝PD21＋RD21－PR22PD1·RD1＝5＋5－82×5×5＝15<6－24＝cos 75°，所以∠PD1R>75°，故C不可能；图3对于D，假设截面是正五边形，则截面中的截线必然分别在5个面内，由于正方体有6个面，分成两两平行的三对，故必然有一对平行面中有两条截线，而根据面面平行的性质可知这两条截线互相平行，但正五边形的边中是不可能有平行的边的，故截面的形状不可能是正五边形，故D不可能.综上所述，选BCD.5.已知正方体ABCD-A1B1C1D1的棱长为2，M为AA1的中点，平面α过点D1且与CM垂直，则()A.CM⊥BDB.BD∥平面αC.平面C1BD∥平面αD.平面α截正方体所得的截面图形的面积为9 2答案ABD解析如图，连接AC，则BD⊥AC.因为BD⊥AM，AM∩AC＝A，AM，AC⊂平面AMC，所以BD⊥平面AMC，又CM⊂平面AMC，所以BD⊥CM，故A正确；取AD的中点E，连接D1E，DM，由平面几何知识可得D1E⊥DM，又CD⊥D1E，DM∩CD＝D，DM，CD⊂平面CDM，所以D1E⊥平面CDM，又CM⊂平面CDM，所以D1E⊥CM.连接B1D1，过点E作EF∥BD，交AB于F，连接B1F，所以CM⊥EF，又D1E∩EF＝E，D1E，EF⊂平面D1EFB1，所以CM⊥平面D1EFB1，所以平面α截正方体所得的截面图形即梯形D1EFB1.由EF∥BD，BD⊄平面α，EF⊂平面α，得BD∥平面α，故B正确；连接AB1，AD1，易知平面AB1D1∥平面C1BD，而平面AB1D1∩平面α＝B1D1，所以平面C1BD与平面α不平行，故C不正确；截面图形为等腰梯形D1EFB1，EF＝2，B1D1＝22，D1E＝B1F＝5，所以截面图形的面积S＝12×(2＋22)×（5）2－⎝⎛⎭⎪⎫22－222＝92，故D正确.6.在正方体ABCD-A1B1C1D1中，N为底面ABCD的中心，P为线段A1D1上的动点(不包括两个端点)，M为线段AP的中点，则()A.CM与PN是异面直线B.CM>PNC.平面PAN⊥平面BDD1B1D.过P，A，C三点的正方体的截面一定是等腰梯形答案BCD解析对于选项A，如图，连接NC，PC，则A，N，C三点共线.又M为AP的中点，N为AC的中点，所以CM与PN共面，故A错误；对于选项B，因为P为线段A1D1上的动点(不包括两个端点)，所以AC>AP.在△MAC中，CM2＝AC2＋AM2－2AC·AM cos∠MAC＝AC2＋14AP2－AC·AP·cos∠MAC.在△PAN中，PN2＝AP2＋AN2－2AP·AN cos∠PAN＝AP2＋1 4AC 2－AP ·AC cos ∠PAN ，则CM 2－PN 2＝34(AC 2－AP 2)>0，所以CM >PN ，故B 正确；对于选项C ，在正方体ABCD-A 1B 1C 1D 1中，易知AC ⊥平面BDD 1B 1，即AN ⊥平面BDD 1B 1，又AN ⊂平面PAN ，所以平面PAN ⊥平面BDD 1B 1，故C 正确； 对于选项D ，连接A 1C 1，在平面A 1B 1C 1D 1内作PK ∥A 1C 1，交C 1D 1于K ，连接KC .在正方体中，A 1C 1∥AC ，所以PK ∥AC ，PK ，AC 共面，所以四边形PKCA 就是过P ，A ，C 三点的正方体的截面，AA 1＝CC 1，A 1P ＝C 1K ，所以AP ＝CK ，即梯形PKCA 为等腰梯形，故D 正确.故选BCD.7.如图，在正四棱柱ABCD-A 1B 1C 1D 1中，AA 1＝2AB ＝2，点P 为线段AD 1上一动点，则下列说法正确的是( )A.直线PB 1∥平面BC 1DB.三棱锥P-BC 1D 的体积为13C.三棱锥D 1-BC 1D 外接球的表面积为3π2D.直线PB 1与平面BCC 1B 1所成角的正弦值的最大值为53 答案 ABD解析 对于A 选项，连接B 1D 1，AB 1，根据正四棱柱的性质可知AD 1∥BC 1，BD ∥B 1D 1，因为BC 1⊄平面AB 1D 1，AD 1⊂平面AB 1D 1，所以BC 1∥平面AB 1D 1，同理得BD ∥平面AB 1D 1，又BC 1∩BD ＝B ，所以平面AB 1D 1∥平面BC 1D ，又PB 1⊂平面AB 1D 1，所以PB 1∥平面BC 1D ，所以A 选项正确；对于B 选项，易知AD 1∥平面BC 1D ，所以V P-BC 1D ＝V A-BC 1D ＝V C 1-ABD ＝13×12×1×1×2＝13，所以B 选项正确；对于C 选项，三棱锥D 1-BC 1D 的外接球即正四棱柱ABCD-A 1B 1C 1D 1的外接球.设外接球的半径为R ，则4R 2＝12＋12＋22＝6，所以外接球的表面积为4πR 2＝6π，所以C 选项错误；对于D 选项，过P 作PE ∥AB ，交BC 1于点E ，则PE ⊥平面BCC 1B 1，连接B 1E ，则∠PB 1E 即直线PB 1与平面BCC 1B 1所成的角，当B 1E 最小时，∠PB 1E 最大，此时B 1E ⊥BC 1，由等面积法得S △BB 1C 1＝12BC 1·B 1E ＝12BB 1·B 1C 1，解得B 1E ＝25，在Rt △PB 1E 中，PE ＝AB ＝1，所以PB 1＝12＋⎝ ⎛⎭⎪⎫252＝35，所以∠PB 1E 的正弦值的最大值为PE PB 1＝53，所以D 选项正确.故选ABD.8.如图，已知正方体ABCD-A 1B 1C 1D 1的棱长为2，E ，F ，G 分别为BC ，CC 1，BB 1的中点，则( )A.直线D1D与直线AF垂直B.直线A1G与平面AEF平行C.平面AEF截正方体ABCD-A1B1C1D1所得的截面的面积为9 2D.点A1和点D到平面AEF的距离相等答案BCD解析对于选项A，假设AF与D1D垂直，又D1D⊥AE，AE∩AF＝A，AE，AF⊂平面AEF，所以D1D⊥平面AEF.因为EF⊂平面AEF，所以D1D⊥EF，这显然是错误的，所以假设不成立，故A错误；图1对于选项B，取B1C1的中点N，连接A1N，GN，如图1所示，易知A1N∥AE，又AE⊂平面AEF，A1N⊄平面AEF，所以A1N∥平面AEF.因为GN∥EF，EF⊂平面AEF，GN⊄平面AEF，所以GN∥平面AEF.又A1N，GN⊂平面A1GN，A1N∩GN＝N，所以平面A1GN∥平面AEF.因为A1G⊂平面A1GN，所以A1G∥平面AEF，故B正确；对于选项C，连接AD1，FD1，如图2所示，因为AD1∥EF，所以四边形AD1FE 为平面AEF截正方体ABCD-A1B1C1D1所得的截面，又AD1＝22＋22＝22，图2EF ＝12＋12＝2，D 1F ＝AE ＝12＋22＝5，所以四边形AD 1FE 为等腰梯形， 高为（5）2－⎝ ⎛⎭⎪⎫222＝322，则S 梯形AD 1FE ＝12×(2＋22)×322＝92，故C 正确；对于选项D ，连接A 1D ，如图2所示，由选项C 可知A 1D 与平面AEF 相交且交点为A 1D 的中点，所以点A 1和点D 到平面AEF 的距离相等，故D 正确.综上，选BCD.9.已知棱长为a 的正方体ABCD-A 1B 1C 1D 1中，M 是B 1C 1的中点，点P 在正方体的表面上运动，且总满足MP ⊥MC ，则下列结论中正确的是( ) A.点P 的轨迹中包含AA 1的中点B.点P 在侧面AA 1D 1D 内的轨迹的长为5a4 C.MP 长度的最大值为21a4D.直线CC 1与直线MP 所成角的余弦值的最大值为55 答案 BCD解析 如图，取A 1D 1的中点E ，分别取A 1A ，B 1B 上靠近A 1，B 1的四等分点F ，G ，连接EM ，EF ，FG ，MG ，易知EM ∥FG 且EM ＝FG ，所以E ，M ，F ，G 四点共面.连接GC ，因为MG 2＝⎝ ⎛⎭⎪⎫a 22＋⎝ ⎛⎭⎪⎫a 42＝5a 216，MC 2＝⎝ ⎛⎭⎪⎫a 22＋a 2＝5a 24，GC 2＝⎝ ⎛⎭⎪⎫3a 42＋a 2＝25a 216，因此MG 2＋MC 2＝GC 2，所以MG ⊥MC ，易知ME ⊥MC ，又MG ∩ME ＝M ，MG ，ME ⊂平面MEFG ，所以MC ⊥平面MEFG ，即点P 的轨迹为四边形MEFG (不含点M )，易知点P 在侧面AA 1D 1D 内的轨迹为EF ，且EF ＝MG ＝5a4，所以A 选项错误，B 选项正确；根据点P 的轨迹可知，当P 与F 重合时，MP 最长，易知FG ⊥平面BB 1C 1C ，则FG ⊥MG ，连接MF ，所以MF ＝a 2＋5a 216＝21a4，故C 选项正确；由于点P 的轨迹为四边形MEFG (不含点M )，所以直线CC 1与直线MP 所成的最小角就是直线CC 1与平面MEFG 所成的角，又向量CC 1→与平面MEFG 的法向量CM →的夹角等于∠C 1CM ，且sin ∠C 1CM ＝a25a 2＝55，所以直线CC 1与平面MEFG 所成角的余弦值为55，即直线CC 1与直线MP 所成角的余弦值的最大值等于55，故D 选项正确.10.如图，长方体ABCD-A 1B 1C 1D 1中，AB ＝BC ＝1，AA 1＝2，M 为AA 1的中点，过B 1M 作长方体的截面α交棱CC 1于N ，则( )A.截面α可能为六边形B.存在点N，使得BN⊥截面αC.若截面α为平行四边形，则1≤CN≤2D.当N与C重合时，截面图形的面积为36 4答案CD解析设N0为棱CC1的中点，当N从C1移动到C时，其过程中存在以下几种情况，如图1，当点N在线段C1N0上时，截面α为平行四边形；当点N在线段N0C上(不包括点N0，C)时，截面α为五边形；当点N与点C重合时，截面α为梯形.图1图2由以上分析可知，对于A，截面α不可能为六边形，所以A错误；对于B，假设BN⊥截面α，因为B1M⊂α，所以BN⊥B1M，所以必有点N，C重合，而BC与平面B1CQM不垂直，所以B错误；对于C，当截面α为平行四边形时，点N在线段C1N0上，则1≤CN≤2，所以C 正确；对于D，当点N与点C重合时，截面α为梯形，如图2，过M作MM′⊥B1C，垂足为M′.设梯形的高为h，B1M′＝x，则在Rt△B1MM′中，由勾股定理，得h2＝(2)2－x2，①同理h 2＝⎝ ⎛⎭⎪⎫522－⎝ ⎛⎭⎪⎫52－x 2，② 由①②，解得x ＝255，h ＝65，所以截面α的面积等于12×⎝⎛⎭⎪⎫5＋52·h ＝12×352×65＝364，所以D 正确. 综上可知，选CD.。
高考数学一轮复习讲练测(新教材新高考)专题8-1空间几何体及其三视图和直观图-教师版
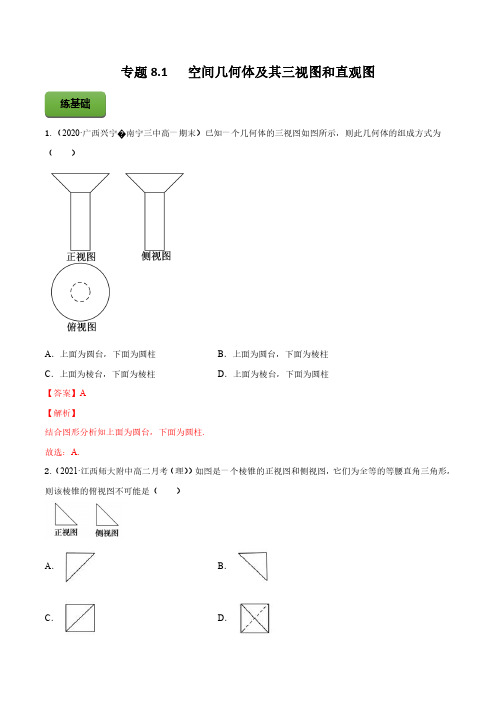
专题8.1空间几何体及其三视图和直观图练基础1.（2020·广西兴宁�南宁三中高一期末）已知一个几何体的三视图如图所示，则此几何体的组成方式为（）A．上面为圆台，下面为圆柱B．上面为圆台，下面为棱柱C．上面为棱台，下面为棱柱D．上面为棱台，下面为圆柱【答案】A【解析】结合图形分析知上面为圆台，下面为圆柱.故选：A.2.（2021·江西师大附中高二月考（理））如图是一个棱锥的正视图和侧视图，它们为全等的等腰直角三角形，则该棱锥的俯视图不可能是（）A．B．C．D．【答案】C【解析】根据棱锥的三视图想象原几何体的结构，可以在正方体中想象描出原几何体，确定其结构．【详解】若几何体为三棱锥，由其正视图和侧视图可知，其底面在下方且为直角三角形，故ABD 均有可能，若几何体是四棱锥，由其正视图和侧视图可知，其底面在下方，且为正方形，俯视图为正方形，但对角线应从左上到右下，C 不正确．故选：C ．3.（2021·江苏高一期末）已知一个圆锥的母线长为2，其侧面积为2π，则该圆锥的高为（）A ．1BC D ．2【答案】C【解析】由侧面积求出圆锥的底面圆半径，再根据勾股定理可求得其高.【详解】设圆锥的底面圆的半径为r ，母线为l ，则2l =，所以其侧面积为22rl r πππ==，解得1r =，==故选：C.4.（2020·河北易县中学高三其他（文））若圆台的母线与高的夹角为6π，且上、下底面半径之差为2，则该圆台的高为（）A ．233B ．2C ．22D ．3【答案】D【解析】设上、下底面半径分别为R ，r ，圆台高为h ，由题可知：tan 6R r h π-=，即233h =，所以23h =．故选：D5.（2020届浙江绍兴市诸暨市高三上期末）某几何体的正视图与侧视图如图所示：则下列两个图形①②中，可能是其俯视图的是（）A．①②都可能B．①可能，②不可能C．①不可能，②可能D．①②都不可能【答案】A【解析】若是①，可能是三棱锥；若是②，可能是棱锥和圆锥的组合；所以①②都有可能，故选：A.6．（2021·石家庄市第十七中学高一月考）如图，某沙漏由上、下两个圆锥组成，每个圆锥的底面直径和高均为12cm ，现有体积为396πcm 的细沙全部漏入下圆锥后，恰好堆成一个盖住沙漏底部的圆锥形沙堆，则此锥形沙堆的高度为（）A ．3cmB ．6cmC ．8cmD ．9cm【答案】C【解析】根据圆锥的体积公式列方程求出沙堆的高．【详解】解：细沙漏入下部后，圆锥形沙堆的底面半径为6r =，设高为h ，则沙堆的体积为216963V h ππ=⋅⋅=圆锥，解得()8h cm =，所以圆锥形沙堆的高度为8cm ．故选：C ．7.（2021·云南弥勒市一中高一月考）如图，正方形OABC 的边长为1，它是水平放置的一个平面图形的直观图，则原图形的周长是（）A ．8B ．6C ．(21D ．(21+【答案】A【解析】根据斜二测画法的规则，得到原图形的形状为平行四边形，进而求得其边长，即可求解.【详解】由斜二测画法的规则，可得原图形为O A B C ''''是一个平行四边形，如图所示，因为水平放置的一个平面图形的直观图OABC 的边长为1的正方形，可得1,OA OB ==1,O A O B ''''==在直角O A B '''△中，可得3A B ''==，所以原图形的周长为11338+++=.故选：A.8．（2021·浙江高三三模）如图，等腰直角三角形ABC 在平面α上方，90BAC ∠= ，若ABC 以BC 为旋转轴旋转，形成的旋转体在平面α内的投影不可能的是（）A ．B ．C ．D ．【答案】C【解析】对直线BC 与平面α的位置关系进行分类讨论，判断出投影的形状，即可得出合适的选项.【详解】若BC α⊥，则形成的旋转体在平面α内的投影如D 选项所示；若//BC α，则形成的旋转体在平面α内的投影为正方形；若BC 与α所成的角的取值范围是0,2π⎛⎫ ⎪⎝⎭时，则形成的旋转体在平面α内的投影如A 、B 选项所示.投影不可能如C 选项所示.故选：C.9．（2020·上海市进才中学高二期末）设MN 是半径为R 的球的直径，则,M N 两点的球面距离是________．【答案】Rπ【解析】MN 是半径为R 的球的直径，则,M N 两点所对的球心角为π，球面距离为R π．故答案为：R π．10．（2020·全国）如图为一几何体的平面展开图，按图中虚线将它折叠起来，画出它的直观图．【答案】见解析【解析】由题设中所给的展开图可以得出，此几何体是一个四棱锥，其底面是一个边长为2的正方形，垂直于底面的侧棱长为2，其直观图如图所示.练提升1.（2021·四川高一期末（理））某圆柱的高为1，底面周长为8，其三视图如图.圆柱表面上的点P在正视图上的对应点为A，圆柱表面上的点Q在左视图上的对应点为B，则在此圆柱侧面上，从P到Q的路径中，最短路径的长度为（）A17B5C．32D．1【答案】B【解析】根据三视图分析出,P Q所在的位置，然后结合圆柱的侧面展开图即可求出结果.【详解】由三视图还原几何体，如图：即点B在距离点A在底面投影的14圆弧处，沿A所在的母线得到如图所示的侧面展开图，圆柱的底面周长即为侧面展开图的长，圆柱的高即为侧面展开图的宽，而线段AB 的距离即为所求P 到Q 的路径中的最短路径，因为底面周长为8,所以1824A B '=⨯=，又因为高为1，则1A A '=，所以2222125AB A A A B ''=+=+=,故选：B.2.【多选题】（2021·宁波市北仑中学高一期中）如图，棱长为a 的正四面体形状的木块，点P 是ACD △的中心．劳动课上需过点P 将该木块锯开，并使得截面平行于棱AB 和CD ，则下列关于截面的说法中正确的是（）A ．截面不是平行四边形B ．截面是矩形C ．截面的面积为229a D ．截面与侧面ABC 的交线平行于侧面ABD【答案】BCD【解析】过点P 构建四边形，通过相关直线间的平行关系进一步证明为平行四边形，找对应线之间的垂直证明截面为矩形，从而计算截面面积【详解】解：如图所示，在正四面体中，4个面均为正三角形，由于点P 为ACD △的中心，所以P 位于CD 的中线的23外，分别取,,,BC AC AD BD 的三等分点，则EM ∥AB ，EF ∥CD ，FN ∥AB ，MN ∥CD ，所以EM ∥FN ，EF ∥MN ，所以截面EFNM 为平行四边形，所以A 错误，延长AP 交CD 于G ，连接BG ，由于P 为ACD △的中心，所以G 为CD 的中点，因为AC AD BC BD ===，所以,AG CD BG CD ⊥⊥，因为AG BG G = ，所以CD ⊥平面ABG ，所以CD AB ⊥，因为EM ∥AB ，EF ∥CD ，所以EM EF ⊥，所以截面EFNM 为矩形，所以B 正确，因为2211,3333MN CD a ME AB a ====，所以2212339S MN ME a a a =⋅=⋅=，所以C 正确，对于D ，截面EFNM ⋂平面ABC ME =，ME ∥AB ，ME ⊄平面ABD ，AB Ì平面ABD ，所以ME ∥平面ABD ，所以D 正确，故选：BCD3.（2021·湖北随州市·广水市一中高一月考）如图所示，矩形O A B C ''''是水平放置一个平面图形的直观图，其6O A ''=，2O C ''=，则原图形是（）A ．正方形B ．矩形C ．菱形D ．梯形【答案】C【解析】由已知得原图为平行四边形，OD BC ^，利用勾股定理计算边长得到OC OA =,可判断原图形的形状.【详解】因为//O A B C ''''，=O A B C ''''，所以直观图还原得//OA BC ，=6OA BC O A ''==，四边形OABC 为平行四边形，OD BC ^，则2C D O C ''''==，2CD ∴=，O D C ''''==2OD O D ''==6OC =，所以6OC OA ==，故原图形为菱形．故选：C.4．（2021·肇州县第二中学高一月考）如图是利用斜二测画法画出的Rt ABO 的直观图，已知4O B ''=，且ABO 的面积为16，过点A '作A C x '''⊥轴于点C '，则A C ''的长为（）A ．BC ．D ．1【答案】A【解析】利用面积公式，求出直观图的高，求出''A B ，然后在直角三角形'''A B C 中求解即可【详解】解：由直观图可知，在Rt ABO 中，2ABO π∠=，因为ABO 的面积为16，4O B OB ''==,所以1162AB OB ⋅=，所以8AB =，所以''4A B =，因为'''4A B C π∠=，A C x '''⊥轴于点C '，所以''''sin 44AC A B π=⋅==故选：A5．（2021·宁夏大学附属中学高一月考）三棱锥S ABC -及其三视图中的正视图和侧视图如图所示，则棱SB 的长为（）A ．B ．CD ．【答案】B【解析】根据几何体的三视图，结合几何体的数量关系，在直角SBD 中，即可求解.【详解】如图所示，根据三棱锥S ABC -及其三视图中的正视图和侧视图，可得底面ABC 中，点D 为AC 的中点，BD =SC ⊥底面ABC ，又由点D 为AC 的中点，且根据侧视图，可得BD AC ⊥，在直角BCD △中，可得4BC ===又由4SC =，在直角SBC 中，可得SB =故选：B.6．（2021·江苏省镇江中学）点P 是平面ABC 外一点，且PA PB PC ==，则点P 在平面ABC 上的射影一定是ABC 的（）A ．外心B ．内心C ．重心D ．垂心【答案】A【解析】过点P 作PO ⊥平面ABC ，因为PA PB PC ==，得到OA OB OC ==，即可求解.【详解】如图所示，过点P 作PO ⊥平面ABC ，可得222222,OA PA PO OB PB PO OC PC PO =-=-=-因为PA PB PC ==，可得OA OB OC ==，所以O 为ABC 的外心.故选：A.7.（2021·上海高二期末）圆锥的高为1，3则过圆锥顶点的截面面积的最大值为____________【答案】2【解析】求出圆锥轴截面顶角大小，判断并求出所求面积最大值．【详解】如图，SAB 是圆锥轴截面，SC 是一条母线，设轴截面顶角为θ，因为圆锥的高为1tan 2θ(0,)θπ∈，所以23θπ=，232ππθ=>，设圆锥母线长为l ，则2l =，截面SBC 的面积为211sin sin 22S SB SC BSC l BSC =⋅∠=∠，因为2(0,]3BSC π∠∈，所以2BSC π∠=时，2max 1222S =⨯=．故答案为：2．8．（2021·浙江绍兴市·高一期末）已知四面体ABCD 的所有棱长均为4，点O 满足OA OB OC OD ===，则以O ABCD 表面所得交线总长度为______.【答案】3【解析】根据正四面体的结构特征求得O 到面的距离，进而利用球的截面的性质求得各面所在平面与球的截面圆的半径，注意与各面的三角形内切圆的半径比较，确定此截面圆是否整个在面所在的三角形内，进而确定球与各面的交线，得到球与四面体表面所得交线总长度．【详解】已知四面体ABCD 的所有棱长均为4，所以四面体ABCD 是正四面体，因为点O 满足OA OB OC OD ===，所以O 为正四面体ABCD 的中心.设正三角BCD 的中心为F ，正三角ACD 的中心为G ，CD 的中点为E ，则连接,,,,AF BG AE BE 则,BG AF O BF AG E ⋂=⋂=．:::1:3,:1:4,OF OA GF AB EF EB OF AF ===∴=则224223BE AE =-=24333BF BE ==，224364()33AF =-，643AF OF ==．因为球O 2O 被平面BCD 截得圆半径为22623(2)()33r PF ==-=，因为正三角形BCD 的边长为4，所以正三角形内切圆半径为232tan 303︒=，故球O 与四面体ABCD 的每一个面所得的交线为正好为内切圆，每个内切圆的周长为4323r π，所以球与四面体ABCD 1633．故答案为：1633π．9.（2020届浙江杭州四中高三上期中）某几何体的三视图如图所示，且该几何体的体积是3，则正视图中的x 的值是_____，最长棱长为_____．【答案】3【解析】由已知中的三视图可得该几何体是一个以直角梯形为底面的四棱锥，且梯形上下边长为1和2，高为2，如图：2AD =，2AB =，1BC =，PA x =，//AD BC ，PA ⊥平面ABCD ，AD AB ⊥，∴底面的面积1(12)232S =⨯+⨯=，∴几何体的体积1333V x ==，可得3x =，最长棱长为：PC故答案为：3．10．（2019·全国高考真题（理））中国有悠久的金石文化，印信是金石文化的代表之一．印信的形状多为长方体、正方体或圆柱体，但南北朝时期的官员独孤信的印信形状是“半正多面体”（图1）.半正多面体是由两种或两种以上的正多边形围成的多面体.半正多面体体现了数学的对称美．图2是一个棱数为48的半正多面体，它的所有顶点都在同一个正方体的表面上，且此正方体的棱长为1．则该半正多面体共有________个面，其棱长为_________．【答案】共26个面.1-.【解析】由图可知第一层与第三层各有9个面，计18个面，第二层共有8个面，所以该半正多面体共有18826+=个面．如图，设该半正多面体的棱长为x ，则AB BE x ==，延长BC 与FE 交于点G ，延长BC 交正方体棱于H ，由半正多面体对称性可知，BGE ∆为等腰直角三角形，22,21)122BG GE CH x GH x x x ∴===∴=⨯+=+=，1x ∴==1．练真题1.（2021·全国高考真题）其侧面展开图为一个半圆，则该圆锥的母线长为（）A ．2B ．C ．4D ．【答案】B【解析】设圆锥的母线长为l ，根据圆锥底面圆的周长等于扇形的弧长可求得l 的值，即为所求.【详解】设圆锥的母线长为l ，由于圆锥底面圆的周长等于扇形的弧长，则2l ππ=l =.故选：B.2．（2021·北京高考真题）定义：24小时内降水在平地上积水厚度（mm ）来判断降雨程度．其中小雨（10mm <），中雨（10mm 25mm -），大雨（25mm 50mm -），暴雨（50mm 100mm -），小明用一个圆锥形容器接了24小时的雨水，如图，则这天降雨属于哪个等级（）A ．小雨B ．中雨C ．大雨D ．暴雨【答案】B【解析】计算出圆锥体积，除以圆面的面积即可得降雨量，即可得解.【详解】由题意，一个半径为()200100mm 2=的圆面内的降雨充满一个底面半径为()20015050mm 2300⨯=，高为()150mm 的圆锥，所以积水厚度()22150150312.5mm 100d ππ⨯⨯==⨯，属于中雨.故选：B.3.（2020·全国高考真题（理））如图是一个多面体的三视图，这个多面体某条棱的一个端点在正视图中对应的点为M ，在俯视图中对应的点为N ，则该端点在侧视图中对应的点为（）A．EB．F C．G D．H【答案】A【解析】根据三视图，画出多面体立体图形，14D D 上的点在正视图中都对应点M ,直线34B C 上的点在俯视图中对应的点为N,∴在正视图中对应M ,在俯视图中对应N 的点是4D ,线段34D D ,上的所有点在侧试图中都对应E ,∴点4D 在侧视图中对应的点为E .故选：A4．(2019年高考全国Ⅲ卷理)如图，点N 为正方形ABCD 的中心，△ECD 为正三角形，平面ECD ⊥平面ABCD ，M 是线段ED 的中点，则()A．BM =EN ，且直线BM ，EN 是相交直线B．BM ≠EN ，且直线BM ，EN 是相交直线C．BM =EN ，且直线BM ，EN 是异面直线D．BM ≠EN ，且直线BM ，EN 是异面直线【答案】B【解析】如图所示，作EO CD ⊥于O ，连接ON ，BD ，易得直线BM ，EN 是三角形EBD 的中线，是相交直线.过M 作MF OD ⊥于F ，连接BF ，平面CDE ⊥平面ABCD ，,EO CD EO ⊥⊂平面CDE ，EO ∴⊥平面ABCD ，MF ⊥平面ABCD ，MFB ∴△与EON △均为直角三角形．设正方形边长为2，易知12EO ON EN ===,，5,,22MF BF BM ==∴=BM EN ∴≠，故选B．5.（2018·北京高考真题（文））某四棱锥的三视图如图所示，在此四棱锥的侧面中，直角三角形的个数为（）A.1B.2C.3D.4【答案】C【解析】分析：根据三视图还原几何体，利用勾股定理求出棱长，再利用勾股定理逆定理判断直角三角形的个数.详解：由三视图可得四棱锥P ABCD -，在四棱锥P ABCD -中，2,2,2,1PD AD CD AB ====，由勾股定理可知：3,PA PC PB BC ====，则在四棱锥中，直角三角形有：,,PAD PCD PAB ∆∆∆共三个，故选C.6.（2021·全国高考真题（理））以图①为正视图，在图②③④⑤中选两个分别作为侧视图和俯视图，组成某个三棱锥的三视图，则所选侧视图和俯视图的编号依次为_________（写出符合要求的一组答案即可）．【答案】③④（答案不唯一）【解析】由题意结合所给的图形确定一组三视图的组合即可.【详解】选择侧视图为③，俯视图为④，如图所示，长方体1111ABCD A B C D -中，12,1AB BC BB ===，,E F 分别为棱11,BC BC 的中点，则正视图①，侧视图③，俯视图④对应的几何体为三棱锥E ADF -.故答案为：③④.。
高考数学立体几何专题复习(含答案)
的中点.
（Ⅰ）证明： PA / / 平面 EDB ； （Ⅱ）求三棱锥 A BDP 的体积.
试卷第 2 页，总 2 页
参考答案
1、【答案】(1)详见解析;(2) . 试题分析（：1）过 B 作 CD 的垂线交 CD 于 F，则
6、如图所示，在直三棱柱 ABC－A1B1C1 中，AC＝3，BC＝4，AB＝5，AA1＝4，点 D 是 AB 的中点． (1)求证：AC1∥平面 CDB1； (2)求异面直线 AC1 与 B1C 所成角的余弦值．
7、如图所示，在三棱锥 A BOC 中，OA 底面 BOC ，OAB OAC 300 ， AB AC 2 ， BC 2 ，
高考数学—立体几何专题复习
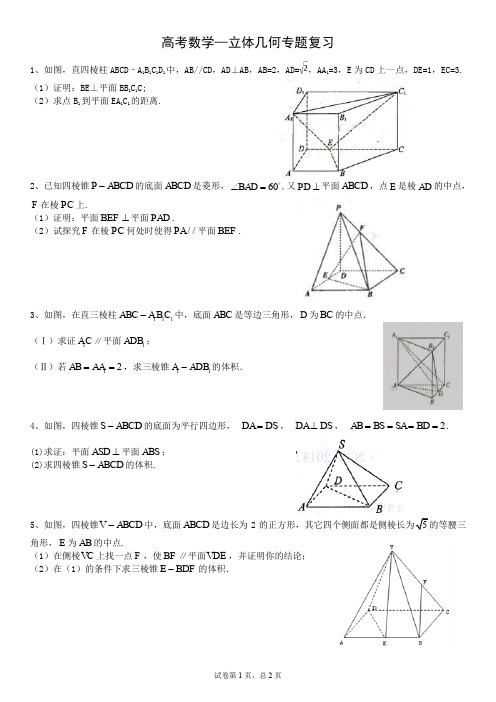
1、如图，直四棱柱 ABCD–A1B1C1D1 中，AB//CD，AD⊥AB，AB=2，AD= ，AA1=3，E 为 CD 上一点，DE=1，EC=3. （1）证明：BE⊥平面 BB1C1C; （2）求点 B1 到平面 EA1C1 的距离.
2、已知四棱锥 P ABCD 的底面 ABCD 是菱形， BAD 60 ,又 PD 平面 ABCD ，点 E 是棱 AD 的中点， F 在棱 PC 上. （1）证明：平面 BEF 平面 PAD . （2）试探究 F 在棱 PC 何处时使得 PA / / 平面 BEF .
答案第 1 页，总 6 页
试题解析：
（1）证明：
PD EB
平面ABCD 平面ABCD
PD
EB
,
又底面 ABCD 是 A 60 的菱形，且点 E 是棱 AD 的中点，所以 EB AD ，
高考数学第一轮复习立体几何专题题库19.doc
241. 已知点P 是正方形ABCD 所在的平面外一点，PD ⊥面AC ，PD=AD=l ，设点C 到面PAB 的距离为d 1，点B 到平面PAC 的距离为d 2，则（ ） （A ）l <d 1 <d 2（B ）d 1< d 2<l （C ）d 1<l < d 2（D ）d 2<d 1<l解析：l d 221=，l d 332=，故d 2<d 1<l ，选D 。
242.如图，正方形ABCD 、ABEF 的边长都是1,而且平面ABCD 、ABEF 互相垂直。
点M 在AC 上移动，点N 在BF 上移动，若CM=BN=a ).20(<<a （1）求MN 的长；（2）当a 为何值时，MN 的长最小； （3）当MN 长最小时，求面MNA 与面MNB 所成的二面角α的大小。
解析：（1）作MP ∥AB 交BC 于点P ，NQ ∥AB 交BE 于点Q ，连接PQ ，依题意可得MP ∥NQ ，且MP=NQ ，即MNQP 是平行四边形。
∴MN=PQ,由已知，CM=BN=a,CB=AB=BE=1,∴2==BF AC ,21,21a BQ a CP ==, 即2aBQ CP ==, ∴=+-==22)1(BQ CP PQ MN )20(21)22()2()21(222<<+-=+-a a a a（2）由（1）知: 2222==MN a 时，当，的中点时，分别移动到即BF AC N M ,, 22的长最小，最小值为MN (3)取MN 的中点G ，连接AG 、BG ，∵AM=AN,BM=BN ，∴AG ⊥MN,BG ⊥MN ，∴∠AGB 即为二面角α的平面角。
又46==BG AG ，所以由余弦定理有 ADE31464621)46()46(cos 22-=∙∙-+=α。
故所求二面角)31arccos(-=α。
243. 如图，边长均为a 的正方形ABCD 、ABEF 所在的平面所成的角为)20(πθθ<<。
2024届一轮复习数学新教材人教A版 第七章立体几何与空间向量必刷小题13 立体几何 课件(37张)
2.下列四个命题中，正确的是 A.各侧面都是全等四边形的棱柱一定是正棱柱 B.对角面是全等矩形的六面体一定是长方体 C.有两侧面垂直于底面的棱柱一定是直棱柱
√D.长方体一定是直四棱柱
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16
7.蹴鞠，又名蹴球，踢圆等，蹴有用脚蹴、踢、蹋的含义，鞠最早系外
包皮革、内实米糠的球.因而蹴鞠就是指古人以脚蹴、蹋、踢皮球的活动，
类似今日的足球.2006年5月20日，蹴鞠已作为非物质文化遗产经国务院
批准列入第一批国家非物质文化遗产名录.已知某鞠的表面上有五个点P，
对于A，由m∥α，m∥n，得到： 若n∥α，过n的平面γ∩α＝l，则n∥l， 又n⊥β，则l⊥β，l⊂α，则α⊥β， 若n⊂α，又n⊥β，则α⊥β.综上，α⊥β，故A正确； 对于B，若m⊥n，m⊥α，n∥β，则α与β相交或平行，故B错误； 对于C，若α⊥β，m⊥α，m⊥n，则n与β相交、平行或n⊂β，故C错误； 对于D，若α⊥β，α∩β＝m，n⊥m，则n与β相交或n⊂β，故D错误.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16
8.某同学画“切面圆柱体”(用与圆柱底面不平行的平面切圆柱，底面与 切面之间的部分叫做切面圆柱体)，发现切面与圆柱侧面的交线是一个椭 圆(如图所示).若该同学所画的椭圆的离心率为12，则“切面”所在平面与 底面所成的角为
π A.12
4.已知m，n表示两条不同的直线，α，β表示两个不同的平面，则下列命 题中正确的是
√A.若m∥α，n⊥β，m∥n，则α⊥β
专题9.5—立体几何—异面直线所成的角1—2022届高三数学一轮复习精讲精练(含答案)
专题9.5—立体几何—异面直线所成的角1一．单选题1．如图，正四棱柱1111ABCD A B C D -满足12AB AA =，点E 在线段1DD 上移动，F 点在线段1BB 上移动，并且满足1DE FB =，则下列结论中正确的是( )A ．直线1AC 与直线EF 可能异面B ．直线EF 与直线AC 所成角随着E 点位置的变化而变化C ．三角形AEF 可能是钝角三角形D ．四棱锥A CEF -的体积保持不变2．如图，设E ，F 分别是正方体1111ABCD A B C D -的棱DC 上两点，且2AB =，1EF =，其中正确的命题为( )A ．直线11DB 与1A D 所成的角为90︒ B ．异面直线11D B 与EF 所成的角为60︒C ．11D B ⊥平面1B EFD ．三棱锥11D B EF -的体积为定值3．在长方体1111ABCD A B C D -中，1AB BC ==，13AA =，则异面直线1AD 与1DB 所成角的余弦值为( ) A 5 B 5 C ．5 D 2 4．在正方体1111ABCD A B C D -中，E 是棱11A B 的中点，则1A B 与DE 所成角的余弦值为(A ．510B ．26C ．55D ．1055．在直三棱柱111ABC A B C -中，12AB AA ==，1BC =，AB BC ⊥，点D 是侧棱1BB 的中点，则异面直线1C D 与直线1AB 所成的角大小为( ) A ．换体6．在直三棱柱111ABC A B C -中，90ACB ∠=︒，1D ，1E 分别是11B C ，11A C 的中点，1CA CB CC ==，则1AE 与1CD 所成角的余弦值为( )A ．12B ．32 C ．35D ．457．如图，在长方体1111ABCD A B C D -中，12AA AD ==，3AB =，点F 在线段11C D 上，且11D F =，则异面直线CD 与BF 所成角的余弦值为( )A ．22B ．33C ．23D ．248．如图，四边形ABCD 为矩形，2AD AB =，E 是BC 的中点，将BAE ∆沿AE 翻折至PAE ∆的位置（点P ∉平面)AECD ，设线段PD 的中点为F ．则在翻折过程中，下列推断不正确的是( )A ．//CF 平面AEPB ．CF 的长度恒定不变C ．AE DP ⊥D ．异面直线CF 与PE 所成角的大小恒定不变 二．多选题9．如图，在正方体1111ABCD A B C D -中，点E 是线段1CD 上的动点，则下列判断正确的是(A ．当点E 与点1D 重合时，1B E AC ⊥B ．当点E 与线段1CD 的中点重合时，1B E 与1AC 异面 C ．无论点E 在线段1CD 的什么位置，都有11AC BE ⊥D ．若异面直线1BE 与AD 所成的角为θ，则cos θ的最大值为6310．已知正方体1111ABCD A B C D -，点P 是棱1CC 的中点，设直线AB 为a ，直线11A D 为b ，则下列判断正确的是( )A ．过点P 有且只有一条直线l 与a ，b 都相交B ．过点P 有且只有一条直线l 与a ，b 都垂直C ．过点P 只有两条直线与a ，b 都成45︒角D ．过点P 只有两条直线与a ，b 都成60︒角11．将正方形ABCD 沿对角线BD 折成直二面角A BD C --，有如下四个结论： ①AC BD ⊥；②ACD ∆是等边三角形；③AB 与平面BCD 所成的角为60︒； ④AB 与CD 所成的角为60︒． 其中正确的结论是( ) A ．①B ．②C ．③D ．④12．如图，边长为1的正方形ABCD 所在平面与正方形ABEF 所在平面互相垂直，动点M ，N 分别在正方形对角线AC 和BF 上移动，且(02)CM BN a a ==<<．则下列结论中正确的有( )A ．当12a =时，ME 与CN 相交 B ．MN 始终与平面BCE 平行C ．异面直线AC 与BF 所成的角为45︒D ．当22a =时，MN 的长最小，最小为22三．填空题13．已知空间中的一个平面与一个正方体的12条棱的夹角都等于α，则cos α= ． 14．如图甲，将三棱锥P ABC -沿三条侧棱剪开后，展开成如图乙所示的形状，其中点1P ，A ，3P 共线，点1P ，B ，2P 共线，点2P ，C ，3P 共线，且1223PP P P =，则在如图甲所示的三棱锥P ABC -中，PA 与BC 所成角的大小为 ．15．如图，在直三棱柱111ABC A B C -中，90BAC ∠=︒，111114AA A B AC ===，点E 是棱1CC 上一点，且113C E CE =，则异面直线1A B 与AE 所成角的余弦值为 ．16．如图，1111ABCD A B C D -是正方体，E ，F 分别是AB ，1BB 的中点，则异面直线1A E 与1C F 所成角的余弦值为 ．四．解答题17．在三棱锥?P ABC 中，M ，N 分别是PA ，BC 的中点，已知2AC PB ==，3MN 求异面直线AC ，PB 所成角的大小．18．如图，在平行六面体1111ABCD A B C D -中，底面是边长为1的正方形，若01160A AB A AD ∠=∠=，且13A A =，若M 是1AA 的中点． （Ⅰ）求证：1//A C 平面MBD ； （Ⅱ）求1A C 的长为；（Ⅲ）求直线1A C 与直线DM 所成角的余弦值．专题9.5—立体几何—异面直线所成的角1答案1．解：如图所示，连接有关线段．设M ，N 为AC ，11A C 的中点，即为上下底面的中心， MN 的中点为O ，则1AC 的中点也是O ，又1DE B F =，由对称性可得O 也是EF 的中点， 所以1AC 与EF 交于点O ，故不是异面直线，故A 错误；由正四棱柱的性质结合线面垂直的判定定理易得AC ⊥平面11BB D D ， 因为EF ⊂平面11BB D D ，AC EF ∴⊥，故B 错误； 设AB a =，则12AA a =，设1DE B F x ==，02x a <<， 易得222AE a x =+，22222(2)54AF a a x a ax x =+-=-+，222222(22)684EF a a x a ax x =+-=-+，因为2222422(2)0AE AF EF ax x x a x +-=-=->， 则EAF ∠为锐角；因为2222222422()0AE EF AF a ax x a x +-=-+=->， 则AEF ∠为锐角，因为2222210124AF EF AE a ax x +-=-+，当32x a =时取得最小值为2222101890a a a a -+=>，则AFE ∠为锐角，故AEF ∆为锐角三角形，故C 错误； 三棱锥A EFC -也可以看做F AOC -和E AOC -的组合体， 由于AOB ∆是固定的，E ，F 到平面AOC 的距离是不变的 (易知1BB ，1DD 平行与平面11)ACC A ，故体积不变，故D 正确． 故选：D ．2．解：对于A ，11D B 不垂直1A D ，故A 错，对于B ，11//EF D C ，11D B 和11D C 所成的角是45︒，异面直线11D B 所成的角45︒，故B 错误， 对于C ，11D B 于EF 不垂直，由此可知11D B 于平面1B EF 不垂直，故C 错， 对于D ，三棱锥11D B EF -的体积为 11113D EFV SB C =⋅1122132=⨯⨯⨯⨯ 23=，为定值， 故D 对， 故选：D ．3．解：建立如图所示的空间直角坐标系， 不妨设1DA =，则有：(0D ，0，0)，(1A ，0，0)，1(0D ，0，1(1B ，1， 所以1(1DB =，1，1((1AD =-，0， 设1DB ，1AD 的夹角为θ， 则11115cos 5||||DB AD DB AD θ⋅==⋅， 即异面直线1AD 与1DB ， 故选：A ．4．解：如图，取1BB 的中点F ，连接EF ，则1//EF A B ，DEF ∴∠（或其补角）即为1A B 与DE 所成角，连接DF ，设正方体的棱长为2，则2EF =，2222213DF =++=，2222213DE =++=，2229292cos 26232DE EF DF DEF DE EF +-+-∴∠===⨯⨯⨯⨯． 1A B ∴与DE 所成角的余弦值为26． 故选：B ．5．解：如图，取AB 的中点E ，连接DE ，则1//DE AB ，则1C DE ∠（或其补角）为异面直线1C D 与直线1AB 所成的角， 1122DE AB ==，12C D =，22211126C E =++=， 12261cos 2222C DE +-∠==-⨯⨯，∴异面直线1C D 与直线1AB 所成的角大小为3π． 故选：C ． 6．解：如图，以C 为坐标原点，分别以CA 、CB 、1CC 所在直线为x 、y 、z 轴建立空间直角坐标系． 设12CA CB CC ===，则(0C ，0，0)，(2A ，0，0)，1(1E ，0，2)，1(0D ，1，2)． 1(1,0,2)AE =-，1(0,1,2)CD =．11111144cos ,5||||55AE CD AE CD AE CD ⋅∴<>===⋅⨯． 1AE ∴与1CD 所成角的余弦值为45． 故选：D ．7．解：以D 为坐标原点距离如图所示空间直角坐标系，则(0D ，0，0)，(0C ，3，0)，(2B ，3，0)，(0F ，1，2)，∴(0,3,0)DC =，(2,2,2)FB =-，63cos ,3||||332DC FB DC FB DC FB ⋅∴<>===⋅⨯．即异面直线CD 与BF 所成角的余弦值为33． 故选：B ．8．解：取AD 的中点M ，连接MF ，MC 交ED 于N ，A ．由题意可知N 为ED 的中点，所以//FM AP ，//FN PE ，所以平面//PAE 平面MFC ，所以A 正确；B ．因为FMC PAE ∠=∠（定值），12FM AP =（定值），MC AE =（定值），在MFC ∆中由余弦定理可知CF 的长是定值，所以B 正确．C ．若AB BE =，则MA ME MD ==，所以90AED ∠=︒，所以AE ED ⊥，若AE DP ⊥，又DEDP D =，则有AE ⊥面PED ，所以有AE PE ⊥，这与AE 不垂直于PE 相矛盾，所以C 不正确；D ．由B 知在翻折过程中MFC ∆的形状不变，点N 的位置也不会发生改变，所以NFC ∠大小不变，又易证//FN PE ，所以NFC ∠是异面直线CF 与PE 所成的角，所以异面直线CF 与PE 所成角的大小恒定不变，故D 正确．故选：C ．9．解：当点E 与点1D 重合时，1//B E BD ，因为AC BD ⊥，1B E AC ∴⊥，∴选项A 正确； 当点E 与线段1CD 的中点重合时，E 是1CD 的中点，1B E 与1AC 都在平面11AB C D 内，1B E 与1AC 相交，∴选项B 错误；建立如图所示的直角坐标系，设正方体棱长为1，则(0A ，0，0)，1(1C ，1，1)，1(1B ，0，1)，(0D ，1，0)， 设(1E a -，1，)a ，01a ，则1(,1,1)B E a a =--，1(1,1,1)AC =，∴11110B E AC a a ⋅=-++-=，11AC B E ∴⊥，∴选项C 正确；(0,1,0)AD =，设异面直线1B E 与AD 所成角为θ，则122221||11cos ||||131(1)2()22B E AD B E AD a a a θ⋅===⋅++--+，当12a =时，cos θ有最大值63，此时点E 是线段1CD 的中点，∴选项D 正确，故选：ACD ．10．解：直线AB 与11A D 是两条互相垂直的异面直线， 点P 不在这两条异面直线中的任何一条上，如图所示， 取1BB 的中点Q ，则11//PQ A D ，且11PQ A D =， 设1A Q 与AB 交于点E ， 则点1A ，1D ，Q ，E ，P 共面， 直线EP 必与11A D 相交于某点F ，由于直线a 与平面11A QPD 仅交于点E ，两点确定一条直线， 则过点P 有且只有一条直线l 与a ，b 都相交， 故选项A 正确；过点P 有且只有一条直线1C C 都与a ，b 成90︒角， 故选项B 正确；分别平移a ，b ，使a 与b 均经过点P ，则有两条互相垂直的直线与a ，b 都成45︒角， 故选项C 正确；假设平面内与a ，b 成60︒角的直线为1l ，2l ，把1l ，2l 绕点P 逐渐竖起，则与a ，b 成60︒角的直线有4条， 故选项D 错误． 故选：ABC ．11．解：取BD 中点，连接AO 、OC ，OA '，设正方形ABCD 边长为a ， 对于①，因为BD OA ⊥，BD OC ⊥，所以BD ⊥平面AOC ，所以BD AC ⊥，所以①对；对于②，因为二面角A BD C --为直二面角，所以AO OC ⊥， 又因为22OA OC a ==，所以AC a =，又因为AD AC a ==，所以②对； 对于③，因为OB 为AB 在平面BCD 内投影，AB 与平面BCD 所成的角4560ABO ∠=︒≠︒， 所以③错；对于④，因为//CD A B '，所以AB 与CD 所成的角为60A BA ∠'=︒，所以④对． 故选：ABD ．12．解：由题意，以B 为坐标原点，BA ，BE ，BC 所在直线为x 轴，y 轴，z 轴，建立空间直角坐标系，如图所示， 由正方形ABCD ，ABFE 的边长1，所以(1A ，0，0)，(0B ，0，0)，(0C ，0，1)，(1D ，0，1)，(0E ，1，0)，(1F ，1，0)， CM BN a ==，所以(2M ，0，12，(2N 2，0)，对于A ，若ME 与CN 相交， 则M 、E 、C 、N 四点共面，故M 、E 、C 、N 四点都在平面ACE 内， 故点N 为AE 与BF 的交点，此时2a ，故A 错误； 对于B ，(0MN =21)2-，平面BCE 的法向量为(1BA =，0，0)，所以0000MN BA ⋅=++=，又MN ⊂/平面BDE ，所以MN 与平面BDE 平行，故B 正确； 对于C ，(1AC =-，0，1)，(1BF =，1，0)，所以cos AC <，10012||||22AC BF BF AC BF ⋅-++>===-⋅，所以AC <，23BF π>=， 所以异面直线AC 与BF 所成的角为3π，故C 错误； 对于D ，22221||()(1)()2222a a MN a =+-=-+， 故所以当22a =时，MN 的长度最小，最小值为22，故D 正确． 故选：BD ．13．解：棱1A A ，11A B ，11A D 与平面11AB D 所成的角相等，∴平面11AB D 就是与正方体的12条棱的夹角均为α的平面．则1A AO α∠=，设棱长为2，12AA =，12A O =，426AO =+=，26cos 36α==， 故答案为：63．14解：13P A P A =，A ∴是13PP 的中点， 同理可知B 是12P P 的中点，C 是23P P 的中点， 2312AB P P ∴=，1212AC PP =，又1223PP P P =，AB AC ∴=，PB PC =， 在图甲中，取BC 的中点D ，连接AD ，PD ， 则AD BC ⊥，PD BC ⊥，又ADPD D =，BC ∴⊥平面PAD ，又PA ⊂平面PAD ，BC PA ∴⊥，PA ∴与BC 所成角的大小为90︒．故答案为：90︒．15．解：以点1A 为原点，建立如图所示的空间直角坐标系1A xyz -， 则1(0A ，0，0)，(4B ，0，4)，(0A ，0，4)，(0E ，4，4)3，则1(4A B =，0，4)，(0AE =，4，8)3-，1cos A B <，112613A B AE AE A B AE⋅->==-⨯， 所以异面直线1A B 与AE 所成角的余弦值为2613， 故答案为：2613．16．解：在正方体1111ABCD A B C D -中，E 、F 是AB 、1BB 的中点，设4AB = 取11A B 的中点H ，1HB 的中点G ，连结GF ，1GC ， GF 、1FC 所成的角即为1A E 与1C F 所成的角．利用勾股定理得：5GF ，125C F =，117GC = 在△1C FG 中，利用余弦定理1520172cos 52525GFC +-∠==⋅⋅． 故答案为：25．17．解：取AB （或)PC 中点Q ，连接QM ．QN ，Q 是AB 中点，N 是BC 中点，//QN AC ⇒，QN =三112AC =， 同理，可得//QM BP ，112QM PB ==， 所以MQN ∠就是异面直线AC 、PB 所成的角或其补角， 在MQN ∆中，1QM QN ==，3MN = 22211(3)1cos 2MQN +-∠=-，120MQN ∠=︒，∴异面直线AC ，PB 所成的角的大小为60︒．18．解：（Ⅰ）如图：连接AC 交BD 于点O ，连接MO ，因为四边形ABCD 为正方形，所以O 为AC 中点， 又因为M 为1AA 中点，所以OM 为△1AAC 的中位线， 所以1//MO AC ，因为MO ⊂面MBD ，所以1//A C 面MBD ， （Ⅱ）在平行六面体1111ABCD A B C D -中，1160A AB A AD ∠=∠=︒，所以11120BCC DCC ∠=∠=︒，又13AA =，1BC DC ==，∴1113||||cos1202CB CC CD CC CD CC ⋅=⋅=︒=-．， ||||cos900CB CD CB CD ⋅=︒=，11CA CB CD CC =++，∴2222211111||()222CA CB CD CC CB CD CC CB CC CD CC CB CD =++=+++⋅+⋅+⋅22231132()2052=+++⨯-⨯+=，∴15AC = （Ⅲ）设直线1A C 与直线DM 所成角为θ， 则111cos |cos ,|||||||A C DM A C DM A C DM θ⋅=<>=，11A C AA AB AD =-++，1||5A C =112DM DA AA =+，2117||()22DM DA AA =+=， ∴11115()()22AC DM AA AB AD DA AA ⋅=-++⋅+=-， ∴5352cos |752θ-==⨯所以直线1A C 与直线DM 35。
高中数学一轮复习：第八章 立体几何(必修2)课后跟踪训练46
课后跟踪训练(四十六)基础巩固练一、选择题1．和两条异面直线都相交的两条直线的位置关系是()A．异面B．相交C．平行D．异面或相交[解析]当两条直线无公共点时，可知两直线异面；当两异面直线中的一条直线与两条直线交于一点时，可知两直线相交，故选D.[答案] D2.如图，α∩β＝l，A，B∈α，C∈β，且C∉l，直线AB∩l＝M，过A，B，C三点的平面记作γ，则γ与β的交线必通过()A．点A B．点BC．点C但不过点M D．点C和点M[解析]∵AB⊂γ，M∈AB，∴M∈γ.又C∈γ，M、C∈β，∴γ与β的交线必通过点C和点M.故选D.[答案] D3．已知正方体ABCD－A1B1C1D1中，O是BD1的中点，直线A1C 交平面AB1D1于点M，则下列结论错误的是()A．A1、M、O三点共线B．M、O、A1、A四点共面C．A、O、C、M四点共面D．B、B1、O、M四点共面[解析]因为O是BD1的中点．由正方体的性质知，O也是A1C 的中点，所以点O在直线A1C上，又直线A1C交平面AB1D1于点M，则A1、M、O三点共线，A正确．又直线与直线外一点确定一个平面，所以B、C正确．故选D.[答案] D4．以下四个命题中，正确命题的个数是()①不共面的四点中，其中任意三点不共线；②若点A，B，C，D 共面，点A，B，C，E共面，则A，B，C，D，E共面；③若直线a，b共面，直线a，c共面，则直线b，c共面；④依次首尾相接的四条线段必共面．A．0 B．1C．2 D．3[解析]对于①，不共面的四点中，其中任意三点不共线，故①正确；对于②，若A，B，C共线时，A，B，C，D，E不一定共面，故②不正确；对于③，b，c也可异面，故③不正确；④是错误的．故选B.[答案] B5．在正四棱柱ABCD－A1B1C1D1中，AA1＝2AB，则异面直线A1B与AD 1所成角的余弦值为( )A.15B.25C.35D.45[解析] 如图，连接BC 1，易证BC 1∥AD 1，则∠A 1BC 1即为异面直线A 1B 与AD 1所成的角或其补角．连接A 1C 1，设AB ＝1，则AA 1＝2，A 1C 1＝2，A 1B ＝BC 1＝5，故cos ∠A 1BC 1＝5＋5－22×5×5＝45.故选D. [答案] D二、填空题6．(2019·陕西汉中调研)若直线a ⊥b ，且直线a ∥平面α，则直线b 与平面α的位置关系是________．[解析] 如图，在正方体中可知，b 与α相交或b ⊂α或b ∥α.[答案] b 与α相交或b ⊂α或b ∥α7．(2019·广东华山模拟)如图所示，在正三棱柱ABC －A 1B 1C 1中，D是AC的中点，AA1∶AB＝2∶1，则异面直线AB1与BD所成的角为________．[解析]取A1C1的中点E，连接B1E，ED，AE，在Rt△AB1E中，∠AB1E即为所求．设AB＝1，则A1A＝2，AB1＝3，B1E＝32，AE＝32，故∠AB1E＝60°.[答案]60°8.(2019·江西上饶月考)如图所示，在正方体ABCD－A1B1C1D1中，M，N分别为棱C1D1，C1C的中点，有以下四结论：①直线AM与CC1是相交直线；②直线AM与BN是平行直线；③直线BN与MB1是异面直线；④直线MN与AC所成的角为60°.其中正确的结论为________(注：把你认为正确的结论号都填上) [解析]由题图可知AM与CC1是异面直线，AM与BN是异面直线，BN与MB1为异面直线．因为D1C∥MN，所以直线MN与AC所成的角就是D1C与AC所成的角，且角为60°.[答案]③④三、解答题9．已知正方体ABCD－A1B1C1D1中，E，F分别为D1C1，C1B1的中点，AC∩BD＝P，A1C1∩EF＝Q.求证：(1)D，B，E，F四点共面；(2)若A1C交平面DBFE于R点，则P，Q，R三点共线．[证明](1)如图所示，因为EF是△D1B1C1的中位线，所以EF∥B1D1.在正方体AC1中，B1D1∥BD，所以EF∥BD.所以EF，BD确定一个平面．即D，B，F，E四点共面．(2)在正方体ABCD－A1B1C1D1中，设平面A1ACC1确定的平面为α，又设平面BDEF为β.因为Q∈A1C1，所以Q∈α.又Q∈EF，所以Q∈β.则Q是α与β的公共点，同理，P点也是α与β的公共点．所以α∩β＝PQ.又A1C∩β＝R，所以R∈A1C，R∈α且R∈β.则R∈PQ，故P，Q，R三点共线．10.(2019·河南许昌模拟)如图所示，在三棱锥P －ABC 中，P A ⊥底面ABC ，D 是PC 的中点．已知∠BAC ＝π2，AB ＝2，AC ＝23，P A ＝2.求：(1)三棱锥P －ABC 的体积；(2)异面直线BC 与AD 所成角的余弦值．[解] (1)S △ABC ＝12×2×23＝23，三棱锥P －ABC 的体积为V ＝13S △ABC ·P A ＝13×23×2＝43 3.(2)如图，取PB 的中点E ，连接DE ，AE ，则ED ∥BC ，所以∠ADE 是异面直线BC 与AD 所成的角(或其补角)．在△ADE 中，DE ＝2，AE ＝2，AD ＝2，cos ∠ADE ＝22＋22－22×2×2＝34. 故异面直线BC 与AD 所成角的余弦值为34.能力提升练11．两条异面直线在同一个平面上的正投影不可能是( )A ．两条相交直线B ．两条平行直线C．两个点D．一条直线和直线外一点[解析]如图，在正方体ABCD－EFGH中，M，N分别为BF，DH的中点，连接MN，DE，CF，EG.当异面直线为EG，MN所在直线时，它们在底面ABCD内的射影为两条相交直线；当异面直线为DE，GF所在直线时，它们在底面ABCD内的射影分别为AD，BC，是两条平行直线；当异面直线为DE，BF所在直线时，它们在底面ABCD内的射影分别为AD和点B，是一条直线和一个点，故选C.[答案] C12．如图，平面α与平面β交于直线l，A，C是平面α内不同的两点，B，D是平面β内不同的两点，且A，B，C，D不在直线l上，M，N分别是线段AB，CD的中点，下列判断正确的是() A．若AB与CD相交，且直线AC平行于l时，则直线BD与l 可能平行也有可能相交B．若AB，CD是异面直线时，则直线MN可能与l平行C．若存在异于AB，CD的直线同时与直线AC，MN，BD都相交，则AB，CD不可能是异面直线D．M，N两点可能重合，但此时直线AC与l不可能相交[解析]对于A，直线BD与l只能平行；对于B，直线MN与l 异面；对于C，AB与CD可能为异面直线．当直线AB与CD的中点M，N重合时，必有直线AC∥l，故不可能相交，综上所述，故选D.[答案] D13．如图所示，在四面体ABCD中，E，F分别为AB，CD的中点，过EF任作一个平面α分别与直线BC，AD相交于点G，H，则下列结论正确的是__________．①对于任意的平面α，都有直线GF，EH，BD相交于同一点；②存在一个平面α0，使得GF∥EH∥BD；③存在一个平面α0，使得点G在线段BC上，点H在线段AD的延长线上．[解析]当H，G分别为AD，BC的中点时，直线GF，EH，BD 平行，所以①错，②正确；若存在一个平面α0，使得点G在线段BC 上，点H在线段AD的延长线上，则平面α0与CD的交点不可能是CD的中点，故③错．[答案]②14.如图，在四棱锥O－ABCD中，底面ABCD是边长为2的正方形，OA⊥底面ABCD，OA＝2，M为OA的中点．(1)求四棱锥O－ABCD的体积；(2)求异面直线OC与MD所成角的正切值的大小．[解] (1)由已知可求得，正方形ABCD 的面积S ＝4，所以，四棱锥O －ABCD 的体积V ＝13×4×2＝83.(2)连接AC ，设线段AC 的中点为E ，连接ME ，DE ，则∠EMD 为异面直线OC 与MD 所成的角(或其补角)，由已知，可得DE ＝2，EM ＝3，MD ＝5，∵(2)2＋(3)2＝(5)2，∴△DEM 为直角三角形，∴tan ∠EMD ＝DE EM ＝23＝63. 拓展延伸练15．(2018·全国卷Ⅰ)已知正方体的棱长为1，每条棱所在直线与平面α所成的角都相等，则α截此正方体所得截面面积的最大值为( ) A.334 B.233 C.324 D.32[解析]记该正方体为ABCD －A ′B ′C ′D ′，正方体的每条棱所在直线与平面α所成的角都相等，即共点的三条棱A ′A ，A ′B ′，A ′D ′与平面α所成的角都相等．如图，连接AB ′，AD ′，B ′D ′，因为三棱锥A ′－AB ′D ′是正三棱锥，所以A ′A ，A ′B ′，A ′D ′与平面AB ′D ′所成的角都相等．分别取C ′D ′，B ′C ′，BB ′，AB ，AD ，DD ′中点的E ，F ，G ，H ，I ，J ，连接EF ，FG ，GH ，IH ，IJ ，JE ，易得E ，F ，G ，H ，I ，J 六点共面，平面EFGHIJ 与平面AB ′D ′平行，且截正方体所得截面的面积最大．又EF ＝FG ＝GH ＝IH ＝IJ＝JE ＝22，所以该正六边形的面积为6×34×⎝ ⎛⎭⎪⎫222＝334，所以α截此正方体所得截面面积的最大值为334，故选A.[答案] A16．(2017·全国卷Ⅲ)a ，b 为空间中两条互相垂直的直线，等腰直角三角形ABC 的直角边AC 所在直线与a ，b 都垂直，斜边AB ，以直线AC 为旋转轴旋转，有下列结论：①当直线AB 与a 成60°角时，AB 与b 成30°角；②当直线AB 与a 成60°角时，AB 与b 成60°角；③直线AB 与a 所成角的最小值为45°；④直线AB 与a 所成角的最大值为60°.其中正确的是________．(填写所有正确结论的编号)[解析]由题意知，AB 是以AC 为轴，BC 为底面半径的圆锥的母线，又AC ⊥a .AC ⊥b ，AC ⊥圆锥底面，所以在底面内可以过点B ，作BD ∥a ，交底面圆C 于点D ，如图所示，连接DE ，则DE ⊥BD ，所以DE ∥b ，连接AD ，设BC ＝1，在等腰△ABD 中，AB ＝AD ＝2，当直线AB 与a成60°角时，∠ABD＝60°，故BD＝2，又在Rt△BDE中，BE＝2，所以DE＝2，过点B作BF∥DE，交圆C于点F，连接AF，EF，所以BF＝DE＝2，所以△ABF为等边三角形，所以∠ABF＝60°，即AB与b成60°角，故②正确，①错误．由最小角定理可知③正确；很明显，可以满足平面ABC⊥直线a，所以直线AB与a所成角的最大值为90°，④错误．所以正确的结论为②③.[答案]②③。
立体几何 大题-2023届高三数学一轮复习
立体几何复习1.（多选）如图，四棱锥P ABCD -中，平面PAD ⊥底面ABCD ，PAD △是等边三角形，底面ABCD 是菱形，且60BAD ∠=︒，M 为棱PD 的中点，N 为菱形ABCD 的中心，下列结论正确的有（ ） A ．直线PB 与平面AMC 平行 B ．直线PB 与直线AD 垂直C ．线段AM 与线段CM 长度相等D ．PB 与AM 所成角的余弦值为24 2.（多选）如图，在长方体ABCD —A 1B 1C 1D 1中，AB ＝4，BC ＝BB 1＝2，E 、F 分别为棱AB 、A 1D 1的中点，则下列说法中正确的有（ ）A ．DB 1⊥CEB ．三棱锥D —CEF 的体积为83C ．若P 是棱C 1D 1上一点，且D 1P ＝1，则E 、C 、P 、F 四点共面D ．平面CEF 截该长方体所得的截面为五边形3.（多选）已知菱形ABCD 的边长为2, ∠ABC=3π,将ΔDAC 沿着对角线AC 折起至ΔD'AC,连接BD'.设二面角D'-AC-B 的大小为θ,则下列说法正确的是（ ）A.若四面体D'ABC 为正四面体，则θ=3π B.四面体D'ABC 的体积最大值为1 C.四面体D'ABC 的表面积最大值为2(3+2) D.当θ=23π时，四面体D'ABC 的外接球的半径为2134.如图，四棱锥P -ABCD 的底面为正方形，PD ⊥底面ABCD ．设平面PAD 与平面PBC 的交线为l ． （1）证明：l ⊥平面PDC ；（2）已知PD =AD =1，Q 为l 上的点，求PB 与平面QCD 所成角的正弦值的最大值．5.如图，点C 是以AB 为直径的圆上的动点（异于,A B ），已知2AB =，2AC =，AE =BEDC 为矩形，平面ABC ⊥平面BEDC .设平面EAD 与平面ABC 的交线为l .（1）证明：l BC ；（2）求平面ADE 与平面ABC 所成的锐二面角的余弦值.6.7. 在如图所示的几何体中，四边形ABCD 为正方形，PA ⊥平面ABCD ，//PA BE ，2BE =，4AB PA ==.（1）求证：//CE 平面PAD ；（2）在棱AB 上是否存在一点F ，使得二面角E PC F --的大小为60︒？如果存在，确定点F 的位置；如果不存在，说明理由.8.如图,四棱锥P -ABCD 中,底面ABCD 是直角梯形,AB ∥DC ,∠BAD =90°,PD =DC =BC =2PA =2AB =2,PD ⊥DC .(1)求证：PA ⊥平面ABCD ；(2)设BM =BD λ(0<λ<1),当二面角A-PM-B 的余弦值为77时,求λ的值.9.如图，四棱锥P ABCD -中，四边形ABCD 是菱形，PA PC =，BD PA ⊥，E 是BC 上一点，且3EC BE =，设AC BD O =.（1）证明：PO ⊥平面ABCD ；（2）若60BAD ∠=︒，PA PE ⊥，求二面角A PE C --的余弦值.10.如图，在四棱锥P ABCD -中，底面ABCD 是菱形，PA ⊥平面ABCD .（1）求证：平面PAC ⊥平面PBD ；（2）若2AP AB ==，60BAD ∠=︒，求二面角A PB D --的余弦值.11.如图，在三棱柱ABC-A 1B 1C 1中，ΔABC 是边长为2的等边三角形，平面ABC ⊥平面AA 1B 1B,A 1A=A 1B,∠A 1AB=60°,O 为AB 的中点，M 为A 1C 1的中点． （1)求证：OM//平面BB 1C 1C;（2)求二面角C 1-BA 1-C 的正弦值．12.如图，在五面体ABCDEF 中，四边形ABEF 为正方形，平面ABEF ⊥平面CDFE ，CD ∥EF ，DF ⊥EF ， EF ＝2CD ＝2．（1）若DF ＝2，求二面角A －CE －F 的正弦值；（2）若平面ACF ⊥平面BCE ，求DF 的长．13.如图，在斜三棱柱111ABC A B C -中，底面是边长为3的等边三角形，12A A =，点1A 在下底面上的射影是ABC ∆的中心O .（1）求证：平面1A AO ⊥平面11BCC B ；（2）求二面角1C AB C --的余弦值.14.如图，在四棱锥P ABCD -中，PA ⊥平面ABCD ，AD CD ⊥，//AD BC ，2PA AD CD ===，3BC =．E为PD的中点，点F在PC上，且13 PFPC=．（Ⅰ）求证：CD⊥平面PAD；（Ⅱ）求二面角F AE P--的余弦值；（Ⅲ）设点G在PB上，且23PGPB=．判断直线AG是否在平面AEF内，说明理由．15.如图，在三棱锥A－BCD中，△ABD与△BCD都为等边三角形，平面ABD⊥平面BCD，M，O分别为AB，BD 的中点，AO∩DM＝G，N在棱CD上且满足2CN＝ND，连接MC，GN．（1）证明：GN∥平面ABC；（2）求直线AC和平面GND所成角的正弦值．16.在多面体ABCDE中，平面ACDE⊥平面ABC，四边形ACDE为直角梯形，CD∥AE，AC⊥AE，AB⊥BC，CD＝1，AE＝AC＝2，F为DE的中点，且点E满足EB4EG=．（1）证明：GF∥平面ABC；（2）当多面体ABCDE的体积最大时，求二面角A—BE—D的余弦值．17一副标准的三角板(图1)中,∠ABC为直角,∠A=60°,∠DEF为直角,DE=EF,BC=DF.把BC与DF重合,拼成一个三棱锥(图2)｡设M是AC的中点,N是BC的中点｡(1)求证:平面ABC⊥平面EMN;(2)若AC=4,二面角E-BC-A为直二面角,求直线EM与平面ABE所成的正弦18.如图四边形ABCD为梯形，AD∥BC，BM⊥AD于M，CN⊥AD于N，∠A=45°，AD=4BC=4，AB=2，现沿CN将△CDN折起，使△ADN为正三角形，且平面AND⊥平面ABCN，过BM的平面与线段DN、DC分别交于E、F．(1)求证：EF⊥DA；(2)在棱DN上(不含端点)是否存在点E，使得直线DB与平面BMEF所成角的正弦值为34，若存在，请确定E点的位置；若不存在，说明理由．19.如图，在四棱锥P—ABCD中，底面ABCD为正方形，PD⊥底面ABCD，M为线段PC的中点，PD＝AD，N为线段BC上的动点．（1）证明：平面MND⊥平面PBC；（2）当点N在线段BC的何位置时，平面MND与平面PAB所成锐二面角的大小为30°？指出点N的位置，并说明理由．。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
101. C B A '''∆是△ABC 在平面α上的射影，那么C B A '''∠和∠ABC 的大小关系是( )(A) C B A '''∠<∠ABC (B) C B A '''∠>∠ABC (C) C B A '''∠≥∠ABC (D) 不能确定解析：D一个直角，当有一条直角边平行于平面时，则射影角可以等于原角大小，但一般情况不等． 102. 已知: 如图, △ABC 中, ∠ACB = 90︒, CD ⊥平面α, AD , BD 和平面α所成的角分别为30︒和45︒, CD = h , 求: D 点到直线AB 的距离。
解析：1、先找出点D 到直线AB 的距离, 即过D 点作 DE ⊥AB , 从图形以及条件可知, 若把DE 放在△ABD 中不易求解。
2、由于CD ⊥平面α, 把DE 转化到直角三角形中求解, 从而转化为先求DE 在平面α内的射影长。
解: 连AC , BC , 过D 作DE ⊥AB , 连CE , 则DE 为D 到直线AB 的距离。
∵CD ⊥α∴AC , BC 分别是AD , BD 在α内的射影。
∴∠DAC , ∠DBC 分别是AD 和BD 与平面α所成的角∴∠DAC = 30︒, ∠DBC = 45︒在Rt △ACD 中,∵CD = h , ∠DAC = 30︒∴AC = 3h 在Rt △BCD 中∵CD = h , ∠DBC = 45︒∴BC = h∵CD ⊥α, DE ⊥AB∴CE ⊥AB 在Rt △ACB 中 AB AC BC h =+=222 S AC BC AB CE =⨯=1212· ∴CE AC BC AB h h h h =⨯==3232· ∴在Rt △DCE 中, DE DC CE h h h =+=+=22223272() ∴点D 到直线AB 的距离为72h 。
103. 已知a 、b 、c 是平面α内相交于一点O 的三条直线，而直线l 和α相交，并且和a 、b 、c 三条直线成等角．求证：l ⊥α证法一：分别在a 、b 、c 上取点A 、B 、C 并使AO = BO = CO ．设l 经过O ，在l 上取一点P ，在△POA 、△POB 、△POC 中，∵ PO 公用，AO = BO = CO ，∠POA =∠POB =∠POC ，∴ △POA ≌△POB ≌△POC∴ PA = PB = PC ．取AB 中点D ．连结OD 、PD ，则OD ⊥AB ，PD ⊥AB ，∵ D OD PD =I∴ AB ⊥平面POD∵ PO ⊂平面POD ．∴ PO ⊥AB ．同理可证 PO ⊥BC∵ α⊂AB ，α⊂BC ，B BC AB =I∴ PO ⊥α，即l ⊥α若l 不经过O 时，可经过O 作l '∥l ．用上述方法证明l '⊥α，∴ l ⊥α．证法二：采用反证法假设l 不和α垂直，则l 和α斜交于O ．同证法一，得到PA = PB = PC ．过P 作α⊥'O P 于O '，则O C O B O A '='='，O 是△ABC 的外心．因为O 也是△ABC 的外心，这样，△ABC 有两个外心，这是不可能的．∴ 假设l 不和α垂直是不成立的．∴ l ⊥α若l 不经过O 点时，过O 作l '∥l ，用上述同样的方法可证l '⊥α，∴ l ⊥α评述：（1）证明线面垂直时，一般都采用直接证法（如证法一），有时也采用反证法（如证法二）或同一法．104. P 是△ABC 所在平面外一点，O 是点P 在平面α上的射影．（1）若PA = PB = PC ，则O 是△ABC 的____________心．（2）若点P 到△ABC 的三边的距离相等，则O 是△ABC _________心．（3）若PA 、PB 、PC 两两垂直，则O 是△ABC _________心．（4）若△ABC 是直角三角形，且PA = PB = PC 则O 是△ABC 的____________心．（5）若△ABC 是等腰三角形，且PA = PB = PC ，则O 是△ABC 的____________心．（6）若P A 、PB 、PC 与平面ABC 所成的角相等，则O 是△ABC 的________心；解析：（1）外心．∵ P A =PB =PC ，∴ OA =OB =OC ，∴ O 是△ABC 的外心．（2）内心（或旁心）．作OD ⊥AB 于D ，OE ⊥BC 于E ，OF ⊥AC 于F ，连结PD 、PE 、PF ．∵ PO ⊥平面ABC ，∴ OD 、OE 、OF 分别为PD 、PE 、PF 在平面ABC 内的射影，由三垂线定理可知，PD ⊥AB ，PE ⊥BC ，PF ⊥AC ．由已知PD =PE =PF ，得OD =OE =OF ，∴ O 是△ABC 的内心．（如图答9-23）（3）垂心．（4）外心．（5）外心（6）外心．P A 与平面ABC 所成的角为∠P AO ，在△P AO 、△PBO 、△PCO 中，PO 是公共边，∠POA =∠POB =∠POC =90°，∠P AO =∠PBO =∠PCO ，∴ △P AO ≌△PBO ≌△PCO ，∴ OA =OB =OC ，∴ O 为△ABC 的外心．（此外心又在等腰三角形的底边高线上）．105. 将矩形ABCD 沿对角线BD 折起来，使点C 的新位置C '在面ABC 上的射影E 恰在AB 上．求证：C B C A '⊥'分析：欲证C B C A '⊥'，只须证C B '与C A '所在平面D C A '垂直；而要证C B '⊥平面D C A '，只须证C B '⊥D C '且C B '⊥AD ．因此，如何利用三垂线定理证明线线垂直就成为关键步骤了．证明：由题意，C B '⊥D C '，又斜线C B '在平面ABCD 上的射影是BA ，∵ BA ⊥AD ，由三垂线定理，得AD B C ⊥'，D DA D C ='I ．∴ C B '⊥平面AD C '，而A C '⊂平面AD C '∴ C B '⊥C A '106. 已知异面直线l 1和l 2，l 1⊥l 2，MN 是l 1和l 2的公垂线，MN = 4，A ∈l 1，B ∈l 2，AM = BN = 2，O 是MN 中点．① 求l 1与OB 的成角．②求A 点到OB 距离．分析：本题若将条件放入立方体的“原型”中，抓住“一个平面四条线”的图形特征及“直线平面垂直”的关键性条件，问题就显得简单明了．解析：（1）如图，画两个相连的正方体，将题目条件一一标在图中．OB 在底面上射影NB ⊥CD ，由三垂线定理，OB ⊥CD ，又CD ∥MA ，∴ OB ⊥MA 即OB 与l 1成90°（2）连结BO 并延长交上底面于E 点．ME = BN ， ∴ ME = 2，又 ON = 2∴ 22==OE OB ． 作AQ ⊥BE ，连结MQ ．对于平面EMO 而言，AM 、AQ 、MQ 分别为垂线、斜线、斜线在平面内的射影，由三垂线逆定理得MQ ⊥EO ．在Rt △MEO 中，22222=⨯=⋅=EO MO ME MQ ． 评述：又在Rt △AMQ 中，62422=+=+=MQ AM AQ ，本题通过补形法使较困难的问题变得明显易解；求点到直线的距离，仍然是利用直线与平面垂直的关键条件，抓住“一个面四条线”的图形特征来解决的．107. 已知各棱长均为a 的正四面体ABCD ，E 是AD 边的中点，连结CE ．求CE 与底面BCD 所成角的正弦值．解析：作AH ⊥底面BCD ，垂足H 是正△BCD 中心，∥连DH 延长交BC 于F ，则平面AHD ⊥平面BCD ，作EO ⊥HD 于O ，连结EC ，则∠ECO 是EC 与底面BCD 所成的角则EO ⊥底面BCD ．a a DF HD 33233232=⨯== a a a HD AD AH 3632222=-=-= a a AH EO 66362121=⨯==，a CE 23= ∴ 322366sin ===∠a a EC EO ECO 108. 已知四面体S －ABC 中，SA ⊥底面ABC ，△ABC 是锐角三角形，H 是点A 在面SBC 上的射影．求证：H 不可能是△SBC 的垂心．分析：本题因不易直接证明，故采用反证法．证明：假设H 是△SBC 的垂心，连结BH ，并延长交SC 于D 点，则BH ⊥SC ∵ AH ⊥平面SBC ，∴ BH 是AB 在平面SBC 内的射影∴ SC ⊥AB （三垂线定理）又∵ SA ⊥底面ABC ，AC 是SC 在面内的射影∴ AB ⊥AC （三垂线定理的逆定理）∴ △ABC 是Rt △与已知△ABC 是锐角三角形相矛盾，于是假设不成立．故H 不可能是△SBC 的垂心．109. 已知ABCD 是边长为4的正方形，E 、F 分别是AB 、AD 的中点，GC 垂直于ABCD 所在的平面，且GC ＝2．求点B 到平面EFG 的距离． A B CH D S解析：如图，连结EG 、FG 、EF 、BD 、AC 、EF 、BD 分别交AC 于H 、O ． 因为ABCD 是正方形，E 、F 分别为AB 和AD 的中点，故EF ∥BD ，H 为AO 的中点．BD 不在平面EFG 上．否则，平面EFG 和平面ABCD 重合，从而点G 在平面的ABCD 上，与题设矛盾．由直线和平面平行的判定定理知BD ∥平面EFG ，所以BD 和平面EFG 的距离就是点B 到平面EFG 的距离． ——4分∵ BD ⊥AC ，∴ EF ⊥HC ．∵ GC ⊥平面ABCD ，∴ EF ⊥GC ，∴ EF ⊥平面HCG ．∴ 平面EFG ⊥平面HCG ，HG 是这两个垂直平面的交线． ——6分 作OK ⊥HG 交HG 于点K ，由两平面垂直的性质定理知OK ⊥平面EFG ，所以线段OK 的长就是点B 到平面EFG 的距离． ——8分 ∵ 正方形ABCD 的边长为4，GC =2，∴ AC=42，HO =2，HC =32．∴ 在Rt △HCG 中，HG =()2222322=+．由于Rt △HKO 和Rt △HCG 有一个锐角是公共的，故Rt △HKO ∽△HCG ．∴ OK =111122222=⨯=⋅HG GC HO ． 即点B 到平面EFG 的距离为11112． ——10分 注：未证明“BD 不在平面EFG 上”不扣分．110.已知：AB与CD为异面直线，AC＝BC，AD＝BD．求证：AB⊥CD．说明：（1）应用判定定理，掌握线线垂直的一般思路．（2）思路：欲证线线垂直，只需证线面垂直，再证线线垂直，而由已知构造线线垂直是关键．（3）教学方法，引导学生分析等腰三角形三线合一的性质构造图形，找到证明方法．证明：如图，取AB中点E，连结CE、DE∵AC＝BC，E为AB中点．∴CE⊥AB同理DE⊥AB，又CE∩DE＝E，且CE⊂平面CDE，DE⊂平面CDE．∴AB⊥平面CDE又CD⊂平面CDE∴AB⊥CD．。