2017级二诊文科
2017年高三-重庆-二诊-文综
2017年春高三考前模拟测试卷文科综合能力测试参考答案本部分共35小题,每小题4分,满分140分。
1.A2.C3.B4.B5.A6.A7.C8.B9.D 10.C11.D 12.A 13.B 14.B 15.D 16.B 17.D 18.C 19.B 20.C21.C 22.A 23.A 24.A 25.B 26.C 27.D 28.A 29.D 30.C 31.C 32.B 33.A 34.B 35.D本部分综合题160分36.(36分)(1)①太阳辐射强;(2分)②气温低;(2分)③气温日较差大;(2分)④降水较少;(2分)⑤多大风。
(2分)(2)地理环境各要素相互联系、相互制约和相互渗透;(2分)湟鱼减少,刚毛藻大量繁殖,水中氧气减少,湖泊水质变坏;(2分)鸟的食物减少,候鸟数量减少。
(2分)(3)降水稀少;(2分)海拔高,气温低;(2分)风力大;(2分)土壤贫瘠,盐碱滩分布广。
(2分)(4)地形平坦,有利于城市的兴建与扩展;(2分)柴达木盆地资源丰富(或附近有丰富的钾盐、石油、煤等资源);(2分)有公路、铁路交汇,对外联系便利。
(2分)(5)湖光山色,景观独特;鸟岛驰名中外(动植物资源独特);少数民族风情;环湖观光,体验活动多样(湖上泛舟、沙岛游乐、露营、骑马观草原)。
(每点2分,答3点得6分)37. (32分)(1)特点:以上察下,以下督上,双向监察。
(2分)影响:促使吏治清明,也限制了皇帝的极端专制;(2分)促进唐朝前期出现“贞观之治”“开元盛世”局面。
(2分)(2)原因:监察体制不合理;监察官员素质不高等。
(4分)解决:兴民权,限制君主和官僚权力。
(4分)体现:准许官民上书言事。
(2分)(3)职权:立法权与监察权。
(2分)理论依据:三权分立学说(分权制衡学说)。
(2分)影响:把分权理论变为了治国的制度,有利于遏制专制独裁。
(2分)(4)问题:严重的官僚主义、文牍主义和脱离实际的现象。
2017年成都二诊文综及答案

成都市2014级高中毕业班第二次诊断性检测文科综合本试卷分选择遜和非选择题两部分。
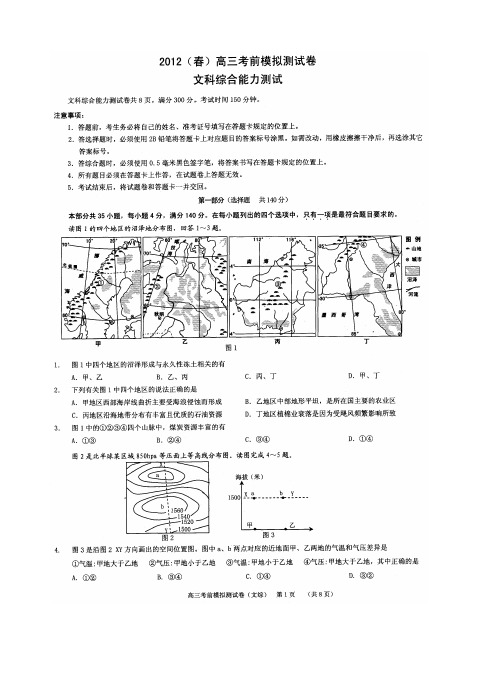
第I卷(选择題》1至7页,第U卷(非选择题)8至12页,共12页;满分300分,考试时间150分钟.注意事项,1.答題前,务必将自己的姓名、考籍号填写在答题卡規定的位置上.2.答选择题时,必须使用2B铅笔将答题卡上对应题目的答案标号涂黑.如需改动, 用橡皮擦擦干净后,再选涂其它答案标号.3.答非选样題时・必须使用0.5毫米黒色签字笔,将签褰书写在答题R规宦的位M上.4.所有题目必须在答题卡上作答.在试題卷上答題无效.5.考试结束后,只将答题卡交回.第I卷(共140分)本卷共35个小趣.每小題4分,共140分.奁毎小通给出的四个选项中,只有一项是符合題目要求的.歩国和澳大利亚都是世界主要的庶林生产和出口国.两国的茂田主要分布在纬度16°以南的平原地区.泰国甘蔑簟产仅为澳大別亚的85%,而泰国吨植耗蔗量为澳大利亚115%,省国蔑桅生产成本大约相同.据此完成1〜3龜.1.澳大利亚甘蔗单产高于泰国的主要族囚是A.气候更温暖湿润B. 土壤更肥沃C.种值技术更先进D.运綸更便捷2.导致秦国蔗帖生产成本与澳大利亚大约相同的主要原因是A.顶料消耗谊B.劳动力工资C.生产技术D.市场需求星3.图1中,能正确表示影响制糖工业区位因索的是A.① D.④图1B.②C・③表14〜6题.14.表中②代表的农作物是A.棉花B.甜菜C.水稻D.小麦5・江西省无农作物③分布的主导因素是A.地形 B.吒候 C.市场 D.交通6.与河北省比较•黑龙江省农作物④分布面积更大的主更匣因是A.平惊面积广大B. 土壤深厚肥沃C.机械化水平髙D.灌溉水源充足图2为某地1. 7月爭温线分布图(筝温距为49).据此完成7〜9題。
田27.图中①地1、7月的温井可能为 A. 8r B.12X? C.169 D. 2or &导致图中②地7月等温线弯曲的因素是 A.洋流R-海陆热力性质 C.地形 D.冬季风的彫晌9.图中R河的汛期可能岀现在A. 3〜5月 B6〜8月 C.9〜11月 D.12〜次年2月2016年11月30日,二十四节气被正式列入联合国我科文组织人类非物庚文化遗产名录•图3为我同华北平原某地(甲地〉和长江中下游平原某地(乙地)二十四节气的平均日瓏时间图•据此完成10〜11越L文科综合•二讼”马试越第2贞(共12页)10.立秋日(8月8 口)前后乙地日照时数大于甲地的主要原因是A.降水就少B 白昼时间长 C.太阳高度大D. 海拔高度低 11.下列节气中.甲地气温最高的是A.立夏 B 夏至 C. 大暑 D.处暑12. 険看城南天府新区建设加快及配套设施的逐步完善,新区的宜居性开始显现,吸引了 众多房企开始在该区域高价囤地,市民也看好该区城房产的市场前景急忙下手習业, 这直接导致了 2016年中秋之后城南存就房交易火爆。
江西省南昌市2017届高三二模测试卷语文试题

江西省南昌市2017届高三二模测试卷语文试题学校_________ 班级__________ 姓名__________ 学号__________一、现代文阅读1. 阅读下面的文字,完成下面小题。
书札的文献价值研究书札也可以称为手札、尺牍、书翰或者书信,诸名之间并无实质性的不同,但又有所区别与侧重。
书札与尺族牍、尺素兼重物质形式与文体形式,相比之下,后二者又更为古雅一些。
这是因为书写尺牍所用之材质;因时代的不同而有所变化。
在纸张未发明之前,书写信函不是用竹简,即是用木牍,偶尔亦用小幅丝帛织物,即为尺素,这就是先秦两汉时期用“简”“牍”“礼”“牒”或“素”等称呼书信的由来。
手札与书札、书翰相近,但书札、书输强调其为书写的作品,而手机强调其出于书写者的亲笔。
书信则侧重其文体内容,着重其社会交往的功能。
但是,这种区别只是相对的,因为不同的人使用这些名词时,各自的理解不尽相同,所以也不免混用。
还有人使用“尺素”或“笺素”之称,在追求古雅之外,又更加强调笺纸的形式种类及其物质文化意义。
例如国家图书馆出版社编有《笺素珍赏》,其副标题就是“国家图书馆藏近现代百位名人手札”。
也有人使用“名人墨迹”这个名称。
从字面上看,“名人墨迹”当然有多种多样的物质形式或文体形式,但手札无疑是其中之荦荦大端。
毫无疑问,书机是浩如烟海、品类繁多的历史文献的一个重要组成部分。
从文献类别上说,书礼文献是写本文献的一种。
所谓写本文献,是相对于印本文献而言的。
一般而言,印本文献刊印之后,即可化身千百,存世者往往不止一本,同一版本者就有相同的文献价值;而写本文献往往只此一本,并无复制本,每一件都是独一无二的。
书札文献也是如此,从这个意义上说,每件书札都是无法复制的,即使作者重抄一遍,其墨迹也不完全一样。
因为独特,所以稀罕;因为稀罕,所以珍贵。
书札的文献价值,主要有如下三个方面:首先是史料价值。
因为出于当事人之手,书札提供了研究相关历史人物与历史事件的第一手史料,这些史料中所披露的人事关系、政事秘辛,往往是不见于正史记载或公开报道的,往往寥寥数行便抵得千言万语。
17届高三文科语文二诊模拟考试试卷

成都七中2016—2017学年下期高2017届“二诊”模拟语文试卷本试卷分第I卷(阅读题)和第Ⅱ卷(表达题)两部分,共150分。
考试时间150分钟。
两卷答案均应写在答题卡上。
第I卷阅读题(70分)一、现代文阅读(35分)(一)阅读下面的文字,完成1~3题。
(9分,每小题3分)中国古代文化以伦理文化为主,最重“礼义”,礼的精神彰显于道德观,礼的形式则所谓“衣冠礼仪”,“文章光华”。
而“道德”一词,重在“德”,“道”是通往“德”的途径。
道德崇高而广大,然古人讲究“践履”(即实践),所以示知广大民众,德教最初或最基本归于一字:孝。
“孝者,教也”,教育之教的字源来自孝,所以《孝经》中有“百善孝为先”的说法。
中国传统文化形成于古代的农耕经济,极重血缘与家庭,而孝敬父母,友于兄弟(所谓的“孝悌”)为其思想核心。
孔子教弟子,也重一“孝”,以之为本,但如何将个体的“孝”发展为“孝文化”,将孝的教育转化为孝的情怀,由此,古人提出了“孝养”“孝顺”与“孝敬”三层次的义理。
《孝经》说:“百善孝为先。
”孝如何表现,首在“养”。
古代是农耕经济,生活取资劳作,“孝”字取“子”负“老”形象,“养儿防老”,天经地义。
今天的老人已有社会保障,但作为儿女,身体发肤,受之父母,养之义不可丢,养之心不可无,落实到物质层面也是必需的。
由此“孝养”的生发,中国文化极重“养”,我们讲“养胃”“养气”“养生”,古人如孟子也说“吾善养吾浩然之气”。
于是我们谈胸襟谓之“涵养”,讲文明称有“修养”,实际都由“孝养”而来。
然而,孝仅限于“养”可否?《论语·为政》所载孔子答弟子问的一段话:“子游问孝。
子曰:‘今之孝者是谓能养,至于犬马皆能有养,不敬,何以别乎?’”是生存之“养”,还是孝道之“养”,前者同“犬马”,后者乃“人伦”,所以关键在一“敬”字,做到了“孝敬”,才是孝文化的核心,人对“孝”有了“敬畏”之心,才能内化为道德的情怀。
古代所推崇的“二十四孝”,其中虽有偏颇,但大多数的故事,显然是这一情怀的形象化表述。
2017届高三第二次诊断考试语文试题 含解析

注意事项:1.本试卷分第Ⅰ卷(阅读题)和第Ⅱ卷(表达题)两部分。
答卷前,考生务必将自己的准考证号、姓名填写在答题卡上。
2.作答时,将答案写在答题卡上。
写在本试卷上无效。
3.考试结束后,将本试卷和答题卡上一并交回。
第Ⅰ卷阅读题一、现代文新阅读(35分)(一)论述类文本阅读(9分,每小题3分)阅读下面的文字,完成下列小题。
孝文化是中国传统文化的重要组成部分。
在中国传统宗法社会和家国一体的社会制度下, 孝文化由家庭伦理、家族伦理扩大到社会伦理和国家伦理乃至整个文化精神体系和文化实践体系,成为人们非自觉的文化认同和社会集体心理意识。
在中国古代,“家”是传统社会的基本单位.孝文化最早是作为家庭伦理规范而存在的,主要调节的是亲子关系,具有归亲、继亲、养亲、敬亲、顺亲、谏亲、侍亲、葬亲、祭亲等丰富内涵。
《孝经》言:“夫孝,天之经也,地之义也,民之行也.”(《孝经·三才》)“孝”被视为天、地、人三才之“道”,不仅维护了家庭关系中长幼、尊卑秩序,而且成为传统社会中最重要的家庭伦理观念,即传统家庭孝道。
传统家庭孝道是一个内容极其繁芜的庞杂体系,从历史视角来看,孝文化在漫长的封建社会受到了较为严重的扭曲和异化,产生了许多消极的影响。
例如,传统孝道将“孝”与“顺”等同,认为孝道就是子女对父母的绝对服从,从而演化为严格的父权制,违背了孝文化的道德本性,扭曲了人性的发展。
又如,在长期的封建社会里,“祭亲”思想被逐渐演化为传统礼教,而成为重形式轻内容、重礼数轻情感的仪式,一些思想甚至被演变为封建迷信,等等。
但是,肃清消极影响,传统孝文化仍不失为中华文化的瑰宝。
在传统社会,孝文化作为家庭伦理最重要的规范,调节着自天子至庶人的行为,并逐渐升华为人们自觉的道德行为,促进了家族和睦与社会和谐。
传统家庭孝道并不是一种封闭的文化形态,而是一种具有开放性和扩展性的伦理道德规范。
具体来说,作为家庭伦理的孝道思想,从调节家庭、家族关系开始,向外推衍而成为社会伦理规范和国家政治规范,完成了从私德向公德的伦理转换.如果说作为私德之孝主要规范的是亲子伦理关系,那么上升为公德的孝,如对四海兄弟的孝悌思想,对国家的孝忠思想、孝廉思想等等,主要规范和协调的便是社会伦理和政治伦理关系,对于协调人际关系、维护社会稳定与促进国家统一等发挥了重要作用.“仁”作为最高的道德原则,是儒家学说的理论核心.以此为逻辑起点,经过推衍和演化,逐步发展为中华文化的核心。
2017成都二诊文科综合试题及答案

成都市2014级高中毕业班第二次诊断性检测文科综合参考答案及评分标准第Ⅰ卷(选择题,共140分)1.C2.B3.C4.A5.B6.D7.B8.C9.D 10.A 11.C 12.C 13.C 14.D 15.B 16.C17.B 18.D 19.A 20.D 21.B 22.C 23.A 24.A25.C 26.B 27.D 28.D 29.C 30.B 31.A 32.B33.C 34.D 35.A第Ⅱ卷(非选择题,共160分)36.(22分)(1)②地低于①地 (1分) 其原因是②地北部没有山脉阻挡冬季风 (北部为平原),受冷空气影响大,所以冬季(一月)气温低于①地(2分)。
③地低于①地(1分)其原因是③地位于云贵高原,海拔高于①地,气温低(2分);同时因地势原因③地冷空气易滞留(冬季③地位于昆明准静止锋冷气团一侧),所以冬季(一月)气温低于①地(2分)。
(2)昼晴,白天气温高,日照强,农作物的光合作用强,生产的有机质多 (2分);夜雨,使夜间温度降低,农作物的呼吸作用减弱,减少营养物质的消耗,从而提高作物的产量和品质(3分);夜间气温低,土壤蒸发和作物蒸腾弱,大量雨水可渗入土壤深层,增加土壤含水量,有利于作物生长(3分)。
(3)①调整产业结构;②加大科技投入,现有工业产品升级换代,③延长产业链,对产品深加工,④开发附加值高的新产品;⑤利用区位优势发展旅游业(每点2分,任答3点给6分,其它答案只有言之有理,可酌情给分,但总分不超过6分)。
37.(24分)(1)特点:全年高温,年降水量丰富 (约2000mm)(2分),旱、雨季分明 (2分)。
原因:3月及前两个月流域内降水较少,河流处于枯水期,流量较小,可降低截流难度,(保障截流安全,节省截流支出)(4分);3月及前两个月降水少,滑坡、泥石流等地质灾害少,便于施工(2分)。
(2)工程建设过程中,能够带动当地建材、交通运输等产业发展(2分);工程建成后提供电力,促进工业发展(2分);工程形成新景观,可带动当地旅游业发展(2分)。
2017届四川省成都市第七中学高三二诊模拟考试语文试卷(解析版)

2017届四川省成都市第七中学高三二诊模拟考试语文试卷(解析版)一、现代文阅读阅读下面的文字,完成问题。
中国古代文化以伦理文化为主,最重‚礼义‛,礼的精神彰显于道德观,礼的形式则所谓‚衣冠礼仪‛,‚文章光华‛。
而‚道德‛一词,重在‚德‛,‚道‛是通往‚德‛的途径。
道德崇高而广大,然古人讲究‚践履‛(即实践),所以示知广大民众,德教最初或最基本归于一字:孝。
‚孝者,教也‛,教育之教的字源来自孝,所以《孝经》中有‚百善孝为先‛ 的说法。
中国传统文化形成于古代的农耕经济,极重血缘与家庭,而孝敬父母,友于兄弟(所谓的‚孝悌‛)为其思想核心。
孔子教弟子,也重一‚孝‛,以之为本,但如何将个体的‚孝‛发展为‚孝文化‛,将孝的教育转化为孝的情怀,由此,古人提出了‚孝养‛‚孝顺‛与‚孝敬‛三层次的义理。
《孝经》说:‚百善孝为先。
‛孝如何表现,首在‚养‛。
古代是农耕经济,生活取资劳作,‚孝‛字取‚子‛负‚老‛形象,‚养儿防老‛,天经地义。
今天的老人已有社会保障,但作为儿女,身体发肤,受之父母,养之义不可丢,养之心不可无,落实到物质层面也是必需的。
由此‚孝养‛的生发,中国文化极重‚养‛,我们讲‚养胃‛‚养气‛‚养生‛,古人如孟子也说‚吾善养吾浩然之气‛。
于是我们谈胸襟谓之‚涵养‛,讲文明称有‚修养‛,实际都由‚孝养‛而来。
然而,孝仅限于‚养‛可否?《论语·为政》所载孔子答弟子问的一段话:‚子游问孝。
子曰:‘今之孝者是谓能养,至于犬马皆能有养,不敬,何以别乎?’‛是生存之‚养‛,还是孝道之‚养‛,前者同‚犬马‛,后者乃‚人伦‛,所以关键在一‚敬‛字,做到了‚孝敬‛,才是孝文化的核心,人对‚孝‛有了‚敬畏‛之心,才能内化为道德的情怀。
古代所推崇的‚二十四孝‛,其中虽有偏颇,但大多数的故事,显然是这一情怀的形象化表述。
在‚孝养‛与‚孝敬‛之间,还有‚孝顺‛,《礼记·中庸》记载孔子曰:‚父母其顺矣。
‛说的是子女对父母之依‚顺‛中的孝‚义‛。
2017年四川省成都市高考数学二诊试卷(文科)(解析版)

2017年省市高考数学二诊试卷〔文科〕一、选择题:本大题共12小题,每题5分,共60分.在每题给出的四个选项中,只有一个是符合题目要求的.1.〔5分〕设集合A=[﹣1,2],B={y|y=x2,x∈A},那么A∩B=〔〕A.[1,4] B.[1,2] C.[﹣1,0] D.[0,2]2.〔5分〕假设复数z1=a+i〔a∈R〕,z2=1﹣i,且为纯虚数,那么z1在复平面所对应的点位于〔〕A.第一象限B.第二象限C.第三象限D.第四象限3.〔5分〕平面向量,的夹角为,且||=1,||=,那么|﹣2|=〔〕A.1 B.C.2 D.4.〔5分〕在等比数列{an }中,a3=6,a3+a5+a7=78,那么a5=〔〕A.12 B.18 C.24 D.365.〔5分〕假设实数x,y满足不等式,那么x﹣y的最大值为〔〕A.﹣5 B.2 C.5 D.76.〔5分〕两位同学约定下午5:30~6:00在图书馆见面,且他们在5:30~6:00之间到达的时刻是等可能的,先到的同学须等待,15分钟后还未见面便离开,那么两位同学能够见面的概率是〔〕A.B.C.D.7.〔5分〕m,n是空间中两条不同的直线,α、β是两个不同的平面,且m⊂α,n⊂β.有以下命题:①假设α∥β,那么m∥n;②假设α∥β,那么m∥β;③假设α∩β=l,且m⊥l,n⊥l,那么α⊥β;④假设α∩β=l,且m⊥l,m⊥n,那么α⊥β.其中真命题的个数是〔〕A.0 B.1 C.2 D.38.〔5分〕函数f〔x〕的定义域为R,当x∈[﹣2,2]时,f〔x〕单调递减,且函数f〔x+2〕为偶函数,那么以下结论正确的选项是〔〕A.f〔π〕<f〔3〕<f〔〕B.f〔π〕<f〔〕<f〔3〕C.f〔〕<f〔3〕<f〔π〕D.f〔〕<f〔π〕<f〔3〕9.〔5分〕执行如下图的程序框图,假设输入a,b,c分别为1,2,0.3,那么输出的结果为〔〕A.1.125 B.1.25 C.1.3125 D.1.37510.〔5分〕设双曲线C:﹣=1〔a>0,b>0〕的左右顶点分别为A1,A2,左右焦点分别为F1,F 2,以F1F2为直径的圆与双曲线左支的一个交点为P,假设以A1A2为直径的圆与PF2相切,那么双曲线C的离心率为〔〕A.B.C.2 D.11.〔5分〕函数f〔x〕=sin〔ωx+2φ〕﹣2sinφcos〔ωx+φ〕〔ω>0,φ∈R〕在〔π,〕上单调递减,那么ω的取值围是〔〕A.〔0,2] B.〔0,] C.[,1] D.[,]12.〔5分〕把平面图形M上的所有点在一个平面上的射影构成的图形M′叫作图形M在这个平面上的射影.如图,在长方体ABCD﹣EFGH中,AB=5,AD=4,AE=3,那么△EBD在平面EBC 上的射影的面积是〔〕A.2 B.C.10 D.30二、填空题:本大题共4小题,每题5分,共20分〕.13.〔5分〕设抛物线C:y2=2x的焦点为F,假设抛物线C上点P的横坐标为2,那么|PF|=.14.〔5分〕在一个容量为5的样本中,数据均为整数,已测出其平均数为10,但墨水污损了两个数据,其中一个数据的十位数字1未污损,即9,10,11,,那么这组数据的方差s2可能的最大值是.15.〔5分〕假设曲线y=lnx+ax2﹣2x〔a为常数〕不存在斜率为负数的切线,那么实数a的取值围是.16.〔5分〕在数列{an }中,a1=1,a1+++…+=an〔n∈N*〕,那么数列{an}的通项公式an=.三、解答题:本大题共5小题,共70分.解答写出文字说明、证明过程或演算过程.17.〔12分〕如图,在平面四边形ABCD中,∠A=,∠B=,AB=6,在AB边上取点E,使得BE=1,连接EC,ED.假设∠CED=,EC=.〔Ⅰ〕求sin∠BCE的值;〔Ⅱ〕求CD的长.18.〔12分〕某项科研活动共进展了5次试验,其数据如表所示:特征量第1次第2次第3次第4次第5次x 555559 551 563 552y 601605 597 599 598〔Ⅰ〕从5次特征量y的试验数据中随机地抽取两个数据,求至少有一个大于600的概率;〔Ⅱ〕求特征量y关于x的线性回归方程=x+;并预测当特征量x为570时特征量y的值.〔附:回归直线的斜率和截距的最小二乘法估计公式分别为=,=﹣〕19.〔12分〕如图,梯形CDEF与△ADE所在的平面垂直,AD⊥DE,CD⊥DE,AB∥CD∥EF,AE=2DE=8,AB=3,EF=9,CD=12,连接BC,BF.〔Ⅰ〕假设G为AD边上一点,DG=DA,求证:EG∥平面BCF;〔Ⅱ〕求多面体ABCDEF的体积.20.〔12分〕在平面直角坐标系xOy中,椭圆E:+=1〔a>b>0〕,圆O:x2+y2=r2〔0<r<b〕.当圆O的一条切线l:y=kx+m与椭圆E相交于A,B两点.〔Ⅰ〕当k=﹣,r=1时,假设点A,B都在坐标轴的正半轴上,求椭圆E的方程;〔Ⅱ〕假设以AB为直径的圆经过坐标原点O,探究a,b,r是否满足+=,并说明理由.21.〔12分〕函数f〔x〕=〔a+〕lnx﹣x+,其中a>0.〔Ⅰ〕假设f〔x〕在〔0,+∞〕上存在极值点,求a的取值围;〔Ⅱ〕设a∈〔1,e],当x1∈〔0,1〕,x2∈〔1,+∞〕时,记f〔x2〕﹣f〔x1〕的最大值为M〔a〕,那么M〔a〕是否存在最大值?假设存在,求出其最大值;假设不存在,请说明理由.[选修4-4:坐标系与参数方程选讲]22.〔10分〕在直角坐标系xOy中,曲线C的参数方程为〔α为参数〕,直线l的参数方程为〔t为参数〕,在以坐标原点O为极点,x轴为正半轴为极轴的极坐标系中,过极点O的射线与曲线C相交于不同于极点的点A,且点A的极坐标为〔2,θ〕,其中θ∈〔,π〕〔Ⅰ〕求θ的值;〔Ⅱ〕假设射线OA与直线l相交于点B,求|AB|的值.[选修4-5:不等式选讲]23.函数f〔x〕=4﹣|x|﹣|x﹣3|〔Ⅰ〕求不等式f〔x+〕≥0的解集;〔Ⅱ〕假设p,q,r为正实数,且++=4,求3p+2q+r的最小值.2017年省市高考数学二诊试卷〔文科〕参考答案与试题解析一、选择题:本大题共12小题,每题5分,共60分.在每题给出的四个选项中,只有一个是符合题目要求的.1.〔5分〕〔2017•模拟〕设集合A=[﹣1,2],B={y|y=x2,x∈A},那么A∩B=〔〕A.[1,4] B.[1,2] C.[﹣1,0] D.[0,2]【分析】先分别求出集合A和B,由此利用交集定义能求出A∩B.【解答】解:∵集合A=[﹣1,2],B={y|y=x2,x∈A}=[0,4],∴A∩B=[0,2].应选:D.【点评】此题考察交集的求法,是根底题,解题时要认真审题,注意交集定义的合理运用.2.〔5分〕〔2017•模拟〕假设复数z1=a+i〔a∈R〕,z2=1﹣i,且为纯虚数,那么z1在复平面所对应的点位于〔〕A.第一象限B.第二象限C.第三象限D.第四象限【分析】利用复数的运算法那么、纯虚数的定义、几何意义即可得出.【解答】解:复数z1=a+i〔a∈R〕,z2=1﹣i,且===+i为纯虚数,∴=0,≠0,∴a=1.那么z1在复平面所对应的点〔1,1〕位于第一象限.应选:A.【点评】此题考察了复数的运算法那么、纯虚数的定义、几何意义,考察了推理能力与计算能力,属于根底题.3.〔5分〕〔2017•模拟〕平面向量,的夹角为,且||=1,||=,那么|﹣2|=〔〕A.1 B.C.2 D.【分析】结合题意设出,的坐标,求出﹣2的坐标,从而求出﹣2的模即可.【解答】解:平面向量,的夹角为,且||=1,||=,不妨设=〔1,0〕,=〔,〕,那么﹣2=〔,﹣〕,故|﹣2|==1,应选:A.【点评】此题考察了向量求模问题,考察向量的坐标运算,是一道根底题.4.〔5分〕〔2017•模拟〕在等比数列{an }中,a3=6,a3+a5+a7=78,那么a5=〔〕A.12 B.18 C.24 D.36【分析】设公比为q,由题意求出公比,再根据等比数列的性质即可求出.【解答】解:设公比为q,∵a3=6,a3+a5+a7=78,∴a3+a3q2+a3q4=78,∴6+6q2+6q4=78,解得q2=3∴a5=a3q2=6×3=18,应选:B【点评】此题考察了等比数列的性质,考察了学生的计算能力,属于根底题.5.〔5分〕〔2017•模拟〕假设实数x,y满足不等式,那么x﹣y的最大值为〔〕A.﹣5 B.2 C.5 D.7【分析】由约束条件作出可行域,化目标函数为直线方程的斜截式,数形结合得到最优解,把最优解的坐标代入目标函数得答案.【解答】解:由约束条件作出可行域如图:由图得A〔0,﹣2〕,令z=x﹣y,化为y=x﹣z,由图可知,当直线y=x﹣z过A时,直线在y轴上的截距最小,z 有最大值为2.应选:B.【点评】此题考察简单的线性规划,考察了数形结合的解题思想方法,是中档题.6.〔5分〕〔2017•模拟〕两位同学约定下午5:30~6:00在图书馆见面,且他们在5:30~6:00之间到达的时刻是等可能的,先到的同学须等待,15分钟后还未见面便离开,那么两位同学能够见面的概率是〔〕A.B.C.D.【分析】由题意知此题是几何概型问题,试验发生包含的所有事件对应的集合是Ω:{〔x,y〕|0≤x≤30,0≤y≤30},做出集合对应的面积是边长为30的正方形面积,写出满足条件的事件对应的集合与面积,根据面积之比计算概率.【解答】解:因为两人谁也没有讲好确切的时间,故样本点由两个数〔甲、乙两人各自到达的时刻〕组成;以5:30作为计算时间的起点建立如下图的平面直角坐标系,设甲、乙各在第x分钟和第y分钟到达,那么样本空间为:Ω:{〔x,y〕|0≤x≤30,0≤y≤30},画成图为一正方形;会面的充要条件是|x﹣y|≤15,即事件A={可以会面}所对应的区域是图中的阴影线局部,∴由几何概型公式知所求概率为面积之比,即P〔A〕==.应选:D.【点评】此题考察了把时间分别用x,y坐标来表示,把时间一维问题转化为平面图形的二维面积问题,计算面积型的几何概型问题.7.〔5分〕〔2017•模拟〕m,n是空间中两条不同的直线,α、β是两个不同的平面,且m⊂α,n⊂β.有以下命题:①假设α∥β,那么m∥n;②假设α∥β,那么m∥β;③假设α∩β=l,且m⊥l,n⊥l,那么α⊥β;④假设α∩β=l,且m⊥l,m⊥n,那么α⊥β.其中真命题的个数是〔〕A.0 B.1 C.2 D.3【分析】根据空间直线和平面,平面和平面平行或垂直的判定定理,分别判断,即可得出结论.【解答】解:①假设α∥β,那么m∥n或m,n异面,不正确;②假设α∥β,根据平面与平面平行的性质,可得m∥β,正确;③假设α∩β=l,且m⊥l,n⊥l,那么α与β不一定垂直,不正确;④假设α∩β=l,且m⊥l,m⊥n,l与n相交那么α⊥β,不正确.应选:B.【点评】此题主要考察命题的真假判断,涉及空间直线和平面,平面和平面平行或垂直的判定,根据相应的判定定理和性质定理是解决此题的关键.8.〔5分〕〔2017•模拟〕函数f〔x〕的定义域为R,当x∈[﹣2,2]时,f〔x〕单调递减,且函数f〔x+2〕为偶函数,那么以下结论正确的选项是〔〕A.f〔π〕<f〔3〕<f〔〕B.f〔π〕<f〔〕<f〔3〕C.f〔〕<f〔3〕<f〔π〕D.f〔〕<f〔π〕<f〔3〕【分析】根据函数的奇偶性,推导出f〔﹣x+2〕=f〔x+2〕,再利用当x∈[﹣2,2]时,f〔x〕单调递减,即可求解.【解答】解:∵y=f〔x+2〕是偶函数,∴f〔﹣x+2〕=f〔x+2〕,∴f〔3〕=f〔1〕,f〔π〕=f〔4﹣π〕,∵4﹣π<1<,当x∈[﹣2,2]时,f〔x〕单调递减,∴f〔4﹣π〕>f〔1〕>f〔〕,∴f〔〕<f〔3〕<f〔π〕,应选C.【点评】此题考察函数单调性、奇偶性,考察学生的计算能力,正确转化是关键.9.〔5分〕〔2017•模拟〕执行如下图的程序框图,假设输入a ,b ,c 分别为1,2,0.3,那么输出的结果为〔 〕A .1.125B .1.25C .1.3125D .1.375【分析】模拟程序的运行,依次写出每次循环得到的a ,b 的值,当a=1.25,b=1.5时满足条件|a ﹣b|<0.3,退出循环,输出的值为1.375. 【解答】解:模拟程序的运行,可得 a=1,b=2,c=0.3执行循环体,m=,不满足条件f 〔m 〕=0,满足条件f 〔a 〕f 〔m 〕<0,b=1.5,不满足条件|a ﹣b|<c ,m=1.25,不满足条件f 〔m 〕=0,不满足条件f 〔a 〕f 〔m 〕<0,a=1.25,满足条件|a ﹣b|<c , 退出循环,输出的值为1.375. 应选:D .【点评】此题考察了程序框图的应用,模拟程序的运行,正确依次写出每次循环得到的a ,b 的值是解题的关键,属于根底题.10.〔5分〕〔2017•模拟〕设双曲线C :﹣=1〔a >0,b >0〕的左右顶点分别为A 1,A 2,左右焦点分别为F 1,F 2,以F 1F 2为直径的圆与双曲线左支的一个交点为P ,假设以A 1A 2为直径的圆与PF2相切,那么双曲线C的离心率为〔〕A.B.C.2 D.【分析】根据双曲线的定义和以及圆的有关性质可得PF1=2a,PF2=4a,再根据勾股定理得到a,c的关系式,即可求出离心率.【解答】解:如下图,由题意可得OQ∥F1P,OQ=OA2=a,OF2=C,F1F2=2c,∴==,∴PF1=2a,∵点P为双曲线左支的一个点,∴PF2﹣PF1=2a,∴PF2=4a,∵以F1F2为直径的圆与双曲线左支的一个交点为P,∴∠F1PF2=90°∴〔2a〕2+〔4a〕2=〔2c〕2,∴=3,∴e==,应选:B【点评】此题要求学生掌握定义:到两个定点的距离之差等于|2a|的点所组成的图形即为双曲线.考察了数形结合思想、此题凸显解析几何的特点:“数研究形,形助数〞,利用几何性质可寻求到简化问题的捷径.11.〔5分〕〔2017•模拟〕函数f〔x〕=sin〔ωx+2φ〕﹣2sinφcos〔ωx+φ〕〔ω>0,φ∈R〕在〔π,〕上单调递减,那么ω的取值围是〔〕A.〔0,2] B.〔0,] C.[,1] D.[,]【分析】利用积化和差公式化简2sinφco s〔ωx+φ〕=sin〔ωx+2φ〕﹣sinωx.可将函数化为y=Asin〔ωx+φ〕的形式,在〔π,〕上单调递减,结合三角函数的图象和性质,建立关系可求ω的取值围.【解答】解:函数f〔x〕=sin〔ωx+2φ〕﹣2sinφcos〔ωx+φ〕〔ω>0,φ∈R〕.化简可得:f〔x〕=sin〔ωx+2φ〕﹣sin〔ωx+2φ〕+sinωx=sinωx,由+,〔k∈Z〕上单调递减,得:+,∴函数f〔x〕的单调减区间为:[,],〔k∈Z〕.∵在〔π,〕上单调递减,可得:∵ω>0,ω≤1.应选C.【点评】此题主要考察对三角函数的化简能力和三角函数的图象和性质的运用,利用三角函数公式将函数进展化简是解决此题的关键.属于中档题.12.〔5分〕〔2017•模拟〕把平面图形M上的所有点在一个平面上的射影构成的图形M′叫作图形M在这个平面上的射影.如图,在长方体ABCD﹣EFGH中,AB=5,AD=4,AE=3,那么△EBD 在平面EBC上的射影的面积是〔〕A.2 B.C.10 D.30【分析】如下图,△EBD在平面EBC上的射影为△OEB,即可求出结论.【解答】解:如下图,△EBD在平面EBC上的射影为△OEB,面积为=2,应选A.【点评】此题考察射影的概念,考察面积的计算,确定△EBD在平面EBC上的射影为△OEB是关键.二、填空题:本大题共4小题,每题5分,共20分〕.13.〔5分〕〔2017•模拟〕设抛物线C:y2=2x的焦点为F,假设抛物线C上点P的横坐标为2,那么|PF|=.【分析】直接利用抛物线的定义,即可求解.【解答】解:抛物线y2=2x上横坐标为2的点到其焦点的距离,就是这点到抛物线的准线的距离.抛物线的准线方程为:x=﹣,所以抛物线y2=2x上横坐标为2的点到其焦点的距离为+2=.故答案为:.【点评】此题考察抛物线的简单性质的应用,抛物线的定义的应用,考察计算能力.14.〔5分〕〔2017•模拟〕在一个容量为5的样本中,数据均为整数,已测出其平均数为10,但墨水污损了两个数据,其中一个数据的十位数字1未污损,即9,10,11,,那么这组数据的方差s2可能的最大值是36 .【分析】设这组数据的最后2个分别是:10+x,y,得到x+y=10,表示出S2,根据x的取值求出S2的最大值即可.【解答】解:设这组数据的最后2个分别是:10+x,y,那么9+10+11+〔10+x〕+y=50,得:x+y=10,故y=10﹣x,故S2=[1+0+1+x2+〔﹣x〕2]=+x2,显然x最大取9时,S2最大是36,故答案为:36.【点评】此题考察了求数据的平均数和方差问题,是一道根底题.15.〔5分〕〔2017•模拟〕假设曲线y=lnx+ax2﹣2x〔a为常数〕不存在斜率为负数的切线,那么实数a的取值围是[,+∞〕.【分析】由题意可知y′≥0在〔0,+∞〕上恒成立,别离参数得a≥,求出右侧函数的最大值即可得出a的围.【解答】解:y′=,x∈〔0,+∞〕,∵曲线y=lnx+ax2﹣2x〔a为常数〕不存在斜率为负数的切线,∴y′=≥0在〔0,+∞〕上恒成立,∴a≥恒成立,x∈〔0,+∞〕.令f〔x〕=,x∈〔0,+∞〕,那么f′〔x〕=,∴当0<x<1时,f′〔x〕>0,当x>1时,f′〔x〕<0,∴f〔x〕在〔0,1〕上单调递增,在〔1,+∞〕上单调递减,∴当x=1时,f〔x〕=取得最大值f〔1〕=,∴a.故答案为[,+∞〕.【点评】此题考察了导数的几何意义,导数与函数单调性的关系,函数最值的计算,属于中档题.16.〔5分〕〔2017•模拟〕在数列{an }中,a1=1,a1+++…+=an〔n∈N*〕,那么数列{an}的通项公式an=.【分析】a1=1,a1+++…+=an〔n∈N*〕,n≥2时,a1+++…+=an﹣1.相减可得:=.再利用递推关系即可得出.【解答】解:∵a1=1,a1+++…+=an〔n∈N*〕,n≥2时,a1+++…+=an﹣1.∴=an ﹣an﹣1,化为:=.∴= (2)1=2.∴an=.故答案为:.【点评】此题考察了数列递推关系、通项公式,考察了推理能力与计算能力,属于中档题.三、解答题:本大题共5小题,共70分.解答写出文字说明、证明过程或演算过程.17.〔12分〕〔2017•模拟〕如图,在平面四边形ABCD中,∠A=,∠B=,AB=6,在AB边上取点E,使得BE=1,连接EC,ED.假设∠CED=,EC=.〔Ⅰ〕求sin∠BCE的值;〔Ⅱ〕求CD的长.【分析】〔Ⅰ〕在△CBE中,正弦定理求出sin∠BCE;〔Ⅱ〕在△CBE中,由余弦定理得CE2=BE2+CB2﹣2BE•CBcos120°,得CB.由余弦定理得CB2=BE2+CE2﹣2BE•CEcos∠BEC⇒cos∠BEC⇒sin∠BEC、cos∠AED在直角△ADE中,求得DE=2,在△CED中,由余弦定理得CD2=CE2+DE2﹣2CE•DEcos120°即可【解答】解:〔Ⅰ〕在△CBE中,由正弦定理得,sin∠BCE=,〔Ⅱ〕在△CBE中,由余弦定理得CE2=BE2+CB2﹣2BE•CBcos120°,即7=1+CB2+CB,解得CB=2.由余弦定理得CB2=BE2+CE2﹣2BE•CEcos∠BEC⇒cos∠BEC=.⇒sin∠BEC=,sin∠AED=sin〔1200+∠BEC〕=,⇒cos∠AED=,在直角△ADE中,AE=5,═cos∠AED=,⇒DE=2,在△CED中,由余弦定理得CD2=CE2+DE2﹣2CE•DEcos120°=49∴CD=7.【点评】此题考察了正余弦定理在解三角形中的应用,是中档题18.〔12分〕〔2017•模拟〕某项科研活动共进展了5次试验,其数据如表所示:特征量第1次第2次第3次第4次第5次x 555559 551 563 552y 601605 597 599 598〔Ⅰ〕从5次特征量y的试验数据中随机地抽取两个数据,求至少有一个大于600的概率;〔Ⅱ〕求特征量y关于x的线性回归方程=x+;并预测当特征量x为570时特征量y的值.〔附:回归直线的斜率和截距的最小二乘法估计公式分别为=,=﹣〕【分析】〔Ⅰ〕利用对立事件的概率公式,可得结论;〔Ⅱ〕求出回归系数,即可求特征量y关于x的线性回归方程=x+;并预测当特征量x为570时特征量y的值.【解答】解:〔Ⅰ〕从5次特征量y的试验数据中随机地抽取两个数据,共有=10种方法,都小于600,有=3种方法,∴至少有一个大于600的概率==0.7;〔Ⅱ〕=554,=600,===0.25,=﹣=461.5,∴=0.25x+461.5,x=570,=604,即当特征量x为570时特征量y的值为604.【点评】此题考察概率的计算,考察独立性检验知识的运用,正确计算是关键.19.〔12分〕〔2017•模拟〕如图,梯形CDEF与△ADE所在的平面垂直,AD⊥DE,CD⊥DE,AB ∥CD∥EF,AE=2DE=8,AB=3,EF=9,CD=12,连接BC,BF.〔Ⅰ〕假设G为AD边上一点,DG=DA,求证:EG∥平面BCF;〔Ⅱ〕求多面体ABCDEF 的体积.【分析】〔Ⅰ〕由可得DA 、DE 、DC 两两互相垂直,以D 为坐标原点,分别以ED 、DC 、DA 所在直线为x ,y ,z 轴建立空间直角坐标系,求出平面BCF 的一个法向量, 由平面法向量与平行证明EG ∥平面BCF ;〔Ⅱ〕把多面体ABCDEF 的体积分解为两个棱锥的体积求解.【解答】〔Ⅰ〕证明:∵梯形CDEF 与△ADE 所在的平面垂直,AD ⊥DE ,∴AD ⊥平面CDEF , 那么AD ⊥DC ,又CD ⊥DE ,∴以D 为坐标原点,分别以ED 、DC 、DA 所在直线为x ,y ,z 轴 建立空间直角坐标系,∵AB ∥CD ∥EF ,AE=2DE=8,AB=3,EF=9,CD=12, 且DG=DA ,∴E 〔﹣4,0,0〕,G 〔0,0,〕,C 〔0,12,0〕, F 〔﹣4,9,0〕,B 〔0,3,〕, ,.设平面BCF 的一个法向量为, 那么由,取z=,得. ,∴.∵EG ⊄平面BCF ,∴EG ∥平面BCF ; 〔Ⅱ〕解:连接BD ,BE , 那么V ABCDEF =V B ﹣CDEF +V B ﹣ADE ==.【点评】此题考察直线与平面平行的判定,训练了利用空间向量证明线面平行,训练了多面体体积的求法,是中档题.20.〔12分〕〔2017•模拟〕在平面直角坐标系xOy 中,椭圆E :+=1〔a >b >0〕,圆O :x 2+y 2=r 2〔0<r <b 〕.当圆O 的一条切线l :y=kx+m 与椭圆E 相交于A ,B 两点.〔Ⅰ〕当k=﹣,r=1时,假设点A ,B 都在坐标轴的正半轴上,求椭圆E 的方程; 〔Ⅱ〕假设以AB 为直径的圆经过坐标原点O ,探究a ,b ,r 是否满足+=,并说明理由. 【分析】〔Ⅰ〕利用点到直线的距离公式求得d==1,即可求得m 的值,由点A ,B 都在坐标轴的正半轴上,即可求得a 和b 的值,求得椭圆方程;〔Ⅱ〕利用点到直线的距离公式,求得m2=r2〔1+k2〕,将直线方程代入椭圆方程,由韦达定理及向量数量积的坐标运算x1x2+y1y2=0,即可求得a,b与r的关系.【解答】解:〔Ⅰ〕当k=﹣,r=1时,那么切线l:y=﹣x+m,即2y+x﹣2m=0,由圆心到l的距离d==1,解得:m=±,点A,B都在坐标轴的正半轴上,那么m>0,∴直线l:y=﹣x+,∴A〔0,〕,B〔,0〕,∴B为椭圆的右顶点,A为椭圆的上顶点,那么a=,b=,∴椭圆方程为:;〔Ⅱ〕a,b,r满足+=成立,理由如下:设点A、B的坐标分别为A〔x1,y1〕、B〔x2,y2〕,直线l与圆x2+y2=r2相切,那么=r,即m2=r2〔1+k2〕,①那么,〔b2+a2k2〕x2+2a2kmx+a2m2﹣a2b2=0.那么x1+x2=﹣,x1x2=,所以y1y2=〔kx1+m〕〔kx2+m〕=k2x1x2+km〔x1+x2〕+m2=,AB为直径的圆经过坐标原点O,那么∠AOB=90°,那么⊥=0,∴x1x2+y1y2=+==0,那么〔a2+b2〕m2=a2b2〔1+k2〕,②将①代入②,=,∴+=.【点评】此题考察椭圆的标准方程,直线与椭圆的位置关系,考察韦达定理,弦长公式,点到直线的距离公式及向量数量积的坐标运算,考察计算能力,属于中档题.21.〔12分〕〔2017•模拟〕函数f〔x〕=〔a+〕lnx﹣x+,其中a>0.〔Ⅰ〕假设f〔x〕在〔0,+∞〕上存在极值点,求a的取值围;〔Ⅱ〕设a∈〔1,e],当x1∈〔0,1〕,x2∈〔1,+∞〕时,记f〔x2〕﹣f〔x1〕的最大值为M〔a〕,那么M〔a〕是否存在最大值?假设存在,求出其最大值;假设不存在,请说明理由.【分析】〔Ⅰ〕求出f′〔x〕=,x∈〔0,+∞〕,由此根据a=1,a>0且a≠1,利用导数性质进展分类讨论,能求出a的取值围.〔Ⅱ〕当a ∈〔1,e]时,,f 〔x 〕在〔0,〕上单调递减,在〔,a 〕上单调递增,在〔a ,+∞〕上单调递减,对∀x 1∈〔0,1〕,有f 〔x 1〕≥f 〔〕,对∀x 2∈〔1,+∞〕,有f 〔x 2〕≤f 〔a 〕,从而[f 〔x 2〕﹣f 〔x 1〕]max =f 〔a 〕﹣f 〔〕,由此能求出M 〔a 〕存在最大值. 【解答】解:〔Ⅰ〕∵f 〔x 〕=〔a+〕lnx ﹣x+,其中a >0, ∴=,x ∈〔0,+∞〕, ①当a=1时,≤0,f 〔x 〕在〔0,+∞〕上单调递减,不存在极值点; ②当a >0时,且a ≠1时,f′〔a 〕=f′〔〕=0, 经检验a ,均为f 〔x 〕的极值点, ∴a ∈〔0,1〕∪〔1,+∞〕. 〔Ⅱ〕当a ∈〔1,e]时,,f 〔x 〕在〔0,〕上单调递减,在〔,a 〕上单调递增, 在〔a ,+∞〕上单调递减,对∀x 1∈〔0,1〕,有f 〔x 1〕≥f 〔〕,对∀x 2∈〔1,+∞〕,有f 〔x 2〕≤f 〔a 〕, ∴[f 〔x 2〕﹣f 〔x 1〕]max =f 〔a 〕﹣f 〔〕, ∴M 〔a 〕=f 〔a 〕﹣f 〔〕=[〔a+〕lna ﹣a+]﹣[〔a+〕ln ﹣+a] =2[〔a+〕lna ﹣a+],a ∈〔1,e],M′〔a 〕=2〔1﹣〕lna+2〔a+〕+2〔﹣1﹣〕 =2〔1﹣〕lna ,a ∈〔1,e].∴M′〔a 〕>0.即M 〔a 〕在〔1,e]上单调递增, ∴[M 〔a 〕]max =M 〔e 〕=2〔e+〕+2〔〕=, ∴M 〔a 〕存在最大值.【点评】此题考察了利用导数研究函数的单调性极值与最值,考察了恒成立问题的等价转化方法,考察了推理能力与计算能力,属于难题.[选修4-4:坐标系与参数方程选讲]22.〔10分〕〔2017•模拟〕在直角坐标系xOy 中,曲线C 的参数方程为〔α为参数〕,直线l 的参数方程为〔t 为参数〕,在以坐标原点O 为极点,x 轴为正半轴为极轴的极坐标系中,过极点O 的射线与曲线C 相交于不同于极点的点A ,且点A 的极坐标为〔2,θ〕,其中θ∈〔,π〕〔Ⅰ〕求θ的值;〔Ⅱ〕假设射线OA与直线l相交于点B,求|AB|的值.【分析】〔Ⅰ〕曲线C的极坐标方程,利用点A的极坐标为〔2,θ〕,θ∈〔,π〕,即可求θ的值;〔Ⅱ〕假设射线OA与直线l相交于点B,求出A,B的坐标,即可求|AB|的值.【解答】解:〔Ⅰ〕曲线C的参数方程为〔α为参数〕,普通方程为x2+〔y﹣2〕2=4,极坐标方程为ρ=4sinθ,∵点A的极坐标为〔2,θ〕,θ∈〔,π〕,∴θ=;〔Ⅱ〕直线l的参数方程为〔t为参数〕,普通方程为x+y﹣4=0,点A的直角坐标为〔﹣,3〕,射线OA的方程为y=﹣x,代入x+y﹣4=0,可得B〔﹣2,6〕,∴|AB|==2.【点评】此题考察三种方程的转化,考察两点间距离公式的运用,属于中档题.[选修4-5:不等式选讲]23.〔2017•模拟〕函数f〔x〕=4﹣|x|﹣|x﹣3|〔Ⅰ〕求不等式f〔x+〕≥0的解集;〔Ⅱ〕假设p,q,r为正实数,且++=4,求3p+2q+r的最小值.【分析】〔I〕由题意,分类讨论,去掉绝对值,解不等式即可;〔Ⅱ〕运用柯西不等式,可3p+2q+r的最小值.【解答】解:〔Ⅰ〕f〔x+〕≥0,即|x+|+|x﹣|≤4,x≤﹣,不等式可化为﹣x﹣﹣x+≤4,∴x≥﹣2,∴﹣2≤x≤﹣;﹣<x<,不等式可化为x+﹣x+≤4恒成立;x≥,不等式可化为x++x﹣≤4,∴x≤2,∴≤x≤2,综上所述,不等式的解集为[﹣2,2];〔Ⅱ〕∵〔++〕〔3p+2q+r〕≥〔1+1+1〕2=9,++=4∴3p+2q+r≥,∴3p+2q+r的最小值为.【点评】此题考察不等式的解法,考察运用柯西不等式,考察运算和推理能力,属于中档题.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
A. x2 + y2 = 1 95
B. x2 − y2 = 1 59
C. x2 + y2 = 1 59
D. x2 − y2 = 1 95
文科数学试题 第1页(共 4 页)
7.已知某产品的销售额 y 与广告费用 x 之间的关系如下表:
x(单位:万元)
0
1
2
3
4
y(单位:万元)
10
15
m
30
35
若根据表中的数据用最小二乘法求得 y 对 x 的回归直线方程为 y = 6.5x + 9 ,则下列说
3.考试结束后,将答题卡交回。
一、选择题:本大题共 12 小题,每小题 5 分,共 60 分。在每小题给出的四个选项中,只 有一项是符合题目要求的。
1.设全集 U={x|x>0},M={x|1<ex<e2},则 UM=
A.(1,2)
B.(2,+∞)
C. (0,1] ∪[2,+ )
D.[2,+ )
2.已知 i 为虚数单位,复数 z 满足 z i =1+ 2i ,则复数 z=
13.直线 l1:ax-(a+1)y-1=0 与直线 4x-6y+3=0 平行,则实数 a 的值
是
.
11 0 4 9
14.某同学在高三学年的五次模拟考试中,其数学成绩的茎叶图如右 12 1 6
图,则该同学数学成绩的方差是
.
15.函数 y = sin(x + ) ( 0, ) 的图象如图所示,则 2
D. x + 2 y − 6 = 0
11.已知 f (x) 为偶函数,且当 x≥0 时, f (x) = x cos x − sin x + 1 x3 ,则满足不等式 3
f (log2 m) + f (log1 m) 2 f (1) 的实数 m 的取值范围为
2
A.( 1 ,2) 2
B.(0,2)
C. (0,1) (1,2) 2
则甲、乙、丙三人恰好到同一景点旅游参观的概率为
A. 1 8
B. 1 4
C. 3 8
D. 1 2
9.双曲线
x2 a2
−
y2 b2
= 1(a>0,b>0)的右焦点为
F,过
F
作与双曲线的两条渐近线平行的直线
且与渐近线分别交于 A,B 两点,若四边形 OAFB(O 为坐标原点)的面积为 bc,则双曲
线的离心率为
0.04 0.03 0.02 0.01
0
5 10 15 20 25 30 时间 t/小时
(2)将每月阅读时间不低于 m 和低于 m 的学生数填入下面的列联表内,并判断能否 在犯错误的概率不超过 0.1 的前提下认为阅读与性别有关.
2×2 列联表
附பைடு நூலகம்:
男 t≥m
女
总计
P(K2≥k0) k0
0.15 2.072
A. 2
B.2
C. 3
D.3
10.已知圆 C: x2 + y2 − 2x − 8 = 0 ,直线 l 经过点 M(2,2),且将圆 C 及其内部区域分为
两部分,若直线 l 使两部分的面积之差最大,则它的方程为
A. x − 2 y + 2 = 0
B. 2x + y − 6 = 0
C. 2x − y − 2 = 0
秘密 ★ 启用前 【考试时间:2020 年 1 月 5 日 15:00—17:00】
绵阳市高中 2017 级第二次诊断性考试
文科数学
注意事项: 1.答卷前,考生务必将自己的姓名、准考证号填写在答题卡上。 2.回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其它答案标号。回答非选择题时,将答案写在答题卡 上。写在本试卷上无效。
A. 5 2
B. 5 2
C. 5
D.5
5.已知为任意角,则“cos2= 1 ”是“sin= 3 ”的
3
3
A.充分不必要条件
B.必要不充分条件
C.充要条件
D.既不充分也不必要
6.已知 M (-2,0),P 是圆 N:x2-4x+y2-32=0 上一动点,线段 MP 的垂直平分线交 NP 于
点 Q,则动点 Q 的轨迹方程为
D. (2,+)
12.函数
f
(x)
=
(2ax
−1)2
− loga (ax
+
2)
在区间[0, 1 a
]上恰有一个零点,则实数
a
的取值范
围是
A. (1 ,1) 32
B. (1,2] [3,+ ) C. (1,2) [3,+ ) D.[2 ,3)
文科数学试题 第2页(共 4 页)
二、填空题:本大题共 4 小题,每小题 5 分,共 20 分.
17.(12 分)
每年的 4 月 23 日为“世界读书日”,某调查机
频率/组距
构对某校学生做了一个是否喜爱阅读的抽样调查, 0.06
该调查机构从该校随机抽查了 100 名不同性别的学 生(其中男生 45 名),统计了每个学生一个月的阅 读时间,其阅读时间 t(小时)的频率分布直方图如图 所示:
(1)求学生每月阅读时间 t 的中位数 m.
A.2-i
B.2+i
C.1-2i
D.i-2
3.已知高一(1)班有学生 45 人,高一(2)班有 50 人,高一(3)班有 55 人,现在要
用分层抽样的方法从这三个班中抽 30 人参加学校“遵纪守法好公民”知识测评,则高
一(2)班被抽出的人数为
A.10
B.12
C.13
D.15
4.已知向量 a=(1,2),b=(-1,x),若 a//b,则∣b∣=
f (x) 在区间[-π,π]上的零点之和为
.
16.过点 M(-1,0)的直线 l 与抛物线 C:y2=4x 交于 A,B
两点(A 在 M,B 之间),若 S△MBF=4S△MAF,则△ABF
的面积为
.
三、解答题:共 70 分。解答应写出文字说明、证明过程或演算步骤。第 17~21 题为必考
题,每个试题考生都必须作答。第 22、23 题为选考题,考生根据要求作答。 (一)必考题:共 60 分。
0.10 2.706
0.05 3.841
t<m
30
总计
45
其中: K2=
n(ad − bc)2
.
(a + b)(b + c)(a + c)(b + d)
18.(12 分)
已知等差数列{an}的公差 d=2,a3>0,且 −3 3 为 a4 与 a7 的等比中项. 数列{bn}的通
法中错误的是
A.产品的销售额与广告费用成正相关 B.该回归直线过点(2,22) C.当广告费用为 10 万元,销售额为 74 万元 D.m 的值是 20 8.甲、乙、丙三位客人在参加中国(绵阳)科技城国际科技博览会期间,计划到绵阳的
九皇山、七曲山大庙两个景点去参观考察,由于时间关系,每个人只能选择一个景点,
