材料力学内力图绘制详细讲解
材料力学第3讲-绘制梁内力图的基本方法
用函数关系表示沿梁轴线各横截面上剪力和弯矩的变化规律， 分别称作剪力方程和弯矩方程.
①剪力方程(Shear- force equation)
FS= FS(x)
②弯矩方程(Bending-moment equation)
构件受弯时，横截面上其作用面垂直于截
面的内力偶矩.
FRAy
m
m
FS M
C
②剪力(Shear force) FS
构件受弯时，横截面上其作用线平行于截面 的内力.
M C
FS
F B
FRB
F FRB
2）梁的内力的正负号规定 (Sign convention for internal force)
m FS
①剪力的正负号规定
左侧梁段 顺时针转向的外力偶引起正值的弯矩 逆时针转向的外力偶引起负值的弯矩
右侧梁段 逆时针转向的外力偶引起正值的弯矩 顺时针转向的外力偶引起负值的弯矩
【例题2-3-4】轴的计例算简图如图所示，已知 F1 = F2 = F = 60kN， a = 230mm，b = 100 mm 和c = 1000 mm. 求 C 、D 点处横截面
M= M(x)
2）剪力图和弯矩图(Shear-force & bending-moment diagrams)
以平行于梁轴的横坐标x表示横截面的位置,以纵坐标表示相
应截面上的剪力和弯矩.这种图线分别称为剪力图和弯矩图 FS(x)
x O
O
x
FS 图的坐标系
M(x) M 图的坐标系
剪力图为正值画在 x 轴上侧,负值画在x 轴下侧
建筑力学5内力内力图
结合内力图和概率论的知识，可以对结构的可靠性进行分析和评估 ，确保结构在各种可能出现的荷载作用下都能保持安全。
利用内力图进行施工模拟
模拟施工过程
通过内力图，可以模拟施工过程 ，预测在施工过程中可能出现的 内力变化和结构变形，从而采取
相应的措施来保证施工安全。
控制施工过程
在施工过程中，通过实时监测结 构的内力变化，可以及时发现施 工中的问题，并采取相应的措施 进行调整和控制，确保施工质量
压力图是关于拱顶和拱脚的直线分布 ，弯矩图是关于拱顶和拱脚的二次函 数分布，剪力图则根据具体情况而定 。
05
CATALOGUE
内力图的应用
利用内力图进行结构设计
确定结构构件的截面尺寸
根据内力图，可以确定结构中各个构件所承受的最大和最小内力 ，从而根据这些值来选择合适的截面尺寸。
优化结构设计
通过分析内力图，可以发现结构中的薄弱环节，从而对结构进行优 化设计，提高结构的承载能力和稳定性。
内力图的绘制方法
解析法
根据结构力学的基本原理，通过 建立数学模型和方程组来求解内
力，并绘制内力图。
实验法
通过实验测试来测量结构的实际内 力，并绘制内力图。实验法通常用 于实际工程中，以验证结构的承载 能力和安全性。
数值分析法
利用计算机数值模拟软件，对结构 进行有限元分析，求解结构的内力 并绘制内力图。数值分析法广泛应 用于工程设计和研究中。
分布力作用下的内力计算
总结词
利用微积分原理计算分布力作用下的内力。
详细描述
分布力作用下，利用微积分原理，将分布力在受力范围内积分，得到内力的总和 ，并确定内力的方向和大小。
弯矩与剪力的计算
材料力学第4讲-利用微分关系绘制梁内力图
在CD和DB段，剪力为负值，弯矩图
1.7 为向下倾斜的直线.
最大弯矩发生在剪力改变正、负号的 C
截面处.说明剪力图和弯矩图是正确的.
27 +
例题3-4-2 一简支梁受均布荷载作用，其集度 q=100kN/m ,如图 所示.试用简
易法作此梁的剪力图和弯矩图. 解：（1） 计算梁的支反力
FRA FRB 0.5 100 1.6 80kN
（1）梁的载荷集度函数、剪力函数和弯矩函数之间的 微分关系
（2）利用微分关系的绘制简单梁的内力图 （3）利用微分关系绘制多跨静定的内力图 （4）根据梁的内力图反推梁的荷载图 2.5 应用叠加原理绘制梁的内力图（待学习） 2.6 刚架和组合变形杆件的内力分析（待学习）
2.4 利用微分关系绘制梁的内力图
dFS ( x) q( x) dx
dM ( x) dx
FS
(
x)
（3）内力的极值点位置的判断 1）最大剪力可能发生在集中力所在截面的一侧;或
发生在剪力图有转折的截面处或杆件的端部.
2）梁上最大弯矩 Mmax可能发生在均布荷载作用区段 内FS(x) = 0 的截面上; 或发生在杆件中部弯矩发生
转折或突变处，或发生在杆件的端部。
将梁分为 AC、CD、DB 三段.
AC和DB上无荷载，CD 段有向下的
均布荷载.
（2）剪力图 AC段 水平直线
FSA右 FRA 80kN
CD段 向右下方的斜直线
FRA
A C
0.2 1
FS
(kN)
80
q
FRB
B
D
1.6
2
+
FSC FRA 80kN
FSD FRB 80kN
材料力学内力图绘制详解
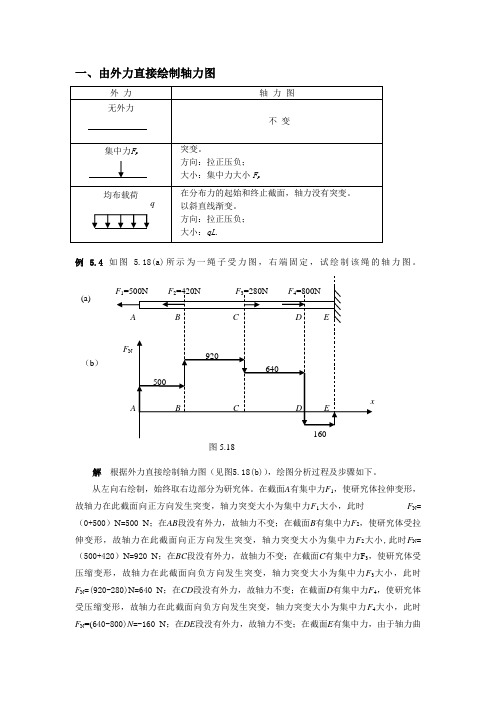
一、由外力直接绘制轴力图例 5.4 如图 5.18(a)所示为一绳子受力图，右端固定，试绘制该绳的轴力图。
解 根据外力直接绘制轴力图（见图5.18(b)），绘图分析过程及步骤如下。
从左向右绘制，始终取右边部分为研究体。
在截面A 有集中力F 1，使研究体拉伸变形，故轴力在此截面向正方向发生突变，轴力突变大小为集中力F 1大小，此时 F N =（0+500）N =500 N ；在AB 段没有外力，故轴力不变；在截面B 有集中力F 2，使研究体受拉伸变形，故轴力在此截面向正方向发生突变，轴力突变大小为集中力F 2大小,此时F N =（500+420）N =920 N ；在BC 段没有外力，故轴力不变；在截面C 有集中力F 3，使研究体受压缩变形，故轴力在此截面向负方向发生突变，轴力突变大小为集中力F 3大小，此时F N =(920-280)N =640 N ；在CD 段没有外力，故轴力不变；在截面D 有集中力F 4，使研究体受压缩变形，故轴力在此截面向负方向发生突变，轴力突变大小为集中力F 4大小，此时 F N =(640-800)N =-160 N ；在DE 段没有外力，故轴力不变；在截面E 有集中力，由于轴力曲（b ）(a)线与轴线围成封闭图形，故轴力突变为0。
例5.5有一根阶梯轴受力如图5.19(a)所示，试绘制阶梯轴的轴力图。
图5.19解从右向左绘制，始终取左变部分为研究体。
根据外力直接绘制轴力图（见图5.19(b)），绘图分析过程及步骤如下：在截面A有集中力F1，使研究体压缩变形，故轴力在此截面向负方向发生突变，轴力突变大小为集中力F1大小,此时F N=（0-10）kN=-10 kN；在AB段有均匀分布载荷，使研究体受拉伸变形，故轴力以斜直线规律向正方向渐变，轴力渐变大小为均匀分布载荷大小，此时F N=（-10+10×2）kN=10 kN；在截面B没有力，故此截面轴力没有变化；在BC段没有外力，故轴力不变；在截面C有集中力F2，使研究体受拉伸变形，故轴力在此截面向正方向发生突变，轴力突变大小为集中力F2大小，此时F N=（10+10）kN=20 kN；在CD段没有外力，故轴力不变；在截面D有集中力，由于轴力曲线与轴线围成封闭图形，故轴力突变为0.二、由外力直接绘制扭矩图制其内力图。
(参考资料)材料力学中内力图的直接画法
材料力学中内力图的直接画法摘要:介绍一种关于材料力学中轴力、扭矩、剪力和弯矩等内力图的直接画法，建立内力的增减与外力方向之间的关系。
关键词:内力图；直接画法；内力；外力。
画内力图是材料力学学习过程中的一个重点，而不少学生在学习这部分内容时感到不好理解，总是不清楚题目要求的截面上的内力应该怎么求。
尤其是弯曲内力中的剪力与弯矩。
为了使同学更好地理解构件的内力、画好内力图,经过摸索与思考，我总结出了关于内力图的一种简单的画法。
本文中约定在各内力图中向上的方向为正向，画图时从左向右画。
希望老师和同学予以指正。
1.轴力、扭矩图轴力图完全可直接根据外力的大小与方向直接画出来。
以水平杆为例，如杆左端有约束，首先求出约束力(外力)，向左的外力会引起轴力增加，而向右的外力会引起轴力减小。
例如:图1中所示的杆的A、B、C、D点分别作用有大小为5P、8P、4P、P的力，方向如图1，试画出杆的轴力图。
解：用截面法求OA段内力N1设置截面如图1.X=OV1-P A+P B-P C-P D=0N1-5P+8P-4P-P=0N1=2P同理，求得AB、BC、CD段内力分别为：N2=-3P,N3=5P,N4=P。
轴力图如图1所示。
如果用直接法，只需要求出O截面的约束力R。
由平衡方程R=2P，方向向左，故O截面的轴力从0增加到2P。
OA段无外力，轴力均为2P。
A截面作用有外力PA=5P，方向向右，轴力在该截面将减小5P，即从2P降为-3P。
AB段无外力，轴力均为-3P。
B截面作用有外力8P，方向向左，该截面轴力将增加8P，即从-3P升到5P。
ＢＣ段轴力为５Ｐ，Ｃ截面有外力４Ｐ，方向向右，轴力在该截面下降４Ｐ。
ＣＤ段轴力为Ｐ，Ｄ截面有外力Ｐ，方向向右，该截面轴力下降Ｐ，最终为Ｏ轴力图终点与ｘ轴重合。
关于扭矩图中扭矩正负的规定，用直接法，将外力偶用右手螺旋法则进行矢量化，矢量沿轴线方向，一水平轴为例，向左的外力偶矩将引起扭矩的增加，向右的外力偶矩将引起扭矩下降，因此在直接法中，扭矩图的画法与轴力图的画法完全一样。
材料力学内力图绘制详解
一、由外力直接绘制轴力图例 如图(a)所示为一绳子受力图，右端固定，试绘制该绳的轴力图。
解 根据外力直接绘制轴力图（见图(b)），绘图分析过程及步骤如下。
从左向右绘制，始终取右边部分为研究体。
在截面A 有集中力F 1，使研究体拉伸变形，故轴力在此截面向正方向发生突变，轴力突变大小为集中力F 1大小，此时 F N =（0+500）N=500 N ；在AB 段没有外力，故轴力不变；在截面B 有集中力F 2，使研究体受拉伸变形，故轴力在此截面向正方向发生突变，轴力突变大小为集中力F 2大小,此时F N =（500+420）（b ）(a)N=920 N；在BC段没有外力，故轴力不变；在截面C有集中力F3，使研究体受压缩变形，故轴力在此截面向负方向发生突变，轴力突变大小为集中力F3大小，此时F N=(920-280)N=640 N；在CD段没有外力，故轴力不变；在截面D有集中力F4，使研究体受压缩变形，故轴力在此截面向负方向发生突变，轴力突变大小为集中力F4大小，此时F N=(640-800)N=-160 N；在DE 段没有外力，故轴力不变；在截面E有集中力，由于轴力曲线与轴线围成封闭图形，故轴力突变为0。
例有一根阶梯轴受力如图(a)所示，试绘制阶梯轴的轴力图。
图解从右向左绘制，始终取左变部分为研究体。
根据外力直接绘制轴力图（见图(b)），绘图分析过程及步骤如下：在截面A有集中力F1，使研究体压缩变形，故轴力在此截面向负方向发生突变，轴力突变大小为集中力F1大小,此时F N=（0-10）kN=-10 kN；在AB段有均匀分布载荷，使研究体受拉伸变形，故轴力以斜直线规律向正方向渐变，轴力渐变大小为均匀分布载荷大小，此时F N=（-10+10×2）kN=10 kN；在截面B没有力，故此截面轴力没有变化；在BC段没有外力，故轴力不变；在截面C有集中力F2，使研究体受拉伸变形，故轴力在此截面向正方向发生突变，轴力突变大小为集中力F2大小，此时F N=（10+10）kN=20 kN；在CD段没有外力，故轴力不变；在截面D有集中力，由于轴力曲线与轴线围成封闭图形，故轴力突变为0.二、由外力直接绘制扭矩图例如图（a）所示圆轴，左端固定、右端自由，受到三个集中力偶作用，试绘制其内力图。
材料力学第4讲-利用微分关系绘制梁内力图
求支座反力的顺序；中间铰接处和刚接处剪力图和弯矩图的特点。
（4）根据梁的内力图反推梁的荷载图
内力图与荷载图的对应关系；微分关系的应用。
2.4（1）梁的荷载集度函数、剪力 函数和弯矩函数之间的微分关系
设梁上作用有任意分布荷载，
其集度 q = q (x) 规定 q (x)向上为正. 将 x 轴的坐标原点取在梁的左端. 假想地用坐标为 x 和 x+dx的两
算出截面C上的剪力为 (3-
24)kN=-5kN,即可确定这条
4m
斜直线（如图所示）. FS/kN 3
M=10kN·m C 2m
F=2kN FRB
B
D
2m
2
x
截面C和B之间梁上无分布载荷,
剪力图为水平线.
5
截面B上有一集中力FRB,从B的左侧到B得右侧,建立了图发生突然变化, 变化的数值即等于FRB.故FRB右侧截面上的剪力为(-5+7)kN=2kN.
x1
等号右边积分的几何意义是x1 , x2两横截面间分布荷载图的面积.
dM ( x) dx
FS
(
x)
若横截面x= x1，x=x2 间无集中力偶作用则得
M ( x2 ) M ( x1 )
x2 x1
FS
(
x
)dx
等号右边积分的几何意义是 x1 , x2两个横截面间剪力图的面积.
例题3-4-1 一简支梁受两个力F作用,如图所示.已知 F= 25.3kN,
dFS ( x) q( x) dx
dM ( x) dx
FS
(
x)
（3）内力的极值点位置的判断 1）最大剪力可能发生在集中力所在截面的一侧;或
材料力学第3讲-绘制梁内力图的基本方法
m dx
②弯矩的正负号规定
(Sign convention for bending moment)
Mm
M
+
当dx 微段的弯曲下凸（即该段的下半
部受拉 ）时,横截面m-m上的弯矩为正；
m
-
当dx 微段的弯曲上凸（即该段的下半 部受压）时,横截面m-m上的弯矩为负.
m
m （受压）
【例题2-3-3】图示梁的计算简图.已知 F1、F2,且 F2 > F1 ,尺寸a、b、c 和 l 亦均为已知.试求梁在E、F 点处横截面处的剪力和弯矩.
B
l
Fx 0 , FRAx 0
MA 0 ,
FRB
Fa l
FRAxA
F B
Fy 0 ,
FRAy
F (l l
a)
FRAy
FRB
求内力——截面法
Fy 0 , MC 0 ,
FS
FRAy
F
(l l
a)
M FRAy x
FRAx A FRAy
剪力
x
1）受弯构件的内力
弯矩
①弯矩(Bending moment)) M
《材料力学》第3讲 绘制梁内力图的基本方法
土木工程学院 马守才 2020年3月
授课提纲
复习与提问：上一次课中我们学习了哪些这门课程的哪
些内容？其中比较重要的内容是什么？ 新课导入：如何对梁进行内力分析？
讲授新课
2. 杆件的内力分析（本单元共有6节，分5次学习） 2.1 轴力方程与轴力图 （已学习） 2.2 扭矩方程与扭矩图 （已学习） 2.3 绘制梁内力图的基本方法 ？√
n
FS
Fi
i 1左（右）
《材料力学》课件4-3平面刚架和曲杆的内力图
感谢您的观看
THANKS
机械工程中的应用
机械零部件
在机械工程中，平面刚架和曲杆结构被广泛应用于各种机械零部件 的设计中，如轴承、齿轮等。
传动系统
在传动系统中，平面刚架和曲杆结构被用于实现动力的传递和分配， 以提高机械设备的效率和稳定性。
航空航天
在航空航天领域中，由于对结构和性能的要求非常高，平面刚架和曲 杆结构也得到了广泛应用，如飞机机身、火箭发动机等。
内力分析的方法包括截面法和节点法。截面 法是通过截取部分杆件进行分析的方法，节 点法则通过分析节点处的平衡状态来确定各 杆件的内力。
内力分析是结构设计和强度校核的 基础，对于保证结构的稳定性和安 全性至关重要。
刚架的内力计算
内力计算是根据已知的力和力矩，计算出各杆 件的内力大小和方向的过程。
内力计算的方法包括静力学方法和动力学方法。 静力学方法适用于分析静载作用下的结构，动 力学方法则适用于分析动态作用下的结构。
内力计算的结果可以用于进一步的结构分析和 设计，如强度校核、稳定性分析和优化设计等。
02
曲杆的内力图
曲杆的组成与分类
曲杆的组成
曲杆由若干直杆和若干节点组成，节 点之间通过直杆连接。
曲杆的分类
根据形状和受力特点，曲杆可分为平 面曲杆和空间曲杆。平面曲杆又可分 为单向弯曲曲杆和双向弯曲曲杆。
曲杆的内力分析
内力的概念
内力是指物体在受力过程中，内部各部分之间相互作用的力量。在材料力学中， 内力通常用截面法来测量。
内力的分析方法
对于曲杆，内力的分析方法主要有截面法和转角法。截面法是通过在曲杆上截 取一个微段，然后分析该微段的受力情况来计算内力；转角法是通过分析节点 或直杆的转角变化来计算内力。
任务十五梁的内力图绘制
任务十五
梁的内力图绘制
任务十五
梁的内力图绘制
3、利用内力方程画内力图
AB段：坐标原点取在左端A点处，距原点A为x1处的任意截面， 其剪力方程和弯矩方程为
Q(x1)=RA－qx1=1.5qa-qx1(0<x1<4a) M(x1)=RAx1-qx21/2=3qa/2x1-q/2x12 (0≤x1≤4a) BC段：坐标原点取在右端C点处，距原点C为x2处的任意截面， 其剪力方程和弯矩方程为 Q(x2)=qx2(0≤x2<2a)
x=a，MC=Pab/l
x=l，MB=0
任务十五
梁的内力图绘制
3、利用内力方程画内力图
从所作的内力图知，若a>b，则在CB段任一截面上的剪力值都 相等且比AC段的要大，其值｜Qmax｜=Pa/l，最大弯矩发生在集中力 P作用的截面上，其值｜Mmax｜=Pab/l 如果集中力P作用在梁的跨中，即a=b=l/2 ｜Qmax｜=P/2 ｜Mmax｜=Pl/4
为了形象地表示剪力和弯矩沿梁轴的变化规律，把剪 力方程和弯矩方程用其图像表示，称为剪力图和弯矩图。 剪力图和弯矩图的画法与轴力图、扭矩图很相似，用平 行于梁轴的横坐标x表示梁横截面的位置，用垂直于梁轴 的纵坐标表示相应截面的剪力和弯矩。 在土建工程中，习惯上将正剪力画在x轴上方，负剪 力画在x轴的下方；正弯矩画在x轴下方，负弯矩画在x轴 的上方，即把弯矩图画在梁受拉的一侧。
材料力学--第2章杆件的内力与内力图
轴力图的画法
画轴力图的步骤：求约束反力、求控制截面上的轴 力、画轴力图。 求任一横截面轴力的简便方法：任一横截面上的轴 力等于该截面一侧杆件上所有外力（包括反力）的代数和； 外力背离截面产生拉力，外力指向截面产生压力。 在分布轴向外力作用下，轴力图为斜直线或曲线。 没有分布轴向外力作用时，整个杆件轴力图为平行于杆件
外加扭力矩Me确定后，应用截面法可以确定横截面上 的内力──扭矩，圆轴两端受外加扭力矩Me作用时，横截 面上将产生分布剪应力，这些剪应力将组成对横截面中心 的合力矩，称为扭矩（twist moment），用Mx表示。
Me Me
Me
Mx
n
－ 右手螺旋定则
第2章 杆件的内力和内力图
◎ 扭矩与扭矩图
如果只在轴的两个端截面作用有外力偶矩，则沿轴线 方向所有横截面上的扭矩都是相同的，并且都等于作用在 轴上的外力偶矩。 当轴的长度方向上有两个以上的外力偶矩作用时，轴
D
E
2
FA
40kN
FN2
F
x
0， FN2 FA 40 0， FN2 50kN(拉)
第2章 杆件的内力和内力图
求CD段内的轴力
◎ 轴力与轴力图
FA
A
40kN B
55kN
25kN
20kN
C
3
D
E
FN3
25kN
20kN
F
x
0， FN3 25 20 0， FN3 5kN(压)
第2章 杆件的内力和内力图
同理，求得AB、 BC、CD段内力分 别为： FN2 B FB FN3 C FC C FC FN4 FN 2F 5F
◎ 轴力与轴力图
材料力学基本第二章 内力与内力图
CB段： BA段：
FN x1 0
FQ x1 F
M x1 Fx1
FN x2 F
FQ x2 0
M x2 F a
0 x1 a
0 x1 a
0 x1 a 0 x2 l
0 x2 l
0 x2 l
2.绘制剪力图和弯矩图
五、平面曲杆的内力图
平面曲杆：轴线为平面曲线的杆件。 内力的符号规定为：弯矩以使曲杆轴线曲率增加者为正，轴力和剪力的符 号规定与前面的相同。
2.6 结论与讨论
结
结论
论 与
• 一个重要概念
讨 论
• 三个微分方程
结
• 一套方法
论
讨论
结
论
与
比较前面三个梁的受力、剪力
讨 论
和弯矩图的相同 之处和不同
之处，从中能得到什么重要结
讨
论？
论
FQ
结
论
与
讨
FQ
论
讨
FQ
论
确定控
结 论 与 讨
制面上剪力 和弯矩有几 种方法？怎
论 样确定弯矩
图上极值点
讨 处的弯矩数
4. 在梁的某一截面上剪力为零，则在这一截面上弯矩有极值。
5. 在梁的某一截面上若作用有集中力，则此处剪力图有突变，突变的值 恰好等于集中力的数值。
6. 在梁的某一截面上若作用有集中力偶，则剪力图不发生变化，但此处 弯矩图会发生突变，突变的值恰好等于集中力偶的数值。
二、剪力、弯矩与载荷集度之间的积分关系
AD段 MeD T3 0
C
d) T3
D
T /Nm
T3 MeD 1018.6 N m e)
1018.6 (+)
材料力学第2章-杆件的内力与内力图
材料力学
刚体平衡概念的扩展和延伸：总体平衡，则其任何局部也必 然是平衡的。
材料力学
截面法
用假想截面从所要
求的截面处将杆截为 两部分 分的平衡
考察其中任意一部
由平衡方程求得横 截面的内力分量
C
F ＝0， F ＝0， M ＝0，
x y C
材料力学
例题2-4（P32)
q
例题2-5(P34)
材料力学
例题2-2
变截面传动轴受外加扭力矩作用，如下图所示。试画出扭矩图。
2M e 5M e 3M e
l
l
解：
2M e M x 2M e M x 3M e 3M e
Mx
Mx
3M e
Mx
＋ －
2M e
x
材料力学
梁(杆件)弯曲变形时的内力
材料力学
弹性体的平衡原理
刚体平衡概念的扩展和延伸：总体平衡，则其任何局部也必 然是平衡的。
材料力学
剪力图与弯矩图的绘制方法与轴力图大体相似，但略有差 异。主要步骤如下：
根据载荷及约束力的作用位置，确定控制面。
应用截面法确定控制面上的剪力和弯矩数值。 建立FQ——x和M——x 坐标系，并将控制面上的剪力 和弯矩值标在相应的坐标系中。 应用平衡微分方程确定各段控制面之间的剪力图和弯矩 图的形状，进而画出剪力图与弯矩图。
试画出：杆件的轴力图。 解：1 求约束反力
FRA A l
FRA
FRA
FRA F2 F1 5kN
2 求AB段轴力
FAB F1 l B F1 FBC F2 C
FAB FRA 5kN
3 求BC段轴力
FBC FRA F1 5 5 10kN
材料力学教材--内力与内力图
F1 1 kN F2 3 kN
例 最大剪力。
L 10 m d 1 m
求图示结构中梁的最大弯矩和
梁中弯矩图呈如图形状，故弯
RA RB
矩极大值出现在 C 截面或 D 截面。
设 C 截面到 A 端距离为 ， 可得 A 端支反力
L L d 1 RA F1 F2 37 4 L L 10 1 M C RA 37 4 2 故有 C 截面弯矩 10
C
YB 14 kN
m
F
0
X C 5 kN
X 0
X B 11 kN
例
画出结构的剪力和弯矩图。
F=5 2 kN/m XXF F
画剪力图
4m 4m
2 kN/m
E XE=8 YF=10 YF Y X XA =11 YEE=4CC=5 C XB B=11 B X =5
YA=4
4m 4m助 学 习 资 料
重 点 与 难 点
◆ 应透彻理解内力符号规定与外力的区别，尤其应熟练掌握轴力和
弯矩的正负规定。 ◆ 截面法是建立内力方程的最基本的方法，应熟练掌握。注意先将 未知内力设正，建立方程时，内力和外力在一起按理论力学的规则进 入方程。因此建立内力方程过程中事实上用了两套符号规定。 ◆ 但是在求某个指定截面的内力时，尽量用更简便的方法，不必通 过建立内力方程求解。 ◆ 计算梁横截面的内力时，应特别注意外力的方向与其引起的内力 符号的关系，以保证内力的正负号正确。 ◆ 正确地计算支座反力是绘制内力图的关键，应确保无误。利用平 衡方程求出支反力后，应进行校核。
例
画出结构的内力图。
A
P1 在 BC 段引起剪力和弯矩。
z
L
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
一、由外力直接绘制轴力图
例 5.4 力图。
解 根据外力直接绘制轴力图（见图5.18(b)），绘图分析过程及步骤如下。
从左向右绘制，始终取右边部分为研究体。
在截面A 有集中力F 1，使研究体拉伸变形，故轴力在此截面向正方向发生突变，轴力突变大小为集中力F 1大小，此时 F N =（0+500）N=500 N ；在AB 段没有外力，故轴力不变；在截面B 有集中力F 2，使研究体受拉伸变形，故轴力在此截面向正方向发生突变，轴力突变大小为集中力F 2大小,此时F N =（500+420）N=920 N ；在BC 段没有外力，故轴力不变；在截面C 有集中力F 3，使研究体受压缩变形，故轴力在此截面向负方向发生突变，轴力突变大小为集中力F 3大小，此时F N =(920-280)N=640 N ；在CD 段没有外力，故轴力不变；在截面D 有集中力F 4，使研究体受压缩变形，故轴力在此截面向负方向发生突变，轴力突变大小为集中力F 4大小，此时 F N =(640-800)N =-160 N ；在DE 段没有外力，故轴力不变；在截面E 有集中力，由于轴力曲线与轴线围成封闭图形，故轴力
（b ）
(a)
突变为0。
例5.5有一根阶梯轴受力如图5.19(a)所示，试绘制阶梯轴的轴力图。
图5.19
解从右向左绘制，始终取左变部分为研究体。
根据外力直接绘制轴力图（见图5.19(b)），绘图分析过程及步骤如下：
在截面A有集中力F1，使研究体压缩变形，故轴力在此截面向负方向发生突变，轴力突变大小为集中力F1大小,此时F N=（0-10）kN=-10 kN；在AB段有均匀分布载荷，使研究体受拉伸变形，故轴力以斜直线规律向正方向渐变，轴力渐变大小为均匀分布载荷大小，此时F N=（-10+10×2）kN=10 kN；在截面B没有力，故此截面轴力没有变化；在BC段没有外力，故轴力不变；在截面C有集中力F2，使研究体受拉伸变形，故轴力在此截面向正方向发生突变，轴力突变大小为集中力F2大小，此时F N=（10+10）kN=20 kN；在CD段没有外力，故轴力不变；在截面D有集中力，由于轴力曲线与轴线围成封闭图形，故轴力突变为0.
二、由外力直接绘制扭矩图
外力扭矩图
无外力
不变
集中力F P突变。
方向：右手螺旋法则，四指指向外力偶方向，拇指离开为正；
大小：集中力偶大小F P
均布力偶在分布力的起始和终止截面，扭矩没有突变。
以斜直线渐变。
方向：右手螺旋法则，四指指向外力偶方向，拇指离开为正；
大小：M q
制其力图。
图5.25
解从右向左绘制，始终取左部分为研究体。
根据外力偶直接绘制扭矩图，绘制分析过程及步骤如下：
在截面A有集中力偶M1，变形方向由右手螺旋法则判断，拇指背离截面，故扭矩在此截面向正方向发生突变，扭矩突变大小为集中力偶M1大小，此时m
kN
1
)1
0(•
=
+
=
x
M；在AB 段无外载荷，故扭矩不变；在截面B有集中力偶M2，变形方向由右手螺旋法则判断，拇指指向截面，故扭矩在此截面向负方向发生突变，扭矩突变大小为集中力偶M2大小此时M x=1-2=-1m
kN•；在BC段无外载荷，故扭矩不变；在截面C有集中力偶M3，变形方向由右手螺旋法则判断，拇指背离截面，故扭矩在此截面向正方向发生突变，扭矩突变大小为集中力偶M3大小m
kN
2
)3
1
(•
=
+
-
=
x
M；在CD段有无外载荷，故扭矩不变；在截面D有集中力，由于扭矩曲线与轴线围成封闭图形，故扭矩突变为零。
扭矩图如图5.25（b）所示。
M q
三、由外力直接绘制剪力图和弯矩图
剪力、弯矩与分布载荷间的关系
例5.10如图5.28(a)所示，简支梁AB，在C点承受集中载荷F=6 kN作用,跨度l=3 m，a，试绘制梁的力图。
2
m
解 （1）求支座反力。
取整段梁为研究对象，受力分析如图5.28(b)，由平衡条件得
0)(A =∑F M ⇒0B =⋅-⋅a F l F
解得
kN 4B =F
0=∑y F ⇒0B A =-+F F F
解得
kN 2A =F
（2）由外力直接绘制力图。
从A 截面开始，有一向上的集中力F A ，故在此截面剪力向上突变，突变大小等于F A ,弯矩没有变化；AC 段没有外力，故剪力在该段没有变化，由于剪力大于零，故在该段弯矩以斜直线规律向正向变化，从截面A 到截面C 弯矩变化大小为AC 段剪力与x 轴围成的面积即
m kN 4A •=•a F ；在截面C 有一向下的集中载荷F ，故在此截面剪力向下突变F ，弯矩没
有变化；在CB 段没有外力，故剪力在该段没有变化，由剪力小于零，则该段弯矩以斜直线规
律向负向变化，从截面C 到截面B 弯矩变化大小为CB 段剪力与x 轴围成的面积即
m kN 4)(B •=-•a l F 变为0。
例5.11 如图5.29(a)所示外伸梁，试计算其力并画出力图。
图5.29
解 （1）先求支座反力。
取整段梁研究，其受力如图5.29(a)，由平衡条件得
∑=-⋅+⋅⇒=020)(2
A B AB q AB F BC F F M
∑=⋅--+⇒=00B A y
AB q F F F F
解得
kN 35,kN 15B A ==F F
（2）由外力直接绘制力图。
从截面A 开始，有一向上的集中力F A ，故在此截面剪力向上突变，突变大小等于F A ,弯矩
没有变化；AB 段有向下的均布力系，故剪力在该段以斜直线规律向下渐渐变化，从截面A 到截面B 剪力值变化q AB ⋅，弯矩以开口向上的抛物线规律渐渐变化，在剪力为零的截面D 弯矩
为极值，从截面A 到截面D 变化值为小三角形面积
m kN 625.52
251515
215•=+⨯
⨯，从截面D 到截面B 变化大三角形面积
m kN 625.152
251525
225•=+⨯
⨯；在截面B 有一向上的集中力F B ，故在该截面剪力向上突变，突变大小等于F B 的大小，弯矩没有变化；BC 段没有外力，故
剪力在该段没有变化，由于剪力大于零，故该段弯矩以斜直线规律向正向变化，从截面C 到截面B 弯矩变化大小为BC 段剪力与x 轴围成的面积。
所绘力图如图5.29(b)、(c)所示。
（3）检查图形是否封闭。
例5.12 如图5.30(a)所示外伸梁，集中力F =10 kN ，均布载荷集度q =10 kN/m ，试利用剪力、弯矩与载荷集度的微分关系绘制出梁的剪力图、弯矩图。
图5.30
解：（1）求A 处约束力。
取整体研究，受力如图5.30(a)，建立平衡方程。
0)(A
=∑F M
⇒05.2D =⨯⋅-⋅-⋅BD q AC F AD F
解得
kN 5.17D =F
∑=+⋅--⇒=010D A y
F q F F F
解得
kN 5.2A =F
（2）由外力直接绘制力图。
从截面A 开始，有一向上的集中力F A ，故在此截面剪力向上突变，突变大小等于F A ,弯矩没有变化；AC 段没有外力，故剪力在该段没有变化，由于剪力大于零，则该段弯矩以斜直线规律向正向变化，从截面C 到截面B 弯矩变化大小为AC 段剪力与x 轴围成的面积；截面C 有一向下的集中力F ，故在此截面剪力向下突变，突变大小等于F 的大小,弯矩没有变化；CD 段没有外力，故剪力在该段没有变化，由于剪力小于零，则该段弯矩以斜直线规律向负向变化，从截面C 到截面D 弯矩变化大小为CD 段剪力与x 轴围成的面积; 截面D 有一向上的集中力F D ，故在此截面剪力向上突变F D ,弯矩没有变化；DB 段有向下的均布力系，故剪力在该段以斜直线规律向下渐渐变化，从截面D 到截面B 剪力值变化DB q ⋅，弯矩以开口向上的抛物线规律渐渐变化，在剪力为零的截面D 弯矩为极值，从截面D 到截面B 变化大小为小三角形面积。
（3）检查图形是否封闭。