拉氏变换练习题(14级)
第4章 拉氏变换作业参考答案

第四章 习题解4-1 根据拉氏变换定义,求下列函数的拉普拉斯变换。
(1)ate --1(2)()()t t 5cos 73sin 2+ (3)tet 3-(4)()t et5cos 4-(5)()[]tb e at --cos 1(6)()tett 22531-++(7)5232++t t (8)()te t 732--δ(9)()t Ω2cos (10)t t e e βα--- (11)()t et5cos 22-(12)()ϕω+t cos解:(1))(111]1[a s s a s s e L at +=+-=-- (2)()()2579657323]5cos 73sin 2[222222+++=+++⨯=+s s s s s s t t L (3)23)3(1][+=-s et L t(4)())](21[)](21[]5cos [)54()54(45544t j t j t t j t j t te e e jL e e e j L t eL --+-----+=+= 25)4(5)541541(212++=+++-+=s j s j s j (5)()[]()]cos []cos 1[at e e L e at L t b t b tb ----=-22)(1ab s a b s ++++=(6)由于1!][+=n ns n t L ,由s 域频移特性得()]53[]531[222222t t t t e t te e L e t t L ----++=++ 3232)2(207)2(10)2(3)2(1+++=+++++=s s s s s s (7)32232526526]523[ss s s s s t t L ++=++=++ (8)()732]32[7+-=--s et L tδ(9)()()22242121]2cos 2121[]cos [Ω+⋅+=Ω+=Ωs ss t L t L (10)))((11][βααββαβα++-=+-+=---s s s s e eL t t(11)在(9)的计算结果基础上由s 域频移特性得()25)2(221)2(21]5cos [222+++⋅++=-s s s t e L t (12)()]sin sin cos cos []cos [ϕωϕωϕωt t L t L -=+222222s i n c o s s i n c o s ωϕωϕωϕωωϕ+-=+-+=s s s s s4-7 求下列函数的拉普拉斯反变换。
第二章_Laplace变换(答案)

积分变换练习题 第二章 Laplace 变换________系_______专业 班级 姓名______ ____学号_______§1 Laplace 变换的概念 §2 Laplace 变换的性质一、选择题1.设()(1)t f t e u t -=-,则[()]f t =L [ ](A )(1)1s e s --- (B )(1)1s e s -++ (C )1s e s -- (D )1se s -+11[(1)][()];1[(1)](1)ss t s u t e u t se e u t s e --+⎛⎫-== ⎪ ⎪ ⎪-= ⎪+⎝⎭由延迟性质可得,再由位移性质可得,L L L2.设2sinh ()tf t t =,则[()]f t =L [ ] (A )1ln 1s s -+ (B )1ln 1s s +- (C )12ln 1s s -+ (D )12ln 1s s +-见课本P84二、填空题1.设2()(2)f t t u t =-,则[]()f t =L。
22''222321[(2)][()];1442[(1)]ss s s u t e u t se s s t u t se s e -⎛⎫-== ⎪ ⎪++ ⎪⎛⎫-== ⎪ ⎪⎝⎭⎝⎭由延迟性质可得,再由象函数的微分性质P83(2.7)可得,L L L 2.设2()t f t t e =,则[]()f t =L。
(1)00''231[](Re()1);112[]1(1)t t st s t te e e dt e dt s s t e s s +∞+∞---⎛⎫===> ⎪- ⎪ ⎪⎛⎫== ⎪ ⎪--⎝⎭⎝⎭⎰⎰再由象函数的微分性质P83(2.7)可得,L L 三、解答题1.求下列函数的Laplace 变换:(1)302()12404t f t t t ≤<⎧⎪=-≤<⎨⎪≥⎩242242422402[()]()3(1)33334ststst st st s s s s s f t f t e dt e dt e dte e e e e e e s s s s s s s+∞----------==+--+=+=-++-=-⎰⎰⎰L(2)3,2()cos ,2t f t t t ππ⎧<⎪⎪=⎨⎪>⎪⎩20222222()22202222[()]()3cos 3333,cos cos()sin 2133[()].1stst st sst stst s s sts ssf t f t e dt e dt te dtee e dt ss se te dt ed ee d s e ef t s s sπππππππτππττππππττττ+∞+∞--------=+∞+∞+∞-+-----==+==-+-=+=-=-+=--++⎰⎰⎰⎰⎰⎰⎰,从而L L(3)()sin2tf t = 222002[()]sin 2sin .241t st s t f t e dt e d s ττττ=+∞+∞--===+⎰⎰L(4)()cos ()sin ()f t t t t u t δ=⋅-⋅200[()][cos ()sin ()]cos ()sin ()1cos sin 1.1st stst stst t f t t t t u t e dtt t e dt t u t e dttete dt s δδ-+∞-+∞+∞--+∞--==⋅-⋅=⋅-⋅=-=-+⎰⎰⎰⎰L2.求以2b 为周期的函数1,0()1,2t bf t b t b<≤⎧=⎨-<≤⎩的Laplace 变换。
拉普拉斯变换(改)

拉普拉斯变换1. 当系统函数)(s H 的极点位于 时,)(t h 绝对可积,系统稳定。
A 、左半平面 B 、右半平面C 、虚轴D 、实轴2011-2012期末卷B2、当系统函数为()()231KH s s K s =+-+时,K 满足 系统稳定。
A 、1K < B 、3K > C 、03K << D 、3K < 2012-2013期末卷A3. 一个连续LTI 因果系统稳定(不包括临界稳定)的条件不包括( ) A .有界输入产生有界输出 B .()h t dt M∞-∞≤⎰,M 为有界正值C .s 平面的右半平面没有极点D .lim ()0t h t →∞=4.某系统的系统函数21()32H s s s K=++-,则常数K 取值范围为( )时系统稳定。
A .2K < B .2K >- C .2K <- D .2K > 5. 如图1所示,电路中()s e t 、()s i t 表示激励源,()u t 、()i t 表示电路的响应,图中a 的网络函数为( ),图中b 的网络函数为( )。
()s e t 1Ω()s i t 1Ω图1A. 211s s s +++B.211s s s +++ C. 2211s ss s ++++D. 221s s s s+++6.象函数()()2211+=+s F s s 的初值()0+f 为( ) A 、0B 、1C 、2D 、37.如果一个因果线性时不变系统的系统函数()H s 的所有极点的实部都小于零,则( ) A 、系统为非稳定系统 B 、()h t <∞ C 、系统为稳定系统D 、()00h t dt ∞=⎰8.象函数()()2211+=+s F s s 的终值()f ∞为( ) A 、0B 、1C 、2D 、39.因果系统的系统函数为()2232H s s s =++,则该系统是( )A 、稳定的B 、不稳定的C 、临界稳定的D 、不确定10. 函数()1t t e e αββα----的拉氏变换为( )A 、11s s αβ+++ B 、s s βα++ C 、s s αβ++D 、()()1s s αβ++11. 象函数()22125s s s s +++的终值为( )A 、0B 、1C 、15D 、1212. 函数sin 2cos t t +的拉氏变换为( ) A 、2211s s ++ B 、()2211s s ++ C 、21s s ++ D 、211s s ++ 13. 象函数231056s s s +++的初值为( ) A 、0B 、3C 、53D 、8514.0cos ()t t ωε的拉氏变换为( )。
拉氏变换详解

3
证:根据拉氏变换的定义有
L[ f (t )] f (t )e dt s f (t )e dt f (t )e
2t
cost 3e
2t
sin t
18
(3)情况3:F(s)有重极点,假若F(s)有L重 极点 p1 ,而其余极点均不相同。 那么
bl bl 1 M (s) b1 F (s) l l 1 D( s ) ( s p1 ) ( s p1 ) s p1 cl 1 cn s pl 1 s pn M (s) 式中b l [ ( s p1 ) l ]s p1 D( s) d M ( s) l bl 1 [ ( s p1 ) ] ds D( s ) s p1
依次类推,可以得到原函数n阶导数的拉氏 变换 L[ f n (t )] s n F (s) s n1 f (0) s n2 f (0) f n1 (0)
4
(3)积分性质
若 L[ f (t )] F ( s )
1
则
式中 f
F ( s) f (0) L[ f (t )dt] s s
19
, bl i
1 d M (s) l { [ ( s p1 ) ]}s p1 i! ds D( s )
l 1
i
1 d M (s) l b1 { [ ( s p1 ) ]}s p1 (l 1)! ds D( s ) 系数cl 1 , , cn , 仍按以前的方法计算
拉氏变换习题集1 (1)(1)

因此r1Leabharlann t2 3et
1 3
e3t
u
t
r2
t
1 3
et
1 3
e3t
u
t
拉普拉斯变换应用
12.已知
r"(t) 5r' (t) 6r(t) 2e' (t) 8e(t),(t) etu(t),r(0 ) 3,r '(0 ) 2
dt
s2 1
s2 1
t d costu(t) d ( s2 ) 2s
dt
ds s2 1 (s2 1)2
5
拉普拉斯变换
4. 求函数 sin tu(t ) 的拉氏变换
解:
sin tu(t ) sin(t )u(t )
sin tu(t ) 1 es
s2 1
6
拉普拉斯变换
a. 解:
t cos t
t cos cost t sin sin t
s cos s2 2
'
s2
sin 2
'
s2 2 cos 2s sin
s2 2 2
4
拉普拉斯变换
3. 求函数 t d cos tu(t) 的拉氏变换 dt
解:
cos tu(t)
s s2 1
d costu(t) s s f (0 ) s2
2r1 (t )
r2
(t )
e(t )
r1 (t )
dr2 (t) dt
2r2 (t)
0
解:对方程组两边应用单边拉式变换得
sR1 s r1(0 ) 2R1 s R2 s 1 s
R1
s
sR2
s
r2
(0
拉氏变换习题课
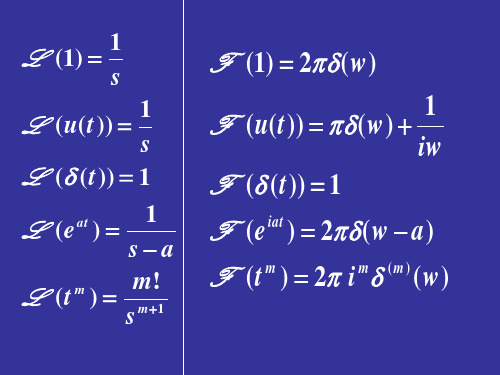
2.( 4 )因为L f ( t) = F ( s) , 由相似性质,有 t L f = aF ( as) a 在利用位移性质, - at t L e f = aF ( as)|s→s+ a s→s+ a = aF ( a(s+ a)
3.
(1)因为(由位移性质)L
s + w0
2 2
|s=β +iw =
β + iw
(β + iw) + w0
2 2
5) f (t ) = e u(t t0 )
iw0t
解: (e u(t t0 ) = F(u(t t0 ) |w→ww ) ) F
iw0t
0
1 ) = e ( + πδ(w)|w→ww iw 1 it ( ww ) ( =e + πδ(w w0 )) i(w w0 )
s2t
s s 1 11 s =L 2 2 2 (10) L 2 2 ( s +1)( s + 4) 3 s +1 s + 2 1 1 s 1 1 s 1 1 L 2 L 2 2 = cost cos2t 3 3 s +1 3 s + 2 3
p100 3.( 2) L
)=
)
u
(t)
L
( f(t)) = L
1 ( u (t)) = s
i 1 snt 2.(1)因为 ct , , L = ar an s 所以由相似性质 有 t 1 1 ar an , ct s a a 1 snat 1 i a 即 L ct = aar an s, a t i a snat 所以 L ct = ar an s t i snat L = at
拉氏变换习题课

at
F (1) 2 ( w )
1 F ( u( t )) ( w ) iw F ( ( t )) 1
F (e ) 2 ( w a )
te- 3tsi 4 由积分性质,L n2tdt 0 1 1 4 s+ 3 - 3t = L te si n2t 2 2 s s s+ 3 + 4
t
1 利用象函数的微分性质,有
sinkt ∞ L = s L sinkt ds= t ∞ k s∞ π s s s s2 + k 2 ds= arctan k |s = 2 - arctan k = arccotk
p100 2.求下列函数的Lapl ace逆变换:
2 F s =
s
s- a s- b
1 a b a - b s- a s- b b aeat - bebt 1 s- b = a - b
st
解:A 部分分式法 : F s = 1 1 L F s = a- b L
e- 3tsin2t ∞ e- 3tsin2t ds 2L = s L t ∞ 2 s+ 3 = ds= arccot 2 2 s (s+ 3) + 4 2
3
f t tL
-1
F s dt s 1 1 -1 2 2 s - 1
bs a
s F ( )) a
拉氏变换详解

t
t
t时,f1 (t ) 1(t ) 0 f1 (t ) f 2 ( )d f1 (t ) 1(t ) f 2 ( )d
0 0
10
t
L[ f 1 (t ) f 2 ( ) d ]
0 t
f 2 ( ) d f 1 ( )e
0 0
s ( )
d d F2 ( s ) F1 ( s )
11
f 2 ( )e
0
s
d f 1 ( )e
0变换
1. 定义:从象函数F(s)求原函数f(t)的运算 1 L [ F ( s )] 。 称为拉氏反变换。记为 由F(s)可按下式求出 1 C j 1 st f (t ) L [ F ( s)] F ( s )e ds(t 0) 2 j C j 式中C是实常数,而且大于F(s)所有极点的 实部。 直接按上式求原函数太复杂,一般都用查 拉氏变换表的方法求拉氏反变换,但F(s)必 12 须是一种能直接查到的原函数的形式。
0
0 st 0
等式两边对s趋向于0取极限
st 左边 lim f ( t ) e dt lim f ( t ) e dt s 0 s 0
f (t ) dt f (t ) 0 lim f (t ) f (0) t
0
右边 lim [ sF ( s ) f (0)] lim sF ( s ) f (0) s 0 s 0 lim f (t ) lim sF ( s ) t s 0
0
0
0
