初三(上)数学提优练习一
九年级数学提优练习题一 试题

轧东卡州北占业市传业学校江都区九年级数学提优练习题一〔〕 教1、把二次根式1(x-1)1x-中根号外的因式移到根号内,结果是__________。
2、观察:11111112,23,34, (334455)+=+=+=请你将发现的规律用含字母表示出来 。
3.假设最简二次根式1a +与42a -是同类二次根式,那么a 的值为 。
4. 假设整数m 满足条件2)1(+m =1+m 且m <52,那么m 的值是 .5.= 。
6、=⎪⎭⎫ ⎝⎛-⎪⎪⎭⎫ ⎝⎛+-=+=x y y x 11111313,则, .7.51=-aa ,那么 aa 1-的值= 。
8. 当x 取______时,2-x -5的值最大,最大值是________. 9.23231+-与的关系是 . 10.如果524-+=+b a b a ,那么b a 2+=___________。
11.假设a <0,那么a a -2= ;假设b <0,化简b a b ab a 32+= 。
12.21+=m ,21-=n ,那么代数式mn n m 322-+的值为 。
13.假设201120121m =-,那么54322011m m m --的值是 .14.a b 、为有理数,m n 、分别为57的整数局部和小数局部,且21amn bn +=,那么2a b += 。
15. 以下各式计算正确的选项是〔 〕A .33431163116=⋅= B . a a a a a --=-⋅--=--111)1(11)1(2〔a <1〕C .53232333=+=+ D .2321321=-++16.计算:①.x x x x 3)1246(÷- ②. abb a ab b 3)23(235÷-⋅ ③.(3 2 -2 3 )2-(3 2 + 2 3 )2④.3〕17、:实数a ,b 在数轴上的位置如下列图a b -18、假设x ,y 为实数,且y =x 41-+14-x +21,求xy y x ++2 -xy y x+-2的值。
初三数学上学期提优1
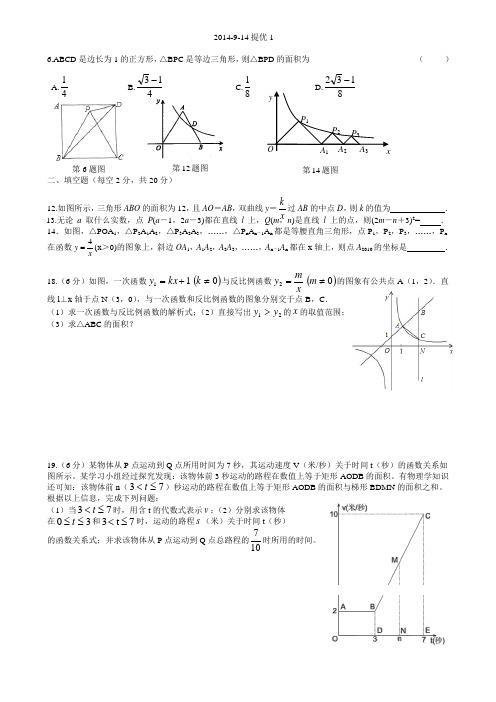
第6题图 第12题图 第14题图2014-9-14提优16.ABCD 是边长为1的正方形,△BPC 是等边三角形,则△BPD 的面积为 ( )A.41 B.413- C.81132-二、填空题(每空2分,共20分)12.如图所示,三角形ABO 的面积为12,且AO =AB ,双曲线y =x k 过AB 的中点D ,则k 的值为 . 13.无论a 取什么实数,点P (a -1,2a -3)都在直线l 上,Q (m ,n )是直线l 上的点,则(2m -n +3)2= .14.如图,△POA 1,△P 2A 1A 2,△P 3A 2A 3,……,△P n A n -1A n 都是等腰直角三角形,点P 1,P 2,P 3,……,P n在函数xy 4=(x >0)的图象上,斜边OA 1,A 1A 2,A 2A 3,……,A n -1A n 都在x 轴上,则点A 2010的坐标是 .18.(6分)如图,一次函数11+=kx y ()0≠k 与反比例函数xm y =2()0≠m 的图象有公共点A (1,2).直线l ⊥x 轴于点N (3,0),与一次函数和反比例函数的图象分别交于点B ,C .(1)求一次函数与反比例函数的解析式;(2)直接写出21y y >的x 的取值范围;(3)求△ABC 的面积?19.(6分)某物体从P 点运动到Q 点所用时间为7秒,其运动速度V (米/秒)关于时间t (秒)的函数关系如图所示。
某学习小组经过探究发现:该物体前3秒运动的路程在数值上等于矩形AODB 的面积。
有物理学知识还可知:该物体前n (73≤<t )秒运动的路程在数值上等于矩形AODB 的面积与梯形BDMN 的面积之和。
根据以上信息,完成下列问题:(1)当73≤<t 时,用含t 的代数式表示v ;(2)分别求该物体在30≤≤t 和3t 7<≤时,运动的路程s (米)关于时间t (秒)的函数关系式;并求该物体从P 点运动到Q 点总路程的710时所用的时间。
初三数学提优测试卷

考试时间:120分钟满分:100分一、选择题(每题5分,共30分)1. 若实数a、b满足a + b = 2,则a^2 + b^2的最小值为:A. 2B. 4C. 6D. 82. 下列各数中,不是无理数的是:A. √3B. πC. 2.5D. √-13. 若x^2 - 4x + 4 = 0,则x的值为:A. 2B. -2C. 4D. -44. 在直角坐标系中,点P(3,4)关于x轴的对称点坐标为:A.(3,-4)B.(-3,4)C.(-3,-4)D.(3,-4)5. 若a、b、c是等差数列,且a + b + c = 15,则abc的最大值为:A. 15B. 20C. 25D. 30二、填空题(每题5分,共20分)6. 若sinα = 0.8,则cosα的值为______。
7. 二项式(x - 2)^5的展开式中,x^3的系数为______。
8. 若等腰三角形的底边长为8,腰长为10,则其面积为______。
9. 在△ABC中,∠A = 60°,∠B = 45°,则∠C的度数为______。
10. 若a、b、c、d是等比数列,且a + b + c + d = 16,则b的值为______。
三、解答题(每题15分,共45分)11. 解方程:2x^2 - 5x - 3 = 0。
12. 已知函数f(x) = x^2 - 4x + 3,求函数f(x)的对称轴和顶点坐标。
13. 在等腰三角形ABC中,AB = AC,∠B = 40°,求∠C的度数。
四、应用题(25分)14. 小明家准备装修客厅,客厅长为5米,宽为4米。
装修公司提供两种方案:方案一:铺满客厅的地面,每平方米需花费100元。
方案二:铺满客厅的地面,每平方米需花费80元,但需在四角各增加一个面积为1平方米的装饰区域。
(1)请计算两种方案的总花费。
(2)若小明家希望总花费不超过4000元,请问他应选择哪种方案?(3)请分析两种方案在美观和实用性方面的优缺点。
苏科版九年级上册 第1章 一元二次方程 专题提优复习训练含答案

苏科版九年级上册一元二次方程章节专题提优复习训练专题一:一元二次方程的求值问题1,关于X的一元二次方程一—一+2/W-1=0的两个实数根分别是芭、x2,且xj+w、?,则(X)-x2)2的值是.2.若公+工―1=0,那么代数式丁+2/_7的值是.3.已知是方程/—3x-4=0的两个实数根,则/+明—3a的值为.4.设a、P是方程。
+1)(工一4)=一5的两实数根,则2-+鼻■= _ .aP5.已知w是方程/+2016x+7=0的两个根,则(m2+2015/?I+6)(H2+2017〃+8)=.6.若冷々是方程/一2%-4=0的两个不相等的实数根,则代数式2芭2-2玉+4+3的值是.7.已知a、夕是方程/_尸1=0的两个实数根,则代数式相+2,_2)的值为.8.关于龙的一元二次方程x2-〃a+5(m-5)=0的两个正实数根分别为%,%2,且2$+/=7,则小的值为.9.设修、心是方程—+4X—3=0的两个根,且2耳(工;+5々一3)+〃=2,贝lja=.10.设不々是方程f+x-3=0的两个根,那么x;-4々2+19的值等于.参考答案1.132.-63.04.475.20086.197.08.2或69.810.0专题二:一元二次方程的系数陷阱问题1.关于尤的一元二次方程(2-。
"+1+/-4=0的一个根为0,贝的值为()A.2B.0C.2或-2D.-22.若关于尤的方程(攵-1),+2>1=0有实数根,则Z的取值范围是()A.女20且攵wlB.女W0且攵wlC.Zr>0D.k>03.已知关于x的一元二次方程(〃-l»2—2x+3=0有实数根,则整数。
的最大值是()A.2B.1C.0D.-14.关于x的方程〃浦-2(3l)x+91=0有实数根,则m的取值范围是.5.关于x的一元二次方程立-2元-1=0有两个不相等的实数根,4的取值范围是.6.已知关于x的一元二次方程(2-2)2/+(2攵+1h+1=0有两个不相等的实数根,则偶数A 的最小值为.7.若关于x的一元二次方程(加-1)/+x+/+23=0有一个根为0,则〃?的值是.8.若关于x的一元二次方程(〃+1)/+1+42-1=。
湘教版-数学-九年级上册-数学第一章反比例函数单元提优
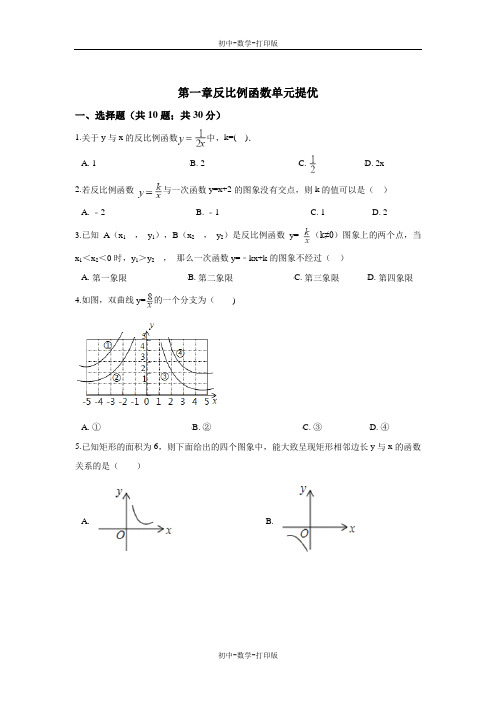
第一章反比例函数单元提优一、选择题(共10题;共30分)1.关于y与x的反比例函数中,k=( ).A. 1B. 2C.D. 2x2.若反比例函数与一次函数y=x+2的图象没有交点,则k的值可以是()A. ﹣2B. ﹣1C. 1D. 23.已知A(x1,y1),B(x2,y2)是反比例函数y= (k≠0)图象上的两个点,当x1<x2<0时,y1>y2,那么一次函数y=﹣kx+k的图象不经过()A. 第一象限B. 第二象限C. 第三象限D. 第四象限4.如图,双曲线y=的一个分支为()A. ①B. ②C. ③D. ④5.已知矩形的面积为6,则下面给出的四个图象中,能大致呈现矩形相邻边长y与x的函数关系的是()A. B.C. D.6.已知A(﹣5,m2),B(﹣2,a),C(﹣0.5,b),D(4,c)都在反比例函数y= 的图象上,则下列判断正确的是()A. m2最大B. a最大C. b最大D. c 最大7.如图所示,已知A(,y1),B(2,y2)为反比例函数y= 图象上的两点,动点P(x,0)在x轴正半轴上运动,当线段AP与线段BP之差达到最大时,点P的坐标是()A. (,0)B. (1,0)C. (,0)D. (,0)8.反比例函数y=的图象如图所示,点M是该函数图象上一点,MN⊥x轴,垂足是点N,如果S△MON=2,则k的值为()A. 2B. -2 C. 4 D. -49.某公司计划新建一个容积V(m3)一定的长方体污水处理池,池的底面积S(m2)与其深度h(m)之间的函数关系式为,这个函数的图象大致是()A. B.C. D.10.反比例函数y=的图象位于平面直角坐标系的()A. 第一、三象限B. 第二、四象限C. 第一、二象限D. 第三、四象限二、填空题(共8题;共24分)11.已知反比例函数y= ,当x>3时,y的取值范围是________.12.正比例函数y1=k1x和反比例函数y2= 交于A、B两点.若A点的坐标为(2,1),则B点的坐标为________.13.如图,已知在平面直角坐标系xOy中,O是坐标原点,点A是函数y= (x<0)图象上一点,AO的延长线交函数y= (x>0,k>0的常数)的图象于点C,点A关于y轴的对称点为A′,点C关于x轴的对称点为C′且点O、A′、C′在同一条直线上,连接CC′,交x轴于点B,连接AB,AA′,A′C′,若△ABC的面积等于6,则由线段AC,CC′,C′A′,A′A所围成的图形的面积等于________.14.将油箱注满k升油后,轿车行驶的总路程S(单位:千米)与平均耗油量a(单位:升/千米)之间是反比例函数关系S= (k是常数,k≠0).已知某轿车油箱注满油后,以平均耗油量为每千米耗油0.1升的速度行驶,可行驶760千米,当平均耗油量为0.08升/千米时,该轿车可以行驶________千米.15.如图,在平面直角坐标系xOy中,反比例函数y= 的图象与一次函数y=k(x﹣2)的图象交点为A(3,2)与B点.若C是y轴上的点,且满足△ABC的面积为10,则C点坐标为________.16.如图,已知双曲线y= 与直线y=﹣x+6相交于A,B两点,过点A作x轴的垂线与过点B作y轴的垂线相交于点C,若△ABC的面积为8,则k的值为________17.如图,点A在反比例函数y= (x>0)图象上,且OA=4,过A作AC⊥x轴,垂足为C,OA的垂直平分线交OC于B.则△ABC的周长为________.18.若一个正比例函数的图象与一个反比例函数图象的一个交点坐标是(2,3),则另一个交点的坐标是________.三、解答题(共6题;共46分)19.当m取何值时,函数是反比例函数?20.已知y与成反比例,且x=4时,y的值为,求y与x之间的函数关系.21.如图,一次函数y=kx+b的图象与x轴交于点A,与反比例函数y= (x>0)的图象交于点B(2,n),过点B作BC⊥x轴于点C,点P(3n﹣4,1)是该反比例函数图象上的一点,且∠PBC=∠ABC,求反比例函数和一次函数的表达式.22.如果函数是反比例函数,求函数的解析式.23.如图,在平面直角坐标系中,已知等边△OAB的顶点A在反比例函数y= (x>0)图象上,当等边△OAB的顶点B在坐标轴上时,求等边△OAB顶点A的坐标和△OAB的面积.24.如图,反比例函数y=(x>0)的图象经过点A(2,1),直线AB与反比例函数图象交与另一点B(1,a),射线AC与y轴交于点C,∠BAC=75°,AD⊥y轴,垂足为D.(1)求反比例函数的解析式;(2)求tan∠DAC的值及直线AC的解析式.参考答案一、选择题1.C2.A3.C4.D5.A6. C7.D8.D9.C 10.A二、填空题11. 0<y<2 12.(﹣2,﹣1)13.10 14.95015.(0,1)或(0,﹣9)16.5 17.2 18.(﹣2,﹣3)三、解答题19.解:∵函数是反比例函数,∴2m+1=1,解得:m=0.20.解:(1)设y= ,将x=4,y=﹣代入解析式,∴﹣= ,∴k=﹣,∴y与x之间的函数关系式为21.解:∵点B(2,n)、P(3n﹣4,1)在反比例函数y= (x>0)的图象上,∴.解得:m=8,n=4.∴反比例函数的表达式为y= .∵m=8,n=4,∴点B(2,4),(8,1).过点P作PD⊥BC,垂足为D,并延长交AB与点P′.在△BDP和△BDP′中,∴△BDP≌△BDP′.∴DP′=DP=6.∴点P′(﹣4,1).将点P′(﹣4,1),B(2,4)代入直线的解析式得:,解得:.∴一次函数的表达式为y= x+322.解:∵是反比例函数,∴2k2+k﹣2=﹣1,解得:k1=,k2=﹣1,∴函数的解析式为:y=或y=.23.解:当点B在x轴上时,如图1,作AC⊥OB于C,∵△AOB是等边三角形,设OC=x,∴AC= x,∴A(x,x),∵顶点A在反比例函数y= (x>0)图象上,∴x• =4 ,∴x=2,∴A(2,2 );当点B在y轴上时,如图2,作AC⊥y轴于C,∵△AOB是等边三角形,设OC=y,∴AC= y,∴A(y,y),∵顶点A在反比例函数y= (x>0)图象上,∴y•y=4 ,∴y=2,∴A(2 ,2);S△AOB=2××4 =4 .24.解:(1)由反比例函数y=(x>0)的图象经过点A(2,1),得:k=2×1=2,∴反比例函数为y=(x>0),(2)作BH⊥AD于H,如图1,把B(1,a)代入反比例函数解析式y=(x>0),得a=2,∴B点坐标为(1,2),∴AH=2﹣1,BH=2﹣1,∴△ABH为等腰直角三角形,∴∠BAH=45°,∵∠BAC=75°,∴∠DAC=∠BAC﹣∠BAH=30°,∴tan∠DAC=tan30°=;∵AD⊥y轴,∴OD=1,AD=2,∵tan∠DAC==,∴CD=2,∴OC=1,∴C点坐标为(0,﹣1),设直线AC的解析式为y=kx+b,把A(2,1)、C(0,﹣1)代入得,解,∴直线AC的解析式为y=x﹣1;初中-数学-打印版初中-数学-打印版。
苏教版九年级上 数学一元二次方程提优测试

初三数学培优讲义例1、 若,28,1422=++=++x xy y y xy x 则=+y x ___________。
练习1、方程1)1(32=-++x x x 的所有整数解的个数是 ( )A 、2B 、3C 、4D 、5例2、已知实数x,y 满足3,3242424=+=-y y x x ,则444y y +的值为( )A 、7B 、2171+C 、2137+D 、5例3【实际背景】 预警方案确定:设克玉米价格当月的克猪肉价格当月的500500=W .如果当月W <6,则下个月...要采取措施防止“猪贱伤农”. 【数据收集】 今年2月~5月玉米、猪肉价格统计表【问题解决】(1)若今年3月的猪肉价格比上月下降的百分数与5月的猪肉价格比上月下降的百分数相等,求3月的猪肉价格m ;(2)若今年6月及以后月份,玉米价格增长的规律不变,而每月的猪肉价格按照5月的猪肉价格比上月下降的百分数继续下降,请你预测7月时是否要采取措施防止“猪贱伤农”;(3)若今年6月及以后月份,每月玉米价格增长率是当月猪肉价格增长率的2倍,而每月的猪肉价格增长率都为a ,则到7月时只用5.5元就可以买到500克猪肉和500克玉米.请你预测8月时是否要采取措施防止“猪贱伤农”.例4、如图,已知点A 从(1,0)出发,以1个单位长度/秒的速度沿x 轴向正方向运动,以O 、A 为顶点在x 轴的上方作菱形OABC ,且∠AOC =60º;同时点G 从点D (8,0)出发,以2个单位长度/秒的速度沿x 轴向负方向运动,以D 、G 为顶点在x 轴的上方作正方形DEFG .设点A 运动了t 秒.求:(1)点B 的坐标(用含t 的代数式表示);(2)当点A 在运动的过程中,当t 为何值时,点O 、B 、E 在同一直线上;(3)当点A 在运动的过程中,是否存在t ,使得以点C 、G 、D 为顶点的三角形为等腰三角形?若存在,求出t 的值;若不存在,请说明理由.月 份2 3 4 5 玉米价格(元/500克)0.7 0.8 0.9 1 猪肉价格(元/500克)7.5 m 6.25 6 1G F E D C B A Ox yA B D C P Q M N练习:1.受季节影响,某种商品每件按原售价降价10%后,又降价a 元,现在每件的售价为b 元,那么该商品每件的原价为 ( ) A.110%a b +-元 B.(1-10%)(a+b) C.110%b a --元D.(1-10%)(a-b)2、一个跳水运动员从10米高台上跳水,他每一时刻所在的高度(单位:米)与所用时间(单位:秒)的关系式是)1)(2(5+--=t t h ,求运动员从起跳到入水所用的时间是 ( )A 、-5秒B 、1秒C 、-1秒D 、2秒3、设c b a 、、为互不相等的非零实数,求证:三个方程02,02,02222=++=++=++b ax cx a cx bx c bx ax 不可能都有两个相等的实数根。
初中九年级上数学提优测试(一)试题卷

初中九年级上数学提优测试(一)试题卷一.选择题(共9小题,每小题3分,共27分) 1.若a b <,则下列不等式正确的是( ) A .1a b< B .22ac bc < C .b a -<- D .0b a -<2.若a 、b 是一元二次方程2360x x +-=的两个不相等的根,则23a b -的值是( ) A .15B .15-C .3-D .33.轮船在静水中的航速为40/km h ,它以该航速沿河顺流航行100km 所用时间,和它以该航速沿河逆流航行80km 所用时间相等,设河水的流速/vkm h ,则可列方程为( ) A .100804040v v =+- B .100804040v v =+- C .100804040v v =-+ D .100804040v v=-+ 4.在ABC ∆中,6AC =、8BC =,10AB =,用尺规作图的方法在BC 上确定一点P ,设PC x =,下列作图方法中,不能求出PC 的长的作图是( )A .B .C .D .5.如图,点E 是菱形ABCD 对角线BD 上任一点,点F 是CD 上任一点,连接CE ,EF 当45ABC ∠=︒,10BC =时,CE EF +的最小值是( )A .10B .5C .102D .26.如图,在坐标系中,平行四边形OABC 的边OA 在x 轴的正半轴上,反比例函数(0)ky x x=>的图象经过对角线OB 的中点D 和顶点C .若平行四边形OABC 的面积为12,则k 的值为( ) A .6 B .5C .4D .3CAP7.一次函数1y mx n =+与2y x a =-+的图像如图所示, 则0mx n x a <+<-+的解集为( ) A .23x << B .2x <C .3x >D .02x <<8.如图,已知:在矩形ABCD 中,AD=2,AB =3,点E 、F 分别是AD 的中点和AB 边上的动点,连接EF ,并把△AEF 沿着EF 对折得△GEF ,当F 点从点A 运动至B 时,点G 的运动的轨迹长为( ) A .2πB .32π C .无法计算 D .π9.利用学过的绝对值知识,可将函数23||2y x x =-+转化为y=x 2-3x+2(x ≥0)或y=x 2+3x+2(x ≤0)则下列结论中正确的有( )①当2x >时,y 随x 增大而增大; ②此函数图象有两条对称轴;③函数图象中两个最低点之间的距离为3;④当23||20x x -+<时,x 的取值范围是21x -<<-或12x <<. A .①②③B .①③④C .①③D .③④二.填空题(共5小题,每小题4分,共20分) 10.2019331(1)64|223|()2--+-= .11.已知x ,y ,z 是ABC ∆的三边,且满足2222xy x yz z +=+,则ABC ∆的形状是 .12.小天想要计算一组数据92,90,94,86,99,85的方差20s ,在计算平均数的过程中,将这组数据中的每一个数都减去90,得到一组新数据2,0,4,4-,9,5-,记这组新数据的方差为21s ,则21s 20s (填“>”,“ =”或” <” )GECBD13.在平面直角坐标系中,已知点(3,0)A ,(0,4)B ,将BOA ∆绕点A 按顺时针方向旋转得CDA ∆,连接OD .当DOA OBA ∠=∠时,OD 的长为_______,点D 的坐标为______. 14.四边形ABCD 内接于圆,∠DAB =60°,弦AD =AB ,弦CD 和弦BC 的和为4,则AC 两点的距离为_________,四边形ABCD 的面积为__________.第13题图 第14题图三.解答题(共4小题,满分33分) 15.(7分)先化简再求值:若2a =-,求221(1)1a a a a -÷---的值.16.(8分)2019年1月,旨在加强生活垃圾分类管理,提高生活垃圾减量化、资源化、无害化处理水平及推进生态文明建设的《海宁市生活垃圾分类管理办法》开始施行.为了了解居民对生活垃圾分类相关知识的了解程度,某社区随机抽取了部分本社区居民进行调查,并绘制了如下统计图(不完整)(1)接受调査的总人数为 人,并请补全条形统计图; (2)在扇形统计图中,“了解一点”部分扇形的圆心角是 ︒;(3)若该社区总共有8000名居民,请你估计其中对生活垃圾分类相关知识“了解一点”和“完全不了解”的总人数.ABDC17.(8分)大学生小王相应国家“自主创业”的号召,利用银行小额无息贷款开办了一家饰品店.该店购进一种今年新上市的饰品进行销售,饰品的进价为每件40元,售价为每件60元,每月可卖出300件.市场调查反映:调整价格时,售价每涨1元每月要少卖10件;售价每下降1元每月多卖20件.为获得更大的利润,现将饰品售价调整为60x -(元/件)(0x >即售价下降,0x <即售价上涨),每月饰品销量为y (件),月利润为w (元). (1)求y 与x 之间的函数关系式;(2)如何确定销售价格才能使月利润最大?求最大月利润;18.(10分)我们定义:有一组对角相等而另一组对角不相等的凸四边形叫做“等对角四边形”.(1)已知:如图1,四边形ABCD 是“等对角四边形”, A C ∠≠∠,75A ∠=︒,85D ∠=︒,则C ∠= .(2)已知:在“等对角四边形” ABCD 中,60DAB ∠=︒,90ABC ∠=︒,4AB =,3AD =.求BC 的长.(3)已知:如图2,在平面直角坐标系xOy 中,四边形ABCD 是“等对角四边形”,其中(2,0)A -、(2,0)C 、(1,3)B --,点D 在y 轴上,抛物线2(0)y ax bx c a =++<过点A 、D ,且当-2≤x ≤2时,函数2y ax bx c =++取最大值为3,求二次项系数a 的值.。
九年级数学提优练习(1)

BD1若直角三角形的两直角边长为a 、b ,且满足,则该直角三角形的斜边长为 .2如图,将菱形纸片ABCD 折叠,使点A 恰好落在菱形的对称中心O 处,折痕为EF.若菱形ABCD 的边长为2cm ,∠A=120°,则EF=_________cm 。
3如图,BD 为圆O 的直径,直线ED 为圆O 的切线,A 、C 两点在圆上,AC 平分∠BAD 且交BD 于F 点,若∠ADE =19°,则∠AFB 的度数为 ▲ .4.把一个半径为1cm 的圆O ,从边长为5cm 的正△ABC 的顶点A 处,按顺时针方向沿着三角形ABC 的三边滚动,则圆O 绕△ABC 滚动一周时圆心O 所经过的路线长为 ▲ .5如图,已知反比例函数y=k 1x ( k 1>0)和y=k 2x( k 2<0)。
点A 在y 轴的正半轴上,过点A 作直线BC∥x 轴,且分别与两个反比例函数的图象交于点B 和C ,连接OC 、OB 。
若△BOC 的面积为52,AC :AB=2:3,则k 1= ,k 2= 。
6.已知点P 是抛物线y =ax 2+c 上一个动点且点P 到直线y =-2的距离始终等于PO(O 为坐标原点),则该抛物线的解析式为 ▲ ,7如图,△ABC 是等边三角形,P 是∠ABC 的平分线BD 上一点,PE⊥AB 于点E ,线段BP 的垂直平分线交BC于点F,垂足为点Q .若BF=2,则PE 的长为【 】(7)(8)A . 2B . 2C .D . 38如图,⊙O 的半径OD ⊥弦AB 于点C ,连结AO 并延长交⊙O 于点E ,连结EC .若AB=8,CD=2,则EC 的长为( ) 229如图,有一圆心角为120 、半径长为6cm 的扇形,若将OA 、OB 重合后围成一圆锥侧面,那么圆锥的高是()A .24cm B .35cm C .62cm D .32 c 10如图,P 是边长为1的正六边形对角线CD 上一点,则AP +BP 的最小值为( )DA 、1B 、3C 、2D 、2311如图,正方形ABCD 中,点E 、F 分别在BC 、CD 上,△AEF 是等边三角形,连接AC 交EF 于G ,下列结论:①BE =DF ,②∠DAF =15°,③AC 垂直平分EF ,④BE +DF =EF ,⑤S △CEF =2S △ABE .其中正确的结论有( )个A .2B .3C .4D .512如图,AB 是⊙O 的直径,且AB=10,弦MN 的长为8,若弦MN 的两端在圆上滑动时,始终与AB 相交,记点A 、B 到MN 的距离分别为h 1,h 2,则|h 1-h 2| 等于( ) A 、5 B 、6 C 、7 D 、813如图,某大楼的顶部树有一块广告牌CD ,小李在山坡的坡脚A 处测得广告牌底部D 的仰角为60°,沿坡面AB 向上走到B 处测得广告牌顶部C 的仰角为45°,已知山坡 AB 的坡度i=1:,AB=8米,AE=12米. (1)求点B 距水平面AE 的高度BH ; (2)求广告牌CD 的高度.(测角器的高度忽略不计,结果精确到0.1米,参考数据:≈1.414,≈1.732)14已知:如图,AB 是⊙O 的直径,E 是⊙O 外一点,过点E 作AB 的垂线ED ,交BA 的延长线于点D ,EA 的延长线与⊙O 交于点C ,DE DC =.(1)求证:DC 是⊙O 的切线;(2)若55sin =∠ACD ,⊙O 的半径为5,求AE 的长.15矩形ABCD中,AB=4,AD=3,把矩形沿直线AC折叠,使点B落在点E处,AE交CD 于点F,连接DE.(1)求证:△DEC≌△EDA;(2)求DF的值;(3)如图2,若P为线段EC上一动点,过点P作△AEC的内接矩形,使其定点Q落在线段AE上,定点M、N落在线段AC上,当线段PE的长为何值时,矩形PQMN的面积最大?并求出其最大值.16如图1,Rt△ABC两直角边的边长为AC=3,BC=4.(1)如图2,⊙O与Rt△ABC的边AB相切于点X,与边BC相切于点Y.请你在图2中作出并标明⊙O的圆心(用尺规作图,保留作图痕迹,不写作法和证明)(2)P是这个Rt△ABC上和其内部的动点,以P为圆心的⊙P与Rt△ABC的两条边相切.设⊙P的面积为S,你认为能否确定S的最大值?若能,请你求出S的最大值;若不能,请你说明不能确定S的最大值的理由.17如图①,O为坐标原点,点B在x轴的正半轴上,四边形OACB是平行四边形,sin∠AOB=,反比例函数y=(k>0)在第一象限内的图象经过点A,与BC交于点F.(1)若OA=10,求反比例函数解析式;(2)若点F为BC的中点,且△AOF的面积S=12,求OA的长和点C的坐标;(3)在(2)中的条件下,过点F作EF∥OB,交OA于点E(如图②),点P为直线EF上的一个动点,连接PA,PO.是否存在这样的点P,使以P、O、A为顶点的三角形是直角三角形?若存在,请直接写出所有点P的坐标;若不存在,请说明理由.18在平面直角坐标系xOy 中,已知二次函数214y x mx n =++的图象经过点(2,0)A 和点3(1,)4B -,直线l 经过抛物线的顶点且与y 轴垂直,垂足为Q .(1) 求该二次函数的表达式;(2) 设抛物线上有一动点P 从点B 处出发沿抛物线向上运动,其纵坐标1y 随时间(t t ≥0)的变化规律为1324y t =-+.现以线段OP 为直径作C .①当点P 在起始位置点B 处时,试判断直线l 与C 的位置关系,并说明理由;在点P 运动的过程中,直线l 与C 是否始终保持这种位置关系? 请说明你的理由; ②若在点P 开始运动的同时,直线l 也向上平行移动,且垂足Q 的纵坐标2y 随时间t 的变化规律为213y t =-+,则当t 在什么范围内变化时,直线l 与C 相交? 此时,若直线l 被C 所截得的弦长为a ,试求2a 的最大值.第28题备用图第28题图。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
初三(上)数学提优练习一
1、如图,已知⊙是以数轴的原点为圆心,半径为1的圆,,点在数轴上运动,若过点且与平行的直线与⊙有公共点, 设,则的取值范围是__________.
2、射线QN 与等边△ABC 的两边AB ,BC 分别交于点M ,N ,且AC ∥QN ,AM =MB =2cm ,QM =4cm .动点P 从点Q 出发,沿射线QN 以每秒1cm 的速度向右移动,经过t 秒,以点P 为圆心,
为半径的圆与△ABC 的边相切(切点在边上),请写出t 可取的一切值 (单位:秒).
3、如图,在圆O 上有定点C 和动点P ,位于直径AB 的异侧,过点C 作CP 的垂线,与PB 的延长线交于点Q ,已知:圆O 半径为52,tan ∠ABC =34
,则CQ 的最大值是 。
4、如图,在Rt △ABC 中,∠C =90°,∠A =30°,AB
=D 在线段AC 上(不与点A 、C 重合),过点D 作DE ⊥AC 交AB 边于点E .
(1)当点D 运动到线段AC 中点时,DE = ;
(2)点A 关于点D 的对称点为点F ,以FC 为半径
作⊙C ,当DE = 时,⊙C 与直线AB 相切.
5、已知直线PD 垂直平分⊙O 的半径OA 于点B ,PD 交⊙O
于点
C 、
D ,P
E 是⊙O 的切线,E 为切点,连结AE ,交CD 于点
F .
(1)若⊙O 的半径为8,求CD 的长;
(2)证明:PE =PF ;
(3)若PF =13,sinA =513
,求EF 的长.
O O 45AOB ∠=︒P P OA O OP x =x
6、如图,⊙O是△ABC的外接圆,FH是⊙O 的切线,切点为F,FH∥BC,连结AF交BC 于E,∠ABC的平分线BD交AF于D,连结BF.
(1)证明:AF平分∠BAC;
(2)证明:BF=FD;
(3)若EF=4,DE=3,求AD的长.
7、如图,在△ABC中,AB=AC,以AB为直径作半圆⊙O,交BC于点D,连接AD,过点D作DE⊥AC,垂足为点E,交AB的延长线于点F.
(1)求证:EF是⊙O的切线;
(2)如果⊙O的半径为5,sin∠ADE=4
5,求BF的长.
8、如图,P A为⊙O的切线,A为切点,直线PO交⊙O与点E,F,过点A作PO的垂线AB垂足为D,交⊙O与点B,延长BO与⊙O交与点C,连接AC,BF.(1)求证:PB与⊙O相切;
(2)试探究线段EF,OD,OP之间的数量关系,并加以证明;
(3)若AC=12,tan∠F=1
2
,求cos∠ACB的值.。
