上海市中考数学分类汇编提优含答案

合集下载

上海市各区2018届中考二模数学分类汇编：几何证明专题(含答案)

上海市各区2018届九年级中考二模数学试卷精选汇编几何证明专题宝山区、嘉定区23.（本题满分12分，第（1）小题6分，第（2）小题6分）如图6，在正方形ABCD 中，点M 是边BC 上的一点（不与B 、C 重合），点N 在CD 边的延长线上，且满足︒=∠90MAN ，联结MN 、AC ，MN 与边AD 交于点E . （1）求证；AN AM =；（2）如果NAD CAD ∠=∠2，求证：AE AC AM ⋅=2.23.证明：（1）∵四边形ABCD 是正方形∴AD AB =，︒=∠=∠=∠=∠90BCD ADC B BAD ……1分 ∴︒=∠+∠90MAD MAB ∵︒=∠90MAN∴︒=∠+∠90MAD NAD ∴NAD MAB ∠=∠………1分 ∵︒=∠+∠180ADC ADN ∴︒=∠90ADN ……1分 ∴ADN B ∠=∠……………………1分 ∴△ABM ≌△ADN ………………………1分 ∴AN AM = ……………………………1分（2）∵四边形ABCD 是正方形 ∴AC 平分BCD ∠和BAD ∠ ∴︒=∠=∠4521BCD BCA ，︒=∠=∠=∠4521BAD CAD BAC ……1分 ∵NAD CAD ∠=∠2 ∴︒=∠5.22NAD∵NAD MAB ∠=∠ ∴︒=∠5.22MAB ………1分 ∴︒=∠5.22MAC ∴︒=∠=∠5.22NAE MAC ∵AN AM =,︒=∠90MAN ∴︒=∠45ANE图6图6∴ANE ACM ∠=∠…………………1分 ∴△ACM ∽△ANE …………1分 ∴ANACAE AM =……1分 ∵AN AM =∴AE AC AM ⋅=2…………1分长宁区23．（本题满分12分，第（1）小题5分，第（2）小题7分）如图，在四边形ABCD 中，AD //BC ，E 在BC 的延长线，联结AE 分别交BD 、CD 于点 G 、F ，且AG GF BE AD =．（1）求证：AB //CD ；（2）若BD GD BC ⋅=2，BG =GE ，求证：四边形ABCD 是菱形．23．（本题满分12分，第（1）小题5分，第（2）小题7分）证明：（1）∵BC AD // ∴BG DG BE AD = （2分）∵AG GFBE AD =∴AGGF BG DG = （1分） ∴ CD AB // （2分）（2）∵BC AD //，CD AB //∴四边形ABCD 是平行四边形 ∴BC=AD （1分） ∵ BD GD BC ⋅=2∴ BD GD AD ⋅=2即ADGDBD AD =又 ∵BDA ADG ∠=∠ ∴ADG ∆∽BDA ∆ （1分） ∴ABD DAG ∠=∠∵CD AB // ∴BDC ABD ∠=∠ ∵BC AD // ∴E DAG ∠=∠∵BG =GE ∴E DBC ∠=∠ ∴DBC BDC ∠=∠ （3分）ACDEF GB第23题图∴BC=CD （1分） ∵四边形ABCD 是平行四边形 ∴平行四边形ABCD 是菱形. （1分）崇明区23．（本题满分12分，第(1)、(2)小题满分各6分）如图，AM 是ABC △的中线，点D 是线段AM 上一点（不与点A 重合）．DE AB ∥交BC 于点K ，CE AM ∥，联结AE ．（1）求证：AB CMEK CK=；（2）求证：BD AE =．23．（本题满分12分，每小题6分）（1）证明：∵DE AB ∥∴ ABC EKC =∠∠ ……………………………………………………1分∵CE AM ∥∴ AMB ECK =∠∠ ……………………………………………………1分∴ABM EKC △∽△ ……………………………………………………1分 ∴AB BMEK CK=………………………………………………………1分 ∵ AM 是△ABC 的中线∴BM CM = ………………………………………………………1分∴AB CMEK CK=………………………………………………………1分（2）证明：∵CE AM ∥ ∴DE CMEK CK=………………………………………………………2分（第23题图）ABK MCDE又∵AB CMEK CK=∴DE AB = ………………………………………………………2分又∵DE AB ∥∴四边形ABDE 是平行四边形 …………………………………………1分 ∴BD AE = ………………………………………………………1分奉贤区23．（本题满分12分，每小题满分各6分）已知：如图7，梯形ABCD ，DC ∥AB ，对角线AC 平分∠BCD ，点E 在边CB 的延长线上，EA ⊥AC ，垂足为点A ．（1）求证：B 是EC 的中点；（2）分别延长CD 、EA 相交于点F ，若EC DC AC ⋅=2，求证：FC AC AF AD ::=．黄浦区23．（本题满分12分）如图，点E 、F 分别为菱形ABCD 边AD 、CD 的中点. （1）求证：BE =BF ；（2）当△BEF 为等边三角形时，求证：∠D =2∠A .ACD E图7B23. 证：（1）∵四边形ABCD为菱形，∴AB=BC=AD=CD，∠A=∠C，——————————————————（2分）又E、F是边的中点，∴AE=CF，——————————————————————————（1分）∴△ABE≌△CBF———————————————————————（2分）∴BE=BF. ——————————————————————————（1分）（2）联结AC、BD，AC交BE、BD于点G、O. ——————————（1分）∵△BEF是等边三角形,∴EB=EF，又∵E、F是两边中点，∴AO=12AC=EF=BE.——————————————————————（1分）又△ABD中，BE、AO均为中线，则G为△ABD的重心，∴1133OG AO BE GE===,∴AG=BG，——————————————————————————（1分）又∠AGE=∠BGO，∴△AGE≌△BGO，——————————————————————（1分）∴AE=BO，则AD=BD，∴△ABD是等边三角形，———————————————————（1分）所以∠BAD=60°，则∠ADC=120°，即∠ADC=2∠BAD. —————————————————————（1分）金山区23．（本题满分12分，每小题6分）如图7，已知AD 是△ABC 的中线， M 是AD 的中点，过A 点作AE ∥BC ，CM 的延长线与AE 相交于点E ，与AB 相交于点F ．（1）求证：四边形AEBD 是平行四边形；（2）如果AC =3AF ，求证四边形AEBD 是矩形．23．证明：（1）∵AE //BC ，∴∠AEM =∠DCM ，∠EAM =∠CDM ，……………………（1分）又∵AM=DM ，∴△AME ≌△DMC ，∴AE ＝CD ，…………………………（1分） ∵BD=CD ，∴AE =BD ．……………………………………………………（1分） ∵AE ∥BD ，∴四边形AEBD 是平行四边形．……………………………（2分）（2）∵AE //BC ，∴AF AEFB BC=．…………………………………………………（1分） ∵AE=BD=CD ，∴12AF AE FB BC ==，∴AB=3AF ．……………………………（1分） ∵AC=3AF ，∴AB=AC ，…………………………………………………………（1分）又∵AD 是△ABC 的中线，∴AD ⊥BC ，即∠ADB =90°．……………………（1分） ∴四边形AEBD 是矩形．……………………………………………………（1分）静安区23.（本题满分12分，第（1）小题满分6分，第（2）小题满分6分）已知：如图，在平行四边形ABCD 中， AC 、DB 交于点E ，点F 在BC 的延长线上，联结EF 、DF ，且∠DEF =∠ADC ．EAFMD图7CC第23题图ABDE F（1）求证：DBABBF EF =；（2）如果DF AD BD ⋅=22，求证：平行四边形ABCD 是矩形．23．（本题满分12分，第（1）小题6分，第（2）小题6分）证明：（1）∵平行四边形ABCD ，∴AD //BC ，AB //DC∴∠BAD +∠ADC =180°，……………………………………（1分）又∵∠BEF +∠DEF =180°, ∴∠BAD +∠ADC =∠BEF +∠DEF ……（1分） ∵∠DEF =∠ADC ∴∠BAD =∠BEF ， …………………………（1分） ∵AB //DC ， ∴∠EBF =∠ADB …………………………（1分）∴△ADB ∽△EBF ∴DB ABBF EF = ………………………（2分） (2) ∵△ADB ∽△EBF ,∴BFBEBD AD =, ………………………（1分）在平行四边形ABCD 中，BE =ED =BD 21∴221BD BE BD BF AD =⋅=⋅∴BF AD BD ⋅=22, ………………………………………（1分）又∵DF AD BD ⋅=22∴DF BF =,△DBF 是等腰三角形 …………………………（1分） ∵DE BE =∴FE ⊥BD , 即∠DEF =90° …………………………（1分） ∴∠ADC =∠DEF =90° …………………………（1分） ∴平行四边形ABCD 是矩形 …………………………（1分）闵行区23．（本题满分12分，其中第（1）小题5分，第（2）小题7分）如图，已知在△ABC 中，∠BAC =2∠C ，∠BAC 的平分线AE 与∠ABC 的平分线BD 相交于点F ，FG ∥AC ，联结DG ．（1）求证：BF BC AB BD ⋅=⋅；（2）求证：四边形ADGF 是菱形．AB第23题图DE FABEGCFD（第23题图）23．证明：（1）∵AE 平分∠BAC ，∴∠BAC =2∠BAF =2∠EAC ．∵∠BAC =2∠C ，∴∠BAF =∠C =∠EAC ．…………………………（1分）又∵BD 平分∠ABC ，∴∠ABD =∠DBC ．……………………………（1分） ∵∠ABF =∠C ，∠ABD =∠DBC ，∴ABF CBD ∆∆∽．…………………………………………………（1分） ∴AB BFBC BD=．………………………………………………………（1分） ∴BF BC AB BD ⋅=⋅．………………………………………………（1分）（2）∵FG ∥AC ，∴∠C =∠FGB ，∴∠FGB =∠FAB ．………………（1分）∵∠BAF =∠BGF ，∠ABD =∠GBD ，BF =BF ，∴ABF GBF ∆∆≌．∴AF =FG ，BA =BG ．…………………………（1分） ∵BA =BG ，∠ABD =∠GBD ，BD =BD ，∴ABD GBD ∆∆≌．∴∠BAD =∠BGD ．……………………………（1分） ∵∠BAD =2∠C ，∴∠BGD =2∠C ，∴∠GDC =∠C ，∴∠GDC =∠EAC ，∴AF ∥DG ．……………………………………（1分）又∵FG ∥AC ，∴四边形ADGF 是平行四边形．……………………（1分） ∴AF =FG ．……………………………………………………………（1分） ∴四边形ADGF 是菱形．……………………………………………（1分）普陀区23．（本题满分12分）已知：如图9，梯形ABCD 中，AD ∥BC ，DE ∥AB ，DE 与对角线AC 交于点F ，FG ∥AD ，且FG EF =.（1）求证：四边形ABED 是菱形；（2）联结AE ，又知AC ⊥ED ，求证：212AE EF ED = .ABC DE FG图923．证明：（1）∵ AD ∥BC ，DE ∥AB ，∴四边形ABED 是平行四边形． ··························· （2分）∵FG ∥AD ，∴FG CFAD CA=． ·················································································· （1分）同理EF CFAB CA = ． ··································································································· （1分）得FG AD ＝EF AB∵FG EF =，∴AD AB =． ··················································································· （1分） ∴四边形ABED 是菱形． ························································································· （1分）（2）联结BD ，与AE 交于点H ．∵四边形ABED 是菱形，∴12EH AE =，BD ⊥AE ． ····································· （2分）得90DHE ∠= ．同理90AFE ∠= ．∴DHE AFE ∠∠＝． ······························································································· （1分）又∵AED ∠是公共角，∴△DHE ∽△AFE ． ··················································· （1分）∴EH DEEF AE =． ········································································································ （1分） ∴212AE EF ED = ． ······························································································ （1分）青浦区23.（本题满分12分，第（1）、（2）小题，每小题6分）如图7，在梯形ABCD 中，AD ∥BC ，对角线AC 、BD 交于点M ，点E 在边 BC 上，且DAE DCB ∠=∠，联结AE ，AE 与BD 交于点F ．（1）求证：2DM MF MB =⋅；（2）联结DE ，如果3BF FM =，求证：四边形ABED 是平行四边形.23．证明：（1）∵AD //BC ，∴∠=∠DAE AEB ， ····························································· （1分）∵∠=∠DCB DAE ，∴∠=∠DCB AEB ， ··········································· （1分）MFE DBA图7∴AE //DC ， ···································································································· （1分）∴=FM AMMD MC． ························································································· （1分） ∵AD //BC ，∴=AM DMMC MB， ····································································· （1分） ∴=FM DMMD MB， ························································································· （1分）即2=⋅MD MF MB ．（2）设=FM a ，则=3BF a ，=4BM a ． ························································· （1分）由2=⋅MD MF MB ，得24=⋅MD a a ，∴2=MD a ， ································································································ （1分） ∴3==DF BF a ． ························································································ （1分） ∵AD //BC ，∴1==AF DFEF BF， ····································································· （1分） ∴=AF EF ， ································································································· （1分） ∴四边形ABED 是平行四边形. ······································································ （1分）松江区23.（本题满分12分，第（1）小题满分7分，第（2）小题满分5分）如图，已知梯形ABCD 中，AB ∥CD ，∠D =90°，BE 平分∠ABC ，交CD 于点E ， F 是AB 的中点，联结AE 、EF ，且AE ⊥BE ．求证：（1）四边形BCEF 是菱形；（2）2BE AE AD BC ⋅=⋅.23.（本题满分12分，第（1）小题满分7分，第（2）小题满分5分）证明：(1) ∵BE 平分∠ABC ,∴∠ABE =∠CBE …………………………………………………1分 ∵AE ⊥BE(第23题图)FACD EB∴∠AEB =90°∵F 是AB 的中点 ∴12EF BF AB ==………………………………………………1分 ∴∠FEB =∠FBE …………………………………………………1分∴∠FEB =∠CBE …………………………………………………1分∴EF ∥BC …………………………………………………1分∵AB ∥CD∴四边形BCEF 是平行四边形…………………………1分∵EF BF =∴四边形BCEF 是菱形……………………………………1分(2) ∵四边形BCEF 是菱形,∴BC =BF ∵12BF AB = ∴AB =2BC ………………………………………………1分∵ AB ∥CD∴ ∠DEA =∠EAB∵ ∠D =∠AEB∴ △EDA ∽△AEB ………………………………………2分∴AD AE BE AB = …………………………………………1分 ∴ BE ·AE =AD ·AB∴ 2BE AE AD BC ⋅=⋅…………………………………1分徐汇区23. 在梯形ABCD 中，AD ∥BC ，AB CD =，BD BC =，点E 在对角线BD 上，且DCE DBC ∠=∠.（1）求证：AD BE =；（2）延长CE 交AB 于点F ，如果CF AB ⊥，(第23题图)F A C D E⋅=⋅.求证：4EF FC DE BD杨浦区23、（本题满分12分，第（1）小题6分，第（2）小题6分）已知：如图7，在□ABCD中，点G为对角线AC的中点，过点G的直线EF分别交边AB、CD 于点E、F，过点G的直线MN分别交边AD、BC于点M、N，且∠AGE=∠CGN。

2024年4月上海市中考数学二模题型分类汇编3--- 实际应用含综合与实践(22题)

4 从这两个统计图中能准确求出样本的平均数．
上述结论中错误的是
（填序号）．
（3）估计本次六年级参赛学生中荣获优秀的共有 m 人．学校“环保社团”决定：这 m
名学生都光荣的成为学校的小小环保“宣传员”，从中选派 x 人帮助本年级参赛得分 60 分以
下的学生普及环保知识．经计算，x 与（m－x）的积恰好等于样本容量的 15 倍. 你认为 x
越适宜．我们可通过计算一组 GDP 所有实际值偏离图像上对应点纵坐标值的程度，即偏离方差，来进行模型分析，一般偏离方差越小越适宜．）
例如，分析直线 AB 即 f (x) x 9 上的点：可知 f (1) 10 ， f (2) 11 ， f (3) 12 ， f (4) 13 ，
求得偏离方差
有几种租车方案？
载客量（人/辆）租金（元/辆）
45
1500
33
1200
第 22 题表
（3）在（2）的条件下，选择哪种租车方案最省钱？此时租车的总费用是多少元？
【2024.4 月松江区二模】
22.（本题满分 10 分，第（1）小题 2 分，第（2）小题 4 分，第（3）小题 4 分）一个凸四边形的四条边及两条对角线共 6 条线段中，如果只有两种大小不同的长度，那
和∠θ，通过计算就可以得到大厦的高度.
测量并通过计算得：CD=60 米，cotα=10.667，cotβ=10.161，cotγ=10.159，cotθ=10.254.
（1）教学楼（AB）的高度为
米；
（2）请你在两种方案中选．取．一．种．方．案．，计算出上海中心大厦（SH）的高度（精确到 1 米）.
（第 22 题图 2）（第 22 题图 1）
（1）估计六年级参赛学生中成绩为良好的学生有

上海市各区届中考二模数学分类汇编压轴题专题含答案

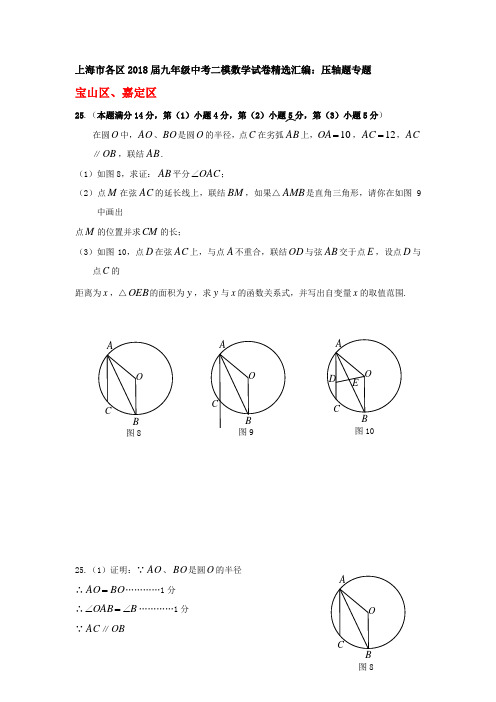
上海市各区2018届九年级中考二模数学试卷精选汇编：压轴题专题宝山区、嘉定区25.（本题满分14分，第（1）小题4分，第（2）小题5分，第（3）小题5分）在圆O 中，AO 、BO 是圆O 的半径，点C 在劣弧AB 上，10=OA ，12=AC ，AC ∥OB ，联结AB .（1）如图8，求证：AB 平分OAC ∠；（2）点M 在弦AC的延长线上，联结BM ，如果△AMB 是直角三角形，请你在如图9中画出点M 的位置并求CM 的长；（3）如图10，点D 在弦AC 上，与点A 不重合，联结OD 与弦AB 交于点E ，设点D 与点C 的距离为x ，△OEB 的面积为y ，求y 与x 的函数关系式，并写出自变量x 的取值范围.25.（1）证明：∵AO 、BO 是圆O 的半径 ∴BO AO =…………1分 ∴B OAB ∠=∠…………1分 ∵AC ∥OB图8图10图8∴B BAC ∠=∠…………1分 ∴BAC OAB ∠=∠∴AB 平分OAC ∠…………1分 (2)解：由题意可知BAM ∠不是直角，所以△AMB 是直角三角形只有以下两种情况:︒=∠90AMB 和︒=∠90ABM① 当︒=∠90AMB ，点M 的位置如图9-1……………1分过点O 作AC OH ⊥,垂足为点H∵OH 经过圆心 ∴AC HC AH 21==∵12=AC ∴6==HC AH 在Rt △AHO 中，222OA HO AH =+ ∵10=OA ∴8=OH∵AC ∥OB ∴︒=∠+∠180OBM AMB ∵︒=∠90AMB ∴︒=∠90OBM ∴四边形OBMH 是矩形 ∴10==HM OB∴4=-=HC HM CM ……………2分 ②当︒=∠90ABM ，点M 的位置如图9-2由①可知58=AB ，552cos =∠CAB 在Rt △ABM 中，552cos ==∠AM AB CAB∴20=AM8=-=AC AM CM ……………2分综上所述，CM 的长为4或8.说明：只要画出一种情况点M 的位置就给1分，两个点都画正确也给1分. （3）过点O 作AB OG ⊥,垂足为点G 由（1）、（2）可知，CAB OAG ∠=∠sin sin 由（2）可得：55sin =∠CAB图10∵10=OA ∴52=OG ……………1分 ∵AC ∥OB ∴ADOBAE BE =……………1分又BE AE -=58,x AD -=12,10=OB∴xBEBE -=-121058 ∴x BE -=22580 ……………1分∴52225802121⨯-⨯=⨯⨯=xOG BE y ∴xy -=22400……………1分自变量x 的取值范围为120<≤x ……………1分长宁区25．（本题满分14分，第（1）小题4分，第（2）小题4分，第（3）小题6分）在圆O 中，C 是弦AB 上的一点，联结OC 并延长，交劣弧AB 于点D ，联结AO 、BO 、AD 、BD . 已知圆O 的半径长为5 ，弦AB 的长为8．（1）如图1，当点D 是弧AB 的中点时，求CD 的长；（2）如图2，设AC =x ，y S S OBDACO=∆∆，求y 关于x 的函数解析式并写出定义域；（3）若四边形AOBD 是梯形，求AD 的长．25.（本题满分14分，第（1）小题4分，第（2）小题4分，第（3）小题6分）解：（1）∵OD 过圆心，点D 是弧AB 的中点，AB =8，∴OD ⊥AB ，（2分）在Rt △AOC 中，，AO =5，∴ （1分），（1分）（2）过点O 作OH ⊥AB ，垂足为点H ，则由（1）可得AH =4，OH =3 ∵AC =x ，∴在Rt △HOC 中，，AO =5， ∴，（1分） ∴（）（3分）（3）①当OB （3分） ②当OA ABC △8AB =10BC =12AC =2AB AD AC =⋅AEF C ∠=∠ABC ∠BE x =CF y =y xGEF △8AB =12AC=2AB AD AC =g 163AD =16201233CD =-=2AB AD AC =g AD AB AB AC =BAC ∠ADB ABC △∽△ABD C =∠∠BD AD BC AB =203BD =BD CD =DBC C =∠∠ABD DBC =∠∠BD ABC ∠A AH BC ∥BD H AH BC∥16432053AD DH AH DC BD BC ====203BD CD ==8AH =163AD DH ==12BH =AH BC∥AH HGBE BG =812BG x BG-=128xBG x =+BEF C EFC=+∠∠∠BEA AEF C EFC +=+∠∠∠∠AEF C =∠∠BEA EFC=∠∠DBC C=∠∠（第25题图） A B C D G EF（备用图）AB C DBEG CFE△∽△BE BGCF EC=12810x x x y x+=-228012x x y -++=GEF GE GF=23GE BE EF CF ==23x y =4BE =EG EF =BE CF =x y =5BE =-FG FE =32GE BE EF CF ==32x y =3BE =-+BC BO BE ⋅=2知AD =1，AB =2. （1）设BC =x ，CD =y ，求y 关于x 的函数关系式，并写出定义域；（2）当∠B =70°时，求∠AEC 的度数；（3）当△ACE 为直角三角形时，求边BC 的长.25. 解：（1）过A 作AH ⊥BC 于H ，————————————————————（1分）由∠D =∠BCD =90°，得四边形ADCH 为矩形.在△BAH 中，AB =2，∠BHA =90°，AH =y ，HB =1x -，所以22221y x =+-，——————————————————————（1分）则()03y x =<<.———————————————（2分）（2）取CD 中点T ，联结TE ，————————————————————（1分）则TE 是梯形中位线，得ET ∥AD ，ET ⊥CD .∴∠AET =∠B =70°. ———————————————————————（1分）又AD =AE =1，∴∠AED =∠ADE =∠DET =35°. ——————————————————（1分）由ET 垂直平分CD ，得∠CET =∠DET =35°，————————————（1分）所以∠AEC =70°＋35°=105°. ——————————————————（1分）（3）当∠AEC =90°时，易知△CBE ≌△CAE ≌△CAD ，得∠BCE =30°，则在△ABH 中，∠B =60°，∠AHB =90°，AB =2，图9AB C D O E备用图ABO 备用图 AB得BH=1，于是BC=2. ——————————————————————（2分）当∠CAE=90°时，易知△CDA∽△BCA，又AC=则AD CAxAC CB=⇒=⇒=2分）易知∠ACE<90°.所以边BC的长为2或12+.——————————————————（1分）金山区25．（本题满分14分，第（1）小题4分，第（2）小题5分，第（3）小题5 分）如图9，已知在梯形ABCD中，AD∥BC，AB=DC=AD=5，3sin5B=，P是线段BC上一点，以P为圆心，PA为半径的⊙P与射线AD的另一个交点为Q，射线PQ与射线CD相交于点E，设BP=x．（1）求证△ABP∽△ECP；（2）如果点Q在线段AD上（与点A、D不重合），设△APQ的面积为y，求y关于x的函数关系式，并写出定义域；（3）如果△QED与△QAP相似，求BP的长．25．解：（1）在⊙P中，PA=PQ，∴∠PAQ ＝∠PQA，……………………………（1分）AB CD图9备用图∵AD ∥BC ，∴∠PAQ ＝∠APB ，∠PQA ＝∠QPC ，∴∠APB ＝∠EPC ，……（1分） ∵梯形ABCD 中，AD ∥BC ，AB =DC ，∴∠B ＝∠C ，…………………………（1分） ∴△APB ∽△ECP ．…………………………………………………………（1分）（2）作AM ⊥BC ，PN ⊥AD ，∵AD ∥BC ，∴AM ∥PN ，∴四边形AMPN 是平行四边形，∴AM =PN ，AN =MP ．………………………………………………………（1分）在Rt △AMB 中，∠AMB =90°，AB =5，sinB =35， ∴AM =3，BM =4，∴PN =3，PM =AN =x -4，……………………………………（1分） ∵PN ⊥AQ ，∴AN =NQ ，∴AQ = 2x -8，……………………………………（1分）∴()1128322y AQ PN x =⋅⋅=⋅-⋅，即312y x =-，………………………（1分）定义域是1342x <<．………………………………………………………（1分）（3）解法一：由△QED 与△QAP 相似，∠AQP ＝∠EQD ，①如果∠PAQ ＝∠DEQ ，∵△APB ∽△ECP ，∴∠PAB ＝∠DEQ ，又∵∠PAQ ＝∠APB ，∴∠PAB ＝∠APB ，∴BP =BA =5．………………………（2分） ②如果∠PAQ ＝∠EDQ ，∵∠PAQ ＝∠APB ，∠EDQ ＝∠C ，∠B ＝∠C ，∴∠B ＝∠APB ，∴ AB =AP ，∵AM ⊥BC ，∴ BM =MP =4，∴ BP =8．………（2分）综上所述BP 的长为5或者8．………………………………………………（1分）解法二：由△QAP 与△QED 相似，∠AQP ＝∠EQD ，在Rt △APN 中，AP PQ ===∵QD ∥PC ，∴EQ EPQD PC=， ∵△APB ∽△ECP ，∴AP EPPB PC=，∴AP EQ PB QD =，①如果AQ EQQP QD =，∴AQ AP QP PB =x=，解得5x =………………………………………………………………………（2分） ②如果AQ DQQP QE =，∴AQ PBQP AP ==解得8x =………………………………………………………………………（2分）综上所述BP 的长为5或者8．…………………………………………………（1分）静安区25．（本题满分14分，第（1）小题满分4分，第（2）小题满分6分，第（3）小题满分4分）如图，平行四边形ABCD 中，已知AB =6，BC =9，31cos =∠ABC ．对角线AC 、BD 交于点O ．动点P 在边AB 上，⊙P 经过点B ,交线段PA 于点E ．设BP = x ．（1）求AC 的长；（2）设⊙O 的半径为y ，当⊙P 与⊙O 外切时，求y 关于x 的函数解析式，并写出定义域；（3）如果AC 是⊙O 的直径，⊙O 经过点E ，求⊙O 与⊙P 的圆心距OP 的长．25．（本题满分14分，第（1）小题4分，第（2）小题6分，第（3）小题4分）解：（1）作AH ⊥BC 于H ，且，AB =6，那么…………（2分）BC =9，HC =9-2=7，， ……………………（1分） ﹒ ………（1分）（2）作OI ⊥AB 于I ，联结PO , AC =BC =9，AO = ∴∠OAB =∠ABC , ∴Rt △AIO 中，∴AI =，IO = ……………………（1分） ∴PI =AB -BP -AI ==， ……………………（1分） ∴Rt △PIO 中，A第25题图B P OC DE·第25题备用图ABOCDDA ·第25题图BP OCHE第25题图……（1分）∵⊙P 与⊙O 外切，∴ ……………………（1分） ∴= …………………………（1分）∵动点P 在边AB 上，⊙P 经过点B ,交线段PA 于点E ．∴定义域：0<x ≤3…………（1分）（3）由题意得：∵点E 在线段AP 上，⊙O 经过点E ，∴⊙O 与⊙P 相交 ∵AO 是⊙O 半径，且AO ＞OI ，∴交点E 存在两种不同的位置，OE =OA = ① 当E 与点A 不重合时，AE 是⊙O 的弦，OI 是弦心距，∵AI =，AE =3， ∴点E 是AB 中点，,,, IO =……………………（2分）② 当E 与点A 重合时，点P 是AB 中点，点O 是AC 中点, ……（2分） ∴或．闵行区25．（本题满分14分，其中第（1）小题4分，第（2）、（3）小题各5分）如图，已知在Rt △ABC 中，∠ACB = 90o，AC =6，BC = 8，点F 在线段AB 上，以点B 为圆心，BF 为半径的圆交BC 于点E ，射线AE 交圆B 于点D （点D 、E 不重合）．（1）如果设BF = x ，EF = y ，求y 与x 之间的函数关系式，并写出它的定义域；（2）如果»»2EDEF ，求ED 的长；（3）联结CD 、BD ，请判断四边形ABDC 是否为直角梯形说明理由．25．解：（1）在Rt △ABC 中，，，∴．……………………………………………………………（1分）（备用图）CBA （第25题图）CBEF DA过E作EH⊥AB，垂足是H，易得：，，．…………………………（1分）在Rt△EHF中，，∴．………………………………………（1分+1分）（2）取的中点P，联结BP交ED于点G∵，P是的中点，∴．∴∠FBE =∠EBP =∠PBD．∵，BP过圆心，∴BG⊥ED，ED =2EG =2DG．…………（1分）又∵∠CEA =∠DEB，∴∠CAE=∠EBP=∠ABC．……………………………………………（1分）又∵BE是公共边，∴．∴．在Rt△CEA中，∵AC = 6，，，∴．……………………………（1分）∴．……………………………………………（1分）∴．……………………………………（1分）（3）四边形ABDC不可能为直角梯形．…………………………………（1分）①当CD∥AB时，如果四边形ABDC是直角梯形，只可能∠ABD =∠CDB = 90o．在Rt△CBD中，∵，∴，．∴，；∴．∴CD不平行于AB，与CD∥AB矛盾．∴四边形ABDC不可能为直角梯形．…………………………（2分）②当AC∥BD时，如果四边形ABDC是直角梯形，只可能∠ACD =∠CDB = 90o．∵AC∥BD，∠ACB = 90o，∴∠ACB =∠CBD = 90o．∴∠ABD =∠ACB +∠BCD > 90o．与∠ACD =∠CDB = 90o矛盾．∴四边形ABDC不可能为直角梯形．…………………………（2分）普陀区25．（本题满分14分）已知P 是O ⊙的直径BA 延长线上的一个动点，P ∠的另一边交O ⊙于点C 、D ，两点位于AB 的上方，AB ＝6，OP m ＝，1sin 3P ＝，如图11所示．另一个半径为6的1O ⊙经过点C 、D ，圆心距1OO n ＝．（1）当6m ＝时，求线段的长；（2）设圆心1O 在直线AB 上方，试用n 的代数式表示m ；（3）△1POO 在点P 的运动过程中，是否能成为以1OO 为腰的等腰三角形，如果能，试求出此时n 的值；如果不能，请说明理由． 25．解：（1）过点O 作OH ⊥CD ，垂足为点H ，联结OC ．在Rt △POH 中，∵1sin 3P ＝，6PO =，∴2OH =． ········· （1分） ∵AB ＝6，∴3OC ＝． ······················ （1分）由勾股定理得CH = ····················· （1分）∵OH ⊥DC，∴2CD CH == ··············· （1分）（2）在Rt △POH 中，∵1sin 3P ＝， PO m ＝，∴3m OH ＝． ········ （1分）在Rt △OCH 中，2293m CH ⎛⎫- ⎪⎝⎭＝． ················ （1分）在Rt △1O CH 中，22363m CH n ⎛⎫-- ⎪⎝⎭＝． ·············· （1分）可得 2236933m m n ⎛⎫⎛⎫--- ⎪ ⎪⎝⎭⎝⎭＝，解得23812n m n -＝． ········· （2分）OAB备用图PDOABC图11（3）△1POO 成为等腰三角形可分以下几种情况：● 当圆心1O 、O 在弦CD 异侧时①1OP OO ＝，即m n ＝，由23812n n n-＝解得9n ＝． ········· （1分）即圆心距等于O ⊙、1O ⊙的半径的和，就有O ⊙、1O ⊙外切不合题意舍去．（1分） ②11O P OO ＝n ＝，解得23m n ＝，即23n 23812n n-＝，解得n ········· （1分） ● 当圆心1O 、O 在弦CD 同侧时,同理可得 28132n m n-＝．∵1POO ∠是钝角，∴只能是m n =，即28132n n n-＝，解得n ． ·· （2分）综上所述，n．青浦区25.（本题满分14分，第（1）小题4分，第（2）小题6分，第（3）小题4分）如图9-1，已知扇形MON，∠MON =90o ，点B 在弧MN 上移动，联结BM ，作OD ⊥BM ，垂足为点D ，C 为线段OD 上一点，且OC =BM ，联结BC 并延长交半径OM 于点A ，设OA = x ，∠COM 的正切值为y ．（1）如图9-2，当AB ⊥OM 时，求证：AM =AC ；（2）求y 关于x 的函数关系式，并写出定义域；（3）当△OAC 为等腰三角形时，求x 的值.图9-1图9-2备用图25．解：（1）∵OD ⊥BM ，AB ⊥OM ，∴∠ODM =∠BAM =90°． ·········· （1分）∵∠ABM +∠M =∠DOM +∠M ，∴∠ABM =∠DOM ． ········· （1分） ∵∠OAC =∠BAM ，OC =BM ，∴△OAC ≌△ABM ， ······················ （1分） ∴AC =AM ． ························· （1分）（2）过点D 作DE=MD MEDMAE)12x2==OA OC DM OE OD OD 2=DM OA ODOE =y0<≤x 111222===DM BM OCx ==OD =DMyOD1=x=x =x α90α︒-α90α︒-α45︒290α∠=>︒BOA 90∠≤︒BOA （1）求CE 的长；（2）P 是 CE 延长线上一点，直线AP 、CD 交于点Q.① 如果△ACQ ∽△CPQ ，求CP 的长；② 如果以点A 为圆心，AQ 为半径的圆与⊙C 相切，求CP 的长.25．（本题满分14分，第（1）小题4分，第（2）小题每个小题各5分）解：（1）∵AE ∥CD∴…………………………………1分 ∵BC=DC∴BE=AE …………………………………1分(第25题图)CBA DE(备用图)CBADE(第25题图)CBA DE设CE =x 则AE =BE =x +2 ∵ ∠ACB =90°， ∴即………………………1分 ∴即…………………………………1分（2）①∵△ACQ ∽△CPQ ，∠QAC>∠P∴∠ACQ=∠P …………………………………1分又∵AE ∥CD ∴∠ACQ=∠CAE∴∠CAE=∠P ………………………………1分 ∴△ACE ∽△PCA ，…………………………1分 ∴…………………………1分即∴ ……………………………1分 ②设CP =t ，则 ∵∠ACB =90°， ∴ ∵AE ∥CD∴……………………………1分即∴……………………………1分若两圆外切，那么此时方程无实数解……………………………1分若两圆内切切，那么 ∴21540160t t -+=CBA DEPQ解之得2015t ±=………………………1分又∵∴2015t +=………………………1分徐汇区25. 已知四边形ABCD 是边长为10的菱形，对角线AC 、BD 相交于点E ，过点C 作CF ∥DB 交AB 延长线于点F ，联结EF 交BC 于点H . （1）如图1，当EF BC ⊥时，求AE 的长；（2）如图2，以EF 为直径作⊙O ，⊙O 经过点C 交边CD 于点G （点C 、G 不重合），设AE 的长为x ，EH 的长为y ；① 求y 关于x 的函数关系式，并写出定义域；③ 联结EG ，当DEG ∆是以DG 为腰的等腰三角形时，求AE 的长.杨浦区25、（本题满分14分，第（1）小题4分，第（2）小题6分，第（3）小题4分）（1）如图9，在梯形ABCD 中，AD 当圆P 过点A 时，求圆P 的半径；（2）分别联结EH 和EA ，当△ABE △CEH 时，以点B 为圆心，r 为半径的圆B 与圆P 相交，试求圆B 的半径r 的取值范围；（3）将劣弧沿直线EH 翻折交BC 于点F ，试通过计算说明线段EH 和EF 的比值为定值，并求出此定值。

上海市中考数学分类汇编专题06：函数及其图象(二次函数)

上海市中考数学分类汇编专题06：函数及其图象（二次函数）姓名:________ 班级:________ 成绩:________一、单选题 (共6题；共12分)1. （2分） (2020九上·秦淮期末) 二次函数y＝3(x－2)2－1的图像顶点坐标是（）A . （－2，1）B . （－2，－1）C . （2，1）D . （2，－1）2. （2分）已知二次函数y=ax2+bx+c（a＜0）的图象如图所示，当﹣5≤x≤0时，下列说法正确的是（）A . 有最小值﹣5、最大值0B . 有最小值﹣3、最大值6C . 有最小值0、最大值6D . 有最小值2、最大值63. （2分）(2016·温州) 如图，半圆O的半径OA＝4，P是OA延长线上一点，线段OP的垂直平分线分别交OP、半圆O于B、C两点，射线PC交半圆O于点D．设PA＝x，CD＝y，则能表示y与x的函数关系的图象是（）A .B .C .D .4. （2分）(2017·桂林) 在平面直角坐标系中，将抛物线y=x2+2x+3绕着它与y轴的交点旋转180°，所得抛物线的解析式是（）A . y=﹣（x+1）2+2B . y=﹣（x﹣1）2+4C . y=﹣（x﹣1）2+2D . y=﹣（x+1）2+45. （2分） (2017九上·芜湖期末) 函数y=ax+b和y=ax2+bx+c在同一直角坐标系内的图象大致是（）A .B .C .D .6. （2分）(2017·青山模拟) 如图，抛物线y=﹣ x2+ x+ 与x轴交于A，B两点，与y轴交于点C．若点P是线段AC上方的抛物线上一动点，当△ACP的面积取得最大值时，点P的坐标是（）A . （4，3）B . （5，）C . （4，）D . （5，3）二、作图题 (共1题；共15分)7. （15分）函数y=ax2（a≠0）与直线y=2x-3的图象交于点（1，b）．求：（1） a和b的值；（2）求抛物线y=ax2的开口方向、对称轴、顶点坐标；（3）作y=ax2的草图．三、综合题 (共9题；共110分)8. （10分） (2019九上·高邮期末) “春节”前夕，某超市购进某种品牌礼品，每盒进价是40元，超市规定每盒售价不得少于45元，设每盒售价为x(元)，每天的销售量y(盒)，y与x成一次的函数关系，经过市场调查获得部分数据如下表：每盒售价为x(元)455055…每天的销售量y(盒)450400350…（1）试求出y与x之间的函数关系式；（2）当每盒售价定为多少元时，每天销售的利润P(元)最大？最大利润是多少？（3）物价部门规定：这种礼品每盒售价不得高于60元，如果超市想要每天获得不低于5250元的利润，那么超市每天至少销售这种礼品多少盒？9. （10分）(2017·青山模拟) 九年级数学兴趣小组经过市场调查，得到某种图书每月的销售与售价的关系为函数关系如下表：售价（元/本）50556065…月销量（本）200018001600 1400…已知该图书的进价为每本30元，设售价为x元．（1）请用含x的式子表示：①销售该图书每本的利润是________元，②月销量是________件．（用x表示直接写出结果）（2）若销售图书的月利润为48000元，则每本图书需要售价多少元？（3）设销售该图书的月利润为y元，那么售价为多少时，当月的利润最大，最大利润是多少？10. （15分）(2017·承德模拟) 某园林专业户计划投资种植花卉及树木，根据市场调查与预测，种植树木的利润y1与投资成本x成正比例关系，种植花卉的利润y2与投资成本x的平方成正比例关系，并得到了表格中的数据；投资量x（万元）2种植树木的利润y1（万元）4种植花卉的利润y2（万元）2（1）分别求出利润y1与y2关于投资量x的函数关系式；（2）如果这位专业户计划以8万元资金投入种植花卉和树木，设他投入种植花卉金额万元，种植花卉和树木共获利润W万元，求出W与m之间的函数关系式，并求他至少获得多少利润？他能获取的最大利润是多少？（3）若该专业户想获利不低于22万元，在（2）的条件下，求出投资种植花卉的金额m的范围．11. （10分） (2018九上·义乌期中) 小明合作学习小组在探究旋转、平移变换.如图△ABC，△DEF均为等腰直角三角形，各顶点坐标分别为A（1，1），B（2，2），C（2，1），D（，0），E（， 0），F（，）.（1）他们将△ABC绕C点按顺时针方向旋转450得到△A1B1C.请你写出点A1，B1的坐标，并判断A1C和DF 的位置关系；（2）他们将△ABC绕原点按顺时针方向旋转450，发现旋转后的三角形恰好有两个顶点落在抛物线上.请你求出符合条件的抛物线解析式；（3）他们继续探究，发现将△ABC绕某个点旋转45，若旋转后的三角形恰好有两个顶点落在抛物线上，则可求出旋转后三角形的直角顶点P的坐标.请你直接写出点P的所有坐标.12. （10分） (2019九上·九龙坡期末) 如图1，抛物线y＝﹣与x轴交于A、B两点，与y 轴交于点C，连接AC、BC.（1）求线段AC的长；（2）如图2，E为抛物线的顶点，F为AC上方的抛物线上一动点，M、N为直线AC上的两动点（M在N的左侧），且MN＝4，作FP⊥AC于点P，FQ∥y轴交AC于点Q.当△FPQ的面积最大时，连接EF、EN、FM，求四边形ENMF周长的最小值.（3）如图3，将△BCO沿x轴负方向平移个单位后得△B'C'O'，再将△B'C'O'绕点O'顺时针旋转α度，得到△B″C″O'（其中0°＜α＜180°），旋转过程中直线B″C″与直线AC交于点G，与x轴交于点H，当△AGH 是等腰三角形时，求α的度数.13. （10分）(2017·兰州模拟) 如图，抛物线y=﹣（x﹣1）2+c与x轴交于A，B（A，B分别在y轴的左右两侧）两点，与y轴的正半轴交于点C，顶点为D，已知A（﹣1，0）．（1）求点B，C的坐标；（2）判断△CDB的形状并说明理由；（3）将△COB沿x轴向右平移t个单位长度（0＜t＜3）得到△QPE．△QPE与△CDB重叠部分（如图中阴影部分）面积为S，求S与t的函数关系式，并写出自变量t的取值范围．14. （15分）(2018·嘉兴模拟) 某公司对一款新高压锅进行测试，放入足量的水和设定某一模式后，在容积不变的情况下，根据温度t(℃)的变化测出高压锅内的压强p(kpa)的大小．压强在加热前是100kpa，达到最大值后高压锅停止加热。

中考数学2022年上海市中考数学真题汇总卷(Ⅱ)(含答案解析)

2022年上海市中考数学真题汇总卷（Ⅱ）考试时间：90分钟；命题人：教研组考生注意： 1、本卷分第I 卷（选择题）和第Ⅱ卷（非选择题）两部分，满分100分，考试时间90分钟2、答卷前，考生务必用0.5毫米黑色签字笔将自己的姓名、班级填写在试卷规定位置上3、答案必须写在试卷各个题目指定区域内相应的位置，如需改动，先划掉原来的答案，然后再写上新的答案；不准使用涂改液、胶带纸、修正带，不按以上要求作答的答案无效。

第I 卷（选择题 30分）一、单选题（10小题，每小题3分，共计30分）1、如果54a b =，那么下列各式错误的是（）A ．54b a =B ．:22:153a b =C ．:5:4a b =D ．528b a = 2、一个长方体的长、宽、高都是整厘米数，棱长总和是64cm ，如果长增加一半，所得的长方体正好能分成3个完全相同的正方体，原来这个长方体的体积是（） A ．3128cm B ．3192cm C ．3256cm D ．3384cm 3、下列分数中，最简分数是（） A ．69 B ．24 C ．46 D ．29 4、下列表述正确的是（） A ．数1a 的倒数是a B ．数a 的倒数是1a C ．一个数的倒数总是比它本身大 D ．一个数的倒数总是比它本身小 5、如图所示，在ABC 中，90BAC ∠=︒，90CDA ∠=︒，则互为余角的角有（）． ·线○封○密○外A．5对B．4对C．3对D．2对6、在正整数1到10中，最小的合数与最大的素数分别是（）A．2，5 B．2，7 C．4，7 D．4，97、下列分数中，大于14且小于13的数是（）A．27B．25C．23D．128、已知C为线段AB延长线上的一点，且13BC AB=，则BC的长为AC长的（）A．34B．13C．12D．149、一根铁丝的长度是7米，如果把它平均分成5段，那么每段的长度是（）A．75米B．15C．57米D．5710、10.2%+等于（）A．1.2%B．1.02%C．1.002%D．100.2%第Ⅱ卷（非选择题 70分）二、填空题（5小题，每小题4分，共计20分）1、一个扇形的圆心角是72︒，则它的面积相当于和它同半径的圆面积的_______．（填几分之几）2、规定一种新运算：对于不小于3的自然数n，（n）表示不是n的因数的最小自然数，如()52=，()83=等等，那么()()615+=_______________．3、如果一个圆的周长为10厘米，那么这个圆的半径等于___________厘米（精确到0.1厘米）．4、定义运算如下：若{}11,a x y =，{}22,b x y =，，则1212a b x x y y ⋅=+，现已知 11,23a ⎧⎫=⎨⎬⎩⎭，1334,b ⎧⎫=⎨⎬⎩⎭，则计算⋅=a b ____________． 5、一套儿童书打七五折后售价为45元，那么这套儿童书的原价为__________元．三、解答题（5小题，每小题10分，共计50分） 1、某班级共有学生36人，其中13同学报名参加乒乓球课外活动班，29的同学报名参加了羽毛球课外活动班．求参加乒乓球课外活动班的同学比参加羽毛球课外活动班的同学多几人？ 2、计算：53 1.9124-+． 3、计算：182 6.3 1.25(3.2)35⨯-⨯- 4、已知a ，b 是实数，定义关于“△”的一种运算如下：a △b ＝（a ﹣b ）2﹣（a +b ）2．（1）小明通过计算发现a △b ＝﹣4ab ，请说明它成立的理由．（2）利用以上信息得x 1x ∆＝，若x 1x +＝3，求（x 1x -）4的值．（3）请判断等式（a △b ）△c ＝a △（b △c ）是否成立？并说明理由． 5、 “五一”长假小明和父母一起去云南旅游，他们到“野象谷”游玩是乘坐缆车进谷的，小明听导游说，这里的缆车单程长为2.35千米，在钢缆上来回均匀地安装188个吊窗，并且这些吊窗按顺序编号：1，2，3，4，…，187，188．小明入谷时乘坐的是45号吊窗，途中他观察迎面而来的吊窗的编号，他先看到142号，过一会他又看到145号，那么当他看到和145号吊窗并排时，他离缆车终点还有多少米？ -参考答案- 一、单选题 1、C 【分析】 ·线○封○密○外根据比例的基本性质判断选项的正确性．【详解】∵54a b =，∴:4:5a b =，C 选项错误．故选：C ．【点睛】本题考查比例的基本性质，解题的关键是熟练运用比例的性质进行判断．2、A【分析】设原长为cm x ，根据如果长增加一半，所得的长方体正好能分成3个完全相同的正方体，得出宽为1130.5cm 2x x ⎛⎫+÷= ⎪⎝⎭，高也是0.5cm x ，再根据棱长总和是64cm ，列出方程即可【详解】解：设原长为cm x ，宽为1130.5cm 2x x ⎛⎫+÷= ⎪⎝⎭，高也是0.5cm x ．由题意可得0.50.5644x x x ++=÷，解得：8x =．所以原来这个长方体的体积为3844128cm ⨯⨯=．故选A ．【点睛】此题属于简单的立方体切拼问题，根据题意得出：原来长方体的长是宽（或高）的2倍，是解答此题的关键；用到的知识点：长方体的棱长总和、长方体体积计算公式．3、D【分析】根据最简分数是分子，分母只有公因数1的分数即可得出答案．【详解】 ∵622142===934263，，， ∴29是最简分数，故选：D ．【点睛】本题主要考查最简分数，掌握最简分数的定义是解题的关键． 4、A 【分析】根据倒数的性质判断下列选项的正确性．【详解】 A 选项正确； B 选项错误，如果0a =就不成立； C 选项错误，2的倒数是12，122<； D 选项错误，12的倒数是2，122>．故选：A ．【点睛】本题考查倒数的性质，解题的关键是掌握倒数的性质． 5、B 【分析】根据若两个角之和等于90，则这两个角互为余角；结合题意，即可找到互为余角的对数．【详解】 ·线○封○密·○外∵90BAC ∠=︒∴90BAD CAD ∠+∠=︒，90B C ∠+∠=︒，∵90CDA ∠=︒∴90B BAD ∠+∠=︒，90C CAD ∠+∠=︒；∴有4对互为余角故选：B ．【点睛】本题考查了余角、直角、直角三角形两锐角互余的知识；解题的关键是熟练掌握余角、直角定义和直角三角形两锐角互余性质，从而完成求解．6、C【分析】由题意根据质数与合数的意义即一个自然数如果只有1和它本身两个因数，这样的数叫做质数．一个自然数，如果除了1和它本身还有别的因数，这样的数叫做合数；由此找出10以内的最小的合数与最大的素数．【详解】解：根据质数、合数的意义可知：在正整数10以内，最小的合数是4，最大的素数7；故选：C ．【点睛】本题考查质数与合数的意义，知道正整数10以内，最小的合数和最大的素数是多少是解答此题的关键．7、A【分析】根据分数的大小比较直接进行求解即可．【详解】解：A 、由121128224=,,484384784==得121473<<，故符合题意； B 、115120224=,,460360560==得112435<<，故不符合题意； C 、由112433<<，故不符合题意； D 、由111432<<，故不符合题意；故选A ．【点睛】本题主要考查分数的大小比较，熟练掌握分数的大小比较是解题的关键． 8、D 【分析】根据题意，画出图形即可得出结论．【详解】解：根据题意，画图如下 ∵13BC AB =设BC=a ，则AB=3a∴AC=AB＋BC=4a ∴BC=14AC 故选D ．【点睛】·线○封○密·○外此题考查的是求线段的关系，掌握各线段的关系是解决此题的关键．9、A【分析】用总长度除以份数即可求解．【详解】解：根据题意得，7÷5=7（米）；5米．答：每份的长度是75故选A．【点睛】本题根据除法平均分的意义，列出除法算式进行求解．10、D【分析】由题意把1可以看作100%，根据加法的意义，把两个数合并成一个数即可．【详解】解：1+0.2%=100.2%．故选：D．【点睛】本题主要考查有理数的加法中百分数加法的计算方法，注意掌握把1看作100%，直接进行计算即可．二、填空题1、15 【分析】根据扇形公式，S=2360n r π和圆的面积公式S=πr 2，分别用字母和所给的数表示出扇形和圆的面积，用扇形的面积除以圆的面积就是要求的答案．【详解】解：扇形的面积是：2272=3605r r ππ，和扇形同半径的圆面积是：πr 2，扇形的面积是它同半径的圆面积的：221()55r r ππ÷=，故答案为：15．【点睛】此题主要考查了扇形和圆面积的公式的实际应用，解答时注意条件中没有告诉的量用字母表示． 2、6 【分析】根据题意可得()()64,152==，然后求解即可．【详解】解：由题意得：()()64,152==，则有()()6154+2=6+=；故答案为6．【点睛】 ·线○封○密○外本题主要考查因数与倍数，熟练掌握求一个数的因数是解题的关键．3、1.6【分析】根据圆周长公式即可求解．【详解】10 1.62r π=≈（厘米），故答案为：1.6．【点睛】本题考查圆的周长，掌握圆的周长公式是解题的关键．4、512【分析】直接依据新定义的运算法则结合分数的乘法和加法计算即可；【详解】解：∵11,23a ⎧⎫=⎨⎬⎩⎭，1334,b ⎧⎫=⎨⎬⎩⎭∴111311235===233464121212⋅=⨯+⨯++a b 故答案为：512【点睛】本题是新定义题，主要考查了分数的乘法和加法运算及理解应用能力，正确的理解题意，熟练掌握分数的乘法和加法运算是解题的关键．5、60【解析】45÷0.75=60(元)故答案为60.三、解答题1、4人【分析】先用乘法求出参加乒乓球课外活动的人数和参加羽毛球课外活动的人数，进而求得问题．【详解】解：参加乒乓球课外活动的人数：136123⨯=（人），参加羽毛球课外活动的人数：23689⨯=（人），多的人数是：12-8=4（人）．【点睛】本题考查了分数的乘法应用题，熟悉想性质和题目的意思是解题的关键．2、17130 【分析】先把第二项和第三项交换位置,再用结合律先算后面两项的差,最后算加法.【详解】解:53 1.9124-+=5 1.90.7512+- =()5 1.90.7512+- =5 1.1512+ =5311220+ ·线○封○密○外=25916060+ =34160 =17130【点睛】完成本题要注意分析式中数据，运用合适的简便方法计算．3、12.7【分析】根据分数与小数的混合运算法则计算即可求解．【详解】解：182 6.3 1.25(3.2)35⨯-⨯-= 6.3 1.25(3.271.6)3⨯-⨯-=14.7 1.25 1.6-⨯=14.72-=12.7【点睛】本题考查了分数与小数的混合运算，掌握混合运算法则是解题关键．4、（1）见解析；（2）-4，25；（3）成立，理由见解析【分析】（1）利用所给公式可得算式（a ﹣b ）2﹣（a +b ）2，然后化简计算即可；（2）根据（1）中的发现，通过计算可得x △1x ＝﹣4，然后把x +1x ＝3代入＝（x ﹣1x ）2﹣（x +1x）2＝﹣4进行计算即可；（3）利用（1）所给规律分别进行计算即可．【详解】（1）a △b ＝（a ﹣b ）2﹣（a +b ）2＝a 2﹣2ab +b 2﹣a 2﹣2ab ﹣b 2＝﹣4ab ．故a △b ＝﹣4ab 成立；（2）由题意得，x △1x ＝（x ﹣1x ）2﹣（x +1x ）2＝﹣4•x 1x ＝﹣4， ∵x +1x ＝3，∴﹣4＝（x ﹣1x ）2﹣（x ﹣1x ）2＝（x ﹣1x ）2﹣32， ∴（x ﹣1x ）2＝5，∴（x ﹣1x ）4＝52＝25，故答案为：﹣4，25；（3）（a △b ）△c ＝a △（b △c ）成立，理由如下： ∵由（1）可知：左边＝（a △b ）△c ＝（﹣4ab ）△c ＝﹣4×（﹣4ab ）×c ＝16abc ，右边＝a △（b △c ）＝a △（﹣4bc ）＝﹣4a ×（﹣4bc ）＝16abc ， ∴（a △b ）△c ＝a △（b △c ）．【点睛】本题考查了新定义下的实数运算，解题的关键是明确题意，找出所求问题需要的条件． 5、他离缆车终点还有1100米．【分析】 ·线○封○密·○外根据题意分析列出式子计算即可；【详解】因为单程是2.35千米，所以来回是4.7千米，来回共有188个吊窗，可求出每个吊窗之间的距离，小明入谷是45号吊窗，当他和145号吊窗并排时，可以求出他终点的距离为：2350212350(14545)11001882⨯-⨯-⨯=（米）．答：他离缆车终点还有1100米．【点睛】本题主要考查了一元一次方程的应用，准确分析是解题的关键．。

最新上海市各区2020届最新中考二模数学分类汇编：选择题专题(含答案)(已纠错)

/ / 上海市各区2018届九年级中考二模数学试卷精选汇编

选择题专题宝山区、嘉定区一、选择题：（本大题共6题，每题4分，满分24分） 1.下列说法中，正确的是（▲）

（A）0是正整数；（B）1是素数；（C）22是分数；（D）722是有理数. 2.关于x的方程022mxx根的情况是（▲）（A）有两个不相等的实数根；（B）有两个相等的实数根；（C）没有实数根；（D）无法确定． 3. 将直线xy2向下平移2个单位，平移后的新直线一定不经过的象限是（▲）（A）第一象限；（B）第二象限；（C）第三象限；（D）第四象限． 4. 下列说法正确的是（▲）（A）一组数据的中位数一定等于该组数据中的某个数据；（B）一组数据的平均数和中位数一定不相等；（C）一组数据的众数可以有几个；（D）一组数据的方差一定大于这组数据的标准差. 5.对角线互相平分且相等的四边形一定是（▲）（A）等腰梯形；（B）矩形；（C）菱形；（D）正方形． 6.已知圆1O的半径长为cm6，圆2O的半径长为cm4，圆心距cmOO321，那么圆1O与圆2O的位置关系是(▲)

（A）外离；（B）外切；（C）相交；（D）内切.

1. D 2. A 3. B 4. C 5. B 6. C 长宁区一、选择题（本大题共6题, 每题4分, 满分24分）【每题只有一个正确选项, 在答题纸相应题号的选项上用2B铅笔正确填涂】 / / 1．函数12xy的图像不经过（ ▲ ）

（A）第一象限；（B）第二象限；（C）第三象限；（D）第四象限． 2．下列式子一定成立的是（ ▲ ）

（A） aaa632；（B）428xxx；

（C） aa121；（D）6321)(aa． 3．下列二次根式中，2的同类二次根式是（ ▲ ）（A）4；（B）x2；（C）92；（D）12． 4．已知一组数据2、x、8、5、5、2的众数是2，那么这组数据的中位数是（ ▲ ）（A） 3.5；（B） 4；（C） 2；（D）6.5． 5．已知圆A的半径长为4，圆B的半径长为7，它们的圆心距为d，要使这两圆没有公共点，那么d的值可以取（ ▲ ）（A） 11；（B） 6；（C） 3；（D）2． 6．已知在四边形ABCD中，AD//BC，对角线AC、BD交于点O，且AC=BD，下列四个命题中真命题是（ ▲ ）（A）若AB=CD，则四边形ABCD一定是等腰梯形；（B）若∠DBC=∠ACB，则四边形ABCD一定是等腰梯形；（C）若ODCOOBAO，则四边形ABCD一定是矩形；（D）若AC⊥BD且AO=OD，则四边形ABCD一定是正方形．一、选择题：（本大题共6题，每题4分，满分24分） 1．B； 2．D； 3．C； 4．A； 5．D； 6．C．崇明区

【2021年】上海市中考数学模拟试题汇编(含答案)

上海市中考数学精选真题预测（含答案）（考试时间100分钟，满分150分）一、选择题：（本大题共6题，每题4分，满分24分） 1、2的倒数是（） A 、 2 B 、 -2 C 、22 D 、 -222、下列算式的运算为2m 的是（）A 、42m m -⋅B 、63m m ÷C 、 21)(-m D 、24m m -3、直线y =（3-π）x 经过的象限是（）A 、一、二象限B 、一、三象限C 、二、三象限D 、二、四象限4、李老师用手机软件记录了某个月（30天）每天走路的步数（单位：万步）它将记录的结果绘制成了如图一所示的统计图，在李老师每天走路的步数这组数据中，众数与中位数分别为（）A 、 1.2与1.3B 、 1.4与1.35C 、 1.4与1.3D 、 1.3与1.35、小明用如图2所示的方法画出了△ABC 全等的△DEF ，他的具体画法是：①画射线DM ，在射线DM 上截取DE =BC ; ②以点D 为圆心，BA 长为半径画弧，以E 为圆心，CA 长为半径画弧，两弧相交于点F ；③联结FD 、FE ; 这样△DEF 就是所要画的三角形，小明这样画的依据是全等三角形判定方法中的（）A 、边角边B 、角边角C 、角角边D 、边边边6、已知两圆相交，它们的圆心距为3，一个圆的半径是2，那么另一个圆的半径长可以是（） A 、 1 B 、 3 C 、 5 D 、7二、填空题：（本大题共12题，每题4分，满分48） 7、计算：（-1）2017+02-4= ；8、函数y =x +2的定义域是；9、方程x =-x 的解是；10、如果抛物线y =a 2x -3的顶点是它的最低点，那么a 的取值范围是； 11、如果抛物线32-=ax y 的顶点是它的最低点，那么a 的取值范围是； 12、如果点P （m -3，1）在反比例函数xy 1=的图像上，那么m 的值是； 13、学校组织“中华经典诗词大赛”，共设有20个试题，其中有关“诗句理解”的试题10个，有关“诗句作者”的试题6个，有关“试卷默写”的试题4个.小杰从中任选一个试题作答，他选中有关“诗句作者”的试题的概率是；14、为了解某区3600名九年级学生的体育训练情况，随机抽取了区内200名九年级学生进行了一次体育模拟测试，把测试结果分为四个等级：A 级：优秀；B 级：良好；C 级：及格；D 级：不及格，并将测试结果绘制成了如图所示的统计图.由此估计全区九年级体育测试成绩可以达到优秀的人数约为；15、在梯形ABCD 中，AD //BC ，AD =21BC ，设AB a →→=，DCb →→=，那么BC →等于（结果用a →、b →的线性组合表示）；16、如果正n 边形的内角是它的中心角的2倍，那么边数n 的值是；17、在等腰ABC ∆中，当顶角A 的大小确定时，它的对边（即底边BC ）与邻边（即腰AB 或AC ）的比值也确定了，我们把这个比值记作T （A ），即()ABBCA A A T =∠∠=的邻边（腰）的对边（底边）.例：T （600）=1，那么T （1200）= ；18、如图，矩形ABCD ，点E 是边AD 上一点，过点E 作EF ⊥BC ，垂足为点F ，将BEF ∆绕着点E 逆时针旋转，使点B 落在边BC 上的点N 处，点F 落在边DC 上的点M 处，如果点M 恰好是边DC 的中点，那么ABAD的值是。

【小初高学习】上海市各区2018届中考二模数学分类汇编：综合计算专题(含答案)

上海市各区2018届九年级中考二模数学试卷精选汇编综合计算宝山区、嘉定区21.（本题满分10分，第（1）小题5分，第（2）小题5分）如图4，在梯形ABCD 中，AD ∥BC ，︒=∠90BAD ，AD AC =. （1）如果BAC ∠︒=∠-10BCA ，求D ∠的度数；（2）若10=AC ，31cot =∠D ，求梯形ABCD 的面积.21.解：（1）∵AD ∥BC∴CAD BCA ∠=∠ …………………1分 ∵BAC ∠︒=∠-10BCA∴BAC ∠︒=∠-10CAD …………………1分 ∵︒=∠90BAD∴BAC ∠︒=∠+90CAD∴︒=∠40CAD …………………1分 ∵AD AC =∴D ACD ∠=∠ …………………1分 ∵︒=∠+∠+∠180CAD D ACD∴︒=∠70D …………………1分(2) 过点C 作AD CH ⊥,垂足为点H ，在Rt △CHD 中，31cot =∠D ∴31cot ==∠CH HD D …………………………1分设x HD =,则x CH 3=，∵AD AC =,10=AC ∴x AH -=10在Rt △CHA 中，222AC CH AH =+ ∴22210)3()10(=+-x x∴2=x ，0=x （舍去）∴2=HD …………1分 ∴6=HC ，8=AH ，10=AD ………………1分图4DCB A图4DCBAH∵︒=∠=∠90CHD BAD ∴AB ∥CH∵AD ∥BC ∴四边形ABCH 是平行四边形 ∴8==AH BC ………1分 ∴梯形ABCD 的面积546)810(21)(21=⨯+=⨯+=CH BC AD S ………1分长宁区21．（本题满分10分，第（1）小题4分，第（2）小题6分）如图，在等腰三角形ABC 中，AB =AC ，点D 在BA 的延长线上，BC =24，135sin =∠ABC ．（1）求AB 的长；（2）若AD =6.5，求DCB ∠的余切值．21．（本题满分10分，第（1）小题4分，第（2）小题6分）解：（1）过点A 作AE ⊥BC ，垂足为点E又∵AB =AC ∴BC BE 21= ∵BC =24 ∴ BE =12 （1分）在ABE Rt ∆中，︒=∠90AEB ，135sin ==∠AB AE ABC （1分）设AE=5k,AB=13k ∵222BE AE AB += ∴1212==k BE∴1=k ， ∴55==k AE ， 1313==k AB （2分）（2）过点D 作DF ⊥BC ，垂足为点F ∵AD=6.5,AB=13 ∴BD=AB+AD=19.5∵AE ⊥BC ，DF ⊥BC ∴ ︒=∠=∠90DFB AEB ∴ DF AE //∴BDABBF BE DF AE == 又 ∵ AE =5，BE =12，AB =13， ∴18,215==BF DF （4分） ∴BF BC CF -= 即61824=-=CF （1分）在DCF Rt ∆中，︒=∠90DFC ，542156cot ===∠DF CF DCB （1分）ADB第21题图崇明区21．（本题满分10分，第(1)、(2)小题满分各5分）已知圆O 的直径12AB =，点C 是圆上一点，且30ABC ∠=︒，点P 是弦BC 上一动点，过点P 作PD OP ⊥交圆O 于点D ．（1）如图1，当PD AB ∥时，求PD 的长；（2）如图2，当BP 平分OPD ∠时，求PC 的长．21．（本题满分10分，每小题5分）（1）解：联结OD∵直径12AB = ∴6OB OD == ……………………………………1分∵PD OP ⊥ ∴90DPO =︒∠∵PD AB ∥ ∴180DPO POB +=︒∠∠ ∴90POB =︒∠ ……1分又∵30ABC =︒∠，6OB =∴30OP OB tan =︒= ………………………………………………1分 ∵在Rt POD △中，222PO PD OD += ……………………………1分∴2226PD +=∴PD =……………………………………………………………1分（2）过点O 作OH BC ⊥，垂足为H （第21题图1）ABOPCD （第21题图2）OABDPC∵OH BC ⊥∴90OHB OHP ==︒∠∠ ∵30ABC =︒∠，6OB =∴132OH OB ==，30BH OB cos =︒= ……………………2分 ∵在⊙O 中，OH BC ⊥∴CH BH == ……………………………………………………1分 ∵BP 平分OPD ∠ ∴1452BPO DPO ==︒∠∠ ∴453PH OH cot =︒= ……………………………………………1分∴3PC CH PH =-=- ………………………………………1分奉贤区21.（本题满分10分，每小题满分各5分）已知：如图6，在△ABC 中，AB =13，AC=8，135cos =∠BAC ，BD ⊥AC ，垂足为点D ，E 是BD 的中点，联结AE 并延长，交边BC 于点F ． (1) 求EAD ∠的余切值； (2) 求BFCF的值． 21、（1）56；（2）58；黄浦区图6ABCD EF21．（本题满分10分）如图，AH 是△ABC 的高，D 是边AB 上一点，CD 与AH 交于点E .已知AB =AC =6，cos B =23， AD ∶DB =1∶2.（1）求△ABC 的面积；（2）求CE ∶DE.21. 解：（1）由AB =AC =6，AH ⊥BC ，得BC =2BH .—————————————————————————（2分）在△ABH 中，AB =6，cosB =23，∠AHB =90°，得BH =2643⨯=，AH=（2分）则BC =8，所以△ABC 面积=182⨯=——————————————（1分）（2）过D 作BC 的平行线交AH 于点F ，———————————————（1分）由AD ∶DB =1∶2，得AD ∶AB =1∶3，则31CE CH BH AB DE DF DF AD ====. ——————————————（4分）金山区21．（本题满分10分，每小题5分）如图5，在矩形ABCD 中，E 是BC 边上的点，AE =BC ，DF ⊥AE ，垂足为F ．（1）求证：AF=BE ；（2）如果BE ∶EC=2∶1，求∠CDF 的余切值．ABCDFE21．解：（1）∵四边形ABCD 是矩形，∴AD =BC ，AD ∥BC ，∠B =90°，∴∠DAF=∠AEB ，……………………………………………………………………（1分）∵AE=BC ，DF ⊥AE ，∴AD=AE ，∠ AFD=∠EBA=90°，………………………（2分） ∴△ADF ≌△EAB ，∴AF =EB ，………………………………………………………（2分）（2）设BE =2k ，EC =k ，则AD =BC =AE =3k ，AF =BE =2k ，…………………………（1分）∵∠ADC =90°，∠AFD =90°，∴∠CDF +∠ADF =90°，∠DAF +∠ADF =90°， ∴∠CDF =∠DAF …………………………………………………………………（2分）在Rt △ADF 中，∠AFD =90°，DF=∴cot ∠CDF =cot ∠DAF=5AF DF ==．………………………………（2分）静安区21．（本题满分10分，第（1）小题满分5分，第（2）小题满分5分）已知：如图，边长为1的正方形ABCD 中，AC 、DB 交于点H ．DE 平分∠ADB ，交AC 于点E ．联结BE 并延长，交边AD 于点F ．（1）求证：DC =EC ；（2）求△EAF 的面积．第21题图21．（本题满分10分, 第（1）小题5分，第（2）小题5分）解：（1）∵正方形ABCD ，∴DC=BC=BA=AD , ∠BAD =∠ADC =∠DCB =∠CBA =90° AH=DH=CH=BH , AC ⊥BD ,∴∠ADH =∠HDC =∠DCH =∠DAE = 45°． …………（2分）又∵DE 平分∠AD B ∴∠ADE =∠EDH∵∠DAE +∠ADE =∠DEC , ∠EDH +∠HDC =∠EDC …………（1分） ∴∠EDC =∠DEC …………（1分） ∴DC =EC …………（1分）（2）∵正方形ABCD ，∴AD ∥BC , ∴△AFE ∽△CBE ∴2)(ECAE S S CEB AEF =∆∆ ………………………………（1分） ∵AB=BC=DC=EC =1，AC =2,∴AE =12- …………………………（1分）Rt △BHC 中， BH =22BC =22, ∴在△BEC 中，BH ⊥EC , 4222121=⨯⨯=∆BEC S ……………………（2分） ∴2)12(42-=∆AEF S , ∴4423)223(42-=-⨯=∆AEF S …………（1分）闵行区21．（本题满分10分，其中第（1）小题4分，第（2）小题6分）已知一次函数24y x =-+的图像与x 轴、y 轴分别交于点A 、B ，以AB 为边在第一象限内作直角三角形ABC ，且∠BAC = 90o ，1tan 2ABC ∠=．（1）求点C 的坐标；第21题图（2）在第一象限内有一点M （1，m ），且点M 与点C 位于直线AB 的同侧，使得ABC ABM S S ∆∆=2，求点M 的坐标．21．解：（1）令0y =，则240x -+=，解得：2x =，∴点A 坐标是（2，0）．令0x =，则4y =，∴点B 坐标是（0，4）．………………………（1分）∴AB ==．………………………………（1分） ∵90BAC ∠=，1tan 2ABC ∠=，∴AC 过C 点作CD ⊥x 轴于点D ，易得OBA DAC ∆∆∽．…………………（1分） ∴2AD =，1CD =，∴点C 坐标是（4，1）．………………………（1分）（2）11522ABC S AB AC ∆=⋅=⨯=．………………………………（1分） ∵2ABM ABC S S ∆∆=，∴52ABM S ∆=．……………………………………（1分）∵(1M ，)m ，∴点M 在直线1x =上；令直线1x =与线段AB 交于点E ，2ME m =-；……………………（1分）分别过点A 、B 作直线1x =的垂线，垂足分别是点F 、G ，∴AF +BG = OA = 2；……………………………………………………（1分）∴111()222ABM BME AME S S S ME BG ME AF ME BG AF ∆∆=+=⋅+⋅=+1152222ME OA ME =⋅=⨯⨯=…………………（1分） ∴52ME =，522m -=，92m =，∴(1M ，92）．……………………（1分）普陀区21．（本题满分10分）如图7，在Rt △ABC 中，90C ∠=，点D 在边BC 上，DE ⊥AB ，点E 为垂足，7AB =，45DAB ∠=，3tan 4B =. （1）求DE 的长；（2）求CDA ∠的余弦值． CD21．解：（1）∵DE ⊥AB ，∴︒=∠90DEA又∵45DAB ∠=，∴AE DE =． ······································································· （1分）在Rt △DEB 中，︒=∠90DEB ，43tan =B ，∴43=BE DE ． ······························· （1分）设x DE 3=，那么x AE 3=，x BE 4=．∵7AB =，∴743=+x x ，解得1=x ． ······························································ （2分） ∴3=DE ． ············································································································· （1分）（2）在Rt △ADE 中，由勾股定理，得23=AD ． ················································ （1分）同理得5=BD ． ······································································································ （1分）在Rt △ABC 中，由43tan =B ，可得54cos =B ．∴528=BC ． ····················· （1分） ∴53=CD ． ············································································································ （1分）∴102cos ==∠AD CD CDA ． ················································································ （1分）即CDA ∠青浦区21. (本题满分10分，第（1）、（2）小题，每小题5分）如图5，在Rt △ABC 中，∠C =90°，AC=3，BC =4，∠ABC 的平分线交边AC 于点D ，延长BD 至点E ，且BD=2DE ，联结AE ．（1）求线段CD 的长；（2）求△ADE 的面积.21．解：（1）过点D 作DH ⊥AB ，垂足为点H ． ································································· （1分）∵BD 平分∠ABC ，∠C =90°，∴DH = DC =x ， ··································································································· （1分）ED A图5则AD =3-x ．∵∠C =90°，AC=3，BC =4，∴AB =5. ····························································· （1分） ∵sin ∠==HD BCBAC AD AB， ∴435=-x x ， ·································································································· （1分） ∴43=x . ·········································································································· （1分）（2）1141052233=⋅=⨯⨯=ABD S AB DH . ···························································· （1分）∵BD=2DE ， ∴2==ABD ADES BDSDE， ····················································································· （3分） ∴1015323=⨯=ADES. ···················································································· （1分）松江区21.（本题满分10分, 每小题各5分）如图，已知△ABC 中，∠B =45°，1tan 2C =， BC =6.（1）求△ABC 面积；（2）AC 的垂直平分线交AC 于点D ，交BC 于点E. 求DE 的长．21.（本题满分10分, 每小题各5分）解：（1）过点A 作AH ⊥BC 于点H …………1分在Rt ABC ∆中，∠B =45°设AH =x ,则BH =x ………………………………1分(第21题图)DA在Rt AHC ∆中，1tan 2AH C HC == ∴HC=2x ………………………………………………………1分∵BC =6∴x+2x =6 得x =2∴AH =2…………………………………………………………1分 ∴162ABC S BC AH ∆=⋅⋅=……………………………………1分 (2)由（1）得AH =2，CH =4在Rt AHC ∆中，AC 2分∵DE 垂直平分AC∴12CD AC == ED ⊥AC …………………………………………………1分在Rt EDC ∆中，1tan 2ED C CD ==……………………………1分∴DE = ………………………………………………1分徐汇区21. 如图，在Rt ABC ∆中，90C ∠=︒，3AC =，4BC =，AD 平分BAC ∠交BC 于点D .（1）求tan DAB ∠；（2）若⊙O 过A 、D 两点，且点O 在边AB 上，用尺规作图的方法确定点O 的位置并求出的⊙O 半径.（保留作图轨迹，不写作法）杨浦区21、（本题满分10分，第（1）小题满分3分，第（2）小题满分7分）已知，如图5，在梯形ABCD中，DC//AB, AD=BC, BD平分∠ABC，∠A=600求：（1）求∠CDB的度数（2）当AD=2时，求对角线BD的长和梯形ABCD的面积。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

目录第一套：上海市各区2018届九年级中考二模选择题13区共78个

第二套：全国各地中考2018选择压轴题汇编13个第三套：上海市2019年中考汇编填空压轴题共13个第四套：2018全国各地中考数学填空压轴题汇编15题第五套：2019上海市各区中考第23题几何证明题专题汇编共13个

第六套：2018上海市各区中考第25题压轴题汇编共13个第七套：2019上海市各区中考第25题压轴题汇编共13个上海市各区2018届九年级中考二模数学试卷精选汇编选择题专题宝山区、嘉定区一、选择题：（本大题共6题，每题4分，满分24分） 1.下列说法中，正确的是（▲）

（A）0是正整数；（B）1是素数；（C）22是分数；（D）722是有理数. 2.关于x的方程022mxx根的情况是（▲）（A）有两个不相等的实数根；（B）有两个相等的实数根；

（C）没有实数根；（D）无法确定． 3. 将直线xy2向下平移2个单位，平移后的新直线一定不经过的象限是（▲）

（A）第一象限；（B）第二象限；（C）第三象限；（D）第四象限．

4. 下列说法正确的是（▲）（A）一组数据的中位数一定等于该组数据中的某个数据；（B）一组数据的平均数和中位数一定不相等；（C）一组数据的众数可以有几个；（D）一组数据的方差一定大于这组数据的标准差. 5.对角线互相平分且相等的四边形一定是（▲）（A）等腰梯形；（B）矩形；（C）菱形；（D）正方形．

6.已知圆1O的半径长为cm6，圆2O的半径长为cm4，圆心距cmOO321，那么圆1O与圆2O的位置关系是(▲)

（A）外离；（B）外切；（C）相交；（D）内切.

1. D 2. A 3. B 4. C 5. B 6. C 长宁区一、选择题（本大题共6题, 每题4分, 满分24分）【每题只有一个正确选项, 在答题纸相应题号的选项上用2B铅笔正确填涂】 1．函数12xy的图像不经过（ ▲ ）（A）第一象限；（B）第二象限；（C）第三象限；（D）第四象限． 2．下列式子一定成立的是（ ▲ ）（A） aaa632；（B）428xxx；

那么d的值可以取（ ▲ ）（A） 11；（B） 6；（C） 3；（D）2． 6．已知在四边形ABCD中，AD//BC，对角线AC、BD交于点O，且AC=BD，下列四个命题中真命题是（ ▲ ）（A）若AB=CD，则四边形ABCD一定是等腰梯形；（B）若∠DBC=∠ACB，则四边形ABCD一定是等腰梯形；（C）若ODCOOBAO，则四边形ABCD一定是矩形；

（D）若AC⊥BD且AO=OD，则四边形ABCD一定是正方形．一、选择题：（本大题共6题，每题4分，满分24分） 1．B； 2．D； 3．C； 4．A； 5．D； 6．C．崇明区一、选择题（本大题共6题，每题4分，满分24分） 1．8的相反数是…………………………………………………………………………………（ ▲ ） (A)18； (B)8； (C)18； (D)

8． 2．下列计算正确的是 …………………………………………………………………………（ ▲ ） (A)235； (B)23aaa； (C)33(2)2aa； (D)632aaa

．

3．今年3月12日，某学校开展植树活动，某植树小组20名同学的年龄情况如下表：年龄（岁） 12 13 14 15 16

人数 1 4 3 7 5 那么这20名同学年龄的众数和中位数分别是……………………………………………（ ▲ ） (A)15,14； (B)15,15； (C)16,14； (D)16,15．

4．某美术社团为练习素描，他们第一次用120元买了若干本相同的画册，第二次用240元在同一家商店买与上一次相同的画册，这次商家每本优惠4元，结果比上次多买了20本．求第一次买了多少本画册？设第一次买了x本画册，列方程正确的是 ………………………（ ▲ ） (A)120240420xx； (B)240120420xx； (C)120240420xx； (D)240120420xx．

5．下列所述图形中，既是轴对称图形又是中心对称图形的是 ……………………………（ ▲ ） (A) 等边三角形； (B) 平行四边形； (C) 菱形； (D) 正五边形． 6．已知ABC△中，D、E分别是AB、AC边上的点，DEBC∥，点F是BC边上一点，联结AF交DE于点G，那么下列结论中一定正确的是 ………………………………………（ ▲ ） (A)EGFGGDAG； (B)EGAEGDAD； (C)EGAGGDGF； (D)EGCFGDBF．

一、选择题：（本大题共6题，每题4分，满分24分） 1．D； 2．B； 3．B； 4．A； 5．C； 6．D. 奉贤区 1．下列二次根式中，与a是同类二次根式的是（）（A）2a；（B）a2；（C）a4；（D）a4． 2．某班要推选学生参加学校的“诗词达人”比赛，有7名学生报名参加班级选拔赛，他们的选拔赛成绩各不相同，现取其中前3名参加学校比赛．小红要判断自己能否参加学校比赛，在知道自己成绩的情况下，还需要知道这7名学生成绩的（）（A）众数；（B）中位数；（C）平均数；（D）方差． 3．下列四个不等式组中，其中一个不等式组的解集在数轴上的正确表示如图1所示，这个不等式组是（）（A）；，32xx （B）；，32xx （C）；，32xx （D）.32xx，

4．如果将直线l1：22xy平移后得到直线l2：xy2，那么下列平移过程正确的是（）（A）将l1向左平移2个单位；（B）将l1向右平移2个单位；（C）将l1向上平移2个单位；（D）将l1向下平移2个单位． 5.将一把直尺和一块含30°和60°角的三角板ABC按如图2所示的位置放置，如果∠CDE=40°,那么∠BAF的大小为（）（A）10°；（B）15°；（C）20°；（D）25°.

6.直线AB、CD相交于点O，射线 OM平分∠AOD，点P在射线OM

图1

图2 上（点P与点O不重合），如果以点P为圆心的圆与直线AB相离，那么圆P与直线CD的位置关系是（）

（A）相离；（B）相切；（C）相交；（D）不确定. 一、选择题： 1、C； 2、B； 3、D； 4、C； 5、A； 6、A；黄浦区一、选择题：（本大题共6题，每题4分，满分24分）【下列各题的四个选项中，有且只有一个是正确的，选择正确项的代号并填涂在答题纸的相应位置上.】 1．下列实数中，介于23与32之间的是（）（A）2；（B）3；（C）227；（D）． 2．下列方程中没有实数根的是（）（A）210xx；（B）210xx；（C）210x；（D）20xx． 3．一个反比例函数与一个一次函数在同一坐标平面内的图像如图示，如果其中的反比例函数解析式为kyx，那么该一次函数可能的解析式是（）（A）ykxk；（B）ykxk；（C）ykxk；（D）ykxk． 4．一个民营企业10名员工的月平均工资如下表，则能较好反映这些员工月平均工资水平的是（）人次 1 1 1 2 1 1 3 工资 30 3 2 1.5 1.2 2 0.8

（工资单位：万元）（A）平均数；（B）中位数；（C）众数；（D）标准差． 5．计算：ABBAuuuruuur（）（A）ABuuur；（B）BAuuur；（C）0r；（D）0． 6．下列命题中，假命题是（）（A）如果一条直线平分弦和弦所对的一条弧，那么这条直线经过圆心，并且垂直于这条弦；（B）如果一条直线平分弦所对的两条弧，那么这条直线经过圆心，并且垂直于这条弦；（C）如果一条直线经过圆心，并且平分弦，那么该直线平分这条弦所对的弧，并且垂直于这条弦；（D）如果一条直线经过圆心，并且垂直弦，那么该直线平分这条弦和弦所对的弧．

一、选择题（本大题6小题，每小题4分，满分24分） 1.A ； 2.B ； 3.B； 4.B； 5.C； 6.C. 金山区 1．下列各数中，相反数等于本身的数是（▲）（A）1；（B）0；（C）1；（D）2． 2．单项式32ab的次数是（▲）（A）2；（B）3 （C）4；（D）5． 3．如果将抛物线22yx向上平移1个单位，那么所得新抛物线的表达式是（▲）（A）221yx；（B）221yx；（C）221yx；（D）221yx． 4．如果一组数据1，2，x，5，6的众数为6，则这组数据的中位数为（▲）（A）1；（B）2 （C）5；（D）6． 5．如图1，□ABCD中，E是BC的中点，设ABauuurr，ADbuuurr，那么向量AEuuur用向量ar、br表示为（▲）

A B D

C E

图1