2018中考数学试题分类汇编 压轴题(全)
2018年全国各地中考数学压轴题汇编:几何综合(西北专版)(解析卷)

2018年全国各地中考数学压轴题汇编(西北专版)几何综合参考答案与试题解析一.选择题(共10小题)1.(2018•陕西)如图,在△ABC中,AC=8,∠ABC=60°,∠C=45°,AD⊥BC,垂足为D,∠ABC的平分线交AD于点E,则AE的长为()A.B.2C.D.3解:∵AD⊥BC,∴∠ADC=∠ADB=90°.在Rt△ADC中,AC=8,∠C=45°,∴AD=CD,∴AD=AC=4.在Rt△ADB中,AD=4,∠ABD=60°,∴BD=AD=.∵BE平分∠ABC,∴∠EBD=30°.在Rt△EBD中,BD=,∠EBD=30°,∴DE=BD=,∴AE=AD﹣DE=.故选:C.2.(2018•兰州)如图,矩形ABCD中,AB=3,BC=4,EF∥DF且BE与DF之间的距离为3,则AE的长是()A.B.C.D.解:如图所示:过点D作DG⊥BE,垂足为G,则GD=3.∵∠A=∠G,∠AEB=∠GED,AB=GD=3,∴△AEB≌△GED.∴AE=EG.设AE=EG=x,则ED=4﹣x,在Rt△DEG中,ED2=GE2+GD2,x2+32=(4﹣x)2,解得:x=.故选:C.3.(2018•陕西)如图,在菱形ABCD中.点E、F、G、H分别是边AB、BC、CD和DA 的中点,连接EF、FG、GH和HE.若EH=2EF,则下列结论正确的是()A.AB=EF B.AB=2EF C.AB=EF D.AB=EF解:连接AC、BD交于O,∵四边形ABCD是菱形,∴AC⊥BD,OA=OC,OB=OD,∵点E、F、G、H分别是边AB、BC、CD和DA的中点,∴EF=AC,EF∥AC,EH=BD,EH∥BD,∴四边形EFGH是矩形,∵EH=2EF,∴OB=2OA,∴AB==OA,∴AB=EF,故选:D.4.(2018•兰州)如图,将▱ABCD沿对角线BD折叠,使点A落在点E处,交BC于点F,若∠ABD=48°,∠CFD=40°,则∠E为()A.102°B.112°C.122°D.92°解:∵AD∥BC,∴∠ADB=∠DBC,由折叠可得∠ADB=∠BDF,∴∠DBC=∠BDF,又∵∠DFC=40°,∴∠DBC=∠BDF=∠ADB=20°,又∵∠ABD=48°,∴△ABD中,∠A=180°﹣20°﹣48°=112°,∴∠E=∠A=112°,故选:B.5.(2018•陕西)如图,△ABC是⊙O的内接三角形,AB=AC,∠BCA=65°,作CD∥AB,并与⊙O相交于点D,连接BD,则∠DBC的大小为()A.15°B.35°C.25°D.45°解:∵AB=AC、∠BCA=65°,∴∠CBA=∠BCA=65°,∠A=50°,∵CD∥AB,∴∠ACD=∠A=50°,又∵∠ABD=∠ACD=50°,∴∠DBC=∠CBA﹣∠ABD=15°,故选:A.6.(2018•白银)如图,点E是正方形ABCD的边DC上一点,把△ADE绕点A顺时针旋转90°到△ABF的位置,若四边形AECF的面积为25,DE=2,则AE的长为()A.5 B.C.7 D.解:∵把△ADE顺时针旋转△ABF的位置,∴四边形AECF的面积等于正方形ABCD的面积等于25,∴AD=DC=5,∵DE=2,∴Rt△ADE中,AE==.故选:D.7.(2018•青海)小桐把一副直角三角尺按如图所示的方式摆放在一起,其中∠E=90°,∠C=90°,∠A=45°,∠D=30°,则∠1+∠2等于()A.150°B.180°C.210°D.270°解:如图:∵∠1=∠D+∠DOA,∠2=∠E+∠EPB,∵∠DOA=∠COP,∠EPB=∠CPO,∴∠1+∠2=∠D+∠E+∠COP+∠CPO=∠D+∠E+180°﹣∠C=30°+90°+180°﹣90°=210°,故选:C.8.(2018•新疆)如图,矩形纸片ABCD中,AB=6cm,BC=8cm.现将其沿AE对折,使得点B落在边AD上的点B1处,折痕与边BC交于点E,则CE的长为()A.6cm B.4cm C.3cm D.2cm解:∵沿AE对折点B落在边AD上的点B1处,∴∠B=∠AB1E=90°,AB=AB1,又∵∠BAD=90°,∴四边形ABEB1是正方形,∴BE=AB=6cm,∴CE=BC﹣BE=8﹣6=2cm.故选:D.9.(2018•白银)如图,⊙A过点O(0,0),C(,0),D(0,1),点B是x轴下方⊙A上的一点,连接BO,BD,则∠OBD的度数是()A.15°B.30°C.45°D.60°解:连接DC,∵C(,0),D(0,1),∴∠DOC=90°,OD=1,OC=,∴∠DCO=30°,∴∠OBD=30°,故选:B.10.(2018•新疆)如图,点P是边长为1的菱形ABCD对角线AC上的一个动点,点M,N分别是AB,BC边上的中点,则MP+PN的最小值是()A.B.1 C.D.2解:如图,作点M关于AC的对称点M′,连接M′N交AC于P,此时MP+NP有最小值,最小值为M′N 的长.∵菱形ABCD关于AC对称,M是AB边上的中点,∴M′是AD的中点,又∵N是BC边上的中点,∴AM′∥BN,AM′=BN,∴四边形ABNM′是平行四边形,∴M′N=AB=1,∴MP+NP=M′N=1,即MP+NP的最小值为1,故选:B.二.填空题(共7小题)11.(2018•陕西)如图,在正五边形ABCDE中,AC与BE相交于点F,则∠AFE的度数为72°.解:∵五边形ABCDE是正五边形,∴∠EAB=∠ABC==108°,∵BA=BC,∴∠BAC=∠BCA=36°,同理∠ABE=36°,∴∠AFE=∠ABF+∠BAF=36°+36°=72°,故答案为:72°.12.(2018•兰州)如图,M、N是正方形ABCD的边CD上的两个动点,满足AM=BN,连接AC交BN于点E,连接DE交AM于点F,连接CF,若正方形的边长为6,则线段CF 的最小值是3﹣3.解:如图,在正方形ABCD中,AD=BC=CD,∠ADC=∠BCD,∠DCE=∠BCE,在Rt△ADM和Rt△BCN中,,∴Rt△ADM≌Rt△BCN(HL),∴∠DAM=∠CBN,在△DCE和△BCE中,,∴△DCE≌△BCE(SAS),∴∠CDE=∠CBE∴∠DCM=∠CDE,∵∠ADF+∠CDE=∠ADC=90°,∴∠DAM+∠ADF=90°,∴∠AFD=180°﹣90°=90°,取AD的中点O,连接OF、OC,则OF=DO=AD=3,在Rt△ODC中,OC==3根据三角形的三边关系,OF+CF>OC,∴当O、F、C三点共线时,CF的长度最小,最小值=OC﹣OF=3﹣3.故答案为:3﹣3.13.(2018•青海)如图,四边形ABCD与四边形EFGH位似,其位似中心为点O,且=,则=.解:∵四边形ABCD与四边形EFGH位似,其位似中心为点O,且=,∴=,则==.故答案为:.14.(2018•陕西)如图,点O是▱ABCD的对称中心,AD>AB,E、F是AB边上的点,且EF=AB;G、H是BC边上的点,且GH=BC,若S1,S2分别表示△EOF和△GOH的面积,则S1与S2之间的等量关系是=.解:∵==,==,∴S1=S△AOB,S2=S△BOC.∵点O是▱ABCD的对称中心,=S△BOC=S▱ABCD,∴S△AOB∴==.即S1与S2之间的等量关系是=.故答案为=.15.(2018•白银)如图,分别以等边三角形的每个顶点为圆心、以边长为半径,在另两个顶点间作一段圆弧,三段圆弧围成的曲边三角形称为勒洛三角形.若等边三角形的边长为a,则勒洛三角形的周长为πa.解:如图.∵△ABC是等边三角形,∴∠A=∠B=∠C=60°,AB=BC=CA=a,∴的长=的长=的长==,∴勒洛三角形的周长为×3=πa.故答案为πa.16.(2018•青海)如图,用一个半径为20cm,面积为150πcm2的扇形铁皮,制作一个无底的圆锥(不计接头损耗),则圆锥的底面半径r为7.5cm.解:解:设铁皮扇形的半径和弧长分别为R、l,圆锥形容器底面半径为r,则由题意得R=20,由Rl=150π得l=15π;由2πr=15π得r=7.5cm.故答案是:7.5cm.17.(2018•新疆)如图,△ABC是⊙O的内接正三角形,⊙O的半径为2,则图中阴影部分的面积是.解:∵△ABC是等边三角形,∴∠C=60°,根据圆周角定理可得∠AOB=2∠C=120°,∴阴影部分的面积是=π,故答案为:三.解答题(共15小题)18.(2018•陕西)如图,已知:在正方形ABCD中,M是BC边上一定点,连接AM.请用尺规作图法,在AM上作一点P,使△DPA∽△ABM.(不写作法,保留作图痕迹)解:如图所示,点P即为所求:∵DP⊥AM,∴∠APD=∠ABM=90°,∵∠BAM+∠PAD=90°,∠PAD+∠ADP=90°,∴∠BAM=∠ADP,∴△DPA∽△ABM.19.(2018•宁夏)已知:AB为⊙O的直径,延长AB到点P,过点P作圆O的切线,切点为C,连接AC,且AC=CP.(1)求∠P的度数;(2)若点D是弧AB的中点,连接CD交AB于点E,且DE•DC=20,求⊙O的面积.(π取3.14)解:(1)连接OC,∵PC为⊙O的切线,∴∠OCP=90°,即∠2+∠P=90°,∵OA=OC,∴∠CAO=∠1,∵AC=CP,∴∠P=∠CAO,又∵∠2是△AOC的一个外角,∴∠2=2∠CAO=2∠P,∴2∠P+∠P=90°,∴∠P=30°;(2)连接AD,∵D为的中点,∴∠ACD=∠DAE,∴△ACD∽△EAD,∴=,即AD2=DC•DE,∵DC•DE=20,∴AD=2,∵=,∴AD=BD,∵AB是⊙O的直径,∴Rt△ADB为等腰直角三角形,∴AB=2,∴OA=AB=,=π•OA2=10π=31.4.∴S⊙O20.(2018•陕西)如图,在Rt△ABC中,∠ACB=90°,以斜边AB上的中线CD为直径作⊙O,分别与AC、BC交于点M、N.(1)过点N作⊙O的切线NE与AB相交于点E,求证:NE⊥AB;(2)连接MD,求证:MD=NB.证明:(1)连接ON,如图,∵CD为斜边AB上的中线,∴CD=AD=DB,∴∠1=∠B,∵OC=ON,∴∠1=∠2,∴∠2=∠B,∴ON∥DB,∵NE为切线,∴ON⊥NE,∴NE⊥AB;(2)连接DN,如图,∵CD为直径,∴∠CMD=∠CND=90°,而∠MCB=90°,∴四边形CMDN为矩形,∴DM=CN,∵DN⊥BC,∠1=∠B,∴CN=BN,∴MD=NB.21.(2018•宁夏)已知点E为正方形ABCD的边AD上一点,连接BE,过点C作CN⊥BE,垂足为M,交AB于点N.(1)求证:△ABE≌△BCN;(2)若N为AB的中点,求tan∠ABE.(1)证明:∵四边形ABCD为正方形∴AB=BC,∠A=∠CBN=90°,∠1+∠2=90°∵CM⊥BE,∴∠2+∠3=90°∴∠1=∠3在△ABE和△BCN中∴△ABE≌△BCN(ASA);(2)∵N为AB中点,∴BN=AB又∵△ABE≌△BCN,∴AE=BN=AB在Rt△ABE中,tan∠ABE═.22.(2018•兰州)如图,在△ABC中,过点C作CD∥AB,E是AC的中点,连接DE并延长,交AB于点F,交CB的延长线于点G,连接AD,CF.(1)求证:四边形AFCD是平行四边形.(2)若GB=3,BC=6,BF=,求AB的长.解:(1)∵E是AC的中点,∴AE=CE,∵AB∥CD,∴∠AFE=∠CDE,在△AEF和△CED中,∵,∴△AEF≌△CED(AAS),∴AF=CD,又AB∥CD,即AF∥CD,∴四边形AFCD是平行四边形;(2)∵AB∥CD,∴△GBF∽△GCD,∴=,即=,解得:CD=,∵四边形AFCD是平行四边形,∴AF=CD=,∴AB=AF+BF=+=6.23.(2018•白银)已知矩形ABCD中,E是AD边上的一个动点,点F,G,H分别是BC,BE,CE的中点.(1)求证:△BGF≌△FHC;(2)设AD=a,当四边形EGFH是正方形时,求矩形ABCD的面积.解:(1)∵点F,G,H分别是BC,BE,CE的中点,∴FH∥BE,FH=BE,FH=BG,∴∠CFH=∠CBG,∵BF=CF,∴△BGF≌△FHC,(2)当四边形EGFH是正方形时,可得:EF⊥GH且EF=GH,∵在△BEC中,点,H分别是BE,CE的中点,∴GH=,且GH∥BC,∴EF⊥BC,∵AD∥BC,AB⊥BC,∴AB=EF=GH=a,∴矩形ABCD的面积=.24.(2018•陕西)问题提出(1)如图①,在△ABC中,∠A=120°,AB=AC=5,则△ABC的外接圆半径R的值为5.问题探究(2)如图②,⊙O的半径为13,弦AB=24,M是AB的中点,P是⊙O上一动点,求PM 的最大值.问题解决(3)如图③所示,AB、AC、是某新区的三条规划路,其中AB=6km,AC=3km,∠BAC=60°,所对的圆心角为60°,新区管委会想在路边建物资总站点P,在AB,AC路边分别建物资分站点E、F,也就是,分别在、线段AB和AC上选取点P、E、F.由于总站工作人员每天都要将物资在各物资站点间按P→E→F→P的路径进行运输,因此,要在各物资站点之间规划道路PE、EF和FP.为了快捷、环保和节约成本.要使得线段PE、EF、FP 之和最短,试求PE+EF+FP的最小值.(各物资站点与所在道路之间的距离、路宽均忽略不计)解:(1)设O是△ABC的外接圆的圆心,∴OA=OB=OC,∵∠A=120°,AB=AC=5,∴△ABO是等边三角形,∴AB=OA=OB=5,(2)当PM⊥AB时,此时PM最大,连接OA,由垂径定理可知:AM=AB=12,∵OA=13,∴由勾股定理可知:OM=5,∴PM=OM+OP=18,(3)设连接AP,OP分别以AB、AC所在直线为对称轴,作出P关于AB的对称点为M,P关于AC的对称点为N,连接MN,交AB于点E,交AC于点F,连接PE、PF,∴AM=AP=AN,∵∠MAB=∠PAB,∠NAC=∠PAC,∴∠BAC=∠PAB+∠PAC=∠MAB+∠NAC=60°,∴∠MAN=120°∴M、P、N在以A为圆心,AP为半径的圆上,设AP=r,易求得:MN=r,∵PE=ME,PF=FN,∴PE+EF+PF=ME+EF+FN=MN=r,∴当AP最小时,PE+EF+PF可取得最小值,∵AP+OP≥OA,∴AP≥OA﹣OP,即点P在OA上时,AP可取得最小值,设AB的中点为Q,∴AQ=AC=3,∵∠BAC=60°,∴AQ=QC=AC=BQ=3,∴∠ABC=∠QCB=30°,∴∠ACB=90°,∴由勾股定理可知:BC=3,∵∠BOC=60°,OB=OC=3,∴△OBC是等边三角形,∴∠OBC=60°,∴∠ABO=90°∴由勾股定理可知:OA=3,∵OP=OB=3,∴AP=r=OA﹣OP=3﹣3,∴PE+EF+PF=MN=r=3﹣9∴PE+EF+PF的最小值为(3﹣9)km.25.(2018•兰州)如图,AB为⊙O的直径,C为⊙O上一点,D为BA延长线上一点,∠ACD=∠B.(1)求证:DC为⊙O的切线;(2)线段DF分别交AC,BC于点E,F且∠CEF=45°,⊙O的半径为5,sinB=,求CF 的长.(1)证明:连接OC,∵AB为⊙O的直径,∴∠ACB=∠BCO+∠OCA=90°,∵OB=OC,∴∠B=∠BCO,∵∠ACD=∠B,∴∠ACD=∠BCO,∴∠ACD+∠OCA=90°,即∠OCD=90°,∴DC为⊙O的切线;(2)解:Rt△ACB中,AB=10,sinB=,∴AC=6,BC=8,∵∠ACD=∠B,∠ADC=∠CDB,∴△CAD∽△BCD,∴,设AD=3x,CD=4x,Rt△OCD中,OC2+CD2=OD2,52+(4x)2=(5+3x)2,x=0(舍)或,∵∠CEF=45°,∠ACB=90°,∴CE=CF,设CF=a,∵∠CEF=∠ACD+∠CDE,∠CFE=∠B+∠BDF,∴∠CDE=∠BDF,∵∠ACD=∠B,∴△CED∽△BFD,∴,∴,a=,∴CF=.26.(2018•青海)如图,在平行四边形ABCD中,E为AB边上的中点,连接DE并延长,交CB的延长线于点F.(1)求证:AD=BF;(2)若平行四边形ABCD的面积为32,试求四边形EBCD的面积.解:(1)∵E是AB边上的中点,∴AE=BE.∵AD∥BC,∴∠ADE=∠F.在△ADE和△BFE中,∠ADE=∠F,∠DEA=∠FEB,AE=BE,∴△ADE≌△BFE.∴AD=BF.(2)过点D作DM⊥AB与M,则DM同时也是平行四边形ABCD的高.=•AB•DM=AB•DM=×32=8,∴S△AED=32﹣8=24.∴S四边形EBCD27.(2018•白银)如图,点O是△ABC的边AB上一点,⊙O与边AC相切于点E,与边BC,AB分别相交于点D,F,且DE=EF.(1)求证:∠C=90°;(2)当BC=3,sinA=时,求AF的长.解:(1)连接OE,BE,∵DE=EF,∴∴∠OBE=∠DBE∵OE=OB,∴∠OEB=∠OBE∴∠OEB=∠DBE,∴OE∥BC∵⊙O与边AC相切于点E,∴OE⊥AC∴BC⊥AC∴∠C=90°(2)在△ABC,∠C=90°,BC=3,sinA=∴AB=5,设⊙O的半径为r,则AO=5﹣r,在Rt△AOE中,sinA===∴r=∴AF=5﹣2×=28.(2018•青海)如图△ABC内接于⊙O,∠B=60°,CD是⊙O的直径,点P是CD延长线上一点,且AP=AC.(2)若PD=,求⊙O的直径.解:(1)证明:连接OA,∵∠B=60°,∴∠AOC=2∠B=120°,又∵OA=OC,∴∠OAC=∠OCA=30°,又∵AP=AC,∴∠P=∠ACP=30°,∴∠OAP=∠AOC﹣∠P=90°,∴OA⊥PA,∴PA是⊙O的切线.(2)在Rt△OAP中,∵∠P=30°,∴PO=2OA=OD+PD,又∵OA=OD,∴PD=OA,∵PD=,∴2OA=2PD=2.∴⊙O的直径为2.29.(2018•新疆)如图,▱ABCD的对角线AC,BD相交于点O.E,F是AC上的两点,并且AE=CF,连接DE,BF.(2)若BD=EF,连接EB,DF,判断四边形EBFD的形状,并说明理由.(1)证明:∵四边形ABCD是平行四边形,∴OA=OC,OB=OD,∵AE=CF,∴OE=OF,在△DEO和△BOF中,∴△DOE≌△BOF.(2)解:结论:四边形EBFD是矩形.理由:∵OD=OB,OE=OF,∴四边形EBFD是平行四边形,∵BD=EF,∴四边形EBFD是矩形.30.(2018•青海)请认真阅读下面的数学小探究系列,完成所提出的问题:(1)探究1:如图1,在等腰直角三角形ABC中,∠ACB=90°,BC=a,将边AB绕点B顺时针旋转90°得到线段BD,连接CD.求证:△BCD的面积为a2.(提示:过点D作BC 边上的高DE,可证△ABC≌△BDE)(2)探究2:如图2,在一般的Rt△ABC中,∠ACB=90°,BC=a,将边AB绕点B顺时针旋转90°得到线段BD,连接CD.请用含a的式子表示△BCD的面积,并说明理由.(3)探究3:如图3,在等腰三角形ABC中,AB=AC,BC=a,将边AB绕点B顺时针旋转90°得到线段BD,连接CD.试探究用含a的式子表示△BCD的面积,要有探究过程.解:(1)如图1,过点D作DE⊥CB交CB的延长线于E,∴∠BED=∠ACB=90°,由旋转知,AB=AD,∠ABD=90°,∴∠ABC+∠DBE=90°,∵∠A+∠ABC=90°,∴∠A=∠DBE,在△ABC和△BDE中,,∴△ABC≌△BDE(AAS)∴BC=DE=a.=BC•DE∵S△BCD=;∴S△BCD(2)△BCD的面积为.理由:如图2,过点D作BC的垂线,与BC的延长线交于点E.∴∠BED=∠ACB=90°,∵线段AB绕点B顺时针旋转90°得到线段BE,∴AB=BD,∠ABD=90°.∴∠ABC+∠DBE=90°.∵∠A+∠ABC=90°.∴∠A=∠DBE.在△ABC和△BDE中,,∴△ABC≌△BDE(AAS)∴BC=DE=a.=BC•DE∵S△BCD=;∴S△BCD(3)如图3,过点A作AF⊥BC与F,过点D作DE⊥BC的延长线于点E,∴∠AFB=∠E=90°,BF=BC=a.∴∠FAB+∠ABF=90°.∵∠ABD=90°,∴∠ABF+∠DBE=90°,∴∠FAB=∠EBD.∵线段BD是由线段AB旋转得到的,∴AB=BD.在△AFB和△BED中,,∴△AFB≌△BED(AAS),∴BF=DE=a.∵S△BCD=BC•DE=•a•a=a2.∴△BCD 的面积为.31.(2018•宁夏)空间任意选定一点O,以点O为端点,作三条互相垂直的射线ox、oy、oz.这三条互相垂直的射线分别称作x轴、y轴、z轴,统称为坐标轴,它们的方向分别为ox(水平向前)、oy(水平向右)、oz(竖直向上)方向,这样的坐标系称为空间直角坐标系.将相邻三个面的面积记为S1、S2、S3,且S1<S2<S3的小长方体称为单位长方体,现将若干个单位长方体在空间直角坐标系内进行码放,要求码放时将单位长方体S1所在的面与x轴垂直,S2所在的面与y轴垂直,S3所在的面与z轴垂直,如图1所示.若将x轴方向表示的量称为几何体码放的排数,y轴方向表示的量称为几何体码放的列数,z轴方向表示的量称为几何体码放的层数;如图2是由若干个单位长方体在空间直角坐标内码放的一个几何体,其中这个几何体共码放了1排2列6层,用有序数组记作(1,2,6),如图3的几何体码放了2排3列4层,用有序数组记作(2,3,4).这样我们就可用每一个有序数组(x,y,z)表示一种几何体的码放方式.(1)如图4是由若干个单位长方体码放的一个几何体的三视图,则这种码放方式的有序数组为(2,3,2),组成这个几何体的单位长方体的个数为12个;(2)对有序数组性质的理解,下列说法正确的是①②⑤;(只填序号)①每一个有序数组(x,y,z)表示一种几何体的码放方式.②有序数组中x、y、z的乘积就表示几何体中单位长方体的个数.③有序数组不同,所表示几何体的单位长方体个数不同.④不同的有序数组所表示的几何体的体积不同.⑤有序数组中x、y、z每两个乘积的2倍可分别确定几何体表面上S1、S2、S3的个数.(3)为了进一步探究有序数组(x,y,z)的几何体的表面积公式S(x,y,z),某同学针对若干个单位长方体进行码放,制作了下列表格:几何体有序数组单位长方体的个数表面上面积为S1的个数表面上面积为S2的个数表面上面积为S3的个数表面积(1,1,1) 1 2 2 2 2S1+2S2+2S3(1,2,1) 2 4 2 4 4S1+2S2+4S3(3,1,1) 3 2 6 6 2S1+6S2+6S3(2,1,2) 4 4 8 4 4S1+8S2+4S3(1,5,1) 5 10 2 10 10S1+2S2+10S3(1,2,3) 6 12 6 4 12S1+6S2+4S3(1,1,7)7 14 14 2 14S1+14S2+2S3(2,2,2)8 8 8 8 8S1+8S2+8S3………………根据以上规律,请写出有序数组(x,y,z)的几何体表面积计算公式S(x,y,z);(用x、y、z、S1、S2、S3表示)(4)当S1=2,S2=3,S3=4时,对由12个单位长方体码放的几何体进行打包,为了节约外包装材料,对12个单位长方体码放的几何体表面积最小的规律进行探究,根据探究的结果请写出使几何体表面积最小的有序数组,并用几何体表面积公式求出这个最小面积.(缝隙不计)解:(1)这种码放方式的有序数组为(2,3,2),组成这个几何体的单位长方体的个数为2×3×2=12个,故答案为(2,3,2),12;(2)正确的有①②⑤.故答案为①②⑤;(3)S(x,y,z)=2yzS1+2xzS2+2xyS3=2(yzS1+xzS2+xyS3).(4)当S1=2,S2=3,S3=4时S(x,y,z)=2(yzS1+xzS2+xyS3)=2(2yz+3xz+4xy)欲使S(x,y,z)的值最小,不难看出x、y、z应满足x≤y≤z(x、y、z为正整数).在由12个单位长方体码放的几何体中,满足条件的有序数组为(1,1,12),(1,2,6),(1,3,4),(2,2,3).而S(1,1,12)=128,S(1,2,6)=100,S(1,3,4)=96,S(2,2,3)=92所以,由12个单位长方体码放的几何体表面积最小的有序数组为:(2,2,3),最小面积为S(2,2,3)=92.。
决胜2018中考数学压轴题全揭秘精品:(压轴题)专题22 动态几何之动点形成的四边形存

(3)在(2)的条件下,过点 P 作 PF⊥x 轴于点 F,G 为抛物线上一动点,M 为 x 轴上一动点,N 为直线 PF 上一
动点,当以
F、M、G
为顶点的四边形是正方WW.ziyua nku.co m
16.(2016 内蒙古呼伦贝尔市,第 26 题,13 分)如图,抛物线 y x2 2x 3 与 x 轴相交的于 A,B 两点(点 A
在点 B 的左侧),与 y 轴相交于点 C,顶点为 D. (1)直接写出 A,B,C 三点的坐标和抛物线的对称轴; (2)连接 BC,与抛物线的对称轴交于点 E,点 P 为线段 BC 上的一个动点(P 不与 C,B 两点重合),过点 P 作 PF∥DE 交抛物线于点 F,设点 P 的横坐标为 m. ①用含 m 的代数式表示线段 PF 的长,并求出当 m 为何值时,四边形 PEDF 为平行四边形. ②设△BCF 的面积为 S,求 S 与 m 的函数关系式;当 m 为何值时,S 有最大值.
4
11.(2016 山东省东营市)在平面直角坐标系中,平行四边形 ABOC 如图放置,点 A、C 的坐标分别是(0,4)、 (﹣1,0),将此平行四边形绕点 O 顺时针旋转 90°,得到平行四边形 A′B′OC′. (1)若抛物线经过点 C、A、A′,求此抛物线的解析式; (2)点 M 是第一象限内抛物线上的一动点,问:当点 M 在何处时,△AMA′的面积最大?最大面积是多少?并求 出此时 M 的坐标; (3)若 P 为抛物线上一动点,N 为 x 轴上的一动点,点 Q 坐标为(1,0),当 P、N、B、Q 构成平行四边形时, 求点 P 的坐标,当这个平行四边形为矩形时,求点 N 的坐标.
C 三点,其中点 A 的坐标为(0,8),点 B 的坐标为(﹣4,0). (1)求该二次函数的表达式及点 C 的坐标; (2)点 D 的坐标为(0,4),点 F 为该二次函数在第一象限内图象上的动点,连接 CD、CF,以 CD、CF 为邻边 作平行四边形 CDEF,设平行四边形 CDEF 的面积为 S.$来&源: ①求 S 的最大值; ②在点 F 的运动过程中,当点 E 落在该二次函数图象上时,请直接写出此时 S 的值.
上海市各区2018届中考数学二模试卷精选汇编压轴题专题(有答案)
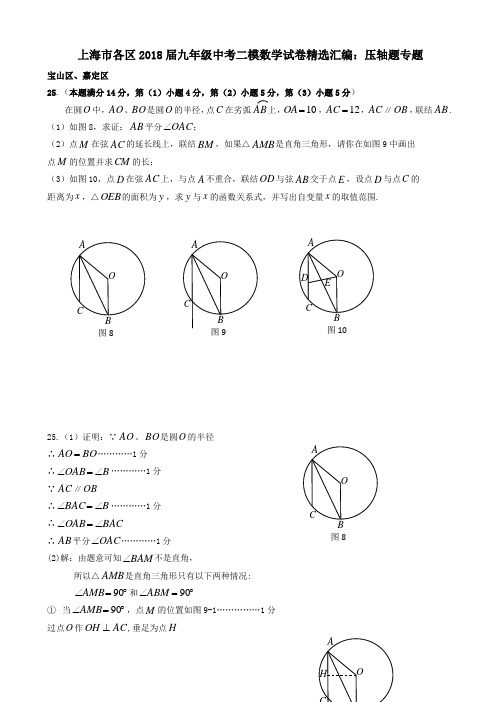
上海市各区2018届九年级中考二模数学试卷精选汇编:压轴题专题宝山区、嘉定区25.(本题满分14分,第(1)小题4分,第(2)小题5分,第(3)小题5分)在圆O 中,AO 、BO 是圆O 的半径,点C 在劣弧AB 上,10=OA,12=AC ,AC ∥OB ,联结AB . (1)如图8,求证:AB 平分OAC ∠;(2)点M 在弦AC 的延长线上,联结BM ,如果△AMB 是直角三角形,请你在如图9中画出 点M 的位置并求CM 的长;(3)如图10,点D 在弦AC 上,与点A 不重合,联结OD 与弦AB 交于点E ,设点D 与点C 的 距离为x ,△OEB 的面积为y ,求y 与x 的函数关系式,并写出自变量x 的取值范围.25.(1)证明:∵AO 、BO 是圆O 的半径 ∴BO AO =…………1分 ∴B OAB ∠=∠…………1分 ∵AC ∥OB∴B BAC ∠=∠…………1分 ∴BAC OAB ∠=∠∴AB 平分OAC ∠…………1分 (2)解:由题意可知BAM ∠不是直角,所以△AMB 是直角三角形只有以下两种情况:︒=∠90AMB 和︒=∠90ABM① 当︒=∠90AMB ,点M 的位置如图9-1……………1分 过点O 作AC OH ⊥,垂足为点H图8图10图8∵OH 经过圆心 ∴AC HC AH 21== ∵12=AC ∴6==HC AH 在Rt △AHO 中,222OA HO AH =+ ∵10=OA ∴8=OH∵AC ∥OB ∴︒=∠+∠180OBM AMB ∵︒=∠90AMB ∴︒=∠90OBM ∴四边形OBMH 是矩形 ∴10==HM OB∴4=-=HC HM CM ……………2分 ②当︒=∠90ABM ,点M 的位置如图9-2 由①可知58=AB ,552cos =∠CAB 在Rt △ABM 中,552cos ==∠AM AB CAB∴20=AM8=-=AC AM CM ……………2分综上所述,CM 的长为4或8.说明:只要画出一种情况点M 的位置就给1分,两个点都画正确也给1分. (3)过点O 作AB OG ⊥,垂足为点G 由(1)、(2)可知,CAB OAG ∠=∠sin sin 由(2)可得:55sin =∠CAB ∵10=OA ∴52=OG ……………1分 ∵AC ∥OB ∴ADOBAE BE =……………1分 又BE AE -=58,x AD -=12,10=OB ∴xBEBE -=-121058 ∴x BE -=22580 ……………1分∴52225802121⨯-⨯=⨯⨯=xOG BE y ∴xy -=22400……………1分自变量x 的取值范围为120<≤x ……………1分图10长宁区25.(本题满分14分,第(1)小题4分,第(2)小题4分,第(3)小题6分)在圆O 中,C 是弦AB 上的一点,联结OC 并延长,交劣弧AB 于点D ,联结AO 、BO 、AD 、BD . 已知圆O 的半径长为5 ,弦AB 的长为8.(1)如图1,当点D 是弧AB 的中点时,求CD 的长; (2)如图2,设AC =x ,y S S OBDACO=∆∆,求y 关于x 的函数解析式并写出定义域; (3)若四边形AOBD 是梯形,求AD 的长.25.(本题满分14分,第(1)小题4分,第(2)小题4分,第(3)小题6分) 解:(1)∵OD 过圆心,点D 是弧AB 的中点,AB =8, ∴OD ⊥AB ,421==AB AC (2分) 在Rt △AOC 中,︒=∠90ACO Θ,AO =5, ∴322=-=AC AO CO (1分)5=OD Θ,2=-=∴OC OD CD (1分)(2)过点O 作OH ⊥AB ,垂足为点H ,则由(1)可得AH =4,OH =3 ∵AC =x ,∴|4|-=x CH在Rt △HOC 中,︒=∠90CHO Θ,AO =5, ∴258|4|322222+-=-+=+=x x x HC HO CO , (1分)∴525882+-⋅-=⋅=⋅==∆∆∆∆∆∆x x x x OD OC BC AC S S S S S S y OBD OBC OBC ACO OBD ACO O AC DBO BA C DBAOxx x x 5402582-+-= (80<<x ) (3分)(3)①当OB //AD 时, 过点A 作AE ⊥OB 交BO 延长线于点E ,过点O 作OF ⊥AD ,垂足为点F , 则OF =AE , AE OB OH AB S ABO ⋅=⋅=∆2121Θ ∴OF OB OH AB AE ==⋅=524 在Rt △AOF 中,︒=∠90AFO Θ,AO =5, ∴5722=-=OF AO AF ∵OF 过圆心,OF ⊥AD ,∴5142==AF AD . (3分) ②当OA //BD 时, 过点B 作BM ⊥OA 交AO 延长线于点M ,过点D 作DG ⊥AO ,垂足为点G , 则由①的方法可得524==BM DG , 在Rt △GOD 中,︒=∠90DGO Θ,DO =5, ∴5722=-=DG DO GO ,518575=-=-=GO AO AG , 在Rt △GAD 中,︒=∠90DGA Θ,∴622=+=DG AG AD ( 3分)综上得6514或=AD 崇明区25.(本题满分14分,第(1)小题4分,第(2)小题4分,第(3)小题6分)如图,已知ABC △中,8AB =,10BC =,12AC =,D 是AC 边上一点,且2AB AD AC =⋅,联结BD ,点E 、F 分别是BC 、AC 上两点(点E 不与B 、C 重合),AEF C ∠=∠,AE 与BD 相交于点G . (1)求证:BD 平分ABC ∠;(2)设BE x =,CF y =,求y 与x 之间的函数关系式; (3)联结FG ,当GEF △是等腰三角形时,求BE 的长度.25.(满分14分,第(1)小题4分,第(2)小题4分,第(3)小题6分)(第25题图)A BCDGEF(备用图)ABCD(1)∵8AB =,12AC = 又∵2AB AD AC =g ∴163AD =∴16201233CD =-= ……………………………1分 ∵2AB AD AC =g ∴AD AB AB AC= 又∵BAC ∠是公共角 ∴ADB ABC △∽△ …………………………1分 ∴ABD C =∠∠,BD ADBC AB= ∴203BD =∴BD CD = ∴DBC C =∠∠ ………………………1分 ∴ABD DBC =∠∠ ∴BD 平分ABC ∠ ………………………1分 (2)过点A 作AH BC ∥交BD 的延长线于点H∵AH BC ∥ ∴16432053AD DH AH DC BD BC ==== ∵203BD CD ==,8AH = ∴163AD DH == ∴12BH = ……1分 ∵AH BC ∥ ∴AH HG BE BG = ∴812BG x BG -= ∴128xBG x =+…1分 ∵BEF C EFC =+∠∠∠ 即BEA AEF C EFC +=+∠∠∠∠ ∵AEF C =∠∠ ∴BEA EFC =∠∠ 又∵DBC C =∠∠∴BEG CFE △∽△ ……………………………………………………………1分∴BE BGCF EC= ∴12810x x x y x +=-∴228012x x y -++= …………………………………………………………1分(3)当△GEF 是等腰三角形时,存在以下三种情况:1° GE GF = 易证23GE BE EF CF == ,即23x y =,得到4BE = ………2分 2° EG EF = 易证BE CF =,即x y =,5BE =-+…………2分 3° FG FE = 易证 32GE BE EF CF == ,即32x y =3BE =-+ ………2分奉贤区25.(本题满分14分,第(1)小题满分5分,第(2)小题满分5分,第(3)小题满分4分)已知:如图9,在半径为2的扇形AOB 中,∠AOB=90°,点C 在半径OB 上,AC 的垂直平分线交OA 于点D ,交弧AB 于点E ,联结BE 、CD .(1)若C 是半径OB 中点,求∠OCD 的正弦值; (2)若E 是弧AB 的中点,求证:BC BO BE ⋅=2;(3)联结CE ,当△DCE 是以CD 为腰的等腰三角形时,求CD 的长.图9备用图ABO备用图ABO黄浦区25.(本题满分14分)如图,四边形ABCD中,∠BCD=∠D=90°,E是边AB的中点.已知AD=1,AB=2.(1)设BC=x,CD=y,求y关于x的函数关系式,并写出定义域;(2)当∠B=70°时,求∠AEC的度数;(3)当△ACE为直角三角形时,求边BC的长.25. 解:(1)过A作AH⊥BC于H,————————————————————(1分)由∠D=∠BCD=90°,得四边形ADCH为矩形.在△BAH 中,AB =2,∠BHA =90°,AH =y ,HB =1x -,所以22221y x =+-,——————————————————————(1分) 则()22303y x x x =-++<<.———————————————(2分)(2)取CD 中点T ,联结TE ,————————————————————(1分) 则TE 是梯形中位线,得ET ∥AD ,ET ⊥CD .∴∠AET =∠B =70°. ———————————————————————(1分) 又AD =AE =1,∴∠AED =∠ADE =∠DET =35°. ——————————————————(1分) 由ET 垂直平分CD ,得∠CET =∠DET =35°,————————————(1分) 所以∠AEC =70°+35°=105°. ——————————————————(1分)(3)当∠AEC =90°时,易知△CBE ≌△CAE ≌△CAD ,得∠BCE =30°, 则在△ABH 中,∠B =60°,∠AHB =90°,AB =2,得BH =1,于是BC =2. ——————————————————————(2分)当∠CAE =90°时,易知△CDA ∽△BCA ,又2224AC BC AB x =-=-,则2241174AD CAx x AC CBx -±=⇒=⇒=-(舍负)—————(2分) 易知∠ACE <90°.所以边BC 的长为2或117+.——————————————————(1分)金山区25.(本题满分14分,第(1)小题4分,第(2)小题5分,第(3)小题5 分)如图9,已知在梯形ABCD 中,AD ∥BC ,AB =DC =AD =5,3sin 5B =,P 是线段BC 上 一点,以P 为圆心,PA 为半径的⊙P 与射线AD 的另一个交点为Q ,射线PQ 与射线CD 相交于点E ,设BP =x .(1)求证△ABP ∽△ECP ;(2)如果点Q 在线段AD 上(与点A 、D 不重合),设△APQ 的面积为y ,求y 关于x 的函数关系式,并写出定义域; (3)如果△QED 与△QAP 相似,求BP 的长.25.解:(1)在⊙P 中,PA =PQ ,∴∠PAQ =∠PQA ,……………………………(1分)∵AD ∥BC ,∴∠PAQ =∠APB ,∠PQA =∠QPC ,∴∠APB =∠EPC ,……(1分) ∵梯形ABCD 中,AD ∥BC ,AB =DC ,∴∠B =∠C ,…………………………(1分) ∴△APB ∽△ECP .…………………………………………………………(1分) (2)作AM ⊥BC ,PN ⊥AD ,∵AD ∥BC ,∴AM ∥PN ,∴四边形AMPN 是平行四边形,∴AM =PN ,AN =MP .………………………………………………………(1分) 在Rt △AMB 中,∠AMB =90°,AB =5,sinB =35, ∴AM =3,BM =4,∴PN =3,PM =AN =x -4,……………………………………(1分) ∵PN ⊥AQ ,∴AN =NQ ,∴AQ = 2x -8,……………………………………(1分) ∴()1128322y AQ PN x =⋅⋅=⋅-⋅,即312y x =-,………………………(1分) 定义域是1342x <<.………………………………………………………(1分) (3)解法一:由△QED 与△QAP 相似,∠AQP =∠EQD ,①如果∠PAQ =∠DEQ ,∵△APB ∽△ECP ,∴∠PAB =∠DEQ ,又∵∠PAQ =∠APB ,∴∠PAB =∠APB ,∴BP =BA =5.………………………(2分)ABCD图9备用图②如果∠PAQ =∠EDQ ,∵∠PAQ =∠APB ,∠EDQ =∠C ,∠B =∠C ,∴∠B =∠APB ,∴ AB =AP ,∵AM ⊥BC ,∴ BM =MP =4,∴ BP =8.………(2分) 综上所述BP 的长为5或者8.………………………………………………(1分) 解法二:由△QAP 与△QED 相似,∠AQP =∠EQD , 在Rt △APN 中,AP PQ ===∵QD ∥PC ,∴EQ EPQD PC=, ∵△APB ∽△ECP ,∴AP EPPB PC=,∴AP EQ PB QD =, ①如果AQ EQ QP QD =,∴AQ AP QP PB =x=,解得5x =………………………………………………………………………(2分) ②如果AQ DQ QP QE =,∴AQ PBQP AP==解得8x =………………………………………………………………………(2分) 综上所述BP 的长为5或者8.…………………………………………………(1分)静安区25.(本题满分14分,第(1)小题满分4分,第(2)小题满分6分,第(3)小题满分4分) 如图,平行四边形ABCD 中,已知AB =6,BC =9,31cos =∠ABC .对角线AC 、BD 交于点O .动点P 在边AB 上,⊙P 经过点B ,交线段PA 于点E .设BP = x .(1) 求AC 的长;(2) 设⊙O 的半径为y ,当⊙P 与⊙O 外切时, 求y 关于x 的函数解析式,并写出定义域; (3) 如果AC 是⊙O 的直径,⊙O 经过点E , 求⊙O 与⊙P 的圆心距OP 的长.25.(本题满分14分,第(1)小题4分,第(2)小题6分,第(3)小题4分) 解:(1)作AH ⊥BC 于H ,且31cos =∠ABC ,AB =6, A 第25题图B P OC DE · 第25题备用图ABOCDDA · POE那么2316cos =⨯=∠⋅=ABC AB BH …………(2分) BC =9,HC =9-2=7,242622=-=AH , ……………………(1分) 9493222=+=+=HC AH AC ﹒ ………(1分)(2)作OI ⊥AB 于I ,联结PO , AC =BC =9,AO =4.5 ∴∠OAB =∠ABC ,∴Rt △AIO 中, 31cos cos ==∠=∠AO AI ABC IAO∴AI =1.5,IO =2322=AI ……………………(1分) ∴PI =AB -BP -AI =6-x -1.5=x -29, ……………………(1分) ∴Rt △PIO 中,41539481918)29()23(2222222+-=+-+=-+=+=x x x x x OI PI OP ……(1分) ∵⊙P 与⊙O 外切,∴y x x x OP +=+-=415392 ……………………(1分) ∴y =x x x x x x -+-=-+-153364214153922…………………………(1分) ∵动点P 在边AB 上,⊙P 经过点B ,交线段PA 于点E .∴定义域:0<x ≤3…………(1分) (3)由题意得:∵点E 在线段AP 上,⊙O 经过点E ,∴⊙O 与⊙P 相交 ∵AO 是⊙O 半径,且AO >OI ,∴交点E 存在两种不同的位置,OE =OA =29① 当E 与点A 不重合时,AE 是⊙O 的弦,OI 是弦心距,∵AI =1.5,AE =3, ∴点E 是AB 中点,321==AB BE ,23==PE BP ,3=PI , IO =23 3327)23(32222==+=+=IO PI OP ……………………(2分)② 当E 与点A 重合时,点P 是AB 中点,点O 是AC 中点,2921==BC OP ……(2分) ∴33=OP 或29. 闵行区25.(本题满分14分,其中第(1)小题4分,第(2)、(3)小题各5分)如图,已知在Rt △ABC 中,∠ACB = 90o,AC =6,BC = 8,点F 在线段AB 上,以点B 为圆心,BF 为半径的圆交BC 于点E ,射线AE 交圆B 于点D (点D 、E 不重合).(1)如果设BF = x ,EF = y ,求y 与x 之间的函数关系式,并写出它的定义域;第25题图(2)(2)如果»»2EDEF =,求ED 的长; (3)联结CD 、BD ,请判断四边形ABDC 是否为直角梯形?说明理由.25.解:(1)在Rt △ABC 中,6AC =,8BC =,90ACB ∠=o∴10AB =.……………………………………………………………(1分) 过E 作EH ⊥AB ,垂足是H , 易得:35EH x =,45BH x =,15FH x =.…………………………(1分) 在Rt △EHF 中,222223155EF EH FH x x ⎛⎫⎛⎫=+=+ ⎪ ⎪⎝⎭⎝⎭,∴(08)y x x =<<.………………………………………(1分+1分) (2)取»ED的中点P ,联结BP 交ED 于点G ∵»»2EDEF =,P 是»ED 的中点,∴»»»EP EF PD ==. ∴∠FBE =∠EBP =∠PBD .∵»»EPEF =,BP 过圆心,∴BG ⊥ED ,ED =2EG =2DG .…………(1分) 又∵∠CEA =∠DEB ,∴∠CAE =∠EBP =∠ABC .……………………………………………(1分)又∵BE 是公共边,∴BEH BEG ∆∆≌.∴35EH EG GD x ===.在Rt △CEA 中,∵AC = 6,8BC =,tan tan AC CECAE ABC BC AC∠=∠==, ∴66339tan 822CE AC CAE ⨯⨯=⋅∠===.……………………………(1分) (备用图)CBA (第25题图)CBEF DADEBACF∴9169782222BE =-=-=.……………………………………………(1分) ∴6672125525ED EG x ===⨯=.……………………………………(1分)(3)四边形ABDC 不可能为直角梯形.…………………………………(1分)①当CD ∥AB 时,如果四边形ABDC 是直角梯形, 只可能∠ABD =∠CDB = 90o. 在Rt △CBD 中,∵8BC =, ∴32cos 5CD BC BCD =⋅∠=, 24sin 5BD BC BCD BE =⋅∠==. ∴321651025CD AB ==,328153245CE BE -==; ∴CD CEAB BE≠. ∴CD 不平行于AB ,与CD ∥AB 矛盾.∴四边形ABDC 不可能为直角梯形.…………………………(2分) ②当AC ∥BD 时,如果四边形ABDC 只可能∠ACD =∠CDB = 90o. ∵AC ∥BD ,∠ACB = 90o, ∴∠ACB =∠CBD = 90o . ∴∠ABD =∠ACB +∠BCD > 90o. 与∠ACD =∠CDB = 90o矛盾.∴四边形ABDC 不可能为直角梯形.…………………………(2分)普陀区25.(本题满分14分)已知P 是O ⊙的直径BA 延长线上的一个动点,P ∠的另一边交O ⊙于点C 、D ,两点位于AB 的上方,AB =6,OP m =,1sin 3P =,如图11所示.另一个半径为6的1O ⊙经过点C 、D ,圆心距1OO n =.(1)当6m =时,求线段CD 的长;(2)设圆心1O 在直线AB 上方,试用n 的代数式表示m ;(3)△1POO 在点P 的运动过程中,是否能成为以1OO 为腰的等腰三角形,如果能,试求出此时n 的值;如果不能,请说明理由.DEBACFDC25.解:(1)过点O 作OH ⊥CD ,垂足为点H ,联结OC .在Rt △POH 中,∵1sin 3P =,6PO =,∴2OH =. ········· (1分) ∵AB =6,∴3OC =. ······················ (1分)由勾股定理得 CH = ····················· (1分)∵OH ⊥DC ,∴2CD CH == ················ (1分) (2)在Rt △POH 中,∵1sin 3P =, PO m =,∴3mOH =. ········ (1分) 在Rt △OCH 中,2293m CH ⎛⎫- ⎪⎝⎭=. ················ (1分)在Rt △1O CH 中,22363m CH n ⎛⎫-- ⎪⎝⎭=. ·············· (1分)可得 2236933m m n ⎛⎫⎛⎫--- ⎪ ⎪⎝⎭⎝⎭=,解得23812n m n -=. ········· (2分)(3)△1POO 成为等腰三角形可分以下几种情况:● 当圆心1O 、O 在弦CD 异侧时①1OP OO =,即m n =,由23812n n n-=解得9n =. ········· (1分)即圆心距等于O ⊙、1O ⊙的半径的和,就有O ⊙、1O ⊙外切不合题意舍去.(1分)②11O P OO =n =,解得23m n =,即23n 23812n n -=,解得n ·········· (1分) ● 当圆心1O 、O 在弦CD 同侧时,同理可得 28132n m n-=.∵1POO ∠是钝角,∴只能是m n =,即28132n n n-=,解得n . ·· (2分)综上所述,n .青浦区25.(本题满分14分,第(1)小题4分,第(2)小题6分,第(3)小题4分)如图9-1,已知扇形MON,∠MON=90o,点B在弧MN上移动,联结BM,作OD⊥BM,垂足为点D,C为线段OD上一点,且OC=BM,联结BC并延长交半径OM于点A,设OA= x,∠COM的正切值为y.(1)如图9-2,当AB⊥OM时,求证:AM =AC;(2)求y关于x的函数关系式,并写出定义域;(3)当△OAC为等腰三角形时,求x的值.25.解:(1)∵OD⊥BM,AB⊥OM,∴∠ODM =∠BAM=90°.··········(1分)∵∠ABM +∠M =∠DOM +∠M,∴∠ABM =∠DOM.·········(1分)∵∠OAC=∠BAM,OC =BM,∴△OAC≌△ABM,······················(1分)∴AC =AM.·························(1分)(2)过点D作DE//AB,交OM于点E.················(1分)∵OB=OM,OD⊥BM,∴BD=DM.················(1分)∵DE//AB,∴=MD MEDM AE,∴AE=EM,∵OM,∴AE=)12x.················(1分)∵DE//AB,∴2==OA OC DMOE OD OD,···················(1分)∴2=DM OAOD OE,∴=y(0<≤x·················(2分)(3)(i)当OA=OC时,∵111222===DM BM OC x,O MNDCBA图9-1ONDCBA图9-2NMO备用图在Rt △ODM中,==OD =DM y OD,1=x=x=x .(2分) (ii )当AO =AC 时,则∠AOC =∠ACO ,∵∠ACO >∠COB ,∠COB =∠AOC ,∴∠ACO >∠AOC ,∴此种情况不存在. ····················· (1分) (ⅲ)当CO =CA 时,则∠COA =∠CAO=α,∵∠CAO >∠M ,∠M =90α︒-,∴α>90α︒-,∴α>45︒,∴290α∠=>︒BOA ,∵90∠≤︒BOA ,∴此种情况不存在. ·· (1分)松江区25.(本题满分14分,第(1)小题4分,第(2)小题每个小题各5分)如图,已知Rt △ABC 中,∠ACB =90°,BC =2,AC =3,以点C 为圆心、CB 为半径的圆交AB 于点D ,过点A 作AE ∥CD ,交BC 延长线于点E.(1)求CE 的长;(2)P 是 CE 延长线上一点,直线AP 、CD 交于点Q.① 如果△ACQ ∽△CPQ ,求CP 的长;② 如果以点A 为圆心,AQ 为半径的圆与⊙C 相切,求CP 的长.25.(本题满分14分,第(1)小题4分,第(2)小题每个小题各5分) 解:(1)∵AE ∥CD∴BC DC BE AE=…………………………………1分 ∵BC=DC∴BE=AE …………………………………1分 设CE =x(第25题图)CBA DE(备用图)CBADECBA DE则AE =BE =x +2 ∵ ∠ACB =90°, ∴222AC CE AE +=即229(2)x x +=+………………………1分 ∴54x =即54CE =…………………………………1分 (2)①∵△ACQ ∽△CPQ ,∠QAC>∠P∴∠ACQ=∠P …………………………………1分 又∵AE ∥CD ∴∠ACQ=∠CAE∴∠CAE=∠P ………………………………1分 ∴△ACE ∽△PCA ,…………………………1分 ∴2AC CE CP =⋅…………………………1分 即2534CP =⋅ ∴365CP =……………………………1分 ②设CP =t ,则54PE t =- ∵∠ACB =90°,∴AP ∵AE ∥CD ∴AQ ECAP EP=……………………………1分5545454t t ==--∴AQ =1分若两圆外切,那么1AQ == 此时方程无实数解……………………………1分CBA DEPQ若两圆内切切,那么2595t AQ +== ∴21540160t t -+= 解之得2041015t ±=………………………1分又∵54t >∴2041015t +=………………………1分徐汇区25. 已知四边形ABCD 是边长为10的菱形,对角线AC 、BD 相交于点E ,过点C 作CF ∥DB 交AB 延长线于点F ,联结EF 交BC 于点H . (1)如图1,当EF BC ⊥时,求AE 的长;(2)如图2,以EF 为直径作⊙O ,⊙O 经过点C 交边CD 于点G (点C 、G 不重合),设AE 的长为x ,EH 的长为y ;① 求y 关于x 的函数关系式,并写出定义域;③ 联结EG ,当DEG ∆是以DG 为腰的等腰三角形时,求AE 的长.杨浦区25、(本题满分14分,第(1)小题4分,第(2)小题6分,第(3)小题4分)如图9,在梯形ABCD中,AD//BC,AB=DC=5,AD=1,BC=9,点P为边BC上一动点,作PH⊥DC,垂足H在边DC上,以点P为圆心PH为半径画圆,交射线PB于点E.(1)当圆P过点A时,求圆P的半径;(2)分别联结EH和EA,当△ABE△CEH时,以点B为圆心,r为半径的圆B与圆P相交,试求圆B的半径r的取值范围;(3)将劣弧沿直线EH翻折交BC于点F,试通过计算说明线段EH和EF的比值为定值,并求出此定值。
2018中考数学专题复习 全等三角形压轴题分类解析(无答案)

三角形综合题归类考点:利用角相等证明垂直1. 已知BE ,CF 是△ABC 的高,且BP=AC ,CQ=AB ,试确定AP 与AQ 的数量关系和位置关系2. 如图,在等腰R t△ABC 中,∠ACB =90°,D 为BC 的中点,DE ⊥AB ,垂足为E ,过点B 作BF ∥AC 交DE 的延长线于点F ,连接CF .(1)求证:CD=BF ;(2)求证:AD ⊥CF ;(3)连接AF ,试判断△ACF 的形状.拓展巩固:如图9所示,△ABC 是等腰直角三角形,∠ACB =90°,AD 是BC 边上的中线,过C 作AD 的垂线,交AB 于点E ,交AD 于点F ,求证:∠ADC =∠BDE .3. 如图1,已知正方形ABCD 的边CD 在正方形DEFG 的边DE 上,连接AE ,GC . (1)试猜想AE 与GC 有怎样的位置关系,并证明你的结论;(2)将正方形DEFG 绕点D 按顺时针方向旋转,使E 点落在BC 边上,如图2,连接AE 和GC .你认为(1)中的结论是否还成立?若成立,给出证明;若不成立,请说明理由.BAC E FQPD A BCDEF图9ABCDE F4.如图1,ABC ∆的边BC 在直线l 上,,AC BC ⊥且,AC BC =EFP ∆的边FP 也 在直线l 上,边EF 与边AC 重合,且EF FP =(1) 在图1中,请你通过观察、测量,猜想并写出AB 与AP 所满足的 数量关系和位置关系;(2) 将EFP ∆沿直线l 向左平移到图2的位置时,EP 交AC 于点Q ,连接 ,AP BQ .猜想并写出BQ 与AP 所满足的数量关系和位置关系,请证明你的猜想; (3)将EFP ∆沿直线l 向左平移到图3的位置时,EP 的延长线交AC 的延长 线于点Q,连结,AP BQ ,你认为(2)中所猜想的BQ 与AP 的数量关系和位置关系和位置关系还成立吗?若成立,给出证明;若不成立,请说明理由.等腰三角形(中考重难点之一) 考点1:等腰三角形性质的应用1. 两个全等的含30,60角的三角板ADE 和三角板ABC ,如图所示放置,,,E A C 三点在一条直线上,连结BD ,取BD 的中点M ,连结,ME MC .试判断EMC ∆的形状,并说明理由. MED CBA压轴题拓展:(三线合一性质的应用)已知Rt ABC ∆中,AC BC =,90C ∠=︒,D 为AB 边的中点,90EDF ∠=︒,EDF ∠绕D 点旋转,它的两边分别交AC 、CB (或它们的延长线)于E 、F .l(1)A B(F) (E)C PABECFPQ (2) lABEC FP l(3)Q当EDF ∠绕D 点旋转到DE AC ⊥于E 时(如图1),易证12DEF CEF ABC S S S ∆∆∆+=.当EDF ∠绕D 点旋转到DE 和AC 不垂直时,在图2和图3这两种情况下,上述结论是否成立? 若成立,请给予证明;若不成立,DEF S ∆,CEF S ∆,ABC S ∆又有怎样的数量关系?请写出你的猜想,不需证明.FEDCBA图1AECF BD图2AECFBD图32. 已知:如图,△ABC 中,∠ABC =45°,CD ⊥AB 于D ,BE 平分∠ABC ,且BE ⊥AC 于E ,与CD 相交于点F ,H 是BC 边的中点,连结DH 与BE 相交于点G 。
2018年全国各地中考数学压轴题汇编:几何综合(浙江专版)(解析卷)

2018年全国各地中考数学压轴题汇编(浙江专版)几何综合参考答案与试题解析1.数学课上,张老师举了下面的例题:例1等腰三角形ABC中,∠A=110°,求∠B的度数.(答案:35°)例2等腰三角形ABC中,∠A=40°,求∠B的度数,(答案:40°或70°或100°)张老师启发同学们进行变式,小敏编了如下一题:变式等腰三角形ABC中,∠A=80°,求∠B的度数.(1)请你解答以上的变式题.(2)解(1)后,小敏发现,∠A的度数不同,得到∠B的度数的个数也可能不同,如果在等腰三角形ABC中,设∠A=x°,当∠B有三个不同的度数时,请你探索x的取值范围.解:(1)若∠A为顶角,则∠B=(180°﹣∠A)÷2=50°;若∠A为底角,∠B为顶角,则∠B=180°﹣2×80°=20°;若∠A为底角,∠B为底角,则∠B=80°;故∠B=50°或20°或80°;(2)分两种情况:①当90≤x<180时,∠A只能为顶角,∴∠B的度数只有一个;②当0<x<90时,若∠A为顶角,则∠B=()°;若∠A为底角,∠B为顶角,则∠B=(180﹣2x)°;若∠A为底角,∠B为底角,则∠B=x°.当≠180﹣2x且180﹣2x≠x且≠x,即x≠60时,∠B有三个不同的度数.2.如图,在Rt△ABC中,点O在斜边AB上,以O为圆心,OB为半径作圆,分别与BC,AB相交于点D,E,连结AD.已知∠CAD=∠B.(1)求证:AD是⊙O的切线.(2)若BC=8,tanB=,求⊙O的半径.(1)证明:连接OD,∵OB=OD,∴∠3=∠B,∵∠B=∠1,∴∠1=∠3,在Rt△ACD中,∠1+∠2=90°,∴∠4=180°﹣(∠2+∠3)=90°,∴OD⊥AD,则AD为圆O的切线;(2)设圆O的半径为r,在Rt△ABC中,AC=BCtanB=4,根据勾股定理得:AB==4,∴OA=4﹣r,在Rt△ACD中,tan∠1=tanB=,∴CD=ACtan∠1=2,根据勾股定理得:AD2=AC2+CD2=16+4=20,在Rt△ADO中,OA2=OD2+AD2,即(4﹣r)2=r2+20,解得:r=.3.如图,在6×6的网格中,每个小正方形的边长为1,点A在格点(小正方形的顶点)上.试在各网格中画出顶点在格点上,面积为6,且符合相应条件的图形.解:符合条件的图形如图所示:4.如图,在四边形ABCD中,E是AB的中点,AD∥EC,∠AED=∠B.(1)求证:△AED≌△EBC.(2)当AB=6时,求CD的长.∴∠A=∠BEC,∵E是AB中点,∴AE=EB,∵∠AED=∠B,∴△AED≌△EBC.(2)解:∵△AED≌△EBC,∴AD=EC,∵AD∥EC,∴四边形AECD是平行四边形,∴CD=AE,∵AB=6,∴CD=AB=3.5.如图,已知AB是⊙O的直径,C,D是⊙O上的点,OC∥BD,交AD于点E,连结BC.(1)求证:AE=ED;(2)若AB=10,∠CBD=36°,求的长.证明:(1)∵AB是⊙O的直径,∴∠ADB=90°,∵OC∥BD,∴∠AEO=∠ADB=90°,即OC⊥AD,∴AE=ED;(2)∵OC⊥AD,∴,∴∠ABC=∠CBD=36°,∴∠AOC=2∠ABC=2×36°=72°,∴.6.如图,在△ABC中,∠ACB=90°,以点B为圆心,BC长为半径画弧,交线段AB于点D;以点A为圆心,AD长为半径画弧,交线段AC于点E,连结CD.(1)若∠A=28°,求∠ACD的度数.(2)设BC=a,AC=b.①线段AD的长是方程x2+2ax﹣b2=0的一个根吗?说明理由.②若AD=EC,求的值.解:(1)∵∠ACB=90°,∠A=28°,∴∠B=62°,∵BD=BC,∴∠BCD=∠BDC=59°,∴∠ACD=90°﹣∠BCD=31°;(2)①由勾股定理得,AB==,∴AD=﹣a,解方程x2+2ax﹣b2=0得,x==﹣a,∴线段AD的长是方程x2+2ax﹣b2=0的一个根;②∵AD=AE,由勾股定理得,a2+b2=(b+a)2,整理得,=.7.在5×3的方格纸中,△ABC的三个顶点都在格点上.(1)在图1中画出线段BD,使BD∥AC,其中D是格点;(2)在图2中画出线段BE,使BE⊥AC,其中E是格点.解:(1)如图所示,线段BD即为所求;(2)如图所示,线段BE即为所求.8.如图,在▱ABCD中,AC是对角线,BE⊥AC,DF⊥AC,垂足分别为点E,F,求证:AE=CF.证明:如图,∵四边形ABCD是平行四边形,∴AB=CD,AB∥CD,∴∠BAE=∠DCF.又BE⊥AC,DF⊥AC,∴∠AEB=∠CFD=90°.在△ABE与△CDF中,,∴得△ABE≌△CDF(AAS),∴AE=CF.9.已知:在△ABC中,AB=AC,D为AC的中点,DE⊥AB,DF⊥BC,垂足分别为点E,F,且DE=DF.求证:△ABC是等边三角形.证明:∵DE⊥AB,DF⊥BC,垂足分别为点E,F,∴∠AED=∠CFD=90°,∵D为AC的中点,∴AD=DC,在Rt△ADE和Rt△CDF中,,∴Rt△ADE≌Rt△CDF,∴∠A=∠C,∴BA=BC,∵AB=AC,∴AB=BC=AC,∴△ABC是等边三角形.10.如图,D是△ABC的BC边上一点,连接AD,作△ABD的外接圆,将△ADC 沿直线AD折叠,点C的对应点E落在BD上.(1)求证:AE=AB.(2)若∠CAB=90°,cos∠ADB=,BE=2,求BC的长.解:(1)由折叠的性质可知,△ADE≌△ADC,∴∠AED=∠ACD,AE=AC,∵∠ABD=∠AED,∴∠ABD=∠ACD,∴AB=AC,∴AE=AB;(2)如图,过A作AH⊥BE于点H,∵AB=AE,BE=2,∴BH=EH=1,∵∠ABE=∠AEB=∠ADB,cos∠ADB=,∴cos∠ABE=cos∠ADB=,∴=.∵∠BAC=90°,AC=AB,∴BC=3.11.在Rt△ABC中,∠ACB=90°,AC=12.点D在直线CB上,以CA,CD为边作矩形ACDE,直线AB与直线CE,DE的交点分别为F,G.(1)如图,点D在线段CB上,四边形ACDE是正方形.①若点G为DE中点,求FG的长.②若DG=GF,求BC的长.(2)已知BC=9,是否存在点D,使得△DFG是等腰三角形?若存在,求该三角形的腰长;若不存在,试说明理由.解:(1)①在正方形ACDE中,DG=GE=6,中Rt△AEG中,AG==6,∵EG∥AC,∴△ACF∽△GEF,∴=,∴==,∴FG=AG=2.②如图1中,正方形ACDE中,AE=ED,∠AEF=∠DEF=45°,∵EF=EF,∴△AEF≌△DEF,∴∠1=∠2,设∠1=∠2=x,∵AE∥BC,∵GF=GD,∴∠3=∠2=x,在△DBF中,∠3+∠FDB+∠B=180°,∴x+(x+90°)+x=180°,解得x=30°,∴∠B=30°,∴在Rt△ABC中,BC==12.(2)在Rt△ABC中,AB===15,如图2中,当点D中线段BC上时,此时只有GF=GD,∵DG∥AC,∴△BDG∽△BCA,设BD=3x,则DG=4x,BG=5x,∴GF=GD=4x,则AF=15﹣9x,∵AE∥CB,∴△AEF∽△BCF,∴=,∴=,整理得:x2﹣6x+5=0,解得x=1或5(舍弃)∴腰长GD为=4x=4.如图3中,当点D中线段BC的延长线上,且直线AB,CE的交点中AE上方时,此时只有GF=DG,设AE=3x,则EG=4x,AG=5x,∴FG=DG=12+4x,∵AE∥BC,∴△AEF∽△BCF,∴=,∴=,解得x=2或﹣2(舍弃),∴腰长DG=4x+12=20.如图4中,当点D在线段BC的延长线上,且直线AB,EC的交点中BD下方时,此时只有DF=DG,过点D作DH⊥FG.设AE=3x,则EG=4x,AG=5x,DG=4x+12,∴FH=GH=DG•cos∠DGB=(4x+12)×=,∴GF=2GH=,∴AF=GF﹣AG=,∵AC∥DG,∴△ACF∽△GEF,∴=,∴=,解得x=或﹣(舍弃),∴腰长GD=4x+12=,如图5中,当点D中线段CB的延长线上时,此时只有DF=DG,作DH⊥AG于H.设AE=3x,则EG=4x,AG=5x,DG=4x﹣12,∴FH=GH=DG•cos∠DGB=,∴FG=2FH=,∴AF=AG﹣FG=,∵AC∥EG,∴△ACF∽△GEF,∴=,∴=,解得x=或﹣(舍弃),∴腰长DG=4x﹣12=,综上所述,等腰三角形△DFG的腰长为4或20或或.12.如图,△ABC是⊙O的内接三角形,点D在上,点E在弦AB上(E不与A重合),且四边形BDCE为菱形.(1)求证:AC=CE;(2)求证:BC2﹣AC2=AB•AC;(3)已知⊙O的半径为3.①若=,求BC的长;②当为何值时,AB•AC的值最大?解:(1)∵四边形EBDC为菱形,∴∠D=∠BEC,∵四边形ABDC是圆的内接四边形,∴∠A+∠D=180°,又∠BEC+∠AEC=180°,∴∠A=∠AEC,∴AC=AE;(2)以点C为圆心,CE长为半径作⊙C,与BC交于点F,于BC延长线交于点G,则CF=CG,由(1)知AC=CE=CD,∴CF=CG=AC,∵四边形AEFG是⊙C的内接四边形,∴∠G+∠AEF=180°,又∵∠AEF+∠BEF=180°,∴∠G=∠BEF,∵∠EBF=∠GBA,∴△BEF∽△BGA,∴=,即BF•BG=BE•AB,∵BF=BC﹣CF=BC﹣AC、BG=BC+CG=BC+AC,BE=CE=AC,∴(BC﹣AC)(BC+AC)=AB•AC,即BC2﹣AC2=AB•AC;(3)设AB=5k、AC=3k,∵BC2﹣AC2=AB•AC,∴BC=2k,连接ED交BC于点M,∵四边形BDCE是菱形,∴DE垂直平分BC,则点E、O、M、D共线,在Rt△DMC中,DC=AC=3k,MC=BC=k,∴DM==k,∴OM=OD﹣DM=3﹣k,在Rt△COM中,由OM2+MC2=OC2得(3﹣k)2+(k)2=32,解得:k=或k=0(舍),∴BC=2k=4;②设OM=d,则MD=3﹣d,MC2=OC2﹣OM2=9﹣d2,∴BC2=(2MC)2=36﹣4d2,AC2=DC2=DM2+CM2=(3﹣d)2+9﹣d2,由(2)得AB•AC=BC2﹣AC2=﹣4d2+6d+18=﹣4(d﹣)2+,∴当x=,即OM=时,AB•AC最大,最大值为,∴DC2=,∴AC=DC=,∴AB=,此时=.13.小敏思考解决如下问题:原题:如图1,点P,Q分别在菱形ABCD的边BC,CD上,∠PAQ=∠B,求证:AP=AQ.(1)小敏进行探索,若将点P,Q的位置特殊化;把∠PAQ绕点A旋转得到∠EAF,使AE⊥BC,点E,F分别在边BC,CD上,如图2.此时她证明了AE=AF,请你证明.(2)受以上(1)的启发,在原题中,添加辅助线:如图3,作AE⊥BC,AF⊥CD,垂足分别为E,F.请你继续完成原题的证明.(3)如果在原题中添加条件:AB=4,∠B=60°,如图1,请你编制一个计算题(不标注新的字母),并直接给出答案(根据编出的问题层次,给不同的得分).(1)证明:∵四边形ABCD是菱形,∴∠B+∠C=180°,∠B=∠D,AB=AD,∵∠EAF=∠B,∴∠EAF+∠C=180°,∴∠AEC+∠AFC=180°,∵AE⊥BC,∴AF⊥CD,在△AEB和△AFD中,,∴△AEB≌△AFD,∴AE=AF;(2)证明:由(1)得,∠PAQ=∠EAF=∠B,AE=AF,∴∠EAP=∠FAQ,在△AEP和△AFQ中,,∴△AEP≌△AFQ,∴AP=AQ;(3)解:已知:AB=4,∠B=60°,求四边形APCQ的面积,解:连接AC、BD交于O,∵∠ABC=60°,BA=BC,∴△ABC为等边三角形,∵AE⊥BC,∴BE=EC,同理,CF=FD,∴四边形AECF的面积=×四边形ABCD的面积,由(2)得,四边形APCQ的面积=四边形AECF的面积,OA=AB=2,OB=AB=2,∴四边形ABCD的面积=×2×2×4=8,∴四边形APCQ的面积=4.14.如图,已知P为锐角∠MAN内部一点,过点P作PB⊥AM于点B,PC⊥AN 于点C,以PB为直径作⊙O,交直线CP于点D,连接AP,BD,AP交⊙O于点E.(1)求证:∠BPD=∠BAC.(2)连接EB,ED,当tan∠MAN=2,AB=2时,在点P的整个运动过程中.①若∠BDE=45°,求PD的长.②若△BED为等腰三角形,求所有满足条件的BD的长.(3)连接OC,EC,OC交AP于点F,当tan∠MAN=1,OC∥BE时,记△OFP 的面积为S1,△CFE的面积为S2,请写出的值.解:(1)∵PB⊥AM、PC⊥AN,∴∠ABP=∠ACP=90°,∴∠BAC+∠BPC=180°,又∠BPD+∠BPC=180°,∴∠BPD=∠BAC;(2)①如图1,∵∠APB=∠BDE=45°,∠ABP=90°,∴BP=AB=2,∵∠BPD=∠BAC,∴tan∠BPD=tan∠BAC,∴=2,∴BP=PD,∴PD=2;②当BD=BE时,∠BED=∠BDE,∴∠BPD=∠BPE=∠BAC,∴tan∠BPE=2,∵AB=2,∴BP=,∴BD=2;当BE=DE时,∠EBD=∠EDB,∵∠APB=∠BDE、∠DBE=∠APC,∴∠APB=∠APC,∴AC=AB=2,过点B作BG⊥AC于点G,得四边形BGCD是矩形,∵AB=2、tan∠BAC=2,∴AG=2,∴BD=CG=2﹣2;当BD=DE时,∠DEB=∠DBE=∠APC,∵∠DEB=∠DPB=∠BAC,∴∠APC=∠BAC,设PD=x,则BD=2x,∴=2,∴,∴x=,∴BD=2x=3,综上所述,当BD=2、3或2﹣2时,△BDE为等腰三角形;(3)如图3,过点O作OH⊥DC于点H,∵tan∠BPD=tan∠MAN=1,∴BD=PD,设BD=PD=2a、PC=2b,则OH=a、CH=a+2b、AC=4a+2b,∵OC∥BE且∠BEP=90°,∴∠PFC=90°,∴∠PAC+∠APC=∠OCH+∠APC=90°,∴∠OCH=∠PAC,∴△ACP∽△CHO,∴=,即OH•AC=CH•PC,∴a(4a+2b)=2b(a+2b),∴a=b,即CP=2a、CH=3a,则OC=a,∵△CPF∽△COH,∴=,即=,则CF=a,OF=OC﹣CF=a,∵BE∥OC且BO=PO,∴OF为△PBE的中位线,∴EF=PF,∴==.15.如图,在Rt△ABC中,AC=BC,∠ACB=90°,点D,E分别在AC,BC上,且CD=CE.(1)如图1,求证:∠CAE=∠CBD;(2)如图2,F是BD的中点,求证:AE⊥CF;(3)如图3,F,G分别是BD,AE的中点,若AC=2,CE=1,求△CGF的面积.解:(1)在△ACE和△BCD中,,∴△ACE≌△BCD,∴∠CAE=∠CBD;(2)如图2,在Rt△BCD中,点F是BD的中点,∴CF=BF,∴∠BCF=∠CBF,由(1)知,∠CAE=∠CBD,∴∠BCF=∠CAE,∴∠CAE+∠ACF=∠BCF+∠ACF=∠BAC=90°,∴∠AMC=90°,∴AE⊥CF;(3)如图3,∵AC=2,∴BC=AC=2,∵CE=1,∴CD=CE=1,在Rt△BCD中,根据勾股定理得,BD==3,∵点F是BD中点,∴CF=DF=BD=,同理:EG=AE=,连接EF,过点F作FH⊥BC,∵∠ACB=90°,点F是BD的中点,∴FH=CD=,=CE•FH=×1×=,∴S△CEF由(2)知,AE⊥CF,=CF•ME=×ME=ME,∴S△CEF∴ME=,∴ME=,∴GM=EG﹣ME=﹣=,=CF•GM=××=.∴S△CFG16.(2018年浙江省宁波市)如图1,直线l:y=﹣x+b与x轴交于点A(4,0),与y轴交于点B,点C是线段OA上一动点(0<AC<).以点A为圆心,AC长为半径作⊙A交x轴于另一点D,交线段AB于点E,连结OE并延长交⊙A于点F.(1)求直线l的函数表达式和tan∠BAO的值;(2)如图2,连结CE,当CE=EF时,①求证:△OCE∽△OEA;②求点E的坐标;(3)当点C在线段OA上运动时,求OE•EF的最大值.解:∵直线l:y=﹣x+b与x轴交于点A(4,0),∴﹣×4+b=0,∴b=3,∴直线l的函数表达式y=﹣x+3,∴B(0,3),∴OA=4,OB=3,在Rt△AOB中,tan∠BAO==;(2)①如图2,连接DF,∵CE=EF,∴∠CDE=∠FDE,∴∠CDF=2∠CDE,∵∠OAE=2∠CDE,∴∠OAE=∠ODF,∵四边形CEFD是⊙O的圆内接四边形,∴∠OEC=∠ODF,∴∠OEC=∠OAE,∵∠COE=∠EOA,∴△COE∽△EOA,②过点E⊥OA于M,由①知,tan∠OAB=,设EM=3m,则AM=4m,∴OM=4﹣4m,AE=5m,∴E(4﹣4m,3m),AC=5m,∴OC=4﹣5m,由①知,△COE∽△EOA,∴,∴OE2=OA•OC=4(4﹣5m)=16﹣20m,∵E(4﹣4m,3m),∴(4﹣4m)2+9m2=25m2﹣32m+16,∴25m2﹣32m+16=16﹣20m,∴m=0(舍)或m=,∴4﹣4m=,3m=,∴(,),(3)如图,设⊙O的半径为r,过点O作OG⊥AB于G,∵A(4,0),B(0,3),∴OA=4,OB=3,∴AB=5,∴AB×OG=OA×OB,∴OG=,∴AG==×=,∴EG=AG﹣AE=﹣r,连接FH,∵EH是⊙O直径,∴EH=2r,∠EFH=90°=∠EGO,∵∠OEG=∠HEF,∴△OEG∽△HEF,∴,∴OE•EF=HE•EG=2r(﹣r)=﹣2(r﹣)2+,∴r=时,OE•EF最大值为.。
最新-全国2018年中考数学试题分类汇编压轴题精品
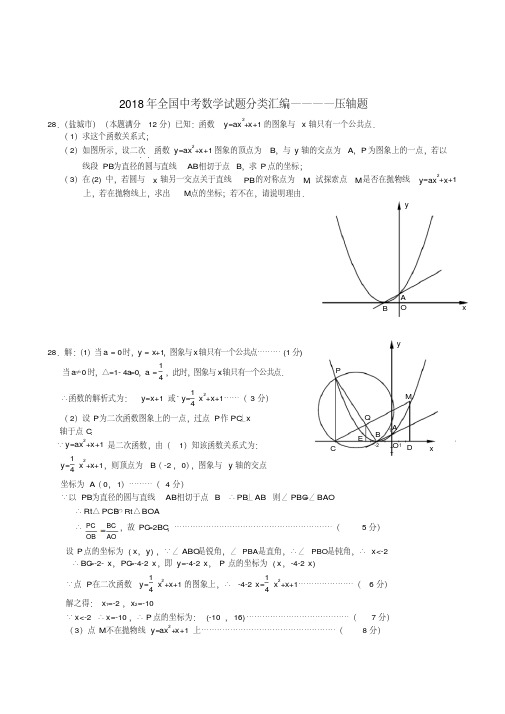
∴ PN=- t 2+3 t
(ⅰ)当 PN=0,即 t= 0 或 t =3 时,以点 P, N, C, D为顶点的多边形是三角形,此三角形的高为
1
1
S=2 DC· AD=2 × 3× 2=3.
(ⅱ)当 PN≠ 0 时,以点 P, N,C, D为顶点的多边形是四边形
∵ PN∥ CD, AD⊥ CD,
1
7
线的对称轴围成的三角形相似
∵点 P在二次函数
1 y=4
x2 +x+1 的图象上,∴
-4-2
1 x=4
x2+x+1…………………(
6 分)
解之得: x1=-2 , x2=-10
∵ x<-2 ∴ x=-10 ,∴ P 点的坐标为: (-10 , 16) …………………………………( 7 分)
( 3)点 M不在抛物线 y=ax2 +x+1 上……………………………………………(
当 t=1 时,此时 N 点的坐标( 1,3 )
当 t=2 时,此时 N 点的坐标( 2,4 )
AD,∴
25.(黄冈市) ( 15 分)已知抛物线 y ax2 bx c( a 0) 顶点为 C( 1,1)且过原点 O.过抛物线上一点
P( x, y)向直线 y
5
作垂线,垂足为
4
( 1)求字母 a, b,c 的值;
( 2)过 P 作直线 x=1 的垂线,可求 P 的纵坐标为 1 ,横坐标为 1 1 3 . 此时, MP= MF= PF= 1,故
4
2
△ MPF为正三角形 .
( 3)存在 . 此时 t = 3 ) 4
24.( 义乌市) 如图 1,已知梯形 OABC,抛物线分别过点
2018年贵州省中考数学压轴题汇编解析:几何综合

2018年全国各地中考数学压轴题汇编(贵州专版)几何综合一.选择题(共6小题)1.(2018•贵阳)如图,在菱形ABCD中,E是AC的中点,EF∥CB,交AB于点F,如果EF=3,那么菱形ABCD的周长为()A.24 B.18 C.12 D.92.(2018•遵义)如图,点P是矩形ABCD的对角线AC上一点,过点P作EF∥BC,分别交AB,CD于E、F,连接PB、PD.若AE=2,PF=8.则图中阴影部分的面积为()A.10 B.12 C.16 D.183.(2018•贵阳)如图,A、B、C是小正方形的顶点,且每个小正方形的边长为1,则tan∠BAC的值为()A.B.1 C.D.4.(2018•遵义)如图,四边形ABCD中,AD∥BC,∠ABC=90°,AB=5,BC=10,连接AC、BD,以BD为直径的圆交AC于点E.若DE=3,则AD的长为()5.(2018•安顺)已知⊙O的直径CD=10cm,AB是⊙O的弦,AB⊥CD,垂足为M,且AB=8cm,则AC的长为()A.2cm B.4cm C.2cm或4cm D.2cm或4cm 6.(2018•铜仁市)在同一平面内,设a、b、c是三条互相平行的直线,已知a与b的距离为4cm,b与c的距离为1cm,则a与c的距离为()A.1cm B.3cm C.5cm或3cm D.1cm或3cm二.填空题(共8小题)7.(2018•贵阳)如图,点M、N分别是正五边形ABCDE的两边AB、BC上的点.且AM=BN,点O是正五边形的中心,则∠MON的度数是度.8.(2018•遵义)如图,△ABC中.点D在BC边上,BD=AD=AC,E为CD的中点.若∠CAE=16°,则∠B为度.9.(2018•贵阳)如图,在△ABC中,BC=6,BC边上的高为4,在△ABC的内部作一个矩形EFGH,使EF在BC边上,另外两个顶点分别在AB、AC边上,则对角线EG长的最小值为.10.(2018•遵义)如图,在菱形ABCD中,∠ABC=120°,将菱形折叠,使点A恰好落在对角线BD上的点G处(不与B、D重合),折痕为EF,若DG=2,BG=6,则BE的长为.11.(2018•安顺)如图,C为半圆内一点,O为圆心,直径AB长为2cm,∠BOC=60°,∠BCO=90°,将△BOC绕圆心O逆时针旋转至△B′OC′,点C′在OA上,则边BC扫过区域12.(2018•黔西南州)已知一个菱形的边长为2,较长的对角线长为2,则这个菱形的面积是.13.(2018•铜仁市)在直角三角形ABC中,∠ACB=90°,D、E是边AB上两点,且CE所在直线垂直平分线段AD,CD平分∠BCE,BC=2,则AB=.14.(2018•黔西南州)如图,已知在△ABC中,BC边上的高AD与AC边上的高BE交于点F,且∠BAC=45°,BD=6,CD=4,则△ABC的面积为60.三.解答题(共9小题)15.(2018•贵阳)如图,在平行四边形ABCD中,AE是BC边上的高,点F是DE的中点,AB与AG关于AE对称,AE与AF关于AG对称.(1)求证:△AEF是等边三角形;(2)若AB=2,求△AFD的面积.16.(2018•遵义)如图,正方形ABCD的对角线交于点O,点E、F分别在AB、BC上(AE <BE),且∠EOF=90°,OE、DA的延长线交于点M,OF、AB的延长线交于点N,连接MN.(1)求证:OM=ON.(2)若正方形ABCD的边长为4,E为OM的中点,求MN的长.17.(2018•贵阳)如图,AB为⊙O的直径,且AB=4,点C在半圆上,OC⊥AB,垂足为点O,P为半圆上任意一点,过P点作PE⊥OC于点E,设△OPE的内心为M,连接OM、PM.(1)求∠OMP的度数;(2)当点P在半圆上从点B运动到点A时,求内心M所经过的路径长.18.(2018•遵义)如图,AB是半圆O的直径,C是AB延长线上的点,AC的垂直平分线交半圆于点D,交AC于点E,连接DA,DC.已知半圆O的半径为3,BC=2.(1)求AD的长.(2)点P是线段AC上一动点,连接DP,作∠DPF=∠DAC,PF交线段CD于点F.当△DPF为等腰三角形时,求AP的长.19.(2018•安顺)如图,在△ABC中,AD是BC边上的中线,E是AD的中点,过点A 作BC的平行线交BE的延长线于点F,连接CF.(1)求证:AF=DC;(2)若AC⊥AB,试判断四边形ADCF的形状,并证明你的结论.20.(2018•铜仁市)如图,在三角形ABC中,AB=6,AC=BC=5,以BC为直径作⊙O交AB于点D,交AC于点G,直线DF是⊙O的切线,D为切点,交CB的延长线于点E.(1)求证:DF⊥AC;(2)求tan∠E的值.21.(2018•安顺)如图,在△ABC中,AB=AC,O为BC的中点,AC与半圆O相切于点D.(1)求证:AB是半圆O所在圆的切线;(2)若cos∠ABC=,AB=12,求半圆O所在圆的半径.22.(2018•贵阳)如图,在矩形ABCD中,AB═2,AD=,P是BC边上的一点,且BP=2CP.(1)用尺规在图①中作出CD边上的中点E,连接AE、BE(保留作图痕迹,不写作法);(2)如图②,在(1)的条件下,判断EB是否平分∠AEC,并说明理由;(3)如图③,在(2)的条件下,连接EP并廷长交AB的廷长线于点F,连接AP,不添加辅助线,△PFB能否由都经过P点的两次变换与△PAE组成一个等腰三角形?如果能,说明理由,并写出两种方法(指出对称轴、旋转中心、旋转方向和平移距离)23.(2018•黔西南州)如图1,已知矩形AOCB,AB=6cm,BC=16cm,动点P从点A出发,以3cm/s的速度向点O运动,直到点O为止;动点Q同时从点C出发,以2cm/s 的速度向点B运动,与点P同时结束运动.(1)点P到达终点O的运动时间是s,此时点Q的运动距离是cm;(2)当运动时间为2s时,P、Q两点的距离为6cm;(3)请你计算出发多久时,点P和点Q之间的距离是10cm;(4)如图2,以点O为坐标原点,OC所在直线为x轴,OA所在直线为y轴,1cm长为单位长度建立平面直角坐标系,连结AC,与PQ相交于点D,若双曲线y=过点D,问k 的值是否会变化?若会变化,说明理由;若不会变化,请求出k的值.2018年全国各地中考数学压轴题汇编(贵州专版)几何综合参考答案与试题解析一.选择题(共6小题)1.(2018•贵阳)如图,在菱形ABCD中,E是AC的中点,EF∥CB,交AB于点F,如果EF=3,那么菱形ABCD的周长为()A.24 B.18 C.12 D.9解:∵E是AC中点,∵EF∥BC,交AB于点F,∴EF是△ABC的中位线,∴EF=BC,∴BC=6,∴菱形ABCD的周长是4×6=24.故选:A.2.(2018•遵义)如图,点P是矩形ABCD的对角线AC上一点,过点P作EF∥BC,分别交AB,CD于E、F,连接PB、PD.若AE=2,PF=8.则图中阴影部分的面积为()A.10 B.12 C.16 D.18解:作PM⊥AD于M,交BC于N.则有四边形AEPM,四边形DFPM,四边形CFPN,四边形BEPN都是矩形,=S△ABC,S△AMP=S△AEP,S△PBE=S△PBN,S△PFD=S△PDM,S△PFC=S△PCN,∴S△ADC=S△PBE=×2×8=8,∴S△DFP8=16,∴S阴=8+故选:C.3.(2018•贵阳)如图,A、B、C是小正方形的顶点,且每个小正方形的边长为1,则tan∠BAC的值为()A.B.1 C.D.解:连接BC,由网格可得AB=BC=,AC=,即AB2+BC2=AC2,∴△ABC为等腰直角三角形,∴∠BAC=45°,则tan∠BAC=1,故选:B.4.(2018•遵义)如图,四边形ABCD中,AD∥BC,∠ABC=90°,AB=5,BC=10,连接AC、BD,以BD为直径的圆交AC于点E.若DE=3,则AD的长为()A.5 B.4 C.3D.2解:如图,在Rt△ABC中,AB=5,BC=10,∴AC=5过点D作DF⊥AC于F,∴∠AFD=∠CBA,∵AD∥BC,∴∠DAF=∠ACB,∴△ADF∽△CAB,∴,∴,设DF=x,则AD=x,在Rt△ABD中,BD==,∵∠DEF=∠DBA,∠DFE=∠DAB=90°,∴△DEF∽△DBA,∴,∴,∴x=2,∴AD=x=2,故选:D.5.(2018•安顺)已知⊙O的直径CD=10cm,AB是⊙O的弦,AB⊥CD,垂足为M,且AB=8cm,则AC的长为()A.2cm B.4cm C.2cm或4cm D.2cm或4cm 解:连接AC,AO,∵⊙O的直径CD=10cm,AB⊥CD,AB=8cm,∴AM=AB=×8=4cm,OD=OC=5cm,当C点位置如图1所示时,∵OA=5cm,AM=4cm,CD⊥AB,∴OM===3cm,∴CM=OC+OM=5+3=8cm,∴AC===4cm;当C点位置如图2所示时,同理可得OM=3cm,∵OC=5cm,∴MC=5﹣3=2cm,在Rt△AMC中,AC===2cm.故选:C.6.(2018•铜仁市)在同一平面内,设a、b、c是三条互相平行的直线,已知a与b的距离为4cm,b与c的距离为1cm,则a与c的距离为()A.1cm B.3cm C.5cm或3cm D.1cm或3cm解:当直线c在a、b之间时,∵a、b、c是三条平行直线,而a与b的距离为4cm,b与c的距离为1cm,∴a与c的距离=4﹣1=3(cm);当直线c不在a、b之间时,∵a、b、c是三条平行直线,而a与b的距离为4cm,b与c的距离为1cm,∴a与c的距离=4+1=5(cm),综上所述,a与c的距离为3cm或3cm.故选:C.二.填空题(共8小题)7.(2018•贵阳)如图,点M、N分别是正五边形ABCDE的两边AB、BC上的点.且AM=BN,点O是正五边形的中心,则∠MON的度数是72度.解:连接OA、OB、OC,∠AOB==72°,∵∠AOB=∠BOC,OA=OB,OB=OC,∴∠OAB=∠OBC,在△AOM和△BON中,∴△AOM≌△BON,∴∠BON=∠AOM,∴∠MON=∠AOB=72°,故答案为:72.8.(2018•遵义)如图,△ABC中.点D在BC边上,BD=AD=AC,E为CD的中点.若∠CAE=16°,则∠B为37度.解:∵AD=AC,点E是CD中点,∴AE⊥CD,∴∠AEC=90°,∴∠C=90°﹣∠CAE=74°,∵AD=AC,∴∠ADC=∠C=74°,∵AD=BD,∴2∠B=∠ADC=74°,∴∠B=37°,故答案为37°.9.(2018•贵阳)如图,在△ABC中,BC=6,BC边上的高为4,在△ABC的内部作一个矩形EFGH,使EF在BC边上,另外两个顶点分别在AB、AC边上,则对角线EG长的最小值为.解:如图,作AQ⊥BC于点Q,交DG于点P,∵四边形DEFG是矩形,∴AQ⊥DG,GF=PQ,设GF=PQ=x,则AP=4﹣x,由DG∥BC知△ADG∽△ABC,∴=,即=,则EF=DG=(4﹣x),∴EG====,∴当x=时,EG取得最小值,最小值为,故答案为:.10.(2018•遵义)如图,在菱形ABCD中,∠ABC=120°,将菱形折叠,使点A恰好落在对角线BD上的点G处(不与B、D重合),折痕为EF,若DG=2,BG=6,则BE的长为2.8.解:作EH⊥BD于H,由折叠的性质可知,EG=EA,由题意得,BD=DG+BG=8,∵四边形ABCD是菱形,∴AD=AB,∠ABD=∠CBD=∠ABC=60°,∴△ABD为等边三角形,∴AB=BD=8,设BE=x,则EG=AE=8﹣x,在Rt△EHB中,BH=x,EH=x,在Rt△EHG中,EG2=EH2+GH2,即(8﹣x)2=(x)2+(6﹣x)2,解得,x=2.8,即BE=2.8,故答案为:2.8.11.(2018•安顺)如图,C 为半圆内一点,O 为圆心,直径AB 长为2cm ,∠BOC=60°,∠BCO=90°,将△BOC 绕圆心O 逆时针旋转至△B′OC′,点C′在OA 上,则边BC 扫过区域(图中阴影部分)的面积为 π cm 2.(结果保留π)解:∵∠BOC=60°,△B′OC′是△BOC 绕圆心O 逆时针旋转得到的,∴∠B′OC′=60°,△BCO=△B′C′O ,∴∠B′OC=60°,∠C′B′O=30°,∴∠B′OB=120°,∵AB=2cm ,∴OB=1cm ,OC′=,∴B′C′=,∴S 扇形B′OB ==π,S 扇形C′OC ==, ∵∴阴影部分面积=S 扇形B′OB +S △B′C′O ﹣S △BCO ﹣S 扇形C′OC =S 扇形B′OB ﹣S 扇形C′OC =π﹣=π;故答案为:π.12.(2018•黔西南州)已知一个菱形的边长为2,较长的对角线长为2,则这个菱形的面积是 2 . 解:依照题意画出图形,如图所示.在Rt△AOB中,AB=2,OB=,∴OA==1,∴AC=2OA=2,=AC•BD=×2×2=2.∴S菱形ABCD故答案为:2.13.(2018•铜仁市)在直角三角形ABC中,∠ACB=90°,D、E是边AB上两点,且CE所在直线垂直平分线段AD,CD平分∠BCE,BC=2,则AB=4.解:∵CE所在直线垂直平分线段AD,∴CE平分∠ACD,∴∠ACE=∠DCE.∵CD平分∠BCE,∴∠DCE=∠DCB.∵∠ACB=90°,∴∠ACE=∠ACB=30°,∴∠A=60°,∴AB===4.故答案为:4.14.(2018•黔西南州)如图,已知在△ABC中,BC边上的高AD与AC边上的高BE交于点F,且∠BAC=45°,BD=6,CD=4,则△ABC的面积为60.解:∵AD⊥BC,BE⊥AC,∴∠AEF=∠BEC=∠BDF=90°,∵∠BAC=45°,∴AE=EB,∵∠EAF+∠C=90°,∠CBE+∠C=90°,∴∠EAF=∠CBE,∴△AEF≌△BEC,∴AF=BC=10,设DF=x.∵△ADC∽△BDF,∴=,∴=,整理得x2+10x﹣24=0,解得x=2或﹣12(舍弃),∴AD=AF+DF=12,=•BC•AD=×10×12=60.∴S△ABC故答案为60.三.解答题(共9小题)15.(2018•贵阳)如图,在平行四边形ABCD中,AE是BC边上的高,点F是DE的中点,AB与AG关于AE对称,AE与AF关于AG对称.(1)求证:△AEF是等边三角形;(2)若AB=2,求△AFD的面积.解:(1)∵AB与AG关于AE对称,∴AE⊥BC,∵四边形ABCD是平行四边形,∴AD∥BC,∴AE⊥AD,即∠DAE=90°,∵点F是DE的中点,即AF是Rt△ADE的中线,∴AF=EF=DF,∵AE与AF关于AG对称,∴AE=AF,则AE=AF=EF,∴△AEF是等边三角形;(2)记AG、EF交点为H,∵△AEF是等边三角形,且AE与AF关于AG对称,∴∠EAG=30°,AG⊥EF,∵AB与AG关于AE对称,∴∠BAE=∠GAE=30°,∠AEB=90°,∵AB=2,∴BE=1、DF=AF=AE=,则EH=AE=、AH=,=××=.∴S△ADF16.(2018•遵义)如图,正方形ABCD的对角线交于点O,点E、F分别在AB、BC上(AE <BE),且∠EOF=90°,OE、DA的延长线交于点M,OF、AB的延长线交于点N,连接MN.(1)求证:OM=ON.(2)若正方形ABCD的边长为4,E为OM的中点,求MN的长.解:(1)∵四边形ABCD是正方形,∴OA=OB,∠DAO=45°,∠OBA=45°,∴∠OAM=∠OBN=135°,∵∠EOF=90°,∠AOB=90°,∴∠AOM=∠BON,∴△OAM≌△OBN(ASA),∴OM=ON;(2)如图,过点O作OH⊥AD于点H,∵正方形的边长为4,∴OH=HA=2,∵E为OM的中点,∴HM=4,则OM==2,∴MN=OM=2.17.(2018•贵阳)如图,AB为⊙O的直径,且AB=4,点C在半圆上,OC⊥AB,垂足为点O,P为半圆上任意一点,过P点作PE⊥OC于点E,设△OPE的内心为M,连接OM、PM.(1)求∠OMP的度数;(2)当点P在半圆上从点B运动到点A时,求内心M所经过的路径长.解:(1)∵△OPE的内心为M,∴∠MOP=∠MOC,∠MPO=∠MPE,∴∠PMO=180°﹣∠MPO﹣∠MOP=180°﹣(∠EOP+∠OPE),∵PE⊥OC,即∠PEO=90°,∴∠PMO=180°﹣(∠EOP+∠OPE)=180°﹣(180°﹣90°)=135°,(2)如图,∵OP=OC,OM=OM,而∠MOP=∠MOC,∴△OPM≌△OCM,∴∠CMO=∠PMO=135°,所以点M在以OC为弦,并且所对的圆周角为135°的两段劣弧上(和);点M在扇形BOC内时,过C、M、O三点作⊙O′,连O′C,O′O,在优弧CO取点D,连DA,DO,∵∠CMO=135°,∴∠CDO=180°﹣135°=45°,∴∠CO′O=90°,而OA=2cm,∴O′O=OC=×2=,∴弧OMC的长==π(cm),同理:点M在扇形AOC内时,同①的方法得,弧ONC的长为πcm,所以内心M所经过的路径长为2×π=πcm.18.(2018•遵义)如图,AB是半圆O的直径,C是AB延长线上的点,AC的垂直平分线交半圆于点D,交AC于点E,连接DA,DC.已知半圆O的半径为3,BC=2.(1)求AD的长.(2)点P是线段AC上一动点,连接DP,作∠DPF=∠DAC,PF交线段CD于点F.当△DPF为等腰三角形时,求AP的长.解:(1)如图1,连接OD,∵OA=OD=3,BC=2,∴AC=8,∵DE是AC的垂直平分线,∴AE=AC=4,∴OE=AE﹣OA=1,在Rt△ODE中,DE==2;在Rt△ADE中,AD==2;(2)当DP=DF时,如图2,点P与A重合,F与C重合,则AP=0;当DP=PF时,如图4,∴∠CDP=∠PFD,∵DE是AC的垂直平分线,∠DPF=∠DAC,∴∠DPF=∠C,∵∠PDF=∠CDP,∴△PDF∽△CDP,∴∠DFP=∠DPC,∴∠CDP=∠CPD,∴CP=CD,∴AP=AC﹣CP=AC﹣CD=AC﹣AD=8﹣2;当PF=DF时,如图3,∴∠FDP=∠FPD,∵∠DPF=∠DAC=∠C,∴△DAC∽△PDC,∴,∴,∴AP=5,即:当△DPF是等腰三角形时,AP的长为0或5或8﹣2.19.(2018•安顺)如图,在△ABC中,AD是BC边上的中线,E是AD的中点,过点A 作BC的平行线交BE的延长线于点F,连接CF.(1)求证:AF=DC;(2)若AC⊥AB,试判断四边形ADCF的形状,并证明你的结论.(1)证明:连接DF,∵E为AD的中点,∴AE=DE,∵AF∥BC,∴∠AFE=∠DBE,在△AFE和△DBE中,,∴△AFE≌△DBE(AAS),∴EF=BE,∵AE=DE,∴四边形AFDB是平行四边形,∴BD=AF,∵AD为中线,∴DC=BD,∴AF=DC;(2)四边形ADCF的形状是菱形,理由如下:∵AF=DC,AF∥BC,∴四边形ADCF是平行四边形,∵∴∵AD为中线∴AD=BC=DC,∴平行四边形ADCF是菱形;20.(2018•铜仁市)如图,在三角形ABC中,AB=6,AC=BC=5,以BC为直径作⊙O交AB于点D,交AC于点G,直线DF是⊙O的切线,D为切点,交CB的延长线于点E.(1)求证:DF⊥AC;(2)求tan∠E的值.(1)证明:如图,连接OC,∵BC是⊙O的直径,∴∠BDC=90°,∴CD⊥AB,∵AC=BC,∴AD=BD,∵OB=OC,∴OD是△ABC的中位线∴OD∥AC,∵DF为⊙O的切线,∴OD⊥DF,∴DF⊥AC;(2)解:如图,连接BG,∵BC是⊙O的直径,∴∠BGC=90°,∵∠EFC=90°=∠BGC,∴EF∥BG,∴∠CBG=∠E,Rt△BDC中,∵BD=3,BC=5,∴CD=4,S△ABC=,6×4=5BG,BG=,由勾股定理得:CG==,∴tan∠CBG=tan∠E===.21.(2018•安顺)如图,在△ABC中,AB=AC,O为BC的中点,AC与半圆O相切于点D.(1)求证:AB是半圆O所在圆的切线;(2)若cos∠ABC=,AB=12,求半圆O所在圆的半径.解:(1)如图,作OE⊥AB于E,连接OD,OA,∵AB=AC,点O是BC的中点,∴∠CAO=∠BAO,∵AC与半圆O相切于D,∴OD⊥AC,∵OE⊥AB,∴OD=OE,∵AB径半圆O的半径的外端点,∴AB是半圆O所在圆的切线;(2)∵AB=AC,O是BC的中点,∴AO⊥BC,在Rt△AOB中,OB=AB•cos∠ABC=12×=8,根据勾股定理得,OA==4,=AB•OE=OB•OA,由三角形的面积得,S△AOB∴OE==,即:半圆O所在圆的半径为.22.(2018•贵阳)如图,在矩形ABCD中,AB═2,AD=,P是BC边上的一点,且BP=2CP.(1)用尺规在图①中作出CD边上的中点E,连接AE、BE(保留作图痕迹,不写作法);(2)如图②,在(1)的条件下,判断EB是否平分∠AEC,并说明理由;(3)如图③,在(2)的条件下,连接EP并廷长交AB的廷长线于点F,连接AP,不添加辅助线,△PFB能否由都经过P点的两次变换与△PAE组成一个等腰三角形?如果能,说明理由,并写出两种方法(指出对称轴、旋转中心、旋转方向和平移距离)解:(1)依题意作出图形如图①所示,(2)EB是平分∠AEC,理由:∵四边形ABCD是矩形,∴∠C=∠D=90°,CD=AB=2,BC=AD=,∵点E是CD的中点,∴DE=CE=CD=1,在△ADE和△BCE中,,∴△ADE≌△BCE,∴∠AED=∠BEC,在Rt△ADE中,AD=,DE=1,∴tan∠AED==,∴∠AED=60°,∴∠BCE=∠AED=60°,∴∠AEB=180°﹣∠AED﹣∠BEC=60°=∠BEC,∴BE平分∠AEC;(3)∵BP=2CP,BC=,∴CP=,BP=,在Rt△CEP中,tan∠CEP==,∴∠CEP=30°,∴∠BEP=30°,∴∠AEP=90°,∵CD∥AB,∴∠F=∠CEP=30°,在Rt△ABP中,tan∠BAP==,∴∠PAB=30°,∴∠EAP=30°=∠F=∠PAB,∵CB⊥AF,∴AP=FP,∴△AEP≌△FBP,∴△PFB能由都经过P点的两次变换与△PAE组成一个等腰三角形,变换的方法为:将△BPF绕点B顺时针旋转120°和△EPA重合,①沿PF折叠,②沿AE 折叠.23.(2018•黔西南州)如图1,已知矩形AOCB,AB=6cm,BC=16cm,动点P从点A出发,以3cm/s的速度向点O运动,直到点O为止;动点Q同时从点C出发,以2cm/s 的速度向点B运动,与点P同时结束运动.(1)点P到达终点O的运动时间是s,此时点Q的运动距离是cm;(2)当运动时间为2s时,P、Q两点的距离为6cm;(3)请你计算出发多久时,点P和点Q之间的距离是10cm;(4)如图2,以点O为坐标原点,OC所在直线为x轴,OA所在直线为y轴,1cm长为单位长度建立平面直角坐标系,连结AC,与PQ相交于点D,若双曲线y=过点D,问k 的值是否会变化?若会变化,说明理由;若不会变化,请求出k的值.解:(1)∵四边形AOCB是矩形,∴OA=BC=16,∵动点P从点A出发,以3cm/s的速度向点O运动,∴,此时,点Q的运动距离是cm(2)如图1,由运动知,AP=3×2=6cm,CQ=2×2=4cm,过点P作PE⊥BC于E,过点Q作QF⊥OA于F,∴四边形APEB是矩形,∴PE=AB=6,BE=6,∴EQ=BC﹣BE﹣CQ=16﹣6﹣4=6,根据勾股定理得,PQ=6,故答案为6;(3)设运动时间为t秒时,由运动知,AP=3t,CQ=2t,同(2)的方法得,PE=6,EQ=16﹣3t﹣2t=16﹣5t,∵点P和点Q之间的距离是10cm,∴62+(16﹣5t)2=100,∴t=或t=;(4)k的值是不会变化,理由:∵四边形AOCB是矩形,∴OC=AB=6,OA=16,∴C(6,0),A(0,16),∴直线AC的解析式为y=﹣x+16①,设运动时间为t,∴AP=3t,CQ=2t,∴OP=16﹣3t,∴P(0,16﹣3t),Q(6,2t),∴PQ解析式为y=x+16﹣3t②,联立①②得,﹣x+16=x+16﹣3t,∴x+x=3t,∴5tx﹣16x+16x=3t,∴x=,∴y=,∴D(,)∴k=×=是定值.. .。
5.14三角形综合题(第5部分)2018年中考数学试题分类汇编(山东四川word解析版)

第五部分图形的性质5.14 三角形综合题【一】知识点清单三角形综合题【二】分类试题汇编及参考答案与解析一、选择题1.(2018年山东省东营市-第10题-3分)如图,点E在△DBC的边DB上,点A在△DBC内部,∠DAE=∠BAC=90°,AD=AE,AB=AC.给出下列结论:①BD=CE;②∠ABD+∠ECB=45°;③BD⊥CE;④BE2=2(AD2+AB2)﹣CD2.其中正确的是()A.①②③④B.②④C.①②③D.①③④【知识考点】全等三角形的判定与性质;勾股定理;等腰直角三角形.【思路分析】只要证明△DAB≌△EAC,利用全等三角形的性质即可一一判断;【解答过程】解:∵∠DAE=∠BAC=90°,∴∠DAB=∠EAC∵AD=AE,AB=AC,∴△DAB≌△EAC,∴BD=CE,∠ABD=∠ECA,故①正确,∴∠ABD+∠ECB=∠ECA+∠ECB=∠ACB=45°,故②正确,∵∠ECB+∠EBC=∠ABD+∠ECB+∠ABC=45°+45°=90°,∴∠CEB=90°,即CE⊥BD,故③正确,∴BE2=BC2﹣EC2=2AB2﹣(CD2﹣DE2)=2AB2﹣CD2+2AD2=2(AD2+AB2)﹣CD2.故④正确,故选:A.【总结归纳】本题考查全等三角形的判定和性质、勾股定理、等腰直角三角形的性质等知识,解题的关键是正确寻找全等三角形解决问题,属于中考选择题中的压轴题.2.(2018年四川省绵阳市-第11题-3分)如图,△ACB和△ECD都是等腰直角三角形,CA=CB,CE=CD,△ACB的顶点A在△ECD的斜边DE上,若的面积为()A B.3C1D.3【知识考点】全等三角形的判定与性质;等腰直角三角形.【思路分析】如图设AB交CD于O,连接BD,作OM⊥DE于M,ON⊥BD于N.想办法求出△AOB 的面积.再求出OA与OB的比值即可解决问题;【解答过程】解:如图设AB交CD于O,连接BD,作OM⊥DE于M,ON⊥BD于N.∵∠ECD=∠ACB=90°,∴∠ECA=∠DCB,∵CE=CD,CA=CB,∴△ECA≌△DCB,∴∠E=∠CDB=45°,AE=BD=,∵∠EDC=45°,∴∠ADB=∠ADC+∠CDB=90°,在Rt△ADB中,AB==2,∴AC=BC=2,∴S△ABC=×2×2=2,∵OD平分∠ADB,OM⊥DE于M,ON⊥BD于N,∴OM=ON,∵====,∴S△AOC=2×=3﹣,故选:D.【总结归纳】本题考查全等三角形的判定和性质、等腰直角三角形的性质、勾股定理、角平分线的性质等知识,解题的关键是学会利用面积法确定线段之间的关系,属于中考选择题中的压轴题.3.(2018年四川省达州市-第8题-3分)如图,△ABC的周长为19,点D,E在边BC上,∠ABC 的平分线垂直于AE,垂足为N,∠ACB的平分线垂直于AD,垂足为M,若BC=7,则MN的长度为()A.32B.2 C.52D.3【知识考点】等腰三角形的判定与性质;三角形中位线定理.【思路分析】证明△BNA≌△BNE,得到BA=BE,即△BAE是等腰三角形,同理△CAD是等腰三角形,根据题意求出DE,根据三角形中位线定理计算即可.【解答过程】解:∵BN平分∠ABC,BN⊥AE,∴∠NBA=∠NBE,∠BNA=∠BNE,在△BNA和△BNE中,∴△BNA≌△BNE,∴BA=BE,∴△BAE是等腰三角形,同理△CAD是等腰三角形,∴点N是AE中点,点M是AD中点(三线合一),∴MN是△ADE的中位线,∵BE+CD=AB+AC=19﹣BC=19﹣7=12,∴DE=BE+CD﹣BC=5,∴MN=DE=.故选:C.【总结归纳】本题考查的是三角形中位线定理、等腰三角形的性质,掌握三角形的中位线平行于第三边,并且等于第三边的一半是解题的关键.二、填空题1.(2018年四川省绵阳市-第18题-3分)如图,在△ABC中,AC=3,BC=4,若AC,BC边上的中线BE,AD垂直相交于O点,则AB=.【知识考点】三角形的重心;勾股定理.【思路分析】利用三角形中线定义得到BD=2,AE=,且可判定点O为△ABC的重心,所以AO=2OD,OB=2OE,利用勾股定理得到BO2+OD2=4,OE2+AO2=,等量代换得到BO2+AO2=4,BO2+AO2=,把两式相加得到BO2+AO2=5,然后再利用勾股定理可计算出AB的长.【解答过程】解:∵AD、BE为AC,BC边上的中线,∴BD=BC=2,AE=AC=,点O为△ABC的重心,∴AO=2OD,OB=2OE,∵BE⊥AD,∴BO2+OD2=BD2=4,OE2+AO2=AE2=,∴BO2+AO2=4,BO2+AO2=,∴BO2+AO2=,∴BO2+AO2=5,∴AB==.故答案为.【总结归纳】本题考查了重心的性质:重心到顶点的距离与重心到对边中点的距离之比为2:1.也考查了勾股定理.2.(2018年四川省泸州市-第16题-3分)如图,等腰△ABC的底边BC=20,面积为120,点F在边BC上,且BF=3FC,EG是腰AC的垂直平分线,若点D在EG上运动,则△CDF周长的最小值为.【知识考点】轴对称﹣最短路线问题;线段垂直平分线的性质;等腰三角形的性质.【思路分析】如图作AH⊥BC于H,连接AD.由EG垂直平分线段AC,推出DA=DC,推出DF+DC=AD+DF,可得当A、D、F共线时,DF+DC的值最小,最小值就是线段AF的长;【解答过程】解:如图作AH⊥BC于H,连接AD.∵EG垂直平分线段AC,∴DA=DC,∴DF+DC=AD+DF,∴当A、D、F共线时,DF+DC的值最小,最小值就是线段AF的长,∵•BC•AH=120,∴AH=12,∵AB=AC,AH⊥BC,∴BH=CH=10,∵BF=3FC,∴CF=FH=5,∴AF===13,∴DF+DC的最小值为13.故答案为13.【总结归纳】本题考查轴对称﹣最短问题、线段的垂直平分线的性质、等腰三角形的性质等知识,解题的关键是学会利用轴对称,解决最短问题,属于中考常考题型.3.(2018年四川省德阳市-第16题-3分)如图,点D为△ABC的AB边上的中点,点E为AD的中点,△ADC为正三角形,给出下列结论,①CB=2CE,②tan∠B=34,③∠ECD=∠DCB,④若AC=2,点P是AB上一动点,点P到AC、BC边的距离分别为d1,d2,则d12+d22的最小值是3.其中正确的结论是(填写正确结论的番号).【知识考点】角平分线的性质;等边三角形的性质;解直角三角形.【思路分析】由题意可得△BCE是含有30°的直角三角形,根据含有30°的直角三角形的性质可判断①②③,易证四边形PMCN是矩形,可得d12+d22=MN2=CP 2,根据垂线段最短,可得CP的值即可求d12+d22的最小值,即可判断④.【解答过程】解:∵D是AB中点∴AD=BD∵△ACD是等边三角形,E是AD中点∴AD=CD,∠ADC=60°=∠ACD,CE⊥AB,∠DCE=30°∴CD=BD∴∠B=∠DCB=30°,且∠DCE=30°,CE⊥AB∴∠ECD=∠DCB,BC=2CE,tan∠B=故①③正确,②错误∵∠DCB=30°,∠ACD=60°∴∠ACB=90°若AC=2,点P是AB上一动点,点P到AC、BC边的距离分别为d1,d2,∴四边形PMCN是矩形∴MN=CP∵d12+d22=MN2=CP2∴当CP为最小值,d12+d22的值最小∴根据垂线段最短,则当CP⊥AB时,d12+d22的值最小此时:∠CAB=60°,AC=2,CP⊥AB∴CP=∴d12+d22=MN2=CP2=3即d12+d22的最小值为3故④正确故答案为①③④【总结归纳】本题考查了解直角三角形,等边三角形的性质和判定,利用垂线段最短求d12+d22的最小值是本题的关键.三、解答题1.(2018年山东省日照市-第22题-13分)问题背景:我们学习等边三角形时得到直角三角形的一个性质:在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半.即:如图1,在Rt△ABC中,∠ACB=90°,∠ABC=30°,则:AC=12 AB.探究结论:小明同学对以上结论作了进一步研究.(1)如图1,连接AB边上中线CE,由于CE=12AB,易得结论:①△ACE为等边三角形;②BE与CE之间的数量关系为.(2)如图2,点D是边CB上任意一点,连接AD,作等边△ADE,且点E在∠ACB的内部,连接BE.试探究线段BE与DE之间的数量关系,写出你的猜想并加以证明.(3)当点D为边CB延长线上任意一点时,在(2)条件的基础上,线段BE与DE之间存在怎样的数量关系?请直接写出你的结论.拓展应用:如图3,在平面直角坐标系xOy中,点A的坐标为(1),点B是x轴正半轴上的一动点,以AB为边作等边△ABC,当C点在第一象限内,且B(2,0)时,求C点的坐标.【知识考点】三角形综合题.【思路分析】探究结论:(1)只要证明△ACE是等边三角形即可解决问题;(2)如图2中,结论:ED=EB.想办法证明EP垂直平分线段AB即可解决问题;(3)结论不变,证明方法类似;拓展应用:利用(2)中结论,可得CO=CB,设C(1,n),根据OC=CB=AB,构建方程即可解决问题;【解答过程】解:探究结论(1)如图1中,∵∠ACB=90°,∠B=30°,∴∠A=60°,∵AC=AB=AE=EB,∴△ACE是等边三角形,∴EC=AE=EB,故答案为EC=EB.(2)如图2中,结论:ED=EB.理由:连接PE.∵△ACP,△ADE都是等边三角形,∴AC=AD=DE,AD=AE,∠CAP=∠DAE=60°,∴∠CAD=∠PAE,∴△CAD≌△PAE,∴∠ACD=∠APE=90°,∴EP⊥AB,∵PA=PB,∴EA=EB,∵DE=AE,∴ED=EB.(3)当点D为边CB延长线上任意一点时,同法可证:ED=EB,故答案为ED=EB.拓展应用:如图3中,作AH⊥x轴于H,CF⊥OB于F,连接OA.∵A(﹣,1),∴∠AOH=30°,由(2)可知,CO=CB,∵CF⊥OB,∴OF=FB=1,∴可以假设C(1,n),∵OC=BC=AB,∴1+n2=1+(+2)2,∴n=2+,∴C(1,2+).【总结归纳】本题考查三角形综合题、等边三角形的判定和性质、全等三角形的判定和性质、勾股定理、线段的垂直平分线的性质等知识,解题的关键是学会添加常用辅助线,构造全等三角形解决问题,属于中考压轴题.2.(2018年山东省淄博市-第23题-9分)(1)操作发现:如图①,小明画了一个等腰三角形ABC,其中AB=AC,在△ABC的外侧分别以AB,AC为腰作了两个等腰直角三角形ABD,ACE,分别取BD,CE,BC的中点M,N,G,连接GM,GN.小明发现了:线段GM与GN的数量关系是;位置关系是.(2)类比思考:如图②,小明在此基础上进行了深入思考.把等腰三角形ABC换为一般的锐角三角形,其中AB>AC,其它条件不变,小明发现的上述结论还成立吗?请说明理由.(3)深入研究:如图③,小明在(2)的基础上,又作了进一步的探究.向△ABC的内侧分别作等腰直角三角形ABD,ACE,其它条件不变,试判断△GMN的形状,并给与证明.【知识考点】三角形综合题.【思路分析】(1)利用SAS判断出△ACD≌△AEB,得出CD=BE,∠ADC=∠ABE,进而判断出∠BDC+∠DBH=90°,即:∠BHD=90°,最后用三角形中位线定理即可得出结论;(2)同(1)的方法即可得出结论;(3)同(1)的方法得出MG=NG,最后利用三角形中位线定理和等量代换即可得出结论.【解答过程】解:(1)连接BE,CD相较于H,∵△ABD和△ACE都是等腰直角三角形,∴AB=AD,AC=AE,∠BAD=∠CAE=90°∴∠CAD=∠BAE,∴△ACD≌△AEB(SAS),∴CD=BE,∠ADC=∠ABE,∴∠BDC+∠DBH=∠BDC+∠ABD+∠ABE=∠BDC+∠ABD+∠ADC=∠ADB+∠ABD=90°,∴∠BHD=90°,∴CD⊥BE,∵点M,G分别是BD,BC的中点,∴MG CD,同理:NG BE,∴MG=NG,MG⊥NG,故答案为:MG=NG,MG⊥NG;(2)连接CD,BE,相较于H,同(1)的方法得,MG=NG,MG⊥NG;(3)连接EB,DC,延长线相交于H,同(1)的方法得,MG=NG,同(1)的方法得,△ABE≌△ADC,∴∠AEB=∠ACD,∴∠CEH+∠ECH=∠AEH﹣∠AEC+180°﹣∠ACD﹣∠ACE=∠ACD﹣45°+180°﹣∠ACD﹣45°=90°,∴∠DHE=90°,同(1)的方法得,MG⊥NG.【总结归纳】此题是三角形综合题,主要考查等腰直角三角形的性质,全等三角形的判定和性质,平行线的判定和性质,三角形的中位线定理,正确作出辅助线用类比的思想解决问题是解本题的关键.3.(2018年四川省自贡市-第25题-12分)如图,已知∠AOB=60°,在∠AOB的平分线OM上有一点C,将一个120°角的顶点与点C重合,它的两条边分别与直线OA、OB相交于点D、E.(1)当∠DCE绕点C旋转到CD与OA垂直时(如图1),请猜想OE+OD与OC的数量关系,并说明理由;(2)当∠DCE绕点C旋转到CD与OA不垂直时,到达图2的位置,(1)中的结论是否成立?并说明理由;(3)当∠DCE绕点C旋转到CD与OA的反向延长线相交时,上述结论是否成立?请在图3中画出图形,若成立,请给于证明;若不成立,线段OD、OE与OC之间又有怎样的数量关系?请写出你的猜想,不需证明.【知识考点】几何变换综合题.【思路分析】(1)先判断出∠OCE=60°,再利用特殊角的三角函数得出OD=OC,同OE=OC,即可得出结论;(2)同(1)的方法得OF+OG=OC,再判断出△CFD≌△CGE,得出DF=EG,最后等量代换即可得出结论;(3)同(2)的方法即可得出结论.【解答过程】解:(1)∵OM是∠AOB的角平分线,∴∠AOC=∠BOC=∠AOB=30°,∵CD⊥OA,∴∠ODC=90°,∴∠OCD=60°,∴∠OCE=∠DCE﹣∠OCD=60°,在Rt△OCD中,OD=OE•cos30°=OC,同理:OE=OC,∴OD+OD=OC;(2)(1)中结论仍然成立,理由:过点C作CF⊥OA于F,CG⊥OB于G,∴∠OFC=∠OGC=90°,∵∠AOB=60°,∴∠FCG=120°,同(1)的方法得,OF=OC,OG=OC,∴OF+OG=OC,∵CF⊥OA,CG⊥OB,且点C是∠AOB的平分线OM上一点,∴CF=CG,∵∠DCE=120°,∠FCG=120°,∴∠DCF=∠ECG,∴△CFD≌△CGE,∴DF=EG,∴OF=OD+DF=OD+EG,OG=OE﹣EG,∴OF+OG=OD+EG+OE﹣EG=OD+OE,∴OD+OE=OC;(3)(1)中结论不成立,结论为:OE﹣OD=OC,理由:过点C作CF⊥OA于F,CG⊥OB于G,∴∠OFC=∠OGC=90°,∵∠AOB=60°,∴∠FCG=120°,同(1)的方法得,OF=OC,OG=OC,∴OF+OG=OC,∵CF⊥OA,CG⊥OB,且点C是∠AOB的平分线OM上一点,∴CF=CG,∵∠DCE=120°,∠FCG=120°,∴∠DCF=∠ECG,∴△CFD≌△CGE,∴DF=EG,∴OF=DF﹣OD=EG﹣OD,OG=OE﹣EG,∴OF+OG=EG﹣OD+OE﹣EG=OE﹣OD,∴OE﹣OD=OC.【总结归纳】此题是几何变换综合题,主要考查了角平分线的定义和定理,全等三角形的判定和性质,特殊角的三角函数直角三角形的性质,正确作出辅助线是解本题的关键.4.(2018年四川省阿坝州/甘孜州-第27题-10分)如图,△ABC中,AB=AC,∠BAC=90°,点D,E分别在AB,BC上,∠EAD=∠EDA,点F为DE的延长线与AC的延长线的交点.(1)求证:DE=EF;(2)判断BD和CF的数量关系,并说明理由;(3)若AB=3,BD的长.【知识考点】三角形综合题.【思路分析】(1)只要证明EA=ED,EA=EF即可解决问题;(2)结论:BD=CF.如图2中,在BE上取一点M,使得ME=CE,连接DM.想办法证明DM=CF,DM=BD即可;(3)如图3中,过点E作EN⊥AD交AD于点N.设BD=x,则DN=,DE=AE=,由∠B=45°,EN⊥BN.推出EN=BN=x+=,在Rt△DEN中,根据DN2+NE2=DE2,构建方程即可解决问题;【解答过程】(1)证明:如图1中,∵∠BAC=90°,∴∠EAD+∠CAE=90°,∠EDA+∠F=90°,∵∠EAD=∠EDA,∴∠EAC=∠F,∴EA=ED,EA=EF,∴DE=EF.(2)解:结论:BD=CF.理由:如图2中,在BE上取一点M,使得ME=CE,连接DM.∵DE=EF.∠DEM=∠CEF,EM=EC.∴△DEM≌△FEC,∴DM=CF,∠MDE=∠F,∴DM∥CF,∴∠BDM=∠BAC=90°,∵AB=AC,∴∠DBM=45°,∴BD=DM,∴BD=CF.(3)如图3中,过点E作EN⊥AD交AD于点N.∵EA=ED,EN⊥AD,∴AN=ND,设BD=x,则DN=,DE=AE=,∵∠B=45°,EN⊥BN.∴EN=BN=x+=,在Rt△DEN中,∵DN2+NE2=DE2,∴()2+()2=()2解得x=1或﹣1(舍弃)∴BD=1.【总结归纳】本题考查三角形综合题、等腰三角形的判定和性质、全等三角形的判定和性质、勾股定理等知识,解题的关键是学会添加常用辅助线,构造全等三角形解决问题,属于中考常考题型.5.(2018年四川省乐山市-第25题-12分)已知Rt△ABC中,∠ACB=90°,点D、E分别在BC、AC边上,连结BE、AD交于点P,设AC=kBD,CD=kAE,k为常数,试探究∠APE的度数:(1)如图1,若k=1,则∠APE的度数为;(2)如图2,若k=试问(1)中的结论是否成立?若成立,请说明理由;若不成立,求出∠APE 的度数.(3)如图3,若k=D、E分别在CB、CA的延长线上,(2)中的结论是否成立,请说明理由.【知识考点】三角形综合题.【思路分析】(1)先判断出四边形ADBF是平行四边形,得出BD=AF,BF=AD,进而判断出△FAE≌△ACD,得出EF=AD=BF,再判断出∠EFB=90°,即可得出结论;(2)先判断出四边形ADBF是平行四边形,得出BD=AF,BF=AD,进而判断出△FAE∽△ACD,再判断出∠EFB=90°,即可得出结论;(3)先判断出四边形ADBF是平行四边形,得出BD=AF,BF=AD,进而判断出△ACD∽△HEA,再判断出∠EFB=90°,即可得出结论;【解答过程】解:(1)如图1,过点A作AF∥CB,过点B作BF∥AD相交于F,连接EF,∴∠FBE=∠APE,∠FAC=∠C=90°,四边形ADBF是平行四边形,∴BD=AF,BF=AD,∵AC=BD,CD=AE,∴AF=AC,∵∠FAC=∠C=90°,∴△FAE≌△ACD,∴EF=AD=BF,∠FEA=∠ADC,∵∠ADC+∠CAD=90°,∴∠FEA+∠CAD=90°=∠EHD,∵AD∥BF,∴∠EFB=90°,∵EF=BF,∴∠FBE=45°,∴∠APE=45°,故答案为:45°.(2)(1)中结论不成立,理由如下:如图2,过点A作AF∥CB,过点B作BF∥AD相交于F,连接EF,∴∠FBE=∠APE,∠FAC=∠C=90°,四边形ADBF是平行四边形,∴BD=AF,BF=AD,∵AC=BD,CD=AE,∴,∵BD=AF,∴,∵∠FAC=∠C=90°,∴△FAE∽△ACD,∴=,∠FEA=∠ADC,∵∠ADC+∠CAD=90°,∴∠FEA+∠CAD=90°=∠EMD,∵AD∥BF,∴∠EFB=90°,在Rt△EFB中,tan∠FBE=,∴∠FBE=30°,∴∠APE=30°,(3)(2)中结论成立,如图3,作EH∥CD,DH∥BE,EH,DH相交于H,连接AH,∴∠APE=∠ADH,∠HEC=∠C=90°,四边形EBDH是平行四边形,∴BE=DH,EH=BD,∵AC=BD,CD=AE,∴,∵∠HEA=∠C=90°,∴△ACD∽△HEA,∴,∠ADC=∠HAE,∵∠CAD+∠ADC=90°,∴∠HAE+∠CAD=90°,∴∠HAD=90°,在Rt△DAH中,tan∠ADH==,∴∠ADH=30°,∴∠APE=30°.【总结归纳】此题是三角形综合题,主要考查了全等三角形的判定和性质,相似三角形的判定和性质,平行四边形的判定和性质,构造全等三角形和相似三角形的判定和性质.6.(2018年四川省攀枝花市-第23题-12分)如图,在△ABC中,AB=7.5,AC=9,S△ABC=814.动点P从A点出发,沿AB方向以每秒5个单位长度的速度向B点匀速运动,动点Q从C点同时出发,以相同的速度沿CA方向向A点匀速运动,当点P运动到B点时,P、Q两点同时停止运动,以PQ为边作正△PQM(P、Q、M按逆时针排序),以QC为边在AC上方作正△QCN,设点P运动时间为t秒.(1)求cosA的值;(2)当△PQM与△QCN的面积满足S△PQM=94S△QCN时,求t的值;(3)当t为何值时,△PQM的某个顶点(Q点除外)落在△QCN的边上.【知识考点】三角形综合题.【思路分析】(1)如图1中,作BE⊥AC于E.利用三角形的面积公式求出BE,利用勾股定理求出AE即可解决问题;(2)如图2中,作PH⊥AC于H.利用S△PQM=S△QCN构建方程即可解决问题;(3)分两种情形①如图3中,当点M落在QN上时,作PH⊥AC于H.②如图4中,当点M在CQ上时,作PH⊥AC于H.分别构建方程求解即可;【解答过程】解:(1)如图1中,作BE⊥AC于E.∵S△ABC=•AC•BE=,∴BE=,在Rt△ABE中,AE==6,∴coaA===.(2)如图2中,作PH⊥AC于H.∵PA=5t,PH=3t,AH=4t,HQ=AC﹣AH﹣CQ=9﹣9t,∴PQ2=PH2+HQ2=9t2+(9﹣9t)2,∵S△PQM=S△QCN,∴•PQ2=וCQ2,∴9t2+(9﹣9t)2=×(5t)2,整理得:5t2﹣18t+9=0,解得t=3(舍弃)或.∴当t=时,满足S△PQM=S△QCN.(3)①如图3中,当点M落在QN上时,作PH⊥AC于H.易知:PM∥AC,∴∠MPQ=∠PQH=60°,∴PH=HQ,∴3t=(9﹣9t),∴t=.②如图4中,当点M在CQ上时,作PH⊥AC于H.同法可得PH=QH,∴3t=(9t﹣9),∴t=,综上所述,当t=s或s时,△PQM的某个顶点(Q点除外)落在△QCN的边上.【总结归纳】本题考查三角形综合题、等边三角形的性质、勾股定理锐角三角函数、解直角三角形等知识,解题的关键是灵活运用所学知识解决问题,学会用分类讨论的思想思考问题,属于中考常考题型.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
综合性问题一、选择题1.(2018·湖北省孝感·3分)如图,△ABC是等边三角形,△ABD是等腰直角三角形,∠BAD=90°,AE⊥BD于点E,连CD分别交AE,AB于点F,G,过点A作AH⊥CD交BD于点H.则下列结论:①∠ADC=15°;②AF=AG;③AH=DF;④△AFG∽△CBG;⑤AF=(﹣1)EF.其中正确结论的个数为()A.5 B.4 C.3 D.2【分析】①由等边三角形与等腰直角三角形知△CAD是等腰三角形且顶角∠CAD=150°,据此可判断;②求出∠AFP和∠FAG度数,从而得出∠AGF度数,据此可判断;③证△ADF≌△BAH即可判断;④由∠AFG=∠CBG=60°、∠AGF=∠CGB 即可得证;⑤设PF=x,则AF=2x、AP==x,设EF=a,由△ADF≌△BAH知BH=AF=2x,根据△ABE是等腰直角三角形之BE=AE=a+2x,据此得出EH=a,证△PAF∽△EAH得=,从而得出a与x的关系即可判断.【解答】解:∵△ABC为等边三角形,△ABD为等腰直角三角形,∴∠BAC=60°、∠BAD=90°、AC=AB=AD,∠ADB=∠ABD=45°,∴△CAD是等腰三角形,且顶角∠CAD=150°,∴∠ADC=15°,故①正确;∵AE⊥BD,即∠AED=90°,∴∠DAE=45°,∴∠AFG=∠ADC+∠DAE=60°,∠FAG=45°,∴∠AGF=75°,由∠AFG≠∠AGF知AF≠AG,故②错误;记AH与CD的交点为P,由AH⊥CD且∠AFG=60°知∠FAP=30°,则∠BAH=∠ADC=15°,在△ADF和△BAH中,∵,∴△ADF≌△BAH(ASA),∴DF=AH,故③正确;∵∠AFG=∠CBG=60°,∠AGF=∠CGB,∴△AFG∽△CBG,故④正确;在Rt△APF中,设PF=x,则AF=2x、AP==x,设EF=a,∵△ADF≌△BAH,∴BH=AF=2x,△ABE中,∵∠AEB=90°、∠ABE=45°,∴BE=AE=AF+EF=a+2x,∴EH=BE﹣BH=a+2x﹣2x=a,∵∠APF=∠AEH=90°,∠FAP=∠HAE,∴△PAF∽△EAH,∴=,即=,整理,得:2x2=(﹣1)ax,由x≠0得2x=(﹣1)a,即AF=(﹣1)EF,故⑤正确;故选:B.【点评】本题主要考查相似三角形的判定与性质,解题的关键是掌握等腰三角形与等边三角形的性质、全等三角形与相似三角形的判定与性质等知识点.2.(2018·山东潍坊·3分)如图,菱形ABCD的边长是4厘米,∠B=60°,动点P以1厘米秒的速度自A点出发沿AB方向运动至B点停止,动点Q以2厘米/秒的速度自B点出发沿折线BCD运动至D点停止.若点P、Q同时出发运动了t秒,记△BPQ的面积为S厘米2,下面图象中能表示S与t之间的函数关系的是()A.B.C.D.【分析】应根据0≤t<2和2≤t<4两种情况进行讨论.把t当作已知数值,就可以求出S,从而得到函数的解析式,进一步即可求解.【解答】解:当0≤t<2时,S=2t××(4﹣t)=﹣t2+4t;当2≤t<4时,S=4××(4﹣t)=﹣2t+8;只有选项D的图形符合.故选:D.【点评】本题主要考查了动点问题的函数图象,利用图形的关系求函数的解析式,注意数形结合是解决本题的关键.3. (2018•安徽•4分)如图,直线都与直线l垂直,垂足分别为M,N,MN=1,正方形ABCD的边长为,对角线AC在直线l上,且点C位于点M处,将正方形ABCD沿l向右平移,直到点A与点N重合为止,记点C平移的距离为x,正方形ABCD的边位于之间分的长度和为y,则y关于x的函数图象大致为()A. B. C. D.【答案】A【解析】【分析】由已知易得AC=2,∠ACD=45°,分0≤x≤1、1<x≤2、2<x≤3三种情况结合等腰直角三角形的性质即可得到相应的函数解析式,由此即可判断.【详解】由正方形的性质,已知正方形ABCD的边长为,易得正方形的对角线AC=2,∠ACD=45°,如图,当0≤x≤1时,y=2,如图,当1<x≤2时,y=2m+2n=2(m+n)= 2,如图,当2<x≤3时,y=2,综上,只有选项A符合,故选A.【点睛】本题考查了动点问题的函数图象,涉及到正方形的性质,等腰直角三角形的性质,勾股定理等,结合图形正确分类是解题的关键.4. (2018·浙江舟山·3分)欧几里得的《原本》记载,形如x2+ax=b2的方程的图解法是;画Rt△ABC,使∠ACB=90°,BC= ,AC=b,再在斜边AB上截取BD= 。
则该方程的一个正根是()A.AC的长B.AD的长C.BC的长D.CD的长【考点】一元二次方程的根,勾股定理【分析】由勾股定理不难得到AC 2+BC 2=AB 2=(AD+BD )2 , 代入b 和a 即可得到答案【解析】【解答】解:在Rt △ABC 中,由勾股定理可得AC 2+BC 2=AB 2=(AD+BD )2 ,因为AC=b ,BD=BC=,所以b 2+=, 整理可得AD 2+aAD=b 2 , 与方程x 2+ax=b 2相同,因为AD 的长度是正数,所以AD 是x 2+ax=b 2的一个正根故答案为B 。
【点评】本题考查了一元二次方程的根与勾股定理的综合运用,注意D 是x 2+ax=b 2的一个正根.5. (2018·重庆·4分) 如图,已知AB 是O e 的直径,点P 在BA 的延长线上,PD 与O e 相切于点D ,过点B 作PD 的垂线交PD 的延长线于点C ,若O e 的半径为4,6BC =,则PA 的长为A .4 B.C .3 D .2.5【考点】圆的切线、相似三角形.【解析】作OH ⊥PC 于点H .易证△POH ∽△PBC ,BC OH PB PO =∴,6484=++∴PA PA ,4=∴PA 【点评】此题考查圆切线与相似的结合,属于基础题3. (2018·重庆(A)·4分) 若数a 使关于x 的不等式组112352x x x x a-+⎧<⎪⎨⎪-≥+⎩有且只有四个整数解,且使关于y 的方程2211y a a y y++=--的解为非负数,则符合条件的所有整数a 的和为( ) A .3- B .2- C .1 D .2【考点】不等式组和分式方程的应用【分析】解关于x 的不等式组,根据题意求出a 的取值范围,然后解关于y 的方程,排除分式方程无解的情况,结合不等式组的结果,找出符合条件的所有整数a 并求其和.【解答】 解不等式⎪⎩⎪⎨⎧+≥<⎪⎩⎪⎨⎧+≥-+<-425253121a x x a x x x x 得,由于不等式有四个整数解,根据题意,,则1420≤+<a ,解得22≤<-a 。
解分式方程2121=-+-+y a y a y 得a y -=2,又需排除分式方程无解的情况,故2≤a 且1≠a .结合不等式组的结果有a 的取值范围为122≠≤<-a a 且,又a 为整数,所以a 的取值为2,0,1-,和为1.故选C【点评】此题考查不等式组和分式方程的应用,需要特别注意分式方程无解情况的考虑,属于中档题二.填空题1.(2018·浙江宁波·4分)如图,正方形ABCD 的边长为8,M 是AB 的中点,P 是BC 边上的动点,连结PM ,以点P 为圆心,PM 长为半径作⊙P.当⊙P 与正方形ABCD 的边相切时,BP的长为 3或4 .【考点】切线的性质、正方形的性质、勾股定理【分析】分两种情形分别求解:如图1中,当⊙P 与直线CD 相切时;如图2中当⊙P 与直线AD 相切时.设切点为K ,连接PK ,则PK⊥AD,四边形PKDC 是矩形;【解答】解:如图1中,当⊙P 与直线CD 相切时,设PC=PM=m .在Rt△PBM中,∵PM2=BM2+PB2,∴x2=42+(8﹣x)2,∴x=5,∴PC=5,BP=BC﹣PC=8﹣5=3.如图2中当⊙P与直线AD相切时.设切点为K,连接PK,则PK⊥AD,四边形PKDC是矩形.∴PM=PK=CD=2BM,∴BM=4,PM=8,在Rt△PBM中,PB==4.综上所述,BP的长为3或4.【点评】本题考查切线的性质、正方形的性质、勾股定理等知识,解题的关键是学会用分类讨论的思想思考问题,学会利用参数构建方程解决问题.2. (2018·浙江宁波·4分)如图,在菱形ABCD中,AB=2,∠B是锐角,AE⊥BC于点E,M是AB的中点,连结MD,ME.若∠EMD=90°,则cosB的值为.【考点】菱形的性质、勾股定理、线段的垂直平分线的性质、全等三角形的判定和性质.【分析】延长DM交CB的延长线于点H.首先证明DE=EH,设BE=x,利用勾股定理构建方程求出x即可解决问题.【解答】解:延长DM交CB的延长线于点H.∵四边形ABCD是菱形,∴AB=BC=AD=2,AD∥CH,∴∠ADM=∠H,∵AM=BM,∠AMD=∠HMB,∴△ADM≌△BHM,∴AD=HB=2,∵EM⊥DH,∴EH=ED,设BE=x,∵AE⊥BC,∴AE⊥AD,∴∠AEB=∠EAD=90°∵AE2=AB2﹣BE2=DE2﹣AD2,∴22﹣x2=(2+x)2﹣22,∴x=﹣1或﹣﹣1(舍弃),∴cosB==,故答案为.【点评】本题考查菱形的性质、勾股定理、线段的垂直平分线的性质、全等三角形的判定和性质等知识,解题的关键是学会添加常用辅助线,构造全等三角形解决问题,属于中考常考题型.3.(2018•湖北荆门•3分)如图,在平面直角坐标系xOy中,函数y=(k>0,x>0)的图象经过菱形OACD的顶点D和边AC的中点E,若菱形OACD的边长为3,则k的值为.【分析】过D作DQ⊥x轴于Q,过C作CM⊥x轴于M,过E作EF⊥x轴于F,设D点的坐标为(a,b),求出C、E的坐标,代入函数解析式,求出a,再根据勾股定理求出b,即可请求出答案.【解答】解:过D作DQ⊥x轴于Q,过C作CM⊥x轴于M,过E作EF⊥x轴于F,设D点的坐标为(a,b)则C点的坐标为(a+3,b),∵E为AC的中点,∴EF=CM=b,AF=AM=OQ=a,E点的坐标为(3+a,b),把D、E的坐标代入y=得:k=ab=(3+a)b,解得:a=2,在Rt△DQO中,由勾股定理得:a2+b2=32,即22+b2=9,解得:b=(负数舍去),∴k=ab=2,故答案为:2.【点评】本题考查了勾股定理、反比例函数图象上点的坐标特征、菱形的性质等知识点,能得出关于a、b的方程是解此题的关键.4.(2018·山东潍坊·3分)如图,正方形ABCD的边长为1,点A与原点重合,点B在y轴的正半轴上,点D在x轴的负半轴上,将正方形ABCD绕点A逆时针旋转30°至正方形AB'C′D′的位置,B'C′与CD相交于点M,则点M的坐标为(﹣1,).【分析】连接AM,由旋转性质知AD=AB′=1、∠BAB′=30°、∠B′AD=60°,证Rt△ADM≌Rt△AB′M得∠DAM=∠B′AD=30°,由DM=ADtan∠DAM可得答案.【解答】解:如图,连接AM,∵将边长为1的正方形ABCD绕点A逆时针旋转30°得到正方形AB'C′D′,∴AD=AB′=1,∠BAB′=30°,∴∠B′AD=60°,在Rt△ADM和Rt△AB′M中,∵,∴Rt△ADM≌Rt△AB′M(HL),∴∠DAM=∠B′AM=∠B′AD=30°,∴DM=ADtan∠DAM=1×=,∴点M的坐标为(﹣1,),故答案为:(﹣1,).【点评】本题主要考查旋转的性质、正方形的性质,解题的关键是掌握旋转变换的不变性与正方形的性质、全等三角形的判定与性质及三角函数的应用.5.(2018·湖北省孝感·3分)如图,在平面直角坐标系中,正方形ABCD的顶点A的坐标为(﹣l,1),点B在x轴正半轴上,点D在第三象限的双曲线y=上,过点C作CE∥x轴交双曲线于点E,连接BE,则△BCE的面积为7 .【分析】作辅助线,构建全等三角形:过D作GH⊥x轴,过A作AG⊥GH,过B作BM⊥HC于M,证明△AGD≌△DHC≌△CMB,根据点D的坐标表示:AG=DH=﹣x﹣1,由DG=BM,列方程可得x的值,表示D和E的坐标,根据三角形面积公式可得结论.【解答】解:过D作GH⊥x轴,过A作AG⊥GH,过B作BM⊥HC于M,设D(x,),∵四边形ABCD是正方形,∴AD=CD=BC,∠ADC=∠DCB=90°,易得△AGD≌△DHC≌△CMB,∴AG=DH=﹣x﹣1,∴DG=BM,∴1﹣=﹣1﹣x﹣,x=﹣2,∴D(﹣2,﹣3),CH=DG=BM=1﹣=4,∵AG=DH=﹣1﹣x=1,∴点E的纵坐标为﹣4,当y=﹣4时,x=﹣,∴E(﹣,﹣4),∴EH=2﹣=,∴CE=CH﹣HE=4﹣=,∴S△CEB=CE•BM=××4=7;故答案为:7.【点评】本题考查正方形的性质、全等三角形的判定和性质、反比例函数的性质等知识,解题的关键是灵活运用所学知识解决问题,学会构建方程解决问题,属于中考填空题的压轴题.6.(2018·山东泰安·3分)如图,在矩形ABCD中,AB=6,BC=10,将矩形ABCD沿BE折叠,点A落在A'处,若EA'的延长线恰好过点C,则sin∠ABE的值为.【分析】先利用勾股定理求出A'C,进而利用勾股定理建立方程求出AE,即可求出BE,最后用三角函数即可得出结论.【解答】解:由折叠知,A'E=AE,A'B=AB=6,∠BA'E=90°,∴∠BA'C=90°,在Rt△A'CB中,A'C==8,设AE=x,则A'E=x,∴DE=10﹣x,CE=A'C+A'E=8+x,在Rt△CDE中,根据勾股定理得,(10﹣x)2+36=(8+x)2,∴x=2,∴AE=2,在Rt△ABE中,根据勾股定理得,BE==2,∴sin∠ABE==,故答案为:.【点评】此题主要考查了折叠的性质,勾股定理,锐角三角函数,充分利用勾股定理求出线段AE是解本题的关键.7.(2018·山东泰安·3分)如图,在△ABC中,AC=6,BC=10,tanC=,点D是AC边上的动点(不与点C重合),过D作DE⊥BC,垂足为E,点F是BD的中点,连接EF,设CD=x,△DEF的面积为S,则S与x之间的函数关系式为S=x2.【分析】可在直角三角形CED中,根据DE、CE的长,求出△BED的面积即可解决问题.【解答】解:(1)在Rt△CDE中,tanC=,CD=x∴DE=x,CE=x,∴BE=10﹣x,∴S△BED=×(10﹣x)•x=﹣x2+3x.∵DF=BF,∴S=S△BED=x2,故答案为S=x2.【点评】本题考查解直角三角形,三角形的面积等知识,解题的关键是熟练掌握基本知识,属于中考常考题型.8.(2018·山东威海·3分)用若干个形状、大小完全相同的矩形纸片围成正方形,4个矩形纸片围成如图①所示的正方形,其阴影部分的面积为12;8个矩形纸片围成如图②所示的正方形,其阴影部分的面积为8;12个矩形纸片围成如图③所示的正方形,其阴影部分的面积为44﹣16.【分析】图①中阴影部分的边长为=2,图②中,阴影部分的边长为=2;设小矩形的长为a,宽为b,依据等量关系即可得到方程组,进而得出a,b的值,即可得到图③中,阴影部分的面积.【解答】解:由图可得,图①中阴影部分的边长为=2,图②中,阴影部分的边长为=2;设小矩形的长为a,宽为b,依题意得,解得,∴图③中,阴影部分的面积为(a﹣3b)2=(4﹣2﹣6)2=44﹣16,1 2 故答案为:44﹣16.【点评】本题主要考查了二元一次方程组的应用以及二次根式的化简,当问题较复杂时,有时设与要求的未知量相关的另一些量为未知数,即为间接设元.无论怎样设元,设几个未知数,就要列几个方程.三.解答题1. (2018•山西•13分)综 合 与 探 究如图,抛物线211433y x x =--与 x 轴交于 A , B 两点(点 A 在点 B 的 左 侧 ), 与 y 轴交于点 C ,连接AC , BC .点 P 是 第 四 象 限 内 抛 物 线 上 的 一 个 动 点 ,点 P 的横坐标为 m ,过 点 P 作 PM ⊥ x 轴 ,垂 足 为点 M , PM 交 BC 于点 Q ,过点 P 作 PE ∥ AC 交 x 轴于点 E ,交 BC 于点 F .( 1) 求 A , B , C 三点的坐标;( 2) 试探究在点 P 的 运 动 的 过 程 中 ,是 否 存 在 这 样 的 点 Q ,使 得 以 A , C , Q 为 顶 点 的 三 角 形 是等腰三角形.若存在,.写出此时点 Q 的 坐 标 ; 若 不 存 在 , 请 说明理由; ( 3) 请用含 m 的 代 数 式 表 示 线 段 QF 的长,并求出 m 为 何 值 时 QF 有最大值 .【考点】 几 何 与 二 次 函 数 综 合【解析】( 1) 解: 由 y = 0 ,得2114=033x x -- 解得 x 1 = -3 , x 2 = 4 . ∴ 点 A , B 的坐标分别为 A(-3,0), B ( 4, 0) 由 x = 0 ,得 y = -4 .∴ 点 C 的 坐 标 为 C ( 0, -4) .( 2) 答: Q ( 5 2 , 5 2 2 - 4) , Q (1,-3) . 2(3)过点F 作FG ⊥PQ 于点G .则FG∥x 轴.由 B(4,0),C(0,-4),得△O B C为等腰直角三角形.∴∠OBC =∠QFG = 45︒ . ∴GQ =FG =FQ .2PE∥AC , ∴∠1 =∠2 .FG∥x轴,∴∠2 =∠3 . ∴∠1 =∠3 .∠FGP =∠AOC = 90︒ , ∴△FGP∽△AOC.2. (2018•山东枣庄•10分)如图1,已知二次函数y=ax2+x+c(a≠0)的图象与y轴交于点A(0,4),与x轴交于点B、C,点C坐标为(8,0),连接AB、AC.(1)请直接写出二次函数y=ax2+x+c的表达式;(2)判断△ABC的形状,并说明理由;(3)若点N在x轴上运动,当以点A、N、C为顶点的三角形是等腰三角形时,请写出此时点N的坐标;(4)如图2,若点N在线段BC上运动(不与点B、C重合),过点N作NM∥AC,交AB于点M,当△AMN 面积最大时,求此时点N的坐标.【分析】(1)根据待定系数法即可求得;(2)根据抛物线的解析式求得B的坐标,然后根据勾股定理分别求得AB2=20,AC2=80,BC10,然后根据勾股定理的逆定理即可证得△ABC是直角三角形.(3)分别以A、C两点为圆心,AC长为半径画弧,与x轴交于三个点,由AC的垂直平分线与x轴交于一个点,即可求得点N的坐标;(4)设点N的坐标为(n,0),则BN=n+2,过M点作MD⊥x轴于点D,根据三角形相似对应边成比例求得MD=(n+2),然后根据S△AMN=S△ABN﹣S△BMN得出关于n的二次函数,根据函数解析式求得即可.【解答】解:(1)∵二次函数y=ax2+x+c的图象与y轴交于点A(0,4),与x轴交于点B、C,点C 坐标为(8,0),∴,解得.∴抛物线表达式:y=﹣x2+x+4;(2)△ABC是直角三角形.令y=0,则﹣x2+x+4=0,解得x1=8,x2=﹣2,∴点B的坐标为(﹣2,0),由已知可得,在Rt△ABO中AB2=BO2+AO2=22+42=20,在Rt△AOC中AC2=AO2+CO2=42+82=80,又∵BC=OB+OC=2+8=10,∴在△ABC中AB2+AC2=20+80=102=BC2∴△ABC是直角三角形.(3)∵A(0,4),C(8,0),∴AC==4,①以A为圆心,以AC长为半径作圆,交x轴于N,此时N的坐标为(﹣8,0),②以C为圆心,以AC长为半径作圆,交x轴于N,此时N的坐标为(8﹣4,0)或(8+4,0)③作AC的垂直平分线,交x轴于N,此时N的坐标为(3,0),综上,若点N在x轴上运动,当以点A、N、C为顶点的三角形是等腰三角形时,点N的坐标分别为(﹣8,0)、(8﹣4,0)、(3,0)、(8+4,0).(4)如图,设点N的坐标为(n,0),则BN=n+2,过M点作MD⊥x轴于点D,∴MD∥OA,∴△BMD∽△BAO,∴=,∵MN∥AC∴=,∴=,∵OA=4,BC=10,BN=n+2∴MD=(n+2),∵S△AMN=S△ABN﹣S△BMN=BN•OA﹣BN•MD=(n+2)×4﹣×(n+2)2=﹣(n﹣3)2+5,当n=3时,△AMN面积最大是5,∴N点坐标为(3,0).∴当△AMN面积最大时,N点坐标为(3,0).【点评】本题是二次函数的综合题,解(1)的关键是待定系数法求解析式,解(2)的关键是勾股定理和逆定理,解(3)的关键是等腰三角形的性质,解(4)的关键是三角形相似的判定和性质以及函数的最值等.3. (2018•山东淄博•8分)如图,以AB为直径的⊙O外接于△ABC,过A点的切线AP与BC的延长线交于点P,∠APB的平分线分别交AB,AC于点D,E,其中AE,BD(AE<BD)的长是一元二次方程x2﹣5x+6=0的两个实数根.(1)求证:PA•BD=PB•AE;(2)在线段BC上是否存在一点M,使得四边形ADME是菱形?若存在,请给予证明,并求其面积;若不存在,说明理由.【考点】MR:圆的综合题.【分析】(1)易证∠APE=∠BPD,∠EAP=∠B,从而可知△PAE∽△PBD,利用相似三角形的性质即可求出答案.(2)过点D作DF⊥PB于点F,作DG⊥AC于点G,易求得AE=2,BD=3,由(1)可知:,从而可知cos∠BDF=cos∠BAC=cos∠APC=,从而可求出AD和DG的长度,进而证明四边形ADFE是菱形,此时F点即为M点,利用平行四边形的面积即可求出菱形ADFE的面积.【解答】解:(1)∵DP平分∠APB,∴∠APE=∠BPD,∵AP与⊙O相切,∴∠BAP=∠BAC+∠EAP=90°,∵AB是⊙O的直径,∴∠ACB=∠BAC+∠B=90°,∴∠EAP=∠B,∴△PAE∽△PBD,∴,∴PA•BD=PB•AE;(2)过点D作DF⊥PB于点F,作DG⊥AC于点G,∵DP平分∠APB,AD⊥AP,DF⊥PB,∴AD=DF,∵∠EAP=∠B,∴∠APC=∠BAC,易证:DF∥AC,∴∠BDF=∠BAC,由于AE,BD(AE<BD)的长是x2﹣5x+6=0,解得:AE=2,BD=3,∴由(1)可知:,∴cos∠APC==,∴cos∠BDF=cos∠APC=,∴,∴DF=2,∴DF=AE,∴四边形ADFE是平行四边形,∵AD=AE,∴四边形ADFE是菱形,此时点F即为M点,∵cos∠BAC=cos∠APC=,∴sin∠BAC=,∴,∴DG=,∴在线段BC上是否存在一点M,使得四边形ADME是菱形其面积为:DG•AE=2×=【点评】本题考查圆的综合问题,涉及圆周角定理,锐角三角函数的定义,平行四边形的判定及其面积公式,相似三角形的判定与性质,综合程度较高,考查学生的灵活运用知识的能力.4.(2018•山东淄博•9分)(1)操作发现:如图①,小明画了一个等腰三角形ABC,其中AB=AC,在△ABC的外侧分别以AB,AC为腰作了两个等腰直角三角形ABD,ACE,分别取BD,CE,BC的中点M,N,G,连接GM,GN.小明发现了:线段GM与GN的数量关系是MG=NG ;位置关系是MG⊥NG .(2)类比思考:如图②,小明在此基础上进行了深入思考.把等腰三角形ABC换为一般的锐角三角形,其中AB>AC,其它条件不变,小明发现的上述结论还成立吗?请说明理由.(3)深入研究:如图③,小明在(2)的基础上,又作了进一步的探究.向△ABC的内侧分别作等腰直角三角形ABD,ACE,其它条件不变,试判断△GMN的形状,并给与证明.【考点】KY:三角形综合题.【分析】(1)利用SAS判断出△ACD≌△AEB,得出CD=BE,∠ADC=∠ABE,进而判断出∠BDC+∠DBH=90°,即:∠BHD=90°,最后用三角形中位线定理即可得出结论;(2)同(1)的方法即可得出结论;(3)同(1)的方法得出MG=NG,最后利用三角形中位线定理和等量代换即可得出结论.【解答】解:(1)连接BE,CD相较于H,∵△ABD和△ACE都是等腰直角三角形,∴AB=AD,AC=AE,∠BAD=∠CAE=90°∴∠CAD=∠BAE,∴△ACD≌△AEB(SAS),∴CD=BE,∠ADC=∠ABE,∴∠BDC+∠DBH=∠BDC+∠ABD+∠ABE=∠BDC+∠ABD+∠ADC=∠ADB+∠ABD=90°,∴∠BHD=90°,∴CD⊥BE,∵点M,G分别是BD,BC的中点,∴MG CD,同理:NG BE,∴MG=NG,MG⊥NG,故答案为:MG=NG,MG⊥NG;(2)连接CD,BE,相较于H,同(1)的方法得,MG=NG,MG⊥NG;(3)连接EB,DC,延长线相交于H,同(1)的方法得,MG=NG,同(1)的方法得,△ABE≌△ADC,∴∠AEB=∠ACD,∴∠CEH+∠ECH=∠AEH﹣∠AEC+180°﹣∠ACD﹣∠ACE=∠ACD﹣45°+180°﹣∠ACD﹣45°=90°,∴∠DHE=90°,同(1)的方法得,MG⊥NG.【点评】此题是三角形综合题,主要考查等腰直角三角形的性质,全等三角形的判定和性质,平行线的判定和性质,三角形的中位线定理,正确作出辅助线用类比的思想解决问题是解本题的关键.5. (2018•山东淄博•9分)如图,抛物线y=ax2+bx经过△OAB的三个顶点,其中点A(1,),点B (3,﹣),O为坐标原点.(1)求这条抛物线所对应的函数表达式;(2)若P(4,m),Q(t,n)为该抛物线上的两点,且n<m,求t的取值范围;(3)若C为线段AB上的一个动点,当点A,点B到直线OC的距离之和最大时,求∠BOC的大小及点C的坐标.【考点】HF:二次函数综合题.【分析】(1)将已知点坐标代入即可;(2)利用抛物线增减性可解问题;(3)观察图形,点A,点B到直线OC的距离之和小于等于AB;同时用点A(1,),点B(3,﹣)求出相关角度.【解答】解:(1)把点A(1,),点B(3,﹣)分别代入y=ax2+bx得解得∴y=﹣(2)由(1)抛物线开口向下,对称轴为直线x=当x>时,y随x的增大而减小∴当t>4时,n<m.(3)如图,设抛物线交x轴于点F分别过点A、B作AD⊥OC于点D,BE⊥OC于点E∵AC≥AD,BC≥BE∴AD+BE ≥AC+BE=AB∴当OC ⊥AB 时,点A ,点B 到直线OC 的距离之和最大. ∵A (1,),点B (3,﹣)∴∠AOF=60°,∠BOF=30° ∴∠AOB=90° ∴∠ABO=30°当OC ⊥AB 时,∠BOC=60° 点C 坐标为(,).【点评】本题考查综合考查用待定系数法求二次函数解析式,抛物线的增减性.解答问题时注意线段最值问题的转化方法.6. (2018•四川成都•9分)在 中,,,,过点 作直线 ,将绕点 顺时针得到 (点 , 的对应点分别为 , )射线,分别交直线于点,.(1)如图1,当 与 重合时,求 的度数;(2)如图2,设与的交点为 ,当 为的中点时,求线段的长;(3)在旋转过程时,当点 分别在,的延长线上时,试探究四边形的面积是否存在最小值.若存在,求出四边形 的最小面积;若不存在,请说明理由.【答案】(1)由旋转的性质得:., , ,,, .(2)为的中点, .由旋转的性质得:,., .,,.(3),最小,即最小,.法一:(几何法)取中点,则..当最小时,最小,,即与重合时,最小.,,,.法二:(代数法)设,.由射影定理得:,当最小,即最小,.当时,“ ”成立,.【考点】三角形的面积,解直角三角形,旋转的性质【解析】【分析】(1)根据旋转的性质可得出,根据已知易证m∥AC,得出∠A'BC是直角,利用特殊角的三角函数值,可求出∠A'CB的度数,就可求出结果。
