2011年全国各地100份中考数学试卷分类汇编第5-- 二元一次方程组及其应用
2011年全国各地中考数学试卷试题分类汇编第5章 二元一次方程组及其应用

2011年全国各地中考数学试卷试题分类汇编第5章 二元一次方程组及其应用一、选择题1. (2011山东泰安,11 ,3分)某班为奖励在校运会上取得较好成绩的运动员,花了400元钱购买甲、乙两种奖品共30件,其中甲种奖品每件16元,乙种奖品每件12元,求甲乙两种奖品各买多少件?该问题中,若设购买甲种奖品x 件,乙种奖品y 件,则方程组正确的是( ) A.⎩⎨⎧x+y=3012x+16y=400B.⎩⎨⎧x+y=3016x+12y=400C.⎩⎨⎧12x+16y=30x+y=400D.⎩⎨⎧16x+12y=30x+y=4002. (2011台湾台北,30)某鞋店有甲、乙两款鞋各30双,甲鞋一双200元,乙鞋一双50元。
该店促销的方式:买一双甲鞋,送一双乙鞋;只买乙鞋没有任何优惠。
若打烊后得知,此两款鞋共卖得1800元,还剩甲鞋x 双、乙鞋y 双,则依题意可列出下列哪一个方程式? A 1800)30(50)30(200=-+-y x B .1800)30(50)30(200=--+-y x x C. 1800)60(50)30(200=--+-y x x D .1800])30(30[50)30(200=---+-y x x 3. (2011台湾全区,9)在早餐店里,王伯伯买5颗馒头,3颗包子,老板少拿2元,只要50元.李太太买了11颗馒头,5颗包子,老板以售价的九折优待,只要90元.若馒头每颗x 元,包子每颗y 元,则下列哪一个二元一次联立方程式可表示题目中的数量关系? A .⎩⎨⎧⨯=++=+9.09051125035y x y x B .⎩⎨⎧÷=++=+9.09051125035y x y xC .⎩⎨⎧⨯=+-=+9.09051125035y x y x D .⎩⎨⎧÷=+-=+9.09051125035y x y x4. (2011湖南益阳,2,4分)二元一次方程21-=x y 有无数多个解,下列四组值中不是..该方程的解的是 A .012x y =⎧⎪⎨=-⎪⎩B .11x y =⎧⎨=⎩C .10x y =⎧⎨=⎩D .11x y =-⎧⎨=-⎩5. (2011四川绵阳9,3)灾后重建,四川从悲壮走向豪迈.灾民发扬伟大的抗震救灾精神,桂花村派男女村民共15 人到山外采购建房所需的水泥,已知男村民一人挑两包,女村民两人抬一包,共购回15 包.请问这次采购派男女村民各多少人?A .男村民3人,女村民12人B .男村民5人,女村民10人C .男村民6人,女村民9人D .男村民7人,女村民8人6. (2011四川凉山州, ,4分)下列方程组中是二元一次方程组的是( )A .12xy x y =⎧⎨+=⎩B . 52313x y y x -=⎧⎪⎨+=⎪⎩C . 20135x z x y +=⎧⎪⎨-=⎪⎩ D .5723z x y =⎧⎪⎨+=⎪⎩7. (2011广东肇庆,4,3分)方程组⎩⎨⎧=+=-422y x y x 的解是A .⎩⎨⎧==21y xB .⎩⎨⎧==13y xC .⎩⎨⎧-==20y xD .⎩⎨⎧==02y x8. (2011山东东营,4,3分)方程组31x y x y +=⎧⎨-=-⎩,的解是A .12.x y =⎧⎨=⎩, B .12.x y =⎧⎨=-⎩, C .21.x y =⎧⎨=⎩, D .01.x y =⎧⎨=-⎩,9. (2011山东枣庄,6,3分)已知2,1x y =⎧⎨=⎩是二元一次方程组7,1ax by ax by +=⎧⎨-=⎩的解,则a b -的值为( )A .-1B .1C .2D .3二、填空题1. (2011安徽芜湖,13,5分)方程组237,38.x y x y +=⎧⎨-=⎩的解是 .2. (2011浙江省,13,3分)如图,母亲节那天,很多同学给妈妈准备了鲜花 和礼盒.从图中信息可知,则买5束鲜花和5个礼盒的总价为 元.3. (2011江西,12,3分)方程组257x y x y ì+=ïïíï-=ïî的解是 .4. (2011福建泉州,12,4分)已知x 、y 满足方程组⎩⎨⎧=+=+,42,52y x y x 则x -y 的值为.5. (2011山东潍坊,15,3分)方程组524050x y x y --=⎧⎨+-=⎩的解是___________________.6. (2011江西南昌,12,3分)方程组257x y x y ì+=ïïíï-=ïî的解是 .7. (2011安徽芜湖,13,5分)方程组237,38.x y x y +=⎧⎨-=⎩的解是 .8. (2011湖北鄂州,7,3分)若关于x ,y 的二元一次方程组3133x y a x y +=+⎧⎨+=⎩的解满足2x y +<,则a 的取值范围为______.9. (2011河北,19,8分)已知.a y x 3y x 3y 2的解的二元一次方程,是关于+=⎩⎨⎧==x求(a+1)(a-1)+7的值三、解答题1. (2011江苏扬州,24,10分)古运河是扬州的母亲河,为打造古运河风光带,现有一段长为180米的河道整治任务由A 、B 两个工程队先后接力完成。
2011年全国各地100份中考数学试卷分类汇编(46专题)(含答案)-46

第16章 频数与频率1. (2011浙江金华,6,3分)学校为了解七年级学生参加课外兴趣小组活动情况,随机调查了40名学生,将结果绘制成了如图所示的频数分布直方图,则参加绘画兴趣小组的频率是( )A .0.1B .0.15C .0.25D .0.3【答案】D2. (2011四川南充市,4,3分)某学校为了了解九年级体能情况,随机选取30名学生测试一分钟仰卧起坐次数,并绘制了如图的直方图,学生仰卧起坐次数在25~30之间的频率为( )(A )0.1 (B )0.17 (C )0.33 (D )0.4次数(次)人数(人)3530252015512103O【答案】D3. (2011浙江温州,7,4分)为了支援地震灾区同学,某校开展捐书活动,九 (1)班40名同学积极 参与.现将捐书数量绘制成频数分布直方图如图所示,则捐书数量在5. 5~6.5组别的频率是( ) A .0.1 B .0.2 C .0.3 D .0.4组别其他舞蹈绘画书法人数1412108642812119【答案】B4. (2011浙江丽水,6,3分)学校为了解七年级学生参加课外兴趣小组活动情况,随机调查了40名学生,将结果绘制成了如图所示的频数分布直方图,则参加绘画兴趣小组的频率是( ) A .0.1 B .0.15 C .0.25 D .0.3【答案】D5. (2011四川内江,13,5分)“Welcome to Senior High School .”(欢迎进入高中),在这段句子的所有英文字母中,字母O 出现的频率是 . 【答案】156. (2011广东东莞,18,7分)李老师为了解班里学生的作息时间,调查班上50名学生上学路上花费的时间,他发现学生所花时间都少于50分钟,然后将调查数据整理,作出如下频数分布直方图的一部分(每 组数据含最小值不含最大值).请根据该频数分布直方图,回答下列问题:(1)此次调查的总体是什么? (2)补全频数分布直方图;(3)该班学生上学路上花费时间在30分钟以上(含30分钟)的人数占全班人数的百分比组别其他舞蹈绘画书法人数1412108642812119是多少?【解】(1)此次调查的总体是:班上50名学生上学路上花费的时间的全体. (2)补全图形,如图所示:(3)该班学生上学路上花费时间在30分钟以上的人数有5人,总人数有50, 5÷50=0.1=10%答:该班学生上学路上花费时间在30分钟以上的人数占全班人数的百分之10.7. (2011广东广州市,22,12分)某中学九年级(3)班50名学生参加平均每周上网时间的调查,由调查结果绘制了频数分布直方图(图6),根据图中信息回答下列问题: (1)求a 的值;(2)用列举法求以下事件的概率:从上网时间在6~10小时的5名学生中随机选取2人,其中至少1人的上网时间在8~10小时.图6 【答案】(1)a =50―6―25―3―2=14(2)设上网时间为6~8小时的三个学生为A 1,A 2,A 3,上网时间为8~10个小时的2名学频数 (学生人数)0 2 4 6 8 10 时间/小时6a 2532生为B1,B2,则共有A1A2,A1A3,A1B1,A1B2,A2A3,A2B1,A2B2A3B1,A3B2B1B210种可能,其中至少1人上网时间在8~10小时的共有7种可能,故P(至少1人的上网时间在8~10小时)=0.78. (2011广东汕头,18,7分)李老师为了解班里学生的作息时间,调查班上50名学生上学路上花费的时间,他发现学生所花时间都少于50分钟,然后将调查数据整理,作出如下频数分布直方图的一部分(每组数据含最小值不含最大值).请根据该频数分布直方图,回答下列问题:(1)此次调查的总体是什么?(2)补全频数分布直方图;(3)该班学生上学路上花费时间在30分钟以上(含30分钟)的人数占全班人数的百分比是多少?【解】(1)此次调查的总体是:班上50名学生上学路上花费的时间的全体.(2)补全图形,如图所示:(3)该班学生上学路上花费时间在30分钟以上的人数有5人,总人数有50,5÷50=0.1=10%答:该班学生上学路上花费时间在30分钟以上的人数占全班人数的百分之10.9. (2011 浙江湖州,21,8) 班主任张老师为了了解学生课堂发言情况,对前一天本班男、女生的发言次数进行了统计,并绘制成如下频数分布折线图(图1) .(1) 请根据图1,回答下列问题:①这个班共有名学生,发言次数是5次的男生有人、女生有人;②男、女生发言次数的中位数分别是次和次.(2) 通过张老师的鼓励,第二天的发言次数比前一天明显增加,全班发言次数变化的人数..的扇形统计图如图2所示.求第二天发言次数增加3次的学生人数和全班增加的发言总次数.【答案】解:(1)①40;2;5 ②4;5.(2)发言次数增加3次的学生人数为:40(120%30%40%)4()⨯---=人.全班增加的发言总次数为40%40130%4024316241252⨯⨯+⨯⨯+⨯=++=(次).10. (2011浙江义乌,20,8分)为了解某市九年级学生学业考试体育成绩,现从中随机抽取部分学生的体育成绩进行分段(A :50分;B :49-45分;C :44-40分;D :39-30分;E :29-0分)统计如下:根据上面提供的信息,回答下列问题:(1)在统计表中,a 的值为 ▲ ,b 的值为 ▲ ,并将统计图补充完整(温馨提示:作图时别忘了用0.5毫米及以上的黑色签字笔涂黑);(2)甲同学说:“我的体育成绩是此次抽样调查所得数据的中位数. ”请问:甲同学的体育成绩应在什么分数段内? ▲ (填相应分数段的字母)(3)如果把成绩在40分以上(含40分)定为优秀,那么该市今年10440名九年级学生中体育成绩为优秀的学生人数约有多少名?【答案】解:(1) 60 , 0.15 (图略) (2) C(3)0.8×10440=8352(名)答:该市九年级考生中体育成绩为优秀的学生人数约有8352名.11. (2011山东聊城,19,8分)今年“世界水日”的主题是“城市用水:应对都市化挑战”.为了解城市居民用水量的情况,小亮随机抽查了阳光小区50户居民去年每户每月的用水分数段 人数(人) 频率A 48 0.2B a 0.25C 84 0.35D 36 bE 12 0.05 学业考试体育成绩(分数段)统计图12243648607284人数分数段A B CD E 0 学业考试体育成绩(分数段)统计表量,将得到的数据整理并绘制了这50户居民去年每月总用水量的折线图和频数、频率分布表如下:注:x 表示50户居民月总用水量(m 3)(1)表中的a =________;d =___________. (2)这50户居民每月总用水量超过550m3的月份占全年月份的百分率是多少(精确到1%)?(3)请根据折线统计图提供的数据,估计该小区去年每户居民平均月用水量是多少?【答案】(1)3,61;(2)这50户居民月总用水量超过550m 3的月份有5个,占全年月份的百分率为(5÷12)×100%=42%(3)(378+641+456+543+550+667+693+600+574+526+423)÷50÷12=109m 3 12. (2011广东省,18,7分)李老师为了解班里学生的作息时间,调查班上50名学生上学路上花费的时间,他发现学生所花时间都少于50分钟,然后将调查数据整理,作出如下频数分布直方图的一部分(每 组数据含最小值不含最大值).请根据该频数分布直方图,回答下列问题:(1)此次调查的总体是什么? (2)补全频数分布直方图;(3)该班学生上学路上花费时间在30分钟以上(含30分钟)的人数占全班人数的百分比是多少?【解】(1)此次调查的总体是:班上50名学生上学路上花费的时间的全体. (2)补全图形,如图所示:组 别 频 数 频 率350<x≤400 1112 400<x≤450 1 112 450<x≤500 2 16500<x≤550 a b550<x≤600 c d 600<x≤650 1 112650<x≤700 2 16(3)该班学生上学路上花费时间在30分钟以上的人数有5人,总人数有50,5÷50=0.1=10%答:该班学生上学路上花费时间在30分钟以上的人数占全班人数的百分之10.13.(2011山东临沂,20,6分)某中学为了解学生的课外阅读情况.就“我最喜爱的课外读物”从文学、艺术、科普和其他四个类别进行了抽样调查(每位同学仅选一项),并根据调查结果制作了尚不完整的频数分布表:类别频数(人数)频率文学m 0.42艺术22 0.11科普66 n其他28合计 1下面是自首届以来各届动漫产品成交金额统计图表(部分未完成):(1)表中m=_________,n=__________;(2)在这次抽样调查中,最喜爱阅读哪类读物的学生最多? 最喜爱阅读哪类读物的学生最少?(3)根据以上调查,试估计该校1200名学生中最喜爱阅读科普读物的学生有多少人?【解】(1)84,0.33;…………………………………………………………………(2分)(2)喜爱阅读文学类的学生最多(84人),喜爱阅读艺术类的学生最少(22人);…………………………………………………………………(4分)(3)1200×0.33=396(人).………………………………………………………(6分)14. (2011浙江省,20,8分)据媒体报道:某市四月份空气质量优良,高举全国榜首,青春中学九年级课外兴趣小组据此提出了“今年究竟能有多少天空气质量达到优良”的问题,他们高举国家环保总局所公布的空气质量级别表(见表1)以及市环保监测站提供的资料,从中随机抽取了今年1-4月份中30天空气综合污染指数,统计数据如下:表I:空气质量级别表空气污染指数0~50 51~100 101~150 151~200 201~250 251~300 大于300空气质量级别Ⅰ级(优)Ⅱ级(良)Ⅲ1(轻微污染)Ⅲ2(轻度污染)Ⅳ1(中度污染)Ⅳ2(中度重污染)Ⅴ(重度污染)空气综合污染指数30,32,40,42,45,45,77,83,85,87,90,113,127,153,16738,45,48,53,57,64,66,77,92,98,130,184,201,235,243请根据空气质量级别表和抽查的空气综合污染指数,解答以下问题:(1) 填写频率分布表中未完成的空格;分组频数统计频数频率0~50 0.3051~100 12 0.40101~150151~200 3 0.10201~250 3 0.10合计30 30 1.00(2) 写出统计数据中的中位数、众数;(3)请根据抽样数据,估计该市今年(按360天计算)空气质量是优良(包括Ⅰ、Ⅱ级)的天数.【答案】(1)分组频数统计频数频率0~50 9 0.3051~100 12 0.40101~150 3 0.10151~200 3 0.10201~250 3 0.10合计30 30 1.00(2) 中位数是80 、众数是45 。
2011全国各省市中考数学试题分类汇编
阅读使人充实,会谈使人敏捷,写作使人精确。
——培根2011全国各省市中考数学试题分类汇编-—函数与一次函数(解答题及答案)三.解答题1.(2011安徽中考)18、在平面直角坐标系中,一蚂蚁从原点O 出发,按向上、向右、向下、向右的方向依次不断移动,每次移动1个单位.其行走路线如下图所示.(1)填写下列各点的坐标:A 1(____,____),A 3(____,____),A 12(___,___);(2)写出点A n 的坐标(n 是正整数);(3)指出蚂蚁从点A 100到A 101的移动方向.2.(2011安徽中考)21. 如图函数11y k x b =+的图象与函数2k y x=(x >0)的图象交于A 、B 两点,与y 轴交于C 点.已知A 点的坐标为(2,1),C 点坐标为(0,3).(1)求函数1y 的表达式和B 点坐标;【解】(2)观察图象,比较当x >0时,1y 和2y 的大小.3.(2011广州中考)14.如图,在平面直角坐标系中,点P 的坐标为(-4,0),⊙P的半径为2,将⊙P 沿x 轴向右平移4个单位长度得⊙P 1.(1)画出⊙P 1,并直接判断⊙P 与⊙P 1的位置关系;(2)设⊙P 1与x 轴正半轴,y 轴正半轴的交点分别为A ,B ,求劣弧AB 与弦AB 围成的图形的面积(结果保留π)4.(2011甘肃兰州)24.(本小题满分7分)如图,一次函数3y kx =+的图像与反比例第18题图 第21题函数m y x=(x >0)的图像交与点P ,PA ⊥x 轴于点A ,PB ⊥y 轴于点B.一次函数的图像分别交x 轴、y 轴于点C 、点D ,且DBP S ∆=27,OC CA =12. (1)求点D 的坐标;(2(3)根据图像写出当x5.(2011广东茂名)某学校要印制一批《学生手册》,甲印刷厂提出:每本收1元印刷费,另收500元制版费;乙印刷厂提出:每本收2元印刷费,不收制版费.(1)分别写出甲、乙两厂的收费甲y (元) 、乙y (元)与印制数量x (本)之间的关系式;(2)问:该学校选择哪间印刷厂印制《学生手册》比较合算?请说明理由. (4分)解:6.(2011广州中考)21.(12分)某商店5月1日举行促销优惠活动,当天到该商店购买商品有两种方案,方案一:用168元购买会员卡成为会员后,凭会员卡购买商店内任何商品,一律按商品价格的8折优惠;方案二:若不购买会员卡,则购买商店内任何商品,一律按商品价格的9.5折优惠。
2011中考1_解二元一次方程组以及简单的三元一次方程组(含答案)

解二元一次方程组以及简单的三元一次方程组一、选择题1. (2011台湾,)若a :b :c =2:3:7,且a -b +3=c -2b ,则c 值为何?( )A .7B .63C .221D .421 分析:先设a =2x ,b =3x ,c =7x ,再由a -b +3=c -2b 得出x 的值,最后代入c =7x 即可.解:设a =2x ,b =3x ,c =7x ,∵a -b +3=c -2b ,∴2x -3x +3=7x -6x ,解得x =23, ∴c =7×23=221, 故选C .点评:本题考查了解三元一次方程组,解题的关键是由题意中的比例式设a =2x ,b =3x ,c =7x ,再求解就容易了.2. (2011,台湾)若二元一次联立方程式的解为x=a ,y=b ,则a+b 之值为何?( )A 、1B 、3C 、4D 、6 分析:将其中一个方程两边乘以一个数,使其与另一方程中x 的系数互为相反数,再将两方程相加,消去一个未知数,达到降元的目的,求出另一个未知数,再用代入法求另一个未知数. 解:,①﹣2×②得,5y=﹣10,y=﹣2,代入②中得,x+4=7,解得,x=3∴a+b=3+(﹣2)=1,故选(A ) 3. (2011东营市)方程组31x y x y +=⎧⎨-=-⎩的解是( ) A 、12x y =⎧⎨=⎩ B 、12x y =⎧⎨=-⎩ C 、21x y =⎧⎨=⎩ D 、01x y =⎧⎨=-⎩分析:解决本题关键是寻找式子间的关系,寻找方法消元,①②相加可消去y ,得到一个关于x 的一元一次方程,解出x 的值,再把x 的值代入方程组中的任意一个式子,都可以求出y 的值解: ,①+②得:2x=2,x=1,把x=1代入①得:1+y=3, y=2,∴方程组的解为:12x y =⎧⎨=⎩ 故选:A ,4. (2011淄博)由方程组63x m y m +=⎧⎨-=⎩可得出x 与y 的关系式是( ) A.x+y=9 B.x+y=3 C.x+y=﹣3 D.x+y=﹣9分析:由①得m=6﹣x ,代入方程②,即可消去m 得到关于x ,y 的关系式.解:()()6132x m y m +=⎧⎪⎨-=⎪⎩由①得:m=6﹣x∴6﹣x=y ﹣3∴x+y=9.故选A .5. (2011•黔南,)已知:|2x+y ﹣3|+2)53(--y x =0,则x 2= .分析:根据非负数的性质列出方程求出x 、y 的值,代入所求代数式计算即可.解:∵|2x+y﹣3|+2)53(--y x =0,∴⎩⎨⎧=--=-+053032y x y x ,解得⎩⎨⎧-==12y x ,∴x 2=4.故答案为4.6.(2011广西崇左)方程组⎩⎨⎧=-=+1375y x y x 的解是 .分析:用加减法解方程组即可.解:⎩⎨⎧=-=+)2(13)1(75y x y x ,(1)+(2)得:8x =8,x =1,把x =1代入(1)得:y =2,∴⎩⎨⎧==21y x , 故答案为:x =1,y =2.二、填空题1. (2011•徐州)方程组⎩⎨⎧3x+y=32x -y=2的解为 . 分析:此题可运用加减消元法解方程组,但为了不出差错,选用加法较好.解:⎩⎨⎧3x+y=3 ①2x -y=2 ②①+②得:5x=5,x=1,把x=1代入第一个方程得:y=0,即⎩⎨⎧x=1y=0.,故答案为:⎩⎨⎧x=1y=0.. 2. (2011潍坊)方程组524050x y x y --=⎧⎨+-=⎩的解是________________. 【分析】由于方程组中两方程y 的系数是倍数关系,且数值较小,故可先用加减消元法再用代入消元法求解.解: 5240(1)50(2)x y x y --=⎧⎨+-=⎩,②×2+①得,7x-14=0,解得x=2; 把x=2代入②得,2+y-5=0,解得y=3.故原方程组的解为: 23x y =⎧⎨=⎩.故答案为 23x y =⎧⎨=⎩.3. (芜湖市)方程组23738x y x y +=⎧⎨-=⎩的解是. 分析:两式相加可化去y ,再将x 的值代入x ﹣3y =8,解得即可.解:23738x y x y +=⎧⎨-=⎩①②,用①+②得:3x =15,即x =5,把x =5代入②得:5﹣3y =8,解得:y =﹣1,∴方程组的解为51x y =⎧⎨=-⎩. 故答案为:51x y =⎧⎨=-⎩.4. (2011十堰)关于x,y 的二元一次方程组⎩⎨⎧=+=+p y x y x 2335的解是正整数,则整数P 的值为 。
2011年全国各地100份中考数学试卷分类汇编(46专题)(含答案)-25

第8章 二次根式一、选择题1. (2011内蒙古乌兰察布,1,3分)如4 的平方根是( )A . 2B . 16 C. ±2 D .±16 【答案】C2. (2011安徽,4,4分)设a =19-1,a 在两个相邻整数之间,则这两个整数是( )A .1和2B .2和3C .3和4D .4和5 【答案】C3. (2011山东菏泽,4,3分)实数a 在数轴上的位置如图所示,则22(4)(11)a a -+-化简后为A . 7B . -7C . 2a -15D . 无法确定a 105第2题图【答案】A 4. (2011山东济宁,1,3分)4的算术平方根是( )A . 2B . -2C . ±2D . 16 【答案】A5. (2011山东济宁,5,3分)若0)3(12=++-+y y x ,则y x -的值为 ( )A .1B .-1C .7D .-7 【答案】C6. (2011山东日照,1,3分)(-2)2的算术平方根是( )(A )2 (B ) ±2 (C )-2 (D )2 【答案】A7. (2011山东泰安,7 ,3分)下列运算正确的是( )A.25=±5B.43-27=1C.18÷2=9D.24·32=6 【答案】D8. (2011山东威海,1,3分)在实数0、3-、2、2-中,最小的是( )A .2-B .3-C .0D .2【答案】A9. (2011山东烟台,5,4分)如果2(21)12a a -=-,则( )A .a <12 B. a ≤12 C. a >12 D. a ≥12【答案】B10.(2011浙江杭州,1,3)下列各式中,正确的是( )A . 2(3)3-=-B .233-=-C .2(3)3±=±D .233=±【答案】B11. (2011浙江省,7,3分)已知21+=m ,21-=n ,则代数式mn n m 322-+的值为( )A .9B .±3C .3D . 5 【答案】C12. (2011台湾台北,4)计算75147-+27之值为何?A .53B .33C .311D . 911 【答案】A13. (2011台湾全区,17)17.计算631254129⨯÷之值为何? A .123 B .63C .33D .433 【答案】B14. (2011广东株洲,1,3分)8的立方根是( ) A .2 B .-2 C .3 D .4 【答案】A15. (2011山东济宁,4,3分)下列各式计算正确的是A .235+=B .2222+=C .33222-=D .1210652-=- 【答案】C16. (2011山东潍坊,1,3分)下面计算正确的是( )A.3333+=B.2733÷=C.235= D.2(2)2-=-【答案】B17. (2011四川成都,1,3分) 4的平方根是 C(A)±16 (B)16 (C )±2 (D)2 【答案】C18. (2011四川宜宾,2,3分)根式3-x 中x 的取值范围是( ) A .x≥3 B .x≤3 C .x <3 D .x >3 【答案】A19. (2011湖南怀化,1,3分)49的平方根为 A .7 B.-7 C.±7 D.±7 【答案】C20.(2011江苏南京,1,2分)9的值等于A .3B .-3C .±3D .3【答案】A21. (2011江苏南通,3,3分)计算327的结果是A. ±33B . 33C . ±3D . 3【答案】D.22. (2011山东临沂,4,3分)计算221-631+8的结果是( ) A .32-23 B .5-2C .5-3D .22【答案】A23. (2011上海,3,4分)下列二次根式中,最简二次根式是( ).(A)15; (B) 0.5; (C) 5; (D) 50 .【答案】C24. (2011四川凉山州,5,4分)已知25523y x x =-+--,则2xy 的值为( ) A .15- B .15 C .152- D . 152【答案】A25. (2011湖北黄石,1,3分)4的值为A.2B.-2C.±2D.不存在 【答案】A26. (2010湖北孝感,4,3分)下列计算正确的是( ) A822-= B.2+3= 5C.236⨯=D.824÷= 【答案】C27. (2011山东滨州,2,3分)若二次根式12x +有意义,则x 的取值范围为( ) A.x ≥12 B. x ≤12 C.x ≥12- D.x ≤12- 【答案】C二、填空题1. (2011安徽芜湖,14,5分)已知a 、b 为两个连续的整数,且28a b <<,则a b += .【答案】112. (2011江苏扬州,10,3分)计算:28-=【答案】23. (2011山东德州12,4分)当2x =时,2211x x x---=_____________. 【答案】224. (2011山东菏泽,9,3分)使41x -有意义的x 的取值范围 是 .【答案】x ≥145. (2011山东日照,15,4分)已知x ,y 为实数,且满足x +1y y ---1)1(=0,那么x 2011-y 2011= . 【答案】-2;6. (2011山东威海,13,3分)计算(508)2-÷的结果是 . 【答案】 37. (2011山东烟台,19,6分)(满分6分)先化简再计算:22121x x x x x x --⎛⎫÷- ⎪+⎝⎭,其中x 是一元二次方程2220x x --=的正数根. 【答案】解:原式=2(1)(1)21(1)x x x x x x x +--+÷+=21(1)x x x x -⋅-=11x -. 解方程得2220x x --=得, 1130x =+>,2130x =-<. 所以原式=1131+-=13(或33). 8. (2011浙江台州,11,5分)若二次根式1-x 有意义,则x 的取值范围是 【答案】x ≥19. (2011江苏泰州,9,3分)16的算术平方根是 . 【答案】410.(2011山东聊城,13,3分)化简:20-5=_____________. 【答案】511. (2011四川内江,加试1,6分)若201120121m =-,则54322011m m m --的值是 . 【答案】012. (2011四川内江,加试3,6分)已知2263(5)36(3)m n m m n -+-=---,则m n -= .【答案】-213. (2011重庆綦江,12,4分)若1x 2-有意义,则x 的取值范围是 . 【答案】:21≥x 14. (2011江苏南京,9,2分)计算(21)(22)+-=_______________. 【答案】212. 15. (2011江苏南通,12,3分)计算:82-= ▲ .【答案】2.16. (2011四川凉山州,25,5分)已知a b 、为有理数,m n 、分别表示57-的整数部分和小数部分,且21amn bn +=,则2a b += 。
2011年全国各地100份中考数学试卷分类汇编(含答案)

方程的应用一、选择题A 组1、(2011年北京四中中考模拟20)某商品原价289元,经连续两次降价后售价为256元,设平均每降价的百分率为x ,则下面所列方程正确的是( )A 、256)x 1(2892=-B 、289)x 1(2562=-C 、256)x 21(289=-D 、289)x 21(256=-答案A2.(2011年浙江仙居)近年来,全国房价不断上涨,某县201 0年4月份的房价平均每平方米为3600元, 比2008年同期的房价平均每平方米上涨了2000元,假设这两年该县房价的平均增长率均为x ,则关于x 的方程为( )A .()212000x +=B .()2200013600x +=C .()()3600200013600x -+=D .()()23600200013600x -+=答案:D3.(浙江省杭州市党山镇中2011年中考数学模拟试卷)某服装厂准备加工400套运动装,在加工完160套后,采用了新技术,使得工作效率比原计划提高了20%,结果共用了18天完成任务,问计划每天加工服装多少套?在这个问题中,设计划每天加工x 套,则根据题意可得方程为 ( )(A ) 18%)201(160400160=+-+x x (B )18%)201(400160=++xx (C ) 18%20160400160=-+xx (D )18%)201(160400400=+-+x x 答案:AB 组1. (2011浙江慈吉 模拟)2010年元旦的到来, 宁波市各大商厦纷纷推出各种优惠以答谢顾客, 其中银泰百货贴出的优惠标语是: 买200元物品, 送100元购物券, 买400元物品送200购物券,……依次类推; 于是小红陪着她的妈妈一起来到大厦买东西, 没过多少时间小红就看中了一件衣服, 一问价钱需要600元. 她心想贵是贵了点,但是能送300元的购物券还是挺划算的, 于是就花600元把这件衣服买了, 同时也得到了300元购物券. 后来小红又用这300元购物券恰好买了一双鞋子, 这时就没有购物券送了. 则下列优惠中, 与小红在这次购物活动中所享受的优惠最接近的是( )A. 5折B. 6折C. 7折D. 8折 答案:C2.(2011湖北省崇阳县城关中学模拟)一种原价均为m 元的商品,甲超市连续两次打八折;乙超市一次性打六折;丙超市第一次打七折,第二次再打九折;若顾客要购买这种商品,最划算应到的超市是( ▲ )A. 甲或乙或丙B. 乙C. 丙D. 乙或丙答案:B3.(2011湖北武汉调考模拟二)黄陂木兰旅游产业发展良好,2008年为640万元,2010年为1000万元,2011年增长率与2008至2010年年平均增长率相同,则2011年旅游收入为( )A.1200万元B.1250万元C.1500万元D.1000万元答案:B4. (2011湖北武汉调考一模)某县为发展教育事业,加强了对教育经费的投入,2 0019年投入3 000万元,预计2011年投入5000万元.设教育经费的年平均增长率为x ,根据题意,下面所列方程正确的是( )A.3000( l+x )2=5000B.3000x 2=5000C.3000( l+x ﹪ )2=5000D.3000(l+x)+3000( l+x)2=5000答案:A5. (2011年杭州市模拟)如图,矩形的长与宽分别为a 和b ,在矩形中截取两个大小相同的圆作为圆柱的上下底面,剩余的矩形作为圆柱的侧面,刚好能组合成一个没有空隙的圆柱,则a 和b 要满足的数量关系是 A.121+=πb a B.122+=πb a C.221+=πb a D.12+=πb a 答案:D6.(2011灌南县新集中学一模)某超市一月份的营业额为200万元,已知第一季度....的总营业第5题额共1000万元, 如果平均每月增长率为x,则由题意列方程应为【 】A .200(1+x)2=1000 B .200+200×2x=1000C .200+200×3x=1000D .200[1+(1+x)+(1+x)2]=1000答案:D二、填空题 A 组1、(2011重庆市纂江县赶水镇)含有同种果蔬但浓度不同的A 、B 两种饮料,A 种饮料重 40千克,B 种饮料重60千克现从这两种饮料中各倒出一部分,且倒出部分的重量相同,再 将每种饮料所倒出的部分与另一种饮料余下的部分混合,如果混合后的两种饮料所含的果蔬 浓度相同,那么从每种饮料中倒出的相同的重量是_____________千克.答案:242、(重庆一中初2011级10—11学年度下期3月月考)某公司生产一种饮料是由A 、B 两种原料液按一定比例配制而成,其中A 原料液的成本价为15元/千克,B 原料液的成本价为10元/千克,按现行价格销售每千克获得70%的利润率.由于市场竞争,物价上涨,A 原料液上涨20%,B 原料液上涨10%,配制后的总成本增加了12%,公司为了拓展市场,打算再投入现总成本的25%做广告宣传,如果要保证每千克利润不变,则此时这种饮料的利润率是__________.答案:50%3、(2011年北京四中三模)某商场销售一批电视机,一月份每台毛利润是售出价的20% (毛利润=售出价-买入价),二月份该商场将每台售出价调低10%(买入价不变),结 果销售台数比一月份增加120%,那么二月份的毛利润总额与一月份毛利润总额的比 是 .答案:11:124.(淮安市启明外国语学校2010-2011学年度第二学期初三数学期中试卷)某种商品原价是120元,经两次降价后的价格是100元,求平均每次降价的百分率.设平均每次降价的百分率为x ,可列方程为 .答案:100)1(1202=-x5、(2011浙江杭州模拟16)由于人民生活水平的不断提高,购买理财产品成为一个热门话题。
2011年全国各地100份中考数学试卷分类汇编

2011 年全国各地100 份中考数学试卷分类汇编
2011 年全国各地100 份中考数学试卷分类汇编
第13 章二次函数
一、选择题
1. (2011 山东滨州,7,3 分)抛物线可以由抛物线平移得到,则下列平移过程正确的是( )
A.先向左平移2 个单位,再向上平移3 个单位
B.先向左平移2 个单位,再向下平移3 个单位
C.先向右平移2 个单位,再向下平移3 个单位
D.先向右平移2 个单位,再向上平移3 个单位
【答案】B
【答案】D
2. (2011 广东广州市,5,3 分)下列函数中,当x>0 时y 值随x 值增大而减小的是().
A.y = x2 B.y = x-1C.y = x D.y =
【答案】D
3. (2011 湖北鄂州,15,3 分)已知函数,则使y=k 成立的x 值恰好有三个,则k 的值为()
A.0 B.1 C.2 D.3
4. (2011 山东德州6,3 分)已知函数(其中)的图象
如下面右图所示,则函数的图象可能正确的是
【答案】D
5. (2011 山东菏泽,8,3 分)如图为抛物线的图像,A、B、C 为抛物线。
2011年全国各地100份中考数学试卷分类汇编(46专题)(含答案)-5
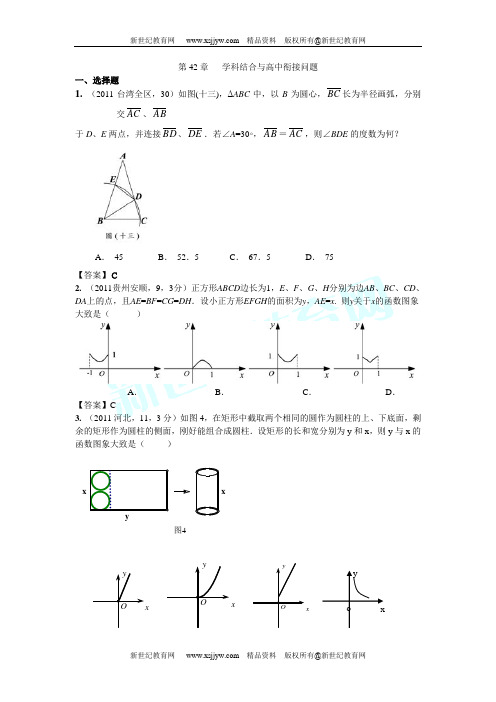
第42章 学科结合与高中衔接问题一、选择题1. (2011台湾全区,30)如图(十三),ΔABC 中,以B 为圆心,BC 长为半径画弧,分别交AC 、AB于D 、E 两点,并连接BD 、DE .若∠A =30∘,AB =AC ,则∠BDE 的度数为何?A . 45B . 52.5C . 67.5D . 75【答案】C2. (2011贵州安顺,9,3分)正方形ABCD 边长为1,E 、F 、G 、H 分别为边AB 、BC 、CD 、DA 上的点,且AE =BF =CG =DH .设小正方形EFGH 的面积为y ,AE =x . 则y 关于x 的函数图象大致是( )A .B .C .D .【答案】C3. (2011河北,11,3分)如图4,在矩形中截取两个相同的圆作为圆柱的上、下底面,剩余的矩形作为圆柱的侧面,刚好能组合成圆柱.设矩形的长和宽分别为y 和x ,则y 与x 的函数图象大致是( )图4xyxxyOxyOxyOoxyA .B .C .D .【答案】A3. (2011重庆市潼南,10,4分) 如图,在平面直角坐标系中,四边形OABC 是菱形, 点C 的坐标为(4,0),∠AOC = 60°,垂直于x 轴的 直线l 从y 轴出发,沿x 轴正方向以每秒1个单位长 度的速度向右平移,设直线l 与菱形OABC 的两边分 别交于点M,N (点M 在点N 的上方),若△OMN 的面积为S ,直线l 的运动时间为t 秒(0≤t ≤4),则 能大致反映S 与t 的函数关系的图象是【答案】C4. (2011台湾台北,23)如图(八),三边均不等长的ABC ∆,若在此三角形内找一点O ,使得OAB ∆、OBC ∆、OCA ∆的面积均相等。
判断下列作法何者正确?A . 作中线AD ,再取AD 的中点OB . 分别作中线AD 、BE ,再取此两中线的交点OC . 分别作AB 、BC 的中垂线,再取此两中垂线的交点OD . 分别作A ∠、B ∠的角平分线,再取此两角平分线的交点O【答案】B 二、填空题 1. 2. 3. 4. 5.三、解答题10题图xy ABC O MN ltsO 242343AtsO242343B tsO242343C tsO242343D1. (2011重庆綦江,26,12分)在如图的直角坐标系中,已知点A (1,0);B (0,-2),将线段AB 绕点A 按逆时针方向旋转90°至AC . ⑴ 求点C 的坐标; ⑵ 若抛物线2212++-=ax x y 经过点C . ①求抛物线的解析式;②在抛物线上是否存在点P (点C 除外)使△ABP 是以AB 为直角边的等腰直角三角形?若存在,求出所有点P 的坐标;若不存在,请说明理由.【答案】:解:(1)过点C 作CD ⊥x 轴,垂足为D ,在△ACD 和△BAO 中,由已知有∠CAD +∠BAO =90°,而∠ABO +∠BAO =90°∴∠CAD =∠ABO ,又∵∠CAD =∠AOB =90°,且由已知有CA =AB ,∴△ACD ≌△BAO ,∴CD =OA =1,AD =BO =2,∴点C 的坐标为(3,-1)(2)①∵抛物线2212++-=ax x y 经过点C (3,-1),∴2332112++⨯-=-a ,解得21=a∴抛物线的解析式为221212++-=x x y 解法一:② i) 当A 为直角顶点时 ,延长CA 至点1P ,使AB AC AP ==1,则△1ABP 是以AB 为直角边的等腰直角三角形,如果点1P 在抛物线上,则1P 满足条件,过点1P 作1P E ⊥x 轴, ∵1AP =AC ,∠1EAP=∠DAC ,∠EA P 1=∠CDA =90°, ∴△A EP 1≌△DCA ,∴AE =AD =2, 1EP =CD=1,∴可求得1P 的坐标为(-1,1),经检验1P 点在抛物线上,因此存在点1P 满足条件; ii ) 当B 点为直角顶点时,过点B 作直线L ⊥BA ,在直线L 上分别取AB BP BP ==32,得到以AB 为直角边的等腰直角△2ABP 和等腰直角△3ABP ,作F P2⊥y 轴,同理可证△F BP 2≌△ABO ∴,22==BO F P BF =OA =1,可得点2P 的坐标为(-2,-1),经检验2P 点在抛物线上,因此存在点2P 满足条件.同理可得点3P 的坐标为(2,-3),经检验3P 点不在抛物线上.综上:抛物线上存在点1P (-1,1),2P (-2,-1)两点,使得△1ABP 和△2ABP是以AB 为直角边的等腰直角三角形.解法二:(2)②(如果有用下面解法的考生可以给满分) i) 当点A 为直角顶点时,易求出直线AC 的解析式为2121+-=x y 由⎪⎪⎩⎪⎪⎨⎧++-=+-=2212121212x x y x y 解之可得1P (-1,1) (已知点C 除外)作E P 1⊥x 轴于E ,则AE =2, E P 1=1, 由勾股定理有又∵AB =5,∴AB AP =1,∴△AB P 1是以AB 为直角边的等腰三角形;ii )当B 点为直角顶点时,过B 作直线L ∥AC 交抛物线于点2P 和点3P ,易求出直线L 的解析式为221--=x y ,由⎪⎪⎩⎪⎪⎨⎧++-=--=221212212x x y x y 解得21-=x 或42=x∴2P (-2,-1),3P (4,-4)作F P 2⊥y 轴于F ,同理可求得AB BP ==52 ∴△AB P 2是以AB 为直角边的等腰三角形作H P 3⊥y 轴于H ,可求得AB BP ≠=+=5242223,∴Rt △3ABP 不是等腰直角三角形,∴点3P 不满足条件.综上:抛物线上存在点1P (-1,1),2P (-2,-1)两点,使得△1ABP 和△2ABP 是以角AB 为直边的等腰直角三角形.2. (2011广东省,22,9分)如图,抛物线2517144y x x =-++与y 轴交于点A ,过点A 的直线与抛物线交于另一点B ,过点B 作BC ⊥x 轴,垂足为点C (3,0). (1)求直线AB 的函数关系式;(2)动点P 在线段OC 上,从原点O 出发以每钞一个单位的速度向C 移动,过点P 作⊥x 轴,交直线AB 于点M ,抛物线于点N ,设点P 移动的时间为t 秒,MN 的长为s 个单位,求s 与t 的函数关系式,并写出t 的取值范围;(3)设(2)的条件下(不考虑点P 与点O ,点G 重合的情况),连接CM ,BN ,当t 为何值时,四边形BCMN 为平等四边形?问对于所求的t 的值,平行四边形BCMN 是否为菱形?说明理由.【解】(1)把x=0代入2517144y x x =-++,得1y =把x=3代入2517144y x x =-++,得52y =, ∴A 、B 两点的坐标分别(0,1)、(3,52)设直线AB 的解析式为y kx b =+,代入A 、B 的坐标,得1532b k b =⎧⎪⎨+=⎪⎩,解得112b k =⎧⎪⎨=⎪⎩ 所以,112y x =+ (2)把x=t 分别代入到112y x =+和2517144y x x =-++ 分别得到点M 、N 的纵坐标为112t +和2517144t t -++ ∴MN=2517144t t -++-(112t +)=251544t t -+ 即251544s t t =-+∵点P 在线段OC 上移动,∴0≤t ≤3.(3)在四边形BCMN 中,∵BC ∥MN∴当BC=MN 时,四边形BCMN 即为平行四边形由25155442t t -+=,得121,2t t == 即当12t =或时,四边形BCMN 为平行四边形当1t =时,PC=2,PM=32,PN=4,由勾股定理求得CM=BN=52,此时BC=CM=MN=BN ,平行四边形BCMN 为菱形; 当2t =时,PC=1,PM=2,由勾股定理求得CM=5,此时BC ≠CM ,平行四边形BCMN 不是菱形;所以,当1t =时,平行四边形BCMN 为菱形.3. (2011湖南怀化,24,10分)在矩形AOBC 中,OB=6,OA=4,分别以OB ,OA 所在直线为x 轴和y 轴建立如图所示的平面直角坐标系,F 是边BC 上的一个动点(不与B ,C 重合),过F 点的反比例函数)0(>=k xky 的图像与AC 边交于点E. (1) 求证:AE×AO=BF×BO ;(2) 若点E 的坐标为(2,4),求经过O 、E 、F 三点的抛物线的解析式;(3) 是否存在这样的点F ,使得将△CEF 沿EF 对折后,C 点恰好落在OB 上?若存在,求出此时的OF 长;若不存在,请说明理由.【答案】(1)证明:由题意知,点E 、F 均在反比例函数)0(>=k xky 图像上,且在第一象限,所以AE×AO=k ,BF×BO=k ,从而AE×AO=BF×BO. (2)将点E 的坐标为(2,4)代入反比例函数)0(>=k xky 得k=8, 所以反比例函数的解析式为xy 8=. ∵OB=6,∴当x=6时,y=34,点F 的坐标为(6,34). 设过点O 、E 、F 三点的二次函数表达式为)0(2≠++=a c bx ax y ,将点O (0,0),E (2、4),F (6,34)三点的坐标代入表达式得: ⎪⎪⎩⎪⎪⎨⎧=++=++=346364240c b a c b a c 解得⎪⎪⎪⎩⎪⎪⎪⎨⎧==-=092694c b a ∴经过O 、E 、F 三点的抛物线的解析式为:x x y 926942+-=. (1) 如图11,将△CEF 沿EF 对折后,C 点恰好落在OB 边于点C′.过点E 作EH ⊥OB 于点H.设CE=n ,CF=m ,则AE=6-n ,BF=4-m 由(1)得AE×AO=BF×BO ∴(6-n)×4=(4-m)×6 ,解得n=1.5m. 由折叠可知,CF=C′F=m ,CE=C′E=1.5m ,∠EC′F=∠C=90°在Rt △EHC′中,∠EC′H+∠C′EH=90°,又∵∠EC′H+∠EC′F+FC′B=180°,∠EC′F=90° ∴∠C′EH=FC′B ∵∠EHC′=C′BF=90° ∴△EC′H ∽△C′FB ,∴FC C E B C EH ''=' ∴5.15.1==''='mmF C C E B C EH , ∵由四边形AEHO 为矩形可得EH=AO=4 ∴C ′B=38. 在Rt △BC′F 中,由勾股定理得,C′F 2=BF 2+C′B 2,即m 2=(4-m)2+238⎪⎭⎫⎝⎛解得:m=926 BF=4-926=910, 在Rt △BOF 中,由勾股定理得,OF 2=BF 2+OB 2,即OF 2=62+2910⎪⎭⎫ ⎝⎛=813016.∴OF=97542∴存在这样的点F ,OF=97542,使得将△CEF 沿EF 对折后,C 点恰好落在OB 上. 4. (2011江苏淮安,28,12分)如图,在Rt △ABC 中,∠C=90°,AC=8,BC=6,点P 在AB 上,AP=2.点E 、F 同时从点P 出发,分别沿PA 、PB 以每秒1个单位长度的速度向点A 、B 匀速运动,点E 到达点A 后立即以原速度沿AB 向点B 运动,点F 运动到点B 时停止,点E 也随之停止.在点E 、F 运动过程中,以EF 为边作正方形EFGH ,使它与△ABC 在线段AB 的同侧,设E 、F 运动的时间为t 秒(t >0),正方形EFGH 与△ABC 重叠部分面积为S .(1)当t=1时,正方形EFGH 的边长是 ;当t=3时,正方形EFGH 的边长是 ;(2)当0<t ≤2时,求S 与t 的函数关系式; (3)直接答出:在整个运动过程中.......,当t 为何值时,S 最大?最大面积是多少?ABCH GP E F【答案】(1)2;6; (2) 当0<t ≤611时(如图),求S 与t 的函数关系式是:S=EFGH S 矩形=(2t )2=4t 2; AB CH GP E F当611<t ≤65时(如图),求S 与t 的函数关系式是:S=EFGH S 矩形-S △HMN =4t 2-12×43×[2t-34(2-t )] 2=2524 t 2+112t -32;当65<t ≤2时(如图),求S 与t 的函数关系式是:S= S △ARF -S △AQE =12×34(2+t ) 2 -12×34(2-t ) 2=3t .(3)由(2)知:若0<t ≤611,则当t=611时S 最大,其最大值S=144121; 若611<t ≤65,则当t=65时S 最大,其最大值S=185; 若65<t ≤2,则当t=2时S 最大,其最大值S=6. 综上所述,当t=2时S 最大,最大面积是6.5. (2011山东临沂,26,13分)如图,已知抛物线经过A (-2,0),B (-3,3)及原点O ,顶点为C .(1)求抛物线的解析式;(2)若点D 在抛物线上,点E 在抛物线的对称轴上,且以A 、O 、D 、E 为顶点的四边形是平行四边形,求点D 的坐标;(3)P 是抛物线上第一象限内的动点,过点P 作PM ⊥x 轴,垂足为M ,是否存在点P 使得以点P 、M 、A 为顶点的三角形与△BOC 相似?若存在,求出点P 的坐标;若不存在,请说明理由.解:(1)∵抛物线过原点O ,∴可设抛物线的解析式为y =ax 2+bx , 将A (-2,0),B (-3,3)代入,得 ⎩⎨⎧.3b 3a 90b 2a 4=-,=-解得⎩⎨⎧.2b 1a =,=∴此抛物线的解析式为y =x 2+2x .……………………(3分)(2)如图,①当AO 为边时,∵以A 、O 、D 、E 为顶点的四边形是平行四边形,∴DE ∥AO ,且DE =AO =2,…………………………………………( 4分) 点E 在对称轴x =-1上,∴点D 的横坐标为1或-3,…………………………………………( 5分) 即符合条件的点D 有两个,分别记为:D 1,D 2, 而当x =1时,y =3;当x =-3时,y =3,∴D 1(1,3),D 2(-3,3).…………………………………………(7分) ②当AO 为对角线时,则DE 与AO 互相平分, 又点E 在对称轴上,且线段AO 的中点横坐标为-1,由对称性知,符合条件的点D 只有一个,即顶点C (-1,,1),综上所述,符合条件的点D 共有三个,分别为D 1(1,3),D 2(-3,3),C (-1,,1).………………………………………………………(8分)③存在.…………………………………………………………………(9分)6. (2011上海,24,12分)已知平面直角坐标系xOy (如图),一次函数334y x =+的图像与y 轴交于点A ,点M 在正比例函数32y x =的图像上,且MO =MA .二次函数y =x 2+bx +c 的图像经过点A 、M .(1)求线段AM 的长;(2)求这个二次函数的解析式;(3)如果点B 在y 轴上,且位于点A 下方,点C 在上述二次函数的图像上,点D 在一次函数334y x =+的图像上,且四边形ABCD 是菱形,求点C 的坐标.【答案】(1)一次函数334y x =+,当x =0时,y =3.所以点A 的坐标为(0,3). 正比例函数32y x =,当y =32时,x =1.所以点M 的坐标为(1,32).如下图,AM =22313122⎛⎫+= ⎪⎝⎭.(2)将点A (0,3)、M (1,32)代入y =x 2+bx +c 中,得 3312c b c =⎧⎪⎨++=⎪⎩,. 解得523b c ⎧=-⎪⎨⎪=⎩,.即这个二次函数的解析式为2532y x x =-+. (3)设B(0,m )(m <3),C(n ,2532n n -+),D(n ,334n +).则AB =3m -,DC =D C y y -=2134n n -,AD =54n .因为四边形ABCD 是菱形,所以AB =DC =AD .所以21334534m n n m n ⎧-=-⎪⎪⎨⎪-=⎪⎩,.解得1130m n =⎧⎨=⎩,;(舍去)12122m n ⎧=⎪⎨⎪=⎩,.将n =2代入2532y x x =-+,得C y =2.所以点C 的坐标为(2,2). 7. (2011四川乐山26,13分)已知顶点为A(1,5)的抛物线2y ax bx c =++经过点B(5,1). (1)求抛物线的解析式;(2)如图(15.1),设C,D 分别是x 轴、y 轴上的两个动点,求四边形ABCD 周长的最小值 (3)在(2)中,当四边形ABCD 的周长最小时,作直线CD.设点P(x,y)(x>0)是直线y=x 上的一个动点,Q 是OP 的中点,以PQ 为斜边按图(15.2)所示构造等腰直角三角形PRQ. ①当△PBR 与直线CD 有公共点时,求x 的取值范围;②在①的条件下,记△PBR 与△COD 的公共部分的面积为S.求S 关于x 的函数关系式,并求S 的最大值。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2011年全国各地100份中考数学试卷分类汇编
2. (2011台湾台北,30)某鞋店有甲、乙两款鞋各30双,甲鞋一双200元,乙鞋一双50
元。
该店促销的方式:买一双甲鞋,送一双乙鞋;只买乙鞋没有任何优惠。
若打烊后得知,此两款鞋共卖得1800元,还剩甲鞋x 双、乙鞋y 双,则依题意可列出下列哪一个方程式?
A 1800)30(50)30(200=-+-y x
B .1800)30(50)30(200=--+-y x x
C. 1800)60(50)30(200=--+-y x x
D .1800])30(30[50)30(200=---+-y x x
3. (2011台湾全区,9)在早餐店里,王伯伯买5颗馒头,3颗包子,老板少拿2元,只要
50元.李太太买了11颗馒头,5颗包子,老板以售价的九折优待,只要90元.若馒头每颗x 元,包子每颗y 元,则下列哪一个二元一次联立方程式可表示题目中的数量关系?
A .⎩⎨⎧⨯=++=+9.09051125035y x y x
B .⎩⎨⎧÷=++=+9
.09051125035y x y x C .⎩⎨⎧⨯=+-=+9.09051125035y x y x D .⎩⎨⎧÷=+-=+9
.09051125035y x y x 4. (2011湖南益阳,2,4分)二元一次方程21-=x y 有无数多个解,下列四组值中不是..该方程的解的是
A .012
x y =⎧⎪⎨=-⎪⎩ B .11x y =⎧⎨=⎩ C .10x y =⎧⎨=⎩ D .11x y =-⎧⎨=-⎩ 5. (2011四川绵阳9,3)灾后重建,四川从悲壮走向豪迈.灾民发扬伟大的抗震救灾精神,桂花村派男女村民共15 人到山外采购建房所需的水泥,已知男村民一人挑两包,女村民两人抬一包,共购回15 包.请问这次采购派男女村民各多少人?
A .男村民3人,女村民12人
B .男村民5人,女村民10人
C .男村民6人,女村民9人
D .男村民7人,女村民8人
7. (2011广东肇庆,4,3分)方程组⎩
⎨⎧=+=-422y x y x 的解是 A .⎩⎨⎧==21y x
B .⎩⎨⎧==13y x
C .⎩⎨⎧-==20y x
D .⎩⎨⎧==0
2y x
9. (2011山东枣庄,6,3分)已知2,1x y =⎧⎨=⎩是二元一次方程组7,1ax by ax by +=⎧⎨-=⎩
的解,则a b -的值为( )
A .-1
B .1
C .2
D .3
二、填空题
1. (2011安徽芜湖,13,5分)方程组237,38.
x y x y +=⎧⎨-=⎩的解是 .
5. (2011山东潍坊,15,3分)方程组524050x y x y --=⎧⎨+-=⎩
的解是___________________. 8. (2011湖北鄂州,7,3分)若关于x ,y 的二元一次方程组3133x y a x y +=+⎧⎨
+=⎩的解满足
2x y +<,则a 的取值范围为______.
【答案】a <4
9. (2011河北,19,8分)已知.a y x 3y x 3y 2的解的二元一次方程,是关于+=⎩⎨
⎧==x 求(a+1)(a-1)+7的值
【答案】将x=2,y=3代入a y x 3+=中,得a=3。
2. (2011山东威海,22,9分)为了参加2011年威海国际铁人三项(游泳、自行车、长跑)系列赛业余组的比赛,李明针对自行车和长跑项目进行专项训练.某次训练中,李明骑自行车的平均速度为每分钟600米,跑步的平均速度为每分钟200米,自行车路段和长跑路段共5千米,用时15分钟.求自行车路段和长跑路段的长度.
答:自行车路段的长度为32千米,长跑路段的长度2千米.
3. (2011山东烟台,20,8分)小华从家里到学校的路是一段平路和一段下坡路.假设他始终保持平路每分钟走60米,下坡路每分钟走80米 ,上坡路每分钟走40米,从家里到学校需10分钟,从学校到家里需15分钟.请问小华家离学校多远?
4. (2011湖南常德,23,8分)某城市规定:出租车起步价允许行驶的最远路程为3千米,
超过3千米的部分按每千米另收费.甲说:“我乘这种出租车走了11千米,付了17元”;乙说:“我乘这种出租车走了23千米,付了35元”.请你算一算这种出租车的起步价是多少元?以及超过3千米后,每千米的车费是多少元?
9. (2011上海,20,10分)解方程组:222,
230.x y x xy y -=⎧⎨--=⎩
10.(2011湖北黄石,20,8分)解方程:0)10553(4222=--+--y x y x。
