2019优化方案高考总复习·数学理第四章第3讲
第3讲 全称量词和存在量词

意 x1∈[0,3],存在 x2∈[1,2]使得 f(x1)≥g(x2)等价于 f(x1)min≥g(x2)min,得 0≥14-m,所以
m≥14.
第21页
栏目导航
高考总复习 一轮复习导学案 ·数学提高版
【解析】 x∈R,sinx+cosx= 2sinx+π4∈[- 2, 2],所以 m<- 2.
第7页
栏目导航
高考总复习 一轮复习导学案 ·数学提高版
第一章 集合与常用逻辑用语、不等式
知识聚焦 1. 全称量词 我们把表示__全__体____的量词称为全称量词. 对应日常语言中的“一切”、“任意的”、“所有的”、“凡是”、“任给”、“对 每一个”等词,用符号“∀”表示. 含有__全__称__量__词____的命题,叫做全称命题.如“对任意实数 x∈M,都有 p(x)成立” 简记成“____∀_x_∈__M__,__p_(_x)________”.
第8页
栏目导航
高考总复习 一轮复习导学案 ·数学提高版
第一章 集合与常用逻辑用语、不等式
2. 存在量词 我们把表示__部__分____的量词称为存在量词. 对应日常语言中的“存在一个”、“至少有一个”、“有个”、“某个”、“有些”、
“有的”等词,用符号“__∃____”表示. 含有__存__在__量__词_ቤተ መጻሕፍቲ ባይዱ__的命题,叫做存在性命题.“存在实数 x0∈M,使 p(x0)成立”简
第22页
栏目导航
高考总复习 一轮复习导学案 ·数学提高版
第一章 集合与常用逻辑用语、不等式
已知 f(x)=ln(x2+1),g(x)=12x-m,若对任意 x1∈[0,3],任意 x2∈[1,2],有 f(x1)≥g(x2),则实数 m 的取值范围是___12_,__+__∞_____.
2019版一轮优化探究物理(人教版)课件:第四章 第3讲 圆周运动
[基础知识•自主梳理]
一、匀速圆周运动及其描述 1.匀速圆周运动 (1)定义:做圆周运动的物体,若在相等的时间内通过的圆弧 长 相等,就是匀速圆周运动. (2)特点:加速度大小不变,方向始终指向 圆心,是变加速运动. (3)条件:合外力大小不变、方向始终与 速度方向垂直且指向圆 心.
2.描述圆周运动的物理量及其关系
=mωa2l,可得 ωa= klg,而转盘的角速度 23klg< klg,小木块 a 未 发生滑动,其所需的向心力由静摩擦力来提供,由牛顿第二定律可得 Ff= mω2l=23kmg,选项 D 错误. 答案:AC
2.[火车转弯分析] (多选)铁路转弯处的弯道半径 r 是根据地 形决定的.弯道处要求外轨比内轨高,其内、外轨高度差 h 的 设计不仅与 r 有关,还与火车在弯道上的行驶速度 v 有关.下 列说法正确的是( ) A.速率 v 一定时,r 越小,要求 h 越大 B.速率 v 一定时,r 越大,要求 h 越大 C.半径 r 一定时,v 越小,要求 h 越大 D.半径 r 一定时,v 越大,要求 h 越大
(2)摩擦或齿轮传动:如图甲、乙所示,两轮边缘接触,接触点 无打滑现象时,两轮边缘线速度大小相等,即 vA=vB.
(3)同轴传动:如图甲、乙所示,绕同一转轴转动的物体,角速 度相同,ωA=ωB,由 v=ωr 知 v 与 r 成正比.
题组突破训练
1.[皮带转动] (多选)变速自行车靠变换 齿轮组合来改变行驶速度.如图所示是某 一变速自行车齿轮转动结构示意图,图中 A 轮有 48 齿,B 轮有 42 齿,C 轮有 18 齿,D 轮有 12 齿,则( ) A.该自行车可变换两种不同挡位 B.该自行车可变换四种不同挡位 C.当 A 轮与 D 轮组合时,两轮的角速度之比 ωA∶ωD=1∶4 D.当 A 轮与 D 轮组合时,两轮的角速度之比 ωA∶ωD=4∶1
精选2019届高考数学北师大版一轮复习讲义:第3讲全称量词与存在量词、逻辑联结词

§1.3简单的逻辑联结词、全称量词与存在量词1.全称量词与存在量词(1)常见的全称量词有“所有”“每一个”“任何”“任意一条”“一切”等.(2)常见的存在量词有“有些”“至少有一个”“有一个”“存在”等.2.全称命题与特称命题(1)含有全称量词的命题叫全称命题.(2)含有存在量词的命题叫特称命题.3.命题的否定(1)全称命题的否定是特称命题;特称命题的否定是全称命题.(2)p或q的否定:非p且非q;p且q的否定:非p或非q.4.简单的逻辑联结词(1)命题中的“且”、“或”、“非”叫作逻辑联结词.(2)简单复合命题的真值表:知识拓展1.含有逻辑联结词的命题真假的判断规律(1)p或q:p,q中有一个为真,则p或q为真,即有真为真.(2)p且q:p,q中有一个为假,则p且q为假,即有假即假.(3)綈p:与p的真假相反,即一真一假,真假相反.2.含有一个量词的命题的否定的规律是“改量词,否结论”.3.命题的否定和否命题的区别:命题“若p,则q”的否定是“若p,则綈q”,否命题是“若綈p,则綈q”.题组一思考辨析1.判断下列结论是否正确(请在括号中打“√”或“×”)(1)命题“3≥2”是真命题.( √)(2)命题p和綈p不可能都是真命题.( √)(3)若命题p,q中至少有一个是真命题,则p或q是真命题.( √)(4)“全等三角形的面积相等”是特称命题.( ×)(5)命题綈(p且q)是假命题,则命题p,q中至少有一个是真命题.( ×)题组二教材改编2.已知p:2是偶数,q:2是质数,则命题綈p,綈q,p或q,p且q中真命题的个数为( )A.1 B.2 C.3 D.4答案 B解析p和q显然都是真命题,所以綈p,綈q都是假命题,p或q,p且q都是真命题.3.命题“正方形都是矩形”的否定是______________________________.答案存在一个正方形,这个正方形不是矩形题组三 易错自纠4.已知命题p ,q ,“綈p 为真”是“p 且q 为假”的( ) A .充分不必要条件 B .必要不充分条件 C .充要条件D .既不充分又不必要条件 答案 A解析 由綈p 为真知,p 为假,可得p 且q 为假;反之,若p 且q 为假,则可能是p 真q 假,从而綈p 为假,故“綈p 为真”是“p 且q 为假”的充分不必要条件,故选A. 5.下列命题中,为真命题的是( ) A .任意x ∈R ,-x 2-1<0 B .存在x ∈R ,x 2+x =-1 C .任意x ∈R ,x 2-x +14>0D .存在x ∈R ,x 2+2x +2<0 答案 A6.若“任意x ∈⎣⎢⎡⎦⎥⎤0,π4,tan x ≤m ”是真命题,则实数m 的最小值为________.答案 1解析 ∵函数y =tan x 在⎣⎢⎡⎦⎥⎤0,π4上是增函数, ∴y max =tan π4=1.依题意知,m ≥y max ,即m ≥1. ∴m 的最小值为1.题型一 含有逻辑联结词的命题的真假判断1.设命题p :函数y =log 2(x 2-2x)的单调增区间是[1,+∞),命题q :函数y =13x+1的值域为(0,1),则下列命题是真命题的为( ) A .p 且q B .p 或q C .p 且(綈q) D .綈q答案 B解析 函数y =log 2(x 2-2x)的递增区间是(2,+∞), 所以命题p 为假命题. 由3x>0,得0<13x +1<1,所以函数y =13x +1的值域为(0,1),故命题q 为真命题.所以p 且q 为假命题,p 或q 为真命题,p 且(綈q)为假命题,綈q 为假命题.故选B.2.(2017·山东)已知命题p :任意x >0,ln(x +1)>0;命题q :若a >b ,则a 2>b 2.下列命题为真命题的是( ) A .p 且q B .p 且(綈q) C .(綈p)且q D .(綈p)且(綈q)答案 B解析 ∵x >0,∴x +1>1,∴ln(x +1)>ln 1=0. ∴命题p 为真命题,∴綈p 为假命题.∵a >b ,取a =1,b =-2,而12=1,(-2)2=4, 此时a 2<b 2,∴命题q 为假命题,∴綈q 为真命题.∴p 且q 为假命题,p 且(綈q)为真命题,(綈p)且q 为假命题,(綈p)且(綈q)为假命题.故选B.3.已知命题p :若平面α⊥平面β,平面γ⊥平面β,则有平面α∥平面γ.命题q :在空间中,对于三条不同的直线a ,b ,c ,若a ⊥b ,b ⊥c ,则a ∥c.对以上两个命题,有以下命题: ①p 且q 为真;②p 或q 为假;③p 或q 为真;④(綈p)或(綈q)为假. 其中,正确的是________.(填序号) 答案 ②解析 命题p 是假命题,这是因为α与γ也可能相交;命题q 也是假命题,这两条直线也可能异面,相交. 思维升华“p 或q ”“p 且q ”“綈p ”等形式命题真假的判断步骤 (1)确定命题的构成形式; (2)判断其中命题p ,q 的真假;(3)确定“p 且q ”“p 或q ”“綈p ”等形式命题的真假.题型二 含有一个量词的命题命题点1 全称命题、特称命题的真假典例 (2017·韶关南雄二模)下列命题中的假命题是( ) A .任意x ∈R,2x -1>0 B .任意x ∈N +,(x -1)2>0 C .存在x ∈R ,lg x<1 D .存在x ∈R ,tan x =2答案 B解析 当x ∈N +时,x -1∈N ,可得(x -1)2≥0,当且仅当x =1时取等号,故B 不正确;易知A ,C ,D 正确,故选B.命题点2 含一个量词的命题的否定典例 (1)命题“任意x ∈R ,⎝ ⎛⎭⎪⎫13x>0”的否定是( )A .存在x ∈R ,⎝ ⎛⎭⎪⎫13x<0B .任意x ∈R ,⎝ ⎛⎭⎪⎫13x≤0C .任意x ∈R ,⎝ ⎛⎭⎪⎫13x<0D .存在x ∈R ,⎝ ⎛⎭⎪⎫13x≤0答案 D解析 全称命题的否定是特称命题,“>”的否定是“≤”.(2)(2017·河北五个一名校联考)命题“存在x ∈R,1<f(x)≤2”的否定形式是( ) A .任意x ∈R,1<f(x)≤2 B .存在x ∈R,1<f(x)≤2C .存在x ∈R ,f(x)≤1或f(x)>2D .任意x ∈R ,f(x)≤1或f(x)>2 答案 D解析 特称命题的否定是全称命题,原命题的否定形式为“任意x ∈R ,f(x)≤1或f(x)>2”.思维升华 (1)判定全称命题“任意x ∈M ,p(x)”是真命题,需要对集合M 中的每一个元素x ,证明p(x)成立;要判断特称命题是真命题,只要在限定集合内找到一个x ,使p(x)成立. (2)对全(特)称命题进行否定的方法①找到命题所含的量词,没有量词的要结合命题的含义先加上量词,再改变量词; ②对原命题的结论进行否定.跟踪训练 (1)下列命题中的真命题是( ) A .存在x ∈R ,使得sin x +cos x =32B .任意x ∈(0,+∞),e x>x +1 C .存在x ∈(-∞,0),2x<3x D .任意x ∈(0,π),sin x>cos x 答案 B解析 ∵sin x +cos x =2sin ⎝ ⎛⎭⎪⎫x +π4≤2<32,故A 错误;设f(x)=e x -x -1,则f ′(x)=e x-1,∴f(x)在(0,+∞)上为增函数,又f(0)=0, ∴任意x ∈(0,+∞),f(x)>0, 即e x>x +1,故B 正确;当x<0时,y =2x 的图像在y =3x 的图像上方,故C 错误;∵当x ∈⎝⎛⎭⎪⎫0,π4时,sin x<cos x ,故D 错误.故选B.(2)(2017·福州质检)已知命题p :“存在x ∈R ,e x-x -1≤0”,则綈p 为( ) A .存在x ∈R ,e x-x -1≥0 B .存在x ∈R ,e x -x -1>0 C .任意x ∈R ,e x -x -1>0 D .任意x ∈R ,e x -x -1≥0 答案 C解析 根据全称命题与特称命题的否定关系,可得綈p 为“任意x ∈R ,e x-x -1>0”,故选C.题型三 含参命题中参数的取值范围典例 (1)已知命题p :关于x 的方程x 2-ax +4=0有实根;命题q :关于x 的函数y =2x 2+ax +4在[3,+∞)上是增函数,若p 且q 是真命题,则实数a 的取值范围是________________. 答案 [-12,-4]∪[4,+∞)解析 若命题p 是真命题,则Δ=a 2-16≥0, 即a ≤-4或a ≥4;若命题q 是真命题, 则-a4≤3,即a ≥-12.∵p 且q 是真命题,∴p ,q 均为真, ∴a 的取值范围是[-12,-4]∪[4,+∞).(2)已知f(x)=ln(x 2+1),g(x)=⎝ ⎛⎭⎪⎫12x -m ,若对任意x 1∈[0,3],存在x 2∈[1,2],使得f(x 1)≥g(x 2),则实数m的取值范围是________________.答案 ⎣⎢⎡⎭⎪⎫14,+∞ 解析 当x ∈[0,3]时,f(x)min =f(0)=0,当x ∈[1,2]时, g(x)min =g(2)=14-m ,由f(x)min ≥g(x)min ,得0≥14-m ,所以m ≥14.引申探究本例(2)中,若将“存在x 2∈[1,2]”改为“任意x 2∈[1,2]”,其他条件不变,则实数m 的取值范围是________________.答案 ⎣⎢⎡⎭⎪⎫12,+∞ 解析 当x ∈[1,2]时,g(x)max =g(1)=12-m ,由f(x)min ≥g(x)max ,得0≥12-m ,∴m ≥12.思维升华 (1)已知含逻辑联结词的命题的真假,可根据每个命题的真假,利用集合的运算求解参数的取值范围.(2)对于含量词的命题中求参数的取值范围的问题,可根据命题的含义,利用函数值域(或最值)解决. 跟踪训练 (1)已知命题“存在x ∈R ,使2x 2+(a -1)x +12≤0”是假命题,则实数a 的取值范围是( )A .(-∞,-1)B .(-1,3)C .(-3,+∞)D .(-3,1)答案 B解析 原命题的否定为任意x ∈R,2x 2+(a -1)x +12>0,由题意知,其为真命题,即Δ=(a -1)2-4×2×12<0,则-2<a -1<2,即-1<a <3.(2)已知p :存在x ∈R ,mx 2+1≤0,q :任意x ∈R ,x 2+mx +1>0,若p 或q 为假命题,则实数m 的取值范围是( ) A .[2,+∞)B .(-∞,-2]C .(-∞,-2]∪[2,+∞)D .[-2,2]答案 A解析 依题意知,p ,q 均为假命题.当p 是假命题时,mx 2+1>0恒成立,则有m ≥0;当q 是假命题时,则有Δ=m 2-4≥0,m ≤-2或m ≥2. 因此由p ,q 均为假命题,得⎩⎪⎨⎪⎧m ≥0,m ≤-2或m ≥2,即m ≥2.常用逻辑用语考点分析有关四种命题及其真假判断、充分必要条件的判断或求参数的取值范围、量词等问题几乎在每年高考中都会出现,多与函数、数列、立体几何、解析几何等知识相结合,难度中等偏下.解决这类问题应熟练把握各类知识的内在联系. 一、命题的真假判断典例 (1)(2017·佛山模拟)已知a ,b 都是实数,那么“a >b ”是“ln a >ln b ”的( ) A .充分不必要条件 B .必要不充分条件 C .充要条件D .既不充分又不必要条件(2)(2018届全国名校大联考)已知命题p :任意x ∈R ,3x<5x;命题q :存在x ∈R ,x 3=1-x 2,则下列命题中为真命题的是( ) A .p 且q B .(綈p)且q C .p 且(綈q)D .(綈p)且(綈q)解析 (1)由ln a >ln b ⇒a >b >0⇒a >b ,故必要性成立.当a =1,b =0时,满足a >b ,但ln b 无意义,所以ln a >ln b 不成立,故充分性不成立. (2)若x =0,则30=50=1,∴p 是假命题, ∵方程x 3=1-x 2有解,∴q 是真命题, ∴(綈p)且q 是真命题. 答案 (1)B (2)B 二、充要条件的判断典例 (1)(2017·广东广雅中学、江西南昌二中联考)已知命题甲是“⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫x ⎪⎪⎪x 2+xx -1≥0”,命题乙是“{x|log 3(2x +1)≤0}”,则下列说法正确的是( ) A .甲是乙的充分条件,但不是乙的必要条件 B .甲是乙的必要条件,但不是乙的充分条件 C .甲是乙的充要条件D .甲既不是乙的充分条件,又不是乙的必要条件(2)(2017·湖北七市联考)已知圆C :(x -1)2+y 2=r 2(r >0).设p :0<r <3,q :圆C 上至多有2个点到直线x -3y +3=0的距离为1,则p 是q 的( ) A .充分不必要条件 B .必要不充分条件 C .充要条件D .既不充分又不必要条件解析 (1)x 2+xx -1≥0等价于x(x +1)(x -1)≥0且x ≠1,解得-1≤x ≤0或x>1.由log 3(2x +1)≤0,得0<2x +1≤1,得-12<x ≤0.∴甲是乙的必要条件,但不是乙的充分条件.故选B.(2)圆C :(x -1)2+y 2=r 2的圆心(1,0)到直线x -3y +3=0的距离d =|1-3×0+3|2=2.当r ∈(0,1)时,直线与圆相离,圆C 上没有到直线的距离为1的点;当r =1时,直线与圆相离,圆C 上只有1个点到直线的距离为1;当r ∈(1,2)时,直线与圆相离,圆C 上有2个点到直线的距离为1;当r =2时,直线与圆相切,圆C 上有2个点到直线的距离为1;当r ∈(2,3)时,直线与圆相交,圆C 上有2个点到直线的距离为1.综上,当r ∈(0,3)时,圆C 上至多有2个点到直线的距离为1,又由圆C 上至多有2个点到直线的距离为1,可得0<r <3,故p 是q 的充要条件,故选C. 答案 (1)B (2)C 三、求参数的取值范围典例 (1)已知命题p :任意x ∈[0,1],a ≥e x,命题q :存在x ∈R ,x 2+4x +a =0,若命题“p 且q ”是真命题,则实数a 的取值范围是__________.(2)已知函数f(x)=x +4x ,g(x)=2x+a ,若任意x 1∈⎣⎢⎡⎦⎥⎤12,3,存在x 2∈[2,3]使得f(x 1)≥g(x 2),则实数a 的取值范围是________.解析 (1)命题“p 且q ”是真命题,p 和q 均是真命题.当p 是真命题时,a ≥(e x)max =e ;当q 为真命题时,Δ=16-4a ≥0,a ≤4,所以a ∈[e,4].(2)∵x ∈⎣⎢⎡⎦⎥⎤12,3,∴f(x)≥2x·4x=4,当且仅当x =2时,f(x)min =4,当x ∈[2,3]时,g(x)min =22+a =4+a ,依题意知f(x)min ≥g(x)min ,即4≥a +4,∴a ≤0. 答案 (1)[e,4] (2)(-∞,0]1.已知命题p :“x>3”是“x 2>9”的充要条件,命题q :“a 2>b 2”是“a>b ”的充要条件,则下列判断正确的是( ) A .p 或q 为真 B .p 且q 为真 C .p 真q 假 D .p 或q 为假答案 D解析 ∵p 假,q 假,∴p 或q 为假.2.设命题p :函数y =sin 2x 的最小正周期为π2;命题q :函数y =cos x 的图像关于直线x =π2对称,则下列判断正确的是( ) A .p 为真 B .綈q 为假 C .p 且q 为假 D .p 或q 为真答案 C解析 函数y =sin 2x 的最小正周期为2π2=π,故命题p 为假命题;x =π2不是y =cos x 的对称轴,故命题q为假命题,故p 且q 为假.故选C.3.(2017·唐山一模)已知命题p :存在x ∈N ,x 3<x 2;命题q :任意a ∈(0,1)∪(1,+∞),函数f(x)=log a (x -1)的图像过点(2,0),则下列判断正确的是( )A .p 假q 真B .p 真q 假C .p 假q 假D .p 真q 真答案 A解析 对任意x ∈N ,x 3≥x 2,∴p 假, 又当x =2时,f(2)=log a 1=0, ∴f(x)的图像过点(2,0),∴q 真.4.(2017·豫西五校联考)若定义域为R 的函数f(x)不是偶函数,则下列命题中一定为真命题的是( ) A .任意x ∈R ,f(-x)≠f(x) B .任意x ∈R ,f(-x)=-f(x) C .存在x ∈R ,f(-x)≠f(x) D .存在x ∈R ,f(-x)=-f(x) 答案 C解析 由题意知任意x ∈R ,f(-x)=f(x)是假命题,则其否定为真命题,存在x ∈R ,f(-x)≠f(x)是真命题,故选C.5.(2017·安庆二模)设命题p :存在x ∈(0,+∞),x +1x >3;命题q :任意x ∈(2,+∞),x 2>2x,则下列命题为真的是( ) A .p 且(綈q) B .(綈p)且q C .p 且q D .(綈p)或q答案 A解析 对于命题p ,当x 0=4时,x 0+1x 0=174>3,故命题p 为真命题;对于命题q ,当x =4时,24=42=16,即存在x ∈(2,+∞),使得2x=x 2成立,故命题q 为假命题,所以p 且(綈q)为真命题,故选A.6.已知命题p :存在α∈R ,cos(π-α)=cos α;命题q :任意x ∈R ,x 2+1>0,则下列结论正确的是( ) A .p 且q 是真命题 B .p 且q 是假命题 C .綈p 是真命题 D .綈q 是真命题答案 A解析 对于p :取α=π2,则cos(π-α)=cos α,所以命题p 是真命题;对于命题q :因为x 2≥0,所以x 2+1>0,所以q 是真命题. 由此可得p 且q 是真命题. 7.下列命题中,真命题是( ) A .存在x ∈R ,e x≤0 B .任意x ∈R,2x>x 2C .a +b =0的充要条件是ab=-1D .“a >1,b >1”是“ab >1”的充分条件 答案 D解析 因为y =e x >0,x ∈R 恒成立,所以A 不正确;因为当x =-5时,2-5<(-5)2,所以B 不正确;“a b=-1”是“a +b =0”的充分不必要条件,C 不正确; 当a >1,b >1时,显然ab >1,D 正确.8.命题p :任意x ∈R ,ax 2+ax +1≥0,若綈p 是真命题,则实数a 的取值范围是( )A .(0,4]B .[0,4]C .(-∞,0]∪[4,+∞)D .(-∞,0)∪(4,+∞) 答案 D解析 因为命题p :任意x ∈R ,ax 2+ax +1≥0,所以綈p :存在x ∈R ,ax 2+ax +1<0,则a <0或⎩⎪⎨⎪⎧ a >0,Δ=a 2-4a >0,解得a <0或a >4. 9.命题“存在n ∈N ,n 2>2n ”的否定是________________.答案 任意n ∈N ,n 2≤2n10.已知函数f(x)的定义域为(a ,b),若“存在x ∈(a ,b),f(x)+f(-x)≠0”是假命题,则f(a +b)=________. 答案 0解析 若“存在x ∈(a ,b),f(x)+f(-x)≠0”是假命题,则“任意x ∈(a ,b),f(x)+f(-x)=0”是真命题,即f(-x)=-f(x),则函数f(x)是奇函数,则a +b =0,即f(a +b)=f(0)=0.11.以下四个命题:①任意x ∈R ,x 2-3x +2>0恒成立;②存在x ∈Q ,x 2=2;③存在x ∈R ,x 2+1=0;④任意x ∈R,4x 2>2x -1+3x 2.其中真命题的个数为________.答案 0解析 ∵x 2-3x +2=0的判别式Δ=(-3)2-4×2>0,∴当x>2或x<1时,x 2-3x +2>0才成立,∴①为假命题;当且仅当x =±2时,x 2=2,∴不存在x ∈Q ,使得x 2=2,∴②为假命题;对任意x ∈R ,x 2+1≠0,∴③为假命题;4x 2-(2x -1+3x 2)=x 2-2x +1=(x -1)2≥0,即当x =1时,4x 2=2x -1+3x 2成立,∴④为假命题.∴①②③④均为假命题.故真命题的个数为0.12.已知命题“任意x ∈R ,x 2-5x +152a>0”的否定为假命题,则实数a 的取值范围是____________. 答案 ⎝ ⎛⎭⎪⎫56,+∞解析 由“任意x ∈R ,x 2-5x +152a>0”的否定为假命题,可知原命题必为真命题,即不等式x 2-5x +152a>0对任意实数x 恒成立.设f(x)=x 2-5x +152a ,则其图像恒在x 轴的上方,故Δ=25-4×152a<0, 解得a>56,即实数a 的取值范围为⎝ ⎛⎭⎪⎫56,+∞.13.已知命题p :-4<x -a<4,命题q :(x -2)(3-x)>0,若綈p 是綈q 的充分不必要条件,则实数a 的取值范围是______.答案 [-1,6]解析 p :-4<x -a<4等价于a -4<x<a +4;q :(x -2)(3-x)>0等价于2<x<3.又綈p 是綈q 的充分不必要条件,即q 是p 的充分不必要条件,所以⎩⎪⎨⎪⎧ a -4≤2,a +4>3,或⎩⎪⎨⎪⎧ a -4<2,a +4≥3,解得-1≤a ≤6.14.下列结论:①若命题p :存在x ∈R ,tan x =1;命题q :任意x ∈R ,x 2-x +1>0,则命题“p 且(綈q)”是假命题;②已知直线l 1:ax +3y -1=0,l 2:x +by +1=0,则l 1⊥l 2的充要条件是a b=-3; ③命题“若x 2-3x +2=0,则x =1”的逆否命题是“若x ≠1,则x 2-3x +2≠0”.其中正确结论的序号为________.答案 ①③解析 ①中命题p 为真命题,命题q 为真命题,所以p 且(綈q)为假命题,故①正确;②当b =a =0时,有l 1⊥l 2,故②不正确;③正确,所以正确结论的序号为①③.15.已知命题p :存在x ∈R ,e x -mx =0,命题q :任意x ∈R ,x 2+mx +1≥0,若p 或(綈q)为假命题,则实数m 的取值范围是________.答案 [0,2]解析 若p 或(綈q)为假命题,则p 假q 真.由e x -mx =0,可得m =e x x ,x ≠0, 设f(x)=e x x,x ≠0,则 f ′(x)=xe x -e x x 2=(x -1)e x x 2, 当x>1时,f ′(x)>0,函数f(x)=e x x 在(1,+∞)上是递增函数;当0<x<1或x<0时,f ′(x)<0,函数f(x)=e x x在(0,1)和(-∞,0)上是递减函数,所以当x =1时,函数取得极小值f(1)=e ,所以函数f(x)=e x x的值域是(-∞,0)∪[e ,+∞),由p 是假命题,可得0≤m<e.当命题q 为真命题时,有Δ=m 2-4≤0,即-2≤m ≤2.所以当p 或(綈q)为假命题时,m 的取值范围是0≤m ≤2.16.已知函数f(x)=x 2-x +1x -1(x ≥2),g(x)=a x (a>1,x ≥2). (1)若存在x ∈[2,+∞),使f(x)=m 成立,则实数m 的取值范围为________________;(2)若任意x 1∈[2,+∞),存在x 2∈[2, +∞),使得f(x 1)=g(x 2),则实数a 的取值范围为_______________. 答案 (1)[3,+∞) (2)(1,3]解析 (1)因为f(x)=x 2-x +1x -1=x +1x -1=x -1+1x -1+1≥2+1=3,当且仅当x =2时等号成立,所以若存在x ∈[2,+∞),使f(x)=m 成立,则实数m 的取值范围为[3,+∞).(2)因为当x ≥2时,f(x)≥3,g(x)≥a 2,若任意x 1∈[2,+∞),存在x 2∈[2,+∞),使得f(x 1)=g(x 2), 则⎩⎪⎨⎪⎧ a 2≤3,a >1, 解得a ∈(1,3].。
第四章玩转铝及其化合物(附带答案解析)-2023年高考化学一轮复习重难点突破讲义
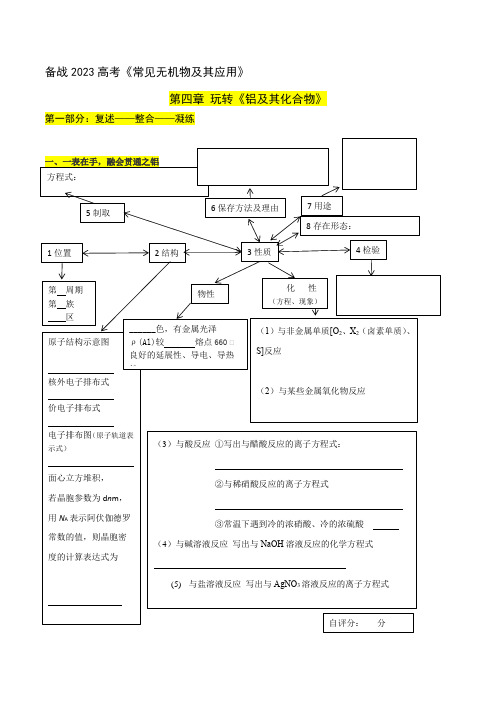
备战2023高考《常见无机物及其应用》第四章玩转《铝及其化合物》第一部分:复述——整合——凝练【核心补充1】【重要的实验】1、铝热反应①在下面方框中画出简易装置图并指出所用试剂的用途 ② 在下面方框中写出实验现象③铝热反应的用途:注:Al 和某些金属氧化物在高温下进行,反应迅速并放出大量的热,新生成的金属单质呈熔融态且易与Al 2O 3分离重要的实验】2、离子检验问题写出检验Al 3+写出检验AlO -2【核心补充2】【Al 的工业冶炼方法】从铝土矿(主要成分是Al 2O 3、含SiO 2、Fe 2O 3、MgO 等杂质)中冶炼铝的两种工艺:要求:1.补全主要微粒或添加的试剂的化学式 2.写出步骤1—5中含铝物质发生反应的离子方程式步骤1: 步骤2: 步骤3: 步骤4: 步骤5: 注:冶炼Al 时只能电解熔融Al 2O 3而不能电解熔融AlCl 3,原因是AlCl 3是共价化合物,熔融态不导电;加入冰晶石(Na 3AlF 6)的目的是降低Al 2O 3的熔化温度。
【核心补充3】【基本图像问题】1.可溶性铝盐溶液与NaOH溶液反应的图像:偏铝酸盐溶液与盐酸反应的图像:2.总结:Al3+、Al(OH)、AlO-2相互转化的比例关系二、一图在手融汇贯通之铝及其化合物连线。
用箭头表示出价类二维图中各物质之间可能存在的转化线,并标清楚反应条件。
+3 Al 2O 3 Al(OH)3 Al Cl 3NaAl O 20 Al单质氧化物氢氧化物盐三、Al 及其化合物易错点全掌控1、结合必要的化学用语解释明矾能净水的原因:2、注意反应的先后顺序当溶液中有多种离子H +、NH 4 +、Mg 2+、Al 3+存在时,向溶液中逐滴加入NaOH 溶液,与NaOH 反应的微粒的先后顺序是: 。
3、离子共存问题 画图连线,标记出微粒间不能大量共存的原因4、从分类观角度总结 既能与酸反应,又能与碱反应的物质 (1)无机物:①金属 如:Al 等 ②两性氧化物 如:Al 2O 3等 ③两性氢氧化物 如:Al(OH)3等④多元弱酸的酸式盐 如:NaHCO 3、KHS 、KHSO 3等⑤弱碱弱酸盐 如:CH 3COONH 4、(NH 4)2CO 3等。
高考数学大一轮复习第四章三角函数解三角形第3讲两角和与差的正弦余弦和正切公式

(教材习题改编)已知
cos
α=-35,α
是第三象限角,则
π cos(4
+α)为( )
A.
2 10
C.7102
B.-
2 10
D.-7102
解析:选 A.因为 cos α=-35,α 是第三象限的角, 所以 sin α=- 1-cos2α=- 1-(-35)2=-45, 所以 cos(π4+α)=cos π4cos α-sin π4sin α= 22·(-35)- 22·(-45) = 102.
又 sin2α+cos2α=1,所以 sin α=255,cos α= 55,则 cosα-π4
=cos αcos π4+sin αsin π4= 55× 22+255× 22=31010.
答案:3
10 10
三角函数公式的直接应用
(1)已知 α∈π2,π,sin α=153,则 tanα+π4=(
2.若 α+β=34π,则(1-tan α)(1-tan β)的值是________. 解析:-1=tan34π=tan(α+β)=1t-antaαn+αttaannββ, 所以 tan αtan β-1=tan α+tan β. 所以 1-tan α-tan β+tan αtan β=2, 即(1-tan α)(1-tan β)=2. 答案:2
三角函数公式的活用 (高频考点) 三角函数公式的活用是高考的热点,高考多以选择题或填空题 的形式出现,研究三角函数的性质和解三角形常应用三角函数 公式.主要命题角度有: (1)两角和与差公式的逆用及变形应用; (2)二倍角公式的活用.
角度一 两角和与差公式的逆用及变形应用
(1)已知 sin α+cos α=13,则 sin2(π4-α)=(
高考数学第3讲 分类与整合思想——巧分善合

33a,
33a,+∞.
大二轮复习 数学(文)
几种常见的由参数变化引起的分类与整合 (1)含有参数的不等式的求解. (2)含有参数的方程的求解. (3)对于解析式系数含参数的函数,求最值或单调性的问题. (4)二元二次方程表示曲线类型的判定等. (5)直线与圆锥曲线位置关系的分类.
大二轮复习 数学(文)
2.(2019·东营模拟)设圆锥曲线 C 的两个焦点分别为 F1,F2,若曲 线 C 上存在点 P 满足|PF1|∶|F1F2|∶|PF2|=4∶3∶2,则曲线 C 的离心 率等于________.
大二轮复习 数学(文)
解析:不妨设|PF1|=4t,|F1F2|=3t,|PF2|=2t,其中,t≠0.若该曲 线为椭圆,则有|PF1|+|PF2|=6t=2a,
解析:选 A.①当 2-a≥2,即 a≤0 时,22-a-2-1=1,解得 a=-1, 则 f(a)=f(-1)=-log2[3-(-1)]=-2; ②当 2-a<2 即 a>0 时,-log2[3-(2-a)]=1, 解得 a=-12,舍去. 所以 f(a)=-2.故选 A.
大二轮复习 数学(文)
(2)(2019·阜阳二模)等比数列{an}中,a1+a4+a7=2,a3+a6+a9=18, 则{an}的前 9 项和 S9=________.
解析:由题意得 q2=aa13++aa46++aa79=9,q=±3, ①当 q=3 时,a2+a5+a8=3(a1+a4+a7)=6, S9=2+6+18=26 ②当 q=-3 时,a2+a5+a8=-3(a1+a4+a7)=-6,S9=2-6+18 =14, 所以 S9=14 或 26. 答案:14 或 26
大二轮复习 数学(文)
2019届高三理科数学第二轮专题复习配套文档专题四 第3讲立体几何中的向量方法

第3讲立体几何中的向量方法[真题再现]1.(2018·课标Ⅰ)如图,四边形ABCD为正方形,E,F分别为AD,BC的中点,以DF为折痕把△DFC使点C到达点P的位置,且PF⊥BF。
(1)证明:平面PEF⊥平面ABFD;(2)求DP与平面ABFD所成角的正弦值.[解](1)证明:由已知可得BF⊥PF,BF⊥EF,所以BF⊥平面PEF.又BF⊂平面ABFD,所以平面PEF⊥平面ABFD。
(2)解:如图,作PH⊥EF,垂足为H.由(1)得,PH⊥平面ABFD。
以H为坐标原点,错误!的方向为y轴正方向,|错误!|为单位长,建立如图所示的空间直角坐标系H.xyz.由(1)可得,DE⊥PE.又DP=2,DE=1,所以PE=错误!.又PF=1,EF=2,所以PE⊥PF.所以PH=错误!,EH=错误!.则H(0,0,0),P错误!,D错误!,错误!=错误!,错误!=错误!.又错误!为平面ABFD的法向量,设DP与平面ABFD所成角为θ,则sin θ=错误!=错误!=错误!。
所以DP与平面ABFD所成角的正弦值为错误!.2.(2018·课标Ⅱ)如图,在三棱锥P-ABC中,AB=BC=22,P A=PB=PC=AC=4,O为AC的中点.(1)证明:PO⊥平面ABC;(2)若点M在棱BC上,且二面角M。
P A-C为30°,求PC与平面P AM所成角的正弦值[解](1)证明:因为P A=PC=AC=4,O为AC的中点,所以OP⊥AC,且OP=2错误!.如图,连接OB.因为AB=BC=错误!AC,所以△ABC为等腰直角三角形,且OB ⊥AC,OB=错误!AC=2。
由OP2+OB2=PB2知PO⊥OB.由OP⊥OB,OP⊥AC,OB∩AC=O,得PO⊥平面ABC.(2)解:如图,以O为坐标原点,错误!的方向为x轴正方向,建立空间直角坐标系O。
xyz。
由已知得O(0,0,0),B(2,0,0),A(0,-2,0),C(0,2,0),P(0,0,2错误!),错误!=(0,2,2错误!).取平面P AC的一个法向量错误!=(2,0,0).设M (a ,2-a,0)(0≤a ≤2),则错误!=(a ,4-a,0).设平面P AM 的法向量为n =(x ,y ,z ).由AP ,→·n =0,错误!·n =0得错误!可取y =错误!a ,得平面P AM 的一个法向量为n =(错误!(a -4),错误!a ,-a ),所以cos 错误!,n =错误!。
优化算法讲座.ppt

Optimization Algorithms
内容
§1 绪 论
§2 最佳食品搭配问题
§3 选址问题VRP
§4 最短路线问题 §5 分派问题 §6 最小费用流和最大流量问题 §7 钢管的订购和运输 §8 赛跑数据的二次规划问题 §9 交通运输问题
2
图: GPS基站安排
3
第一节: 绪 论
x47 x57 x67 v
4
8
7 5
8
1
14
3
13
6
31
例7:钢管的订购和运输
要铺设一条从A1 A2 A15的输送天然气的主管道, 如图1 所示. 经筛选, 可以生产这种主管道钢管的钢厂有S1, S2 ,S7. 图中粗 线表示铁路, 单细线表示公路, 双细线表示要铺设的管道(假设沿管 道线或者原来有公路或者建有施工公路). 圆圈表示火车站, 每段铁 路公路和管道旁的阿拉伯数字表示里程(单位km).
14
Matlab求解
Return
1. 线性规划问题:
linprog
2. 有约束的一元函数的最小值: fminbnd
min f (x) s.t. x1 x x2
3. 无约束多元函数最小值:
fminsearch
4. 有约束的多元函数最小值: fmincon
5. 二次规划问题 :
quadprog
aij x j
bi , i
1, 2,..., n.
xi 0, i 1, 2,..., n.
10
11
4. 根据设计变量的允许值
整数规划(0-1规划)和实数规划。
5. 根据变量具有确定值还是随机值
