常微分方程2010-2011-1(B)答案
常微分方程课后答案

常微分方程 2、11、xy dxdy2=,并求满足初始条件:x=0,y=1的特解、 解:对原式进行变量分离得。
故它的特解为代入得把即两边同时积分得:e e xx y c y x x c y c y xdx dy y22,11,0,ln ,212=====+==,0)1(.22=++dy x dx y 并求满足初始条件:x=0,y=1的特解、解:对原式进行变量分离得:。
故特解是时,代入式子得。
当时显然也是原方程的解当即时,两边同时积分得;当xy c y x y x c y c y x y dy dx x y++=====++=+=+≠=+-1ln 11,11,001ln 1,11ln 0,11123yxy dx dy x y 321++=解:原式可化为:x x y x x yx yx yyxyc c c c x dx x dy y yx ydxdy 2222222232232)1(1)1)(1(),0(ln 1ln 21ln 1ln 2111,0111=++=++≠++-=++=+≠+•+=+)故原方程的解为(即两边积分得故分离变量得显然.0;0;ln ,ln ,ln ln 0110000)1()1(4===-==-+=-++=-=+≠===-++x y c y x xy c y x xy c y y x x dy y y dx x x xy x y xdy y ydx x 故原方程的解为即两边积分时,变量分离是方程的解,当或解:由:10ln 1ln ln 1ln 1,0ln 0)ln (ln :931:8.cos ln sin ln 07ln sgn arcsin ln sgn arcsin 1sgn 11,)1(,,,6ln )1ln(21111,11,,,0)()(:53322222222222c dx dy dx dy xycy ud uu dx x x y u dx xydy x y ydx dy y x x c dy yy yydx dy c x y tgxdx ctgydy ctgxdy tgydx cx x xycx x u dxx x du xdxdu dxdux u dx dy ux y u x y y dx dy xc x arctgu dxx du u u u dx du x u dxdu xu dx dy ux y u x y x y x y dx dy dx x y dy x y e e e e e e ee x y uu xy x u u x yxyy x xx+===+=+-===-•-=--+-=-=+-===-=+•=+•=•=--=+===-+=+-=++=++-++=++===+-==-++-+--两边积分解:变量分离:。
研究生数理方程期末试题-10-11-1-A-答案
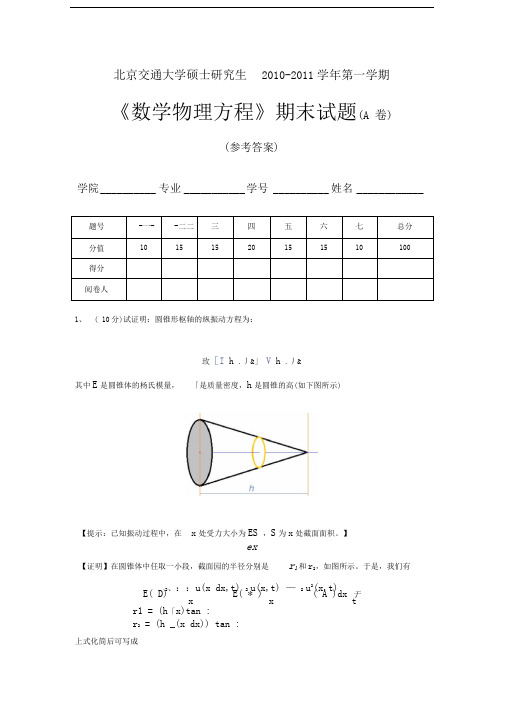
北京交通大学硕士研究生2010-2011学年第一学期《数学物理方程》期末试题(A 卷)(参考答案)学院__________ 专业___________ 学号 __________ 姓名____________1、( 10分)试证明:圆锥形枢轴的纵振动方程为:玫[I h .丿&」V h .丿&其中E是圆锥体的杨氏模量,「是质量密度,h是圆锥的高(如下图所示)【提示:已知振动过程中,在x处受力大小为ES ,S为x处截面面积。
】ex【证明】在圆锥体中任取一小段,截面园的半径分别是r1和r2,如图所示。
于是,我们有2、::u(x dx,t) 2 u(x,t) — 2 u2(x,t)E( D) E( * ) ( A )dx 于x x t r1 = (h「x)tan :r2= (h _(x dx)) tan :上式化简后可写成22::U(X,t)2::u(x,t) 2, ;u (x,t)E[(h -x)卜亠 & -(h -'X) 〔x J - - (h -'X)dx 2从而有E ::[(^x)2;:U(x ,t)H-(^x)2::u2(x,t) .x :X:t 或成2::[(1「)2汽("]“2(1「)小叩).xh ::x h ;:t其中a^E,证明完毕。
2、 (20分)考虑横截面为矩形的散热片, 它的一边y=b 处于较高温度U ,其它三边y=0.x = 0和x = a 则处于冷却介质中,因而保持较低的温度 u o 。
试求该截面上的稳定温度分布u(x,y),即求解以下定解问题:u|y 卫二 %, u|y 生二 U, 0 x a. 【提示:可以令u(x, y)二u 0 v(x, y),然后再用分离变量方法求解。
】【解】令u(x, y) v(x, y),则原定解问题变为Wl x£=0, V=0, 0cy <b;v|y/0, v|y 子U _u °,0 x a.分离变量:f 2\dU;:2U=0, 0 : x : a, 0 : y : b;y=0, 0 : x :: a, 0 : y : b;■ 2y »2 -2v(x,y) =X(x)Y(y)代入方程得到关于X和Y的常微分方程以及关于X的定解条件:X X = 0,X(0) =0,X(a) =0;Y - Y =0可以判定,特征值(n =1,,2,3J||)特征函数n 二X(x) = X n(x) =C n S in—x (n=1,,2,3JI|)利用特征值、可以求得丫(y) =Y n(y) =A n e叨B n^;y(n = 1,,2,3,l|l) 于是求得特征解n r n iy n,1V n(x,y)=(代e= B n e^ )sin x (n =1,,2,3JI|)a形式解为n -y _j-y门二v(x, y)二為V n(x, y)二為(A n e~ B n e^ )sin x吕 3r Q Qv(x,0)=迟(An+B n)sinO0 bv(x,b)八(A n e吗B n en =1pg na )sin——x 二U -u0得到A nB n =0八也如二 4 “,、A e aB e a(U - u。
常微分方程第三版习题答案

常微分方程第三版习题答案常微分方程是数学中的一个重要分支,它研究的是描述自然界中变化规律的方程。
在学习常微分方程的过程中,习题是非常重要的一部分,通过解习题可以加深对理论知识的理解和应用能力的培养。
本文将为大家提供《常微分方程第三版》习题的部分答案,希望能对大家的学习有所帮助。
1. 习题一1.1 解:首先,我们根据题意列出方程:$\frac{dy}{dt} = 2y + t^2$这是一个一阶线性常微分方程,我们可以使用常数变易法来求解。
令$y = u(t)e^{2t}$,则$\frac{dy}{dt} = \frac{du}{dt}e^{2t} + 2ue^{2t}$将上述结果代入原方程,得到:$\frac{du}{dt}e^{2t} + 2ue^{2t} = 2(u(t)e^{2t}) + t^2$化简得到:$\frac{du}{dt}e^{2t} = t^2$两边同时除以$e^{2t}$,得到:$\frac{du}{dt} = t^2e^{-2t}$对上式两边同时积分,得到:$u = -\frac{1}{4}t^2e^{-2t} + C$将$u$代入$y = u(t)e^{2t}$,得到最终的解:$y = (-\frac{1}{4}t^2e^{-2t} + C)e^{2t}$1.2 解:首先,我们根据题意列出方程:$\frac{dy}{dt} = \frac{t}{y}$这是一个一阶可分离变量的常微分方程,我们可以通过分离变量来求解。
将方程变形,得到:$ydy = tdt$对上式两边同时积分,得到:$\frac{1}{2}y^2 = \frac{1}{2}t^2 + C$解得:$y^2 = t^2 + C$由于题目中给出了初始条件$y(0) = 1$,将初始条件代入上式,得到:$1 = 0 + C$解得:$C = 1$将$C$代入$y^2 = t^2 + C$,得到最终的解:$y^2 = t^2 + 1$2. 习题二2.1 解:首先,我们根据题意列出方程:$\frac{dy}{dt} = 2ty + t^2$这是一个一阶线性常微分方程,我们可以使用常数变易法来求解。
复变函数与积分变换期末考试题

哈尔滨工程大学本科生考试试卷( 2010-2011 年 第一 学期)2011-01-04得分评卷人选择题(每小题2分,共10分)一、1、00Im Im limz z z z z z →-=- ( ).A.i B.i - C.0 D.不存在2、若0(1)n n n a z ∞=-∑在3z =发散,则它在 ( ).A . 1z =-收敛 B.2z =收敛 C . 2z i =发散 D . 均不正确3、已知函数212()1cos f z z z=--,则0z =,z =∞分别是()f z 的 ( ).A.二阶极点、孤立奇点 B.二阶极点、非孤立奇点 C.可去奇点、孤立奇点 D.可去奇点、非孤立奇点4、映射3z iw z i-=+在02z i =处的旋转角为 ( ). A./2π- B.0 C ./2π D . π5、下列命题或论断中,正确的个数是 ( ).I :Ln z Ln z =Ⅱ:设()(,)(,)f z u x y iv x y =+解析,则u -是v 的共轭调和函数III :()(,)(,)f z u x y iv x y =+的导数()f z '存在的充要条件是,u v 的偏导数分别存在Ⅳ:()tan(1/)f z z =在任意圆环域0z R <<不能展开为洛朗级数A.0 B.1 C.2 D.3得分评卷人填空题(每小题2分,共10分)二、6、设z i e i =,则Re z = .7、若函数32(,)v x y x axy =+为某一解析函数的虚部,则常数=a .8、设函数cos ze z 的泰勒展开式为∑∞=0n n n z c ,则它的收敛半径为 .9、设信号()(1)f t t δ=-,则通过Fourier 变换得到的频谱函数()F ω= .10、设1()(1)F s s s =-,则通过Laplace 逆变换得到()f t = . 得分评卷人计算题Ⅰ(每小题5分,共25分)三、11、函数33()23f z x i y =+在何处可导?何处解析?12、设()(,)(,)f z u x y iv x y =+是解析函数,且22()(4)u v x y x xy y -=-++,求()f z .13、计算积分()n Cz z dz +⎰,其中:1C z =为负向,n 为整数.14、计算积分(21)(2)C zdzz z +-⎰,其中:3C z =为正向.15、利用留数定理计算定积分201cos d πθθ+⎰.得分评卷人计算题Ⅱ(每小题6分,共18分)四、16、求函数23()32z f z z z -=-+在下列要求下的级数(泰勒或者洛朗级数)展开:(1) 圆1z <内;(2) 环12z <<内;(3) 环11z <-<∞内.17、设2321sin (),:32C e f z d C z iz ξξξξπξξ=-=-⎰正向,试求:(1) ()f z 在复平面上除去3z =的点处的函数表达式; (2) ()f i '及()f i π.18、按照要求逐步完成下列有关保形映射的问题.(1) Z 平面阴影部分是角形区域/6arg /6z ππ-<<,如下图所示。
常微分方程 习题答案

常微分方程习题答案常微分方程(ODEs)是数学中的一个重要分支,研究方程中的未知函数的导数与自变量之间的关系。
在实际应用中,ODEs广泛用于描述各种自然现象和工程问题,如物理学中的运动学、天体力学、电路理论等。
本文将通过一些常见的ODEs习题,探讨其解答方法和相关概念。
1. 一阶线性常微分方程考虑形如$y'+p(x)y=q(x)$的一阶线性常微分方程,其中$p(x)$和$q(x)$是已知函数。
我们可以使用常数变易法来求解该方程。
首先求出齐次方程$y'+p(x)y=0$的通解$y_h(x)$,然后寻找特解$y_p(x)$,使得$y_p(x)$满足原方程。
最后,将通解$y_h(x)$和特解$y_p(x)$相加,即可得到原方程的通解。
2. 高阶常微分方程高阶常微分方程是指包含未知函数的高阶导数的方程。
考虑形如$y^{(n)}+a_1y^{(n-1)}+\ldots+a_ny=f(x)$的齐次线性常微分方程,其中$a_1,\ldots,a_n$是已知常数,$f(x)$是已知函数。
我们可以使用特征方程的方法来求解该方程。
首先求出齐次方程的特征方程$r^n+a_1r^{n-1}+\ldots+a_n=0$的根$r_1,\ldots,r_n$,然后根据根的性质得到齐次方程的通解$y_h(x)$。
接下来,我们需要找到一个特解$y_p(x)$,使得$y_p(x)$满足原方程。
最后,将通解$y_h(x)$和特解$y_p(x)$相加,即可得到原方程的通解。
3. 常见的ODEs应用常微分方程在各个领域都有广泛的应用。
例如,在物理学中,牛顿第二定律$F=ma$可以转化为二阶常微分方程$m\frac{{d^2x}}{{dt^2}}=F(x,t)$,其中$x(t)$表示物体的位置。
在天体力学中,开普勒定律可以通过常微分方程来描述行星的运动。
在电路理论中,基尔霍夫电流定律和电压定律可以转化为常微分方程,用于分析电路中的电流和电压。
常微分方程试题及答案

常微分方程试题及答案一、单项选择题(每题5分,共20分)1. 下列哪一项不是常微分方程的特点?A. 未知函数是连续的B. 未知函数是可微的C. 未知函数的导数是未知的D. 方程中包含未知函数的导数答案:A2. 常微分方程的解是指满足方程的函数,下列哪一项不是解的性质?A. 唯一性B. 存在性C. 可微性D. 可积性答案:D3. 一阶线性微分方程的一般形式是:A. \( y' + p(x)y = q(x) \)B. \( y' = p(x)y + q(x) \)C. \( y' - p(x)y = q(x) \)D. \( y' + p(x)y = q(x) \) 或 \( y' - p(x)y = q(x) \)答案:A4. 已知微分方程 \( y'' - y = 0 \) 的一个特解是 \( y = e^x \),那么它的通解是:A. \( y = C_1e^x + C_2e^{-x} \)B. \( y = C_1e^x + C_2 \)C. \( y = C_1e^x + C_2e^x \)D. \( y = C_1 + C_2e^{-x} \)答案:A二、填空题(每题5分,共20分)1. 微分方程 \( y'' + y' + y = 0 \) 的通解是 \( y = C_1e^{-x}+ C_2e^{-\frac{1}{2}x} \),其中 \( C_1 \) 和 \( C_2 \) 是常数。
2. 微分方程 \( y'' - 4y = 0 \) 的通解是 \( y = C_1\cos(2x) +C_2\sin(2x) \),其中 \( C_1 \) 和 \( C_2 \) 是常数。
3. 微分方程 \( y'' + 4y = 0 \) 的通解是 \( y = C_1\cos(2x) +C_2\sin(2x) \),其中 \( C_1 \) 和 \( C_2 \) 是常数。
常微分方程标准答案-一二章

习题1.24. 给定一阶微分方程2dyx dx=, (1). 求出它的通解; (2). 求通过点()1,4的特解; (3). 求出与直线23y x =+相切的解; (4). 求出满足条件102ydx =⎰的解;(5). 绘出(2),(3),(4)中的解得图形。
解:(1). 通解显然为2,y x c c =+∈;(2). 把1,4x y ==代入2y x c =+得3c =,故通过点()1,4的特解为23y x =+;(3). 因为所求直线与直线23y x =+相切,所以223y x cy x ⎧=+⎨=+⎩只有唯一解,即223x c x +=+只有唯一实根,从而4c =,故与直线23y x =+相切的解是24y x =+;(4). 把2y x c =+代入12ydx =⎰即得5c =,故满足条件12ydx =⎰的解是253y x =+;(5). 图形如下:-1.5-1-0.500.51 1.512345675. 求下列两个微分方程的公共解:242422,2y y x x y x x x y y ''=+-=++--解:由2424222y x x x x x y y +-=++--可得()()222210y x xy -++=所以2y x =或212y x =--,2y x =代入原微分方程满足,而212y x =--代入原微分方程不满足,故所求公共解是代入原微分方程不满足。
6. 求微分方程20y xy y ''+-=的直线积分曲线。
解:设所求直线积分曲线是y kx b =+,则将其代入原微分方程可得2200010k b k xk kx b k b k b k k -=⎧+--=⇒⇒====⎨-=⎩或所以所求直线积分曲线是0y =或1y x =+。
8. 试建立分别具有下列性质的曲线所满足的微分方程:(2). 曲线上任一点的切线介于两坐标轴之间的部分等于定长l ; (5). 曲线上任一点的切线的纵截距等于切点横坐标的平方。
常微分课后答案第一章

常微分课后答案第一章yx C x C y x C x C y 2222121sin cos ,cos sin ωωωωωωωωω-=--=''+-=',所以0222=+y dxyd ω,故xCx C y ωωsin cos 21+=为方程的解.(6)yB x A y B x A y 22)sin(,)cos(ωωωωω-=+-=''+=',故0222=+y dxyd ω,因此)sin(B x A y +=ω为方程的解.3.验证下列各函数是相应微分方程的解:(1)xxy sin =,x y y x cos =+'; (2)212x Cy -+=,xxy y x2)1(2=+'-(C 是任意常数);(3)x Ce y =,02=+'-''y y y (C 是任意常数); (4)xe y =,xx xe ye y ey 2212-=-+'-;(5)x y sin =,0cos sin sin 222=-+-+'x x x y yy ;(6)xy 1-=,1222++='xy y x y x ; (7)12+=xy ,xy x yy 2)1(22++-=';(8))()(x f x g y =,)()()()(2x f x g y x g x f y '-'='.证明 (1)因为2sin cos x xx x y -=',所以xxxx x x x y y x cos sin sin cos =+-=+'.(2)由于21xCx y --=',故xx C x xCx x xy y x 2)12(1)1()1(2222=-++--⋅-=+'-.(3)由于xCe y =',xCe y ='',于是022=+-=+'-''x x x Ce Ce Ce y y y .(4)由xe y =',因此xx x x x x x x e e e e e e ye y e y 22212)(2-=⋅-+⋅=-+'--.(5)因为x y cos =',所以cos sin sin sin 2sin cos cos sin sin 22222=-+⋅-+=-+-+'x x x x x x x x x y y y . (6)从21xy =',得1111122222++=+⎪⎭⎫⎝⎛-⋅+⎪⎭⎫ ⎝⎛-⋅=='xy y x x x x x y x .(7)由x y 2=',得到xy x y x x x x x y 2)1(2)1)(1()1(2222222++-=+++-+=='.(8))()()()()()()()()()()()()()()(222x f x g y x g x f x f x g x f x g x g x f x f x g x f x g x f y '-'='-⎪⎪⎭⎫ ⎝⎛⋅'='-'='.4.给定一阶微分方程x dx dy 2=, (1)求出它的通解; (2)求通过点)4,1(的特解; (3)求出与直线32+=x y 相切的解;(4)求出满足条件210=⎰ydx 的解;(5)绘出(2),(3),(4)中的解的图形. 解 (1)通解 Cx xdx y +==⎰22.(2)由41==x y ,得到3=C ,所以过点)4,1(的特解为32+=xy .(3)这时122=⇒=x x ,切点坐标为)5,1(,由51==x y ,得到4=C ,所以与直线32+=x y 相切的解为42+=xy .(4)由231)31()(131210=+=+=+=⎰⎰C Cx x dx C x ydx ,得到35=C ,故满足条件21=⎰ydx 的解为352+=xy .(5)如图1-1所示.-3-2-1123x24681012y图1-15.求下列两个微分方程的公共解: (1)422x x yy -+=';(2)2422y y x xx y --++='.解 公共解必须满足2424222y y x x x x x y --++=-+,即 022242=-+-x y x y ,得到2x y =或212--=x y 是微分方程422x x y y -+='和2422y y x x x y --++='的公共解.6.求微分方程02=-'+'y y x y 的直线积分曲线.解 设直线积分曲线为0=++C By Ax ,两边对x 求导得,0='+y B A ,若0=B ,则0=A ,得到0=C ,不可能.故必有0≠B ,则B Ay -=',代入原方程有02=++⎪⎭⎫ ⎝⎛-+-B Cx B A B A x B A ,或)(22=-++B AB C x B A BA ,所以,⎪⎪⎩⎪⎪⎨⎧=-=+0,022BA B C B AB A ,得到⎩⎨⎧==0,0C A 或B C A -==.所求直线积分曲线为0=y 和1+=x y . 7.微分方程32224xy y y x=-',证明其积分曲线关于坐标原点)0,0(成中心对称的曲线,也是此微分方程的积分曲线.证明 设0),(=y x F 是微分方程32224xy y y x =-'的积分曲线,则与其关于坐标原点)0,0(成中心对称的曲线是),(=--y x F .由于),(=y x F 适合微分方程32224xy y y x =-',故3222),(),(4xyy y x F y x F x y x =-⎥⎥⎦⎤⎢⎢⎣⎡-⋅,分别以y x --,代yx ,,亦有3222))(()(),(),()(4y x y y x F y x F x y x --=--⎥⎥⎦⎤⎢⎢⎣⎡-----⋅-,而由0),(=--y x F ,得到),(),(y x F y x F y yx -----=',从而0),(=--y x F 也是此微分方程的积分曲线.8.物体在空气中的冷却速度与物体和空气的温差成比例,如果物体在20分钟内由100C 冷至60C ,那么,在多久的时间内,这个物体的温度达到30C ?假设空气的温度为20C . 解 设物体在时刻t 的温度为)(t u u =,20=au,微分方程为)(au u k dtdu --=,解得ktaCe u u -+= ,根据初始条件10000===u ut ,得80=-=a u uC ,因此 kta a e u u u u --+=)(0,根据60,201===uu t ,得到ka a e u u u u2001)(--+=,由此202ln ln 20110=--=a a u u u u k ,所以得到t e u 202ln 8020-+=,当30=u 时,解出60=t (分钟)1=(小时).在1小时的时间内,这个物体的温度达到30C .9.试建立分别具有下列性质的曲线所满足的微分方程:(1)曲线上任一点的切线与该点的向径夹角为α;(2)曲线上任一点的切线介于两坐标轴之间的部分等于定长l ;(3)曲线上任一点的切线与两坐标轴所围成的三角形的面积都等于常数2a ;(4)曲线上任一点的切线介于两坐标轴之间的部分被切点等分;(5)曲线上任一点的切线的纵截距等于切点横坐标的平方;(6)曲线上任一点的切线的纵截距是切点的横坐标和纵坐标的等差中项;(7)曲线上任一点的切线的斜率与切点的横坐标成正比.(提示:过点),(y x d 的横截距和纵截距分别为'-yy x 和y x y '-).解 (1)曲线上任一点为),(y x ,则xy y x yy '+-'=1tan α,即ααtan tan y x x y y -+='. (2)曲线上任一点),(y x 处的切线方程为yy x Y X y -'=-',与两坐标轴交点为),0(y x y '-和)0,(y yy x '-',两点间距离为l y x y y y y x ='-+⎪⎪⎭⎫ ⎝⎛'-'22)(,即 222)()(l y x y y y x ='-+'-. (3)由(2),有221a y x y y yy x ='-'-',或y a y y x '=-'222)(.(4)由(2),有2y x y y '-=,或0=+'y y x .(5)由(2),2xy xy='-.(6)同样由(2),2yxy xy +='-,或xy xy='-2.(7)易得kxy='(k为常数且0>k).。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
《 常微分方程 》试卷(B)答案:
一. 填空题(每小题3分, 共15分)
1. )2,1(),1,0(),0,0(;
2. 5220
121x x -; 3. )2
,2(ππ-; 4. 0=-'+''-'''y y y y ; 5. ⎪⎪⎭
⎫ ⎝⎛+--+----t t t t t t t t e e e e e e e e 444423)(2(33251.
二.单项选择题(每小题3分, 共15分)
1. C
2.B
3. D 4 . C 5. A
三. 求下列微分方程的解 ( 共36分)
1. 分离变量: 2211x xdx y ydy
+=+ (3分)
两边积分,得通解
.1122c x y ++=+ (7分)
2. 令 ,1-=y z 则 (2分)
,11-+-=z x
x dx dz (3分) ,11x e x
c x z -+-= (5分) 得通解:x e x c x y --+-=111. (7分) 有特解:0=y .
3.令 ,0sin )21(,cos =+==x y
N x M (1分) ,21y
M x N y M +=-∂∂-∂∂ 积分因子 .)(2y e y y u = (4分) 通解: .sin 2c x e y y
= (7分)
4.令t e x =, 则原方程变为
t y dt dy dt
y d =+-222. (4.1) (2分) 特征根:1=λ(二重). 通解:.21t t te c e c y +=(3分)
方程(4.1)特解设为:B At y +=1, (5分)
代入方程(4.1),可得: .2,1==B A
(4.1)的通解为:221+++=t te c e c y t t (7分)
所求通解为:.2ln ln 21+++=x x x c x c y (8分)
5. 解: 令 ,'p y = 代入方程可得: ,01122=-+-p dx
dp x 分离变量, 可得 )1(,11222≠--=-p x dx p dp
, (2分)
两边积分, 得:
,sin 1cos )arcsin sin(arcsin arcsin 12111c x c x c x p c x p -+-=+-=⇒+-= (4分)
从而 ,sin 1cos 121c x c x dx
dy -+-= 通解为 .)1(arcsin sin 2
1cos 21 22112c x x x c c x y +-++-= (6分) 当 12=p 时, 有 ,1'±=y 可得: c x y +±=也为原方程的解. (7分)
四. 特征根:.,21i i -==λλ (2分) i =1λ对应特征向量 ⎪⎪⎭
⎫ ⎝⎛-i 1;i -=2λ 对应特征向量 ⎪⎪⎭⎫ ⎝⎛i 1; (4分) 基解矩阵 ⎪⎪⎭⎫ ⎝
⎛-=Φ--it it it it ie ie e e t )(, ⎪⎪⎭⎫ ⎝⎛-=Φ-1121)0(1i i i , ⎪⎪⎭
⎫ ⎝⎛-=ΦΦ=-t t t t t At cos sin sin cos )0()()exp(1 (6分) .|)cos |ln cos sin |cos |ln sin cos )()0()()(0⎪⎪⎭⎫ ⎝⎛+-=+=-⎰t t t t t t t t ds s f e e t s t A t
At ϕϕ (10分)
五. .2)(22)(2634by y x b a ax xy a b dt
dV --+--= (2分) 取 ,1,1==b a 则 22),(y x y x V += 定正. (4分) 6422y x dt
dV --= 定负, (6分) 故零解渐近稳定. (8分) 六. 证明:(反证法)
(1) 若 ,0)(01
='x y 则 )(1x y 为初值问题 0)()(0)()(010
1⎩⎨⎧='==+'+''x y x y y x q y x p y 的解, 而零解也为此初值问题的解, 由解的唯一性知, ,0)(1=x y 矛盾.
(4分)
(2) 若有公共零点 ,0)()(,02010==x y x y x 则
0, )()()()()](),([02
010*******=''=x y x y x y x y x y x y W 因此 )(1x y 与 )(2x y 线性相关, 矛盾. (8分)
七. 证明: 特征根: .2,121-=-=λλ
对应齐次线性方程通解: .221t t e c e c x --+= (2分)
常数变易: .)()(221t t e t c e t c x --+= 代入原方程, 取
⎩⎨⎧=-+-=+----)
()2)(('))(('0)(')('221221t f e t c e t c e t c e t c t t t t (3分) 解出 .)()(,)()(022011⎰⎰-=+=t
s t s ds s f e c t c ds s f e c t c (4分) 于是 .)()()(0220221⎰⎰-----++=t s t t s t t t ds s f e e ds s f e e e c e c t ϕ (5分)
由于 ,|)(|)(00t t s t t s e ds s f e e ds
s f e ⎰⎰≤而
, |)(| ( 0,|)(|lim |)(| ( ,0|)(|lim 000⎪⎩⎪⎨⎧∞===⎰⎰⎰∞++∞→+∞+∞→时)当收敛时)当ds s f e e t f e ds s f e e ds s f e s t t t s t t s
t 得到,0)(lim 0=⎰+∞→t t
s t e ds
s f e 同理可得, ,0)(lim 202=⎰+∞→t t s t e ds s f e 于是 .0)(lim =+∞
→t t ϕ (8分)。
