第一章质点运动学(第一次课)
合集下载
第1章-质点运动学
为了描述速 度随时间
z A.
(t )
.B
的变化情况,定义:质点
的平均加速度为
(t t )
O
a t
y
24
x
质点的(瞬时)加速度定义为:
d d r a lim 2 t 0 t dt dt
2
即:质点在某时刻或某位置的(瞬时)加速度等于
速度矢量 对时间的一阶导数,或等于矢径 r 对时
第一篇 力 学
1
内容提要
第一章 运动学 第二章 质点动力学(牛顿运动定律) 第三章 刚体力学
第四章 振动学基础
第五章 第六章 波动学基础
狭义相对论
2
第1章 质点运动学
§1-1 参考系、坐标系和理想模型
运动的可认知性——绝对运动与相对静止的辩证统一
案例讨论:关于物质运动属性的两种哲学论断 赫拉克利特:“人不能两次踏进同一条河流”
y
y
位置矢量 r 的大小(即质点P到原点o的距离)为
2 2 2 r r x y z
方向余弦: cos=x/r, cos=y/r, cos=z/r 式中 , , 取小于180°的值。
z
r
P(x,y,z)
z
C
cos2 + cos2 + cos2 =1
x
A
运动方程
—— 轨道方程。
11
消去时间t得:x2+y2=62
§1-3 位移 速 度
一.位移和路程
如图所示,质点沿曲线C运动。时刻t在A点,时 刻t+t在B点。 从起点A到终点B的有向线 段AB=r,称为质点在时间t内 的位移。 而A到B的路径长度S为 路程。
z A.
(t )
.B
的变化情况,定义:质点
的平均加速度为
(t t )
O
a t
y
24
x
质点的(瞬时)加速度定义为:
d d r a lim 2 t 0 t dt dt
2
即:质点在某时刻或某位置的(瞬时)加速度等于
速度矢量 对时间的一阶导数,或等于矢径 r 对时
第一篇 力 学
1
内容提要
第一章 运动学 第二章 质点动力学(牛顿运动定律) 第三章 刚体力学
第四章 振动学基础
第五章 第六章 波动学基础
狭义相对论
2
第1章 质点运动学
§1-1 参考系、坐标系和理想模型
运动的可认知性——绝对运动与相对静止的辩证统一
案例讨论:关于物质运动属性的两种哲学论断 赫拉克利特:“人不能两次踏进同一条河流”
y
y
位置矢量 r 的大小(即质点P到原点o的距离)为
2 2 2 r r x y z
方向余弦: cos=x/r, cos=y/r, cos=z/r 式中 , , 取小于180°的值。
z
r
P(x,y,z)
z
C
cos2 + cos2 + cos2 =1
x
A
运动方程
—— 轨道方程。
11
消去时间t得:x2+y2=62
§1-3 位移 速 度
一.位移和路程
如图所示,质点沿曲线C运动。时刻t在A点,时 刻t+t在B点。 从起点A到终点B的有向线 段AB=r,称为质点在时间t内 的位移。 而A到B的路径长度S为 路程。
上海理工大学 大学物理 第一章 质点运动学(1)

y
v0
y
v0
v0 x v0 cos v0 y v0 sin
质点在运动过程中 加速度始终为: 质点在任一时刻的 运动速度为:
O
v0x
y x
m
x
m
a gj
v (v0 cos )i (v0 sin gt) j
因为
dr v dt
1 2 t r v dt (v0t cos )i (v0t sin gt ) j 0 2
质点运动的轨迹可以看成v0方向的匀速直线运动和自由落体运 动的叠加;
x v0t cos 1 2 y v0t sin gt 2
1 x2 y xtg g 2 2 2 v0 cos
从上述方程式看,x,y构成一条抛物线,所以抛体运动又称为 “抛物线运动”。
1 x y xtg g 2 2 2 v0 cos
上述抛物线与x轴相交两点,其中x=0处为起点,另一交点的x 坐标为: 2 v0 sin 2 xm
2
g
可以令sin2=1,即=450时射程最远。
xm是上述抛物运动的射程。当初速度v0一定时,欲使射程最大,
同样,我们也可以根据运动速度求出ym,即上述抛物运动最高 点,此时Vy=0
v y v0 sin gt t (v0 sin ) / g
x
z
v v x v y vz
v v
称速率。
v x i v y j vz k
例1 设质点的运动方程为 r(t ) x(t )i y(t ) j ,其中
(1) 求t =3s 时的速度。(2)作出质点的运动轨迹图。
解:(1) 速度分量为:v x
第1章 质点运动学
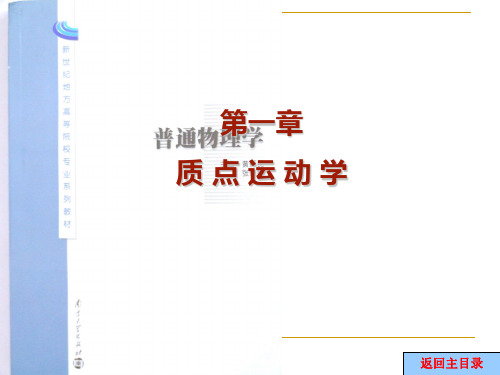
100t
4
t3
0
3
x x0
t
t0 vx (t)dt 0
t
(100t
4
t3 )dt
50t 2
1
t4
0
3
3
第一章 质点运动学
1-5 曲线运动
一、匀速圆周运动
1、匀速圆周运动的加速度
A v B
vA B vB
设质△|量=圆点 t|时vvv周处|存'刻。的在在,质半圆。v质点径周根点从为上据在PR点的加Q,运P处速处圆动,度,心到速的速为Q度定度O点为义,为有vv可v在,速;' 得t其度时在瞬中增刻t+时|,v
解:由
a
ann a
v2 R
n
dv dt
v
ds dt
20
0.6t 2 (m
/
s)
当t=1s时
an
v2 r
(20 0.6)2 200
m / s2
1.88m / s2
a
dv dt
1.2t
1.2m / s2
a a2 an2 2.23m / s2
dt
v0 v
0
v
v e(1.0s1 )t 0
由速度的定义: v
dy dt
v e(1.0s1 )t 0
y
t
dy v0 e dt (1.0s1 )t
y 10 1 e( 1.0s1 )t
0
0
由以上结果, t 时, v 0,此时y 10m。
但实际情况是:t 9.2s时, v 0,此时y 10m。
加速度分量
加速度大小 加速度余弦方向
a | a| a2x a2y a2z
大学物理第1章质点运动学

则有
ax 2 R cost;
a y 2 R sint
加速度的大小
2 2 2 2 2 2 a ax a2 ( R cos t ) ( R sin t ) R y
根据矢量的点积运算,分别计算
v r [(R sint )i (R cost ) j ] [(R cost )i ( R sint ) j ] 0 2 2 v a [(R sint )i (R cost ) j ] [( R cost )i ( R sint ) j ] 0
大学物理
第一章 质点运动学
1.1 运动学的一些基本概念 1.1.1、参考系(reference frame)和坐标系(coordinate) 参考系:为了描述物体的运动而选取的参考标准物体。 (运动描述的相对性) 坐标系:直角坐标系、自然坐标系、极坐标系、球坐标系等. 说明 在运动学中,参考系的选择是任意的;在动力学中则不然 1.1.2、时间和空间的计量 1、时间及其计量 时间表征物理事件的顺序性和物质运动的持续性。时间测量的 标准单位是秒。1967年定义秒为铯—133原子基态的两个超精细 能级之间跃迁辐射周期的9192631770倍。量度时间范围从宇宙 年龄1018s(约200亿年)到微观粒子的最短寿命 10-24s.极限的时 间间隔为普朗克时间10-43s,小于此时间,现有的时间概念就不适 用了。
运动学中的两类问题
1、已知质点的运动学方程求质点的速度、加速度等问
题常称为运动学第一类问题.
r r (t )
微分
v, a
2、由加速度和初始条件求速度方程和运动方程的问题称 为运动学的第二类问题.
a , v0 , r0
第1章-质点运动学

述
位移
rrrBArxBxBAii
rA
yA
yB
j j
y
yB A r
r y A A
rB
B
yB yA
(xB xA)i ( yB yA) j
xi yj
o
xA
xB x
xB xA
若质点r 在 (三x维B 空x间A中)i运动( yB
yA)
j
(zB
z A )k
位移的大小为 r x2 y2 z2
23
1-2 求解运动学问题举例
例3 有 一个球体在某液体中竖直下落, 其初速度
为 v0 10 j , 它的加速度为 a 1.0v j. 问:(1)经
过多少时间后可以认为小球已停止运动, (2)此球体
在停止运动前经历的路程有多长?
解:由加速度定义
v dv 1.0
t
dt
,
v v0
0
a dv 1.0v dt
v v2
位矢量
t
0,
t 0
0,
tv
rv
a
dv dt
v2 r
en
2ren
法向单 位矢量
vB
r
o
en
v
vB
vA et r
vA
31
1-3 圆周运动
三alitlami tm 变00速litdmdv圆vvvt0tt周nt运vtavt动dvdttrev2ttleeit切mntv向a0nn加aaevn速tntneen度t 和法向v加2v速tove度2vnrevtv1vn1
一 圆周运动的角速度和角加速度
角坐标 (t)
角速度 (t) d (t)
dt
速率
位移
rrrBArxBxBAii
rA
yA
yB
j j
y
yB A r
r y A A
rB
B
yB yA
(xB xA)i ( yB yA) j
xi yj
o
xA
xB x
xB xA
若质点r 在 (三x维B 空x间A中)i运动( yB
yA)
j
(zB
z A )k
位移的大小为 r x2 y2 z2
23
1-2 求解运动学问题举例
例3 有 一个球体在某液体中竖直下落, 其初速度
为 v0 10 j , 它的加速度为 a 1.0v j. 问:(1)经
过多少时间后可以认为小球已停止运动, (2)此球体
在停止运动前经历的路程有多长?
解:由加速度定义
v dv 1.0
t
dt
,
v v0
0
a dv 1.0v dt
v v2
位矢量
t
0,
t 0
0,
tv
rv
a
dv dt
v2 r
en
2ren
法向单 位矢量
vB
r
o
en
v
vB
vA et r
vA
31
1-3 圆周运动
三alitlami tm 变00速litdmdv圆vvvt0tt周nt运vtavt动dvdttrev2ttleeit切mntv向a0nn加aaevn速tntneen度t 和法向v加2v速tove度2vnrevtv1vn1
一 圆周运动的角速度和角加速度
角坐标 (t)
角速度 (t) d (t)
dt
速率
大学物理——第1章-质点运动学

沿逆时针方向转动角位移取正, 沿顺时针方向转动角位移取负.
21
★ 角速度 ω 大小: ω = lim 单位:rad/s ★ 角加速度 β
v
θ dθ = t →0 t dt
v
ω dω d2θ 大小: β = lim = = 2 t →0 t dt dt
单位:rad/s2
22
★ 线量与角量的关系
dS = R dθ
16
取CF的长度等于CD
v v v v vτ vn v v v = lim + lim 加速度: a = lim = aτ + an t →0 t →0 t →0 t t t
v v 当 t →0 时,B点无限接近A点,vA与 vB v v 的夹角 θ 趋近于零,vτ 的极限方向与 vA v 相同,是A点处圆周的切线方向;vn的极 v 限方向垂直于 vA ,沿圆轨道的半径,指向
y
v v v r = r′ + R
v v v dr dr ′ dR 求导: = + dt dt dt
o
y′ M v u v v r′ r v o′ R
x′
z′
x
z v称为质点M的绝对速度, v称为质点M的相对速度, υ υ′
v 称为牵连速度. u
27
v v υ =υ′ +u
v
in 例1-6 一人向东前进,其速率为 υ1 = 50m/ m ,觉得风从 正南方吹来;假若他把速率增大为υ2 = 75m/ m , in
t
9
初始条件:t = 0 , x = 5m 【不定积分方法】
速度表达式是: v = 4+ 2t
x = ∫ vdt = ∫ (4 + 2t)dt = 4t + t 2 + C
21
★ 角速度 ω 大小: ω = lim 单位:rad/s ★ 角加速度 β
v
θ dθ = t →0 t dt
v
ω dω d2θ 大小: β = lim = = 2 t →0 t dt dt
单位:rad/s2
22
★ 线量与角量的关系
dS = R dθ
16
取CF的长度等于CD
v v v v vτ vn v v v = lim + lim 加速度: a = lim = aτ + an t →0 t →0 t →0 t t t
v v 当 t →0 时,B点无限接近A点,vA与 vB v v 的夹角 θ 趋近于零,vτ 的极限方向与 vA v 相同,是A点处圆周的切线方向;vn的极 v 限方向垂直于 vA ,沿圆轨道的半径,指向
y
v v v r = r′ + R
v v v dr dr ′ dR 求导: = + dt dt dt
o
y′ M v u v v r′ r v o′ R
x′
z′
x
z v称为质点M的绝对速度, v称为质点M的相对速度, υ υ′
v 称为牵连速度. u
27
v v υ =υ′ +u
v
in 例1-6 一人向东前进,其速率为 υ1 = 50m/ m ,觉得风从 正南方吹来;假若他把速率增大为υ2 = 75m/ m , in
t
9
初始条件:t = 0 , x = 5m 【不定积分方法】
速度表达式是: v = 4+ 2t
x = ∫ vdt = ∫ (4 + 2t)dt = 4t + t 2 + C
第一章 质点运动学

16
物理学
已知:x(t ) 1.0t 2.0,y(t ) 0.25t 2 2.0, 解 (1) 由题意可得
dx dy vx 1.0, vy 0.5t dt dt t 3s 时速度为 v 1.0i 1.5 j
速度 v 与
x 轴之间的夹角
第一章 质点运动学
第一章 质点运动学
14
物理学
讨论 一运动质点在某瞬 y 时位于矢径 r ( x, y ) 的 y 端点处,其速度大小为
dr ( A) dt dr ( C) dt
注意
dr (B) dt
r (t )
x
o
x
dx 2 dy 2 ( D) ( ) ( ) dt dt
dr dr dt dt
1.5 0 arctan 56.3 1.0
17
物理学
x(t ) 1.0t 2.0, (2)运动方程 2 y(t ) 0.25t 2.0,
消去参数 t 可得轨迹方程为
y 0.25x x 3.0
2
轨迹图 t 4s
y/m
6 2
t 4s
t 2s 4
-6 -4 -2 0
dx B v A v x i i vi dt l dy vB v y j j o dt 2 2 2 x y l dx dy 两边求导得 2 x 2y 0 dt dt
第一章 质点运动学
解
y
A
v
x
20
物理学
dy x dx y 即 dt y dt B x dx vB j y dt dx o v dt vB vtan j
物理学
已知:x(t ) 1.0t 2.0,y(t ) 0.25t 2 2.0, 解 (1) 由题意可得
dx dy vx 1.0, vy 0.5t dt dt t 3s 时速度为 v 1.0i 1.5 j
速度 v 与
x 轴之间的夹角
第一章 质点运动学
第一章 质点运动学
14
物理学
讨论 一运动质点在某瞬 y 时位于矢径 r ( x, y ) 的 y 端点处,其速度大小为
dr ( A) dt dr ( C) dt
注意
dr (B) dt
r (t )
x
o
x
dx 2 dy 2 ( D) ( ) ( ) dt dt
dr dr dt dt
1.5 0 arctan 56.3 1.0
17
物理学
x(t ) 1.0t 2.0, (2)运动方程 2 y(t ) 0.25t 2.0,
消去参数 t 可得轨迹方程为
y 0.25x x 3.0
2
轨迹图 t 4s
y/m
6 2
t 4s
t 2s 4
-6 -4 -2 0
dx B v A v x i i vi dt l dy vB v y j j o dt 2 2 2 x y l dx dy 两边求导得 2 x 2y 0 dt dt
第一章 质点运动学
解
y
A
v
x
20
物理学
dy x dx y 即 dt y dt B x dx vB j y dt dx o v dt vB vtan j
第一章 质点运动学1

第一章 质点运动学 教学基本要求
一 掌握位置矢量、位移、加速度等描述质点运 动及运动变化的物理量 . 理解这些物理量的矢量性、 瞬时性和相对性 . 二 理解运动方程的物理意义及作用 . 掌握运用 运动方程确定质点的位置、位移、速度和加速度的方 法,以及已知质点运动的加速度和初始条件求速度、 运动方程的方法 . 三 能计算质点作圆周运动时的角速度、角加 速度、切向加速度和法向加速度 . 四 理解伽利略速度变换式, 并会用它求简单的质 点相对运动问题 .
2 2
2
讨论 位移与路程
(A)P1P2 两点间的路程 s ' 是不唯一的, 可以是 s或 是唯一的. 而位移r (B) 一般情况, 位移 大小不等于路程.
y
r (t1 )
O
s
'
p1 r
r (t2 )
s
p2
(C)什么情况 r s?
r s
z
x
不改变方向的直线运动; 当 t 0 时 r s .
三
速度
1 平均速度
在t 时间内, 质点从点 A 运动到点 B, 其位移为
y
B
r (t t)
s r
A
r r (t t ) r (t ) ( xB xA )i ( yB y A ) j o xi yj
r (t)
P2
r
r xi yj zk z 2 2 2 r x y z
注意
P ( x1 , y1 , z1 ) 1 P2 ( x2 , y2 , z2 )
x
r r
2
位矢长度的变化
2 2
r x2 y2 z 2 x1 y1 z1
一 掌握位置矢量、位移、加速度等描述质点运 动及运动变化的物理量 . 理解这些物理量的矢量性、 瞬时性和相对性 . 二 理解运动方程的物理意义及作用 . 掌握运用 运动方程确定质点的位置、位移、速度和加速度的方 法,以及已知质点运动的加速度和初始条件求速度、 运动方程的方法 . 三 能计算质点作圆周运动时的角速度、角加 速度、切向加速度和法向加速度 . 四 理解伽利略速度变换式, 并会用它求简单的质 点相对运动问题 .
2 2
2
讨论 位移与路程
(A)P1P2 两点间的路程 s ' 是不唯一的, 可以是 s或 是唯一的. 而位移r (B) 一般情况, 位移 大小不等于路程.
y
r (t1 )
O
s
'
p1 r
r (t2 )
s
p2
(C)什么情况 r s?
r s
z
x
不改变方向的直线运动; 当 t 0 时 r s .
三
速度
1 平均速度
在t 时间内, 质点从点 A 运动到点 B, 其位移为
y
B
r (t t)
s r
A
r r (t t ) r (t ) ( xB xA )i ( yB y A ) j o xi yj
r (t)
P2
r
r xi yj zk z 2 2 2 r x y z
注意
P ( x1 , y1 , z1 ) 1 P2 ( x2 , y2 , z2 )
x
r r
2
位矢长度的变化
2 2
r x2 y2 z 2 x1 y1 z1
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
四、轨迹与轨迹方程
1 2 如:对xOy平面内的平抛运动,质点的位矢 r v0ti gt j 2 x v0t 其分量为 1 2 y 2 gt
质点运动时所经过的空间点的集合称为轨迹 (或轨迹曲线)。
1.2.2 位移矢量
一、定义
在一般情况下,质点在一个时间段内位置的 变化可以用质点初时刻位置指向末时刻位置的矢量 来描写,这个矢量叫位移矢量 r 。
d 3)角速度 dt d 4)角加速度 dt 基本定义式
o
P(t )
参考方向
如圆周运动
圆周运动时,由于轨迹确定,用这套物理量较为方便。
§1.2 描写运动的四个物理量
1.2.1 位置矢量 1.2.2 位移矢量
1.2.3 速度矢量
1.2.4 加速度矢量
1.2.1 位置矢量
一、定义 坐标原点指向质点p的 矢量来确定质点位置。
二、位置矢量的分解 设 p 点 在 x、y、z 三 个 坐 标 轴上的坐标为x、y、z。则位 置矢量为
r xi yj zk
二、表示方法
r r2 r1 x x2 x1 y y2 y1 z z z 2 1
三、路程
质点运动过程中 经过轨迹长度叫做路程 。常用s或Δs表示。 在△t →0时,路程等于 位移的大小ds= dr
s
1.2.3 速度矢量
一、定义 位移矢量与时间的比 ,用
§1.1 参考系、质点
1.1.1 力学与机械运动
一、力学 机械运动规律 二、机械运动的定义 位变与形变 三、力学所包含的学科 运动学:是描写运动的一门学问,物体 是怎么运动的 动力学 :是关于运动本质规律的学问, 物体为什么是这样运动的
1.1.2 参考系、质点
一、质点的定义
一个只有质量而没有形状和大小的几何点 二、实际物体可视为质点的条件 当物体的形状和大小对运动没有影响或其影 响可以忽略的情况下,该物体就可以当成质点
在无限短时间内速度增量与时间的比
dvx d x ax dt dt 2 dv y d 2 y 2 a y dt dt dvz d 2 z 2 az dt dt
1.2.5其他物理量 角位移 角速度 角加速度
1)角位置
2)角位移
Q(t t )
三、实际物体可视为多个或无限多个质点的组合
实际物体总是由原子、分子组成的,若将每 个原子或分子看成质点,物体就可以认为是由多个 质点组成的。
1.1.3 参考系
一、参照系的定义 为了描写物体的运动而选作为参考的 物体或没有相对运动的物体群,叫参照系 (或参考系) 二、运动描述的相对性
1.1.4 坐标系
大小: 方向余弦:
r r x2 y2 z2
x y z cos ;cos ;cos r r r
三、运动方程(t ) j z (t )k 质点位置随时间的变化关系
x x(t ) 分量形式 : y y (t ) z z (t )
一、定义 量化后的参照系 二、常用的坐标系
Y Z Y
o o X X
平面直角坐标系
三维直角坐标系
2、自然坐标系 自然坐标系是以质点运动轨迹的切向和法 向作为坐标轴的方向建立的坐标系。由于随着质 点的运动,不同时刻质点所在位置处轨迹的切向 和法向是不同的,因此自然坐标系是活动坐标系。 它随质点运动而变化。
一、定义
一段时间内速度的增量与时间的比。
二、速度增量的概念
在考察的时间段内,质点末时刻的速度(简称为末速度) 与初时刻的速度(简称为初速度)的矢量差叫做速度增量。
三、平均加速度
v a t
四、瞬时加速度
2 v dv d r a lim 2 t 0 t dt dt 2
第一章 质点运动学(一)
梁鸿东 物理与电子工程学院
◆ 学习目标
理解参考系和坐标系的概念
参考系和坐标系、质点
掌握位移、瞬时速度和瞬时加速度概念;
位置矢量和位移矢量、瞬时速度和瞬时加速度
掌握已知加速度和初始条件求解速度、运动方程的 方法; 理解角速度、角加速度及其与线量的关系;
角位移、角速度和角加速度、线量与角量间的关系
v
表示
二、数学计算公式 r v 1、平均速度 t r dr v lim 2、瞬时速度: t 0 t dt 3、速度的分量形式
三、速度的方向 沿着轨道的切向,且 指向前进的一侧。 四、速率 质点所走过的路程与 时间的比 。 速率等于速度矢量的 大小
1.2.4 加速度矢量
