2002高教社杯全国大学生数学建模竞赛
高教社杯全国大学生数学建模竞赛B题论文

碎纸片的拼接复原摘要本文利用Manhattan距离,聚类分析,图像处理等方法解决了碎纸片的拼接复原问题。
由于碎纸机产生的碎纸片是边缘规则且等大的矩形,此时碎纸片拼接方法就不能利用碎片边缘的尖角特征等基于边界几何特征的拼接方法,而要利用碎片内的字迹断线或碎片内的文字位置搜索与之匹配的相邻碎纸片。
拼接碎片前利用数学软件MATLAB软件对碎片图像进行数据化处理,得到对应的像素矩阵,后设置阈值对像素矩阵进行二值化处理,得到相应的0-1矩阵。
下面分别对三个问题的解决方法和算法实现做简单的阐述:问题一,分别对附件1和附件2的碎片数据进行处理得到相应的0-1矩阵,依次计算某个0-1矩阵最右边一列组成向量与其他所有0-1矩阵的最左边向量的Manhattan距离,可以得到某个最小距离值、说明最小距离值对应的碎片是可与基准碎片拼接的,最终得到碎片拼接完整的图像。
问题二,同样对于附件3和附件4中的碎片数据进行处理得到相应的数值矩阵,并计算得到每个碎片顶部空白高度和文字高度,即指每行像素点都为255的行数、一行中存在像素点为非255的行数,根据空白高度和文字高度对碎片进行聚类分类,聚类阀值取3像素,得到11组像素矩阵,进而得到11类可能在同一行的碎片类。
其中对附件4中的英文的处理中,我们还采用水平像素投影累积的方法,进一步分类出可能在同一行的碎片类。
用问题一的方法,计算Manhattan 距离可以对每一类碎片按次序排列好,得到11行已经排列好的碎片,再应用曼哈顿距离在竖直方向上进行聚合得到完整的图像。
问题三,首先,对于附件5中的碎片数据我们采用正反相接,本文将b面最左边的一列像素拼接到a面最右边的一列像素的下面,构成360×1的向量,再把其他的碎片采用相同的办法得到360×1的向量,再用问题一的方法,计算出各碎片之间的Manhattan距离。
其次,根据每个碎片顶部的空白高度或者文字高度对碎片进行区间分类,得到22组矩阵,然后应用曼哈顿距离将得到的22组矩阵聚成两类,每类各包含两面的11组矩阵,最后利用Manhattan距离在竖直方向上进行聚合得到完整的图像。
高教社杯数学建模竞赛时间

高教社杯数学建模竞赛时间1.引言1.1 概述数学建模竞赛一直是高等教育领域中备受关注和重视的一项活动。
作为培养学生综合素养和创新能力的重要环节,数学建模竞赛在培养学生解决实际问题的能力和思维方式上起着至关重要的作用。
高教社杯数学建模竞赛作为国内一项具有广泛影响力的竞赛,每年吸引了大量的学生和教师参与其中。
在竞赛中,参赛者需要通过三天的考试,在规定的时间内解决给定的实际问题,并完成相应的模型构建和分析。
这不仅考验了参赛者的数学基础知识和技巧,更需要他们具备良好的逻辑思维和创新意识。
此外,高教社杯数学建模竞赛着重于培养学生的团队协作精神和沟通能力,每个团队都需要合理分工和紧密配合,才能在有限的时间内完成任务。
这种团队合作的模式既能增进同学们之间的交流与合作,也能培养他们解决实际问题的能力。
在这个竞赛中取得优异成绩的学生不仅仅只是获得了荣誉和奖励,更重要的是他们通过竞赛的经历锻炼了自己的思维和动手能力,提高了解决实际问题的能力。
这对于他们未来的学习和工作都具有重要的意义。
因此,本文将对高教社杯数学建模竞赛的时间安排进行详细的探讨和分析。
通过对竞赛的背景、规则以及竞赛效果的评价等方面的介绍,旨在帮助读者更好地了解和认识这一竞赛,并对未来的竞赛发展提出一些建设性的意见和建议。
文章结构部分的内容示例:1.2 文章结构本文主要分为三个部分,即引言、正文和结论。
引言部分首先对文章的主题进行概述,介绍高教社杯数学建模竞赛的背景和重要性。
然后对本文的结构进行说明,明确各个部分的目的和内容安排。
最后,介绍本文的目的,即通过对竞赛时间的分析和评价,总结竞赛效果,并对未来竞赛的发展提出展望。
正文部分将详细介绍高教社杯数学建模竞赛的背景,包括竞赛的发起机构、目的和历史背景,以及竞赛在数学教育领域的重要作用。
接着,对竞赛规则进行详细说明,包括竞赛的参与条件、题目类型和评分标准等内容。
同时,还会探讨竞赛规则对参赛者和教育机构的影响,以及竞赛规则的改进空间和挑战。
历年全国大学生数学建模竞赛成绩

本科
贵州赛区三等奖
宋琴刘兵向程波
教练组
专科
贵州赛区三等奖
柏玉顺周春艳朱志群
教练组
本科
成功参赛奖
杨国源陈娟钱冬梅
教练组
本科
成功参赛奖
罗永国胡忠贤陈超
教练组
教练组
本科
云贵赛区三等奖
陈军、吴德宪、刘江
教练组
本科
云贵赛区三等奖
施婧、夏万阳、赵庆福
教练组
专科
云贵赛区三等奖
朱红、朱志群、曾加敏
教练组
本科
云贵赛区成功参赛奖
熊进、李志能、李秀琴
教练组
本科
云贵赛区成功参赛奖
何强、张祥、钱东梅
教练组
本科
云贵赛区成功参赛奖
吴昊、汪山志、李松
教练组
2007年9月
本科
全国二等奖
历年全国大学生数学建模竞赛成绩
年份
级别
奖项
获奖人
指导教师
2000年9月
大专
贵州赛区一等奖
杨振钦苏文英先艳
教练组
大专
贵州赛区二等奖
林艺颜平张丽荣
教练组
本科
贵州赛区成功参赛奖
杜永新韩立书陈闯
教练组
2001年9月
大专
全国二等奖
李扬陈媛刘览
李伟
大专
贵州赛区一等奖
何曼妮朱有国张军
左建军丁虹
大专
贵州赛区一等奖
张静龙新聂瞬林
安育成
专科
贵州赛二等奖
吴、勾廷远、梅桂森
安育成
专科
贵州赛二等奖
周芳琴、胡连海、宗彦
安育成
2006年9月
本科
全国大学生数学建模竞赛题选

全国大学生数学建模竞赛题选2001年C题基金使用计划某校基金会有一笔数额为M元的基金,打算将其存入银行或购买国库券。
当前银行存款及各期国库券的利率见下表。
假设国库券每年至少发行一次,发行时间不定。
取款政策参考银行的现行政策。
校基金会计划在n年内每年用部分本息奖励优秀师生,要求每年的奖金额大致相同,且在n年末仍保留原基金数额。
校基金会希望获得最佳的基金使用计划,以提高每年的奖金额。
请你帮助校基金会在如下情况下设计基金使用方案,并对M=5000万元,n=10年给出具体结果:1.只存款不购国库券;2.可存款也可购国库券。
3.学校在基金到位后的第3年要举行百年校庆,基金会希望这一年的奖金比其2003年C 题2002年5月1日,“武汉国际抢渡长江挑战赛”在江城隆重举行,参赛的国内外选手共186人。
虽然选手中专业人员将近一半,但仅34人到达终点。
与此形成鲜明对比的是,于1934年9月9日在武汉首次举办的横渡长江游泳竞赛,参赛的44人中,却有40人到达终点。
究其原因,关键在于游泳者能否根据自己的速度,合理地选择游泳方向。
假设竞渡区域两岸为平行线,它们之间的垂直距离为1160米,从起点正对岸到终点的距离为1000米,见图1。
具体问题如下:1. 假定在竞渡过程中游泳者的速度大小和方向不变,水流速度为1.89米/秒。
已知第一名的成绩为14分8秒,求她游泳的路线,游泳速度的大小和方向;已知一游泳者速度大小为1.5米/秒,求他的游泳方向并估计他的成绩。
2. 在(1)的假设下,如果游泳者始终以和岸边垂直的方向游, 他(她)们能否到达终点?根据你们的数学模型说明为什么1934年 和2002年能游到终点的人数的百分比有如此大的差别;给出能够成功到达终点的选手的条件。
图1. 渡江示意图3. 若流速沿离岸边距离的分布为 (设从武昌汉阳门垂直向上为 y 轴正向) :⎪⎩⎪⎨⎧≤≤<<≤≤=米米秒,米米米秒,米米米秒,米1160960/47.1960200/11.22000/47.1)(0y y y y v游泳者的速度大小(1.5米/秒)仍全程保持不变,试为他选择游泳方向和路线,估计他的成绩。
中国大学生数学建模竞赛发展史
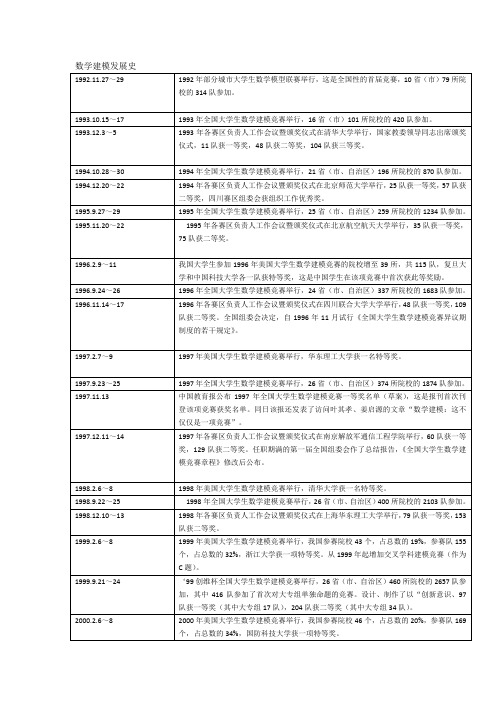
2000网易杯全国大学生数学建模竞赛举行,27省(市、自治区)517所院校的3210队参加,其中608队参加大专组竞赛,香港城市大学有1个队首次参赛
2000.12.6~8
2000年各赛区负责人工作会议暨颁奖仪式在中山大学珠海校区举行,119队获一等奖(其中大专组23队),245队获二等奖(其中大专组55队)。
1998年全国大学生数学建模竞赛举行,26省(市、自治区)400所院校的2103队参加。
1998.12.10~13
1998年各赛区负责人工作会议暨颁奖仪式在上海华东理工大学举行,79队获一等奖,153队获二等奖。
1999.2.6~8
1999年美国大学生数学建模竞赛举行,我国参赛院校43个,占总数的19%,参赛队155个,占总数的32%,浙江大学获一项特等奖。从1999年起增加交叉学科建模竞赛(作为C题)。
2003.2
2003年美国大学生数学建模竞赛(MCM)和交叉学科竞赛(ICM)举行,我国共参加300队,占总数的47%,浙江大学、北京大学、东南大学、东华大学各一队获特等奖。
2003.9.22~25
2003高教社杯全国大学生数学建模竞赛举行,30省(市、自治区)637所院校的5406队参加。
2003.12.6~7
2003年各赛区工作会议暨颁奖仪式在厦门举行,厦门大学承办,608队获全国奖,其中本科组一等奖151队,二等奖306队,大专组一等奖48队,二等奖103队。
2004.2
2004年美国大学生数学建模竞赛(MCM)和交叉学科竞赛(ICM)举行,我国共参加398队,占总数的54%,成都电子科技大学一队获特等奖。
数学建模发展史
1992.11.27~29
1992年部分城市大学生数学模型联赛举行,这是全国性的首届竞赛,10省(市)79所院校的314队参加。
2002高教社杯全国大学生数学建模竞赛获奖名单

北京师范大学
郭沁苗廖丹徐海英
指导小组
74
北京师范大学
杨唯张庆辉李朝瑞
指导小组
75
北京邮电大学
赵乃峰徐清爽张鹏
罗守山
76
北京邮电大学
吴云峰郭群峰郭晶
贺祖国
77
北京邮电大学
洪珺王玮李武军
贺祖国
78
北京邮电大学
欧阳坚王莹刘莉莉
贺祖国
79
北京邮电大学
王天琦梁宇鹏张深秋
贺祖国
80
北京邮电大学
朱晓暄黄蔚蓝杨晓光
113
解放军信息工程大学
王琳李立群田园
指导教师组
114
解放军信息工程大学
邢赛鹏兰明敬王冕
指导教师组
115
解放军炮兵学院
黄琪汪金华陈虎
数模教练组
116
解放军炮兵学院
黎明曦王伦夫李智华
数模教练组
117
解放军蚌埠坦克学院
杜国红侯进国陈志东
杨生武
118
解放军理工大学
洪梅王益柏陈维
教练组
二等奖274名(排名以学校笔划为序)
四川师范大学
李志江 付 宇 吴 倩
孙峪怀
89
四川师范大学
王益青 冯向东 李 妍
赵 凌
90
四川师范大学
高 尉 张武梅 郭秀红
杨 春
91
四川师范学院
文志平 周 军 郭小林
陈豫眉
92
四川轻化工学院
刘自山 万帮睿 周 畅
冯家竹
93
宁波大学
祝成林大成朱张广
数模组
94
甘肃工业大学
袁强徐波夏培
刘树群等
2002年全国大学生数学建模竞赛

2002年全国大学生数学建模竞赛及第六届大学生电子设计竞赛总结2002年高教社杯全国大学生数学建模竞赛和山东省第六届大学生电子设计竞赛在教育部高教司、中国工业与应用数学学会和省教育厅的正确领导下,在各高校教务处和广大学生的积极参与下,各项工作圆满完成并达到了预期的目标。
一、基本情况在年初的2001年全国大学生数学建模、电子设计竞赛山东赛区表彰会上,教育厅副厅长刘向信对开展这两项有意义的活动给予了充分肯定,对进一步培养学生创新精神和动手能力做了重要指示。
教育厅高教处每年从省组委会的建设到评审专家的遴选聘用,从竞赛经费的支持到教学研究立项、教学成果的评选,从指导教师培训到优胜队的推荐,从教学工作会议的动员到颁奖会的总结,事事处处都严格要求、一丝不苟,做到热心指导、大力帮助。
各高校也在政策和经费上向大学生竞赛倾斜,如山东大学去年和今年就投入25万元建设数学建模创新实验室,投入40万元建设电子设计创新实验室,中国海洋大学、济南大学、山东科技大学、曲阜师范大学、山东建工学院、山东电专等高校都投入20万元—30万元的经费建设数学或电子实验室。
今年参加全国大学生数学建模竞赛的学校有25所,有142支代表队参赛。
海军潜艇学院、中国煤炭经济学院、山东农业大学、聊城大学等4所院校首次参赛,参赛学校比去年增加了20%,参赛队数比去年增加了30%,获得全国一等奖2项、全国二等奖13项,并有40多个队获得赛区奖,收到了较好的效果。
在大家的共同努力下,山东赛区在继去年获得全国大学生电子设计竞赛优秀组织奖后,今年又获得了全国大学生数学建模竞赛优秀组织奖。
今年在广州周立功单片机发展有限公司的支持下,我们举办了第六届大学生电子设计竞赛,组织形式和竞赛要求与全国竞赛完全相同,赛题从9道应征试题中挑选并完善了6道,参赛学校有17所,有86支代表队参赛。
今年海军潜艇学院和山东交通学院首次参赛,参赛代表队也比去年增加了20%,收到了较好的效果。
2002高教社杯全国大学生数学建模竞赛

2002高教社杯全国大学生数学建模竞赛A 题 车灯线光源的优化设计 参考答案注意:以下答案是命题人给出的,仅供参考。
各评阅组应根据对题目的理解及学生的解答,自主地进行评阅。
一. 假设和简化 (略)二. 模型的建立建立坐标系如下图,记线光源长度为l ,功率为W ,B,C 点的光强度分别为)(l h B W 和)(l h C W ,先求)(l h B 和)(l h C 的表达式,再建立整个问题的数学模型.以下均以毫米为单位,由所给信息不难求出车灯反射面方程为6022y x z +=,焦点坐标为(0,0,15)。
1) 位于点P(0,w,15)的单位能量的点光源反射到点C(0, 2600, 25015)的能量设反射点的坐标为Q )60,,(22y x y x +.记入射向量为a ,该点反射面外法线方向为b ,不难得到反射向量c满足.22b bba a c ⋅-= 记222y x r +=,由)1,30/,30/(),1560,,(2-=--=y x b r w y x a从而得),,(z y x c c c c =的表达式)900(6081000036001800900)9002(90022242222++-+=+--=+=r wy r r c r r y w c r xyw c z y x注意到反射光通过C 点,应有60/25015,2600,2r kc y kc x kc z y x -=-=-=其中k 为常数. 从上述第一式可解得0=x 或wyr k 29002+-=.由此得反射点坐标满足以下两组方程:⎪⎩⎪⎨⎧--±=-=⎪⎩⎪⎨=--++-+++-223459005200)2600(133750.021060000001350810000)8100009360000()46800001498200(1800)2600(y y x w w y w y w y w y y w y通过计算可知,存在56.10-≈C w ,当Cw w 0>时第一组方程不存在满足2236≤r 的实根,即无反射点. 而当C w w 0<时,有两个反射点2,1),60/,,0(2=i y y Q i i i .而第二组方程仅当5609.18119.3-<<-w 时存在满足2236≤r 的一对实根,即有两个反射点),60,,(22y x y x +±记为43,Q Q . 若反射点的坐标为),,(z y x Q ,则位于点)15,,0(w P 的单位能量点光源经Q 点反射到C点的能量密度(单位面积的能量, 正比于光强度)为 24cos PQL πβ=其中2222)1560/()(-+-+=r w y x PQ而β为反射向量与z 轴的夹角,.60/25015cos 2QCr -=β2))(),(l h l h C B 的表达式长l 的具有单位能量的线光源位于点)15,,0(w P 的长dw 的微小线光源段反射到C 点的能量密度为 ,/)()(41l w f w E i i ∑==其中⎪⎩⎪⎨⎧=--∉--∈=⎪⎩⎪⎨⎧=-∉-∈=4,3,]5609.1,8119.3[,0]5609.1,8119.3[,4cos )(2,1,],30[,0],2/[,4cos )(20002i w w PQ w f i w w w l w PQ w f iii C Ci i i πβπβ长l 的具有单位能量的线光源反射到C 点的能量密度为 .)()(2/2/⎰-=l l C dw w E l h类似可得)(l h B 的表达式.相应的反射点方程为⎪⎩⎪⎨⎧--±=-=⎪⎩⎪⎨=--++-+++-223459002600)1300(137500.010530000001350810000)8100004680000()23400001498200(1800)1300(y y x w w y w y w y w y y w y相应的,78.00-≈Bw 而第二组方程的有两个反射点的范围为].7800005.0,906.1[--∈w3) 优化设计的数学模型设线光源的功率为W , 则它反射到B 点和C 点的能量密度分别为W l h B ⋅)(和W l h C ⋅)(.问题的数学模型为:⎪⎩⎪⎨⎧≥≥≤≤1)(2)(..min 00W l h W l h t s W C B l l三. 模型的求解)(),(l h l h C B 可以用数值积分求得. )(l h B 应具备下列性质:⎪⎩⎪⎨⎧≤<↓≤≤↑=<<=0''0,,20,0)(l l l l l l w l l l h B BB BB B 其中B l 为起亮值,'B l 为最大值点,0l 为考察的最大范围,例如取为20mm 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2002高教社杯全国大学生数学建模竞赛
A 题 车灯线光源的优化设计 参考答案
注意:以下答案是命题人给出的,仅供参考。
各评阅组应根据对题目的理解及学生的解答,自主地进行评阅。
一. 假设和简化 (略)
二. 模型的建立
建立坐标系如下图,记线光源长度为l ,功率为W ,B,C 点的光强度分别为)(l h B W 和
)(l h C W ,先求)(l h B 和)(l h C 的表达式,再建立整个问题的数学模型.
以下均以毫米为单位,由所给信息不难求出车灯反射面方程为60
2
2y x z +=,焦点坐标为
(0,0,15)。
1) 位于点P(0,w,15)的单位能量的点光源反射到点C(0, 2600, 25015)的能量
设反射点的坐标为Q )60,
,(2
2y x y x +.记入射向量为a ,该点反射面外法线方向为b ,不难得到反射向量c
满足
.22b b
b
a a c ⋅-= 记2
22y x r +=,由
)
1,30/,30/(),
1560,,(2-=--=y x b r w y x a
从而得),,(z y x c c c c =
的表达式
)
900(6081000036001800900
)
9002(900
22242
222
++-+=
+--=+=r wy r r c r r y w c r xyw c z y x
注意到反射光通过C 点,应有
60
/25015,
2600,
2r kc y kc x kc z y x -=-=-=
其中k 为常数. 从上述第一式可解得0=x 或wy
r k 2900
2+-=.由此得反射点坐标满足以下两
组方程:
⎪⎩
⎪⎨
⎧
--±=-=⎪⎩⎪⎨
=--++-+++-223459005200)2600(133750.021060000001350810000
)8100009360000()46800001498200(1800)2600(y y x w w y w y w y w y y w y
通过计算可知,存在56.10-≈C w ,当C
w w 0
>时第一组方程不存在满足2236≤r 的实根,即无反射点. 而当C w w 0<时,有两个反射点2,1),60/,,0(2=i y y Q i i i .
而第二组方程仅当5609.18119.3-<<-w 时存在满足2
236≤r 的一对实根,即有两
个反射点),60
,
,(2
2y x y x +±记为43,Q Q . 若反射点的坐标为),,(z y x Q ,则位于点)15,,0(w P 的单位能量点光源经Q 点反射到C
点的能量密度(单位面积的能量, 正比于光强度)为 2
4cos PQ
L πβ=
其中
2222)1560/()(-+-+=
r w y x PQ
而β为反射向量与z 轴的夹角,
.60
/25015cos 2QC
r -=β
2))(),(l h l h C B 的表达式
长l 的具有单位能量的线光源位于点)15,,0(w P 的长dw 的微小线光源段反射到C 点的能量密度为 ,/)()(4
1
l w f w E i i ∑==
其中
⎪⎩
⎪
⎨⎧=--∉--∈=⎪⎩⎪⎨⎧=-∉-∈=4
,3,]5609.1,8119.3[,0]5609.1,8119.3[,4cos )(2
,1,],30[,0],2/[,4cos )(20002
i w w PQ w f i w w w l w PQ w f i
i
i C C
i i i πβπβ
长l 的具有单位能量的线光源反射到C 点的能量密度为 .)()(2
/2
/⎰-=
l l C dw w E l h
类似可得)(l h B 的表达式.相应的反射点方程为
⎪⎩
⎪⎨
⎧
--±=-=⎪⎩⎪⎨
=--++-+++-223459002600)1300(137500.010530000001350810000
)8100004680000()23400001498200(1800)1300(y y x w w y w y w y w y y w y
相应的,78.00-≈B
w 而第二组方程的有两个反射点的范围为].7800005
.0,906.1[--∈w
3) 优化设计的数学模型
设线光源的功率为W , 则它反射到B 点和C 点的能量密度分别为W l h B ⋅)(和W l h C ⋅)(.问题的数学模型为:
⎪⎩
⎪⎨⎧≥≥≤≤1
)(2)(.
.min 0
0W l h W l h t s W C B l l
三. 模型的求解
)(),(l h l h C B 可以用数值积分求得. )(l h B 应具备下列性质:
⎪⎩
⎪⎨⎧≤<↓≤≤↑=<<=0
''
0,,20,0)(l l l l l l w l l l h B B
B B
B B 其中B l 为起亮值,'
B l 为最大值点,0l 为考察的最大范围,例如取为20mm 。
)(l h
C 也有类似的
性质,且起亮值和最大值点均相应地右移.数值求解)(2)(l h l h C B =,记其解为*l l =,再求出
'',C B l l ,不难看出'
'C
B l l <且*l 落在),(''
C B l l 之中。
令)(/2)(/1***l h l h w B C ==现证*w 为问题之最优值。
事实上,对可行域中任一),(w l ,
当,*l l ≥有,)(/2)(/2**w l h H l h H w B B =>≥(用到*l l ≥时↓B h )。
当*l l <,有**)(/)(/w l h H l h H w C C =>≥,(用到*l l <时↑c h )。
这就证明了*w 的确是最小值。
事实上数值结果为62.3,22.6,16.3*'
'
≈≈≈l l l C B .
四. 反射光亮区的计算
分别将线光源和车灯反射面离散化为点光源和面元的集合,计算每一点光源关于每一车灯反射面元的反射光线,判断其是否与车灯反射面相交,若相交,一次反射光不能到达测试屏,否则求出该反射光线与反射屏平面的交点,即为反射亮点。
所有这些亮点的集合即为反射光亮区。
亮区的上半部分由下图所示(横坐标为x 轴,纵坐标为y 轴,单位为mm),下半部分与上半部分是关于x 轴对称的.
五. 注记
(1) 计算))(( ),(l h l h C B 的另一方法是建立问题的数值模型用数值模拟的方法加以解决.具体的做法是: 在得到反射光线和反射到测试屏上能量的数学模型后, 分别将线光源和车灯反射面离散化为点光源和面元的集合,在测试屏B(或C)点附近取一微小面元.计算每一点光源关于每一车灯反射面元的反射光线,将所有能到达该面元的反射光线的反射能量迭加起来,除以面元的面积即为B(或C)点的反射能量密度.
但用这样的方法必须十分注意结果的检验,注意计算精度(必须考察线光源和反射面的剖分密度和测试屏B(或C)点附近小面元的取法等).
(2) 以上参考答案中没有考虑线光源本身对反射光线的遮挡问题,即假设线光源是透明的。
如果假设线光源是不透明的,似乎更符合现实。
此时需要考虑线光源本身对反射光线的遮挡,计算会更复杂些,计算结果也会有所不同。
