九年级数学上册(人教版)配套精品教学课件 23.2.1 中心对称
合集下载
九年级数学人教版上册23.2.1中心对称课件(共19张PPT)

(2)以BC边的中点为对称中心。 九年级数学 上册
相等 在△AOB与△ A′ O B′中 (1)PA与PA′的数量关系是__。 区别:中心对称的旋转角度都是180°,一般的旋转的旋转角度不固定,中心对称是特殊的旋转.
例1(4) 已知四边形ABCD和点O,画四边形A′B′C′D′,使它与已知四边形关于这一点对称。
九年级数学 上册
旋转概念: 把一个平面图形绕着平面内某一点O 转动一个角 度,叫做图形的旋转.这个定点O 叫旋转中心,转 动的角叫做旋转角.
如果图形上的点P经过旋转变为点P′,那么这两个点 P和P′叫做这个旋转的对应点.
A
F
E
B
O
C
D 轴对称
轴对称是指, 把一个图形沿着某一条直线折叠能与另一个图 形完全重合,那么就说这两个图形关于这条直线对称或轴对称.
在两个图形上。
C
A
B
对称中心:点A
D
对称点:点B和点D 点C和点E
E
了解中心对称的概念
问题1 如图,线段 AC,BD 相交于点 O,OA=OC,OB=OD.把 △OCD 绕
点 O 旋转 180°,你有什么发现?
两个图案能够完全重合在一起.
问题2
(1)图形中旋转中心是哪一点?
(点 O)
A
D
(2)旋转的角度是多少?
问题1 如图,线段 AC,BD 相交于点 O,OA=OC,OB=OD.把 △OCD 绕点 O 旋转 180°,你有什么发现?
中心对称的作图 九年级数学 上册
对称点:点B和点D 点C和点E
(1)关于中心对称的两个图形,对称点连线都经过对称中心,并且被对称中心平分。 点B和点D 九年级数学 上册 联系:中心对称和一般的旋转都是绕着某一点进行旋转;
相等 在△AOB与△ A′ O B′中 (1)PA与PA′的数量关系是__。 区别:中心对称的旋转角度都是180°,一般的旋转的旋转角度不固定,中心对称是特殊的旋转.
例1(4) 已知四边形ABCD和点O,画四边形A′B′C′D′,使它与已知四边形关于这一点对称。
九年级数学 上册
旋转概念: 把一个平面图形绕着平面内某一点O 转动一个角 度,叫做图形的旋转.这个定点O 叫旋转中心,转 动的角叫做旋转角.
如果图形上的点P经过旋转变为点P′,那么这两个点 P和P′叫做这个旋转的对应点.
A
F
E
B
O
C
D 轴对称
轴对称是指, 把一个图形沿着某一条直线折叠能与另一个图 形完全重合,那么就说这两个图形关于这条直线对称或轴对称.
在两个图形上。
C
A
B
对称中心:点A
D
对称点:点B和点D 点C和点E
E
了解中心对称的概念
问题1 如图,线段 AC,BD 相交于点 O,OA=OC,OB=OD.把 △OCD 绕
点 O 旋转 180°,你有什么发现?
两个图案能够完全重合在一起.
问题2
(1)图形中旋转中心是哪一点?
(点 O)
A
D
(2)旋转的角度是多少?
问题1 如图,线段 AC,BD 相交于点 O,OA=OC,OB=OD.把 △OCD 绕点 O 旋转 180°,你有什么发现?
中心对称的作图 九年级数学 上册
对称点:点B和点D 点C和点E
(1)关于中心对称的两个图形,对称点连线都经过对称中心,并且被对称中心平分。 点B和点D 九年级数学 上册 联系:中心对称和一般的旋转都是绕着某一点进行旋转;
上册中心对称人教版九年级数学全一册完美课件

上册 23.2.1 中心对称-2020秋人教版九年级数学全 一册课 件(共2 3张PPT )
(2)如答图②,画出其中一个即可. 第 8 题答图②
上册 23.2.1 中心对称-2020秋人教版九年级数学全 一册课 件(共2 3张PPT )
上册 23.2.1 中心对称-2020秋人教版九年级数学全 一册课 件(共2 3张PPT )
①∠BAC=∠B1A1C1;②AC=A1C1;③OA=OA1;
④△ABC 与△A1B1C1 的面积相等.
其中正确的有( D )
A.1 个
B.2 个
C.3 个
D.4 个
图23-2-2
上册 23.2.1 中心对称-2020秋人教版九年级数学全 一册课 件(共2 3张PPT )
上册 23.2.1 中心对称-2020秋人教版九年级数学全 一册课 件(共2 3张PPT )
上册 23.2.1 中心对称-2020秋人教版九年级数学全 一册课 件(共2 3张PPT )
图 23-2-6
上册 23.2.1 中心对称-2020秋人教版九年级数学全 一册课 件(共2 3张PPT )
解:(1)如答图①所示,△A1B1C 是所求的三角形.
第 8题 答 图 ① 上册 23.2.1 中心对称-2020秋人教版九年级数学全 一册课 件(共2 3张PPT )
23.2 中心对称 23.2.1 中心对称
1.下列的每组数中,两个数字成中心对称的是( D )
A
B
C
D
2.下列英语缩写中,是中心对称的是( A )
A.SOS
B.JAL
C.CNC
D.SAR
上册 23.2.1 中心对称-2020秋人教版九年级数学全 一册课 件(共2 3张PPT )
九年级上册数学23.2.1-中心对称ppt课件

先下 提示:圆的中心对称性 后下
趣味题2:如图,有一组数排列成方阵,试计算这 组数的和.
12345 23456 34567 45678 56789
10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10
答案: 25×10÷2=125
当堂练习
1.判断正误: (1)轴对称的两个图形一定是全等形,但全等的两
个图形不一定是轴对称的图形.( √ ) (2)成中心对称的两个图形一定是全等形.但全等
的两个图形不一定是成中心对称的图形. ( √ ) (3)全等的两个图形,不是成中心对称的图形,就
是成轴对称的图形. ( × )
2.如下所示的4组图形中,左边数字与右边数字成中心 对称的有( D )
2.同理,可作出点B,C,D的对应点B',C',D';
3.顺次连接A',B',C',D',则四边形A'B'C'D'即为所作.
C D
B' A'
O
D'
A
B
C'
考考你:如图,已知△ABC与△A′B′C′中心对称,找出 它们的对称中心O.
C
B A
A′ B′
C′
解法1:根据观察,B、B′应是对应点,连接BB′,用 刻度尺找出BB′的中点O,则点O即为所求(如图).
Miss White : What can you do , John ? John : I can ( do some Kung fu ).
A. sing English songs
B. do some Kung fu
趣味题2:如图,有一组数排列成方阵,试计算这 组数的和.
12345 23456 34567 45678 56789
10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10
答案: 25×10÷2=125
当堂练习
1.判断正误: (1)轴对称的两个图形一定是全等形,但全等的两
个图形不一定是轴对称的图形.( √ ) (2)成中心对称的两个图形一定是全等形.但全等
的两个图形不一定是成中心对称的图形. ( √ ) (3)全等的两个图形,不是成中心对称的图形,就
是成轴对称的图形. ( × )
2.如下所示的4组图形中,左边数字与右边数字成中心 对称的有( D )
2.同理,可作出点B,C,D的对应点B',C',D';
3.顺次连接A',B',C',D',则四边形A'B'C'D'即为所作.
C D
B' A'
O
D'
A
B
C'
考考你:如图,已知△ABC与△A′B′C′中心对称,找出 它们的对称中心O.
C
B A
A′ B′
C′
解法1:根据观察,B、B′应是对应点,连接BB′,用 刻度尺找出BB′的中点O,则点O即为所求(如图).
Miss White : What can you do , John ? John : I can ( do some Kung fu ).
A. sing English songs
B. do some Kung fu
新人教版初中数学九年级上册《中心对称》优质教学课件

O
图1
引入新知
问题1 (2)如图2,线段AC,BD相交于点O,OA=OC, OB=OD.把△OCD绕点O逆时针(或顺时针)方向旋 转180°,你有什么发现?
A
D
B
O
C 图2
引入新知
问题2 你能说说上述两个旋转的 共同点吗?
180°
O
图1
A
180°
D
B
O
C
图2
引入新知
180°
问题2
你能说说上述两个旋转的
复习回顾
• 旋转的性质: 旋转前、后的图形全等.
A
B C
A'
O
C'
B'
复习回顾
• 旋转的作图: 明确旋转中心; 明确旋转方向; 明确旋转角度.
A
B C
A'
O
C'
B'
引入新知
问题1 (1)如图1,把其中一个图案绕点O逆时针方向 旋转180°,你有什么发现?
O
图1
引入新知
问题1 (1)如图1,把其中一个图案绕点O逆时针方向 旋转180°,你有什么发现?若是顺时针方向旋转 180°呢?
巩固落实
法1:如图15,连接AD,取AD的中点O, 则点O即为所求.
F
E
A
O
D
B
C
图图1511
巩固落实
法2:如图16,连接AD、CF相交于点O, 则点O即为所求.
F
A O
B
C
图图1126
E D
巩固落实
练习
如图17,△ABC与△A'B'C'关于某一个点成
中心对称,点 A,B的对称点分别为点A'和B'.
图1
引入新知
问题1 (2)如图2,线段AC,BD相交于点O,OA=OC, OB=OD.把△OCD绕点O逆时针(或顺时针)方向旋 转180°,你有什么发现?
A
D
B
O
C 图2
引入新知
问题2 你能说说上述两个旋转的 共同点吗?
180°
O
图1
A
180°
D
B
O
C
图2
引入新知
180°
问题2
你能说说上述两个旋转的
复习回顾
• 旋转的性质: 旋转前、后的图形全等.
A
B C
A'
O
C'
B'
复习回顾
• 旋转的作图: 明确旋转中心; 明确旋转方向; 明确旋转角度.
A
B C
A'
O
C'
B'
引入新知
问题1 (1)如图1,把其中一个图案绕点O逆时针方向 旋转180°,你有什么发现?
O
图1
引入新知
问题1 (1)如图1,把其中一个图案绕点O逆时针方向 旋转180°,你有什么发现?若是顺时针方向旋转 180°呢?
巩固落实
法1:如图15,连接AD,取AD的中点O, 则点O即为所求.
F
E
A
O
D
B
C
图图1511
巩固落实
法2:如图16,连接AD、CF相交于点O, 则点O即为所求.
F
A O
B
C
图图1126
E D
巩固落实
练习
如图17,△ABC与△A'B'C'关于某一个点成
中心对称,点 A,B的对称点分别为点A'和B'.
人教版九年级数学上册 23.2.1 中心对称 教学课件(共38张PPT)
N
F
B
B.
M
A
O
G
CA
C
E
D
D
6. 画△A′B′C′,使△A′B′C′和△ABC关于点O 成中心对称。
A
C′
B′
O
B
C
A′ △A′B′C′即为所求的三角形。
拓展资料 中心对称的应用
广告商标
工艺品(如:地毯、挂毯)
电扇的扇叶
车轮
齿轮
风车
课堂小结
1. 中心对称与轴对称的区别和联系?
轴对称
有一条对称轴——直线
图形沿对称轴对折 (翻折180°)后重合
对称点的连线被 对称轴垂直平分
中心对称
有一个对称中心——点
图形绕对称中心旋 转180°后重合
对称点连线经过对称中 心,且被对称中心平分
2. 中心对称的两条基本性质:
(1)关于中心对称的两个图形,对应点所 连线都经过对称中心,而且被对称中心所平 分。
(2)关于中心对称的两个图形是全等图形 及其它们的应用。
教学目标
【知识与能力】
了解中心对称、对称中心、关于中心的对称 点等概念。 通过具体实例认识两个图形关于某一点成中 心对称的本质:就是一个图形绕一点旋转180° 而成。 作出中心对称的图形。
【过程与方法】
利用中心对称的特征作出某一图形成中心对称 的图形,确定对称中心的位置。 培养学生独立思考、自学能力。 培养学生通过体验、感受中心对称的概念和性 质,培养学生的概括能力和动手能力。 通过对中心对称概念的概括和性质的探索和应 用培养学生的探索能力和空间想象能力。
8. 矩形ABCD中,AB=3,BC=4,若将矩 形折叠,使C点和A点重合,求折痕EF的长。
F
B
B.
M
A
O
G
CA
C
E
D
D
6. 画△A′B′C′,使△A′B′C′和△ABC关于点O 成中心对称。
A
C′
B′
O
B
C
A′ △A′B′C′即为所求的三角形。
拓展资料 中心对称的应用
广告商标
工艺品(如:地毯、挂毯)
电扇的扇叶
车轮
齿轮
风车
课堂小结
1. 中心对称与轴对称的区别和联系?
轴对称
有一条对称轴——直线
图形沿对称轴对折 (翻折180°)后重合
对称点的连线被 对称轴垂直平分
中心对称
有一个对称中心——点
图形绕对称中心旋 转180°后重合
对称点连线经过对称中 心,且被对称中心平分
2. 中心对称的两条基本性质:
(1)关于中心对称的两个图形,对应点所 连线都经过对称中心,而且被对称中心所平 分。
(2)关于中心对称的两个图形是全等图形 及其它们的应用。
教学目标
【知识与能力】
了解中心对称、对称中心、关于中心的对称 点等概念。 通过具体实例认识两个图形关于某一点成中 心对称的本质:就是一个图形绕一点旋转180° 而成。 作出中心对称的图形。
【过程与方法】
利用中心对称的特征作出某一图形成中心对称 的图形,确定对称中心的位置。 培养学生独立思考、自学能力。 培养学生通过体验、感受中心对称的概念和性 质,培养学生的概括能力和动手能力。 通过对中心对称概念的概括和性质的探索和应 用培养学生的探索能力和空间想象能力。
8. 矩形ABCD中,AB=3,BC=4,若将矩 形折叠,使C点和A点重合,求折痕EF的长。
人教版九年级数学上册课件:23.2中心对称--2.1中心对称(共28张PPT)

19
知识点三:中心对称作图
典例讲评
(1)如图①,选择点O为对称中 心,画出点A关于点O的对称点A;
解:(1)如图①,连接AO,在AO的延 长线上截取OA′=OA,即可以求得点 A关于点O的对称点A′.
O A′ A
①
20
知识点三:中心对称作图
典例讲评
C
(2)如图②,选择点O为对称中
A
B′ A′
心,画出与△ABC关于点O对称的
B ②O
△A′B′C′.
解:(2)如图②,作出A,B,C三
C′
点关于点O的对称点A′,B′,C′, 作已知图形关于某一
依次连接A′B′,B′C′,C′A′,就可 点对称的图形,其作图步
得到与△ABC关于点O对称的 △A′B′C′.
骤简记为:连接、延长、 截取相等线段、连点成图.
21
知识点三:中心对称作图
而且被 对称中心 所平分。 2.关于中心对称的两个图形是 全等形 。
B
∵∆ABC和∆A′B′C′关于点O成中心对称 A ∴OA=OA′,OB=OB′,OC=OC′
∆ABC ∆A′B′C′
C
O C′
A′
B′
11
知识点二:中心对称的性质
归纳总结
(1)因为中心对称是一种特殊的旋 转变换,所以具备旋转的一切性 质. (2)成中心对称的两个图形,其对 应线段互相平行(或在同一条直 线上)且相等.
15
知识点二:中心对称的性质
学以致用
2.如图,在平面直角坐标系中,点
P(1,1),N(2,0),△MNP和△M1N1P1 的顶点都在格点上,△MNP与 △M1N1P1关于某一点成中心对称, 则对称中心的坐标为 (2,1) .
知识点三:中心对称作图
典例讲评
(1)如图①,选择点O为对称中 心,画出点A关于点O的对称点A;
解:(1)如图①,连接AO,在AO的延 长线上截取OA′=OA,即可以求得点 A关于点O的对称点A′.
O A′ A
①
20
知识点三:中心对称作图
典例讲评
C
(2)如图②,选择点O为对称中
A
B′ A′
心,画出与△ABC关于点O对称的
B ②O
△A′B′C′.
解:(2)如图②,作出A,B,C三
C′
点关于点O的对称点A′,B′,C′, 作已知图形关于某一
依次连接A′B′,B′C′,C′A′,就可 点对称的图形,其作图步
得到与△ABC关于点O对称的 △A′B′C′.
骤简记为:连接、延长、 截取相等线段、连点成图.
21
知识点三:中心对称作图
而且被 对称中心 所平分。 2.关于中心对称的两个图形是 全等形 。
B
∵∆ABC和∆A′B′C′关于点O成中心对称 A ∴OA=OA′,OB=OB′,OC=OC′
∆ABC ∆A′B′C′
C
O C′
A′
B′
11
知识点二:中心对称的性质
归纳总结
(1)因为中心对称是一种特殊的旋 转变换,所以具备旋转的一切性 质. (2)成中心对称的两个图形,其对 应线段互相平行(或在同一条直 线上)且相等.
15
知识点二:中心对称的性质
学以致用
2.如图,在平面直角坐标系中,点
P(1,1),N(2,0),△MNP和△M1N1P1 的顶点都在格点上,△MNP与 △M1N1P1关于某一点成中心对称, 则对称中心的坐标为 (2,1) .
人教版九年级数学上册23.2.1中心对称(22张PPT)

中心D的对称点为C(B′)
(B′) C
A′
D
(2)连结A′B′、A′C′.
则△A′B′C′为所求作的三角形, 如图所示.
B (C′)
三检测
1、找出下列图形的对称中心
2、怎样判别两个图形关于某一点成中心对 称呢?如果两个图形的对应点连成的线段
都经 过某一点,并且被该点平分,那 么这两个图形一定关于这一点成中心对 称。
发现: 两个图案重合; △OCD与△OAB 重合
A
D
O
B
23.2-2
C
像这样,把一个图形绕某一个点旋转180º,如果 它能够与另一个图形重合,那么就说这两个图形关 于这个点对称或中心对称;这个点叫做对称中心;
这两个图形中的对应点叫做关于中心的对称点 例如: 图23.2-2中△OCD和△OAB关于点0对称, 点C与点A是关于点O的对称点。
布置作业
教科书第 66 页,练习 1,2 题.
说说你在本节课的收获
(1) 关于中心对称的两个图形,对称点所连 线段都经过对称中心,而且被对称中心所平 分;
(2) 关于中心对称的两个图形是全等图形.
(1) 画一个点关于某点(对称中心)的对称点 的画法是先连接这个点与对称中心并延长一倍即 可。
(2) 画一个图形关于某点的对称图形的画法 是先画出图形中的几个特殊点(如多边形的顶点、 线段的端点,圆的圆心等)关于某点的对称点, 然后再顺次连结有关对称点即可。
形呢?
例1: 如图,选择点O为对称中心,画出点A 关于点O的对称点A′;
A
O
A′
●
●
●
连接AO, OA = OA′
在AO的延长线上截取OA
′即=O可A求得点A关于点O的对称
人教版九年级上册数学 23.2.1 中心对称教学课件(共22张PPT)

You have to believe in yourself. That's the secret of success. 人必须相信自己,这是成功的秘诀。
探究 旋转三角板,画关于点O对称的两个三角形:
第一步,画出△ABC;
第二步,以三角板的一个顶点O为中心,把三角板旋 转180°,画出△A′B′C′;
9、要学生做的事,教职员躬亲共做;要学生学的知识,教职员躬亲共学;要学生守的规则,教职员躬亲共守。21.8.2421.8.24Tuesday, August 24, 2021 10、阅读一切好书如同和过去最杰出的人谈话。20:27:1520:27:1520:278/24/2021 8:27:15 PM
16、教学的目的是培养学生自己学习,自己研究,用自己的头脑来想,用自己的眼睛看,用自己的手来做这种精神。2021年8月24日星期二8时27分15秒20:27:1524 August 2021 17、儿童是中心,教育的措施便围绕他们而组织起来。下午8时27分15秒下午8时27分20:27:1521.8.24
新人教版数学九年级 上册
第二十三章 旋 转
23.2.1 中心对称
复习引入,回忆知识
1、旋转的三要素:_旋__转_中__心__,旋__转_方__向__, _旋__转_角__。
2、时钟的指针在不停地转动,从12:00 到12:10,分针旋转了多少度?
—从中1心这2:对是称一00。种到特1殊2:的旋30转呢—?
A D
B
.O
C
(1)
A
B
.
o
E D
C
(2)
你知道吗?
2、图中的两个四边形关于某点对称,找出它 们的对称中心。
中考链接: 1.(2015.贵港)下列各组图形中,成中心对
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
√)
(2)成中心对称的两个图形一定是全等形.但全等的 两个图形不一定是成中心对称的图形. ( √ ) (3)全等的两个图形,不是成中心对称的图形,就是 成轴对称的图形. ( ×)
2.如下所示的4组图形中,左边数字与右边数字成中心对称的有
(D )
A.1组
B.2组
C.3组
D.4组
3.如图,已知△AOB与△DOC成中心对称,△AOB的面积 是6,AB=3,则△DOC中CD边上的高是( B ) A.2 C.6 B.4 D.8 A C O B D
C
D
O
B
填一填:
A
O 是对称 如图,△OCD与△OAB关于点O中心对称 ,则____ 中心,点A与_____ C 是对称点, 点B与____ D 是对称点.
归纳总结
1.中心对称是一种特殊的旋转.特殊在其旋转角是180 °. 2.中心对称是两个图形之间一种特殊的位置关系.
二 探究中心对称的性质
如图,旋转三角尺,画出△ABC关于点O中心对称的△A′B′C′ .
(3)如图,选择点O为对称中心,画出与△ABC关于点O
对称的△A′B′C′. C
A B O A′
B′
△A′B′C′为所求作的三角形
C′
考考你
如图,已知△ABC与△A′B′C′中心对称,找出它们的对称中
心O. C B′ B A C′ A′
解法1:根据观察,B、B′应是对应点,连接BB′,用刻度尺找出
4.如图,已知等边三角形ABC和点O,画△A′B′C′,使△A′B′C′和
△ABC关于点O成中心对称.
A
C′ O
B
B′
C
A′
课堂小结
概念
旋转角是180°
中心对称
性质
1.对称中心与两对称点三点共线; 2.成中心对称的两个图形是全等形
作图
应用1:作中心对称图形; 应用2:找出对称中心.
课后作业
见《学练优》本课时练习
三 性质应用
典例精析
例1 (1)已知A点和O点,画出点A关于点O的对称点A'. O A A' 第一步:连接AO, 第二步:延长AO至A',使OA'=OA, 则A'是所求的点.
(2)已知线段AB和O点,画出线段AB关于点O的对称线段A' B' .
B'
A
O
A' B 简记为:一连接;二延长;三截取等长;四连线 .
导入新课
观察与思考
1.从A旋转到B,旋转中心 D 是?旋转角是多少度呢?
C
B
2.从A旋转到C呢?
o
A 3.从A旋转到D呢?
讲授新课
一 中心对称的概念
C
O D 重 合
O
重 合
B
A 像这样,把一个图形绕某一个点旋转180º,如果它能够与另一个 图形重合,那么就说这两个图形关于这个点对称或中心对称;这个 点叫做对称中心;这两个图形中的对应点叫做关于中心的对称点.
配套精品教学课件/人教版
九年级数学(上)
授课老师:XX XX XX 授课日期:201X.XX.XX
九年级数学上册(人教版) 配套精品教学课件
第二十三章 旋转
23.2 中心对称
23.2.1 中心对称
导入新课 讲授新课 当堂练习 课堂小结
学习目标
1.理解中心对称的定义. 2.探究中心对称的性质.(难点) 3.掌握中心对称的性质及其应用.(重点)
BB′的中点O,则点O即为所求(如图).
C O B A C′ B′
A′
解法2:根据观察,B、B′及C、C′应是两组对应点,连接BB′、 CC′,BB′、CC′相交于点O,则点O即为所求(如图).
C O B′ B A′
A
C′
注意:如果限制只用直尺作图,我们用解法2.
四 中心对称与轴对称的区别与联系
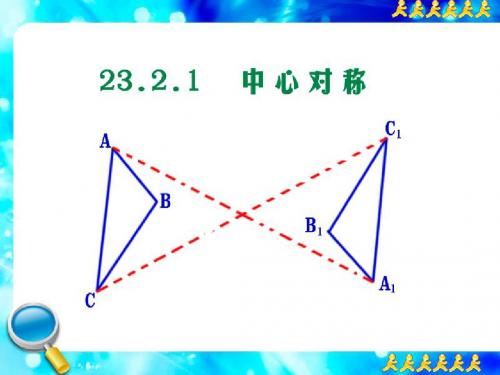
A O B C 中心对称
C1
B1
A1
轴 对 1 2
称
有一条对称轴 ——直线 图形沿轴对折(翻转 180° ) 翻转后和另一个图形重合
有一个对称中心 ——点
图形绕中心旋转 180° 旋转后和另一个图形重合
3
当堂练习
1.判断正误: (1)轴对称的两个图形一定是全等形,但全等的两个
图形不一定是轴对称的图形.(
C A B
O B′ C′
●
A′
找一找: 下图中△A′B′C′与△ABC关于点O是成中心对称,你能
从图中找到哪些等量关系?
(1) OA=OA′、OB=OB′、 OC=OC′ (2)△ABC≌△A′B′C′
归纳总结
中心对称的性质 1.中心对称的两个图形,对称点所连线段经过对称中 心,而且被对称中心所平分. (即对称点与对称中心三点共线) 2.中心对称的两个图形是全等形.
配套精品教学课件/人教版
九年级数学(上)
授课老师:XX XX XX 授课日期:201X.XX.XX
