【精】2020学年四川省南充市白塔中学高二上学期期中数学试卷和解析(理科)
四川省南充市高坪区白塔中学2019_2020学年高二数学上学期期中试题文(含解析)

四川省南充市高坪区白塔中学2019-2020学年高二数学上学期期中试题 文(含解析)第Ⅰ卷(选择题共60分)一、选择题:(共12小题,每小题5分,共60分.在每个小题给出的四个选项中,只有一项是符合题目要求的一项).1.直线12,l l 方程分别为3420,220x y x y +-=++=,直线12,l l 倾斜角分别为12,αα,则( )A. 12αα>B. 12αα<C. 12αα=D. 不确定 【答案】A【解析】【分析】求出两条直线的斜率后可得它们的倾斜角的大小.【详解】直线1l 的斜率为134k =-,直线2l 的斜率为22k =-, 故13tan 4α=-,2tan 2α=-,因为21tan tan 0αα<<, 故212a παπ<<<,故选A.【点睛】对于直线方程()00Ax By C B ++=≠,其斜率为A k B =-,注意直线的倾斜角α与斜率的关系为:(1)当0,,22ππαπ⎡⎫⎛⎫∈⎪ ⎪⎢⎣⎭⎝⎭ 时,tan k α=;(2)当2πα=时,斜率不存在.2.我市修建经济适用房.已知我市顺庆、高坪、嘉陵三个区分别有低收入家庭360户、270户、180户,若首批经济适用房中有90套住房用于解决住房紧张问题,采用分层抽样的方法决定各区户数,则应从顺庆区中抽取低收入家庭的户数为( )A. 40B. 36C. 30D. 20 【答案】A【解析】【分析】先求出每个个体被抽到的概率,用顺庆区的低收入家庭数量乘以每个个体被抽到的概率,即得应从顺庆区中抽取低收入家庭的户数.【详解】顺庆、高坪、嘉陵三个区分别有低收入家庭360户、270户、180户,∴对应的户数比为:360:270:1804:3:2=,则应从顺庆区中抽取低收入家庭的户数为44909040 4329⨯=⨯=++.故选:A.【点睛】本题考查分层抽样的定义,属于基础题.3.执行所示程序后输出的结果是:A. -1B. 0C. 1D. 2 【答案】B【解析】当n=5,S=0时,满足进入循环的条件,执行完循环体后,S=5,n=4;当n=4,S=5时,满足进入循环的条件,执行完循环体后,S=9,n=3;当n=3,S=9时,满足进入循环的条件,执行完循环体后,S=12,n=2;当n=2,S=12时,满足进入循环条件,执行完循环体后,S=14,n=1;当n=1,S=14时,满足进入循环的条件,执行完循环体后,S=15,n=0;当n=0,S=15时,不满足进入循环的条件,退出循环体后,输出n=0故选B.4.阅读如图所示的程序框图,运行相应的程序,输出的i值等于A. 2B. 3C. 4D. 5【答案】C【解析】【详解】根据框图的循环结构依次可得:1=⨯===+=;a S i122,2,1122=⨯==+==+=;a S i228,2810,2133=⨯==+==+=,3224,102434,314a S ii=.故C正确.跳出循环,输出4【易错点晴】本题主要考查的是程序框图,属于容易题.解题时一定要抓住重要条件S>”,否则很容易出现错误.在给出程序框图求解输出结果的试题中只要按照程序“11框图规定的运算方法逐次计算,直到达到输出条件即可.5.某篮球队甲、乙两名运动员练习罚球,每人练习10组,每组罚球40个.命中个数的茎叶图如下图,则下面结论中错误..的一个是()A. 甲的极差是29B. 甲的中位数是24C. 甲罚球命中率比乙高D. 乙的众数是21【答案】B【解析】【分析】通过茎叶图找出甲的最大值及最小值求出极差判断出A 对;找出甲中间的两个数,求出这两个数的平均数即数据的中位数,判断出D 错;根据图的数据分布,判断出甲的平均值比乙的平均值大,判断出C 对.【详解】由茎叶图知甲的最大值为37,最小值为8,所以甲的极差为29,故A 对甲中间的两个数为22,24,所以甲的中位数为2224232+=故B 不对 甲的命中个数集中在20而乙的命中个数集中在10和20,所以甲的平均数大,故C 对 乙的数据中出现次数最多的是21,所以D 对故选:B .【点睛】茎叶图的优点是保留了原始数据,便于记录及表示,能反映数据在各段上的分布情况.茎叶图不能直接反映总体的分布情况,这就需要通过茎叶图给出的数据求出数据的数字特征,进一步估计总体情况.6.设点B 是点()2,3,5A -关于平面xOy 的对称点,则AB 等于( )B. 10 D. 38 【答案】B【解析】【分析】利用空间中的两个点关于xOy 平面对称时的坐标关系可求B 的坐标,再利用两点之间的距离公式可求AB .【详解】因为点B 是点()2,3,5A -关于平面xOy 的对称点,故()2,3,5B --,故10AB ==, 故选B.【点睛】本题考查空间中关于坐标平面对称的点的坐标关系,此类问题属于基础题.7.圆22(4)9x y -+=和圆22(3)4x y +-=的公切线有( )A. 1条B. 2条C. 3条D. 4条【答案】C【解析】【分析】 求出两圆的圆心和半径,根据两圆的圆心距小于半径之和,可得两圆相交,由此可得两圆的公切线的条数.【详解】解答:圆22(4)9x y -+=,表示以()4,0为圆心,半径等于3的圆。
四川省2020年高二上学期期中数学试卷(理科)A卷(精编)

四川省2020年高二上学期期中数学试卷(理科)A卷姓名:________ 班级:________ 成绩:________一、选择题 (共12题;共24分)1. (2分)过与轴的交点,且倾斜角等于该直线倾斜角一半的直线方程为()A .B .C .D .2. (2分)直线与圆有两个不同交点的一个充分不必要条件是()A .B .C .D .3. (2分) (2016高二上·绍兴期中) 水平放置的△ABC的直观图如图,其中B′O′=C′O′=1,A′O′= ,那么原△ABC是一个()A . 等边三角形B . 直角三角形C . 三边中只有两边相等的等腰三角形D . 三边互不相等的三角形4. (2分)两直线 - =1与 - =1的图象可能是图中的哪一个()A .B .C .D .5. (2分)空间四边形ABCD的各顶点坐标分别是, E,F分别是AB与CD的中点,则EF的长为()A .B .C .D . 36. (2分)下列四个结论:⑴两条不同的直线都和同一个平面平行,则这两条直线平行.⑵两条不同的直线没有公共点,则这两条直线平行.⑶两条不同直线都和第三条直线垂直,则这两条直线平行.⑷一条直线和一个平面内无数条直线没有公共点,则这条直线和这个平面平行.其中正确的个数为()A . 0B . 1C . 2D . 37. (2分) (2019高二上·大同月考) 过圆锥的高的两个三等分点作平行于底面的截面,它们把圆锥的侧面分成的三部分的面积之比为()A . 1﹕2﹕3B . 1﹕3﹕5C . 1﹕2﹕4D . 1﹕3﹕98. (2分)(2019·黄山模拟) 在《九章算术》中,将四个面都是直角三角形的四面体称为鳖膈,在鳖膈A-BCD 中,AB⊥平面BCD,BC⊥CD,且AB=BC=CD,M为AD的中点,则异面直线BM与CD夹角的余弦值为()A .B .C .D .9. (2分)规定表示两个数中的最小的数,若函数的图像关于直线对称,则的值是()A . -1B . 1C . 2D . -210. (2分)(2017·武邑模拟) 记曲线y= 与x轴所围成的区域为D,若曲线y=ax(x﹣2)(a <0)把D的面积均分为两等份,则a的值为()A . ﹣B . ﹣C . ﹣D . ﹣11. (2分) (2018高二下·四川期中) 到两坐标轴的距离相等的动点的轨迹方程是()A .B .C .D .12. (2分)(2019·宝安模拟) 某空间几何体的三视图如图所示,则该几何体的体积为()A . 1B . 2C . 4D . 8二、填空题 (共4题;共6分)13. (2分) (2016高二上·温州期中) 已知圆柱的底面直径和高都等于球的直径,则球的表面积与圆柱的表面积之比是________,球的体积与圆柱的体积之比是________14. (1分) (2016高二上·武城期中) 若⊙O1:x2+y2=5与⊙O2:(x﹣m)2+y2=20(m∈R)相交于A、B两点,且两圆在点A处的切线互相垂直,则线段AB的长度是________.15. (2分)已知直线l1:ax+2y+6=0,l2:x+(a﹣1)y+a2﹣1=0,若l1⊥l2 ,则a= ________ ,若l1∥l2 ,则l1与l2的距离为________16. (1分) (2019高一下·梅河口月考) 下列四个正方体图形中,,为正方体的两个顶点,,,分别为其所在的棱的中点,能得出平面的图形的序号是________三、解答题 (共6题;共60分)17. (15分) (2019高二上·德州月考) 如图,在正方体的棱长为,为棱的中点.(1)求四棱锥的体积(2)求证:面(3)求证:面面18. (5分)正方形中心为G(﹣1,0),一边所在直线的斜率为3,且此正方形的面积为14.4,求此正方形各边所在的直线方程.19. (10分)如图,在三棱柱ABC﹣A1B1C1中,已知AB⊥侧面BB1C1C,BC=1,CC1=2,BC1= .(1)求证:BC1⊥平面ABC;(2)当二面角A﹣CC1﹣B为时,求三棱柱ABC﹣A1B1C1的体积.20. (10分) (2020高一下·重庆期末) 已知圆,(1)求过点且被圆所截得的弦长为的直线的方程;(2)若为直线上的动点,且圆上存在两个不同的点到点的距离为2,求点的横坐标的取值范围.21. (10分) (2016高一上·西安期末) 在四棱锥P﹣ABCD中,底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC,E是PC的中点,过E点做EF⊥PB交PB于点F.求证:(1)PA∥平面DEB;(2)PB⊥平面DEF.22. (10分) (2017高二上·南通开学考) 已知圆C:x2+y2+2x-4y+3=0.(1)若圆C的切线在x轴、y轴上的截距相等,求切线的方程;(2)从圆C外一点P(x1 , y1)向圆引一条切线,切点为M,O为坐标原点,且有|PM|=|PO|,求使|PM|最小的点P的坐标.参考答案一、选择题 (共12题;共24分)1-1、2-1、3-1、4-1、5-1、6-1、7-1、8-1、9-1、10-1、11-1、12-1、二、填空题 (共4题;共6分)13-1、14-1、15-1、16-1、三、解答题 (共6题;共60分) 17-1、17-2、17-3、18-1、19-1、19-2、20-1、20-2、21-1、21-2、22-1、22-2、。
四川省南充市2020年高二上学期期中数学试卷(理科)(II)卷

四川省南充市 2020 年高二上学期期中数学试卷(理科)(II)卷姓名:________班级:________成绩:________一、 选择题 (共 12 题;共 24 分)1. (2 分) (2019 高二上·长春月考) 命题“∃ x∈Z,使 x2+2x+m≤0”的否定是( ) A . ∀ x∈Z,都有 x2+2x+m≤0B . ∃ x∈Z,使 x2+2x+m>0C . ∀ x∈Z,都有 x2+2x+m>0 D . 不存在 x∈Z,使 x2+2x+m>02. (2 分) (2015 高三上·潍坊期中) 已知命题 p:∀ x>1, 列命题为真命题的是( )x>0,命题 q:∃ x∈R,x3≥3x . 则下A . p∨qB . p∨(¬q)C . p∧(¬q)D . (¬p)∧q3. (2 分) (2016 高二上·黄陵期中) 下列命题中的假命题是( )A . ∃ x∈R,lg x=0B . ∃ x∈R,tan x=1C . ∀ x∈R,x3>0D . ∀ x∈R,2x>04. (2 分) 已知 是等比数列,前 n 项和为 ,,则 ( )A.第 1 页 共 11 页B. C. D.5. (2 分) (2016 高二下·黔南期末) 已知 F1、F2 分别是双曲线的左右焦点,A 为双曲线的右顶点,线段 AF2 的垂直平分线交双曲线与 P,且|PF1|=3|PF2|,则该双曲线的离心率是( )A.B.C.D. 6. (2 分) (2015 高二上·怀仁期末) 在等腰梯形 ABCD 中,AB∥CD,且|AB|=2,|AD|=1,|CD|=2x 其中 x∈ (0,1),以 A,B 为焦点且过点 D 的双曲线的离心率为 e1 , 以 C,D 为焦点且过点 A 的椭圆的离心率为 e2 , 若 对任意 x∈(0,1)不等式 t<e1+e2 恒成立,则 t 的最大值为( )A.B. C.2D.7. (2 分) 如图,已知双曲线 C: ﹣ =1(a>0,b>0)的右顶点为 A,O 为坐标原点,以 A 为圆心的圆 与双曲线 C 的某渐近线交于两点 P、Q,若∠PAQ=60°且 =3 , 则双曲线 C 的离心率为( )第 2 页 共 11 页A. B. C. D.8. (2 分) (2020·淮北模拟) 已知双曲线的右焦点为,点,为双曲线左支上的动点,且周长的最小值为 16,则双曲线的离心率为( )A.2B.C.D. 9. (2 分) 若抛物线 A . 0个 B . 1个 C . 2个 D . 4个的焦点是 F,准线是 L,则经过点 F、M(4,4)且与 l 相切的圆共有 ( )10. (2 分) (2017·湖北模拟) 已知 O 为坐标原点,双曲线第 3 页 共 11 页上有一点 P,过点 P 作两条渐近线的平行线,与两条渐近线的交点分别为 A,B,若平行四边形 PAOB 的面积为 1,则双曲线的离心率为( ) A.B.C.D. 11. (2 分) (2016 高二上·大庆期中) 下列说法中正确的是( ) A . 若| |=| |,则 、 的长度相同,方向相同或相反 B . 若向量 是向量 的相反向量,则| |=| | C . 空间向量的减法满足结合律 D . 在四边形 ABCD 中,一定有 + =12. (2 分) (2016·天津模拟) 已知双曲线=1(a,b>0)抛物线 y2=4x 共焦点,双曲线与抛物线的一公共点到抛物线准线的距离为 2,双曲线的离心率为 e,则 2e﹣b2 的值是( )A . +1B . 2 ﹣2C . 4﹣2 D.4二、 填空题 (共 4 题;共 4 分)13. (1 分) (2017 高二下·濮阳期末) 过抛物线 y2=2px(p>0)的焦点 F 作倾斜角为 30°的直线交抛物线 于 A、B 两点,若线段 AB 的长为 8,则 p=________.14. (1 分) 若命题“存在 x∈R,ax2+4x+a≤0”为假命题,则实数 a 的取值范围是________ 15. (1 分) 在抛物线 y2=2px 上,横坐标为 4 的点到焦点的距离为 5,则 p 的值为________第 4 页 共 11 页16. (1 分) (2016 高二上·临川期中) 已知椭圆的方程为 左焦点且斜率为 1 的直线与该椭圆相交与 A,B 两点,则三、 解答题 (共 6 题;共 60 分)17. (10 分) 解答题=1,其左右焦点分别为 F1 , F2 , 过其 =________.(1) 求经过点的 P( , ),Q(,1)的椭圆的标准方程;(2) 求与椭圆 + =1 有公共焦点,且离心率 e= 的双曲线的标准方程.18. (10 分) (2019 高二上·德惠期中) 命题 :方程有实数解,命题 :方程表示焦点在 轴上的椭圆.(1) 若命题 为真,求 的取值范围;(2) 若命题为真,求 的取值范围.19. (10 分) (2017·成安模拟) 曲线 C1 上任意一点 M 满足|MF1|+|MF2|=4,其中 F1(﹣ ,0),F2( , 0)抛物线 C2 的焦点是直线 y=x﹣1 与 x 轴的交点,顶点为原点 O.(1) 求 C1,C2 的标准方程;(2) 请问是否存在直线 l 满足条件:①过 C2 的焦点 F;②与 C1 交于不同两点 M,N,且满足 若存在,求出直线 l 的方程;若不存在,说明理由.⊥?20. (10 分) 已知向量 =(cosx,﹣1), =( sinx,﹣ ).(1) 当时,求的值;(2) 已知在锐角△ABC 中,a,b,c 分别为角 A,B,C 的对边, • ,求 f(B)的取值范围.c=2asin(A+B),函数 f(x)=( + )21. (10 分) (2019 高二上·唐山月考) 已知一动圆与圆 :内切.第 5 页 共 11 页外切,且与圆 :(1) 求动圆圆心 的轨迹方程 ;(2) 过点能否作一条直线 与 交于 , 两点,且点 是线段出直线 方程;若不存在,说明理由.的中点,若存在,求22. (10 分) (2017 高二上·阜宁月考) 如图,A、B 分别是椭圆 焦点,点 P 在椭圆上,且位于 x 轴上方,PA⊥PF.的左、右端点,F 是椭圆的右(1) 点 P 的坐标; (2) 设 M 是椭圆长轴 AB 上的一点,M 到直线 AP 的距离等于 MB,求椭圆上的点到点 M 的距离 d 的最小值.第 6 页 共 11 页一、 选择题 (共 12 题;共 24 分)1-1、 2-1、 3-1、 4-1、 5-1、 6-1、 7-1、 8-1、 9-1、 10-1、 11-1、 12-1、二、 填空题 (共 4 题;共 4 分)13-1、 14-1、 15-1、参考答案第 7 页 共 11 页16-1、三、 解答题 (共 6 题;共 60 分)17-1、17-2、 18-1、 18-2、第 8 页 共 11 页19-1、19-2、 20-1、第 9 页 共 11 页20-2、 21-1、 21-2、第 10 页 共 11 页22-1、22-2、第11 页共11 页。
2020-2021学年四川省南充高级中学高二上学期期中考试数学(理)试卷及答案

2020-2021学年四川省南充高级中学高二上学期期中考试数学(理)试卷★祝考试顺利★(含答案)(时间:120分钟 满分:150分)一、选择题(本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项 是符合题目要求的)1.若点()2,1A ,圆的一般方程为222410x y x y ++-+=,则点A 与圆位置关系( )A .圆外B .圆内且不是圆心C .圆上D .圆心2.直线250x y +-=的纵截距是( )A .5B .-5C .52-D .52- 3.已知数列{}n a 满足11a =,16n n a a +=+,在5a =( )A .25B .30C .32D .644.已知m n 、是不重合直线,αβγ、、是不重合平面,则下列说法①若αγβγ⊥⊥、,则α∥β ②m n αα⊥⊥、,则m ∥n③若α∥β、γ∥β,则γ∥α ④若m αββ⊥⊥、,则m ∥α正确的是A .①③B .②③C .①④D .②④5.设变量y ,x 满足约束条件⎩⎨⎧x +2y ≥2,2x +y ≤4,4x -y ≥-1,则目标函数y x z -3=的最大值是( ) A .-6 B .23 C .6 D .-326.如图,网格纸上小正方形的边长为1,粗实线画出的是某几何体的三视图,则该几何体的体积为( )A .36B .72C .108D .2167.若点()12--,A 在直线30mx ny ++=上,其中m n 、均为正数,则12m n+的最小值为 ( ) A .2 B .43 C .6D .838.在三棱锥A BCD -中,AB ⊥面,4,BCD AB AD BC CD ====,则三棱锥 A BCD -的外接球表面积是( )A . BC .5πD .20π 9.已知圆()221:(1)-39C x y ++=和222:-42-110C x y x y ++=,则这两个圆的公共弦长为( )A .125B .245C .95D .1510. ABC ∆中,内角C ,B ,A 的对边分别为,,,c b a 1,22cos ,a b a C ==sin C =, 则ABC ∆的面积为( )A. 2B. 4C. 2或4 211.已知直线()()():21110l k x k y k R ++++=∈与圆()()221225x y -+-=交于A ,B两点,则弦长AB 的取值范围是( )A .[]4,10B .[]3,5C .[]8,10D .[]6,1012. 四棱锥ABCD S -中,底面是边长为22的菱形 60∠=BAD ABCD ,,SA ⊥平面ABCD ,且SA =E 是边BC 的中点,动点P 在四棱锥ABCD S -表面上运动,并且总保持,AC PE ⊥则动点P 的轨迹周长为( )A .242+B .342+C .222+D .322+二、填空题(本大题共4小题,每小题5分,共20分,把答案填在题中横线上)13.已知一个圆柱的表面积等于侧面积的32,且其轴截面的周长为16,则该圆柱的体积为______.。
四川省绵阳市2020版高二上学期期中数学试卷(理科)(II)卷

四川省绵阳市2020版高二上学期期中数学试卷(理科)(II)卷姓名:________ 班级:________ 成绩:________一、选择题: (共12题;共24分)1. (2分)一个多面体的直观图、主视图、左视图、俯视图如下,、分别为、的中点.下列结论中正确的个数有()①直线与相交. ②. ③//平面.④三棱锥的体积为.A . 4个B . 3个C . 2个D . 1个2. (2分)在空间直角坐标系中,点关于x轴的对称点的坐标为()A .B .C .D .3. (2分)设A,B,C,D是空间不共面的四点,且满足,,,则△BCD 是()A . 钝角三角形B . 锐角三角形C . 直角三角形D . 不确定4. (2分)如果正方体的棱长为a,那么四面体的体积是()A .B .C .D .5. (2分)已知异面直线a与b所成角为锐角,下列结论不正确的是()A . 不存在一个平面α使得a⊂α,b⊂αB . 存在一个平面α使得a∥α,b∥αC . 不存在一个平面α使得a⊥α,b⊥αD . 存在一个平面α使得a∥α,b⊥α6. (2分) (2016高一下·武邑期中) 某几何体的三视图如图所示,则它的体积为()A . 8﹣B . 8﹣C . 8﹣2πD .7. (2分) (2016高二上·鞍山期中) 直三棱柱ABC﹣A1B1C1中,若∠BAC=90°,AB=AC=AA1 ,则异面直线BA1与AC1所成的角等于()A . 30°B . 45°C . 60°D . 90°8. (2分)已知一个几何体的正视图和俯视图如图所示,正视图是边长为2a的正三角形,俯视图是边长为a 的正六边形,则该几何体侧视图的面积为()A .B .C . 3D .9. (2分)圆锥的母线长为6,轴截面的顶角为120度,过两条母线作截面,则截面面积的最大值为()A . 9B . 18C . 18D . 910. (2分)已知三棱锥ABCD中,AB⊥CD,且AB与平面BCD成60°角.当的值取到最大值时,二面角A﹣CD﹣B的大小为()A . 30°B . 45°C . 60°D . 90°11. (2分)(2018·呼和浩特模拟) 已知球半径为,设是球面上四个点,其中,则棱锥的体积的最大值为()A .B .C .D .12. (2分)某四面体的三视图如图所示.该四面体的六条棱的长度中,最大的是()A .B .C .D .二、填空题: (共4题;共4分)13. (1分) (2017高二下·寿光期中) ∠AOB在平面α内,OC是平面α的一条斜线,若已知∠AOB=∠BOC=∠COA=60°,则OC与平面α所成的角的余弦值等于________.14. (1分) (2016高一下·南京期末) 正三棱柱ABC﹣A1B1C1的底面边长为2,高为3,点P为侧棱BB1上一点,则三棱锥A﹣CPC1的体积是________.15. (1分)在棱长为a的正方体ABCD﹣A1B1C1D1中,M是AB的中点,则点C到平面A1DM的距离为________.16. (1分)已知直二面角α﹣l﹣β,点A∈α,AC⊥l,C为垂足,点B∈β,BD⊥l,D为垂足.若AB=2,AC=BD=1,则CD=________三、解答题: (共6题;共40分)17. (10分) (2019高三上·上海月考) 如图,在所有棱长都等于2的正三棱柱中,点是的中点,求:(1)异面直线与所成角的大小;(2)直线与平面所成角的大小.18. (10分) (2016高二下·卢龙期末) 如图,在直三棱柱ABC﹣A1B1C1中,点D是BC的中点.(1)求证:A1B∥平面ADC1;(2)若AB⊥AC,AB=AC=1,AA1=2,求平面ADC1与ABA1所成二面角的正弦值.19. (5分)如图,AB是圆O的直径,点C在圆O上,矩形DCBE所在的平面垂直于圆O所在的平面,AB=4,BE=1.(1)证明:平面ADE⊥平面ACD;(2)当三棱锥C﹣ADE的体积最大时,求点C到平面ADE的距离.20. (5分)如图所示,在直四棱柱ABCD﹣A1B1C1D1中,DB=BC,DB⊥AC,点M是棱BB1上一点.(1)求证:B1D1∥面A1BD;(2)求证:MD⊥AC;(3)试确定点M的位置,使得平面DMC1⊥平面CC1D1D.21. (5分)如图,在四边形ABCD中,△ABC是边长为2的等边三角形,AD丄DC,AD=DC,E、F是平面ABCD 同一侧的两点,BE丄平面ABCD,DF丄平面ABCD,且DF=1.(Ⅰ)若AE丄CF,求BE的值;(Ⅱ)求当BE为何值时,二面角E﹣AC﹣F的大小是60°.22. (5分)已知E、F、G、H分别为空间四边形ABCD的边AB、BC、CD、DA上的点,且EE=2,EH=1,四边形EFGH为平行四边形.(Ⅰ)求证:EH∥BD;(Ⅱ)连结AC,若AC⊥BD,求FH的长度.参考答案一、选择题: (共12题;共24分)1-1、2-1、3-1、4-1、5-1、6-1、7-1、8-1、9-1、10-1、11-1、12-1、二、填空题: (共4题;共4分)13-1、14-1、15-1、16-1、三、解答题: (共6题;共40分) 17-1、17-2、18-1、18-2、19-1、20-1、21-1、22-1、。
四川省南充市白塔中学2019 2020高二数学上学期期中试题理
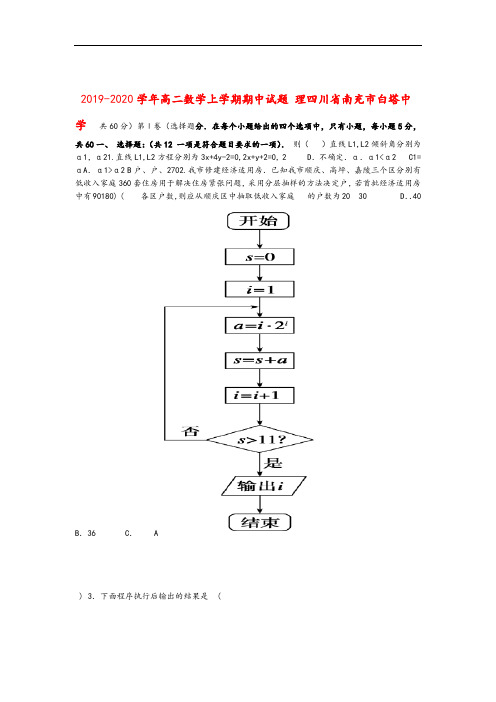
2019-2020学年高二数学上学期期中试题理四川省南充市白塔中学共60分)第Ⅰ卷(选择题分.在每个小题给出的四个选项中,只有小题,每小题5分,共60一、选择题:(共12 一项是符合题目要求的一项).则()直线L1,L2倾斜角分别为α1,α21.直线L1,L2方程分别为3x+4y-2=0,2x+y+2=0, 2 D.不确定.α.α1<α2 C1=αA.α1>α2 B户、户、2702.我市修建经济适用房.已知我市顺庆、高坪、嘉陵三个区分别有低收入家庭360套住房用于解决住房紧张问题,采用分层抽样的方法决定户,若首批经济适用房中有90180) ( 各区户数,则应从顺庆区中抽取低收入家庭的户数为20 30 D..40B.36 C. A) 3.下面程序执行后输出的结果是 (0 ..-1 B n=5 A 2.. S=01 D CWHILE S<15S=S+n n=n-1WEND PRINT nENDi) 值等于(4.阅读如右图所示的程序框图,运行相应的程序,则输出的54 D..3 C.A.2 B个.命中个数的茎叶40105.某篮球队甲、乙两名运动员练习罚球,每人练习组,每组罚球) 图如下图,则下面结论中错误的是(29 .甲的极差是A21 .乙的众数是B .甲罚球命中率比乙高C24.甲的中位数是D xOy( )等于的对称点,则B是点A(2,-3,5)关于平面|AB|6.设点381038 D. 10 C..A . B22)R?,(ab22OO1y???(xa1)(??2)?b4b?y?)ax(?()?,:.已知圆7,:21- 1 -那么两圆公切线的条数()A.0 B.1 C.2 D.38.从一批产品中取出三件产品,设A={三件产品全不是次品},B={三件产品全是次品},C= {三件产品至少有一件是次品},则下列结论正确的是()A.A与C互斥 B. A与B互为对立事件 C.B与C互斥 D.任何两个均互斥yx已知这组数据的平均,9.,105次上班途中所花的时间(单位:分钟)分别为,,119.某人yx) -的值为|数为10,方差为2,则|(4.2 C.3DA.1 B.10.已知过点A(-2,m)和B(m,4)的直线与直线2x+y-1=0平行,则m+6的值为()A.0 B.-8 C.-2 D.10?22,Mx?0?y???x?y??M,?所确定当约束条件M=311.时的平面区域内整点(横坐标纵坐标均为整?x?y?M.??数的点)的个数为(C )(A)9(B)13(C)16 (D)18l:x?4y?222C:x?y?1交于A、与圆B12..如图直线两点,O为坐标原点,若直线OA 、????cos?cos=( ) OB的倾斜角分别为,则、24D))17 ((B)13 ()(AC1717二、填空题:(共4小题,每小题5分,共20分).ABCDABCDAABD-则此动点在三棱锥中,13.在长方体-有一动点在此长方体内随机运动,11111内的概率为xy-2≤0-2??xy?+1≥0-zyxxy的最大值时最优解为.14.若=,满足约束条件3 +2,则??y≤022=4相切于A、B两点,则四边形xPBPA2x+y+10=015.P在直线上,、与圆+yPAOB面积的最小值为- 2 -????0B,?A10,1R?a0??:lax?y?1?0l:x?ay1,给出如已知直线,,,和两点,16.21下结论其中真命题的序号是all BA分别经过定点;①当和变化时, 与21all为何值时,都互相垂直;②不论与21MB?MA ll2M的最大值是交于点,则③如果;与21103PB?PA xy?2P为直线上的点,则④的最小值是.56小题,共70分。
四川省2020年高二上学期期中数学试卷(理科)(I)卷(精编)

四川省2020年高二上学期期中数学试卷(理科)(I)卷姓名:________ 班级:________ 成绩:________一、选择题 (共12题;共24分)1. (2分) (2016高二上·和平期中) 设Sn是等差数列{an}的前n项和,若a1+a3+a5=3,则S5=()A . 5B . 7C . 9D . 112. (2分)已知命题p:在△ABC中,“C>B”是“sinC>sinB”的充分不必要条件;命题q:“a>b”是“ac2>bc2”的充分不必要条件,则下列选项中正确的是()A . p真q假B . p假q真C . “”为假D . “”为真3. (2分)数列{an}满足a1=3,an+1=2an+3•2n+1 ,则an=()A . (3n﹣1)•2nB . (6n﹣3)•2n﹣1C . 3(2n﹣1)•2n+1D . (3n﹣2)•2n﹣14. (2分) (2017高二上·延安期末) 已知a>0,b>0,a+b=2,则的最小值是()A .B . 4C .D . 55. (2分) (2016高二上·和平期中) 已知正实数a,b满足a+2b=1,则的最小值为()A .B . 4C .D .6. (2分)(2017·石景山模拟) 如图,将正三角形ABC分割成m个边长为1的小正三角形和一个灰色菱形,这个灰色菱形可以分割成n个边长为1的小正三角形.若m:n=47:25,则三角形ABC的边长是()A . 10B . 11C . 12D . 137. (2分) (2016高二上·高青期中) 已知变量x,y满足约束条件,则目标函数z=ax+by(a >0,b>0)的最小值为2,则 + 的最小值为()A . 2B . 4C .D .8. (2分) (2019高二上·天河期末) 二面角为60°,A、B是棱上的两点,AC、BD分别在半平面内,,,且AB=AC=,BD=,则CD的长为()A .B .C .D .9. (2分) (2019高二上·吉林月考) 如图是由容量为100的样本得到的频率分布直方图.其中前4组的频率成等比数列,后6组的频数成等差数列,设最大频率为a,在到之间的数据个数为b,则a,b的值分别为()A . 0.27,78B . 0.27,83C . 2.7,78D . 2.7,8310. (2分) (2019高三上·佛山月考) 在△ABC中,角A,B,C的对边分别为a,b,c,且满足(b-a)sinA=(b-c)(sinB+sinC),则角C等于()A .B .C .D .11. (2分) (2016高一上·惠城期中) 函数y=lgx﹣的零点所在的大致区间是()A . (6,7)B . (7,8)C . (8,9)D . (9,10)12. (2分)已知函数f(x)的定义域为R,若存在常数m>0,对任意x∈R,有|f(x)|≤m|x|,则称函数f(x)为F﹣函数.给出下列函数:①f(x)=x2;②;③f(x)=2x;④f(x)=sin2x.其中是F﹣函数的序号为()A . ①②B . ①③C . ②④D . ③④二、填空题 (共4题;共4分)13. (1分)(2019·揭阳模拟) 已知数列满足,,则数列中最大项的值为________.14. (1分)若ABC中,AC=, A=45度,C=75度,则BC=________.15. (1分) (2016高二上·灌云期中) 不等式﹣x2+2x>0的解集是________.16. (1分)已知连续2n+1(n∈N*)个正整数总和为a,且这些数中后n个数的平方和与前n个数的平方和之差为b.若,则n的值为________三、解答题 (共6题;共45分)17. (5分) (2016高一下·宜昌期中) 已知 =(2cosx,sinx﹣cosx), =( sinx,sinx+cosx),记函数f(x)= • .(Ⅰ)求f(x)的表达式,以及f(x)取最大值时x的取值集合;(Ⅱ)设△ABC三内角A,B,C的对应边分别为a,b,c,若a+b=2 ,c= ,f(C)=2,求△ABC的面积.18. (10分) (2019高一上·辽宁月考) 已知函数().(1)证明的单调性;(2)若函数为奇函数,当时,恒成立,求实数的取值范围.19. (5分)(2017·济宁模拟) 已知数列{an}的前n项和Sn= (an﹣1),数列{bn}满足bn+2=2bn+1﹣bn ,且b6=a3 , b60=a5 ,其中n∈N*.(Ⅰ)求数列{an},{bn}的通项公式;(Ⅱ)若cn=(﹣1)nbnbn+1 ,求数列{cn}的前n项和Tn .20. (5分) (2016高一下·双流期中) 如图,某观测站在港口A的南偏西40°方向的C处,测得一船在距观测站31海里的B处,正沿着从港口出发的一条南偏东20°的航线上向港口A开去,当船走了20海里到达D处,此时观测站又测得CD等于21海里,问此时船离港口A处还有多远?21. (10分) (2019高二上·北京期中) 数列中,,对任意且有 .(1)设,证明:数列为等比数列,并求的通项公式.(2)求的前项和 .22. (10分) (2020高二下·莲湖期末) 已知.(1)当时,求不等式的解集;(2)当取得最小值为9时,求a的值,并求出此时的取值范围.参考答案一、选择题 (共12题;共24分)1-1、2-1、3-1、4-1、5-1、6-1、7-1、8-1、9-1、10-1、11-1、12-1、二、填空题 (共4题;共4分)13-1、14-1、15-1、16-1、三、解答题 (共6题;共45分) 17-1、18-1、18-2、19-1、20-1、21-1、21-2、22-1、22-2、。
四川省南充高中学年高二数学上学期期中考试(理) 人教版

南充高中2020学年高二上学期期中考试数学试题(理科)(考试时间:120分钟,)一、选择题(5×12)1.如果a<0,b>0,那么下列不等式中正确的是A、B、C、D、2.直线的倾斜角的大小为A、120°B、30°C、60°D、150°3.若A、B、) C、D、4.直线与直线互相垂直,则a的值为A、2B、C、D、5.若α、β满足,则的取值范围是A、B、C、D、6.已知,则A、B、C、D、7.设直线的方程为,则直线的倾斜角的范围是A、[0,B、C、D、8.设函数,若,则的取值范围是A、B、C、D、9.若点(4,a)到直线的距离不大于3,则a的取值范围是A、B、C、D、10.过点的直线与x轴正半轴、y轴正半轴分别交于A、B两点,则面积取最小时直线的方程为A、B、C、D、11.已知,A、B、C、D、12.当,不等式恒成立,则实数m的取值范围是A、B、C、D、二、填空题(4×4)13.已知则的最小值是。
14.设a、b、c为直角三角形的三边长,c为斜边,若点(m、n)在直线ax+by+2c=0上,则。
15.已知:实系数一元二次方程的两个根为,且,则的取值范围是。
(用区间表示)16.已知变量满足约束条件,则的取值范围是题号 1 2 3 4 5 6 7 8 9 10 11 12 答案、 14、、、19.(12分)设的顶点,内角的平分线所在直线方程为,AB边上的中线所在直线方程为;(1)求B点坐标;(2)求BC所在直线方程。
20.(12分)某工厂制造甲、乙两种产品,已知制造甲产品1kg要用煤 9吨,电力4kW,劳力(按工作日计算)3个;制造乙产品1kg要用煤4吨,电力5kW,劳力10个,又知制成甲产品1kg可获利7万元,制成乙产品1kg可获利12万元。
现在此工厂有煤360吨,电力200kW,劳力300个,在这种条件下应生产甲、乙两种产品各多少千克,才能获得最大经济效益?21.(12分)已知关于x的不等式的解集为A,且;(1)求实数a的取值范围;(2)求集合A。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2018-2019学年四川省南充市白塔中学高二(上)期中数学试卷(理科)一、选择题(本大题共12小题,每小题5分,共60分)1.(5分)在空间直角坐标系中,已知点Q(﹣3,1,4),则点Q关于xOz面的对称点的坐标为()A.(3,﹣1,﹣4) B.(﹣3,﹣1,﹣4)C.(3,1,4)D.(﹣3,﹣1,4)2.(5分)为了了解某社区居民是否准备收看奥运会开幕式,某记者分别从社区的60~70岁,40~50岁,20~30岁的三个年龄段中的160,240,X人中,采用分层抽样的方法共抽出了30人进行调查,若60~70岁这个年龄段中抽查了8人,那么x为()A.90 B.120 C.180 D.2003.(5分)已知直线l1的方程为3x+4y﹣7=0,直线l2的方程为6x+8y+1=0,则直线l1与l2的距离为()A.B.C.4 D.84.(5分)若某中学高二年级8个班参加合唱比赛的得分如茎叶图所示,则这组数据的中位数是()A.91.5 B.92.5 C.91 D.925.(5分)4张卡片上分别写有数字1,2,3,4,从这4张卡片中随机抽取2张,则取出的2张卡片上的数字之和为奇数的概率为()A.B.C.D.6.(5分)若变量x、y满足约束条件,则z=2x﹣y+1的最小值等于()A.﹣ B.﹣2 C.﹣ D.27.(5分)直线l过点A(3,4)且与点B(﹣3,2)的距离最远,那么l的方程为()A.3x﹣y﹣13=0 B.3x﹣y+13=0 C.3x+y﹣13=0 D.3x+y+13=08.(5分)运行如图的程序框图,设输出数据构成的集合为A,从集合A中任取一个元素a,则函数y=x a,x∈[0,+∞)是增函数的概率为()A.B.C.D.9.(5分)如图,直线y=ax﹣的图象可能是()A.B. C.D.10.(5分)样本数据:﹣2,﹣1,0,1,2的方差为()A.B.2 C.1 D.2.511.(5分)P在直线2x+y+10=0上,PA、PB与圆x2+y2=4相切于A、B两点,则四边形PAOB面积的最小值为()A.24 B.16 C.8 D.412.(5分)Rt△ABC中,斜边BC为4,以BC中点为圆心,作半径为1的圆,分别交BC于P、Q 两点,则|AP|2+|AQ|2+|PQ|2的值为()A.4+B.3+C.D.14二、填空题(本大题共4小题,每小题5分,共20分)13.(5分)把十进制数89(10)化为五进制数,则89(10)=(5).14.(5分)用辗转相除法求出153和119的最大公约数是.15.(5分)在棱长为3的正方体内任取一个点,则这个点到各面的距离都大于1的概率为.16.(5分)已知m∈R,则直线(m﹣1)x+(2m﹣1)y=m﹣4与圆x2+y2﹣10x+4y+20=0的位置关系为.三、解答题(本大题共6小题,满分70分,解答题写出必要的文字说明、推演步骤)17.(10分)已知直线l经过点A(﹣1,﹣3),且其倾斜角等于直线x﹣y=0的倾斜角的4倍.求直线l的方程并用一般式表示.18.(12分)某中学团委组织了“弘扬奥运精神,爱我中华”的知识竞赛,从参加考试的学生中抽出60名学生,将其成绩(均为整数)分成六段[40,50),[50,60),…,[90,100]后画出如下部分频率分布直方图.观察图形给出的信息,回答下列问题:(1)求第四小组的频率,并补全这个频率分布直方图;(2)估计这次考试的及格率(60分及以上为及格)和平均分;(3)从成绩是[40,50)和[90,100]的学生中选两人,求他们在同一分数段的概率.19.(12分)已知△ABC中,A(1,3),AB、AC边上的中线所在直线方程分别为x﹣2y+1=0和y ﹣1=0,求△ABC各边所在直线方程.20.(12分)已知坐标平面上点M(x,y)与两个定点M1(26,1),M2(2,1)的距离之比等于5.(1)求点M的轨迹方程,并说明轨迹是什么图形;(2)记(1)中的轨迹为C,过点A(﹣2,3)的直线l被C所截得的线段的长为8,求直线l的方程.21.(12分)已知P(﹣2,﹣3)和以Q为圆心的圆(x﹣4)2+(y﹣2)2=9.(1)求出以PQ为直径的圆Q1的一般式方程.(2)若圆Q和圆Q1交于A、B两点,直线PA、PB是以Q为圆心的圆的切线吗?为什么?(3)求直线AB的方程.22.(12分)有定点P(6,4)及定直线l:y=4x,Q是l上在第一象限内的点.PQ交x轴的正半轴于M点,问点Q在什么位置时,△OMQ的面积最小,并求出最小值.2018-2019学年四川省南充市白塔中学高二(上)期中数学试卷(理科)参考答案与试题解析一、选择题(本大题共12小题,每小题5分,共60分)1.(5分)在空间直角坐标系中,已知点Q(﹣3,1,4),则点Q关于xOz面的对称点的坐标为()A.(3,﹣1,﹣4) B.(﹣3,﹣1,﹣4)C.(3,1,4)D.(﹣3,﹣1,4)【解答】解:根据空间直角坐标系中,点关于坐标面对称的特点知点关于那一个面对称,则面上所包含的两个字母的符号不变,不包含的那个字母对应的数字要变,∴Q(﹣3,1,4),关于xoz面的对称点坐标(﹣3,﹣1,4)故选:D.2.(5分)为了了解某社区居民是否准备收看奥运会开幕式,某记者分别从社区的60~70岁,40~50岁,20~30岁的三个年龄段中的160,240,X人中,采用分层抽样的方法共抽出了30人进行调查,若60~70岁这个年龄段中抽查了8人,那么x为()A.90 B.120 C.180 D.200【解答】解:60~70岁,40~50岁,20~30岁的三个年龄段中的160,240,X人中可以抽取30人,每个个体被抽到的概率等于:,∵在60~70岁这个年龄段中抽查了8人,可知×160=8,解得x=200,故选:D.3.(5分)已知直线l1的方程为3x+4y﹣7=0,直线l2的方程为6x+8y+1=0,则直线l1与l2的距离为()A.B.C.4 D.8【解答】解:由题意可得:直线l1的方程为6x+8y﹣14=0,因为直线l2的方程为6x+8y+1=0,所以根据两条平行线间的距离公式d=可得:直线l1与l2的距离为=.故选:B.4.(5分)若某中学高二年级8个班参加合唱比赛的得分如茎叶图所示,则这组数据的中位数是()A.91.5 B.92.5 C.91 D.92【解答】解:由茎叶图知样本数据共有8个,按照从小到大的顺序为:87,89,90,91,92,93,94,96.在中间两位的数据是91,92;所以样本的中位数是(91+92)÷2=91.5.故选:A.5.(5分)4张卡片上分别写有数字1,2,3,4,从这4张卡片中随机抽取2张,则取出的2张卡片上的数字之和为奇数的概率为()A.B.C.D.【解答】解:4张卡片上分别写有数字1,2,3,4,从这4张卡片中随机抽取2张,基本事件总数n==6,取出的2张卡片上的数字之和为奇数包含的基本事件个数m==4,∴取出的2张卡片上的数字之和为奇数的概率为=.故选:C.6.(5分)若变量x、y满足约束条件,则z=2x﹣y+1的最小值等于()A.﹣ B.﹣2 C.﹣ D.2【解答】解:由z=2x﹣y+1,得y=2x﹣z+1,作出不等式对应的可行域(阴影部分),平移直线y=2x﹣z+1,由平移可知当直线y=2x﹣z+1,经过点B时,直线y=2x﹣z+1的截距最大,此时z取得最小值,由,解得,即C(﹣1,).将C的坐标代入z=2x﹣y+1,得z=﹣2﹣+1=﹣,即目标函数z=2x﹣y+1的最小值为﹣.故选:C.7.(5分)直线l过点A(3,4)且与点B(﹣3,2)的距离最远,那么l的方程为()A.3x﹣y﹣13=0 B.3x﹣y+13=0 C.3x+y﹣13=0 D.3x+y+13=0【解答】解:∵线l过点A(3,4)且与点B(﹣3,2)的距离最远,∴直线l的斜率为:==﹣3,∴直线l的方程为y﹣4=﹣3(x﹣3),即3x+y﹣13=0,故选:C.8.(5分)运行如图的程序框图,设输出数据构成的集合为A,从集合A中任取一个元素a,则函数y=x a,x∈[0,+∞)是增函数的概率为()A.B.C.D.【解答】解:由框图可知A={3,0,﹣1,8,15},其中基本事件的总数为5,设集合中满足“函数y=xα,x∈[0,+∞)是增函数”为事件E,当函数y=xα,x∈[0,+∞)是增函数时,α>0事件E包含基本事件为3,则.故选:C.9.(5分)如图,直线y=ax﹣的图象可能是()A.B. C.D.【解答】解:方程直线的可以看作一次函数,其斜率a和截距异号,只有A符合,其斜率和截距都为负.故选:A.10.(5分)样本数据:﹣2,﹣1,0,1,2的方差为()A.B.2 C.1 D.2.5【解答】解:样本数据:﹣2,﹣1,0,1,2的平均数为:=(﹣2﹣1+0+1+2)=0,∴方差为:S2=[(﹣2﹣0)2+(﹣1﹣0)2+(0﹣0)2+(1﹣0)2+(2﹣0)2]=2.故选:B.11.(5分)P在直线2x+y+10=0上,PA、PB与圆x2+y2=4相切于A、B两点,则四边形PAOB面积的最小值为()A.24 B.16 C.8 D.4【解答】解:由圆x2+y2=4,得到圆心(0,0),半径r=2,由题意可得:PA=PB,PA⊥OA,PB⊥OB,∴S PAOB=2S△PAO=,在Rt△PAO中,由勾股定理可得:PA2=PO2﹣r2=PO2﹣4,当PO最小时,PA最小,此时所求的面积也最小,点P是直线l:2x+y+10=0上的动点,当PO⊥l时,PO有最小值d=,PA=4,所求四边形PAOB的面积的最小值为8.故选:C.12.(5分)Rt△ABC中,斜边BC为4,以BC中点为圆心,作半径为1的圆,分别交BC于P、Q 两点,则|AP|2+|AQ|2+|PQ|2的值为()A.4+B.3+C.D.14【解答】解:由题意,OA=OB=2,OP=OQ=1△AOP中,根据余弦定理AP2=OA2+OP2﹣2OA•OPcos∠AOP同理△AOQ中,AQ2=OA2+OQ2﹣2OA•OQcos∠AOQ因为∠AOP+∠AOQ=180°,所以|AP|2+|AQ|2+|PQ|2=2OA2+2OP2+PQ2=2×22+2×12+(2×1)2=14.故选:D.二、填空题(本大题共4小题,每小题5分,共20分)13.(5分)把十进制数89(10)化为五进制数,则89(10)=324(5).【解答】解:89÷5=17+4,余数是4,17÷5=3+2,余数是2,3÷5=0+3,余数是3.故89(10)=324(5),故答案为:324.14.(5分)用辗转相除法求出153和119的最大公约数是17.【解答】解:153=119×1+34,119=34×3+17,34=17×2.∴153与119的最大公约数是17.故答案为17.15.(5分)在棱长为3的正方体内任取一个点,则这个点到各面的距离都大于1的概率为.【解答】解:在正方体内,到各面的距离大于1的点位于一个边长为1的小正方体内,小正方体的体积为1,大正方体的体积为33=27,∴所求概率为.故答案为:.16.(5分)已知m∈R,则直线(m﹣1)x+(2m﹣1)y=m﹣4与圆x2+y2﹣10x+4y+20=0的位置关系为相交.【解答】解:直线(m﹣1)x+(2m﹣1)y=m﹣4,可化为m(x+2y﹣1)+(﹣x﹣y+4)=0,由,可得x=7,y=﹣3∴直线(m﹣1)x+(2m﹣1)y=m﹣4恒过(7,﹣3)而72+(﹣3)2﹣70+4×(﹣3)+20=﹣4<0∴点(7,﹣3)在圆x2+y2﹣10x+4y+20内则直线直线(m﹣1)x+(2m﹣1)y=m﹣4与圆x2+y2﹣10x+4y+20=0相交.故答案为:相交.三、解答题(本大题共6小题,满分70分,解答题写出必要的文字说明、推演步骤)17.(10分)已知直线l经过点A(﹣1,﹣3),且其倾斜角等于直线x﹣y=0的倾斜角的4倍.求直线l的方程并用一般式表示.【解答】解:假设直线x﹣y=0的倾斜角是A,那么有tanA=,A=,设过A点直线的倾斜角是B,那么B=4A=,那么直线L的斜率k=tanB=tan4A=tan=﹣,∴直线方程是:y+3=﹣(x+1),即:直线方程为x+y+3+=0.18.(12分)某中学团委组织了“弘扬奥运精神,爱我中华”的知识竞赛,从参加考试的学生中抽出60名学生,将其成绩(均为整数)分成六段[40,50),[50,60),…,[90,100]后画出如下部分频率分布直方图.观察图形给出的信息,回答下列问题:(1)求第四小组的频率,并补全这个频率分布直方图;(2)估计这次考试的及格率(60分及以上为及格)和平均分;(3)从成绩是[40,50)和[90,100]的学生中选两人,求他们在同一分数段的概率.【解答】解:(1)第一小组的频率为0.010×10=0.1,第二小组的频率为0.015×10=0.15,第三小组的频率为0.015×10=0.15,第五小组的频率为0.025×10=0.25,第六小组的频率为0.005×10=0.05,所以第四小组的频率为1﹣0.1﹣0.15﹣0.15﹣0.25﹣0.05=0.3.频率/组距=0.3÷10=0.03,故频率分布直方图如图(2)平均分超过60分的频率为0.15+0.25+0.05+0.3=0.75,所以估计这次考试的及格率为75%.第一组人数0.10×60=6,第二组人数0.15×60=9,第三组人数0.15×60=9,第四组人数0.3×60=18,第五组人数0.25×60=15,第六组人数0.05×60=3,所以平均分为=71.(3)成绩在[40,50)的有6人,在[90,100]的有3人,从中选两人有,他们在同一分数段的有,所以他们在同一分数段的概率是.19.(12分)已知△ABC中,A(1,3),AB、AC边上的中线所在直线方程分别为x﹣2y+1=0和y ﹣1=0,求△ABC各边所在直线方程.【解答】解:设B(x B,1)则AB的中点∵D在中线CD:x﹣2y+1=0上∴,解得x B=5,故B(5,1).同样,因点C在直线x﹣2y+1=0上,可以设C为(2y C﹣1,y C),根据=1,解出y C=﹣1,所以C(﹣3,﹣1).根据两点式,得直线AB的方程为y﹣3=(x﹣1);直线BC的方程为y﹣1=(x﹣5);直线AC的方程为y﹣3=(x﹣1)化简得△ABC中直线AB:x+2y﹣7=0,直线BC:x﹣4y﹣1=0,直线AC:x﹣y+2=0.20.(12分)已知坐标平面上点M(x,y)与两个定点M1(26,1),M2(2,1)的距离之比等于5.(1)求点M的轨迹方程,并说明轨迹是什么图形;(2)记(1)中的轨迹为C,过点A(﹣2,3)的直线l被C所截得的线段的长为8,求直线l的方程.【解答】解:(1)由题意坐标平面上点M(x,y)与两个定点M1(26,1),M2(2,1)的距离之比等于5,得=5.,化简得x2+y2﹣2x﹣2y﹣23=0.即(x﹣1)2+(y﹣1)2=25.∴点M的轨迹方程是(x﹣1)2+(y﹣1)2=25,所求轨迹是以(1,1)为圆心,以5为半径的圆.(2)当直线l的斜率不存在时,过点A(﹣2,3)的直线l:x=﹣2,此时过点A(﹣2,3)的直线l被圆所截得的线段的长为:2=8,∴l:x=﹣2符合题意.当直线l的斜率存在时,设过点A(﹣2,3)的直线l的方程为y﹣3=k(x+2),即kx﹣y+2k+3=0,圆心到l的距离d=,由题意,得+42=52,解得k=.∴直线l的方程为x﹣y+=0.即5x﹣12y+46=0.综上,直线l的方程为x=﹣2,或5x﹣12y+46=0.21.(12分)已知P(﹣2,﹣3)和以Q为圆心的圆(x﹣4)2+(y﹣2)2=9.(1)求出以PQ为直径的圆Q1的一般式方程.(2)若圆Q和圆Q1交于A、B两点,直线PA、PB是以Q为圆心的圆的切线吗?为什么?(3)求直线AB的方程.【解答】解:(1)由圆(x﹣4)2+(y﹣2)2=9可得圆心Q(4,2).∴线段PQ的中点Q1(1,﹣),|PQ1|=.∴以PQ为直径,Q1为圆心的圆的方程为(x﹣1)2+(y+)2=;(2)∵∠PAQ是以PQ为直径的圆周角,∴∠PAQ=90°.∴直线PA是以Q为圆心的圆的切线.同理PB是以Q为圆心的圆的切线.(3)由于交点A,B既在圆(x﹣4)2+(y﹣2)2=9上,又在圆(x﹣1)2+(y+)2=上.两方程相减可得:6x+5y=25,即为直线AB的方程.22.(12分)有定点P(6,4)及定直线l:y=4x,Q是l上在第一象限内的点.PQ交x轴的正半轴于M点,问点Q在什么位置时,△OMQ的面积最小,并求出最小值.【解答】解:设Q(a,4a),则直线PQ的方程为y﹣4=(x﹣6),令y=0,得到x=OM=,所以当a>1,即a+1>0,a﹣1>0时,△OMQ的面积S=××4a=10×[]=10×[(a﹣1)+]+20≥10×2+20=40,当且仅当(a﹣1)=时(a=2)取等号;所以当Q的坐标为(2,8)时,面积S的最小值为40.赠送初中数学几何模型【模型五】垂直弦模型:图形特征:运用举例:1.已知A、B、C、D是⊙O上的四个点.(1)如图1,若∠ADC=∠BCD=90°,AD=CD,求证AC⊥BD;(2)如图2,若AC⊥BD,垂足为E,AB=2,DC=4,求⊙O的半径.2.如图,已知四边形ABCD内接于⊙O,对角线AC⊥BD于P,设⊙O的半径是2。
