07第四章多组分系统热力学-1
第四章 多组分系统1

B B B B B
B
(2)
此式与前式相减得:
n dX 0 除以 n= n → x dX 0
等TP,
B
B
B
B
B
B
B
——吉布斯-杜亥姆方程
B
例:
二组分系统, nAdX A nB dX B =0
或
xAdX A xB dX B =0
5.偏摩尔量间函数关系
H B = U B p VB
G=G(T,P,nA,nB,……nk)
G G ) P ,n dT + ( )T , n dP dG= ( T P
+
B A
k
G ( )T , P,nC dnB nB
G G 组成不变:有 ( ) P,n S, ( )T ,n V T p
dG=-SdT+VdP+
B
G 定义式:μ B= ( )T , P ,nC nB
X 引起系统容量性质 dX 的改变值 ( )T , p ,nC nB
注意:
1)必须在等 TP 下的偏微商
其它条件下不是偏摩尔量
X XB =( )T , p ,nC nB
GB
X ( )T ,V ,nC ≠ X B nB
G ( )T ,V ,nC nB
=
G ( )T , p ,nC nB
k
Z Z dp dZ= ( ) p ,nA ,nB ,n C nk dT + ( ) p T Z Z )T , p ,nA ,nC nK dnB +( ) p ,nB ,n C nk dnA + ( nB nA Z + ……+ ( )T , p ,nA ,nB , nk 1 dnk nk
物理化学:第4章_多组分系统热力学_
真实混合物:实曲线
Vm xBVB xCVC VB (VC VB)xC
当混合物组成改变时,两组 分偏摩尔体积随之改变,且二者 变化相互关联。
组成接近某纯组分,其偏摩 尔体积也接近该纯组分摩尔体积。
5. 吉布斯 − 杜亥姆方程
对广度量 X (T , p, nB, nC , nD ,) 求全微分:
dX
X T
p,nB
dT
X p
T ,nB
dp
B
X nB
dnB T , p,nC
恒温、恒压
另一方面,由加和公式
,恒温恒压下求导:
比较两式,得
或
或
吉布斯-杜亥姆方程--在一定温度压力下,当混合物
组成变化时,各组分偏摩尔量变化的相互依赖关系。
➢ 系统中各组分的偏摩尔量并非完全独立,而是相 互依存的。
➢ 例:固体溶解、过饱和溶液析出、…
组分B在α、β两相中迁移达平衡的条件:该组分
在两相中的化学势相等。
➢ 物质总是从其化学势高的相向化学势低的相迁移, 直至物质迁移达平衡时为止,此时系统中每个组分在 其所处的相中的化学势相等。
化学势 判据
② 化学平衡
<0:自发不可逆; =0:平衡、可逆
任一化学反应,假定系统已处于相平衡,
任一组分B在每个相中的化学势都相等: Bα B
B
B
整个系统中B组分物质的量的变化量: dnBα dnB
α
BdnB
B
化学平衡时
平衡条件:与化学反应达到平衡的方式无关。
§4.3 气体组分的化学势
1、纯理想气体的化学势 2、理想气体混合物中任一组分的化学势 3、纯真实气体的化学势 4、真实气体混合物中任一组分的化学势
物理化学4 多组分体系热力学 1

几点说明
(1)偏摩尔量只对体系中某组分才具有的,对整体而 言无所谓偏摩尔量的概念; (2)只有体系的广度性质才有偏摩尔量(质量除外) ; (3)偏摩尔量本身是强度性质; (4)注意右下角标的条件; (5)任何偏摩尔量都是T、p、组成的函数; (6)纯物质的偏摩尔量就是摩尔量; (7)偏摩尔量可能是负值。 (8)偏摩尔量是1mol B对整体热力学性质的贡献量, 而不应该理解为它在混合体系中所具有的量。
分类
气态混合物:空气 混合物液态混合物:甲醇 + 乙醇 固态混合物:Cu + Ni 气态溶液:萘溶解于高压CO 2中 非电解质溶液:糖水 − − − 本章 溶液液态溶液 电解质溶液:盐水 - - -电化学 固态溶液:单体溶解于聚合物中 − − − 又称固溶体
§4-2 化学势 化学势μ μB
• 4-2-1 化学势定义 • 4-2-2 平衡判据与平衡条件 • 4-2-3 理想气体的化学势表达式
4-2-1 化学势定义
混合物或溶液中,组分B的偏摩尔吉布斯函数 GB在化学热力学中有特殊的重要性,又把它叫 做化学势,用符号μB表示。
∂G µ B = GB = ∂nB T , p ,nc≠B
dX = ∑ X B dnB
B =1 k
( 2)
• 可得Gibbs-Duhem方程:
∑ n dX
B B=1
k
B
=0
∑ x dX
B B=1
k
B
=0
Gibbs-Duhem方程的意义: (1) 某一偏摩尔量的变化可从其它偏摩尔量的变 化中求得。 (2) 对一个含有K个组分的均相体系,K个偏摩 尔量Xi中,只有 K-1个是独立的。
如果在溶液中不按比例地添加各组分,则溶液浓 度会发生改变,这时各组分的物质的量和偏摩尔量均 会改变。 根据集合公式
第四章- 多组分系统热力学

平衡
单组分多相系统
自 发 ( 恒T、 恒V、W ' 0) d n 0
平衡
(2)恒T、恒V且W’=0时:
d A S dT pd V
d n B B
B
dA
自发 (恒T、恒V、W' 0) d n 0 B B
组成表示法
1、物质B的摩尔分数 x B (mole fraction)
xB
nB / nB
B
xB 1
B
无量纲
2、物质B的质量分数 wB (mass percent)
wB mB / mB
B
WB 1
B
无量纲
3、物质B的(体积)摩尔浓度
c B (volume molality)
第四章 多组分系统热力学
Chapter 4 Thermodynamics of Muiticomponent systems
引
言
前几章介绍了简单系统发生PVT变化、相变化 和化学变化时热力学理论以及W、Q、 U、 H、 A、 G 的计算。
简单系统: 纯物质系统或组成不变的系统。
多组分系统:多组分、且组成发生变化的系统. 本章讨论其热力学规律。
§4-1 偏摩尔量
1. 2. 3. 4. 5. 6.
问题的提出 偏摩尔量 偏摩尔量的实验测定 偏摩尔量与摩尔量的区别 吉布斯–杜亥姆方程(Gibbs-Duhem) 偏摩尔量之间的关系
1.问题的提出 T、p一定时,100ml水+100ml乙醇混合= 200ml混合物?
答案:不相等!
G G dT dp G B dnB T p B p ,nC T ,nC
第四章 多组分系统热力学习题

第四章多组分系统热力学选择题1。
在373。
15K和101325Pa•下水的化学势与水蒸气化学位的关系为(A) μ(水)=μ(汽) (B)μ(水)<μ(汽)(C)μ(水)>μ(汽)(D) 无法确定答案:A。
两相平衡,化学势相等.2.下列哪种现象不属于稀溶液的依数性(A) 凝固点降低(B)沸点升高(C) 渗透压(D)蒸气压升高答案:D。
稀溶液的依数性之一为蒸气压下降.3.98K时,A、B两种气体在水中的亨利常数分别为 k1和 k2,且k1> k2,则当P1=P2时,A、B在水中的溶解量C1 和 C2 的关系为(A) C1> C2 (B) C1< C2 (C) C1= C2 (D)不能确定答案:B4.将非挥发性溶质溶于溶剂中形成稀溶液时,将引起(A) 沸点升高 (B)熔点升高 (C)蒸气压升高 (D) 都不对答案:A.稀溶液的依数性包括沸点升高、凝固点下降、蒸气压下降和渗透压。
5。
涉及纯物质标准状态的下列说法中不正确的是(A)纯理想气体的标准状态就是标准压力P(100KPa)下的状态(B) 纯液体物质的标准状态就是标准压力P(100KPa)下的纯液体(C)纯固体物质的标准状态就是标准压力P(100KPa)下的纯固体(D)不同的物质在相同温度下都处于标准状态时,它们的同一热力学函数值都应相同答案:D6。
稀溶液的依数性包括蒸汽压下降、沸点升高、凝固点降低和渗透压,下面的陈述都与它们有关,其中正确的是(A)只有溶质不挥发的稀溶液才有这些依数性(B)所有依数性都与溶液中溶质的浓度成正比(C) 所有依数性都与溶剂的性质无关(D)所有依数性都与溶质的性质有关答案:B7。
关于亨利系数,下面的说法中正确的是(A) 其值与温度、浓度和压力有关(B) 其值只与温度、溶质性质和浓度标度有关(C)其值与溶剂性质、温度和浓度大小有关(D)其值与温度、溶剂和溶质的性质及浓度标度等因素都有关答案:D8. 定义偏摩尔量时规定的条件是(A)等温等压(B)等熵等压(C) 等温, 溶液浓度不变 (D)等温等压,溶液浓度不变答案:D9。
多组分系统

第四章 多组分系统热力学及其在溶液中的应用§4.1 引 言1.基本概念1)多组分系统:由两种或两种以上物质所组成的系统。
(多组分系统可以是单相的也可以是多相的。
)2)混合物:由两种或两种相互均匀混合而构成的系统。
(可以是气相、液相或固相) 3)溶 液(1)定义:由两种或两种以上物质在分子级别呈均匀混合而成的系统。
(2)溶液组分命名:溶质,溶剂。
(3)分类:(1)固态溶液、液态溶液。
(2)电解质溶液、非电解质溶液。
(4)应注意问题:形成溶液后,一般溶质、溶剂受力 情况与纯组分受力情况不同,所以对它们研究方法是不同的。
2.溶液中物质受力情况溶剂-溶剂 f 11 ,溶质-溶质 f 22 ,溶剂-溶质 f 12。
1) 纯态: 溶质 f 22 溶剂 f 11 2) 稀溶液: 溶质 f 22 溶剂 f 11 3) 中等浓度: 溶质 f 22,f 12 溶剂 f 12, f 11 4) 高浓度: 溶质 f 22 溶剂 f 12 3.受力变化同热效应关系1) 放热2) 吸热3) 不吸热不放热§4.2 多组分系统的组成表示法1.组成表示法1)B 的质量浓度:单位体积混合物中所含B 的质量。
1211,22f f f >121122,f f f <121122f f f ==()B B m Vρ=单位 与T 有关2)B 的质量分数:单位质量混合物中所含B 的质量。
单位为1,与T 无关3)B 的浓度:单位体积混合物中所含B 的物质的量。
单位 或 同T 有关。
4)B 的摩尔分数( 或):组分B 的物质的量与混合物中总物质的量的比值。
单位为1,与T 无关液体用 ,气体用5)溶质B 的质量摩尔浓度:每千克溶剂中所含溶质的物质的量。
单位 与T 无关。
6)溶质B 的摩尔比:单位物质的量的溶剂中所含溶质的物质的量。
单位为1,与T 无关。
2.常用的浓度表示法之间的关系 1) 与 的关系:若取1000 g 溶剂对稀溶液 2) 与 关系:-3kg m ⋅B B W w W =B Bn c V =-3mol m ⋅-3mol dm ⋅B x B y B B n x n=B x By ()BB A n m m =⋅-1mol kg BB A n r n =B x B m B BB A B n n x n n n ==+∑AB B A B BB A10001000m x m m M M m M ==++∑∑A B 1000M m <<∑B AB 1000m M x =B x BC A B B BW W c M ρρ=-=-∑∑AB B B B A AB B B B B BB A A c c c M x W c M c M c M c c M M ρρ===--+++∑∑∑∑∑()B AB A B Bc M x c M M ρ=+-∑若溶液很稀则3) 同 的关系: 取 取若溶液很稀则 若 取 对水§4.3 偏摩尔量1.偏摩尔量的定义 1. 问题的引出对简单均相系统 ,要描述其状态,只需要两个状态性质(T 、p )就可以了。
第4章多组分系统热力学分解

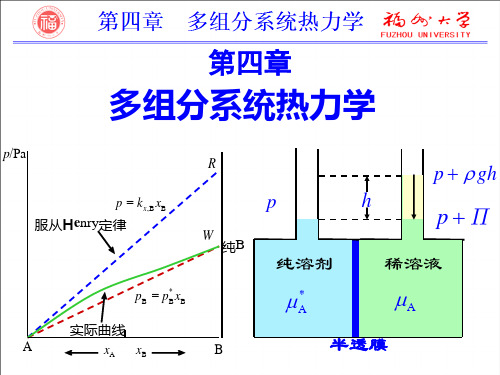
p/Pa
R
p gh
p
p = kx,B xB 服从Henry定律
h
W
pP
稀溶液
纯B
纯溶剂
* A
* pB = pB xB
A
半透膜
A
实际曲线 xA xB
B
基本内容
§ 4.1 § 4.2 § 4.3 § 4.4 § 4.5 § 4.6 § 4.7 § 4.8 § 4.9 偏摩尔量 化学势 气体组分的化学势 逸度及逸度因子 拉乌尔定律和亨利定律 理想液态混合物 理想稀溶液 活度与活度因子 稀溶液的依数性
GB 骣 ¶G 琪 =琪 桫 ¶n B
T ,p ,n C
因此:
T ,n B
禳 骣 镲 ?G 镲 琪 = 睚 琪 ?nB 镲 镲 铪p桫 禳 镲 抖 骣G 镲 琪 = 睚 琪 桫p 抖 n 镲 B 镲 铪 骣 ¶V 琪 =琪 桫 ¶n B
T ,p ,n C T ,n B
T ,n B T ,p ,n C
V nBVm , B nCVm ,C
理想混合溶液
★将0.5摩尔的水与0.5摩尔的乙醇混合,溶液体积:
V≠(0.5×18.09十0.5×58.35)cm3 =38.22cm3 =37.2cm3
实际混合溶液 V nBVm n V ,B C m,C
★乙醇与水溶液混合的体积与浓度的关系
多组分系统可以是单相的也可以是多相的。
但对多组分多相系统可以拆解为多个多组分单相系统来研究。
多组分单相系统:是由两种或两种以上物质以分子大小粒
子相互均匀混合成一相的系统。
混合物——系统中的各组分以同等条件予以研究 溶 液——系统中的组分区分为溶剂和溶质予以研究
物理化学 第四章 多组分系统热力学

Vm
T,p一定
V*m,C VC
V*m,B VB
d c· b·
0 B
a xC
C
图4.1.2 二组分液态混合物的 偏摩尔体积示意图
若B,C形成真实液态混合物: 则混合物体积为由V*m,B至V*m,C的曲线。对于任一 组成a时,两组分的偏摩尔体积可用下法表示: 过组成点a所对应的系统体积点d作Vm-xC曲线的 切线,此切线在左右两纵坐标上的截距即分别 为该组成下两组分的偏摩尔体积VB,VC。
B
系统中各广度量的偏摩尔量: 对于多组分系统中的组分B,有: 偏摩尔体积: VB=(ƽV/ƽnB)T,p,n C 偏摩尔热力学能: UB=(ƽU/ƽnB)T,p,n C 偏摩尔焓: HB=(ƽH/ƽnB)T,p,n C 偏摩尔熵: SB=(ƽS/ƽnB)T,p,n C 偏摩尔亥姆霍兹函数:AB=(ƽA/ƽnB)T,p,n C 偏摩尔吉布斯函数: GB=(ƽG/ƽnB)T,p,n
C
几点说明: (1)偏摩尔量为两个广度性质之比,所以为强度 性质; (2)偏摩尔量的定义中明确是在恒温、恒压及系 统组成不变的条件下,偏导数式的下标为T,p 时才是偏摩尔量; (3)同一物质在相同温度、压力但组成不同的多 组分均相系统中,偏摩尔量不同; (4)若系统为单组分系统,则该组分的偏摩尔量 与该组分的摩尔量相等,即: XB=X*B,m
C
=VB (数学知识:二阶偏导与求导的顺序无关) 得证。
4.2化学势 4.2化学势
1.化学势的定义 混合物(或溶液中)组分B的偏摩尔吉布斯函数GB 定义为B的化学势,用符号μB表示:
μB = GB=(ƽG/ƽnB)T,p,n
def
C
对于纯物质,其化学势等于它的摩尔吉布斯函 数。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
U n B S,V ,nC nB
同理还可得
B n B S, p ,n
H
C nB
15
和
B
A n B
T ,V , nC nB
于是化学势就有4个偏微商表达式:
*
解释: 不同组分的分子的结构, 大小和性质不同, 使纯态(B-B, C-C)和混合态(B-B, C-C, B-C)的分子间距不同(涉及V 等), 分 子间相互作用能也不同(涉及U, H, S, A, G等). 因此, 需用新的物理量偏摩尔量的概念取代纯物质的摩尔量. 5
偏摩尔体积VB 实验还表明, 水和乙醇的偏摩尔体积还与混合物的组成有 关. 只有在一定温度, 压力和确定组成的混合物中, 各组分 才有确定的偏摩尔体积. 为此, 有如下偏摩尔体积的定义:
若dT=0, dp=0 则
dX X BdnB
B
若各组分按一定比例同时微量地加入以形成混合物, 则 XB 为常数, 从 nB = 0到 nB = nB积分上式, 得偏摩尔量的集合公式:
X nB X B
B
如,混合物或溶液的体积 V=nBVB+nCVC+… 混合物或溶液的内能 U=nBUB+nCUC+…
dU TdS pdV BdnB
B
dH TdS Vdp BdnB
B
dA SdT pdV BdnB
B
以上4式为均相系统的更为普遍的热力学基本方程. 既适用于变组成的封闭系统, 也适用于敞开系统.
写出函数 U = f ( S, V, nB, nC, nD…) 的全微分式, 并与上 列对应方程对比, 可得
注意:每个偏微分的下标, 也即求偏导的条件; 特别注意与
各相应偏摩尔量的区别和联系.
纯物质的化学势等于该物质的摩尔吉布斯函数, 即
G * * B Gm ,B (T , p) n B T , p
16
2. 化学势判据及应用
恒温恒压下, 系统内发生相变化(或化学变化)时,
x
B
B
dX B 0
若为B, C二组分混合物或溶液, 则 xBdXB= – xCdXC 可见, 当混合物组成发生微小变化, 如果一组分的偏摩尔体积 增大, 则另一组分的偏摩尔体积一定减小. 12
5. 偏摩尔量之间的函数关系 混合物或溶液中同一组分, 它的不同偏摩尔量之间的关系 与纯物质各摩尔量间的关系相同. 如 纯组分: H =U +pV
• 在一定温度, 压力下, 1mol组分B在确定组成的混合物 中对体积的贡献值VB , 等于在无限大量(有限值)该组 成的混合物中加入1mol B引起的系统体积的增加值; • 也等于在有限量的该组成的混合物中加入dnB的B组分 引起系统体积增加 dV 折合成加入 1mol B 时的增量, 用数学式表示:
11
4. 吉布斯 - 杜亥姆方程
(可略)
X nB X B
B
恒温恒压下对集合公式 求全微分, 得 将上式与式
dX X BdnB nBdX B
B B
dX X BdnB
B
比较, 得
nBdX B 0
B
吉布斯-杜亥姆 (Gibbs -Duhem)方程
除以
n
n
B
B
得
VB V n B T , p,nc nB
nC’ ≠nB 表示除了nB外, 其余组分均不变.
6
2. 偏摩尔量
以 X 代表 V, U, H, S, A, G 这些广延性质之一, 对多组分系统 其全微分 X= f (T, p, nB, nC, …)
dp T , nB ;nC dnC T , p , nB ;nD X X dX dT T p , n ;n p B C X n B X dnB n C T , p , nC ;nD
在组成不变的条件下, 与dG =-SdT + Vdp对比, 得
G S , T p ,nC
G V p T ,nC
于是得
dG SdT Vdp BdnB
B
14
由dU = d(G-pV+TS), dH = d(G +TS), dA = d(G-pV), 又得
真实液态混合物
理想稀溶液 真实溶液
固态溶液(相平衡章)
电解质溶液在下册第七章电化学中讨论.
2
§4.1 偏摩尔量
§4.2 化 学 势 §4.3 气体组分的化学势
§4.4 拉乌尔定律和亨利定律
3
§4.1 偏摩尔量
1. 问题的提出
Partial molar quantity
单组分纯物质, 系统的广延性质V, U, H, S, A, G 都有其 相应的摩尔量:
• 任何偏摩尔量都是T, p和组成的函数.
10
3. 偏摩尔量的测定举例
(可略)
以二组分的偏摩尔体积为例.
斜率法: 向一定量 nC 的液态组分 C 中不断加入组分 B, 测出不同 nB 时的混合物的体积 V , 作 V-nB 曲线.
由曲线上某点的切线斜率得到相应组成 ( xB)下 VB, 再 用集合公式求出VC : VC = (V-nBVB)/nC . 截距法: 作 Vm-xB 曲线, 在曲线上任一点作切线, 与两边 纵坐标的交点就是两个组分的偏摩尔体积. 至于UB , HB , AB , GB等, 只能得到其变化值.
dnB dnB
dG
B
且
dnB 0
BdnB BdnB B dnB ( B B )dnB
B B
在一定T, p下, 若
则 dG = 0, 组分 B 在α, β两相中达成平衡.
若
B B
*
*
是(准)强度性质.
但在液态混合物或溶液中,组分B的单位量的VB , UB , HB , SB , AB, GB 与同温同压下单独存在时相应的摩尔量通常并不相等. 4
例如, 25℃,101.325kPa时, 将1摩尔58.35cm3 C2H5OH(l) 和1摩 尔18.09cm3 H2O(l) 混合后体积减少了2.04cm3. ( = 76.44-74.40)
9
关于偏摩尔量的几点说明:
• 偏摩尔量的含义是: 偏摩尔量XB是在T, p以及除nB外所有 其他组分的量都保持不变的条件下, 任意广延性质X 随nB 的变化率. 也可理解为在恒温恒压下, 向大量的某一定组成 的混合物或溶液中加入单位量的B (1mol B)时引起系统的 广延性质 X 的改变量.
• 只有系统的广延性质才有偏摩尔量, 而偏摩尔量则成为准 强度性质. 如UB , HB , GB 的单位为J· -1. mol • 只有在恒温恒压下, 某广延性质对nB的偏微分才叫偏摩尔 量.
则 dG < 0, 组分B有从α相转移到β相的自发趋势.
结论: 在恒温恒压下若任一物质B在两相中的化学势不相等, 则该组分必然从化学势高的那一相向化学势低的那一相转移, 即朝着化学势减小的方向进行: 若每一组分在两相的化学势 都分别相等, 则两相处于平衡状态. 18
§4.3 气体组分的化学势
1. 理想气体的化学势 标准化学势 B : 物质B 在标准态下的化学势. 特别提醒: 任何状态的组分B的化学势都将以其同温下的标准 化学势为基准来表示. 尽管的绝对值仍未知, 但下章将要学 习的化学平衡规律只须知道下列加和值即可满足需要:
定义
def X XB n B
T , p ,nC nB
ห้องสมุดไป่ตู้
XB偏摩尔量
该式表示在恒温恒压和除B组分以外其它组分的含量都不 变的条件下, 任一广延性质 X 随 B 组分物质的量的变化率, 即 每单位量引起 X 的增量(折合值, 对应于该一定状态). 7
偏摩尔体积 偏摩尔内能
T , p ,nC nB
注意:下标均为
T , p, n n C B
SB
在其它任何条件 下的变化率都不 是偏摩尔量.
偏摩尔亥姆霍兹函数 偏摩尔吉布斯函数
AB
GB
G n B
T , p,nC nB
8
将XB 代入前述全微分式, 得
X X dX dT dp X BdnB X CdnC ... T p,nC p T ,nC
18.09cm3 H2O*(l) 58.35cm3
C2H5OH *(l)
*
74.40cm3
H 2O C2H5OH(l)
VH2O =17.0cm3/mol VC2H5OH = 57.4 cm3/mol
表明: V H 2 O V m H 2 O, l ; V C 2 H 5 OH V m C 2 H 5 OH, l
化学势的定义式
B
def
Chemical potential
G GB n B T , p , nC nB
1. 基本热力学公式 对多组分组成可变的单相系统 G=f (T, p, nB, nC , ……)
G G G dG dT dp n p T ,n T p,nC B B C dnB T , p ,nC nB
B
U n B H n B S,V ,nC nB A n B S, p,nC nB G n B T ,V ,nC nB T , p,nC nB
