北师大版2017初中一年级(下册)数学 第二章 相交线与平行线 第二节 第2课时 内错角 同旁内角(PPT课件)
北师大版七年级数学下册第二章相交线与平行线2.1两条直线的位置关系课件课件

AB C
Da
垂线的性质(2)
连接直线外一点与直线上各点的 所有线段中,垂线段最短。
简单说成:垂线段最短.
2、
3、在数学课上,同学们在练习过点B、作线段AC 所在直线的垂线段时,有一部分同学画出下 列四种图形,请你数一数,错误的个数为
如图:一辆汽车在直线形的 公路上由A向B行驶, M、N 分别是位于公路AB两侧的两
北京师范大学出版社数学七年级下册
第二章 相交线与平行线
§2.1.2 两条直线的位置关系(二)
找不同
指出下列几组相交的直线中,不同的一组
(1)
(2)
(3)
(4)
探究新知:
垂直:当两条直线相交所成的四个角中,
有一个角是直角时,这两条直线互相垂直, 其中一条直线叫另一条直线的垂线,它们的 交点叫垂足。
D
所学校。汽车行驶时,会对
C
公路两旁的学校造成一定的 噪音 影响。当汽车行驶到何 处时,分别对两个学校影响 最大?在图中标出来。
课堂 小结 记作:AB⊥CD ,垂足为O
画出两条互相垂直的直线吗? 列四种图形,请你数一数,错误的个数为 第二章 相交线与平行线 平面内,过一点有且只有一条直线于已知直线垂直。
不管数学的任一分支是多么抽象,总有一天会应用在这实际世界上
垂直:当两条直线相交所成的四个角中,有一个角是直角时,这两条直线互相垂直,其中一条直线叫另一条直线的垂线,它们的交点 叫垂足。 (1)画出直线m和点A; 记作:AB⊥CD ,垂足为O
直线吗,试试看吧!请说明理由。 公路两旁的学校造成一定的
(2)过点A画直线m的垂线,你能画多 你有几种画法?
▪ 1.你学到了哪些知识? 公路两旁的学校造成一定的
北师大版初一(下)数学第二章相交线与平行线教案:相交线与平行线讲义(含解析)

北师大版初一(下)数学第二章相交线与平行线教案:相交线与平行线讲义(含解析)把握对顶角和邻补角的概念;把握垂线段的定义及其画法;3.把握三线八角的定义和找法;4.把握平行线的性质与判定.相交线在同一平面内,两条直线的位置关系有_________和________。
(2)相交:在同一平面内,有__________的两条直线称为相交线。
(3)邻补角:①定义:有公共顶点,且有一条公共边,另一条边互为反向延长线,具有这种位置关系的两个角,互为邻补角。
②性质:位置——互为邻角数量——互为补角(两角之和为180°)(4)对顶角:①定义:有一个公共顶点,同时有一个角的两边分别是另一个角两边的反向延长线,具有这种位置关系的两个角,互为对顶角②性质:对顶角相等几何语言:∵∠1+∠2=180°∠2+∠3=180°∴∠1=∠3(同角的补角相等)两直线相交所成的四个角中存在几种不同关系的角,它们的概念及性质如下表:注意点:⑴对顶角是成对显现的,对顶角是具有专门位置关系的两个角;⑵假如∠α与∠β是对顶角,那么一定有∠α=∠β;反之假如∠α=∠β,那么∠α与∠β不一定是对顶角⑶假如∠α与∠β互为邻补角,则一定有_____________;反之假如∠α+∠β=180°,则∠α与∠β不一定是邻补角。
(4)两直线相交形成的四个角中,每一个角的邻补角有两个,而对顶角只有一个。
2.垂线⑴定义,当两条直线相交所成的四个角中,有一个角是直角时,就说这两条直线互相垂直,其中的一条直线叫做另一条直线的垂线,它们的交点叫做_______。
符号语言记作:如图所示:AB⊥CD,垂足为O垂线性质1:过一点_______________一条直线与已知直线垂直。
垂线性质2:连接直线外一点与直线上各点的所有线段中,垂线段最短。
简称:_______________。
3.垂线的画法:(1)过直线上一点画已知直线的垂线;(2)过直线外一点画已知直线的垂线。
新版北师大初中数学教材目录

新版北师大初中数学教材目录七年级上册第一章丰富的图形世界1.生活中的立体图形 2.展开与折叠3.截一个几何体 4.从三个不同方向看物体的形状第二章有理数及其运算1.有理数 2.数轴 3.绝对值4.有理数的加法 5.有理数的减法6.有理数的加减混合运算 7.有理数的乘法8.有理数的除法 9.有理数的乘方 10.科学计数法11.有理数的混合运算 12.用计算器进行运算第三章整式及其加减1.字母表示数 2.代数式 3.整式4.整式的加减 5.探索与表达规律第四章基本平面图形1.线段、射线、直线 2.比较线段的长短3.角 4.角的比较 5.多边形和圆的初步认识第五章一元一次方程1.认识一元一次方程 2.求解一元一次方程3.应用一元一次方程——水箱变高了4.应用一元一次方程——打折销售5.应用一元一次方程——“希望工程”义演6.应用一元一次方程——追赶小明第六章数据的收集与整理1.数据的收集 2.普查和抽样调查3.数据的表示 4.统计图的选择七年级下册第一章整式的乘除1.同底数幂的乘法 2.幂的乘方与积的乘方3.同底数幂的除法 4.整式的乘法5.平方差公式 6.完全平方公式 7.整式的除法第二章相交线与平行线1.两条直线的位置关系 2.探索直线平行的条件3.平行线的性质 4.用尺规作角第三章三角形1.认识三角形 2.图形的全等 3.探索三角形全等的条件4.用尺规作三角形 5.利用三角形全等测距离第四章变量之间的关系1.用表格表示的变量间关系 2.用关系式表示的变量间关系3.用图像表示的变量间关系第五章生活中的轴对称1.轴对称现象 2.探索轴对称的性质3.简单轴对称图形 4.利用轴对称进行设计第六章频率与概率1.感受可能性 2.频率的稳定性 3.等可能事件的概率八年级上册第一章勾股定理1.探索勾股定理 2.一定是直角三角形吗 3.勾股定理的应用第二章实数1.认识无理数 2.平方根 3.立方根 4.估算5.用计算器开方 6.实数 7.二次根式第三章位置与坐标1.确定位置 2.平面直角坐标系 3.轴对称与坐标变化第四章一次函数1.函数 2.一次函数与正比例函数 3.一次函数的图象4.一次函数的应用第五章二元一次方程组1.认识二元一次方程组 2.求解二元一次方程组3.应用二元一次方程组——鸡兔同笼4.应用二元一次方程组——增收节支5.应用二元一次方程组——里程碑上的数6.二元一次方程与一次函数7.用二元一次方程组确定一次函数表达式8.三元一次方程组第六章数据的分析1.平均数 2.中位数与众数3.从统计图分析数据的集中趋势 4.数据的离散程度第七章平行线的证明1.为什么要证明 2.定义与命题 3.平行线的判定4.平行线的性质 5.三角形内角和定理八年级下册第一章证明(二)1.等腰三角形 2.直角三角形 3.线段的垂直平分线 4.角平分线第二章一元一次不等式和一元一次不等式组1.不等关系 2.不等式的基本性质3.不等式的解集 4.一元一次不等式5.一元一次不等式与一次函数 6.一元一次不等式组第三章图形的平移与旋转1.图形的平移 2.图形的旋转 3.中心对称 4.简单的图案设计第四章因式分解1.因式分解 2.提公因式法 3.运用公式法第五章分式1.认识分式 2.分式的乘除法 3.分式的加减法 4.分式方程第六章平行四边形1.平行四边形的性质 2.平行四边形的判别3.三角形的中位线 4.多边形的内角和与外角和九年级上册第一章特殊的平行四边形1.菱形的性质与判定 2.矩形的性质与判定 3.正方形的的性质与判定第二章一元二次方程1.认识一元二次方程 2.配方法 3.公式法4.因式分解法 5.一元二次方程的应用第三章相似图形1.成比例线段 2.平行线分线段成比例 3.相似多边形4.相似三角形的判定 5.黄金分割 6.测量旗杆的高度7.相似三角形的性质 8.图形的放大与缩小第四章视图与投影1.投影 2.视图第五章反比例函数1.反比例函数 2.反比例函数的图象与性质 3.反比例函数的应用第六章对概率的进一步研究1.游戏公平吗 2.投针试验 3.生日相同的概率九年级下册第一章直角三角形的边角关系1.从梯子的倾斜程度谈起 2.特殊角的三角函数值3.三角函数的有关计算 4.船有触礁的危险吗 5.测量物体的高度第二章二次函数1.二次函数所描述的关系 2.二次函数的图像与性质 3.确定二次函数的表达式4.最大面积是多少 5.何时获得最大利润 6.二次函数与一元二次方程第三章圆1.圆 2.圆的对称性 3.垂径定理 4.圆周角与圆心角的关系5.确定圆的条件 6.直线和圆的位置关系 7.切线长定理8.圆内接正多边形 9.弧长及扇形的面积第四章统计与概率1.视力的变化 2.生活中的概率 3.统计与概率的应用。
新北师大版七年级数学下册《二章 相交线与平行线 1 两条直线的位置关系 对顶角、余角和补角》课件_15

巩固反馈
1.下列各图中,∠1和∠2是对顶角的是(D )
1 2
A
12
B
1
C2
2.如图所示,有一个破损的扇形零
件,利用图中的量角器可以量出这
个扇形零件的圆心角的度数吗?你
能说出所量角的度数是多少吗?为
什么?
400
1 2
D
2 1
数学活动三
动手实践 探究新知
1
13
900
2
定义: 如果两个角的和等于180°,如果两个角的和等于90°, 那么称这两个角互为补角. 那么称这两个角互为余角.
注意:互为补角和互为余角指两个角之间 的数量关系,与它们的位置无关.
巩固反馈
∠α 5° 32° 145° x°( x<90)
∠α的余角 85° 58°
不存在 90° x°
∠α的补角 175° 148° 35°
180° x°
通过上述计算,你发现了什么?
180° x°( 90 x°)=90° 一个锐角的补角比它的余角大90°.
E D
A
B
O
C
作业布置
必做题:1.课本P40习题2.1: 1,2,3,4,5题 选做题:2.下图由两块相同的直角三角板拼 成,其中
∠FDE=∠AOB=900,点O在FD上,DE在直线AB上, 请找出相等的角、互余的角、互补的角.
F
注意事项:
O
1.独立、高效完成.
2.整理错题.
3.反思解惑.
A
D BE
数学活动四
动手实践 探究新知
跟着老师的视频一起折一折,画一画。
数学活动四
动手实践 探究新知
C
北师大版数学七年级下册《平行线的性质》相交线与平行线(第2课时)

5.已知AB⊥BF,CD⊥BF,∠1= ∠2,试说明∠3=∠E.
解: 因为∠1=∠2
(已知),
所以AB∥EF
(内错角相等,两直线平行).
A1 C3
因为AB⊥BF,CD⊥BF,
所以AB∥CD
E
(垂直于同一条直线的两条直线平行).
所以EF∥CD
(平行于同一条直线的两条直线平行).
所以 ∠3= ∠E
(两直线平行,内错角相等).
(两直线平行,同旁内角互补)
所以∠AGD=180°-∠BAC=180°-70°=110°.
如图,AB//CD,试解决下列问题: (1)如图1,∠1+∠2=__1_80°___; (2)如图2,∠1+∠2+∠3=__3_60°__;
(3)如图3,∠1+∠2+∠3+∠4=_ 54_0_°__;
(4)如图4,试探究∠1+∠2+∠3+∠4+…+∠n
B
D 2F
6.如图,EF∥AD,∠1=∠2,∠BAC=70 °,求∠AGD
的度数.
C
解: 因为EF∥AD, (已知)
所以∠2=∠3. (两直线平行,同位角相等)
D F
1
G
又因为∠1=∠2,
(已知)
B
所以∠1=∠3. (等量代换)
所以DG∥AB. (内错角相等,两直线平行)
2
E
3A
所以∠BAC+∠AGD=180°.
可得AC∥MD.
例2 如图,AB∥CD,如果∠1=∠2,那么EF与AB
平行吗?说说你的理由.
解:因为∠1= ∠2, 根据“内错角相等,两直线 平行” ,
所以EF∥CD. 又因为AB∥CD,
根据“平行于同一条直线的两条直线平行”,
北师版七年级下册数学 第2章 相交线与平行线 垂线的定义与性质

感悟新知
3.如图,三条直线相交于点O, 若CO⊥AB,∠1=56°,则∠2等于( ) B A.30° B.34° C.45° D.56°
知1-练
感悟新知
4. 如图,点O在直线AB上,且OC⊥OD,若 ∠COA=36°,则∠DOB的大小为( ) B A.36° B.54° C.55° D.44°
知1-练
感悟新知
知1-讲
特别提醒: 垂直和垂线是两个不同的概念,垂直是两条直线的位置关系, 是相交的一种特殊情况,特殊在夹角为直角,而垂线是一条直 线.
感悟新知
如图例,1 CO⊥AB于点O,∠AOE=∠COF,则射 线OE,OF是什么位置关系?请说明理由.
导引:要判断OE,OF是什么位置关 系,其实质是说明OE,OF是 否垂直,即要看∠EOF是否为 90°;要让∠EOF=90°,需说明∠EOF= ∠AOC或∠EOF=∠BOC都可,这样就把问题 转化为说明∠AOE=∠COF(已知)了.
画出两条互相垂直的直线吗? (2)如果只有直尺,你能在右图方格
纸上画出两条互相垂直的直线吗? (3)你能用折纸的方法折出互相垂直的直线吗?试试看!
感悟新知
1.垂线的画法:
知2-讲
经过一点(已知直线上或直线外),画已知直线的垂线,步骤
如下:
(1)靠线:让直角三角板的一条直角边与已知直线重合;
(2)过点:沿直线移动,使直角三角板的另一条直角边经过已知点;
第2章相交线与平行线
2.1两条直线的位置关系
第2课时垂线的定 义与性质
学习目标
1 课时讲解
垂直的定义 垂线的画法 垂线的性质
2 课时流程
逐点 导讲练
课堂 小结
作业 提升
课时导入
北师大版初中数学一年级下2.1两条直线的位置关系 课件(共34张PPT)

动手实践二
DO
C
12
34
图2-2
AN B 图2-3
打台球时,选择适当的方向,用白球击打红球, 反弹后的红球会直接入袋,此时∠1=∠2,将图 2-2抽象成成图2-3,ON与DC交于点O, ∠DON=∠CON=900,∠1=∠2
DO
C
12
34
AN B
图2-2
图2-3
小组合作交流,解决下列问题:在图2-3中
通常用“⊥”表 示两直线垂直。
C
A OB D
记作AB⊥CD, 垂足为点O.
m
O
记作l⊥m, 垂足为点O.
动手画一画1
工具1:你能借助三角尺或者量角器,在一 张白纸上画出两条互相垂直的直线吗? 工具2:如果只有直尺,你能在方格纸上画出 两条互相垂直的直线吗?请说出你的画法和 理由. 工具3:你能用折纸的方法折出互相垂直的 直线吗,试试看吧!请说明理由。
问题1:
①你能借助三角尺, 在一张白纸上画出两 条互相垂直的直线?
②怎样用量角器画出 两条互相垂直的直线
问题2:如果只有直尺,你能在方格纸上 画出两条互相垂直的直线吗? 说说你的画法和理由.
问题3: 你能用折纸的方法折出互相垂直的 直线吗,试试看吧!请说明理由。
动手画一画2
问题1:请画出直线m和点A,你有几种画 法? 问题2:过点A画直线m的垂线你能画出多 少条?请用你自己的语言概括你的发现。
E
D
A
O
B
C
2.1─11
你学到了哪些知识? 一、定义: 1、对顶角 2、互为补角,余角
二、性质: 对顶角相等 同角或等角的余角相等 同角或等角的补角相等
(二)
问题:
课前导入
新北师大版七年级数学下册第二章相交线与平行线知识点梳理汇总
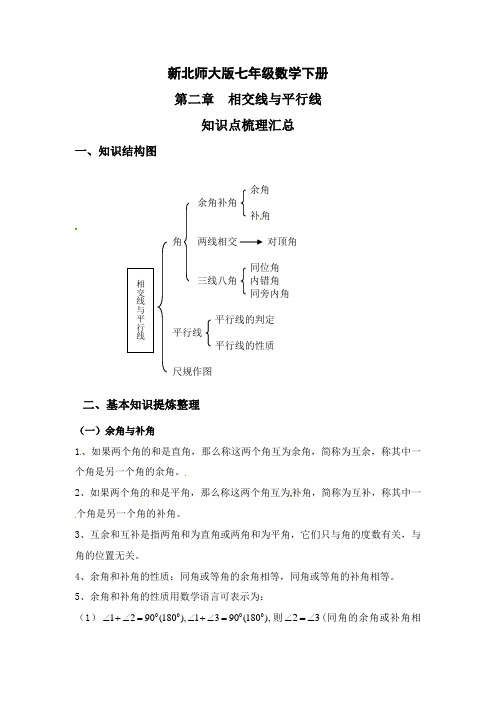
新北师大版七年级数学下册第二章相交线与平行线知识点梳理汇总一、知识结构图余角余角补角补角角两线相交对顶角同位角三线八角内错角同旁内角平行线的判定平行线平行线的性质尺规作图二、基本知识提炼整理(一)余角与补角1、如果两个角的和是直角,那么称这两个角互为余角,简称为互余,称其中一个角是另一个角的余角。
2、如果两个角的和是平角,那么称这两个角互为补角,简称为互补,称其中一个角是另一个角的补角。
3、互余和互补是指两角和为直角或两角和为平角,它们只与角的度数有关,与角的位置无关。
4、余角和补角的性质:同角或等角的余角相等,同角或等角的补角相等。
5、余角和补角的性质用数学语言可表示为:(1)00001290(180),1390(180),∠+∠=∠+∠=则23∠=∠(同角的余角或补角相等)。
(2)0000∠+∠=∠+∠=且14,1290(180),3490(180),∠=∠则23∠=∠(等角的余角(或补角)相等)。
6、余角和补角的性质是证明两角相等的一个重要方法。
(二)对顶角1、两条直线相交成四个角,其中不相邻的两个角是对顶角。
2、一个角的两边分别是另一个角的两边的反向延长线,这两个角叫做对顶角。
3、对顶角的性质:对顶角相等。
4、对顶角的性质在今后的推理说明中应用非常广泛,它是证明两个角相等的依据及重要桥梁。
5、对顶角是从位置上定义的,对顶角一定相等,但相等的角不一定是对顶角。
(三)同位角、内错角、同旁内角1、两条直线被第三条直线所截,形成了8个角。
2、同位角:两个角都在两条直线的同侧,并且在第三条直线(截线)的同旁,这样的一对角叫做同位角。
3、内错角:两个角都在两条直线之间,并且在第三条直线(截线)的两旁,这样的一对角叫做内错角。
4、同旁内角:两个角都在两条直线之间,并且在第三条直线(截线)的同旁,这样的一对角叫同旁内角。
5、这三种角只与位置有关,与大小无关,通常情况下,它们之间不存在固定的大小关系。
(四)六类角1、补角、余角、对顶角、同位角、内错角、同旁内角六类角都是对两角来说的。
