山东省德州市武城县八年级数学上册12.3角的平分线的性质课后训练新版新人教版
人教版八年级数学(上册)12.3角的平分线的性质(第1课时) 课时习题(附参考答案)
12.3角的平分线的性质
(第1课时)
1. 用尺规作下列角的平分线:
2. 画出三角形三个内角的平分线
你发现了什么特点吗? .
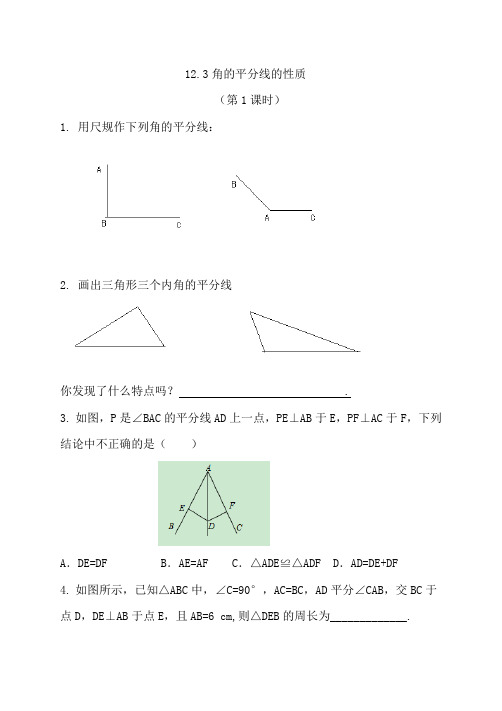
3.如图,P是∠BAC的平分线AD上一点,PE⊥AB于E,PF⊥AC于F,下列结论中不正确的是()
A.DE=DF B.AE=AF C.△ADE≌△ADF D.AD=DE+DF
4.如图所示,已知△ABC中,∠C=90°,AC=BC,AD平分∠CAB,交BC于点D,DE⊥AB于点E,且AB=6 cm,则△DEB的周长为_____________.
5.如图,已知AB∥CD,O为∠A、∠C的角平分线的交点,OE⊥AC于E,且OE=2,则两平行线间AB、CD的距离等于。
6.如图,已知BD是∠ABC的内角平分线,CD是∠ACB的外角平分线,由D 出发,作点D到BC、AC和AB的垂线DE、DF和DG,垂足分别为E、F、G,则DE、DF、DG的关系是。
7.如图,∠AOP=∠BOP,AD⊥OB于D,BC⊥OA于C,AD与BC交于点P。
求证:AP=BP。
参考答案
1.略
2.三角形的三条角平分线相交于一点.
3.D
4. 6
5. 4
6.DE=DF=DG.
7.证明:∵∠AOP=∠BOP,AD⊥OB于D,BC⊥OA于C,∴PC=PD 在△PAC与△PBD中,
∵∠APC=∠BPD,∠ACP=∠BDP,PC=PD
∴△PAC≌△PBD,即AP=BP.。
新人教版八年级数学上册12.3角的平分线的性质(第1课时)课时同步习题(含答案)

12.3 角的平分线的性质一、选择题1. 用尺规作已知角的平分线的理论依据是( )A .SASB .AASC .SSSD .ASA2. 如图,∠1=∠2,PD ⊥OA ,PE ⊥OB ,垂足分别为D ,E ,下列结论错误的是( )A 、PD =PEB 、OD =OEC 、∠DPO=∠EPOD 、PD =OD 3. 如图,Rt △ABC 中,∠C =90°,∠ABC 的平分线BD 交AC 于D ,若CD =3cm ,则点D 到AB 的距离DE 是( )A .5cmB .4cmC .3cmD .2cm4. 如图,△ABC 中,∠C =90°,AC =BC ,AD 平分∠CAB 交BC 于D ,DE ⊥AB 于E ,且AB =6㎝,则△DEB 的周长为( )A. 4㎝B. 6㎝C. 10㎝D. 不能确定 21D A PO EB第2题图 第3题图 第4题图 5.如图,OP 平分AOB ∠,PA OA ⊥,PB OB ⊥,垂足分别为A ,B .下列结论中不一定成立的是( ) A.PA PB = B.PO 平分APB ∠ C.OA OB = D.AB 垂直平分OP6.如图,AD 是△ABC 中∠BAC 的平分线,DE ⊥A B 于点E ,DF ⊥AC 交AC 于点F .S △ABC =7,DE=2,AB=4,则AC 长是( )第5题图 第6题图 第7题图7.如图,AD 是△ABC 的角平分线,DF ⊥AB ,垂足为F ,DE=DG ,△ADG 和△AED 的面积分别为50和39,则△EDF 的面积为( )DCA EBF E O D C ABA 、11B 、5.5C 、7D 、3.5 8.已知:如图,△ABC 中,∠C =90o ,点O 为△ABC 的三条角平分线的交点,OD ⊥BC ,OE ⊥AC ,OF ⊥AB ,点D 、E 、F 分别是垂足,且AB =10cm ,BC =8cm ,CA =6cm ,则点O 到三边AB 、AC 和BC 的距离分别等于( ) (A )2cm 、2cm 、2cm . (B )3cm 、3cm 、3cm .(C )4cm 、4cm 、4cm . (D )2cm 、3cm 、5cm .二、填空题 9.如图,P 是∠AOB 的角平分线上的一点,PC ⊥OA 于点C ,PD ⊥OB 于点D ,写出图中一对相等的线段(只需写出一对即可) .10.如图,在△ABC 中,∠A =90°,BD 平分∠ABC ,AD =2 cm ,则点D 到BC 的距离为________cm .11 .如图,OP 平分∠MON ,PA ⊥ON 于点A ,点Q 是射线OM 上一个动点,若PA=3,则PQ 的最小值为 .第9题图 第10题图 第11题图12.如图,在Rt △ABC 中,∠A=90°,∠ABC 的平分线BD 交AC 于点D ,AD=3,BC=10,则△BDC 的面积是 .第12题图 第13题图 第15题图13.如图,在Rt △ABC 中,∠C=90°,若BC=10,AD 平分∠BAC 交BC 于点D ,且BD :CD=3:2,则点D 到线段AB 的距离为 .14.已知△ABC 中,AD 是角平分线,AB=5,AC=3,且S △ADC =6,则S △ABD = .15.如图,AD 是△ABC 的角平分线,DE ⊥AB ,DF ⊥AC ,垂足分别为点E ,F ,连接EF ,则EF 与AD 的关系是 .16.通过学习我们已经知道三角形的三条内角平分线是交于一点的.如图,P 是△ABC 的内角平分线的交点,已知P 点到AB 边的距离为1,△ABC 的周长为10,则△ABC 的面积为 .17.如图,AD ∥BC ,∠ABC 的角平分线BP 与∠BAD 的角平分线AP 相交于点P ,作PE ⊥AB 于点E .若PE=2,则两平行线AD 与BC 间的距离为 .第16题图 第17题图 第18题图18. 如图,△ABC 的三边AB 、BC 、CA 长分别为40、50、60.其三条角平分线交于点O ,则S △ABO :S △BCO :S △CAO = .三、解答题19.已知:AD 是△ABC 的角平分线,DE ⊥AB ,DF ⊥AC ,垂足分别是E 、F ,BD =CD ,求证:∠B =∠C. 20. 如图,画∠AOB=90°,并画∠AOB 的平分线OCP 上,使三角尺的两条直角边与∠AOB 的两边分别相交于点E 、F21.如图,AB ∥CD ,以点A 为圆心,小于AC 长为半径作圆弧,分别交AB ,AC 于E ,F 两点,再分别以E ,F 为圆心,大于EF 长为半径作圆弧,两条圆弧交于点P ,作射线AP ,交CD 于点M .(1)若∠ACD=114°,求∠MAB 的度数;(2)若CN ⊥AM ,垂足为N ,求证:△ACN ≌△MCN .22. 如图,已知△ABC 中,AB=AC ,BE 平分∠ABC 交AC 于E ,若∠A=90°,那么BC 、B A 、AE 三者之间有何关系?并加以证明.23. 如图,△ABC中,D为BC的中点,DE⊥BC交∠BAC的平分线AE于点E,EF⊥AB于F,EG⊥A G交AC的延长线于G.求证:BF=CG.12.3 角的平分线的性质第1课时角的平分线的性质一、选择题1.C2.D3.C4.B5.D6.B7.B8.A二、填空题9.PC=PD(答案不唯一)10. 2 11. 3 12. 15 13. 4 14. 1015. AD垂直平分EF 16. 5 17. 4 18. 4:5:6三、解答题19.证明:∵AD是△ABC的角平分线,DE⊥AB,DF⊥AC,∴DE=DF,在Rt△DEB与Rt△DFC中,BD=CD,DE=DF,∴Rt△DEB≌Rt△DFC(HL),∴∠B=∠C.理由是:过点∴∠ACD+∠CAB=18的平分线,∴∠MAB=∠CAB=33°22 . 解:BC、BA、AE三者之间的关系:BC=BA+AE,理由如下:过E作ED⊥BC交BC于点D,∵BE平分∠ABC,BA⊥CA,∴AE=DE,∠EDC=∠A=∠BDE=90°,∵在Rt△BAE和Rt△BDE中,∴Rt△BAE≌Rt△BDE(HL),∴BA=BD,∵AB=AC,∠A=90°∴∠C=45°,∴∠CED=45°=∠C,∴DE=CD,∵AE=DE,∴AE=CD=DE,∴BC=BD+DC=BA+AE.∵EF⊥AB EG⊥A G,。
八年级数学上册第十二章全等三角形12-3角的平分线的性质同步练习含解析新版新人教版

《12.3 角的平分线的性质》一、填空题1.如图,∠B=∠D=90゜,根据角平分线性质填空:(1)若∠1=∠2,则______=______.(2)若∠3=∠4,则______=______.2.如图,BD是∠ABC的平分线,DE⊥AB于E,DF⊥BC于F,AB=12,BC=15,S△ABD=36,则S△BCD=______.3.如图,△ABC的三边AB、BC、CA长分别是20、30、40,其三条角平分线将△ABC分成三个三角形,则S△ABO:S△BCO:S△CAO等于______.4.如图,AD是△ABC的角平分线,若AB=2AC.则S△ABD:S△ACD=______.二、选择题5.如图,已知点P、D、E分别在OC、OA、OB上,下列推理:①∵OC平分∠AOB,∴PD=PE;②∵OC平分∠AOB,PD⊥OA,PE⊥OB,∴PD=PE;③∵PD⊥OA,PE⊥OB,∴PD=PE;其中正确的个数有()A.0个B.1个C.2个D.3个6.如图△ABC中,∠ACB=90゜,AD平分∠BAC交BC于D,DE垂直AB于E,若DE=1.5cm,BD=3cm,则BC=()A.3cm B.7.5cm C.6cm D.4.5cm7.在△ABC中,∠C=90゜,AD平分∠BAC交BC于D,BD:DC=3:2,点D到AB的距离为6,则BC长为()A.10 B.20 C.15 D.258.如图,在△ABC中,∠B、∠C的角平分线交于点0,OD⊥AB于D,OE⊥AC于E,则OD与OE的大小关系是()A.OD>OE B.OD<OE C.OD=OE D.不能确定三、解答题9.如图,△ABC中,∠C=90゜,AD是∠BAC的平分线,DE⊥AB于E,F在AC上,且BE=CF,求证:(1)DE=DC;(2)BD=DF.10.如图,四边形ABCD中,AB=AD,CB=CD,点P是AC上一点,PE⊥BC于E,PF⊥CD于F,求证:PE=PF.11.已知,如图,BD是∠ABC的平分线,AB=BC,点P在BD上,PM⊥AD,PN⊥CD,垂足分别是M、N.试说明:PM=PN.12.如图,BD是∠ABC的平分线,DE⊥AB于E,S△ABC=90,AB=18,BC=12,求DE的长.13.如图.已知在△ABC中,∠A、∠B的角平分线交于点O,过O作OP⊥BC于P,OQ⊥AC于Q,OR⊥AB 于R,AB=7,BC=8,AC=9.(1)求BP、CQ、AR的长.(2)若BO的延长线交AC于E,CO的延长线交AB于F,若∠A=60゜,求证:OE=OF.《12.3 角的平分线的性质》参考答案与试题解析一、填空题1.如图,∠B=∠D=90゜,根据角平分线性质填空:(1)若∠1=∠2,则BC = DC .(2)若∠3=∠4,则AB = AD .【考点】角平分线的性质.【分析】(1)根据角平分线性质推出即可;(2)根据角平分线性质推出即可.【解答】解:(1)∵∠B=∠D=90°,∴AB⊥BC,AD⊥DC,∵∠1=∠2,∴BC=CD,故答案为:BC,DC.(2)∵AB⊥BC,AD⊥DC,∵∠3=∠4,∴AB=AD,故答案为:AB,AD.【点评】本题考查了角平分线性质的应用,注意:角平分线上的点到角两边距离相等.2.如图,BD是∠ABC的平分线,DE⊥AB于E,DF⊥BC于F,AB=12,BC=15,S△ABD=36,则S△BCD= 45 .【考点】角平分线的性质.【分析】首先根据△ABD的面积计算出DE的长,再根据角平分线上的点到角两边的距离相等可得DE=DF,然后计算出DF的长,再利用三角形的面积公式计算出△BCD的面积即可.【解答】解:∵S△ABD=36,∴•AB•ED=36,×12×ED=36,解得:DE=6,∵BD是∠ABC的平分线,DE⊥AB于E,DF⊥BC于F,∴DE=DF,∴DF=6,∵BC=15,∴S△BCD=•CB•DF=×15×6=45,故答案为:45.【点评】此题主要考查了角平分线的性质,关键是掌握角平分线上的点到角两边的距离相等.3.如图,△ABC的三边AB、BC、CA长分别是20、30、40,其三条角平分线将△ABC分成三个三角形,则S△ABO:S△BCO:S△CAO等于2:3:4 .【考点】角平分线的性质;三角形的面积.【专题】常规题型.【分析】由角平分线的性质可得,点O到三角形三边的距离相等,即三个三角形的AB、BC、CA的高相等,利用面积公式即可求解.【解答】解:过点O作OD⊥AC于D,OE⊥AB于E,OF⊥BC于F,∵O是三角形三条角平分线的交点,∴OD=OE=OF,∵AB=20,BC=30,AC=40,∴S△ABO:S△BCO:S△CAO=2:3:4.故答案为:2:3:4.【点评】此题主要考查角平分线的性质和三角形面积的求法,难度不大,作辅助线很关键.4.如图,AD是△ABC的角平分线,若AB=2AC.则S△ABD:S△ACD= 2 .【考点】角平分线的性质.【分析】过D作DM⊥AC于M,DN⊥AB于N,根据角平分线性质得出DM=DN,根据三角形面积公式求出即可.【解答】解:过D作DM⊥AC于M,DN⊥AB于N,∵AD是△ABC的角平分线,∴DM=DN,∴S△ABD:S△ACD=(AB×DN):(AC×DM)=AB:AC=2AC:AC=2,故答案为:2.【点评】本题考查了角平分线性质的应用,注意:角平分线上的点到角两边的距离相等.二、选择题5.如图,已知点P、D、E分别在OC、OA、OB上,下列推理:①∵OC平分∠AOB,∴PD=PE;②∵OC平分∠AOB,PD⊥OA,PE⊥OB,∴PD=PE;③∵PD⊥OA,PE⊥OB,∴PD=PE;其中正确的个数有()A.0个B.1个C.2个D.3个【考点】角平分线的性质.【分析】直接根据角平分线的性质进行解答即可.【解答】解:∵OC平分∠AOB,PD⊥OA,PE⊥OB,∴PD=PE.故选B.【点评】本题考查的是角平分线的性质,即角平分线上的点到角两边的距离相等.6.如图△ABC中,∠ACB=90゜,AD平分∠BAC交BC于D,DE垂直AB于E,若DE=1.5cm,BD=3cm,则BC=()A.3cm B.7.5cm C.6cm D.4.5cm【考点】角平分线的性质.【分析】根据角平分线的性质得出CD长,代入BC=BD+DC求出即可.【解答】解:∵∠ACB=90°,∴AC⊥BC,∵DE⊥AB,AD平分∠BAC,∴DE=DC=1.5cm,∵BD=3cm,∴BC=BD+DC=3cm+1.5cm=4.5cm,故选D.【点评】本题考查了角平分线性质的应用,注意:角平分线上的点到角两边的距离相等.7.在△ABC中,∠C=90゜,AD平分∠BAC交BC于D,BD:DC=3:2,点D到AB的距离为6,则BC长为()A.10 B.20 C.15 D.25【考点】角平分线的性质.【分析】过点D作DE⊥AB于E,根据角平分线上的点到角的两边的距离相等可得DC=DE,然后求出BD 的长,再根据BC=BD+DE代入数据进行计算即可得解.【解答】解:如图,过点D作DE⊥AB于E,∵点D到AB的距离为6,∴DE=6,∵∠C=90°,AD平分∠BAC交BC于D,∴DC=DE=6,∵BD:DC=3:2,∴BD=×3=9,∴BC=BD+DE=9+6=15.故选C.【点评】本题考查了角平分线上的点到角的两边的距离相等的性质,熟记性质是解题的关键,作出图形更形象直观.8.如图,在△ABC中,∠B、∠C的角平分线交于点0,OD⊥AB于D,OE⊥AC于E,则OD与OE的大小关系是()A.OD>OE B.OD<OE C.OD=OE D.不能确定【考点】角平分线的性质.【分析】根据三角形的角平分线相交于一点,连接AO,则AO平分∠BAC,然后根据角平分线上的点到角的两边的距离相等解答.【解答】解:如图,连接AO,∵∠B、∠C的角平分线交于点0,∴AO平分∠BAC,∵OD⊥AB,OE⊥AC,∴OD=OE.故选C.【点评】本题考查了角平分线上的点到角的两边的距离相等的性质,根据三角形的角平分线相交于一点作辅助线并判断出AO平分∠BAC是解题的关键.三、解答题9.如图,△ABC中,∠C=90゜,AD是∠BAC的平分线,DE⊥AB于E,F在AC上,且BE=CF,求证:(1)DE=DC;(2)BD=DF.【考点】角平分线的性质;全等三角形的判定与性质.【专题】证明题.【分析】(1)根据角平分线上的点到角的两边的距离相等证明即可;(2)利用“边角边”证明△BDE和△FDC全等,再根据全等三角形对应边相等证明即可.【解答】证明:(1)∵∠C=90°,AD是∠BAC的平分线,DE⊥AB,∴DE=DC;(2)在△BDE和△FDC中,,∴△BDE≌△FDC(SAS),∴BD=DF.【点评】本题考查了角平分线上的点到角的两边的距离相等的性质,全等三角形的判定与性质,是基础题,熟记性质是解题的关键.10.如图,四边形ABCD中,AB=AD,CB=CD,点P是AC上一点,PE⊥BC于E,PF⊥CD于F,求证:PE=PF.【考点】全等三角形的判定与性质;角平分线的性质.【专题】证明题.【分析】根据“SSS”可得到△ABC≌△ADC,则∠BCA=∠DCA,再利用角平分线的性质即可得到结论.【解答】证明:在△ABC和△ADC中,,∴△ABC≌△ADC(SSS),∴∠BCA=∠DCA,∵PE⊥BC于E,PF⊥CD于F,∴PE=PF.【点评】本题考查了全等三角形的判定与性质:三边都对应相等的两三角形全等;全等三角形的对应边相等,对应角相等.角平分线的性质:角的平分线上的点到角的两边的距离相等.11.已知,如图,BD是∠ABC的平分线,AB=BC,点P在BD上,PM⊥AD,PN⊥CD,垂足分别是M、N.试说明:PM=PN.【考点】角平分线的性质;全等三角形的判定与性质.【专题】证明题.【分析】根据角平分线的性质以及已知条件证得△ABD≌△CBD(SAS),然后由全等三角形的对应角相等推知∠ADB=∠CDB;再由垂直的性质和全等三角形的判定定理AAS判定△PMD≌△PND,最后根据全等三角形的对应边相等推知PM=PN.【解答】证明:在△ABD和△CBD中,AB=BC(已知),∠ABD=∠CBD(角平分线的性质),BD=BD(公共边),∴△ABD≌△CBD(SAS),∴∠ADB=∠CDB(全等三角形的对应角相等);∵PM⊥AD,PN⊥CD,∴∠PMD=∠PND=90°;又∵PD=PD(公共边),∴△PMD≌△PND(AAS),∴PM=PN(全等三角形的对应边相等).【点评】本题考查了角平分线的性质、全等三角形的判定与性质.由已知证明△ABD≌△CBD是解决的关键.12.如图,BD是∠ABC的平分线,DE⊥AB于E,S△ABC=90,AB=18,BC=12,求DE的长.【考点】角平分线的性质.【分析】过点D作DF⊥BC于F,根据角平分线上的点到角的两边的距离相等可得DE=DF,然后根据三角形的面积列出方程求解即可.【解答】解:如图,过点D作DF⊥BC于F,∵BD是∠ABC的平分线,DE⊥AB,∴DE=DF,∴S△ABC=AB•DE+BC•DF=90,即×18•DE+×12•DE=90,解得DE=6.【点评】本题考查了角平分线上的点到角的两边的距离相等的性质,三角形的面积,熟记性质并作出辅助线是解题的关键.13.如图.已知在△ABC中,∠A、∠B的角平分线交于点O,过O作OP⊥BC于P,OQ⊥AC于Q,OR⊥AB 于R,AB=7,BC=8,AC=9.(1)求BP、CQ、AR的长.(2)若BO的延长线交AC于E,CO的延长线交AB于F,若∠A=60゜,求证:OE=OF.【考点】角平分线的性质;全等三角形的判定与性质.【分析】(1)根据角平分线性质得出OR=OQ=OP,根据勾股定理起床AR=AQ,CQ=CP,BR=BP,得出方程组,求出即可;(2)过O作OM⊥AC于肘,ON⊥AB于N,求出OM=ON,证出△FON≌△EOM即可.【解答】解:连接AO,OB,OC,∵OP⊥BC,OQ⊥AC,OR⊥AB,∠A、∠B的角平分线交于点O,∴OR=OQ,OR=OP,∴由勾股定理得:AR2=OA2﹣OR2,AQ2=AO2﹣OQ2,∴AR=AQ,同理BR=BP,CQ=CP,即O在∠ACB角平分线上,设BP=BR=x,CP=CQ=y,AQ=AR=z,则x=3,y=5,z=4,∴BP=3,CQ=5,AR=4.(2)过O作OM⊥AC于M,ON⊥AB于N,∵O在∠A的平分线,∴OM=ON,∠ANO=∠AMO=90°,∵∠A=60°,∴∠NOM=120°,∵O在∠ACB、∠ABC的角平分线上,∴∠EBC+∠FCB=(∠ABC+∠ACB)=×(180°﹣∠A)=60°,∴∠FON=∠EOM,在△FON和△EOM中∴△FON≌△EOM,∴OE=OF.【点评】本题考查了角平分线性质和全等三角形的性质和判定的应用,注意:角平分线上的点到角两边的距离相等.。
八年级数学上册 12.3 角的平分线的性质学案(新版)新人教版

12.3角的平分线的性质自学案(一)学习目标1.会用尺规作一个角的平分线,知道作法的合理性;2.探索并证明角的平分线的性质;3.能用角的平分线的性质解决简单问题。
(二)学习重点探索并证明角的平分线的性质。
(三)学习难点能用角的平分线的性质解决简单问题。
(四)课前预习1.点P 是∠BAC 内一点,PE ⊥AB 于点E ,PF ⊥AC 于点F ,由PE=PF ,PA=PA 得到△PEA ≌△PFA 的理由是( )A.HLB.ASAC.AASD.SAS2.如图,两条笔直的公路l 1,l 2相交于点O,村庄C 的村民在公路的旁边建三个加工厂A,B,D,已AB=BC=CD=DA=5千米,村庄C 到公路l 1的距离为4千米,则村庄C 到公路l 2的距离是( )A.3千米B.4千米C.5千米D.6千米3.如图,OP 平分AOB ∠,OA PA ⊥,OB PB ⊥,垂足分别为A,B 。
下列结论中不一定成立的是( )。
A.PA=PBB.PO 平分APB ∠C.OA=OBD.AB 垂直平分OP4.如图所示,AB ∥CD ,O 为∠BAC 、∠ACD 的平分线的交点,OE ⊥AC 于E ,且OE =5,则AB 与CD 间的距离等于____.5.如图,现有一块三角形的空地,其三条边长分别是20m,30m,40m.现要把它分成面积比为2∶3∶4的三部分,分别种植不同种类的花,请你设计一种方案,并简单说明理由.(五)疑惑摘要预习之后,你还有哪些没有弄清的问题,请记下来,课堂上我们共同探讨。
探究案典型例题例1、如图,BC、AD分别垂直OA、OB,BC和AD相交于E,且OE平分∠AOB. 求证:EA=EB.例2、如图,在△ABC中,∠C=90° AD是∠BAC的平分线,DE⊥AB于E,F在AC上,BD=DF.求证:CF=EB.训练案课后作业一、选择题1.如图,∠1=∠2,PD⊥OA于点D,PE⊥OB于点E,则下列结论错误的是( )A.PD=PEB.OD=OEC.PD=ODD.∠OPD=∠OPE2.如图,Rt△ABC中,∠C=90°,∠ABC的平分线BD交AC于点D.若CD=3cm,则点D到AB的距离DE是( )A.5cmB.4cmC.3cmD.2cm3.尺规作一个角的平分线的示意图如图所示,则能说明∠AOC=∠BOC的依据是( )A.SSSB.ASAC.AASD.角平分线上的点到角两边的距离相等4.如图,点D,P,E分别在OA,OC,OB上,且PD=PE,以下不能得出OC平分∠AOB的是( )A.OD=OEB.∠DPO=∠EPOC.∠ODP=∠OEPD.PD⊥OA,PE⊥OB二、填空题5.在Rt△ABC中,∠C=90°,若BC=10,AD平分∠BAC交BC于点D, 且BD∶CD=3∶2,则点D到线段AB的距离为.6.如图,AD是△ABC中∠BAC的平分线,DE⊥AB交AB于点E,DF⊥AC交AC于点F,S△ABC=7,DE=2,AB=4,则AC的长是.7.如图,△ABC的外角∠ACD的平分线CP与内角∠ABC的平分线BP交于点P,若∠BPC=40°,则∠CAP= .8.如图,DB⊥AB,DC⊥AC,BD=DC,∠BAC=80°,则∠ADC的度数是.三、解答题9.如图,D是△ABC外角∠ACE的平分线上的一点,DF⊥AC于F,DE⊥BC交BC的延长线于E,求证:CF=CE.10.如图,∠1=∠2,AE⊥OB于E,BD⊥OA于D,AE与BD相交于点C.求证:AC=BC.11.已知:如图,BE=CF,BF⊥AC于点F,CE⊥AB于点E,BF和CE交于点D,求证:AD平分∠BAC.四、拓展提高如图,四边形ABDC中,∠D=∠B=90゜,点O为BD的中点,且OA平分∠BAC.(1)求证:OC平分∠ACD;(2)求证:OA⊥OC;(3)求证:AB+CD=AC.。
人教版数学八年级上册知识分类训练-12.3-角平分线的性质(含详案)

人教版八年级上册知识分类训练12.3 角平分线的性质1、角平分线的定义:一条射线把一个角分成两个相等的角,这条射线叫做这个角的平分线。
2、角平分线的性质:角的平分线上的点到这个角的两边的距离相等。
用数学语言表示为:∵ QD⊥OA,QE⊥OB,点Q在∠AOB的平分线上∴ QD=QE4、角平分线的判定方法:角的内部到角的两边的距离相等的点在角的平分线上。
用数学语言表示为:∵ QD⊥OA,QE⊥OB,QD=QE.∴点Q在∠AOB的平分线上.5、尺规作角的平分线:画法:①以O为圆心,适当长为半径作弧,交OA于M,交OB于N.②分别以M,N为圆心.大于 1/2 MN的长为半径作弧.两弧在∠AOB的内部交于C.③作射线OC.所以,射线OC即为所求.针对训练1.如图,OC平分∠AOB,点P在OC上,PD⊥OB,PD=2,则点P到OA的距离是( )A.4B.3C.2D.12.如图,在Rt△ABC中,∠C=90°,以点A为圆心,适当长为半径作弧,分别交AB,AC 于点D,E,再分别以点D,E,为圆心,以大于DE的长度为半径作弧,两弧交于点F,作射线AF交BC于点G,若AB=12,CG=3,则△ABG的面积是( )A.12B.18C.24D.363.如图,OP平分∠MON,PA⊥ON于点A,点Q是射线OM上的一个动点.若PA=4,则PQ的长不可能是( )A.3.9B.4C.4.3D.5.54.如图,△ABC的∠B的外角的平分线BD与∠C的外角的平分线CE相交于点P,若点P 到AC的距离为3,则点P到AB的距离为( )A.1B.2C.3D.45.如图,在四边形ABCD中,∠A=90°,AD=4,BC=6,对角线BD平分∠ABC,则△BCD 的面积为( )A.15B.12C.8D.66.如图,已知△ABC的周长是18cm,∠ABC和∠ACB的角平分线交于点O,OD⊥BC于点D,若OD=3cm,则△ABC的面积是( )cm2.A.24B.27C.30D.337.如图,在△ABC中,AD是∠BAC的角平分线,若BA=5,AC=2,S△ABC=14,则S△ABD = .8.如图,在Rt△ABC中,∠C=90°,BD是∠ABC的角平分线,如果AB=10,△ADB的面积是15,则CD的长为 .9.如图,在Rt△ABC中,∠ACB=90°,AD平分∠CAB,若CD=4,则点D到AB的距离为 .10.如图,射线OC是∠AOB的角平分线,D是射线OC上一点,DP⊥OA于点P,DP=5,若点Q是射线OB上一点,OQ=4,则△ODQ的面积是 .11.如图,在△ABC中,BD是△ABC的角平分线,DE⊥AB于点E,DE=2.AB=6.BC=4,求△ABC的面积.12.如图在△ABC中,∠B=∠C,点D是BC的中点,DE⊥AB于点,DF⊥AC于点F.求证:AD是△ABC的角平分线.13.如图,CB=CD,∠D+∠ABC=180°,CE⊥AD于E,CF⊥AB交AB的延长线于点F.求证:AC平分∠DAB.14.如图,△ABC中,∠BAC=90°,AD⊥BC,垂足为D.(1)求作∠ABC的平分线,分别交AD,AC于P,Q两点;(要求:尺规作图,保留作图痕迹,不写作法)(2)证明AP=AQ.15.已知:如图,OC是∠AOB的平分线,P是OC上的一点,PD⊥OA,PE⊥OB,垂足分别为D、E,点F是OC上的另一点,连接DF,EF.求证:DF=EF.16.如图,四边形ABCD中,∠B=∠C=90°,点E为BC的中点,且AE平分∠BAD.(1)求证:DE平分∠ADC;(2)求证:AB+CD=AD.17.如图,△ABC中,点D在边BC延长线上,∠ACB=110°,∠ABC的平分线交AD于点E,过点E作EH⊥BD,垂足为H,且∠CEH=55°.(1)求∠ACE的度数;(2)求证:AE平分∠CAF;(3)若AC+CD=14,AB=8.5,且S△ACD=21,求△ABE的面积.参考答案1.解:过P作PE⊥AO于E,∵OC平分∠AOB,点P在OC上,PD⊥OB,∴PE=PD=2,∴点P到OA的距离是2.故选:C.2.解:过点G作GH⊥AB于点H,根据题意得,AF是∠CAB的角平分线,∵∠C=90°,∴AC⊥CG,∵GH⊥AB,∴CG=GH,∵CG=3,∴,故选:B.3.解:∵OP平分∠MON,PA⊥ON于点A,PA=4,∴当PQ⊥AM时,PQ=PA=4,∴PQ≥4,∴PQ的长不可能3.9.故选:A.4.解:过P作PQ⊥AC于Q,PW⊥BC于W,PR⊥AB于R,∵△ABC的∠B的外角的平分线BD与∠C的外角的平分线CE相交于点P,∴PQ=PW,PW=PR,∴PR=PQ,∵点P到AC的距离为3,∴PQ=PR=3,则点P到AB的距离为3,故选:C.5.解:过点D作DE⊥BC,垂足为E,∵BD平分∠ABC,DE⊥BC,DA⊥AB,∴DE=DA=4,∵BC=6,∴△BCD的面积=BC•DE=×6×4=12,故选:B.6.解:过O点作OE⊥AB于E,OF⊥AC于F,连接OA,如图,∵OB平分∠ABC,OD⊥BC,OE⊥AB,∴OE=OD=3,同理可得OF=OD=3,∴S△ABC=S△OAB+S△OBC+S△OAC=×OE×AB+×OD×BC+×OF×AC=(AB+BC+AC),∵△ABC的周长是18,∴S△ABC=×18=27(cm2).故选:B.7.解:过点D作DE⊥AB,DF⊥AC于点E,F,∵AD是∠BAC的角平分线,∴DE=DF,设DE=DF=h,∵BA=5,AC=2,S△ABC=14,∴AB•h+AC•h=14,即×5h+×2h=14,解得h=4,∴S△ABD=AB•DE=×5×4=10.故答案为:10.8.解:如图,过点D作DE⊥AB于点E,∵AB=10,△ADB的面积是15,∴,∴DE=3,在Rt△ABC中,∠C=90°,BD是∠ABC的角平分线,∴CD=DE=3,故答案为:3.9.解:过点D,作DE⊥AB,交AB于点E,∵∠ACB=90°,AD平分∠CAB,∴DE=CD=4,故答案为:4.10.解:作DH⊥OB于点H,∵OC是∠AOB的角平分线,DP⊥OA,DH⊥OB,∴DH=DP=5,∴△ODQ的面积=OQ•DH=4×5=10,故答案为:10.11.解:如图,过点D作DF⊥BC于点F.∵BD是△ABC的角平分线,DE⊥AB,DF⊥BC,∴DF=DE=2,又∵AB=6,BC=4,∴=.12.证明:∵点D是BC的中点,∴BD=CD,∵DE⊥AB,DF⊥AC,∴∠BED=∠CFD=90°,在△BED和△CFD中,,∴△BED≌△CFD(AAS),∴DE=DF,即点D到AB和AC的距离相等,∴AD是△ABC的角平分线.13.证明:∵CE⊥AD于E,CF⊥AB,∴∠DEC=∠CFB=90°,∵∠D+∠ABC=180°,∠CBF+∠ABC=180°,∴∠D=∠CBF,在△CDE与△CBF中,,∴△CDE≌△CBF(AAS),∴CE=CF,∴AC平分∠DAB.14.(1)解:如图所示,BQ为所求作;(2)证明:∵BQ平分∠ABC,∴∠ABQ=∠CBQ,∵∠BAC=90°∴∠AQP+∠ABQ=90°,∵AD⊥BC,∴∠ADB=90°,∴∠CBQ+∠BPD=90°,∵∠ABQ=∠CBQ,∴∠AQP=∠BPD,又∵∠BPD=∠APQ,∴∠AQP=∠APQ,∴AP=AQ.15.证明:∵OP是∠AOB的平分线,PD⊥OA,PE⊥OB,∴PD=PE,在Rt△OPD和Rt△OPE中,,∴Rt△OPD≌Rt△OPE(HL),∴OD=OE,∵OC是∠AOB的平分线,∴∠DOF=∠EOF,在△ODF和△OEF中,,∴△ODF≌△OEF(SAS),∴DF=EF.16.证明:(1)如图,过点E作EF⊥AD于F,∵∠B=90°,AE平分∠DAB,∴BE=EF,∵E是BC的中点,∴BE=CE,∴CE=EF,又∵∠C=90°,EF⊥AD,∴DE是∠ADC的平分线.(2)∵AE平分∠BAD,DE平分∠ADC,EF⊥AD,∠B=∠C=90°,∴AB=AF,DC=DF,∴AB+CD=AF+FD=AD.17.(1)解:∵∠ACB=110°,∴∠ACD=180°﹣110°=70°,∵EH⊥BD,∴∠CHE=90°,∵∠CEH=55°,∴∠ECH=90°﹣55°=35°,∴∠ACE=180°﹣35°﹣110°=35°;(2)证明:过E点分别作EM⊥BF于M,EN⊥AC与N,∵BE平分∠ABC,∴EM=EH,∵∠ACE=∠ECH=40°,∴CE平分∠ACD,∴EN=EH,∴EM=EN,∴AE平分∠CAF;(3)解:∵AC+CD=14,S△ACD=21,EM=EN=EH,∴S△ACD=S△ACE+S△CED=AC•EN+CD•EH=(AC+CD)•EM=21,即,解得EM=3,∵AB=8.5,∴S△ABE=AB•EM=.。
人教版八年级数学上册练习 12.3《角的平分线的性质》

12.3 角的平分线的性质1.如图11-100所示,在Rt △ABC中,∠C=90°,AD是角平分线,DE⊥AB于点E,下列结论错误的是()A.BD+DE=BC B.DE平分∠ADBC.DA平分∠EDC D.DE+AC>AD2.如图11-101所示,在△ABC中,AD平分∠BAC,DE⊥AB于E,DF⊥AC 于F,则下列结论中错误的是()A.DE=DF B.AD上任意一点到E,F两点的距离相等C.AE=AF D.BD=DC3.如图11-102所示,BE⊥AC于E,CF⊥AB于F,AE=AF,BE与CF交于点D,则:①△ABE≌△ACF;②△BDF≌△CDE;③点D在∠BAC的平分线上.以上结论正确的是()A.①B.②C.①②D.①②③4.如图11-103所示,△ABC中,P,Q分别是BC,AC上的点,作PR⊥AB,P S⊥AC,垂足分别是R,S,若A Q=P Q,P R=P S,下面三个结沦:①A S=A R:②Q P∥AR;③△B R P≌△C S P.其中正确的是()A.①③B.②③C.①②D.①②③5.在△ABC中,∠C=90°,AD平分∠BA C,BC=10 cm,BD=7 cm,则点D 到AB的距离是.6.如图11-104所示,在直线l上找一点,使这点到∠AOB的两边OA,OB的距离相等,则这个点是.7.如图11-105所示,已知O为∠BAC的平分线与∠ACD的平分线的交点,OE⊥AC于E,若OE=2,则点O到AB的距离与点O到CD的距离的和是.8.如图11-106所示,已知△ABC的角平分线BM,CN相交于点P,求证点P 到AB,BC,CA的距离相等.9.如图1l-107所示,BD是∠ABC的平分线,BA=BC,点P在BD上,且PM⊥AD,PN⊥CD.求证PM=PN.10.如图11-108所示,BF⊥AC于点F,CE⊥AB于点E,BF与CE交于D,且BD=CD.(1)求证D在∠BAC的平分线上;(2)若将条件:BD=CD和结论:D在∠BAC的平分线上互换,结论成立吗?试说明理由.11.如图11-109所示,点B,C在∠A的两边上,且AC=AB,P为∠A内一点,PC=PB,PE⊥AB、PF⊥AC,垂足分别为E,F.求证PE=PF.12.如图11-110所示,已知点B,C分别在∠MAN的两边上,BD⊥AM,CE⊥AN,垂足分别为D,E,BD,CE相交于点F,且BF=CF.求证点F在∠A的平分线上.(提示:在同一个三角形中,等边对等角,等角对等边)13.如图11-111所示,在△ABC中,∠C=90°,AC=BC,AD平分∠CAB,交BC于D,能否在AB上确定一点E,使△BDE的周长等于AB的长?请说明理由.参考答案1.B[提示:由AD 是∠BAC 的平分线,DE ⊥AB ,∠C =90°,可知DC =DE ,所以BD +DE =BD +CD =BC ,选项A 成立;DE +AC =DC +AC >AD ,选项D 成立;由AD 平分∠BAC ,∠DEA =90°,∠C =90°,可知∠EDA =∠CDA ,所以选项C 成立.]2.D [提示:利用角平分线的性质及全等三角形的有关知识可解本题.]3.D [提示:由ASA 可知Rt △ABE ≌Rt △ACF ,从而AC =AB ,又AE =AF ,故CE =BF ,从而可由AAS 得Rt △DFB ≌Rt △DEC ,有DE =DF ,又DE ,DF 分别垂直于AC ,AB ,故点D 在∠BAC 的平分线上.故①②③均正确.]4.C[提示:连接AP ,由P R =P S 及已知条件易证Rt △A R P ≌Rt △A S P (HL ),故A R =A S ,∠R AP =∠S AP ,又Q A =Q P ,故∠Q AP =∠Q PA =∠RAP .从而P Q ∥A R ,但无法证明△B R P ≌△C S P .]5.3 cm[提示:由AD 平分∠BAC 知D 到AB ,AC 的距离相等,又BC =10 cm ,BD =7 cm ,故CD =3 ,又∠ACD =90°,则点D 到AC 的距离即是CD 的长,为3 cm ,故D 到AB 的距离也是3 cm .]6.∠AOB 的平分线与直线l 的交点7.4[提示:过O 分别作AB ,CD 的垂线.则点O 到AB ,CD 的距离均等于OE ,故它们的和为4.]8.证明:过P 点分别作PE ⊥AB 于E ,PF ⊥ BC 于 F ,PG ⊥CA 于G .∵BM 平分∠ABC ,∴PE =PF .同理PF =PC .∴PE =PF =PG ,即点P 到AB ,BC ,CA 的距离相等.9.证明:∵BD 是∠ABC 的平分线,∴∠ABD =∠CBD .在△ABD 和△CBD 中,ABD CBD BD BD ⎧⎪∠=∠⎨⎪=⎩A B =A B (已知)(已证)∴△ABD ≌△CBD (SAS ).∴∠ADB =∠CDB (全等三角形的对应角相等),即DB 是∠ADC 的平分线.又∵PM ⊥AD ,PN ⊥ DC ,∴PM =PN .10.(1)证明:∵BF ⊥AC ,CE ⊥AB ,∴∠BED =∠CFD =90°.在Rt △BED(公共边)和Rt △CFD 中()BED CFD EDB FDC BD CD ∠=∠⎧⎪∠=∠⎨⎪=⎩已知(对顶角相等)∴Rt △BED ≌Rt △CFD(AAS ).∴DE =DF (全等三角形的对应边相等).∴D 在∠ BAC 的平分线上(到角的两边距离相等的点在角的平分线上).(2)解:成立.理由如下:∵点D 在∠BAC 的平分线上,且BF ⊥AC ,CE ⊥AB ,∴DE =DF ,∠BED =∠CFD =90°.在Rt △BED 和Rt △CFD 中,BED CFD DE DF EDB FDC ∠=∠⎧⎪=⎨⎪∠=∠⎩, ∴Rt △BED ≌Rt △CFD (A S A ). ∴BD =DC (全等三角形的对应边相等).11.证明:连接AP ,在Rt △ABP 和△ACP 中,AB AC AP AP PB PC =⎧⎪=⎨⎪=⎩,,(公共边),∴△ABP ≌△ACP (SSS )∴∠BAP =∠CAP .又∵PE ⊥AB ,PF ⊥AC ,∴PE =PF .12.证明:如图11-112所示,连接BC ,作射线AF .∵BD ⊥AM ,CE ⊥AN ,∴∠ADB =∠AEC =∠BDC =∠CEB =90°.∵BF =CF ,∵∠DBC =∠ECB .又∵BC =CB ,∴△BCD ≌△CBE .∴BD =CE ,∴EF =DF ,∴点F 在∠CAB 的平分线上.13.解:能.过D 作DE ⊥AB ,交AB 于E 点,则E 点即可满足要求.理由:∵AD 平分∠CAB ,CD ⊥AC ,DE ⊥AB ,∴CD =DE .在Rt △ACD 和Rt △AED 中,,,CD DE AD AD =⎧⎨=⎩∴Rt △ACD ≌Rt △AED (HL )∴AC =AE .∵AC =BC ,.BC =AE .∴△BDE 的周长=BD +DE +EB =BD +DC +EB =BC +EB =AE +EB =AB .(已证)。
八年级数学上册12.3角平分线的性质(讲+练)(8大题型)-【重要笔记】2022-2023学年八年级

12.3 角平分线的性质角的平分线的性质角的平分线的性质:角的平分线上的点到角两边的距离相等。
注意:用符号语言表示角的平分线的性质定理:若CD平分∠ADB,点P是CD上一点,且PE⊥AD于点E,PF⊥BD于点F,则PE=PF.角的平分线的尺规作图角平分线的尺规作图(1)以O为圆心,适当长为半径画弧,交OA于D,交OB于E.(2)分别以D、E为圆心,大于12DE的长为半径画弧,两弧在∠AOB内部交于点C.(3)画射线OC.射线OC即为所求.题型1:作已知角的平分线1.尺规作图:已知:∠CBA,求作∠CAB的平分线.【变式1-1】如图,在直线MN上求作一点P,使点P到射线OA和OB的距离相等。
(不写作法,保留作图痕迹)【变式1-2】如图,在Rt△ABC中,△C=90°.(1)作△BAC的平分线AD交边BC于点D.(尺规作图,保留作图痕迹,不写作法).(2)在(1)的条件下,若△BAC=28°,求△ADB的度数.题型2:角平分线的性质的应用-证明线段2.如图,已知OE平分△AOB,BC△OA于点C,AD△OB于点D,求证:EA=EB.【变式2-1】如图,点D、B分别在△A的两边上,C是△A内一点,AB = AD,BC = CD,CE△AD于E,CF△AF于F.求证:CE = CF.【变式2-2】已知:如图,OC是△AOB的平分线,P是OC上的一点,PD△OA,PE△OB,垂足分别为D、E,点F是OC上的另一点,连接DF,EF.求证:DF=EF.题型3:角平分线的性质的应用-和差关系3.如图,在△ABC中,△C=90°,△CAD=△BAD,DE△AB于E,点F在边AC 上,连接DF.(1)求证:AC=AE;(2)若AC=8,AB=10,求DE的长;(3)若CF=BE,直接写出线段AB,AF,EB的数量关系.【变式3-1】如图,△ABC的边BC的垂直平分线DE交△ABC的外角平分线AD于点D,DF△AB于点F,且AB>AC,试探究BF、AC、AF之间的数量关系,并说明理由.【变式3-2】题型4:角平分线的性质的应用-面积相关4.如图,BD是ΔABC的角平分线,DE⊥AB垂足为E,ΔABC的面积为70,AB= 16,BC=12,求DE的长.【变式4-1】如图,AD是△ABC的角平分线,DF△AB,垂足为F,如图DE=DG,△ADG和△AED的面积分别为50和38,求△EDF的面积【变式4-2】如图,在ΔABC中,AD为∠BAC的平分线,DE⊥AB于点E,DF⊥AC于点F,若ΔABC的面积为21cm2,AB=8cm,AC=6cm,求DE的值.角的平分线的判定角平分线的判定:角的内部到角两边距离相等的点在角的平分线上.注意:用符号语言表示角的平分线的判定:若PE⊥AD于点E,PF⊥BD于点F,PE=PF,则PD平分∠ADB题型5:角平分线的判定5.如图,∠B=∠C=90°,M是BC的中点,DM平分∠ADC,求证:AM平分∠DAB.【变式5-1】如图所示,PA=PB,△1+△2=180°.求证:OP平分△AOB.【变式5-2】如图所示,AP、CP分别是△ABC外角△MAC和△NCA的平分线,它们交于点P.求证:BP为△MBN的平分线.题型7:角平分线的性质与判定综合6.如图,已知点A、C分别在△GBE的边BG、BE上,且AB=AC,AD△BE,△GBE的平分线与AD交于点D,连接CD.求证:(1)AB=AD;(2)CD平分△ACE.【变式6-1】如图,已知△ABC中BC边的垂直平分线DE与∠BAC的平分线交于点E,EF⊥AB交AB的延长线于点F,BG⊥AC交AC于点G.求证.(1)BF=CG.(2)若AB=6,AC=8,求AF的长度.【变式6-2】如图,在△ABC外作两个大小不同的等腰直角三角形,其中∠DAB=∠CAE=90°,AB=AD,AC=AE.连接DC、BE交于F点.(1)求证:△DAC△△BAE.(2)直线DC、BE是否互相垂直,请说明理由.(3)求证:AF平分∠DFE.【变式6-3】如图1,射线BD交△ABC的外角平分线CE于点P,已知△A=78°,△BPC=39°,BC=7,AB=4.(1)求证:BD平分△ABC;(2)如图2,AC的垂直平分线交BD于点Q,交AC于点G,QM△BC于点M,求MC的长度.题型7:角平分线的实际应用7.某地有两条相交叉的公路,计划修建一个饭馆:希望饭馆点P既在MN这条公路上,又到直线OA、OB的距离相等.你能确定饭馆应该建在什么位置吗?(保留作图痕迹)【变式7-1】如图:某地要在三条公路围成的一块平地上修建一个公园,要使公园到三条公路的距离相等,应在何处修建?(使用尺规作图,保留作图痕迹)并证明你的观点.【变式7-2】太和中学校园内有一块直角三角形(Rt △ABC)空地,如图所示,园艺师傅以角平分线AD为界,在其两侧分别种上了不同的花草,在△ABD区域内种植了月季花,在△ACD区域内种植了牡丹花,并量得两直角边AB=10m,AC=6m,分别求月季花与牡丹花两种花草的种植面积.题型8:三角形中的角平分线8.已知△ABC的三条角平分线相交于点O,过点O作OD△BC,OE△AC,OF△AB.求证:OD=OE=OF.【变式8-1】如图,△ABC中,AB=6,AC=7,BD、CD分别平分△ABC、△ACB,过点D作直线平行于BC,交AB、AC于E、F. 求△AEF的周长.【变式8-2】如图,△ABC的三边AB、BC、CA长分别是20、30、40,其三条角平分线将△ABC分为三个三角形,则S△ABO:S△BCO:S△CAO等于?【变式8-3】如图①,在△ABC中,△ABC和△ACB的平分线交于点O,△A=α.(1)如图①,若△A=50°,求△BOC的度数.(2)如图②,连接OA,求证:OA平分△BAC.(3)如图③,若射线BO与△ACB的外角平分线交于点P,求证OC△PC.一、单选题1.如图,在△ABC中,△C=90°,BD平分△ABC,交AC于点D;若DC=3,AB=8则△ABD的面积是()A.8B.12C.16D.242.如图,OP平分△MON,PA△ON于点A,点Q是射线OM上的一个动点,若PA= 4,则PQ的长不可能是()A.3.5B.4C.4.5D.53.如图,已知点O是△ABC内一点,且点O到三边的距离相等,△A=40°,则△BOC=()A.110°B.120°C.130°D.140°4.如图,在四边形ABCD中,AB=CD,BA和CD的延长线交于点E,若点P使得S△PAB=S△PCD,则满足此条件的点P()A.有且只有1个B.有且只有2个C.组成△E的平分线D.组成△E的平分线所在的直线(E点除外)5.如图,在Rt△ACB中,∠ACB=90°,BC=12,BD=2CD,AD平分∠BAC,则点D到AB的距离等于()A.3B.4C.5D.9二、填空题6.如图,在△ABC中,BE平分△ABC交AC于点E,AF△BC于点F,BE、AF交于点P,若AB=9,PF=3,则△ABP的面积是.7.如图,已知△COB=2△AOC,OD平分△AOB,且△COD=18°,则△AOB的度数为.8.如图,在Rt△ABC中,∠ACB=90°, AC=6, BC=8, AB=10, AD是∠BAC的平分线.若P, Q分别是AD和AC上的动点,则PC+PQ的最小值是.9.如图,OP平分△AOB,PM△OA于M,点D在OB上,DH△OP于H.若OD=4,OP=7,PM=3,则DH的长为.三、作图题10.如图,电信部门要在S区修建一座电视信号发射塔.按照设计要求,发射塔到两个城镇A,B的距离必须相等,到两条高速公路m和n的距离也必须相等.发射塔应修建在什么位置?请用尺规作图标出它的位置.四、解答题11.如图,已知AD⊥BC于点D,E是延长线BA上一点,且EC⊥BC于点C,若∠ACE=∠E.求证:AD平分∠BAC.12.如图,在△ABC中,AD为△BAC的平分线,DE△AB于E,DF△AC于F,△ABC 面积是28cm2,AB=20cm,AC=8cm,求DE的长.13.如图,点P是△AOB的角平分线OC上一点,PE△OA,OE=12cm,点G是线段OP的中点,连接EG,点F是射线OB上的一个动点,若PF的最小值为4cm,求△PGE的面积.14.如图,直线AB△CD,点E在CD上,点O、点F在AB上,连接OE,过点F作FH△OE于点H.(1)尺规作图:作△EOF的角平分线OG交CD于点G;(不写作法,保留作图痕迹,并标明字母)(2)在(1)的条件下,已知△OFH=20°,求△OGD的度数.15.如图,△ABC和△EBD中,△ABC=△DBE=90°,AB=CB,BE=BD,连接AE,CD,AE与CD交于点M,AE与BC交于点N.(1)求证:AE=CD;(2)求证:AE△CD;(3)连接BM,有以下两个结论:①BM平分△CBE;②MB平分△AMD,其中正确的一个是(请写序号),并给出证明过程.。
八年级数学上册12.3角的平分线的性质课后训练新版新人教版

角的平分线的性质课后训练基础巩固1.作∠AOB的平分线OC,合理的顺序是( ).①作射线OC;②以O为圆心,适当长为半径画弧,交OA于点D,交OB于点E;③分别以点D,E为圆心,大于的长为半径画弧,两弧在∠AOB内交于点C.A.①②③ B.②①③C.②③① D.③②①2.三角形中到三边距离相等的点是( ).A.三条边的垂直平分线的交点B.三条高的交点C.三条中线的交点D.三条内角平分线的交点3.如图,∠1=∠2,PD⊥OA,PE⊥OB,垂足分别为D,E,下列结论错误的是( ).A.PD=PEB.OD=OEC.∠DPO=∠EPOD.PD=OD4.如图,在△ABC中,∠ACB=90°,BE平分∠ABC,DE⊥AB于点D,如果AC=3 cm,那么AE +DE等于( ).A.2 cm B.3 cmC.4 cmD.5 cm5.在△ABC中,∠C=90°,点O为△ABC三条角平分线的交点,OD⊥BC于点D,OE⊥AC于点E,OF⊥AB于点F,且AB=10 cm,BC=8 cm,AC=6 cm,则点O到三边AB,AC,BC的距离分别为( ).A.2 cm,2 cm,2 c m B.3 cm,3 cm,3 cmC.4 cm,4 cm,4 cmD.2 cm,3 cm,5 cm能力提升6.如图所示,∠AOB=60°,CD⊥OA于点D,CE⊥OB于点E,且CD=CE,则∠DCO=________.7.在△ABC中,∠C=90°,AD平分∠BAC交BC于点D,若BC=32,且BD∶CD=9∶7,则D到AB的距离为__________.8.点O是△ABC内一点,且点O到三边的距离相等,∠A=60°,则∠BOC的度数为__________.9.如图,BN是∠ABC的平分线,点P在BN上,点D,E分别在AB,BC上,∠BDP+∠BEP=180°,且∠BDP,∠BEP都不是直角,求证:PD=PE.10.如图,在△ABC中,∠C=90°,AD平分∠BAC,DE⊥AB于点E,点F在AC上,BD=DF.(1)试说明CF=EB的理由;(2)请你判断AE,AF与BE的大小关系,并说明理由.11.如图,木工师傅常用角尺来作任意一个角的平分线,请你设计一个方案,只用角尺来作∠AOB 的平分线,并说明理由.12.已知:如图所示,BF与CE相交于点D,BD=CD,BF⊥AC于点F,CE⊥AB于点E,求证:点D在∠BAC的平分线上.参考答案1.C。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
角的平分线的性质
课后训练
基础巩固
1.作∠AOB的平分线OC,合理的顺序是( ).
①作射线OC;②以O为圆心,适当长为半径画弧,交OA于点D,交OB于点E;③分别以点D,
E为圆心,大于1
2
DE的长为半径画弧,两弧在∠AOB内交于点C.
A.①②③ B.②①③
C.②③① D.③②①
2.三角形中到三边距离相等的点是( ).
A.三条边的垂直平分线的交点B.三条高的交点
C.三条中线的交点D.三条内角平分线的交点
3.如图,∠1=∠2,PD⊥OA,PE⊥OB,垂足分别为D,E,下列结论错误的是( ).
A.PD=PE
B.OD=OE
C.∠DPO=∠EPO
D.PD=OD
4.如图,在△ABC中,∠ACB=90°,BE平分∠ABC,DE⊥AB于点D,如果AC=3 cm,那么AE +DE等于( ).
A.2 cm B.3 cm C.4 cm D.5 cm
5.在△ABC中,∠C=90°,点O为△ABC三条角平分线的交点,OD⊥BC于点D,OE⊥AC于点E,OF⊥AB于点F,且AB=10 cm,BC=8 cm,AC=6 cm,则点O到三边AB,AC,BC的距离分别为( ).A.2 cm,2 cm,2 c m B.3 cm,3 cm,3 cm
C.4 cm,4 cm,4 cm D.2 cm,3 cm,5 cm
能力提升
6.如图所示,∠AOB=60°,CD⊥OA于点D,CE⊥OB于点E,且CD=CE,则∠DCO=________.
7.在△ABC中,∠C=90°,AD平分∠BAC交BC于点D,若BC=32,且BD∶CD=9∶7,则D到AB的距离为__________.
8.点O是△ABC内一点,且点O到三边的距离相等,∠A=60°,则∠BOC的度数为__________.9.如图,BN是∠ABC的平分线,点P在BN上,点D,E分别在AB,BC上,∠BDP+∠BEP=180°,且∠BDP,∠BEP都不是直角,求证:PD=PE.
10.如图,在△ABC中,∠C=90°,AD平分∠BAC,DE⊥AB于点E,点F在AC上,BD=DF.
(1)试说明CF=EB的理由;
(2)请你判断AE,AF与BE的大小关系,并说明理由.
11.如图,木工师傅常用角尺来作任意一个角的平分线,请你设计一个方案,只用角尺来作∠AOB 的平分线,并说明理由.
12.已知:如图所示,BF与CE相交于点D,BD=CD,BF⊥AC于点F,CE⊥AB于点E,求证:点D在∠BAC的平分线上.
参考答案
1.C
2.D点拨:由角的平分线的性质知,到角两边距离相等的点在角的平分线上,所以到三角形三边距离相等的点是三条内角平分线的交点.
3.D 点拨:由角平分线的性质得PE=PD,进而可证△PEO≌△PDO,得OE=OD,∠DPO=∠EPO,但PD=OD是错误的.
4.B 点拨:因为BE平分∠ABC,∠ACB=90°,DE⊥AB于点D,
所以DE=EC,AE+DE=AE+EC=AC=3 cm.
5.A 点拨:因为点O为△ABC三条角平分线的交点,OD⊥BC于点D,OE⊥AC于点E,OF⊥AB 于点F,
所以设点O到三边AB,AC,BC的距离为x cm.
由三角形的面积公式得,1
2
×6x+
1
2
×8x+
1
2
×10x=
1
2
×6×8,
解得x=2(cm).
6.60°点拨:因为CD⊥OA于点D,CE⊥OB于点E,且CD=CE,所以OC为∠AOB的平分线.
所以∠AOC=30°.
所以∠DCO=60°.
7.14 点拨:设BD=9x,CD=7x,
所以9x+7x=32,解得x=2.
所以BD=18,CD=14.由于AD平分∠BAC交BC于点D,
则点D到AB的距离等于CD=14.
8.120°点拨:点O到三边的距离相等,
所以点O是三个内角的平分线的交点.
又因为∠A=60°,
所以∠B+∠C=120°,1
2
∠B+
1
2
∠C=60°.
所以∠BOC=180°-60°=120°.
9.证明:如图,过点P分别作PF⊥AB于点F,PG⊥BC于点G,
∵BN是∠ABC的平分线,
∴PF=PG.
又∵∠BDP+∠BEP=180°,∠PEG+∠BEP=180°,∴∠BDP=∠PEG.在△PFD和△PGE中,
∵
,
,
,
FDP GEP
PFD PGE PF PG
∠=∠
⎧
⎪
∠=∠
⎨
⎪=
⎩
∴△PFD≌△PGE(AAS).
∴PD=PE.
10.解:(1)∵∠C=90°,
∴DC⊥AC.
∵AD平分∠BAC,DE⊥AB,
∴DC=DE,∠DEB=∠C=90°.在Rt△DCF与Rt△DEB中,
∵
,
, DF DB DC DE
=
⎧
⎨
=
⎩
∴Rt△DCF≌Rt△DEB(HL).
∴CF=EB.
(2)AE=AF+BE.
理由如下:∵AD平分∠BAC,
∴∠CAD=∠EAD.
又∵AD=AD,∠C=∠DEA=90°,
∴△ACD≌△AED(AAS).
∴AC=AE.
由(1)知BE=CF,
∴AC=AF+CF=AF+BE.
∴AE=AF+BE.
11.解:方案:如图,(1)在射线OA上截取OM为一定的长度a,在OB上截取ON=a;
(2)分别过点M,N作OA,OB的垂线,设交点为P;
(3)连接OP,则OP就是∠AOB的平分线.
理由:在Rt△OMP和Rt△ONP中,OM=ON,OP=OP,
所以Rt△OMP≌Rt△ONP(HL).所以∠MOP=∠NOP.
12.证明:∵BF⊥AC,CE⊥AB,∴∠BED=∠CFD=90°.
在△BDE和△CDF中,
∵
,
,
,
BED CFD
BDE CDF BD CD
∠=∠
⎧
⎪
∠=∠
⎨
⎪=
⎩
∴△BDE≌△CDF(A AS).
∴DE=DF.
∵BF⊥AC,CE⊥AB,
∴∠BAD=∠CAD,即点D在∠BAC的平分线上.。
