2018年高考数学一轮复习经典高考小题狂练7
2018版考前三个月高考数学理科全国通用总复习文档:解答题滚动练7 含解析 精品

解答题滚动练71.盒内有大小相同的9个球,其中2个红色球,3个白色球,4个黑色球,规定取出1个红色球得1分,取出1个白色球得0分,取出1个黑色球得-1分.现从盒内任取3个球. (1)求取出的3个球中至少有一个红球的概率; (2)求取出的3个球得分之和恰好为1分的概率; (3)设ξ为取出的3个球中白色球的个数,求ξ的分布列.解 (1)由题意知本题是一个古典概型,记事件A 为“取出的3个球中至少有一个红球”,则事件A 的对立事件A 为“取出的3个球中没有红球”,因为试验发生包含的所有事件为从9个球中任取3个球有C 39种结果,满足A 的条件有C 37种结果,所以P (A )=1-P (A )=1-C 37C 39=712. (2)满足条件取出的3个球得分之和恰好为1分有两种结果,包括取出1个红色球,2个白色球和取出2个红色球,1个黑色球,记“取出1个红色球,2个白色球”为事件B ,有C 12C 23种结果.“取出2个红色球,1个黑色球”为事件C ,有C 22C 14种结果.其中事件B 和C 是互斥事件,则P (B ∪C )=P (B )+P (C )=C 12C 23C 39+C 22C 14C 39=542.(3)ξ可能的取值为0,1,2,3,则P (ξ=0)=C 36C 39=521,P (ξ=1)=C 13C 26C 39=1528,P (ξ=2)=C 23C 16C 39=314,P (ξ=3)=C 33C 39=184.ξ的分布列为2.已知等差数列{a n }的前n 项和为S n ,且满足a 6+a 8=-10,S 10=-35. (1)求数列{a n }的通项公式;(2)求数列⎩⎨⎧⎭⎬⎫a n 2n -1的前n 项和T n .解 (1)由题设可得⎩⎪⎨⎪⎧a 1+6d =-5,2a 1+9d =-7,解得⎩⎪⎨⎪⎧a 1=1,d =-1,所以a n =1-(n -1)=2-n . (2)因为a n 2n -1=12n -2-n ·12n -1,所以T n =2+1+12+…+12n -2-⎝⎛⎭⎫1+2×12+3×122+…+n ·12n -1, 令S n =2+1+12+…+12n -2,S n ′=1+2×12+3×122+…+n ·12n -1,则T n =S n -S n ′,因为S n =2+1+12+…+12n -2=2⎝⎛⎭⎫1-12n 12=4⎝⎛⎭⎫1-12n =4-12n -2, S n ′=1+2×12+3×122+…+n ·12n -1,① 所以12S n ′=12+2×122+3×123+…+n ·12n ,②由①-②,得12S n ′=1+12+122+123+…+12n -1-n ·12n =1-12n1-12-n ·12n =2-12n -1-n ·12n , 所以S n ′=4-12n -2-n ·12n -1,因此T n =S n -S n ′=n2n -1.3.过点C (2,2)作一直线与抛物线y 2=4x 交于A ,B 两点,点P 是抛物线y 2=4x 上到直线l :y =x +2的距离最小的点,直线AP 与直线l 交于点Q .(1)求点P 的坐标;(2)求证:直线BQ 平行于抛物线的对称轴. (1)解 设点P 的坐标为(x 0,y 0),则y 20=4x 0, 所以点P 到直线l 的距离d =||x 0-y 0+22=⎪⎪⎪⎪y 204-y 0+22=||(y 0-2)2+442≥22. 当且仅当y 0=2时等号成立,此时P 点坐标为(1,2).(2)证明 设点A 的坐标为⎝⎛⎭⎫y 214,y 1,显然y 1≠2.当y 1=-2时,A 点坐标为(1,-2),直线AP 的方程为x =1; 当y 1≠-2时,直线AP 的方程为y -2=y 1-2y 214-1(x -1),化简得4x -(y 1+2)y +2y 1=0.综上,直线AP 的方程为4x -(y 1+2)y +2y 1=0.与直线l 的方程y =x +2联立,可得点Q 的纵坐标为y Q =2y 1-8y 1-2.当y 21=8时,直线AC 的方程为x =2,可得B 点的纵坐标为y B =-y 1. 此时y Q =2y 1-8y 1-2=2-4y 1-2=2-4()y 1+2y 21-4=-y 1,即知BQ ∥x 轴,当y 21≠8时,直线AC 的方程为y -2=y 1-2y 214-2(x -2), 化简得(4y 1-8)x -(y 21-8)y +(2y 21-8y 1)=0,与抛物线方程y 2=4x 联立,消去x ,可得(y 1-2)y 2-(y 21-8)y +(2y 21-8y 1)=0,所以点B 的纵坐标为y B =y 21-8y 1-2-y 1=2y 1-8y 1-2.从而可得BQ ∥x 轴, 所以BQ ∥x 轴.4.已知函数f (x )=a ln x +x 2-x ,其中a ∈R . (1)当a >0时,讨论f (x )的单调性;(2)当x ≥1时,f (x )≥0恒成立,求a 的取值范围. 解 (1)函数f (x )=a ln x +x 2-x 的定义域为(0,+∞), f ′(x )=ax +2x -1=2x 2-x +a x,设g (x )=2x 2-x +a ,Δ=1-8a .①当a ≥18时,Δ≤0,g (x )≥0成立,故f ′(x )≥0成立,f (x )在(0,+∞)上为增函数;②当0<a <18时,Δ>0,令g (x )=0,得x 1=1-1-8a 4,x 2=1+1-8a 4.显然x 2>x 1>0,当x ∈(0,x 1)时,g (x )>0,f ′(x )>0,f (x )为增函数, 当x ∈(x 1,x 2)时,g (x )<0,f ′(x )<0,f (x )为减函数, 当x ∈(x 2,+∞)时,g (x )>0,f ′(x )>0,f (x )为增函数, 综上,当a ≥18时,f (x )在(0,+∞)上为增函数,当0<a <18时,f (x )在⎝ ⎛⎭⎪⎫0,1-1-8a 4,⎝ ⎛⎭⎪⎫1+1-8a 4,+∞上为增函数,在⎝⎛⎭⎪⎫1-1-8a 4,1+1-8a 4上为减函数.(2)显然f (1)=0,由x ≥1可知,当a ≥0时,a ln x ≥0,x 2-x ≥0,故f (x )≥0成立; 当a <0时,Δ=1-8a >0.令g (x )=0,得x 1=1-1-8a 4,x 2=1+1-8a4.显然x 1<0,x 2>0,当x ∈(0,x 2)时,g (x )<0,f ′(x )<0,f (x )为减函数, 当x ∈(x 2,+∞)时,g (x )>0,f ′(x )>0,f (x )为增函数;若-1≤a <0,则x 2≤1,当x ≥1时,f (x )为增函数,故f (x )≥f (1)=0成立; 若a <-1,则x 2>1,由f (x )在(0,x 2)上为减函数可知, 当x ∈(1,x 2)时,f (x )为减函数, f (x )<f (1)=0与题意不符,舍去. 综上,a 的取值范围是[-1,+∞).。
2018版高考数学(人教A版文科)一轮复习真题演练集训:第七章 不等式7-1含解析

真题演练集训1.[2016·北京卷]已知x,y∈R,且x>y>0,则( )A。
错误!-错误!>0B.sin x-sin y>0C.错误!x-错误!y<0D.ln x+ln y>0答案:C解析:解法一:因为x〉y〉0,选项A,取x=1,y=错误!,则错误!-错误!=1-2=-1〈0,排除A;选项B,取x=π,y=错误!,则sin x-sin y =sin π-sin 错误!=-1<0,排除B;选项D,取x=2,y=错误!,则ln x+ln y=ln(xy)=ln 1=0,排除D。
故选C.解法二:因为函数y=错误!x在R上单调递减,且x>y〉0,所以错误! x<错误!y,即错误!x-错误!y〈0,故选C。
2.[2016·新课标全国卷Ⅰ]若a>b>1,0<c〈1,则( )A.a c〈b c B.ab c<ba cC.a log b c〈b log a c D.log a c〈log b c答案:C解析:对于选项A,考虑幂函数y=x c,因为c〉0,所以y=x c为增函数,又a〉b〉1,所以a c〉b c,故A错;对于选项B,ab c〈ba c⇔错误!c〈错误!,又y=错误!x是减函数,故B错;对于选项D,由对数函数的性质可知D错,故选C.3.[2014·辽宁卷]当x∈[-2,1]时,不等式ax3-x2+4x +3≥0恒成立,则实数a的取值范围是( )A.[-5,-3]B。
错误!C.[-6,-2]D.[-4,-3]答案:C解析:当x=0时,ax3-x2+4x+3≥0变为3≥0恒成立,即a∈R,当x∈(0,1]时,ax3≥x2-4x-3,a≥错误!,∴a≥错误!max。
设φ(x)=错误!,φ′(x)=错误!=-错误!=-错误!>0,∴φ(x)在(0,1]上递增,φ(x)max=φ(1)=-6.∴a≥-6。
当x∈[-2,0)时,a≤错误!,∴a≤错误!min.仍设φ(x)=错误!,φ′(x)=-x-9x+1x4,当x∈[-2,-1)时,φ′(x)<0;当x∈(-1,0)时,φ′(x)>0。
2018版高考数学(人教A版理科)一轮复习真题演练集训第七章 不等式 7-2 Word版含答案
真题演练集训
.若变量,满足(\\(+≤,-≤,≥,))则+的最大值是( )
.
.
.
.
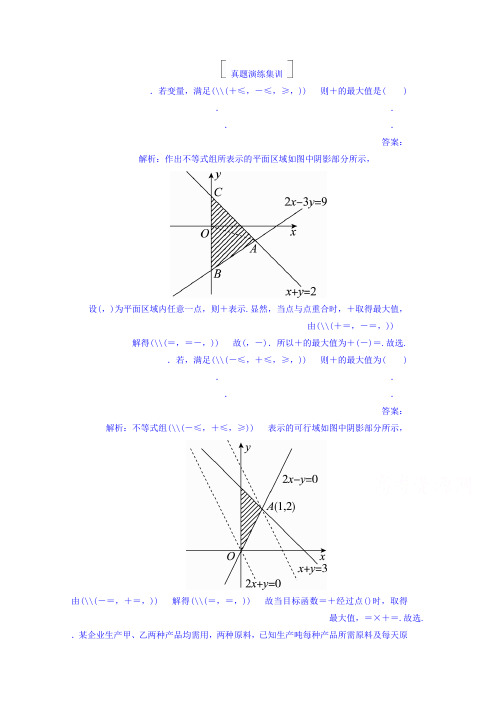
答案:解析:作出不等式组所表示的平面区域如图中阴影部分所示,
设(,)为平面区域内任意一点,则+表示.显然,当点与点重合时,+取得最大值,
由(\\(+=,-=,))
解得(\\(=,=-,))故(,-).所以+的最大值为+(-)=.故选.
.若,满足(\\(-≤,+≤,≥,))则+的最大值为( )
.
.
.
.
答案:解析:不等式组(\\(-≤,+≤,≥))表示的可行域如图中阴影部分所示,
由(\\(-=,+=,))解得(\\(=,=,))故当目标函数=+经过点()时,取得
最大值,=×+=.故选..某企业生产甲、乙两种产品均需用,两种原料,已知生产吨每种产品所需原料及每天原
料的可用限额如表所示.如果生产吨甲、乙产品可获利润分别为万元、万元,则该企业每天可
获得最大利润为( )
万元
.万元.万元
答案:
解析:
设每天生产甲、乙产品分别为吨、吨,每天所获利润为万元,则有
(\\(+≤,+≤,≥,≥,))目标函数为=+,作出可行域如图中阴影部分所示,由图形可知,当直线=+经过点()时,取最大值,最大值为×+×=(万元)..不等式组(\\(+≥,-≤))的解集记为,有下面四个命题:
:∀(,)∈,+≥-;
:∃(,)∈,+≥;
:∀(,)∈,+≤;
:∃(,)∈,+≤-.
其中的真命题是( )
.,.,
.,.,
答案:
解析:作出不等式组表示的可行域,如图中阴影部分所示.。
2018版高考数学(人教A版文科)一轮复习真题演练集训第七章不等式7-1Word版含解析

真题演练集训1.[2016·北京卷]已知x ,y ∈R ,且x >y >0,则( ) A.1x -1y >0B .sin x -sin y >0C.⎝ ⎛⎭⎪⎫12x -⎝ ⎛⎭⎪⎫12y <0 D .ln x +ln y >0答案:C解析:解法一:因为x >y >0,选项A ,取x =1,y =12,则1x -1y =1-2=-1<0,排除A ;选项B ,取x =π,y =π2,则sin x -sin y =sinπ-sin π2=-1<0,排除B ;选项D ,取x =2,y =12,则ln x +ln y =ln(xy )=ln 1=0,排除D.故选C.解法二:因为函数y =⎝ ⎛⎭⎪⎫12x 在R 上单调递减,且x >y >0,所以⎝ ⎛⎭⎪⎫12x <⎝ ⎛⎭⎪⎫12y ,即⎝ ⎛⎭⎪⎫12x -⎝ ⎛⎭⎪⎫12y <0,故选C. 2.[2016·新课标全国卷Ⅰ]若a >b >1,0<c <1,则( )A .a c <b cB .ab c <ba cC .a log b c <b log a cD .log a c <log b c 答案:C解析:对于选项A ,考虑幂函数y =x c ,因为c >0,所以y =x c 为增函数,又a >b >1,所以a c >b c ,故A 错;对于选项B ,ab c <ba c⇔⎝ ⎛⎭⎪⎫b a c <b a ,又y =⎝ ⎛⎭⎪⎫b a x 是减函数,故B 错;对于选项D ,由对数函数的性质可知D 错,故选C.3.[2014·辽宁卷]当x ∈[-2,1]时,不等式ax 3-x 2+4x +3≥0恒成立,则实数a 的取值范围是( )A .[-5,-3] B.⎣⎢⎡⎦⎥⎤-6,-98C .[-6,-2]D .[-4,-3]答案:C解析:当x =0时,ax 3-x 2+4x +3≥0变为3≥0恒成立,即a∈R ,当x ∈(0,1]时,ax 3≥x 2-4x -3,a ≥x 2-4x -3x 3,∴a ≥⎣⎢⎡⎦⎥⎤x 2-4x -3x 3max .设φ(x )=x 2-4x -3x 3,φ′(x )=(2x -4)x 3-(x 2-4x -3)3x 2x 6=-x 2-8x -9x 4=-(x -9)(x +1)x 4>0,∴φ(x )在(0,1]上递增,φ(x )max =φ(1)=-6.∴a ≥-6.当x ∈[-2,0)时,a ≤x 2-4x -3x 3,∴a ≤⎣⎢⎡⎦⎥⎤x 2-4x -3x 3min .仍设φ(x )=x 2-4x -3x 3,φ′(x )=-(x -9)(x +1)x 4,当x ∈[-2,-1)时,φ′(x )<0;当x ∈(-1,0)时,φ′(x )>0.∴当x =-1时,φ(x )有极小值,即为最小值.而φ(x )min =φ(-1)=1+4-3-1=-2, ∴a ≤-2.综上可知a 的取值范围为[-6,-2].4.[2015·辽宁卷]不等式2x 2-x <4的解集为________. 答案:{x |-1<x <2}(或(-1,2))解析:∵<4,∴<22,∴ x 2-x <2,即x 2-x -2<0,∴ -1<x <2.5.[2014·江苏卷]已知函数f (x )=x 2+mx -1,若对于任意x ∈[m ,m +1],都有f (x )<0成立,则实数m 的取值范围是________.答案:⎝ ⎛⎭⎪⎫-22,0 解析:由题可得,f (x )<0对于x ∈[m ,m +1]恒成立,即⎩⎪⎨⎪⎧f (m )=2m 2-1<0,f (m +1)=2m 2+3m <0, 解得-22<m <0.。
2018高三数学小题狂做系列(第一辑):2018高三理科数学小题狂做(7)

2018高三理科数学小题狂做(7)一、选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.)1、已知集合{}21x x A =-<<,{}220x x x B =-≤,则A B =( )A .{}01x x <<B .{}01x x ≤<C .{}11x x -<≤D .{}21x x -<≤2、复数=( )A .)2i B .1i + C .i D .i -3、点()1,1M 到抛物线2y ax =准线的距离为2,则a 的值为( ) A .14 B .112- C .14或112- D .14-或112 4、设n S 是公差不为零的等差数列{}n a 的前n 项和,且10a >,若59S S =,则当n S 最大时,n =( )A .6B .7C .10D .9 5、执行如图所示的程序框图,要使输出的S 值小于1,则输入的t 值不能是下面的( ) A .2012 B .2013 C .2014 D .2015 6、下列命题中正确命题的个数是( )①对于命题:p R x ∃∈,使得210x x +-<,则:p ⌝R x ∀∈,均有210x x +->②p 是q 的必要不充分条件,则p ⌝是q ⌝的充分不必要条件③命题“若x y =,则sin sin x y =”的逆否命题为真命题④“1m =-”是“直线1:l ()2110mx m y +-+=与直线2:l 330x my ++=垂直”的充要条件A .1个B .2个C .3个D .4个 7、如图,网格纸上小正方形的边长为1,若粗线画出的是某几何体的三视图,则此几何体的体积为( )A .6B .8C .10D .128、设双曲线的一个焦点为F ,虚轴的一个端点为B ,焦点F 到一条渐近线的距离为d ,若F B ≥,则双曲线离心率的取值范围是( )A.( B.)+∞ C .(]1,3 D.)+∞9、不等式组2204x y -≤≤⎧⎨≤≤⎩表示的点集记为A ,不等式组220x y y x -+≥⎧⎨≥⎩表示的点集记为B ,在A 中任取一点P ,则P∈B 的概率为( )A .932B .732 C .916 D .71610、设二项式12nx ⎛⎫- ⎪⎝⎭(n *∈N )展开式的二项式系数和与各项系数和分别为n a ,n b ,则1212nna a ab b b ++⋅⋅⋅+=++⋅⋅⋅+( ) A .123n -+ B .()1221n -+ C .12n + D .111、已知数列{}n a 满足3215334n a n n m =-++,若数列的最小项为1,则m 的值为( )A .14B .13C .14-D .13-12、已知函数())()()0ln 10x f x x x ≥=⎪--<⎩,若函数()()F x f x kx =-有且只有两个零点,则k 的取值范围为( )A .()0,1B .10,2⎛⎫ ⎪⎝⎭C .1,12⎛⎫⎪⎝⎭D .()1,+∞二、填空题(本大题共4小题,每小题5分,共20分.)13、向量a ,b 满足1a =,2b =,()()2a b a b +⊥-,则向量a 与b 的夹角 为 .14、三棱柱111C C AB -A B 各顶点都在一个球面上,侧棱与底面垂直,C 120∠A B =,C C A =B =,14AA =,则这个球的表面积为 .15、某校高一开设4门选修课,有4名同学,每人只选一门,恰有2门课程没有同学选修,共有 种不同选课方案(用数字作答).16、已知函数()()sin 2cos y x x πϕπϕ=+-+(0ϕπ<<)的图象关于直线1x =对称,则sin 2ϕ= .2018高三理科数学小题狂做(7)参考答案一、选择题(本大题共12小题,每小题5分,满分60分.在每小题给出的四个选项中,只有一项是符合题目要求的.)13、9014、64π15、8416、4 5 -。
2018届北师大版高三数学一轮复习练习第七章不等式第1讲Word版含解析

基础巩固题组(建议用时:40分钟)一、选择题1.若f (x )=3x 2-x +1,g (x )=2x 2+x -1,则f (x ),g (x )的大小关系是( )A.f (x )=g (x )B.f (x )>g (x )C.f (x )<g (x )D.随x 的值变化而变化解析 f (x )-g (x )=x 2-2x +2=(x -1)2+1>0⇒f (x )>g (x ).答案 B2.已知下列四个条件:①b >0>a ,②0>a >b ,③a >0>b ,④a >b >0,能推出1a <1b 成立的有( )A.1个B.2个C.3个D.4个解析 运用倒数性质,由a >b ,ab >0可得1a <1b ,②、④正确.又正数大于负数,①正确,③错误,故选C.答案 C3.(2017·河北省三市联考)若集合A ={x |3+2x -x 2>0},集合B ={x |2x <2},则A ∩B 等于( )A.(1,3)B.(-∞,-1)C.(-1,1)D.(-3,1)解析 依题意,可求得A =(-1,3),B =(-∞,1),∴A ∩B =(-1,1).答案 C4.若集合A ={x |ax 2-ax +1<0}=∅,则实数a 的取值范围是( )A.{a |0<a <4}B.{a |0≤a <4}C.{a |0<a ≤4}D.{a |0≤a ≤4}解析 由题意知a =0时,满足条件.a ≠0时,由⎩⎨⎧a >0,Δ=a 2-4a ≤0,得0<a ≤4,所以0≤a ≤4. 答案 D5.已知函数f (x )=-x 2+ax +b 2-b +1(a ∈R ,b ∈R ),对任意实数x 都有f (1-x )=f (1+x )成立,若当x ∈[-1,1]时,f (x )>0恒成立,则b 的取值范围是( )A.(-1,0)B.(2,+∞)C.(-∞,-1)∪(2,+∞)D.不能确定 解析 由f (1-x )=f (1+x )知f (x )的图像关于直线x =1对称,即a 2=1,解得a =2.又因为f (x )开口向下,所以当x ∈[-1,1]时,f (x )为增函数,所以f (x )min =f (-1)=-1-2+b 2-b +1=b 2-b -2,f (x )>0恒成立,即b 2-b -2>0恒成立,解得b <-1或b >2.答案 C二、填空题6.已知函数f (x )=⎩⎨⎧x 2+2x ,x ≥0,-x 2+2x ,x <0,则不等式f (x )>3的解集为________. 解析 由题意知⎩⎨⎧x ≥0,x 2+2x >3或⎩⎨⎧x <0,-x 2+2x >3,解得x >1.故原不等式的解集为{x |x >1}.答案 {x |x >1}7.(2016·合肥模拟)若关于x 的不等式ax >b 的解集为⎝ ⎛⎭⎪⎫-∞,15,则关于x 的不等式ax 2+bx -45a >0的解集为________.解析 由已知ax >b 的解集为⎝⎛⎭⎪⎫-∞,15,可知a <0,且b a =15,将不等式ax 2+bx -45a >0两边同除以a ,得x 2+b a x -45<0,即x 2+15x -45<0,解得-1<x <45,故不等式ax 2+bx -45a >0的解集为⎝ ⎛⎭⎪⎫-1,45. 答案 ⎝ ⎛⎭⎪⎫-1,45 8.不等式a 2+8b 2≥λb (a +b )对于任意的a ,b ∈R 恒成立,则实数λ的取值范围为________.解析 因为a 2+8b 2≥λb (a +b )对于任意的a ,b ∈R 恒成立,所以a 2+8b 2-λb (a +b )≥0对于任意的a ,b ∈R 恒成立,即a 2-λba +(8-λ)b 2≥0恒成立, 由二次不等式的性质可得,Δ=λ2b 2+4(λ-8)b 2=b 2(λ2+4λ-32)≤0,所以(λ+8)(λ-4)≤0,解得-8≤λ≤4.答案 [-8,4]三、解答题9.已知f (x )=-3x 2+a (6-a )x +6.(1)解关于a 的不等式f (1)>0;(2)若不等式f (x )>b 的解集为(-1,3),求实数a ,b 的值.解 (1)由题意知f (1)=-3+a (6-a )+6=-a 2+6a +3>0,即a 2-6a -3<0,解得3-23<a <3+2 3.所以不等式的解集为{a |3-23<a <3+23}.(2)∵f (x )>b 的解集为(-1,3),∴方程-3x 2+a (6-a )x +6-b =0的两根为-1,3,∴⎩⎪⎨⎪⎧(-1)+3=a (6-a )3,(-1)×3=-6-b 3,解得⎩⎨⎧a =3±3,b =-3. 即a 的值为3±3,b 的值为-3.10.某商品每件成本价为80元,售价为100元,每天售出100件.若售价降低x成(1成=10%),售出商品数量就增加85x 成.要求售价不能低于成本价.(1)设该商店一天的营业额为y ,试求y 与x 之间的函数关系式y =f (x ),并写出定义域;(2)若再要求该商品一天营业额至少为10 260元,求x 的取值范围.解 (1)由题意得,y =100⎝ ⎛⎭⎪⎫1-x 10·100⎝ ⎛⎭⎪⎫1+850x . 因为售价不能低于成本价,所以100⎝ ⎛⎭⎪⎫1-x 10-80≥0. 所以y =f (x )=40(10-x )(25+4x ),定义域为x ∈[0,2].(2)由题意得40(10-x )(25+4x )≥10 260,化简得8x 2-30x +13≤0.解得12≤x ≤134.所以x 的取值范围是⎣⎢⎡⎦⎥⎤12,2. 能力提升题组(建议用时:20分钟)11.下面四个条件中,使a >b 成立的充分而不必要条件是( )A.a >b +1B.a >b -1C.a 2>b 2D.a 3>b 3解析 A 项:若a >b +1,则必有a >b ,反之,当a =2,b =1时,满足a >b ,但不能推出a >b +1,故a >b +1是a >b 成立的充分而不必要条件;B 项:当a =b =1时,满足a >b -1,反之,由a >b -1不能推出a >b ;C 项:当a =-2,b =1时,满足a 2>b 2,但a >b 不成立;D 项:a >b 是a 3>b 3的充要条件,综上所述答案选A.答案 A12.(2017·湛江调研)已知函数f (x )=ax 2+bx +c (a ≠0),若不等式f (x )<0的解集为⎩⎨⎧⎭⎬⎫x |x <12或x >3,则f (e x )>0(e 是自然对数的底数)的解集是( )A.{x |x <-ln 2或x >ln 3}B.{x |ln 2<x <ln 3}C.{x |x <ln 3}D.{x |-ln 2<x <ln 3} 解析 法一 依题意可得f (x )=a ⎝ ⎛⎭⎪⎫x -12(x -3)(a <0),则f (e x )=a ⎝ ⎛⎭⎪⎫e x -12(e x -3)(a <0),由f (e x )=a ⎝ ⎛⎭⎪⎫e x -12(e x -3)>0,可得12<e x <3, 解得-ln 2<x <ln 3,故选D.法二 由题知,f (x )>0的解集为⎩⎨⎧⎭⎬⎫x |12<x <3, 令12<e x <3,得-ln 2<x <ln 3,故选D.答案 D13.若不等式x 2+ax -2>0在区间[1,5]上有解,则实数a 的取值范围是________. 解析 设f (x )=x 2+ax -2,由题知:Δ=a 2+8>0,所以方程x 2+ax -2=0恒有一正一负两根,于是不等式x 2+ax -2>0在区间[1,5]上有解的充要条件是f (5)>0,即a ∈⎝ ⎛⎭⎪⎫-235,+∞. 答案 ⎝ ⎛⎭⎪⎫-235,+∞ 14.解关于x 的不等式ax 2-(2a +1)x +2<0(a ∈R ).解 原不等式可化为(ax -1)(x -2)<0.(1)当a >0时,原不等式可以化为a (x -2)⎝ ⎛⎭⎪⎫x -1a <0,根据不等式的性质,这个不等式等价于(x -2)·⎝ ⎛⎭⎪⎫x -1a <0.当0<a <12时,2<1a ,则原不等式的解集是⎩⎨⎧⎭⎬⎫x |2<x <1a ; 当a =12时,原不等式的解集是∅;当a >12时,1a <2,则原不等式的解集是⎩⎨⎧⎭⎬⎫x ⎪⎪⎪1a <x <2. (2)当a =0时,原不等式为-(x -2)<0,解得x >2,即原不等式的解集是{x |x >2}.(3)当a <0时,原不等式可以化为a (x -2)⎝ ⎛⎭⎪⎫x -1a <0, 根据不等式的性质,这个不等式等价于(x -2)·⎝ ⎛⎭⎪⎫x -1a >0, 由于1a <2,故原不等式的解集是⎩⎨⎧⎭⎬⎫x |x <1a 或x >2. 综上所述,当a <0时,不等式的解集为⎩⎨⎧⎭⎬⎫x |x <1a 或x >2; 当a =0时,不等式的解集为{x |x >2};当0<a <12时,不等式的解集为⎩⎨⎧⎭⎬⎫x |2<x <1a ;当a =12时,不等式的解集为∅;当a >12时,不等式的解集为⎩⎨⎧⎭⎬⎫x |1a <x <2.。
2018高考数学(文科)习题 第七章 不等式 课时撬分练7-2 word版含答案

………………………………………………………………………………………………时间:45分钟基础组1.不等式x -2x 2-1<0的解集为( ) A .{x |1<x <2}B .{x |x <2且x ≠1}C .{x |-1<x <2且x ≠1}D .{x |x <-1或1<x <2}答案 D 解析x -2x 2-1<0⇔(x -1)(x +1)(x -2)<0⇔x <-1或1<x <2,故选D. 2.已知不等式x 2-2x -3<0的解集为A ,不等式x 2+x -6<0的解集是B ,不等式x 2+ax +b<0的解集是A ∩B ,那么a +b 等于( ) A .-3 B .1 C .-1 D .3答案 A解析 由题意,A ={x |-1<x <3},B ={x |-3<x <2},A ∩B ={x |-1<x <2},则不等式x2+ax +b <0的解集为{x |-1<x <2}.由根与系数的关系可知,a =-1,b =-2,所以a +b =-3,故选A.3. 若不等式(a -a 2)(x 2+1)+x ≤0对一切x ∈(0,2]恒成立,则a 的取值范围为( )点击观看解答视频A.⎝ ⎛⎦⎥⎤-∞,1-32B.⎣⎢⎡⎭⎪⎫1+32,+∞C.⎝ ⎛⎦⎥⎤-∞,1-32∪⎣⎢⎡⎭⎪⎫1+32,+∞D.⎣⎢⎡⎦⎥⎤1-32,1+32答案 C解析 ∵x ∈(0,2],∴a 2-a ≥x x 2+1=1x +1x.要使a 2-a ≥1x +1x在x ∈(0,2]时恒成立,则a 2-a ≥⎝ ⎛⎭⎪⎪⎫1x +1x max ,由基本不等式得x +1x ≥2,当且仅当x =1时,等号成立,即⎝ ⎛⎭⎪⎪⎫1x +1x max =12.故a 2-a ≥12,解得a ≤1-32或a ≥1+32,故选C.4.不等式x -12x +1≤0的解集为( )A.⎝ ⎛⎦⎥⎤-12,1 B.⎣⎢⎡⎦⎥⎤-12,1C.⎝⎛⎭⎪⎫-∞,-12∪[)1,+∞ D.⎝⎛⎦⎥⎤-∞,-12∪不等式x 2-2x +5≥a 2-3a 对任意实数x 恒成立,则实数a 的取值范围为( )A .B .(-∞,-2]∪∪答案 A解析 x 2-2x +5=(x -1)2+4的最小值为4,所以x 2-2x +5≥a 2-3a 对任意实数x 恒成立,只需a 2-3a ≤4,解得-1≤a ≤4.6.若函数f (x )=x 2+ax -3a -9对任意x ∈R 恒有f (x )≥0,则f (1)等于( ) A .6 B .5 C .4 D .3答案 C解析 由题意可得,Δ=a 2-4(-3a -9)≤0, 即(a +6)2≤0,又(a +6)2≥0,∴a +6=0, ∴a =-6,∴f (x )=x 2-6x +9, ∴f (1)=1-6+9=4.故选C. 7.不等式x -2x +1≤0的解集是( ) A .(-∞,-1)∪(-1,2] B .C .(-∞,-1)∪ 答案D 解析x -2x +1≤0⇔(x +1)(x -2)≤0,且x ≠-1,即x ∈(-1,2],故选D. 8. 已知f (x )=⎩⎪⎨⎪⎧2-x ,x ≤0,x 2-6x +2,x >0,则关于x 的不等式f (3-x 2)<f (2x )的解集为( )点击观看解答视频A.(-3,-3)B.(-3,1)C.(-∞,2-3)∪(2+3,+∞)D.(-3,1)∪(2+3,+∞)答案 D解析画出函数f(x)的图象如图所示,可知函数f(x)在(-∞,3)上是减函数,在(3,+∞)上是增函数.∵3-x2≤3,故分以下几种情形:(1)若3-x2≤0且2x≤0,即x≤-3,则2-(3-x2)<2-2x,∴-3<x<1.∴-3<x≤-3;(2)若-3<x≤0,则0<3-x2≤3,2x≤0,观察图象知f(3-x2)<f(2x)恒成立;(3)若0<x≤3,则2x<3-x2或3-(3-x2)<2x-3(3-x2离对称轴x=3比2x离对称轴近),解得0<x<1;(4)若x>3,则3-x2<0,2x>0,要求2-(3-x2)<(2x)2-6×2x+2,解得x>2+ 3.综上,得关于x的不等式f(3-x2)<f(2x)的解集为(-3,1)∪(2+3,+∞).9.若不等式x2-(2+m)x+m-1>0对任意m∈恒成立,则x的取值范围是________.答案(-∞,-1)∪(3,+∞)解析把不等式化为(1-x)m+x2-2x-1>0.设f(m)=(1-x)m+x2-2x-1,则问题转化为关于m的一次函数.f(m)在区间上大于0恒成立,只需⎩⎪⎨⎪⎧f -1>0,f1>0即⎩⎪⎨⎪⎧x 2-x -2>0,x 2-3x >0⇒⎩⎪⎨⎪⎧x <-1或x >2,x <0或x >3,解得x <-1或x >3,故x 的取值范围是(-∞,-1)∪(3,+∞).10.若关于x 的不等式ax -b >0的解集为(-∞,1),则关于x 的不等式(ax +b )(x -2)>0的解集为________.答案 (-1,2)解析 由题意可得a =b <0,故(ax +b )(x -2)>0等价于(x +1)(x -2)<0,解得-1<x <2,故所求不等式的解集为(-1,2).11.二次函数f (x )满足f (2)=-1,f (-1)=-1,且f (x )的最大值为8,试解不等式f (x )>-1.解 由于f (2)=f (-1)=-1,根据二次函数的对称性,则对称轴为x =2+-12=12,又知最大值为8.可设f (x )=a (x -12)2+8,将f (2)=-1代入得,a =-4. ∴f (x )=-4(x -12)2+8.由f (x )>-1,-4x 2+4x +7>-1, 即x 2-x -2<0,∴解集为{x |-1<x <2}.12.已知不等式ax 2-3x +6>4的解集为{x |x <1或x >b }. (1)求a ,b ;(2)解不等式ax 2-(ac +b )x +bc <0.解 (1)因为不等式ax 2-3x +6>4的解集为{x |x <1或x >b },所以x 1=1与x 2=b 是方程ax 2-3x +2=0的两个实数根,且b >1.由根与系数的关系,得⎩⎪⎨⎪⎧1+b =3a,1×b =2a.解得⎩⎪⎨⎪⎧a =1,b =2.(2)原不等式化为:x 2-(2+c )x +2c <0,即(x -2)(x -c )<0.①当c >2时,不等式的解集为{x |2<x <c }; ②当c <2时,不等式的解集为{x |c <x <2}; ③当c =2时,不等式的解集为∅.能力组13. 在R 上定义运算⊗:x ⊗y =x (1-y ).若不等式(x -a )⊗(x +a )<1对任意实数x 成立,则( )点击观看解答视频A .-1<a <1B .0<a <2C .-12<a <32D .-32<a <12答案 C解析 根据题意有(x -a )⊗(x +a )=(x -a )(1-x -a ),∵不等式(x -a )⊗(x +a )<1对任意实数x 成立,则(x -a )(1-x -a )<1对任意实数x 成立, 即使x 2-x -a 2+a +1>0对任意实数x 成立, 所以Δ=1-4(-a 2+a +1)<0, 解得-12<a <32,故选C.14.已知关于x 的不等式ax 2+bx +c <0的解集是⎩⎨⎧x ⎪⎪⎪⎭⎬⎫x <-2或x >-12,则ax 2-bx +c >0的解集为________.答案 ⎝ ⎛⎭⎪⎫12,2解析 由题意知,-2,-12是方程ax 2+bx +c =0的两个根,且a <0,故⎩⎪⎨⎪⎧4a -2b +c =0,14a -12b +c =0,解得a =c ,b =52c ,所以不等式ax 2-bx +c >0即为2x 2-5x +2<0,故解集为⎩⎨⎧x ⎪⎪⎪⎭⎬⎫12<x <2.15.某小型服装厂生产一种风衣,日销货量x 件与货价p 元/件之间的关系为p =160-2x ,生产x 件所需成本为C =500+30x 元,则该厂日产量为________时,日获利不少于1300元.答案 20件至45件解析 由题意,得(160-2x )x -(500+30x )≥1300,化简得x 2-65x +900≤0,解之得20≤x ≤45.因此,该厂日产量在20件至45件时,日获利不少于1300元.故填20件至45件.16.已知关于x 的不等式kx 2-2x +6k <0(k ≠0). (1)若不等式的解集为{x |x <-3或x >-2},求k 的值;(2)若不等式的解集为⎩⎨⎧x ⎪⎪⎪⎭⎬⎫x ∈R ,x ≠1k ,求k 的值;(3)若不等式的解集为R ,求k 的取值范围; (4)若不等式的解集为∅,求k 的取值范围.解 (1)由不等式的解集为{x |x <-3或x >-2}可知k <0,且-3与-2是方程kx 2-2x +6k =0的两根,∴(-3)+(-2)=2k ,解得k =-25.(2)由不等式的解集为⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫x ⎪⎪⎪x ∈R ,x ≠1k 可知⎩⎪⎨⎪⎧k <0,Δ=4-24k 2=0,解得k =-66. (3)依题意知⎩⎪⎨⎪⎧k <0,Δ=4-24k 2<0,解得k <-66. (4)依题意知⎩⎪⎨⎪⎧k >0,Δ=4-24k 2≤0,解得k ≥66.我知道,自己这么做,确实违逆了当时身边卷起的一股股大潮。
2018年高考数学一轮复习经典高考小题狂练16

.
解法一: 判别式法 令 t 2a b , b t 2a 代入 a 2 b2 ab 3 得 7a2 5at t2 3 0
关于 a 的一元二次方程有解得
25t 2 28 t 2 3 0 ,即 t2 28
所以 t 2a b 2 7 ,当且仅当
a 5 t 5 2a b 14 14
2a b 2 7
解法二: 化齐次式
AC2 BC2 9 AC BC
2
当且仅当 AC BC 5 时,等号成立,故最长边为 5
感知高考刺金 238 题
如 图 , C, D 在 半 径 为 1 的 O 上 , 线 段 AB 是 O 的 直 径 , 则 AC BD 的 取 值 范 围
是
.
解法一:极化恒等式角度
AC BD AD DC BD DC DB
(这里的 就是向量夹角,由于三点不同,故 cos
1,1 )
当
0 时有 2 2 2
11
1
当
0 时有 2 2 2
11
1
画出可行域如图,
于是将 y
2
3
2 视为可行域 内的
,
到 点 3, 0 的 距 离 的 平 方 , 易 得 当
,
2, 1 时, y 2 ,当
时, y
,故
2
2
3
2
解法二: OC OA OB 2 2 cos 1 2
于是
2
3
2
2
3
2 2 cos 1 2
2
2
2
cos 3
cos 3
cos 3
10
10
2
2
2
2
解法三: 由 OA OB CO 0 可以构造三角形法则
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
(ii )若 a b 6 时,满足 综上, a b 2
a b 0 ,恒成立 2
故 要 使 对 x1 0 , x2 x1 , g x2
ba8
f x1 成 立 只 需 a b ab
,画出可行域可 得 2
2a b 7
2.( 1)若复数 z 与其共轭复数 z 满足 z
5 5 , z z 2 ,则 z
z
(2)若函数 f x 解:( 1) 2
ab 1 0
故f x
max 1 a b , 1 a b
max
b 1 a , 4a b 1 0 ,又结合 a 2 ,
b 1 a , 4a b 1 0
可以从规划视角来解题,以 a 为横坐标, b 为横坐标建系,
画出可行域
4a b 1 a2
0
如图 1 所示,
目标函数 b 1 a
b1a
2
视为可行域内的点
2
a,b 到直线 x y 1 0 的距离的
即 12
2a c
8 ac
5
a c 30
所以 a c a c cos AOC 24
解法二: 同前, O , A, C, B 四点共圆
由正弦定理得 R
5
3
3
, sin ABC , tan ABC
3
5
4
又a c
a c cos AOC
2S OAC tan
8 S OAC
3
所以当且仅当 AOC 为等腰三角形时, S OAC max S NAC 9
道底 AB 的张角 最大时,采集效果最好,则采集效果 最 好 时 位 置 C 到 AB 的 距 离
是
。
解:以抛物线顶点为原点建系,则抛物线方程为
2
x
4y , A 4, 6 , B 4, 6 ,C x, y
设 ACB
,则 cos
CA CB CA CB
且 S ABC
1 86 y
2
1 CA CB sin
5
2
4c 4a
2.( 1)将二项式 ( x
1 ) n 的展开式按 x 的降幂排列,若前三项系数成等差数列,则该
24 x
展开式中 x 的指数是整数的项共有
个。
(2)无重复数字的五位数 a1a2a3a4a5 , 当 a1<a2 , a2 >a3, a3<a4, a4>a5 时称为波形数,
则由 1,2,3,4,5 任意组成的一个没有重复数字的五位数是波形数的概率为
感知高考刺金 131
1.函数 f x
4x x 0 , g x x1
1 xa
2
x b , a b ,若对 x1 0 , x2 x1 ,
g x2 f x1 ,则 2a b 的最大值为
。
解: g x
1 b a ,x b
2
x
a
b ,a
x
b, f x
2
1 a b ,x a
2
4x
4
4
x0
x1
x1
若使对 x1 0 , x2 x1 , g x2
x a 的图象总在 F x ln x
x 图象的上方,求实数
(2) x a ln x
x 对 x 0 且 x 1 恒成立,
。 a 的取值集合。
故 a x x ln x , x 1 或 a x x ln x ,0 x 1
min
min
令 g( x) x x ln x ,,, ,得 a 1
感知高考刺金 132
现要求第
三、四两节课中每节课恰有两位教师开课 (不考虑教师所开课的班级和内容) ,则不同的开
课方案共有
种。
解:若只有甲乙两人开课,他们两人每人开设两节,只有一种方案;
若甲乙两人开课,丙丁中有一人开课,则有
C21 A12 A12 8 种方案;
若甲乙两人中有一人开课,丙丁两人均开课,有
12
A2 A2
4 种方案;
右 支 于 P, Q 两 点 , 若 P F1 F1 F2 , 且 3 PF2 2 QF2 , 则 双 曲 线 的 离 心 率
为
。
解:如图所示,标出两个焦点三角形各边的长度, M 是 PF2 的中点,则在 Rt PF1M , Rt F1MQ
中,利用勾股定理得
2
2
2
2
F1M 2c c a 3c a
所以 5c2 12ac 7a2 0 即e 7
2 倍,显然当 a,b 取点 2, 1 时 b 1 a min 2 2 2
同理,可行域
4a b 1 a2
0
如图 1
2
视为可行域内的点
2
a, b 到直线
的 2 倍,显然当 a, b 取点 2, 1 时 b 1 a min 2 综上, M a, b 2
x y 1 0 的距离
( 2)解法一:规划视角
t a 和 y2
t a 的图象,两者取其大,则显然当
t 0 时,
f1 a b 1 2
2 ab1 2
a3b a1
M a, b 2
f 1 a b1 2
2 a b1 2 a 3 b a1
a f
2
1 a2 4b 2 4
8 a2 4b 8
a2
a2
2b
2
4
4
显然又是一个规划问题了。
以 a 为横坐标, b 为横坐标建系,画出可行域如图中 ABC 的蓝色部分。这里画图时注意到
证法二:绝对值不等式
fx
max f 1 , f 1 max 1 a b , 1 a b
max
1a b 1a b 1a b 1ab
2
2
解法三: M a,b max 1 a b , 1 a b
a2
令 b 1 t ,则 M a,b g t max t a , t a
在同一个坐标系中画出 y1 g t min a 2 故 M a, b 2
若甲乙丙丁四人全部开课,每人一节,有
C42C
2 2
6 种方案;
故共有 19 种
( 2 ) 若 二 项 式 3x 2
n
2 (n 3x
N*) 展 开 式 中 含 有 常 数 项 , 则 n 的 最 小 取 值
是
。
解: 7
感知高考刺金 134
x2 y2 1.已知双曲线 a2 b2 1 a 0,b 0 的左、右焦点分别为 F1, F2 ,过 F2 的直线交双曲线的
1.已知 f x
2
x
2
2a 1 x
2
a
4a
5 ,若 f x 的最大值是 g a ,则关于 a 的不等式
log 1 g a 3 0 的解集是
。
2
解:令
2
1x
t
0,1 ,则 x2 1 t 2
所以 f t
t2 2at a2 4a 6
t
2
a
2a2
4a
6
当 a 0 时, g a f 0 a 2 4a 6
当 0 a 1 时, g a
故 a c 的最大值为 24。
解法三: 同前, O , A, C, B 四点共圆
2 AC 2 由极化恒等式 a c OE
4
2 AC 2 故 a c OE
4
2
NE 3 24
2.( 1)“预祝大家高考满堂红”这句话,如图所示形式排列,
从“预”字读起,只允许逐字..沿水平向右或竖直向下方向读,
则读完整句话的不同读法共有 答案: 28 256 种
2
再由
| z |=
5
得
骣珑珑珑桫a
+ 2
2
2鼢鼢鼢+
骣2 - a 桫2
2
=
25 .
解得 a = ? 46 . (2)解:由 f (x) x3 bx2 cx得 f (x) 3x2 2bx c .
由 x 0 是函数 f ( x) 的一个极值点知 f (0) c 0 . 又由 f (x) 图像经过点 A(3,0) 得 f (3) 27 9b 3c 0 . 所以 b = - 3 . f (x) x3 3x2 . 由 l1 / / l 2 得 f (x1) f (x2) 3x12 6x1 3x22 6x2 .
可以取到,所以 a b
0
min
又由( 1)的逆否命题可知当 M a,b
2 时,必有 a 2 ,
f1 1 a b 2
且
4 1 a b 1 a b 2 2b
f 1 1a b 2
3b1
(i )若 0 b 1,则 a b 2 1 3
(ii )若 3 b 0 ,则 a 2
1,1 , f a 2
a2 b M a, b 2
。
解:( 1) 3 个
(2)五个数任意排列,有
5
A5 120 种不同排法
若将 5 排在 a2 位置, 4 排在 a4 位置,其余三个数任意排,有 A33 6 种
5 与 4 交换位置,又有 6 种; 若将 5 排在 a2 位置, 3 排在 a4 位置,则 4 只能排在 a1 位置,其余两个数有
交换位置,又有 2 种;
种.
预祝 大家高 考满 堂红 祝大家高考满堂红 大家高考满堂红 家高考满堂红 高考满堂红 考满堂红 满堂红 堂红 红
(2)
x
1
x
8
1 的展开式中
x5 的系数是
。
解: 14
感知高考刺金 136
2015 年浙江第 18 题
设函数 f x x2 ax b a,b R ,记 M a,b 为 y f x 在 1,1 上的最大值
2
所以两式相除得 tan
8y 6
x2 16
2
