2013年名牌高校自主招生及高中数学联赛辅导专题讲座

合集下载

第一讲开启我的竞赛之路

第一讲开启我的竞赛之路一．初识数学竞赛前一段时间，我们组织竞赛报名时，没想到会有这么多人报名，竟然达到了近 300 名同学！这是由于多数同学对竞赛的特点不了解造成的。

数学竞赛是一种思维的竞赛，是一种其试题的难度要远比高考数学高出很多，技巧与方法的升华，是一种课堂知识在课外的拓展。

思维的含量也远比普通高考大得多。

整套数学竞赛试卷分为了一试和二试两个环节：其中，一试部分是高考部分的内容，但比高考要难一些，与高校自主招生试题的难度差不多，分为了填空题与解答题，没有选择题，其中填空题每小题 8 分，共64 分，解答题有三道，第一道试题 16 分，第二道与第三道试题和 20 分，共 56 分.一试的分值是 120 分；这其中三道解答试题中必有一道是圆锥曲线的试题，另两道试题主要是从不等式、数列、函数中选择。

二试部分的内容是完全与高考不着边，共 4 道大题，分别考查代数、平面几何、初等数论和组合。

前两道试题每道题 40 分，后两道试题每道题 50 分，共 180分。

整套试卷满分 300 分，一般情况下，能够获得 150 分以上就可以获得一等奖.原来数学竞赛获得一等奖的同学就真接具备了高校的保送资格或高考加 20 分。

但从 2014 年开始，取消保送，至于加分与否，到目前为止山东省还没有出台具体的政策. 二．我校最近几年的数学竞赛与自主招生成绩我是从 2006年开始进行竞赛辅导的，当年的竞赛有我和现在高三一位老师颜景海老师一起负责，2006 年 10 月，我校张昊（就读于山东大学，在正在山东大学读研）同学荣获全这在当时就创造了我们济宁市的一个记录（注：原来我市从来没有过全国二等奖），国二等奖，张长城（就读于南京大学，现正在南京大学读研）、刘悦（就读于中国海洋大学，现在中国海洋读研）；有了一个好的开端，一切就顺利了，从 2007 年起学校把竞赛工作放给我一个人。

在 2007 年的竞赛考试中，我校取得了四名全国二等奖，三名全国三等奖的成绩，在 2008 年的数学竞赛中，我校岳爱珍同学获得全国一等奖（保送西安交通大学，现在西安交通大学读研），4 名全国三等奖，这份成绩开创了济宁市一等奖的先例；2009 年由于忙于高三的班主任工作，没有进行辅导工作，我校成绩是两个三等奖； 2010 年，卷土重来，经过一年的精心准备与同学们的辛勤努力，我校杨若涛同学以 217 分的总成绩获得了山东省和第一名并入选全国高中数学竞赛的冬令营（现就读于中国科技大学华罗庚班），张浩同学获以山东省第 21 名的成绩获得了保送资格（后来高考加 20 分，现就读于中南大学）。

自主招生专题——一类不定方程问题

龙源期刊网
自主招生专题——一类不定方程问题
作者：任念兵
来源：《中学数学杂志(高中版)》2013年第04期
如火如荼的高校自主招生考试越来越受到广大学生和家长的重视，对自主招生试题的研究也成为一线数学教师日常教学研究的重要内容数论问题虽然在高考中要求较低，但却是自主招生的热点，其中有一类不定方程问题频繁出现在各名牌大学自主招生考试中，本文试以朴素的不等式估值来统一处理这类问题.
对于这类形如∑ni=11xi=C的不定方程的正整数解问题，可以考虑将未知数xi排序，再利用简单的不等式估计每个式子的值，从而缩小xi的取值范围，最终得到符合要求的正整数解
无独有偶，2年上海交通大学也考过此题，而此题的各种变形形式则屡屡出现在各名牌大学自主招生考试题中.
例1（211年复旦大学）设正整数n可以等于4个不同的正整数的倒数之和，则这样的n
的个数是（）.
作者简介任念兵（1981—），男，安徽安庆人，中学一级教师，从事高中数学教学与研究，曾获全国高中数学青年教师教学评优一等奖，发表教学文章4余篇.。

湖南常德市一中高中数学竞赛讲座：第一讲技巧方程无答案

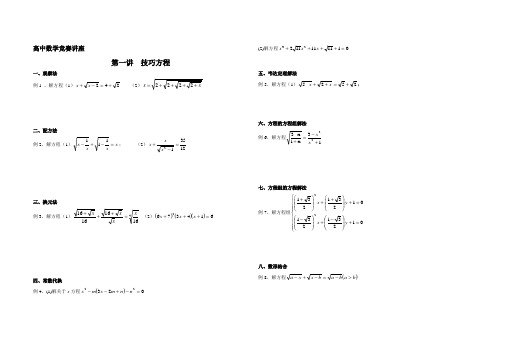
高中数学竞赛讲座第一讲技巧方程一、观察法例1 、解方程（1）242+=-+x x （2）x x ++++=2222二、配方法例2、解方程（1）x xx x =-+-111；（2）123512=-+x x x三、换元法例3、解方程（1）416161616x xx x =+++ （2）()()()6143762=+++x x x四、常数代换例4、(1)解关于x 方程()02322=-+--n n m x m x(2)解方程01111111223=++++x x x五、韦达定理解法例5、解方程（1）252-5+=++x x ;六、方程的方程组解法例6、解方程13x 1x -322+-=+x x七、方程组的方程解法例7、解方程组⎪⎪⎪⎩⎪⎪⎪⎨⎧=+⎪⎪⎭⎫ ⎝⎛-+⎪⎪⎭⎫⎝⎛-=+⎪⎪⎭⎫⎝⎛++⎪⎪⎭⎫⎝⎛+012312310123123122y x y x八、数形结合例8、解方程()b a b a b x x a >-=-+-九、方程的不等式解法例9、解方程012sin 22=+-xx x π十、技巧方程组例10、（1）解方程组⎪⎩⎪⎨⎧--=--+=yx x y yx x y 1-3（2）已知实数n x x x ,,,21 满足1112222211+==+=+n n x x x x x x ，且3101112121=+++++++n n x x x x x x ，求n x十一、不定方程求定解例11、（1）求方程的整数解：3222=+y x（2）解方程()z y x z y x ++=-+-+-2193421练习解下列方程或方程组： 1、14-53=-+x x ； 2、44121=++++x x x3、21212=--+-+x x x x4、⎪⎩⎪⎨⎧=-++=++-+08123132y xy y y x y x5、⎪⎪⎩⎪⎪⎨⎧-+-=-+-=y y y x x x x y 111111 6、⎪⎩⎪⎨⎧=++=++=++431222222zx x z yz z y xy y x7、求方程7322=+-+yxy x y x 的所有整数解。

高二自主招生讲座(解析几何)

2014自主招生（数学）解读与备考2013、12一、先看一个问题：例1、（2011年自主招生华约数学试题14）已知双曲线2222:1(0,0)x y C a b a b-=>>，12F F 、分别为C 的左、右焦点。

P 为C 右支上一点，且12=,3F PF π∠ 12F PF ∆的面积为2．（Ⅰ）求C 的离心率e ；（Ⅱ）设A 为C 的左顶点，Q 为第一象限内C 上的任意一点，问是否存在常数(0)λλ>,使得22QF A QAF λ∠=∠恒成立。

若存在，求出λ的值；若不存在，请说明理由．谈几个问题：1、北约考察的重点：研究能力（意识与方法）；2、谈谈题是怎么编的（1）、机器（2）、理论结论1、设F 为圆锥曲线焦点，其相应准线为l ，作一直线交圆锥曲线于P A 、两点，交l 于M ，则FM 平分AFP ∠（或其外角）。

点(0,1),E 且与椭圆相交于,C D 两点.① 求椭圆方程；② 若直线l 与x 轴相交于点G ，且,GC DE =求k 的值；③ 设A 为椭圆的下顶点，,AC AD k k 分别为直线,AC AD 的斜率. 证明对任意的k ，恒有2AC AD k k ⋅=-xy结论2、设),(00y x P 为椭圆)0(12222>>=+b a by a x 上一定点，PB PA 、为它的任意两条弦，斜率分别为21,k k 。

若12k k λ⋅=（注：22b a λ≠），则直线AB 过定点（2222002222,a b a b x y a b a bλλλλ++---）。

例3、已知椭圆22221(0)x y a b a b +=>>的离心率是，且经过点(2,1)M ．直线1(0)2y x m m =+<与椭圆相交于A ，B 两点．（1）求椭圆的方程；（2）求△MAB 的内心的横坐标．结论3、设),(00y x P 为椭圆)0(12222>>=+b a by a x 上一定点，PB PA 、为它的任意两条弦，斜率分别为21,k k ，若021=+k k ，则直线AB 的斜率是定值0202y a x b k =。

高中数学竞赛专题讲座(解析几何)

高中数学竞赛专题讲座（解析几何）一、基础知识1．椭圆的定义，第一定义：平面上到两个定点的距离之和等于定长（大于两个定点之间的距离）的点的轨迹，即|PF 1|+|PF 2|=2a (2a>|F 1F 2|=2c). 第二定义：平面上到一个定点的距离与到一条定直线的距离之比为同一个常数e(0<e<1)的点的轨迹（其中定点不在定直线上），即e dPF =||(0<e<1). 第三定义：在直角坐标平面给定两圆c 1: x 2+y 2=a 2, c 2: x 2+y 2=b 2, a, b ∈R +且a ≠b 。

从原点出发的射线交圆c 1于P ，交圆c 2于Q ，过P 引y 轴的平行线，过Q 引x 轴的平行线，两条线的交点的轨迹即为椭圆。

2．椭圆的方程，如果以椭圆的中心为原点，焦点所在的直线为坐标轴建立坐标系，由定义可求得它的标准方程，若焦点在x 轴上，列标准方程为 ~12222=+b y a x (a>b>0)，参数方程为⎩⎨⎧==θθsin cos b y a x （θ为参数）。

若焦点在y 轴上，列标准方程为12222=+b y a y (a>b>0)。

3．椭圆中的相关概念，对于中心在原点，焦点在x 轴上的椭圆12222=+by a x ， a 称半长轴长，b 称半短轴长，c 称为半焦距，长轴端点、短轴端点、两个焦点的坐标分别为(±a, 0), (0, ±b), (±c, 0)；与左焦点对应的准线（即第二定义中的定直线）为c a x 2-=，与右焦点对应的准线为c a x 2=；定义中的比e 称为离心率，且ace =，由c 2+b 2=a 2知0<e<1.椭圆有两条对称轴，分别是长轴、短轴。

:4．椭圆的焦半径公式：对于椭圆=+2222by a x 1(a>b>0), F 1(-c, 0), F 2(c, 0)是它的两焦点。

2013年高校自主招生培训

5.2012年自主招生新变化
(2)高水平大学自主选拔（简称AAA）学业能力测试
AAA测试的指导思想 · AAA测试的命题以现行中学教学大纲为参照，重点在于考察学生对于知识的综合应用能力和学习能力，不以超出中学大纲的知识为主要考察目标。
5.2012年自主招生新变化
(2)高水平大学自主选拔（简称AAA）学业能力测试 AAA测试的科目
门类面试类、文科类需面试
笔试、面试武汉大学、湖南大学等
4、自主招生考试内容笔试：
内容难度、内容均与高考大纲要求相符难度、内容均超出高考大纲要求内容超出高考大纲，但难度不高考查目的代表学校注重对考生的基础知识、基本能力和基础素质的湖南大学等考查
考题不死扣高中课本，而是具有一定深度和广度，可以拉开考生区分度考查学生对理论知识的应用能力和技巧
90 80 70 60 50 40 30 20 10 0 东部西部北部
•
第一季度第二季度第三季度第四季度
•
5.2012年自主招生新变化
(2)高水平大学自主选拔（简称AAA）学业能力测试
AAA测试的时间安排 • · 考试当天，上午进行阅读与写作的测试。全部试卷及答题卡在开考时一并下发，开考3小时后一并收回。 • · 下午进行数学、自然科学/人文与社会的测试。两科试卷及答题卡在开考时一并下发，开考3小时后一并收回。 • · 考试时间 2012年2月11日
(4)卓越人才培养自主选拔录取学业能力测试
• 时间：2012年2月12日 • 上午：社会科学（涵盖语文与英语）考试时间：150分钟，满分：150分； • 下午：数学(测试内容以高中数学教学内容为主) 考试时间：90分钟，满分：100分；自然科学（涵盖物理与化学，文科生不考）考试时间：90分钟，满分：100分。

2013太原市数学竞赛辅导讲义

2013山西省数学会数学自主招生辅导讲义数列与极限太原五中王彩凤{}{}{}{}5353334442531. (2012n n n n n n a b a b n S S a as T T b b -+-+例卓越联盟）设是等差数列，是等比数列，记满足，的前项和分别为,T ,若a =b ,a =b ,且=5,则=________{}432156.(5,n a a a a a a +--=+例2 2012北大保送）正项等比数列，满足a 求的最小值.2333121212320132012{}2{}=-2012n n nn a a a a a a a a a a a a 例3.（全国高中联赛）已知数列的各项均为非零实数，且对于任意的正整数n ，都有（++）=++(1)当n=3时，求所有满足条件的三项组成的数列，，；（）是否存在满足条件的无穷数列，使得？若存在，求出这样的无穷数列的一个通项公式；若不存在，说明理由。

22222012201311114201212(1)1222013,k a k k k k a a =++++++-⎛⎫∈ ⎪⎝⎭例：（联赛预赛）设求证：例5.（2010赛题）在一个有限项的实数列中，任何7个连续项的和都是负数，任何11个连续项的和都是正数，试问这样一个数列至多有多少项？例6.（2010全国联赛题）证明32520x x +-=恰有一个实数根r,且存在唯一的严格递增正整数数列{}n a ，使得31225a a a r r r =+++123412341234123411111m m m mm a a a a a a a a a a a a m a a a a =+++≥+++例7：若正整数使得对任意一组满足的正数，，，都有成立，则正整数的最小值是___________{}221112323412.20111,-33(1)1)(1))(1))(1)4n n n n n n n n a a a a a a n a a a a a a a a a +++<=+≥--+--+--<例8（江苏）数列满足：0<求证：(((11.i n +≥≥例9（2010山西预赛）设x 0,i=1,2,n,约定x =x 证明:121211.12n kk k n nk k k k a a a kn a A ==+++≤--<∑∑例10（2010全国联赛一试）给定整数n>2,设正实数a ,a ,,a 满足 a 1,k=1,2,n.记A =,k=1,2,,n证明:1112123{a }111111112482n n n n n a a a a a +≥例11：数列中，已知=2,且对一切正整数n 都有a =a a a +1求证：+++++++对一切正整数n 都成立*1212*2121*1{a },1(1)(1()21(1)()211()1()12n n n n n n nn n n nn n k n N c a c a c a p S p pa p f n S p f n f n n N pp p f k n N p p --=∈++++-=-=++∈⎡⎤++≤≤-∈⎢⎥-⎣⎦∑例12：已知数列各项均不为零，其前n 项和为s 且对任意都有为大于的常数），记（1）试比较与的大小（）；（2）求证：(2n-1)f(n)（）.12,11212551.:,,(2)(1)==0(2)=12n=2000,=2011;300n n k k n n nn n n n a a a n a a a a a a a a a +≥-+++≥例13数列A 满足=1(k=1,2,n-1),则称A 为E 数列.记S(A )=写出一个满足，且S(A )>0的E 数列A ；若，证明：E 数列A 是递增数列的充要条件是（）对于任意给定的整数n(n 2),是否存在首项为的E 数列A ，使得S(A )=？如果存在，写n 出一个满足条件的E 数列A ；如果不存在，说明理由。

高三培优讲义13 自主招生中的三角函数

高一培优讲义13 自主招生中的三角函数
1.（2011北约）在三角形ABC中，求证： .
2.（2009北京大学）存不存在使得为等差数列？
3.（2008清华大学）求 .
4.（2012北约）求使得 .
在上有唯一解的 .
5.（2012华约）设 .
6.（2012华约）如果，
那么的取值范围：（）
A B C D
7.（清华大学）已知为等差数列，为等比数列，
求的值.
8.（浙江大学）已知：为三角形的三个内角
求证：
9.（2010年清华大学等五校联考）在中，已知，外接圆半径 .
（Ⅰ）求角的大小；
（Ⅱ）求面积的最大值.
10.（2012卓越）y= ________.
11.（2011卓约）在中, 是角的平分线,且 .
14.（2011卓约）已知则 ()
A. B. C . D.
15.（2013卓约）在中，三个内角、、所对边分别为、、．
已知．
（1）求角的大小；（2）求的最大值．
16.（2014北约）证明：．
17.（2014华约）函数的最大值为1,最小值为 ,求的值.
18.（2014卓越）设，函数，
(1)求的取值范围;
(2)若 ,问为何值时, 最短?
12.（2011卓约）已知 ABC不是直角三角形.
（1）证明：tanA+tanB+tanC=tanAtanBtanC；
（2）若，且sin2A，sin2B，sin2C的倒数成等差数列.
求cos 的值.
13.（2011华约）若的最小值和最大值分别为( )
．（1）若 [ ]，求在ቤተ መጻሕፍቲ ባይዱ间上的最大值；

2013自主招生卓越联盟自主招生备战攻略

2013自主招生卓越联盟自主招生备战攻略
来源：广州日报二
2013年自主招生申请开始，再过三个月又到了几大自招联盟考试的时候，每个自主招生联盟各有自己的出题规律的难度范围，整理各大自招联盟出题特点，有意向报考的同学可进行参考。

卓越自主招生联盟出题特点
“卓越”的考试科目为数学100分，自然科学(含物理和化学，100分)，社会科学(含语文和英语，150分)。

文科考生不参加自然科学测试。

某教育机构的老师团队认为，“卓越”数学试题比高考稍难，相当于高考压轴题水平。

语文试题仅包含常规高考中的阅读和作文版块。

英语难度同“华约”一样，题量大，要求学生知识面宽广。

物理和化学看重学生的实验能力及动手能力，物理较为实在，不会有过多的偏题怪题，注重基础和实际应用。

学大教育衡艳华老师认为，广东考生青睐“卓越”联盟中的华工，可以研读“卓越联盟”过往自招试题，适当再看一些竞赛的初试题。

2013高三数学专题讲座

第1讲选择题的解题方法与技巧解法特点概述选择题是高考数学试卷的三大解法之一．选择题的分数一般占全卷的40%左右，高考数学选择题的基本特点是：(1)绝大部分数学选择题属于低中档题，且一般按由易到难的顺序排列，主要的数学思想和数学方法能通过它得到充分的体现和应用，并且因为它还有相对难度(如思维层次、解题方法的优劣选择，解题速度的快慢等)，所以选择题已成为具有较好区分度的基本解法之一．(2)选择题具有概括性强、知识覆盖面广、小巧灵活及有一定的综合性和深度等特点，且每一题几乎都有两种或两种以上的解法，能有效地检测学生的思维层次及观察、分析、判断和推理能力．目前，高考数学选择题采用的是一元选择题(即有且只有一个正确答案)，由选择题的结构特点，决定了解选择题除常规方法外还有一些特殊的方法．解选择题的基本原则是：“小题不能大做”，要充分利用题目中(包括题干和选项)提供的各种信息，排除干扰，利用矛盾，作出正确的判断．数学选择题的求解，一般有两条思路：一是从题干出发考虑，探求结果；二是从题干和选择支联合考虑或从选择支出发探求是否满足题干条件．解答数学选择题的主要方法包括直接对照法、概念辨析法、图象分析法、特例检验法、排除法、逆向思维法等，这些方法既是数学思维的具体体现，也是解题的有效手段．直接对照型选择题是直接从题设条件出发，利用已知条件、相关概念、性质、公式、公理、定理、法则等基础知识，通过严谨推理、准确运算、合理验证，从而直接得出正确结论，然后对照题目所给出的选项“对号入座”，从而确定正确的选择支．这类选择题往往是由计算题、应用题或证明题改编而来，其基本求解策略是由因导果，直接求解．解法一直接对照法例1 设定义在R上的函数f(x)满足f(x)²f(x＋2)＝13，若f(1)＝2，则f(99)等于( )A ．13B ．2 C.132 D.213思维启迪：先求f (x )的周期。

解析 ∵f (x ＋2)＝13f (x ) ∴f (x ＋4)＝13f (x ＋2)＝1313f (x )＝f (x )．∴函数f (x )为周期函数，且T ＝4. ∴f (99)＝f (4³24＋3)＝f (3)＝13f (1)＝132.探究提高直接法是解选择题的最基本方法，运用直接法时,要注意充分挖掘题设条件的特点，利用有关性质和已有的结论，迅速得到所需结论．如本题通过分析条件得到f (x )是周期为4的函数，利用周期性是快速解答此题的关键．变式训练1函数f (x )对于任意实数x 满足条件f (x ＋2)＝1f (x )，若f (1)＝－5，则f (f (5))的值为 ( )A ．5B ．－5 C.15 D ．－15解析由f (x ＋2)＝1f (x )，得f (x ＋4)＝1f (x ＋2)＝f (x )，所以f (x )是以4为周期的函数，所以f (5)＝f (1)＝－5，从而f (f (5))＝f (－5)＝f (－1)＝1f (－1＋2)＝1f (1)＝－15.例2 设双曲线x 2a 2－y 2b2＝1的一条渐近线与抛物线y ＝x 2＋1只有一个公共点，则双曲线的离心率为( )A.54 B ．5 C.52D. 5思维启迪：求双曲线的一条渐近线的斜率即ba的值，尽而求离心率．解析：设双曲线的渐近线方程为y ＝kx ，这条直线与抛物线y ＝x 2＋1相切，联立⎩⎪⎨⎪⎧y ＝kxy ＝x 2＋1，整理得x 2－kx ＋1＝0，则Δ＝k 2－4＝0，解得k ＝±2，即b a ＝2，故双曲线的离心率e ＝c a＝c 2a 2＝a 2＋b 2a 2＝1＋(b a)2＝ 5.变式训练2 已知双曲线C ：x 2a 2－y 2b2＝1(a >0，b >0)，以C 的右焦点为圆心且与C 的渐近线相切的圆的半径是 ( )A ．aB ．b C.ab D.a 2＋b 2解析： x 2a 2－y 2b 2＝1的其中一条渐近线方程为：y ＝－bax ，即bx ＋ay ＝0，而焦点坐标为(c,0)，根据点到直线的距离d ＝|b ³a 2＋b 2|a 2＋b 2＝b .故选B.解法二：概念辨析法概念辨析是从题设条件出发，通过对数学概念的辨析，进行少量运算或推理，直接选择出正确结论的方法．这类题目常涉及一些似是而非、很容易混淆的概念或性质，这需要考生在平时注意辨析有关概念，准确区分相应概念的内涵与外延，同时在审题时要多加小心，准确审题以保证正确选择．一般说来，这类题目运算量小，侧重判断，下笔容易，但稍不留意则易误入命题者设置的“陷阱”．例3 已知非零向量a ＝(x 1，y 1)，b ＝(x 2，y 2)，给出下列条件，①a ＝kb (k ∈R)；②x 1x 2＋y 1y 2＝0；③(a＋3b )∥(2a －b )；④a²b ＝|a||b |；⑤x 21y 22＋x 22y 21≤2x 1x 2y 1y 2.其中能够使得a∥b 的个数是 ( )A ．1B ．2C ．3D ．4解析：显然①是正确的，这是共线向量的基本定理；②是错误的，这是两个向量垂直的条件；③是正确的，因为由(a ＋3b )∥(2a －b )，可得(a ＋3b )＝λ(2a －b )，当λ≠12时，整理得a ＝λ＋32λ－1b ，故a ∥b ，当λ＝12时也可得到a ∥b ；④是正确的，若设两个向量的夹角为θ，则由a²b ＝|a||b |cos θ，可知cos θ＝1，从而θ＝0，所以a∥b ；⑤是正确的，由x 21y 22＋x 22y 21≤2x 1x 2y 1y 2，可得(x 1y 2－x 2y 1)2≤0，从而x 1y 2－x 2y 1＝0，于是a∥b .变式训练3 关于平面向量a ，b ，c ，有下列三个命题： ①若a²b ＝a²c ，则b ＝c .②若a ＝(1，k )，b ＝(－2,6)，a ∥b ，则k ＝－3.③非零向量a 和b 满足|a |＝|b |＝|a －b |，则a 与a ＋b 的夹角为 60°.则假命题为 ( ) A ．①② B ．①③ C ．②③ D ．①②③解析: ①a²b ＝a²c ⇔a²(b －c )＝0，a 与b －c 可以垂直，而不一定有b ＝c ，故①为假命题． ②∵a∥b ，∴1³6＝－2k .∴k ＝－3.故②为真命题．③由平行四边形法则知围成菱形且夹角为60°，a ＋b 为其对角线上的向量，a 与a ＋b 夹角为30°，故③为假命题．解法三数形结合法“数”与“形”是数学这座高楼大厦的两块最重要的基石，二者在内容上互相联系、在方法上互相渗透、在一定条件下可以互相转化，而数形结合法正是在这一学科特点的基础上发展而来的．在解答选择题的过程中，可以先根据题意，做出草图，然后参照图形的做法、形状、位置、性质，综合图象的特征，得出结论．例4 (2012²海南)用min{a ，b ，c }表示a ，b ，c 三个数中的最小值．设f (x )＝min{2x ，x ＋2,10－x }(x ≥0)，则f (x )的最大值为 ( )A ．4B ．5C ．6D ．7思维启迪：画出函数f (x )的图象，观察最高点求出纵坐标即可．本题运用图象来求值，直观、易懂．解析由题意知函数f (x )是三个函数y1＝2x ，y 2＝x ＋2，y 3＝10－x 中的较小者，作出三个函数在同一个坐标系之下的图象(如图中实线部分为f (x )的图象)可知A (4,6)为函数f (x )图象的最高点．变式训练 4 (2010²湖北）设集合A ＝⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫(x ，y )⎪⎪⎪x 24＋y 216＝1，B ＝{}(x ，y )|y ＝3x ，则A ∩B 的子集的个数是( )A ．4B ．3C ．2D ．1解析集合A 中的元素是椭圆x 24＋y 216＝1上的点，集合B 中的元素是函数y ＝3x 的图象上的点．由数形结合，可知A ∩B 中有2个元素，因此A ∩B 的子集的个数为4.例5 函数f (x )＝1－|2x －1|，则方程f (x )²2x ＝1的实根的个数是 ( ) A ．0 B ．1 C ．2 D ．3思维启迪：若直接求解方程显然不可能，考虑到方程可转化为f (x )＝⎝ ⎛⎭⎪⎫12x ，而函数y ＝f (x )和y ＝⎝ ⎛⎭⎪⎫12x的图象又都可以画出，故可以利用数形结合的方法，通过两个函数图象交点的个数确定相应方程的根的个数．解析方程f (x )²2x＝1可化为f (x )＝⎝ ⎛⎭⎪⎫12x，在同一坐标系下分别画出函数y＝f (x )和y ＝⎝ ⎛⎭⎪⎫12x的图象，如图所示．可以发现其图象有两个交点，因此方程f (x )＝⎝ ⎛⎭⎪⎫12x有两个实数根．变式训练5 函数y ＝|log 12x |的定义域为[a ，b ]，值域为[0,2]，则区间[a ，b ]的长度b －a 的最小值是( )A ．2 B.32 C ．3 D.34解析作出函数y ＝|log 12x |的图象，如图所示，由y ＝0解得x ＝1；由y＝2，解得x ＝4或x ＝14.所以区间[a ，b ]的长度b －a 的最小值为1－14＝34.解法四特例检验法特例检验(也称特例法或特殊值法)是用特殊值(或特殊图形、特殊位置)代替题设普遍条件，得出特殊结论，再对各个选项进行检验，从而做出正确的选择．常用的特例有特殊数值、特殊数列、特殊函数、特殊图形、特殊角、特殊位置等．特例检验是解答选择题的最佳方法之一，适用于解答“对某一集合的所有元素、某种关系恒成立”，这样以全称判断形式出现的题目，其原理是“结论若在某种特殊情况下不真，则它在一般情况下也不真”，利用“小题小做”或“小题巧做”的解题策略．例6 已知A 、B 、C 、D 是抛物线y 2＝8x 上的点，F 是抛物线的焦点，且FA →＋FB →＋FC →＋FD →＝0，则|FA →|＋|FB →|＋|FC →|＋|FD →|的值为 ( )A ．2B ．4C ．8D ．16 解析取特殊位置，AB ，CD 为抛物线的通径，显然FA →＋FB →＋FC →＋FD →＝0，则|FA →|＋|FB →|＋|FC →|＋|FD →|＝4p ＝16，故选D.探究提高本题直接求解较难，利用特殊位置法，则简便易行．利用特殊检验法的关键是所选特例要符合条件．变式训练6 已知P 、Q 是椭圆3x 2＋5y 2＝1上满足∠POQ ＝90°的两个动点，则1OP 2＋1OQ 2等于 ( )A ．34B ．8 C.815 D.34225解析取两特殊点P (33，0)、Q (0，55)即两个端点，则1OP 2＋1OQ 2＝3＋5＝8.故选B.例7 数列{a n }成等比数列的充要条件是 ( ) A ．a n ＋1＝a n q (q 为常数)B ．a 2n ＋1＝a n ²a n ＋2≠0C ．a n ＝a 1q n －1(q 为常数)D ．a n ＋1＝a n ²a n ＋2解析考查特殊数列0,0，…，0，…，不是等比数列，但此数列显然适合A ，C ，D 项．故选B.探究提高判断一个数列是否为等比数列的基本方法是定义法，也就是看a n ＋1a n是否为常数，但应注意检验一个数列为等比数列的必要条件是否成立．变式训练7 已知等差数列{a n }的前n 项和为S n ，若a 2n a n ＝4n －12n －1，则S 2nS n的值为 ( )A ．2B ．3C ．4D ．8 解析方法一 (特殊值检验法)取n ＝1，得a 2a 1＝31，∴a 1＋a 2a 1＝41＝4，于是，当n ＝1时，S 2n S n ＝S 2S 1＝a 1＋a 2a 1＝4.方法二 (特殊式检验法)注意到a 2n a n ＝4n －12n －1＝2²2n －12²n －1，取a n ＝2n －1，S 2nS n ＝1＋(4n －1)2²2n 1＋(2n －1)2²n ＝4. 方法三 (直接求解法)由a 2n a n ＝4n －12n －1，得a 2n －a n a n ＝2n 2n －1，即nd a n ＝2n 2n －1，∴a n ＝d (2n －1)2，于是，S 2n S n ＝a 1＋a 2n2²2n a 1＋a n2²n＝2²a 1＋a 2na 1＋a n＝2²d 2＋d2(4n －1)d 2＋d2(2n －1)＝4. 答案 C解法五排除法数学选择题的解题本质就是去伪存真，舍弃不符合题目要求的选项，找到符合题意的正确结论．筛选法(又叫排除法)就是通过观察分析或推理运算各项提供的信息或通过特例，对于错误的选项，逐一剔除，从而获得正确的结论．例8 方程ax 2＋2x ＋1＝0至少有一个负根的充要条件是( ) A ．0<a ≤1 B ．a <1C ．a ≤1D ．0<a ≤1或a <0 解析当a ＝0时，x ＝－12，故排除A 、D.当a ＝1时，x ＝－1，排除B. 故选C.探究提高选择具有代表性的值对选项进行排除是解决本题的关键．对“至少有一个负根”的充要条件取值进行验证要比直接运算方便、易行．不但缩短时间，同时提高解题效率．变式训练8 已知函数f (x )＝mx 2＋(m －3)x ＋1的图象与x 轴的交点至少有一个在原点右侧，则实数m 的取值范围是( )A ．(0,1)B ．(0,1]C ．(－∞，1)D ．(－∞，1] 解析令m ＝0，由f (x )＝0得x ＝13适合，排除A 、B.令m ＝1，由f (x )＝0得：x ＝1适合，排除C. 解法六估算法由于选择题提供了唯一正确的选择支，解答又无需过程．因此，有些题目，不必进行准确的计算,只需对其数值特点和取值界限作出适当的估计，便能作出正确的判断，这就是估算法．估算法往往可以减少运算量，但是加强了思维的层次．例9 若A 为不等式组⎩⎪⎨⎪⎧x ≤0y ≥0y －x ≤2表示的平面区域，则当a 从－2连续变化到1时，动直线x ＋y ＝a 扫过A 中的那部分区域的面积为 ( ) A.34 B ．1 C.74D ．2解析如图知区域的面积是△OAB 去掉一个小直角三角形．阴影部分面积比1大，比S △OAB ＝12³2³2＝2小，故选C 项．探究提高： “估算法”的关键是应该确定结果所在的大致范围，否则“估算”就没有意义．本题的关键在所求值应该比△AOB 的面积小且大于其面积的一半．选择题解题规律及方法总结：1．解选择题的基本方法有直接法、排除法、特例（值）验证法和数形结合法．但大部分选择题的解法是直接法，在解选择题时要根据题干和选择支两方面的特点灵活运用上述一种或几种方法“巧解”，在“小题小做”、“小题巧做”上做文章，切忌盲目地采用直接法．2．由于选择题供选答案多、信息量大、正误混杂、迷惑性强，稍不留心就会误入“陷阱”，应该从正反两个方向肯定、否定、筛选、验证，既谨慎选择，又大胆跳跃．3．作为平时训练，解完一道题后，还应考虑一下能不能用其他方法进行“巧算”，并注意及时总结，这样才能有效地提高解选择题的能力.知能提升演练1．已知集合A ＝{1,3,5,7,9}，B ＝{0,3,6,9,12}，则A ∩(∁N B )等于 ( ) A ．{1,5,7} B ．{3,5,7} C ．{1,3,9} D ．{1,2,3} 解析由于3∈∁N B ，所以3∈A ∩(∁N B ) ∴排除B 、C 、D ，故选A.2．已知向量a ，b 不共线，c ＝ka ＋b (k ∈R)，d ＝a －b .如果c ∥d ，那么 ( ) A ．k ＝1且c 与d 同向 B ．k ＝1且c 与d 反向 C ．k ＝－1且c 与d 同向 D ．k ＝－1且c 与d 反向解析当k ＝1时，c ＝a ＋b ，不存在实数λ，使得a ＝λb .所以c 与d 不共线，与c ∥d 矛盾．排除A 、B ；当k ＝－1时，c ＝－a ＋b ＝－(a －b )＝－d ，所以c ∥d ，且c 与d 反向．故应选D.3．已知函数y ＝tan ωx 在⎝ ⎛⎭⎪⎫－π2，π2内是减函数，则( )A ．0<ω≤1B ．－1≤ω<0C ．ω≥1D ．ω≤－1解析可用排除法，∵当ω>0时正切函数在其定义域内各长度为一个周期的连续区间内为增函数，∴排除A 、C ，又当|ω|>1时正切函数的最小正周期长度小于π，∴y ＝tan ωx 在⎝ ⎛⎭⎪⎫－π2，π2内不连续，在这个区间内不是减函数，这样排除D ，故选B.4．已知向量OB →＝(2,0)，向量OC →＝(2,2)，向量CA →＝(2cos α，2sin α)，则向量OA →与向量OB →的夹角的取值范围是 ( )A ．[0，π4]B ．[5π12，π2]C ．[π4，5π12]D ．[π12，5π12]解析 ∵|CA →|=2，∴A 的轨迹是⊙C ，半径为2.由图可知∠COB ＝π4，设向量OA →与向量OB →的夹角为θ，则π4－π6≤θ≤π4＋π6，故选D.5．设函数y ＝f (x )在(－∞，＋∞)内有定义，对于给定的正数K ，定义函数f K (x )＝⎩⎪⎨⎪⎧f (x )，f (x )≤K ，K ，f (x )>K .取函数f (x )＝2－|x |，当K ＝12时，函数f K (x )的单调递增区间为 ( )A ．(－∞，0)B ．(0，＋∞)C ．(－∞，－1)D ．(1，＋∞) 解析函数f (x )＝2－|x |＝(12)|x |，作图f (x )≤K ＝12⇒x ∈(－∞，－1]∪[1,＋∞),故在(－∞,－1)上是单调递增的, 选C 项．6．设x ，y ∈R，用2y 是1＋x 和1－x 的等比中项，则动点(x ，y )的轨迹为除去x 轴上点的 ( )A ．一条直线B ．一个圆C ．双曲线的一支D ．一个椭圆解析 (2y )2＝(1－x )(1＋x )(y ≠0)得x 2＋4y 2＝1(y ≠0)．7．(2011²福建)若点O 和点F (－2,0)分别为双曲线x 2a2－y 2＝1(a >0)的中心和左焦点，点P 为双曲线右支上的任意一点，则OP →²FP →的取值范围为 ( ) A ．[3－23，＋∞) B．[3＋23，＋∞) C ．[－74，＋∞) D ．[74，＋∞)解析由c ＝2得a 2＋1＝4，∴a 2＝3，∴双曲线方程为x 23－y 2＝1.设P (x ，y )(x ≥3)，OP →²FP →＝(x ，y )²(x ＋2，y )＝x 2＋2x ＋y 2＝x 2＋2x ＋x 23－1＝43x 2＋2x －1(x ≥3)．令g (x )＝43x 2＋2x －1(x ≥3)，则g (x )在[3，＋∞)上单调递增．g (x )min ＝g (3)＝3＋2 3.8．已知等差数列{a n }满足a 1＋a 2＋…＋a 101＝0，则有( ) A ．a 1＋a 101>0 B ．a 2＋a 102<0 C ．a 3＋a 99＝0 D ．a 51＝51 解析取满足题意的特殊数列a n ＝0，则a 3＋a 99＝0，故选C.9．在等差数列{a n }中，若a 2＋a 4＋a 6＋a 8＋a 10＝80，则a 7－12a 8的值为 ( )A ．4B ．6C ．8D ．10 解析令等差数列{a n }为常数列a n ＝16. 显然a 7－12a 8＝16－8＝8. 故选C.10．若1a <1b <0，则下列不等式：①a ＋b <ab ；②|a |>|b |；③a <b ；④b a ＋ab>2中，正确的不等式是( )A ．①②B ．②③C ．①④D ．③④解析取a ＝－1，b ＝－2，则②、③不正确，所以A 、B 、D 错误，故选C.11.(2011²全国)如图，质点P 在半径为2的圆周上逆时针运动，其初始位置为P 0(2，－2)，角速度为1，那么点P 到x 轴距离d 关于时间t 的函数图象大致为 ( )解析观察并联想P 运动轨迹与d 的关系，当t ＝0时，d ＝2，排除A 、D ；当开始运动时d 递减，排除B.12．若函数f (x )＝⎪⎪⎪⎪⎪⎪x 2x 2＋1－a ＋4a 的最小值等于3，则实数a 的值等于( )A. 34 B ．1 C. 34或1 D ．不存在这样的a解析方法一直接对照法令x 2x 2＋1＝t ，则t ∈[0,1)．若a ≥1，则f (x )＝|t －a |＋4a ＝5a －t 不存在最小值；若0≤a <1，则f (x )＝|t －a |＋4a ，当t ＝a 时取得最小值4a ，于是4a ＝3，得a ＝34符合题意；若a <0，f (x )＝|t －a |＋4a ＝t ＋3a ，当t ＝0时取得最小值3a ，于是3a ＝3，得a ＝1不符合题意．综上可知，a ＝34.方法二试验法若a ＝1，则f (x )＝⎪⎪⎪⎪⎪⎪x 2x 2＋1－1＋4>4，显然函数的最小值不是3，故排除选项B 、C ；若a ＝34，f (x )＝⎪⎪⎪⎪⎪⎪x 2x 2＋1－34＋3，这时只要令x 2x 2＋1－34＝0，即x ＝±3，函数可取得最小值3，因此A 项正确，D 项错误．13．已知sin θ＝m －3m ＋5，cos θ＝4－2m m ＋5(π2<θ<π)，则tan θ2等于( )A. m －39－m B ．|m －39－m | C. 13D ．5解析由于受条件sin 2θ＋cos 2θ＝1的制约，故m 为一确定的值，于是sin θ，cos θ的值应与m 的值无关，进而tan θ2的值与m 无关，又π2<θ<π，π4<θ2<π2，∴tan θ2>1，故选D 项．14．已知函数y ＝f (x )，y ＝g (x )的导函数的图象如下图，那么y ＝f (x )，y ＝g (x )图象可能是( )解析从导函数的图象可知两个函数在x 0处斜率相同，可以排除B 项，再者导函数的函数值反映的是原函数增加的快慢，可明显看出y ＝f (x )的导函数是减函数，所以原函数应该增加的越来越慢，排除A 、C 两项，最后只有D 项，可以验证y ＝g (x )导函数是增函数，增加越来越快．答案 D第2讲填空题的解题方法与技巧解法特点概述填空题是高考试卷中的三大解法之一，和选择题一样，属于客观性试题．它只要求写出结果而不需要写出解答过程．在整个高考试卷中，填空题的难度一般为中等．不同省份的试卷所占分值的比重有所不同．1．填空题的类型填空题主要考查学生的基础知识、基本技能以及分析问题和解决问题的能力，具有小巧灵活、结构简单、概念性强、运算量不大、不需要写出求解过程而只需要写出结论等特点．从填写内容看，主要有两类：一类是定量填写，一类是定性填写．2．填空题的特征填空题不要求写出计算或推理过程，只需要将结论直接写出的“求解题”．填空题与选择题也有质的区别：第一，表现为填空题没有备选项，因此，解答时有不受诱误干扰之好处，但也有缺乏提示之不足；第二，填空题的结构往往是在一个正确的命题或断言中，抽出其中的一些内容 (既可以是条件，也可以是结论)，留下空位，让考生独立填上，考查方法比较灵活．从历年高考成绩看，填空题得分率一直不很高，因为填空题的结果必须是数值准确、形式规范、表达式最简，稍有毛病，便是零分．因此，解填空题要求在“快速、准确”上下功夫，由于填空题不需要写出具体的推理、计算过程，因此要想“快速”解答填空题，则千万不可“小题大做”，而要达到“准确”，则必须合理灵活地运用恰当的方法，在“巧”字上下功夫．3．解填空题的基本原则解填空题的基本原则是“小题不能大做”，基本策略是“巧做”．解填空题的常用方法有：直接法、数形结合法、特殊化法、等价转化法、构造法、合情推理法等．解题方法例析解法一直接法直接法就是从题设条件出发，运用定义、定理、公式、性质、法则等知识，通过变形、推理、计算等，得出正确结论，使用此法时，要善于透过现象看本质，自觉地、有意识地采用灵活、简捷的解法．例1 在等差数列{a n }中，a 1＝－3,11a 5＝5a 8－13，则数列 {a n }的前n 项和S n 的最小值为________．解析设公差为d ，则11(－3＋4d )＝5(－3＋7d )－13， ∴d ＝59.∴数列{a n }为递增数列．令a n ≤0，∴－3＋(n －1)²59≤0，∴n ≤325，∵n ∈N *.∴前6项均为负值，∴S n 的最小值为S 6＝－293. 答案－293探究提高: 本题运用直接法，直接利用等差数列的通项公式判断出数列的项的符号，进而确定前几项的和最小，最后利用等差数列的求和公式求得最小值．变式训练1 设S n 是等差数列{a n }的前n 项和，已知a 2＝3，a 6 ＝11，则S 7＝________. 方法一 S 7＝7(a 1＋a 7)2＝7(a 2＋a 6)2＝7³(3＋11)2＝49. 故填49.方法二由⎩⎪⎨⎪⎧a 2＝a 1＋d ＝3，a 6＝a 1＋5d ＝11可得⎩⎪⎨⎪⎧a 1＝1，d ＝2，∴a 7＝1＋6³2＝13.∴ S 7＝7(a 1＋a 7)2＝7×(1＋13)2＝49. 故填49.解法二特殊值法特殊值法在考试中应用起来比较方便，它的实施过程是从特殊到一般，优点是简便易行．当暗示答案是一个“定值”时，就可以取一个特殊数值、特殊位置、特殊图形、特殊关系、特殊数列或特殊函数值来将字母具体化，把一般形式变为特殊形式．当题目的条件是从一般性的角度给出时，特例法尤其有效．例2 已知△ABC 的三个内角A 、B 、C 的对边分别为a 、b 、c ，且满足(sin A －sin C )(a ＋c )b＝sin A －sin B ，则C ＝_______.思维启迪: 题目中给出了△ABC 的边和角满足的一个关系式，由此关系式来确定角C 的大小，因此可考虑一些特殊的三角形是否满足关系式，如：等边三角形、直角三角形等，若满足，则可求出此时角C 的大小．解析容易发现当△ABC 是一个等边三角形时，满足(sin A －sin C )(a ＋c )b＝sin A －sin B ，而此时C＝60°，故角C 的大小为60°.探究提高: 特殊值法的理论依据是：若对所有值都成立，那么对特殊值也成立，我们就可以利用填空题不需要过程只需要结果这一“弱点”，“以偏概全”来求值．在解决一些与三角形、四边形等平面图形有关的填空题时，可根据题意，选择其中的特殊图形(如正三角形、正方形)等解决问题．此题还可用直接法求解如下：由(sin A －sin C )(a ＋c )b＝sin A －sin B 可得(a －c )(a ＋c )b ＝a －b ，整理得，a 2－c 2＝ab －b 2，即a 2＋b 2－c 2＝ab .由余弦定理，得cos C ＝a 2＋b 2－c22ab＝12，所以C ＝60°. 变式训练2在△ABC 中，角A 、B 、C 所对的边分别为a 、b 、c ，如果a 、b 、c 成等差数列，则cos A ＋cos C1＋cos A cos C＝________.解析方法一取特殊值a ＝3，b ＝4，c ＝5，则cos A ＝45，cos C ＝0，cos A ＋cos C 1＋cos A cos C ＝45.方法二取特殊角A ＝B ＝C ＝π3，cos A ＝cos C ＝12，cos A ＋cos C 1＋cos A cos C ＝45.例3 如图所示，在△ABC 中,AO 是BC 边上的中线，K 为AO 上一点，且OA →＝2AK →, 过点K 的直线分别交直线AB 、AC 于不同的两点M 、N ，若AB →＝mAM →，AC →＝nAN →，则m ＋n ＝________.思维启迪:题目中过点K 的直线是任意的，因此m 和n 的值是变化的，但从题意看m ＋n 的值是一个定值，故可取一条特殊的直线进行求解．解析当过点K 的直线与BC 平行时，MN 就是△ABC 的一条中位线(∵OA →＝2AK →，∴K 是AO 的中点)．这时由于有AB →＝mAM →，AC →＝nAN →，因此m ＝n ＝2，故m ＋n ＝4. 答案 4探究提高: 本题在解答中，充分考虑了“直线虽然任意,但m ＋n 的值却是定值”这一信息，通过取直线的一个特殊位置得到了问题的解,显得非常简单,在求解这类填空题时，就要善于捕捉这样的有效信息,帮助我们解决问题．变式训练3 设O 是△ABC 内部一点，且OA →＋OC →＝－2OB →，则△AOB 与△AOC 的面积之比为______．解析采用特殊位置，可令△ABC 为正三角形，则根据OA →＋OC →＝－2OB →可知，O 是△ABC 的中心，则OA ＝OB ＝OC ，所以△AOB ≌△AOC ，即△AOB 与△AOC 的面积之比为1. 解法三图象分析法(数形结合法)依据特殊数量关系所对应的图形位置、特征，利用图形直观性求解的填空题，称为图象分析型填空题，这类问题的几何意义一般较为明显．由于填空题不要求写出解答过程，因而有些问题可以借助于图形，然后参照图形的形状、位置、性质，综合图象的特征，进行直观地分析，加上简单的运算，一般就可以得出正确的答案．事实上许多问题都可以转化为数与形的结合，利用数形结合法解题既浅显易懂，又能节省时间．利用数形结合的思想解决问题能很好地考查考生对基础知识的掌握程度及灵活处理问题的能力，此类问题为近年来高考考查的热点内容．例 4 已知方程(x 2－2x ＋m )(x 2－2x ＋n )＝0的四个根组成一个首项为14的等差数列，则|m －n |的值等于________．思维启迪:考虑到原方程的四个根，其实是抛物线y ＝x 2－2x ＋m 与y ＝x 2－2x ＋n 和x 轴四个交点的横坐标，所以可以利用图象进行求解．解析如图所示，易知抛物线y ＝x 2－2x ＋m 与y ＝x 2－2x ＋n 有相同的对称轴x ＝1，它们与x 轴的四个交点依次为A 、B 、C 、D .因为x A ＝14，则x D ＝74.又|AB |＝|BC |＝|CD |，所以x B ＝34，x C ＝54.故|m －n |＝|14³74－34³54|＝12.探究提高本题是数列问题，但由于和方程的根有关系，故可借助数形结合的方法进行求解，因此在解题时，我们要认真分析题目特点，充分挖掘其中的有用信息，寻求最简捷的解法．变式训练4 已知定义在R 上的奇函数f (x )满足f (x －4)＝－f (x ),且在区间[0,2]上是增函数，若方程f (x )＝m (m >0)，在区间[－8,8]上有四个不同的根x 1，x 2，x 3，x 4，则x 1＋x 2＋x 3＋x 4＝________.解析因为定义在R 上的奇函数，满足f (x －4)＝－f (x )，所以f (4－x )＝f (x )．因此，函数图象关于直线x ＝2对称且f (0)＝0，由f (x －4)＝－f (x )知f (x －8)＝f (x )，所以函数是以8为周期的周期函数．又因为f (x )在区间[0,2]上是增函数，所以f (x )在区间[－2,0]上也是增函数，如图所示，那么方程f (x )＝m (m >0)在区间[－8,8]上有四个不同的根x 1，x 2，x 3,x 4，不妨设x 1<x 2<x 3<x 4.由对称性知x 1＋x 2＝－12，x 3＋x 4＝4，所以x 1＋x 2＋x 3＋x 4＝－12＋4＝－8.例5 函数y ＝f (x )的图象如图所示，其定义域为[－4,4]，那么不等式f (x )sin x≤0的解集为_______________．解析 f (x )sin x ≤0⇔⎩⎪⎨⎪⎧f (x )≤0，sin x >0，或⎩⎪⎨⎪⎧f (x )≥0，sin x <0，在给出的坐标系中，再作出y ＝sin x 在[－4,4]上的图象，如图所示,观察图象即可得到所求的解集为[－4，－π)∪(－π，0)∪[π2，π)．探究提高与函数有关的填空题，依据题目条件，灵活地应用函数图象解答问题，往往可使抽象复杂的代数问题变得形象直观，使问题快速获解．变式训练5 不等式（|x |-2）²sin x <0，x ∈[-π,2π］的解集为 .解析在同一坐标系中分别作出y =|x |- 2 与y=sin x 的图象：根据图象可得不等式的解集为：解法四等价转化法将所给的命题进行等价转化，使之成为一种容易理解的语言或容易求解的模式．通过转化，使问题化繁为简、化陌生为熟悉，将问题等价转化成便于解决的问题，从而得出正确的结果．例6 设函数f (x )＝⎩⎪⎨⎪⎧x 2－4x ＋6， x ≥03x ＋4， x <0，若互不相等的实数x 1，x 2，x 3满足f (x 1)＝f (x 2)＝f (x 3)，则x 1＋x 2＋x 3的取值范围是________．思维启迪:π)2,(π)2π,0()2ππ,( -将问题转化为y ＝m 与y ＝f (x )有三个不同的交点，再研究三个交点的横坐标之和的取值范围．解析本题可转化为直线y ＝m 与函数f (x )的图象有三个交点,y ＝x 2－4x ＋6在[0,＋∞)的最小值为f (2)＝2，故2<m <4，易知x 1,x 2，x 3中必有一负二正，不妨设x 1，x 2>0，由于y ＝x 2－4x ＋6的对称轴为x ＝2,则x 1＋x 2＝4，令3x ＋4＝2，得x ＝－23，则－23<x 3<0，故－23＋4<x 1＋x 2＋x 3<0＋4，即x 1＋x 2＋x 3的取值范围是(103，4)．探究提高等价转化法的关键是要明确转化的方向或者说转化的目标．本题转化的关键就是将研究x 1＋x 2＋x 3的取值范围问题转化成了直线y ＝m 与曲线y ＝f (x )有三个交点的问题，将数的问题转化成了形的问题，从而利用图形的性质解决．变式训练6 已知关于x 的不等式ax －1x ＋1<0的解集是(－∞,－1)∪(－12，＋∞)，则a 的值为________．解析将ax －1x ＋1<0转化为(x ＋1)(ax －1)<0,其解集是(－∞,－1)∪(－12，＋∞)，当且仅当x ＝－12是方程ax －1＝0的解，得a ＝－2. 解法五构造法构造型填空题的求解，需要利用已知条件和结论的特殊性构造出新的数学模型，从而简化推理与计算过程，使较复杂的数学问题得到简捷的解决，它来源于对基础知识和基本方法的积累，需要从一般的方法原理中进行提炼概括，积极联想，横向类比，从曾经遇到过的类似问题中寻找灵感，构造出相应的函数、概率、几何等具体的数学模型，使问题快速解决．例7 函数f (x )＝2sin(x ＋π4)＋2x 2＋x2x 2＋cos x 的最大值为M ，最小值为m ，则M ＋m ＝________.思维启迪:直接求f (x )的最大值、最小值显然不可取．化简f (x )＝1＋x ＋sin x 2x 2＋cos x ，构造新函数g (x )＝x ＋sin x2x 2＋cos x利用g (x )的奇偶性求解．解析: 根据分子和分母同次的特点，分子展开，得到部分分式，f (x )＝1＋x ＋sin x2x 2＋cos x，f (x )－1为奇函数，则m －1＝－(M －1)，∴M ＋m ＝2.探究提高:整体思考，联想奇函数，利用其对称性简化求解，这是整体观念与构造思维的一种应用．注意到分式类函数的结构特征，借助分式类函数最值的处理方法，部分分式法，变形发现辅助函数为奇函数，整体处理最大值和最小值的问题以使问题简单化，这种构造特殊函数模型的方法来源于对函数性质应用的深刻理解．变式训练7 已知函数f (x )＝sin x cos x ＋sin x cos x ＋3，若f (lg a )＝4，则f (lg 1a )的值等于________．解析: f (x )＝sin x cos x ＋sin x cos x ＋3＝12sin 2x ＋tan x ＋3，若令g (x )＝12sin 2x ＋tan x ，则g (x )是一个奇函数．由f (lg a )＝4,得g (lg a )＋3＝4,∴g (lg a )＝1.于是g (lg 1a )=g (－lg a )＝－g (lg a )＝－1，故f (lg 1a )＝g (lg 1a)＋3＝－1＋3＝2.例8 已知a 、b 是正实数，且满足ab ＝a ＋b ＋3，则a ＋b 的取值范围是__________．思维启迪:考虑到已知条件中出现了两个正数a 和b 的乘积ab 以及和a ＋b ，可与一元二次方程的根联系起来构造方程进行求解．解析: ∵a 、b 是正实数且ab ＝a ＋b ＋3，故a 、b 可视为一元二次方程x 2－mx ＋m ＋3＝0的两个根，其中a ＋b ＝m ，ab ＝m ＋3.要使方程有两个正根，应有⎩⎪⎨⎪⎧Δ＝m 2－4m －12≥0，m >0，m ＋3>0，解得m ≥6，即a ＋b ≥6，故a ＋b 的取值范围是[6，＋∞)．。

2013年高考备考讲座提纲--数学解读会

18
19
20
21
导数问题
立体几何
数列问题
丌等式问题
以核辐射背景的概率统计
抛物线问题
知识要求
1.极值点 1.线线 2.已知单调平行性求参数值 2.求体积
1.通项 2.前n项和
1.证明 3 .证明
求轨 1求概率迹 2求EX 3求EX的最小值
11理科
函数题（包括导数不等式三角函数）占了44分， 29.3％
复数
双曲线
奇偶性
线性规划
极坐标
三视图
命题的否定
集合中的排列组合
三角函数问题
函数图象
11理科
填空题知识考点
11
12
13
14
15
程序框图
二项式定理
向量
三角形中的三角函数
直线过整点问题
11理科
解答题
问题背景
16
17
1.角 2.面积
1.单调性和极值 2丌等式证明
1.线面平行 2线面垂直 2.求体积
1.求椭囿方程 2. 求角平分线方程 3 对称问题
等差数列证明
10理科
函数题（包括导数不等式三角函数）占了44分， 29.33％
解析几何占了22分，14.7％
立体几何占了23分，15.3％概率统计占了23分，15.3％
研读考纲把握规律高效备考
合肥一中刘昱
2013年高考备考讲座提纲
一、安徽卷考试说明二、四年（09--12)高考试题回顾三、几年来高考不变的规律
四、2013年高考数学试题命制趋势展望五、高考试题的分单元分析及备考建议六、目前学生数学复习中可能存在的问题

高中数学竞赛专题讲座

高中数学竞赛专题讲座主要涉及高中数学竞赛中的重点、难点和热点问题，旨在提高学生的数学思维能力和解题技巧。

以下是一些高中数学竞赛专题讲座的常见内容：1.集合与容斥原理：集合是数学中基本的概念之一，而容斥原理是集合论中的重要原理之一。

在讲座中，可以介绍集合的基本概念、集合的表示方法、集合的运算、容斥原理等。

2.组合数学：组合数学是数学竞赛中的重要内容之一，包括排列、组合、组合恒等式、组合计数、组合优化等问题。

在讲座中，可以介绍这些问题的解决方法，如递归法、数学归纳法等。

3.数学归纳法及其应用：数学归纳法是一种重要的证明方法，适用于证明与自然数有关的命题。

在讲座中，可以介绍数学归纳法的原理、应用场景和常见问题，如归纳法中的恒等式证明等。

4.数列与数列求和：数列是数学中的重要概念之一，而数列求和是数学竞赛中的常见问题。

在讲座中，可以介绍数列的基本概念、数列的表示方法、数列的通项公式和求和公式等。

5.不等式及其性质：不等式是数学竞赛中常见的问题之一，涉及的知识点较多。

在讲座中，可以介绍不等式的基本性质、基本不等式和常见的解题技巧，如放缩法等。

6.几何证明与解析几何：几何证明是数学竞赛中的重要内容之一，而解析几何是通过代数方法研究几何问题的方法之一。

在讲座中，可以介绍平面几何和解析几何的基本概念、性质和解题方法。

7.概率与统计：概率与统计是数学竞赛中的常见问题之一，包括随机事件的概率、随机变量的分布和统计数据的分析等。

在讲座中，可以介绍这些问题的解决方法，如公式法、模拟法等。

总之，高中数学竞赛专题讲座涉及的知识点较多，需要学生在日常学习中不断积累和巩固基础知识点，提高自己的数学思维能力和解题技巧。

同时，也需要教师根据学生的实际情况和竞赛要求，制定合理的教学计划和教学方法，帮助学生更好地掌握数学竞赛的相关知识和技能。

2013年自主招生本月开始考前备考注重民生内容

2013年自主招生本月开始考前备考注重民生内容备受考生和家长关注的2013年高校自主招生即将开始，考生又将迎来新一轮激烈竞争。

具备高校自招资格的考生最终被高校认定，将享受到高考降分录取等优惠政策。

目前自招的高校已达80多所。

考生如何根据自己的实际情况，更为科学合理地选择？昨天，记者采访了富有经验的名师、大连育明高中教务处主任张敬燕。

考生家长首先明确参加自招的目的：是要冲高，还是要保底。

成绩稳定的考生可以冲高，利用自招的降分优惠来冲一所更好的大学，成绩不稳定的考生要实行保底策略，通过自招更稳妥地进入心仪的高校。

对于目标院校的选择，要结合考生的学习成绩来认真定位。

可以根据高一、高二的成绩，以及高三期中考试成绩来确定目标高校。

在海选学校阶段，一种做法是，考生根据自己的成绩水平、对高校的喜好程度，在自招院校中先选定一批目标院校，再根据目标院校的招生简章作进一步筛选，看看自己符合哪几所的报名条件。

另一种做法，可以先阅读高校自招简章，看自己符合哪些学校的报名条件，最后根据自己的成绩和对高校的喜好程度来筛选，确定目标。

无论你选择哪个或哪几个目标高校，都要准备很多的申请材料。

一般来说高校自主选拔录取的《招生简章》要在11月份开始陆续公布，若等简章下来后再准备，时间就很仓促了。

考生可以到网上查询一下各高校往年的自招章程作个参考，等最新简章发布后再作调整。

参加自招需要的材料准备要遵循一个原则：在精不在多。

在准备申请材料时，要认真对待申请材料的每个细节，实事求是，不能夸大其词。

自招笔试的试题，要么灵活多变，要么题量极大，一般不用作特殊的准备。

但还是能有一些规律可循：社会热点经常会作为考试材料出现，这就需要考生平时注意这方面的积累。

一些陈旧的，不存在争议的，与热点联系偏远的一定不会进入试题。

考试主要考查学生的学习潜力、合作意识、社会公德、奉献精神，无论多特殊的学校，也会尊重社会认可的普世价值，有关民生的内容肯定会考。

同时，考前一周左右辅导一下孩子的面试。