人教版高三数学(文)上学期第二次月考试题
高三数学上学期第二次月考试题文含解析试题

卜人入州八九几市潮王学校一中2021届高三年级第二次月考数学试卷〔文科〕第一卷〔一共60分〕一、选择题:本大题一一共12个小题,每一小题5分,一共60分.在每一小题给出的四个选项里面,只有一项为哪一项哪一项符合题目要求的.1.复数的一共轭复数是〔〕A. B. C. D.【答案】C【解析】,∴复数的一共轭复数是应选:C点睛:除法的关键是分子分母同乘以分母的一共轭复数,解题中要注意把的幂写成最简形式.2.假设,且,那么角的终边位于〔〕A.第一象限B.第二象限C.第三象限D.第四象限【答案】B【解析】∵sinα>0,那么角α的终边位于一二象限或者y轴的非负半轴,∵由tanα<0,∴角α的终边位于二四象限,∴角α的终边位于第二象限.应选择B.3.函数,其中为实数,假设对恒成立,且,那么的单调递增区间是〔〕A.向左平移个长度单位B.向右平移个长度单位C.向左平移个长度单位D.向右平移个长度单位【答案】A【解析】假设对恒成立,那么为函数的函数的最值,即2×+φ=kπ+,k∈Z,那么φ=kπ+,k∈Z,又f〔〕>f〔π〕,sin〔π+φ〕=﹣sinφ>sin〔2π+φ〕=sinφ,sinφ<0.令k=﹣1,此时φ=﹣,满足条件sinφ<0,令2x﹣∈[2kπ﹣,2kπ+],k∈Z,解得:x∈[kπ+,kπ+]〔k∈Z〕.那么f〔x〕的单调递增区间是[kπ+,kπ+]〔k∈Z〕.应选C.4.A. B.-1C. D.1【答案】D【解析】,应选:D.5.在中,角所对边长分别为,假设,那么的最小值为〔〕A. B. C.D.【答案】C考点:余弦定理。
6.,那么A.9B.3C.1D.2【答案】C【解析】试题分析:,可得,即,又解得,,.应选B.考点:1、向量的模,2、向量的数量积的运算.7.函数,其中,假设的值域是,那么实数的取值范围是〔〕A. B. C. D.【答案】D【解析】∵的值域是,∴由函数的图象和性质可知≤≤,可解得a∈.应选:D.8.假设,,且,那么的值是〔〕A. B. C.或者 D.或者【答案】A【解析】∵,∴,又0<<,∴2α∈〔,π〕,即α∈〔,〕,∴β﹣α∈〔,〕,∴cos2α=﹣=﹣;又,∴β﹣α∈〔,π〕,∴cos〔β﹣α〕=﹣=﹣,∴cos〔α+β〕=cos[2α+〔β﹣α〕]=cos2αcos〔β﹣α〕﹣sin2αsin〔β﹣α〕=﹣×〔﹣〕﹣×=.又α∈〔,〕,,∴〔α+β〕∈〔,2π〕,∴α+β=,应选:A.点睛:求角问题一般包含三步:第一步明确此角的某个三角函数值,第二步根据条件限制角的范围;第三步求出此角.9.某班设计了一个八边形的班徽〔如图〕,它由腰长为1,顶角为的四个等腰三角形,及其底边构成的正方形所组成,该八边形的面积为〔〕A. B.C. D.【答案】A【解析】试题分析:利用余弦定理求出正方形面积;利用三角形知识得出四个等腰三角形面积;故八边形面积.故此题正确答案为A.考点:余弦定理和三角形面积的求解.【方法点晴】此题是一道关于三角函数在几何中的应用的题目,掌握正余弦定理是解题的关键;首先根据三角形面积公式求出个三角形的面积;接下来利用余弦定理可求出正方形的边长的平方,进而得到正方形的面积,最后得到答案.10.函数,其中为实数,假设对恒成立,且,那么的单调递增区间是〔〕A. B.C. D.【答案】C【解析】假设对恒成立,那么为函数的函数的最值,即2×+φ=kπ+,k∈Z,那么φ=kπ+,k∈Z,又f〔〕>f〔π〕,sin〔π+φ〕=﹣sinφ>sin〔2π+φ〕=sinφ,sinφ<0.令k=﹣1,此时φ=﹣,满足条件sinφ<0,令2x﹣∈[2kπ﹣,2kπ+],k∈Z,解得:x∈[kπ+,kπ+]〔k∈Z〕.那么f〔x〕的单调递增区间是[kπ+,kπ+]〔k∈Z〕.应选C.11.在矩形中,,,为矩形内一点,且,假设,那么的最大值为〔〕A.B. C. D.【答案】C【解析】如图,设∠PAE=θ,,那么:;又;∴;∴;∴的最大值为.应选B.12.假设,实数满足方程组那么〔〕A.0B.C.D.1【答案】D【解析】,由②化简得:8y3﹣〔1+cos2y〕+2y+3=0,整理得:﹣8y3+cos2y﹣2y﹣2=0,即〔﹣2y〕3+cos〔﹣2y〕+〔﹣2y〕﹣2=0,设t=﹣2y,那么有t3+cost+t﹣2=0,与方程①比照得:t=x,即x=﹣2y,∴x+2y=0,那么cos〔x+2y〕=1.应选D点睛:解题关键根据两个方程的构造特点,构造新函数借助新函数的性质明确x与y的关系,从而得到的值.第二卷〔一共90分〕二、填空题〔每一小题5分,总分值是20分,将答案填在答题纸上〕13.在中,,且的面积为,那么__________.【答案】【解析】根据题意,的面积为:,那么,在中,由余弦定理有:.1021年在召开的国际数学家大会,会标是以我国古代数学家赵爽的弦图为根底设计的,弦图是由四个全等直角三角形与一个小正方形拼成的一个大正方形〔如图〕.假设小正方形的面积为1,大正方形的面积为25,直角三角形中较小的锐角为,那么的值等于__________.【答案】【解析】试题分析:由题意得,大正方形的边长为5,小正方形的边长为1,∴1=5cosα-5sinα,∴cosα-sinα=.由于α为锐角,cos2α+sin2α=1,∴cosα=,sinα=,∴考点:此题考察三角函数的应用点评:用三角函数来表示正方形的边长,列方程求解15.如图,是边长为4的正方形,动点在以为直径的圆弧上,那么的取值范围是__________.【答案】【解析】以AB中点为坐标原点,AB所在直线为x轴建立如图坐标系那么圆弧APB方程为x2+y2=4,〔y≥0〕,C〔2,4〕,D〔﹣2,4〕因此设P〔2cosα,2sinα〕,α∈[0,π]∴=〔2﹣2cosα,4﹣2sinα〕,=〔﹣2﹣2cosα,4﹣2sinα〕,由此可得=〔2﹣2cosα〕〔﹣2﹣2cosα〕+〔4﹣2sinα〕〔4﹣2sinα〕=4cos2α﹣4+16﹣16sinα+4sin2α=16﹣16sinα化简得=16﹣16sinα∵α∈[0,π],sinα∈[0,1]∴当α=0或者π时,取最大值为16;当α=时,取最小值为0.由此可得的取值范围是[0,16]故答案为:[0,16]点睛:向量有三种表达形式,几何形式,代数形式,符号形式,三种形式对应着处理平面向量问题的三种策略.16.如图,在平面斜坐标系中,,斜坐标定义:假设〔其中,分别是轴,轴的单位向量〕,那么叫做的斜坐标.〔1〕得斜坐标为,那么__________.〔2〕在此坐标系内,,动点满足,那么的轨迹方程是__________.【答案】(1).1(2).【解析】〔1〕∵,∴1.........................故答案为:1;y=x三、解答题〔本大题一一共6小题,一共70分.解容许写出文字说明、证明过程或者演算步骤.〕17.设的内角所对边的长分别为,且有.〔1〕求角的大小;〔2〕假设,为的中点,求的长.【答案】(1)(2)【解析】试题分析:〔Ⅰ〕根据2sinBcosA=sinAcosC+cosAsinC,可得2sinBcosA=sin〔A+C〕,从而可得2sinBcosA=sinB,由此可求求角A的大小;〔Ⅱ〕利用b=2,c=1,A=,可求a的值,进而可求B=,利用D为BC的中点,可求AD的长.试题解析:〔1〕∵,∴,∵,∴,∴,∴,∵,∴;〔2〕∵,,∴,∴,∴,∵为的中点,∴.点睛:解三角形问题,多为边和角的求值问题,这就需要根据正、余弦定理结合条件灵敏转化边和角之间的关系,从而到达解决问题的目的.其根本步骤是:第一步:定条件,即确定三角形中的和所求,在图形中标出来,然后确定转化的方向.第二步:定工具,即根据条件和所求合理选择转化的工具,施行边角之间的互化.第三步:求结果.18.在中,.〔1〕求的值;〔2〕假设,求在方向上的投影.【答案】(1)(2)【解析】试题分析:〔1〕根据降幂公式,代入化简得到,再根据两角和的余弦公式化简为,〔2〕根据投影公式在方向上的投影为,所以根据正弦定理求,再求,根据余弦定理求,代入即可.试题解析:(1)由,可得,即,∴〔2〕由正弦定理得,由题意知,∴,∴.由余弦定理得,解得〔舍〕在方向上的投影:.19.函数的图象关于直线对称,且图象上相邻两个最高点的间隔为.〔1〕求和的值.〔2〕假设,求的值.【答案】(1),(2)【解析】试题分析:〔1〕由两个相邻的最高点的间隔可求得周期,那么,函数为,由函数关于直线对称,可知,结合可求得的值;〔2〕对进展三角恒等变换,可求得的值,又为锐角,可求得,再利用三角恒等变换求得值.试题解析:〔1〕由题意可得函数的最小正周期为,再根据图象关于直线对称,可得结合,可得〔2〕再根据考点:三角函数的周期与初相,三角恒等变换.20.函数.假设的最小正周期为.〔1〕求的单调递增区间;〔2〕在中,角的对边分别是满足,求函数的取值范围.【答案】(1)(2)【解析】试题分析:〔1〕利用正弦、余弦的二倍角公式以及两角和公式把化简成,通过的最小正周期求出,得到的解析式,再通过正弦函数的单调性求出答案;〔2〕根据正弦定理及,求出,进而求出,得到的范围,把代入根据正弦函数的单调性,求出函数的取值范围.试题解析:(1)f(x)=sinωx cosωx+cos2ωx-=sin,∵T==4π,∴ω=,∴f(x)=sin,∴f(x)的单调递增区间为(k∈Z).(2)∵(2a-c)cos B=b cos C,∴2sin A cos B-sin C cos B=sin B cos C,2sin A cos B=sin(B+C)=sin A,∴cos B=,∴B=.∵f(A)=sin,0<A<,∴,∴f(A)∈.21.如图,在直角坐标系中,点是单位圆上的动点,过点作轴的垂线与射线交于点,与轴交于点,记,且.〔1〕假设,求.〔2〕求面积的最大值.【答案】(1)(2)【解析】试题分析:﹙1﹚同角三角的根本关系求得的值,再利用两角差的余弦公式求得的值.(2)利用用割补法求的面积,再利用正弦函数的值域,求得它的最值.试题解析:〔1〕依题意得,所以,因为,且,所以,所以.〔2〕由三角函数定义,得,从而.,.因为,所以当时,“=〞成立,所以面积的最大值为.22.函数.〔1〕假设函数的最大值为6,求常数的值;〔2〕假设函数有两个零点和,求的取值范围,并求和的值;〔3〕在〔1〕的条件下,假设,讨论函数的零点个数.【答案】(1)(2),(3)没有零点【解析】试题分析:〔1〕利用二倍角的正弦公式,两角和的正弦公式化简解析式,由x的范围求出的范围,由正弦函数的最大值和条件列出方程,求出m的值;〔2〕由x的范围求出z=的范围,函数在上有两个零点方程在上有两解,再转化为两个函数图象有两个交点,由正弦函数的图象列出不等式,求出m的范围,由正弦函数的图象和对称性求出x1与x2的和;〔3〕由〔1〕求出f〔x〕的最小值,求出当t≥2时〔t﹣1〕f〔x〕的范围,利用商的关系、两角差的正切公式化简,由x的范围、正切函数的性质求出范围,即可判断出函数g〔x〕的零点个数.试题解析:〔1〕由题意得,,,∵,∴,那么,∴时,,解得;〔2〕令,∵,∴,函数在上有两个零点方程在上有两解,即函数与在上有两个交点由图象可知,解得由图象可知,∴解得;〔3〕在〔1〕的条件下,,且,那么,当时,〔当且时取等号〕,,∵,∴,〔当时取等号〕,所以当时,函数有一个零点,当时,恒成立,函数没有零点。
新人教版高三上学期第二次月考数学(文)试卷(含答案)
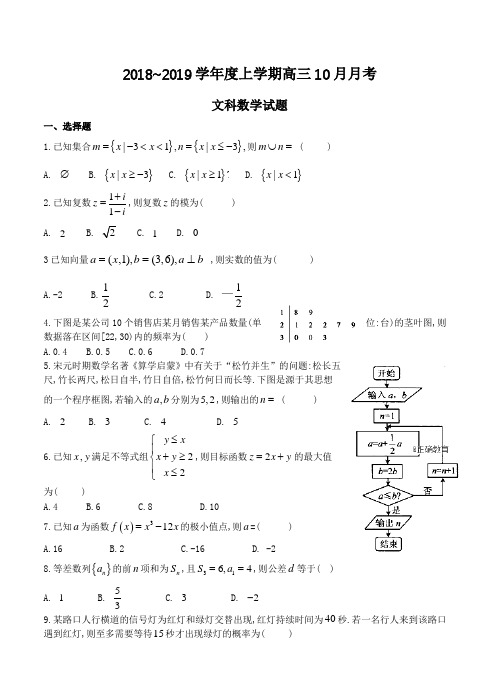
2018~2019学年度上学期高三10月月考文科数学试题一、选择题1.已知集合{}{}31,|,|3m x x n x x =-<<=≤-则m n ⋃= ( ) A.∅B.{}|3x x ≥- C.{}|1?x x ≥ D.{}|1x x <2.已知复数11iz i+=-,则复数z 的模为( ) A.2C.1D.0 3已知向量(,1),(3,6),ax b a b ==⊥ ,则实数的值为( )A.-2B.12C.2D. 12— 4.下图是某公司10个销售店某月销售某产品数量(单位:台)的茎叶图,则数据落在区间[22,30)内的频率为( ) A.0.4 B.0.5 C.0.6 D.0.75.宋元时期数学名著《算学启蒙》中有关于“松竹并生”的问题:松长五尺,竹长两尺,松日自半,竹日自倍,松竹何日而长等.下图是源于其思想的一个程序框图,若输入的,a b 分别为5,2,则输出的n = ( ) A.2B.3C.4D.56.已知 ,x y 满足不等式组22y x x y x ⎧≤+≥≤⎪⎨⎪⎩,则目标函数2z x y =+的最大值为( )A.4B.6C.8D.107.已知a 为函数()312f x x x =-的极小值点,则a =( )A.16B.2C.-16D. -28.等差数列{}n a 的前n 项和为n S ,且316,4S a ==,则公差d 等于( ) A.1B.53C.3D.2- 9.某路口人行横道的信号灯为红灯和绿灯交替出现,红灯持续时间为40秒.若一名行人来到该路口遇到红灯,则至多需要等待15秒才出现绿灯的概率为()A.710B.58C.310D.3810.如下图,在ABC ∆中,1,3AN NC P =是BN 上的一点,若29AP mAB AC =+,则实数m 的值为( )A.13B.19C.3D.1 11.设0,0a b >>.若1a b +=,则1122a b+的最小值是( ) A.1B.18C.2D.4 12.已知函数()()2112x x f x x x a e e --+=-++有唯一零点,则a = ( ) A.1B.12C.13D.12- 二、填空题13.若命题2:,log 0p x R x ∀∈≥,则p ⌝是__________。
高三数学上学期第二次月考试题 文 新人教-新版

—————————— 新学期 新成绩 新目标 新方向 ——————————2019学年度第一学期第二次月考高三数学(文)试题(满分150分,时间120分钟)一、选择题(每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.)1. 已知集合{}{}2|21,|450,A x x B x x x =-<≤=+-≤则B C A =A. {|52}x x -≤≤-B. {|52}x x -≤<-C. {|52}x x -<≤-D. {|52}x x -<<-2. 已知函数23,0(),0x x f x m x x ⎧<⎪=⎨-≥⎪⎩,给出下列两个命题: 命题:(,0)p m ∃∈-∞,方程()0f x =有解.命题:q 若19m =,则((1))0f f -=.那么,下列命题为真命题的是 A. p q ∧B. ()p q ⌝∧C. ()p q ∧⌝D. ()()p q ⌝∧⌝3. 在ABC ∆中,22,60,2AB AC BAC BD DC ==∠==,则AD BC ⋅=A. 1B. -1D.24. 已知某棱锥的三视图如图所示,则该棱锥的表面积为A. 2B. 3+C. 2+D. 3+5. 函数sin 3()33x xxf x -=-的图象大致为6. 已知函数()sin(2)(0)f x x ϕπϕ=+-<<,将函数()f x 的图象向左平移3π个单位长度后所得的函数图象关于直线x π=对称,则函数()f x A. 在区间[,]63ππ-上单调递减B. 在区间[,]36ππ-上单调递减 C. 在区间[,]36ππ-上单调递增D. 在区间[,]63ππ-上单调递增 7. 已知函数|1|1()()2x f x m -=+,若()2f x >恒成立,则 1.10.9(2),(3),a f b f ==2()c f m -=三者的大小关系为A. a b c <<B. a c b <<C. b a c <<D. c b a <<8. 圆心在直线220x y --=上,且过点(3, 1)的圆与直线20x y --=相切,则该圆的标准方程为A. 22(2)(2)x y -+-=B. 22(1)(1)2x y +++= C. 22(2)(2)2x y -+-=D. 22(2)(1)2x y ++-=9. 数列{}n a 满足11a =,对任意的n ∈N *都有11n n a a a n +=++,则122016111...a a a +++= A.20152016B.20162017C.40332017D.4032201710. 已知偶函数()(0)f x x ≠的导函数为()f x ',且满足(1)0f =,当0x >时,()2()x f x f x '<-,则使()0f x >成立的x 的取值范围为 A. (,1)(0,1)-∞- B. (1,0)(0,1)- C. (1,0)(1,)-+∞D. (,1)(1,)-∞-+∞11. 若点O 和点(2,0)F -分别为双曲线2221(0)x y a a-=>的中心和左焦点,点P 为双曲线右支上的任意一点,则⋅的取值范围为A. [3)-+∞B. [3)++∞C. 7[,)4-+∞D. 7[,)4+∞12. 已知函数()f x 是定义在R 上的奇函数,且当0x >时,()(3)0f x f x -++=;当(0,3)x ∈时,ln ()e xf x x=,其中e 是自然对数的底数,且 2.72e ≈,则方程6()0f x x -=在[-9,9]上的解的个数为A. 4B. 5C. 6D. 7二、填空题:(本大题共4小题,每小题5分,共20分,把答案填在题中横线上)13.已知函数()y f x =满足条件(2)(2)f x f x +=-,当且[0,1]x ∈时,()52xf x =+,则151(log )6253f ⨯= . 14. 已知实数,x y 满足不等式组23032x y x y y --≥⎧⎪+≤⎨⎪≥-⎩,则22y x z x +=的取值范围是 .15. 球O 与棱长为2的正四面体各条棱都相切,设正四面体的体积为1V ,球的体积为2V ,则12V V = .16. 已知椭圆22221(0)x y a b a b+=>>的左、右焦点分别为12,F F ,点P 为以12||F F 为直径的圆与椭圆的一个交点,且P 到x 轴的距离为22a c,则该椭圆的离心率为 .三、解答题:(本大题共5个题,要求写出必要的推理、证明、计算过程) 17.(本题满分12分)在ABC ∆中,,,a b c 分别为角A ,B ,C 所对的边,sin sin sin c a c bB C A--=+. (Ⅰ)求角A ;(Ⅱ)若ABC a S ∆==11b c+的值. 18.(本题满分12分)各项均为正数的数列{}n a 满足122n n a S =+,其中n S 为数列{}n a 前n 项和,且23,2a a 为等差数列{}n b 的前两项.(Ⅰ)求数列{},{}n n a b 的通项公式;(Ⅱ)设2n n n c a b +=,试求数列{}n c 的n 项和n T . 19.(本题满分12分)已知四棱锥P -ABCD 中,底面ABCD 是直角梯形,AD//BC ,AB ⊥AD ,且PD ⊥平面ABCD ,AB =2AD =2,M 在BC 上且BM =4MC =4. (Ⅰ)求证:平面PAM ⊥平面PBD ;(Ⅱ)若N 为PM 中点,PD =2,求三棱锥N -PCD 的体积.20.(本题满分12分)已知焦点在y 轴上的抛物线C 经过点P (-2,1). (Ⅰ)求抛物线C 的标准方程;(Ⅱ)过点M (2,4)的直线l 与抛物线交于点A ,B ,设直线PA ,PB 的斜率分别为12,k k ,判断1234k k +是否为定值,并说明理由 21.(本题满分12分)已知函数1()ln 2f x m x x x=++. (Ⅰ)若1m =-,求曲线()y f x =在点(1,(1)f )处的切线方程;(Ⅱ)若对任意的[0,1],[2,]m x e ∈∈关于x 的不等式()(2)f x n x ≤+恒成立,求实数n 的取值范围.请考生在(22).(23)两题中任选一题作答,如果多答,则按做的第一题记分.作答时用2B 铅笔在答题卡上把所选题目对应题号右侧的方框涂黑. 22.(本题满分10分)选修4-4:坐标系与参数方程在直角坐标系xoy 中,直线l 经过点(1,0)P ,倾斜角为6π.以坐标原点O 为极点,以x 轴的正半轴为极轴,建立极坐标系,曲线C 的极坐标方程为4cos()3πρθ=+.(1)写出直线l 的参数方程和曲线C 的直角坐标方程;(2)设直线l 与曲线C 相交于A ,B 两点,求|PA|+|PB|的值.23.(本小题满分10分)选修4-5:不等式选讲已知函数()|21||1|f x x x =-++. (1)解不等式()3f x ≤;(2)记函数()()|1|g x f x x =++的值域为M ,若t M ∈,证明:2313t t t+≥+.。
高三数学上学期第二次月考试题 文 试题

卜人入州八九几市潮王学校汪清县第HY 学2021届高三数学上学期第二次月考试题文 本卷须知:1.2.请将答案正确填写上在答题卡上1.{P =-,{}sin ,Q y y θθ==∈R ,那么PQ =〔〕A .∅B .{}0C .{}1,0-D .{- 2.复数2)1(=+zi ,求=z 〔〕 A .1 B .2 C .2 D .43.条件:24p x -<<,条件()():20q x x a ++<;假设q 是p 的必要而不充分条件,那么a 的取值范围是〔〕A .()4,+∞B .(),4-∞-C .(],4-∞-D .[)4,+∞ ABC ∆中,角A,B,C 所对角为a,b,c.假设B a b sin 2=,那么角A 等于〔〕A .3πB .6πC .4πD .656ππ或 5.等差数列{}n a 中,n S 为n a 的前n 项和,208=a ,567=S ,那么12a =〔〕 A .2 B .32 C .36D .40 6.假设43tan =α,那么αα2sin 2cos 2+=〔〕A .2564 B .2548 C .1 D .25167假设点102⎛⎫ ⎪⎝⎭,到直线():300l x y m m ++=>m =〔〕A .7B .172C .14D .178.向量a ,b 满足1=a ,+=a b ,)1=-b ,那么a ,b 的夹角等于〔〕A .3πB .6πC .23πD .56π 9.执行如下列图的程序框图,输出的值是S 〔〕A .43B .55C .61D .81 10.设x ,y 满足约束条件22024010x y x y x +-≥⎧⎪-+≥⎨⎪-≤⎩,那么目的函数32z x y =-的最小值为〔〕A .6-B .4-C .2D .2-11.直线l :y x m =+与曲线x =m 的取值范围是〔〕A.⎡-⎣ B.(1-⎤⎦ C.⎡⎣ D.(⎤⎦12.函数2)(+=ax x f ,x x x g 2)(2-=,对[]11,2x ∀∈-,[]2,12-∈∃x ,使)()(21x g x f =,那么a 的取值范围是〔〕A .⎥⎦⎤ ⎝⎛21,0 B .⎥⎦⎤⎢⎣⎡-21,1 C .[)+∞⋃⎥⎦⎤ ⎝⎛-∞-,323, D .[)+∞,313.设(1,2)a =,(1,1)b =,c a kb =+.假设b c ⊥,那么实数k 的值等于. 14.{}n a 为等比数列,212=a ,453=⋅a a ,那么=q _______ 15.设函数x x f cos )(=,先将()y f x =纵坐标不变,横坐标变为原来的2倍,再将图象向右平移3π个单位长度后得)(x g y =,那么)(x g y =的对称中心为________ )1,0(,1log )3(≠>-=+a a y x a 且的图像恒过定点A ,假设点A 在直线01=++ny mx 上,其中0>mn ,那么nm 21+的最小值为. 17.〔10分〕在ABC ∆中,角,,A B C 的对边分别为,,a b c ,4a =,23B π=,sin 2sin b C B =.〔1〕求b 的值;〔2〕求ABC ∆的面积. 18.(本小题12分)圆C 经过点()2,1A -和直线10x y +-=相切,且圆心在直线2y x =-上.〔1〕求圆C 的方程;〔2〕假设直线22y x =-与圆C 交于A ,B 两点,求弦AB 的长19.〔本小题12分〕数列{}n a 的前n 项和为n S ,且满足n n S n +=2,*∈N n (1)求{}n a 的通项公式;(2)求数列⎭⎬⎫⎩⎨⎧+n a n )1(1的前n 项和. 20.〔12分〕在ABC ∆中,内角,,A B C 所对的边分别是,,a b c ,sin 4sin 5sin b B a B a A =+.〔1〕假设c=,求角C 的大小;〔2〕假设2a =,且ABC ∆的面积为,求ABC ∆的周长.21.(本小题总分值是12分)数列}{n a 的首项11=a ,前n 项和为n S ,且121+=+n n S a . 〔1〕求数列}{n a 的通项公式;〔2〕设13log +=n n a b ,求数列}{n n b a +的前n 项和n T .22.(本小题总分值是12分)函数()1x f x e a -=+,函数()ln ,g x ax x a R =+∈.〔1〕求函数()y g x =的单调区间;〔2〕假设不等式()()1f x g x ≥+在[)1,+∞上恒成立,务实数a 的取值范围;文科数学答案 第一卷一、选择题〔此题一共12小题,每一小题5分,一共60分,只有一个选项正确,请把答案写在答题卷上..........〕 1-6:ACBBAD7-12:AACDCB 第二卷二、填空题〔此题一共4小题,每一小题5分,一共20分,请把答案写在答题卷上..........〕13.32 14.2±15.Z k kx ∈+),0,342(π 16.⎪⎭⎫⎢⎣⎡49,21 三、解答题〔此题一共6个小题,一共70分.解容许写出必要的文字说明、证明过程或者演算步骤,请把答案写在答题卷上〕17.解:〔1〕由Z k k x k ∈+≤-≤+,23263122πππππ 得函数的单调递减区间为:Z k k k ∈++],56,26[ππππ〔2〕由135cos 1310)23(==+απα得:f 那么:6533)cos(-=+βα 18.解:〔1〕根据题意可得:n a n 2=〔2〕设⎭⎬⎫⎩⎨⎧+n a n )1(1的前n 项和为n T 由〔1〕得:)111(21)1(121)1(1+-⨯=+⨯=+n n n n a n n 那么)1(2)111(21)1113121211(21+=+-=+-+⋯+-+-=n n n n n T n 19.解:(1)解法一:∵P 是等腰直角三角形PBC 的直角顶点,且BC =2,∴∠PCB =,PC =,又∵∠ACB =,∴∠ACP =,在△PAC 中,由余弦定理得PA2=AC2+PC2-2AC·PCcos=5,∴PA =.解法二:依题意建立如图直角坐标系,那么有C(0,0),B(2,0),A(0,3),∵△PBC 是等腰直角三角形,∠ACB =,∴∠ACP =,∠PBC =,∴直线PC 的方程为y =x ,直线PB 的方程为y =-x +2,由得P(1,1),∴PA ==,(2)在△PBC 中,∠BPC =,∠PCB =θ,∴∠PBC =-θ,由正弦定理得==,∴PB =sinθ,PC =sin ,∴△PBC 的面积S(θ)=PB·PCsin=sin sinθ=2sinθcosθ-sin2θ=sin2θ+cos2θ-=sin -,θ∈,∴当θ=时,△PBC 面积的最大值为.20.解:〔〕由方程x bx ax 22=+有两个相等的实数根得=∆(b-2)2=0,那么b=2,. 由)3()1(x f x f -=-知对称轴方程为12=-=ab x , 那么.2)(,12x x x f a +-=-=故,知1411)1()(≤≤+--=n x x f 即41≤n , 而抛物线x x y 22+-=的对称轴为x=1,那么41≤n 时, )(x f 在[m,n]上为增函数.假设满足题设条件的m,n 存在, 那么,4)(4)(⎩⎨⎧==n n f m m f 即⎩⎨⎧=+-=+-,424222n n n m m m 解得⎩⎨⎧-==-==,2020n n m m 或或 又m <n,所以存在符合题意0;2=-=n m21.解:21.解析:〔1〕()gx 的定义域为(0,)+∞ ∵()ln ,gx ax x a R =+∈,()11ax g x a x x '+∴=+=, 当0a ≥时,()0g x '≥在(0,)+∞上恒成立∴g(x)的增区间()0,+∞,无减区间,当0a <时,令()0g x '≥得10x a <<-, 令()0g x '<得1xa >-, ∴()g x 的增区间10,a ⎛⎫- ⎪⎝⎭,减区间1,a ⎛⎫-+∞ ⎪⎝⎭; 〔2〕()()1f x g x ≥+,即1ln 10x e x a ax --+--≥在[)1,+∞上恒成立, 设()1ln 1x F x e x a ax -=-+--,考虑到()10F =,()11x F x e a x--'=-,在[)1,+∞上为增函数, ∵1x ≥,11e 0x x --≥, ∴当0a≤时,()0F x '≥,()F x 在[)1,+∞上为增函数,()0F x ≥恒成立 当0a >时,()10F '<,()'F x '在[)1,+∞上为增函数,()01,x ∃∈+∞,在()01,x 上,()0F x '<,()F x 递减,()0F x <,这时不合题意,综上所述,0a ≤;22.解:(1)由x =cosα+sinα得2222cos sin cos 2sin c ()os sin x αααααα=+=++,所以曲线M 可化为y =x2-1,x ∈[2,2],由ρsin=t 得ρsinθ+ρcosθ=t ,所以ρsinθ+ρcosθ=t ,所以曲线N 可化为x +y =t.(2)假设曲线M ,N 有公一共点,那么当直线N 过点)1,2(,时满足要求,此时t =12+,并且向左下方平行挪动直到相切之前总有公一共点,相切时仍然只有一个公一共点,联立,得x2+x -1-t =0,由Δ=1+4(1+t)=0,解得t =-.综上可求得t 的取值范围是-≤t≤12+.。
高三数学上学期第二次月考试题 文含解析

卜人入州八九几市潮王学校上高县第二2021届高三数学上学期第二次月考试题文〔含解析〕一.选择题〔本大题一一共12小题,每一小题5分,一共60分〕 1.集合P={|x 0x ≥},Q={x |102x x +≥-},那么P∩Q=〔〕 A.〔-∞,2〕 B.[0,+)∞ C.[)2,+∞D.〔2,+∞〕【答案】D 【解析】 【分析】求出Q 中不等式的解集确定集合Q ,找出P 与Q 的交集即可. 【详解】由Q 中的不等式变形得:()()120x x +-≥,且20x -≠,解得:1x ≤-或者2x >,即Q (,1](2,)=-∞-⋃+∞, 应选:D .【点睛】此题考察了交集及其运算,纯熟掌握交集的定义是解此题的关键.0(0,)x ∃∈+∞,00ln 1x x =-〞的否认是〔〕A.0(0,)x ∃∈+∞,00ln 1x x ≠-B.0(0,)x ∃∉+∞,00ln 1x x =-C.(0,)x ∀∈+∞,ln 1x x ≠-D.(0,)x ∀∉+∞,ln 1x x =-【答案】C 【解析】(0,)x ∀∈+∞,ln 1x x ≠-3.在锐角△ABC 中,角、、A B C 所对的边长分别为a b c 、、,那么A B >是tanA tanB >成立的()条件: A.充分不必要 B.必要不充分C.充要D.既不充分也不必要 【答案】C 【解析】 【分析】 利用正切函数tan y x =在区间()0,90︒︒上的单调性证明充分条件和必要条件即可.【详解】由于正切函数tan y x =在区间()0,90︒︒上单调递增900A B ︒>>>︒⇒tanA tanB >,所以A B >是tanA tanB >成立的充分条件 tanA tanB A B >⇒>,所以A B >是tanA tanB >成立的必要条件综上,A B >是tanA tanB >成立的充要条件应选C.【点睛】此题主要考察了充要条件的判断,属于根底题. 4.以下函数中,既是偶函数又在区间()0,∞+上单调递增的函数是〔〕A.()22x x f x -=-B.()21f x x =-C.()12log f x x =D.()sin f x x x =【答案】B 【解析】 【分析】分析各选项里面函数的奇偶性与单调性,可得出正确选项. 【详解】对于A 选项,函数()y f x =的定义域为R ,()()22x x f x f x --=-=-,该函数为奇函数,不符合题意;对于B 选项,函数()y f x =的定义域为R ,()()()2211f x x x f x -=--=-=,该函数为偶函数,且该函数在()0,∞+上单调递增,符合题意;对于C 选项,函数()y f x =的定义域为()0,∞+,该函数为非奇非偶函数,不符合题意;对于D 选项,函数()y f x =的定义域为R ,()()()sin sin f x x x x x f x -=--==,该函数为偶函数,由于()()20f f ππ==,所以,该函数在()0,∞+上不可能为增函数,不符合题意.应选:B.【点睛】此题考察函数奇偶性与单调性的判断,考察函数单调性与奇偶性定义的应用,属于中等题. 5.函数 f 〔x 〕=lnx+2x-6的零点x 0所在区间是〔〕 A.()0,1B.()1,2C.()2,3D.()3,4【答案】C 【解析】 【分析】判断函数是连续增函数,利用函数的指导品牌定理,从而得到函数f 〔x 〕=lnx+2x-6的零点所在的区间. 【详解】∵连续函数f 〔x 〕=lnx+2x-6是增函数,∴f〔2〕=ln2+4-6=ln2-2<0,f 〔3〕=ln3>0, ∴f〔2〕•f〔3〕<0,故函数f 〔x 〕=lnx+2x-6的零点所在的区间为〔2,3〕, 应选:C .【点睛】此题主要考察函数的零点的断定定理的应用,属于根底题.y x m =-+是曲线23ln y x x =-的一条切线,那么m 的值是〔〕A.0B.2C.1D.3【答案】B 【解析】 【分析】根据切线的斜率的几何意义可知0003|21x x y x x ='=-=-,求出切点,代入切线即可求出m .【详解】设切点为00(,)x y因为切线y x m =-+,所以0003|21x x y x x ='=-=-, 解得0031,2x x ==-〔舍去〕 代入曲线23ln y x x =-得01y =,所以切点为1,1()代入切线方程可得11m =-+,解得2m =. 应选B.【点睛】此题主要考察了函数导数的几何意义,函数的切线方程,属于中档题.()()212log 6f x x ax =++在[)2,-+∞上是减函数,那么a 的取值范围为A.[)4,+∞ B.[)4,5C.[)4,8D.[)8,+∞【答案】B 【解析】 【分析】 令t =26x ax ++,那么由题意可得函数t 在区间[-2,+∞〕上为增函数且t 〔-2〕>0,由此解得实数a的取值范围. 【详解】令t =26x ax ++,那么函数g 〔t 〕12log =t 在区间〔0,+∞〕上为减函数,可得函数t 在区间[2,+∞〕上为增函数且t 〔-2〕>0,故有()2224260a t a >⎧-≤⎪⎨⎪-=-+⎩, 解得﹣4≤a <5, 应选:B .【点睛】此题主要考察复合函数的单调性,要注意函数的定义域及复合函数单调性的结论:同增异减的应用,此题属于根底题.()2sin 1xf x x =+的图象大致为〔〕 A. B.C. D.【答案】A 【解析】 利用排除法: 由函数的解析式可得:()()f x f x -=-,函数为奇函数,函数图象关于坐标原点对称,选项CD 错误;当2x π=时,22sin12021142f ππππ⎛⎫==> ⎪⎝⎭⎛⎫++ ⎪⎝⎭,选项B 错误, 此题选择A 选项.点睛:函数图象的识辨可从以下方面入手:(1)从函数的定义域,判断图象的左右位置;从函数的值域,判断图象的上下位置.(2)从函数的单调性,判断图象的变化趋势.(3)从函数的奇偶性,判断图象的对称性.(4)从函数的特征点,排除不合要求的图象.利用上述方法排除、挑选选项.R 上的函数()f x 满足()()f x f x =-,且当(,0)x ∈-∞时,()()0f x xf x '+>成立,假设()()0.20.233,(ln 2)(ln 2)a f b f =⋅=⋅,3311(log )(log ),,,99c f a b c =⋅则的大小关系是〔〕A.a b c >>B.c b a >>C.c a b >>D.a c b >>【答案】A 【解析】 【分析】构造函数()()F x xf x =,利用导数及题设条件得出()F x 在(,0)-∞上的单调性,结合函数()F x 的奇偶性确定()F x 在R 上单调性,根据单调性即可比较,,a b c 的大小关系.【详解】由()()f x f x =-知函数()f x 为偶函数,设()()F x xf x =,那么()F x 为奇函数,当(,0)x ∈-∞时,()()()0F x f x xf x ''=+>,所以()F x 在(,0)-∞上为递增函数,所以()F x 在R 上是递增函数.因为0.231log 20ln 2139=-<<<<,所以()0.321log (ln 2)39F F F ⎛⎫<< ⎪⎝⎭,即c b a <<,应选A .【点睛】此题主要考察了利用函数的单调性比较大小,关键在于构造新函数()()F x xf x =,通过函数()f x 的奇偶性,判断()F x 的各种性质,可得()F x 在R 上是递增函数,因此只需比较自变量的大小关系,通过分别对各个自变量与临界值0,1作比较,判断出三者的关系,即可得到函数值的大小关系.()2222,2{log ,2x x x f x x x -+≤=>,假设0R x ∃∈,使得()2054f x m m ≤-成立,那么实数m 的取值范围为〔〕A.11,4⎡⎤-⎢⎥⎣⎦B.1,14⎡⎤⎢⎥⎣⎦C.12,4⎡⎤-⎢⎥⎣⎦D.1,13⎡⎤⎢⎥⎣⎦【答案】B 【解析】由函数的解析式可得函数的最小值为:()11f =,那么要考察的不等式转化为:2154m m ≤-,解得:114m ≤≤,即实数m 的取值范围为1,14⎡⎤⎢⎥⎣⎦. 此题选择B 选项.点睛:(1)求分段函数的函数值,要先确定要求值的自变量属于哪一段区间,然后代入该段的解析式求值,当出现f (f (a ))的形式时,应从内到外依次求值.(2)当给出函数值求自变量的值时,先假设所求的值在分段函数定义区间的各段上,然后求出相应自变量的值,切记要代入检验,看所求的自变量的值是否满足相应段自变量的取值范围.()f x ,当0x >时,满足()()()2372,0233,2log x x f x f x x ⎧--<≤⎪⎪=⎨⎪->⎪⎩,那么()()()()1232020(f f f f +++⋯+=)A.25logB.25log -C.2-D.0【答案】B 【解析】 【分析】通过计算前几项,利用归纳推理,可得3,4,...,2020n =的函数值以3为周期,利用周期计算可得其和. 【详解】定义域为R 的奇函数()f x ,可得()()f x f x -=-,当0x >时,满足()()()23log 72,0233,2x x f x f x x ⎧--<≤⎪⎪=⎨⎪->⎪⎩,可得32x >时,()()3f x f x =-, 那么()21log 5f =-,()()()2211log 5f f f =-=-=, ()()300f f ==, ()()241log 5f f ==-,()()()()25211log 5f f f f ==-=-=,()()()6300f f f ===, ()()()2741log 5f f f ===-,()()()()28211log 5f f f f ==-=-=,226730log 5log 5=⨯⨯-=-,应选B.【点睛】此题主要考察归纳推理、函数的奇偶性、周期性的应用,属于难题.〔1〕函数的单调性与奇偶性相结合,注意函数的单调性及奇偶性的定义,以及奇、偶函数图象的对称性. 〔2〕周期性与奇偶性相结合,此类问题多考察求值问题,常利用奇偶性及周期性进展交换,将所求函数值的自变量转化到解析式的函数定义域内求解;〔3〕周期性、奇偶性与单调性相结合,解决此类问题通常先利用周期性转化自变量所在的区间,然后利用奇偶性和单调性求解.()()2log 1f x x =+的图象向右平移一个单位,所得图象与函数()g x 的图象关于直线y x =对称;偶函数()hx 满足()()11h x h x -=--,当[]0,1x ∈时,()()1h x g x =-;假设函数()()y k f x h x =⋅-有五个零点,那么正数k 的取值范围是〔〕A.()3log 2,1B.[)3log 2,1C.61log 2,2⎛⎫ ⎪⎝⎭D.61log 2,2⎛⎤ ⎥⎝⎦【答案】C 【解析】分析:由题意分别确定函数f (x )的图象性质和函数h (x )图象的性质,然后数形结合得到关于k 的不等式组,求解不等式组即可求得最终结果. 详解:曲线()()2log 1f x x =+右移一个单位,得()21log y f x x =-=,所以g (x )=2x,h (x -1)=h (-x -1)=h (x +1),那么函数h (x )的周期为2.当x ∈[0,1]时,()21x hx =-,y =kf (x )-h (x )有五个零点,等价于函数y =kf (x )与函数y =h (x )的图象有五个公一共点.绘制函数图像如下列图,由图像知kf 〔3〕<1且kf 〔5〕>1,即:22log 41log 61k k <⎧⎨>⎩,求解不等式组可得:61log 22k <<. 即k 的取值范围是612,2log ⎛⎫ ⎪⎝⎭。
2021年高三上学期第二次月考数学文含答案

2021年高三上学期第二次月考数学文含答案一、选择题:本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中。
只有一项是符合题目要求的.山东省1.已知集合,那么集合等于()A、 B、 C、 D、2.求:的值是 ( )A、 B、 C、 D、3.函数且的图象一定过定点()A、B、C、D、4.曲线在点处的切线方程为()A.B.C.D.5.命题“,”的否定是()A.,B.,C.,D.,6.下列函数在定义域内为奇函数的是()A. B. C. D.7.计算()A.B.C.D.8.函数的图象如图1所示,则的图象可能是()9.在中,,.若点满足,则()A.B.C.D.10.要得到函数的图象,只需将函数的图象上所有的点A.横坐标伸长到原来的2倍(纵坐标不变),再向左平行移动个单位长度B.横坐标缩短到原来的倍(纵坐标不变),再向右平行移动个单位长度C.横坐标缩短到原来的倍(纵坐标不变),再向左平行移动个单位长度D.横坐标伸长到原来的2倍(纵坐标不变),再向右平行移动个单位长度二、填空题:本大题共5小题,每小题5分,共25分.11.函数是周期函数,它的周期是__ .12.在单位圆中,面积为1的扇形所对的圆心角的弧度数为_ .13.已知命题,命题成立,若“p∧q”为真命题,则实数m的取值范围是_ _ .14. 求值:23456cos cos cos cos cos cos777777ππππππ=_ _ .15. 已知下列给出的四个结论:①命题“若,则方程有实数根”的逆否命题为:“若方程无实数根,则≤0”;②;③在△ABC中,“”是“”的充要条件;④设则是为偶函数”的充分而不必要条件;则其中正确命题的序号为_________________(写出所有正确命题的序号).三、解答题:本大题共6个小题,共75分.解答应写文字说明、证明过程或演算步骤,把答案填写在答题纸的相应位置.16.(本小题满分12分)(1)已知中,分别是角的对边,,则等于多少?(2)在中,分别是角的对边,若,求边上的高是多少?17.(本小题满分12分)已知函数,(1)求函数的极值;(2)若对,都有≥恒成立,求出的范围;(3),有≥成立,求出的范围;18.(本小题满分12分)已知函数ππ1 ()cos()cos()sin cos334f x x x x x=+--+,(1)求函数的对称轴所在直线的方程;(2)求函数单调递增区间.19.(本小题满分12分)某工厂有一批货物由海上从甲地运往乙地,已知轮船的最大航行速度为60海里/小时,甲地至乙地之间的海上航行距离为600海里,每小时的运输成本由燃料费和其它费用组成,轮船每小时的燃料费与轮船速度的平方成正比,比例系数为0.5,其它费用为每小时1250元.(1)请把全程运输成本(元)表示为速度(海里/小时)的函数,并指明定义域;(2)为使全程运输成本最小,轮船应以多大速度行驶?20.(本小题满分13分)(1)在中,分别是角的对边,其中是边上的高,请同学们利用所学知识给出这个不等式:≥的证明.(2)在中,是边上的高,已知,并且该三角形的周长是;①求证:;②求此三角形面积的最大值.21.(本小题满分14分)已知函数.(I)判断的单调性;(Ⅱ)求函数的零点的个数;(III)令,若函数在(0,)内有极值,求实数a的取值范围.参考答案11、答案: 12、答案:2 13、答案: 14、答案: 15、答案:①②④; 16.【答案】(1)由正弦定理:,则:, 解得: … … … 3分又由于是三角形中的角,且由于,于是:或 … … 6分 (2)由余弦定理:,这样,… … 9分 由面积公式,解得: … … 12分(2),… … … 7分因此在区间的最大值是,最小值是,≥… … … 10分 (3)由(2)得:≥… … … 12分 18、【答案】(Ⅰ)ππ11()cos()cos()sin 23324f x x x x =+--+1111(cos )(cos )sin 22224x x x x x =+-+… … … 6分令,解得,… … … 8分(II)由 ,得函数的 单调递增区间为 … … … 12分19.【答案】 (1)由题意得:2600750000(12500.5)300y x x x x=+=+,即:… … … 6分(2)由(1)知,令,解得x =50,或x =-50(舍去).… … …8分当时,,当时,(均值不等式法同样给分,但要考虑定义域), … … … 10分因此,函数,在x =50处取得极小值,也是最小值.故为使全程运输成本最小,轮船应以50海里/小时的速度行驶. … … … 12分 20.【答案】要证明:≥,即证明:≥,利用余弦定理和正弦定理即证明:≥,即证明:≥222222sin C 2(1cos C)2(1cosC)(1cosC)ab ab ab c c c -+-==,因为,即证明:≥,完全平方式得证. … … … 6分 (2) ,使用正弦定理,.… … 9分(3)≥,解得:≤,于是:≤,最大值… … 13分21.【答案】设,则有两个不同的根,且一根在内,不妨设,由于,所以,…………………12分由于,则只需,即………13分解得:………………………………………………………14分40650 9ECA 黊33060 8124 脤35739 8B9B 讛25107 6213 戓24130 5E42 幂34930 8872 衲34484 86B4 蚴n32613 7F65 罥38780 977C 靼%24745 60A9 悩。
2021-2022年高三上学期第二次月考数学(文)试题含答案

2021年高三上学期第二次月考数学(文)试题含答案1、 命题“对任意,都有”的否定为( )A .对任意,使得B .不存在,使得C .存在,使得D .存在,使得2、已知集合,,则( )A .[1,2)B .C .[0,1]D .3、若sin 60333,log cos 60,log tan 60a b c ︒==︒=︒,则( )A. B. C. D.4、某三棱锥的三视图如图2所示,则该三棱锥的体积是( )A .B .C .D . 5、下面是关于公差的等差数列的四个命题:其中的真命题为 ( ) A . B . C . D . 6、设函数,将的图像向右平移个单位,使得到 的图像关于对称,则的最小值为( ) A. B. C. D.7、设是定义在上的函数,如果对于任意给定的等比数列,有 仍是等比数列,则称为“保等比数列函数”.现有定义在上的如下函数: ①; ②; ③; ④,则其中是“保等比数列函数”的的序号为( )A . ①②B . ③④C . ①③D . ②④ 8、 若、、均为单位向量,且,则的最小值为( )A .B .1C .D .9. 设实数x ,y 满足约束条件,12002y x y x ⎧≤⎪⎪≥⎨⎪≤≤⎪⎩且目标函数z=ax+by (a>0,b>0)的最大值为1,则的最小值为 ( ) A. 4 B. 8 C. 9 D. 610.如图,直角梯形ABCD 中,A =90°,B =45°,底边AB =5,高AD =3,点E 由B 沿折线BCD 向点D 移动,EMAB 于M ,ENAD 于N ,设BM =,矩形AMEN 的面积为,那么与的函数关系的图像大致是( )第Ⅱ卷 非选择题(共100分)二、填空题: 把答案填写在答题卡相应的题号后的横线上(本大题共5小题,每小题5分,共25分) 11、如果,则12、某住宅小区计划植树不少于100棵,若第一天植2棵,以后每天植树的棵树是前一天的2倍,则需要的最少天数n(n∈)等于_____________.13、点P (x ,y )在直线上,则的最小值为 .14、如果函数在上至少取得最小值1008次,则正数的最小值是______________. 15. 定义“正对数”:,现有四个命题:①若,则; ②若,则 ③若,则 ④若,则其中的真命题有____________ (写出所有真命题的序号)三、解答题:解答应写出文字说明、证明过程或演算步骤(本大题共6小题,共75分) 16、(本小题满分12分)记函数的定义域为A ,的定义域为B ,求集合A 、B 、。
高三数学上学期第二次月考试卷 理(含解析)-人教版高三全册数学试题

2015-2016学年某某省马某某市红星中学高三(上)第二次月考数学试卷(理科)一、选择题:本大题共12小题,每小题5分,在每小题给同的四个选项中,只有一项是符合题目要求的.1.设全集U是实数集R,M={x|y=ln(x2﹣2x) },N={y|y=},则图中阴影部分表示的集合是( )A.{x|﹣2≤x<2} B.{x|1<x≤2}C.{x|1≤x≤2}D.{x|x<1}2.已知函数f(x)=且f(a)=﹣3,则f(6﹣a)=( ) A.﹣B.﹣C.﹣D.﹣3.给出如下命题,正确的序号是( )A.命题:∀x∈R,x2≠x的否定是:∃x0∈R,使得x02≠xB.命题:若x≥2且y≥3,则x+y≥5的否命题为:若x<2且y<3,则x+y<5C.若ω=1是函数f(x)=cosωx在区间[0,π]上单调递减的充分不必要条件D.命题:∃x0∈R,x02+a<0为假命题,则实数a的取值X围是a>04.已知某几何体的三视图如图所示,其中,正(主)视图,侧(左)视图均是由三角形与半圆构成,俯视图由圆与内接三角形构成,根据图中的数据可得此几何体的体积为( )A.B.C.D.5.设F1、F2为椭圆+y2=1的左、右焦点,过椭圆中心任作一直线与椭圆交于P、Q两点,当四边形PF1QF2面积最大时,•的值等于( )A.0 B.2 C.4 D.﹣26.设a=log37,b=21.1,c=0.83.1,则( )A.b<a<c B.c<a<b C.c<b<a D.a<c<b7.执行如图所示的程序框图,如果输入P=153,Q=63,则输出的P的值是( )A.2 B.3 C.9 D.278.若点(16,tanθ)在函数y=log2x的图象上,则=( ) A.B.C.4 D.49.已知函数f(x)=()x﹣log3x,若实数x0是方程f(x)=0的解,且x0<x1,则f(x1)的值( )A.恒为负B.等于零C.恒为正D.不大于零10.已知数列{a n}的前n项和为S n,过点P(n,S n)和Q(n+1,S n+1)(n∈N*)的直线的斜率为3n﹣2,则a2+a4+a5+a9的值等于( )A.52 B.40 C.26 D.2011.函数y=e|lnx|﹣|x﹣1|的图象大致是( )A.B. C.D.12.已知定义在R上的奇函数f(x),其导函数为f′(x),对任意正实数x满足xf′(x)>2f(﹣x),若g(x)=x2f(x),则不等式g(x)<g(1﹣3x)的解集是( )A.(,+∞)B.(﹣∞,)C.(0,)D.(﹣∞,)∪(,+∞)二、填空题:本大题共4小题,每小题5分.13.计算:()+lg+lg70+=__________.14.设变量x,y满足约束条件,则z=x﹣3y的最小值是__________.15.已知定义在R上的奇函数f(x)满足f(x﹣4)=﹣f(x),且在区间[0,2]上是增函数.若方程f(x)=m(m>0)在区间[﹣8,8]上有四个不同的根x1,x2,x3,x4,则x1+x2+x3+x4=__________.16.关于函数f(x)=(x≠0),有下列命题:①f(x)的最小值是lg2;②其图象关于y轴对称;③当x>0时,f(x)是增函数;当x<0时,f(x)是减函数;④f(x)在区间(﹣1,0)和(1,+∞)上是增函数,其中所有正确结论的序号是__________.三、解答题:解答应写出文字说明,证明过程或演算步骤.17.已知p:|1﹣|≤2;q:x2﹣2x+1﹣m2≤0(m>0),若¬p是¬q的必要不充分条件,某某数m的取值X围.18.已知函数f(x)=﹣x2+2ex+m﹣1,g(x)=x+(x>0).(1)若y=g(x)﹣m有零点,求m的取值X围;(2)确定m的取值X围,使得g(x)﹣f(x)=0有两个相异实根.19.已知函数f(x)=log a(x+1)(a>1),若函数y=g(x)的图象上任意一点P关于原点的对称点Q的轨迹恰好是函数f(x)的图象.(1)写出函数g(x)的解析式;(2)当x∈[0,1)时,总有f(x)+g(x)≥m成立,求m的取值X围.20.某机床厂今年初用98万元购进一台数控机床,并立即投入使用,计划第一年维修、保养费用12万元,从第二年开始,每年的维修、保养修费用比上一年增加4万元,该机床使用后,每年的总收入为50万元,设使用x年后数控机床的盈利总额y元.(1)写出y与x之间的函数关系式;(2)从第几年开始,该机床开始盈利?(3)使用若干年后,对机床的处理有两种方案:①当年平均盈利额达到最大值时,以30万元价格处理该机床;②当盈利额达到最大值时,以12万元价格处理该机床.问哪种方案处理较为合理?请说明理由.21.已知函数f(x)=+xlnx,g(x)=x3﹣x2﹣3.(1)讨论函数h(x)=的单调性;(2)如果对任意的s,t∈[,2],都有f(s)≥g(t)成立,某某数a的取值X围.四、选做题:请考生在第22、23题中任选一题作答,如果多做,则按所做的第一题记分.22.已知曲线C1的参数方程是(θ为参数)以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线C2的极坐标方程是ρ=﹣4cosθ.(1)求曲线C1与C2交点的极坐标;(2)A、B两点分别在曲线C1与C2上,当|AB|最大时,求△OAB的面积(O为坐标原点).23.已知不等式|2x+2|﹣|x﹣1|>a.(1)当a=0时,求不等式的解集(2)若不等式在区间[﹣4,2]内无解.某某数a的取值X围.2015-2016学年某某省马某某市红星中学高三(上)第二次月考数学试卷(理科)一、选择题:本大题共12小题,每小题5分,在每小题给同的四个选项中,只有一项是符合题目要求的.1.设全集U是实数集R,M={x|y=ln(x2﹣2x) },N={y|y=},则图中阴影部分表示的集合是( )A.{x|﹣2≤x<2} B.{x|1<x≤2}C.{x|1≤x≤2}D.{x|x<1}【考点】Venn图表达集合的关系及运算.【专题】应用题;集合思想;定义法;集合.【分析】由图知,阴影部分表示的集合中的元素是在集合N中的元素但不在集合M中的元素组成的,即N∩C U M.【解答】解:由韦恩图知阴影部分表示的集合为N∩(C U M)M={x|y=ln(x2﹣2x) }∴x2﹣2x>0,解得x<0,或x>2,∴M={x|x<0,或x>2},∴C U M={x|0≤x≤2}=[0,2],N={y|y=}={y|y≥1}=[1,+∞),∴N∩(C U M)=[1,2],故选:C【点评】本小题主要考查Venn图表达集合的关系及运算、二次不等式的解法等基础知识,属于基础题2.已知函数f(x)=且f(a)=﹣3,则f(6﹣a)=( ) A.﹣B.﹣C.﹣D.﹣【考点】分段函数的应用;函数的零点.【专题】函数的性质及应用.【分析】由f(a)=﹣3,结合指数和对数的运算性质,求得a=7,再由分段函数求得f(6﹣a)的值.【解答】解:函数f(x)=且f(a)=﹣3,若a≤1,则2a﹣1﹣2=﹣3,即有2a﹣1=﹣1<0,方程无解;若a>1,则﹣log2(a+1)=﹣3,解得a=7,则f(6﹣a)=f(﹣1)=2﹣1﹣1﹣2=﹣.故选:A.【点评】本题考查分段函数的运用:求函数值,主要考查指数和对数的运算性质,属于中档题.3.给出如下命题,正确的序号是( )A.命题:∀x∈R,x2≠x的否定是:∃x0∈R,使得x02≠xB.命题:若x≥2且y≥3,则x+y≥5的否命题为:若x<2且y<3,则x+y<5C.若ω=1是函数f(x)=cosωx在区间[0,π]上单调递减的充分不必要条件D.命题:∃x0∈R,x02+a<0为假命题,则实数a的取值X围是a>0【考点】命题的真假判断与应用.【专题】计算题;规律型;简易逻辑.【分析】利用命题的否定判断A的正误;四种命题的逆否关系判断B的正误;充要条件判断C 的正误;命题的真假判断D的正误;【解答】解:对于A,命题:∀x∈R,x2≠x的否定是:∃x0∈R,使得x02≠x0,不满足命题的否定形式,所以不正确;对于B,命题:若x≥2且y≥3,则x+y≥5的否命题为:若x<2且y<3,则x+y<5,不满足否命题的形式,所以不正确;对于C,若ω=1是函数f(x)=cosx在区间[0,π]上单调递减的,而函数f(x)=cosωx在区间[0,π]上单调递减的,ω≤1,所以ω=1是函数f(x)=cosωx在区间[0,π]上单调递减的充分不必要条件,正确.对于D,命题:∃x0∈R,x02+a<0为假命题,则命题:a≥0,∀x∈R,x2+a≥0是真命题;所以,命题:∃x0∈R,x02+a<0为假命题,则实数a的取值X围是a>0,不正确;故选:C.【点评】本题考查命题的真假的判断与应用,基本知识的考查.4.已知某几何体的三视图如图所示,其中,正(主)视图,侧(左)视图均是由三角形与半圆构成,俯视图由圆与内接三角形构成,根据图中的数据可得此几何体的体积为( )A.B.C.D.【考点】由三视图求面积、体积.【专题】图表型.【分析】先由三视图还原成原来的几何体,再根据三视图中的长度关系,找到几何体中的长度关系,进而可以求几何体的体积.【解答】解:由三视图可得该几何体的上部分是一个三棱锥,下部分是半球,所以根据三视图中的数据可得:V=××=,故选C.【点评】本题考点是由三视图求几何体的面积、体积,考查对三视图的理解与应用,主要考查三视图与实物图之间的关系,用三视图中的数据还原出实物图的数据,再根据相关的公式求表面积与体积,本题求的是组合体的体积,一般组合体的体积要分部分来求.三视图的投影规则是:“主视、俯视长对正;主视、左视高平齐,左视、俯视宽相等”.三视图是高考的新增考点,不时出现在高考试题中,应予以重视.5.设F1、F2为椭圆+y2=1的左、右焦点,过椭圆中心任作一直线与椭圆交于P、Q两点,当四边形PF1QF2面积最大时,•的值等于( )A.0 B.2 C.4 D.﹣2【考点】椭圆的简单性质.【专题】计算题.【分析】通过题意可推断出当P、Q分别在椭圆短轴端点时,四边形PF1QF2面积最大.进而可根据椭圆的方程求得焦点的坐标和P的坐标,进而求得和,则•的值可求得.【解答】解:根据题意可知当P、Q分别在椭圆短轴端点时,四边形PF1QF2面积最大.这时,F1(﹣,0),F2(,0),P(0,1),∴=(﹣,﹣1),=(,﹣1),∴•=﹣2.故选D【点评】本题主要考查了椭圆的简单性质.考查了学生数形结合的思想和分析问题的能力.6.设a=log37,b=21.1,c=0.83.1,则( )A.b<a<c B.c<a<b C.c<b<a D.a<c<b【考点】对数值大小的比较.【专题】函数的性质及应用.【分析】分别讨论a,b,c的取值X围,即可比较大小.【解答】解:1<log37<2,b=21.1>2,c=0.83.1<1,则c<a<b,故选:B.【点评】本题主要考查函数值的大小比较,根据指数和对数的性质即可得到结论.7.执行如图所示的程序框图,如果输入P=153,Q=63,则输出的P的值是( )A.2 B.3 C.9 D.27【考点】程序框图.【专题】图表型;算法和程序框图.【分析】模拟执行程序,依次写出每次循环得到的R,P,Q的值,当Q=0时,满足条件Q=0,退出循环,输出P的值为3.【解答】解:模拟执行程序,可得P=153,Q=63不满足条件Q=0,R=27,P=63,Q=27不满足条件Q=0,R=9,P=27,Q=9不满足条件Q=0,R=0,P=9,Q=0满足条件Q=0,退出循环,输出P的值为9.故选:C.【点评】本题主要考查了程序框图和算法,依次写出每次循环得到的R,P,Q的值是解题的关键,属于基本知识的考查.8.若点(16,tanθ)在函数y=log2x的图象上,则=( ) A.B.C.4 D.4【考点】三角函数的化简求值.【专题】计算题;转化思想;转化法;三角函数的求值.【分析】先根据对数的运算性质求出tanθ,再化简代值计算即可.【解答】解:点(16,tanθ)在函数y=log2x的图象上,∴tanθ=log216=4,∴====,故选:B.【点评】本题考查了二倍角公式,函数值的求法,以及对数的运算性质,属于基础题.9.已知函数f(x)=()x﹣log3x,若实数x0是方程f(x)=0的解,且x0<x1,则f(x1)的值( )A.恒为负B.等于零C.恒为正D.不大于零【考点】函数的零点与方程根的关系.【专题】函数的性质及应用.【分析】由函数的性质可知,f(x)=()x﹣log3x在(0,+∞)上是减函数,且可得f(x0)=0,由0<x0<x1,可得f(x1)<f(x0)=0,即可判断【解答】解:∵实数x0是方程f(x)=0的解,∴f(x0)=0.∵函数y()x,y=log3x在(0,+∞)上分别具有单调递减、单调递增,∴函数f(x)在(0,+∞)上是减函数.又∵0<x0<x1,∴f(x1)<f(x0)=0.∴f(x1)的值恒为负.故选A.【点评】本题主要考查了函数的单调性的简单应用,解题的关键是准确判断函数f(x)的单调性并能灵活应用.10.已知数列{a n}的前n项和为S n,过点P(n,S n)和Q(n+1,S n+1)(n∈N*)的直线的斜率为3n﹣2,则a2+a4+a5+a9的值等于( )A.52 B.40 C.26 D.20【考点】数列的求和.【专题】等差数列与等比数列.【分析】首先根据题中的已知条件已知数列{a n}的前n项和为S n,过点P(n,S n)和Q(n+1,S n+1)(n∈N*)的直线的斜率为3n﹣2,进一步求出数列的通项公式,然后根据通项公式求出各项的值,最后确定结果.【解答】解:已知数列{a n}的前n项和为S n,过点P(n,S n)和Q(n+1,S n+1)(n∈N*)的直线的斜率为3n﹣2则:∴a n=3n﹣5a2+a4+a5+a9=40故选:B【点评】本题考查的知识点:根据点的斜率求出数列的通项公式,由通项公式求数列的项.11.函数y=e|lnx|﹣|x﹣1|的图象大致是( )A.B. C.D.【考点】对数的运算性质;函数的图象与图象变化.【分析】根据函数y=e|lnx|﹣|x﹣1|知必过点(1,1),再对函数进行求导观察其导数的符号进而知原函数的单调性,得到答案.【解答】解:由y=e|lnx|﹣|x﹣1|可知:函数过点(1,1),当0<x<1时,y=e﹣lnx﹣1+x=+x﹣1,y′=﹣+1<0.∴y=e﹣lnx﹣1+x为减函数;若当x>1时,y=e lnx﹣x+1=1,故选D.【点评】本题主要考查函数的求导与函数单调性的关系.12.已知定义在R上的奇函数f(x),其导函数为f′(x),对任意正实数x满足xf′(x)>2f(﹣x),若g(x)=x2f(x),则不等式g(x)<g(1﹣3x)的解集是( )A.(,+∞)B.(﹣∞,)C.(0,)D.(﹣∞,)∪(,+∞)【考点】函数奇偶性的性质.【专题】转化思想;数学模型法;函数的性质及应用;导数的综合应用.【分析】f(x)是定义在R上的奇函数,可得:f(﹣x)=﹣f(x).对任意正实数x满足xf′(x)>2f(﹣x),可得:xf′(x)+2f(x)>0,由g(x)=x2f(x),可得g′(x)>0.可得函数g(x)在(0,+∞)上单调递增.即可得出.【解答】解:∵f(x)是定义在R上的奇函数,∴f(﹣x)=﹣f(x).对任意正实数x满足xf′(x)>2f(﹣x),∴xf′(x)+2f(x)>0,∵g(x)=x2f(x),∴g′(x)=2xf(x)+x2f′(x)>0.∴函数g(x)在(0,+∞)上单调递增.又g(0)=0,g(﹣x)=x2f(﹣x)=﹣g(x),∴函数g(x)是R上的奇函数,∴g(x)是R上的增函数.由不等式g(x)<g(1﹣3x),∴x<1﹣3x,解得.∴不等式g(x)<g(1﹣3x)的解集为:.故选:B.【点评】本题考查了函数的奇偶性与单调性,考查了推理能力与计算能力,属于中档题.二、填空题:本大题共4小题,每小题5分.13.计算:()+lg+lg70+=.【考点】对数的运算性质;有理数指数幂的化简求值.【专题】计算题;函数思想;定义法;函数的性质及应用.【分析】根据对数和幂的运算性质计算即可.【解答】解:()+lg+lg70+=+lg()+1﹣lg3=+lg+1=+1+1=,故答案为:.【点评】本题考查了对数和幂的运算性质,关键是掌握性质,属于基础题.14.设变量x,y满足约束条件,则z=x﹣3y的最小值是﹣8.【考点】简单线性规划.【专题】不等式的解法及应用.【分析】将z=x﹣3y变形为,此式可看作是斜率为,纵截距为的一系列平行直线,当最大时,z最小.作出原不等式组表示的平面区域,让直线向此平面区域平移,可探求纵截距的最大值.【解答】解:由z=x﹣3y,得,此式可看作是斜率为,纵截距为的直线,当最大时,z最小.画出直线y=x,x+2y=2,x=﹣2,从而可标出不等式组表示的平面区域,如右图所示.由图知,当动直线经过点P时,z最小,此时由,得P(﹣2,2),从而z min=﹣2﹣3×2=﹣8,即z=x﹣3y的最小值是﹣8.故答案为:﹣8.【点评】本题考查了线性规划的应用,为高考常考的题型,求解此类问题的一般步骤是:(1)作出已知不等式组表示的平面区域;(2)运用化归思想及数形结合思想,将目标函数的最值问题转化为平面中几何量的最值问题处理.15.已知定义在R上的奇函数f(x)满足f(x﹣4)=﹣f(x),且在区间[0,2]上是增函数.若方程f(x)=m(m>0)在区间[﹣8,8]上有四个不同的根x1,x2,x3,x4,则x1+x2+x3+x4=﹣8.【考点】奇偶性与单调性的综合;函数的周期性.【专题】数形结合.【分析】由条件“f(x﹣4)=﹣f(x)”得f(x+8)=f(x),说明此函数是周期函数,又是奇函数,且在[0,2]上为增函数,由这些画出示意图,由图可解决问题.【解答】解:此函数是周期函数,又是奇函数,且在[0,2]上为增函数,综合条件得函数的示意图,由图看出,四个交点中两个交点的横坐标之和为2×(﹣6),另两个交点的横坐标之和为2×2,所以x1+x2+x3+x4=﹣8.故答案为﹣8.【点评】数形结合是数学解题中常用的思想方法,能够变抽象思维为形象思维,有助于把握数学问题的本质;另外,由于使用了数形结合的方法,很多问题便迎刃而解,且解法简捷.16.关于函数f(x)=(x≠0),有下列命题:①f(x)的最小值是lg2;②其图象关于y轴对称;③当x>0时,f(x)是增函数;当x<0时,f(x)是减函数;④f(x)在区间(﹣1,0)和(1,+∞)上是增函数,其中所有正确结论的序号是①②④.【考点】命题的真假判断与应用;奇偶性与单调性的综合.【专题】函数思想;定义法;函数的性质及应用.【分析】是结合复合函数单调性的关系进行判断.②根据基本由函数奇偶性的定义判断函数为偶函数判断;③利用对勾函数的单调性判断;④由对勾函数的最值及函数奇偶性的性质进行判断即可.【解答】解:①函数f(x)=lg,(x∈R且x≠0).∵=2,∴f(x)=lg≥2,即f(x)的最小值是lg2,故①正确,②∵f(﹣x)==f(x),∴函数f(x)为偶函数,图象关于y轴对称,故②正确;③当x>0时,t(x)=,在(0,1)上单调递减,在(1,+∞)上得到递增,∴f(x)=lg在(0,1)上单调递减,在(1,+∞)上得到递增,故③错误;④∵函数f(x)是偶函数,由③知f(x)在(0,1)上单调递减,在(1,+∞)上得到递增,∴在(﹣1,0)上单调递增,在(﹣∞,﹣1)上得到递减,故④正确,故答案为:①②④【点评】本题考查了命题的真假判断与应用,考查了函数奇偶性的性质,考查了复合函数的单调性,是中档题.三、解答题:解答应写出文字说明,证明过程或演算步骤.17.已知p:|1﹣|≤2;q:x2﹣2x+1﹣m2≤0(m>0),若¬p是¬q的必要不充分条件,某某数m的取值X围.【考点】必要条件;绝对值不等式的解法.【专题】规律型.【分析】先求出命题p,q的等价条件,利用¬p是¬q的必要不充分条件转化为q是p的必要不充分条件,建立条件关系即可求出m的取值X围.【解答】解:由||=,得|x﹣4|≤6,即﹣6≤x﹣4≤6,∴﹣2≤x≤10,即p:﹣2≤x≤10,由x2+2x+1﹣m2≤0得[x+(1﹣m)][x+(1+m)]≤0,即1﹣m≤x≤1+m,(m>0),∴q:1﹣m≤x≤1+m,(m>0),∵¬p是¬q的必要不充分条件,∴q是p的必要不充分条件.即,且等号不能同时取,∴,解得m≥9.【点评】本题主要考查充分条件和必要条件的应用,将¬p是¬q的必要不充分条件转化为q 是p的必要不充分条件是解决本题的关键.18.已知函数f(x)=﹣x2+2ex+m﹣1,g(x)=x+(x>0).(1)若y=g(x)﹣m有零点,求m的取值X围;(2)确定m的取值X围,使得g(x)﹣f(x)=0有两个相异实根.【考点】函数零点的判定定理;根的存在性及根的个数判断.【专题】计算题;函数的性质及应用;导数的综合应用;不等式的解法及应用.【分析】(1)由基本不等式可得g(x)=x+≥2=2e,从而求m的取值X围;(2)令F(x)=g(x)﹣f(x)=x++x2﹣2ex﹣m+1,求导F′(x)=1﹣+2x﹣2e=(x﹣e)(+2);从而判断函数的单调性及最值,从而确定m的取值X围.【解答】解:(1)∵g(x)=x+≥2=2e;(当且仅当x=,即x=e时,等号成立)∴若使函数y=g(x)﹣m有零点,则m≥2e;故m的取值X围为[2e,+∞);(2)令F(x)=g(x)﹣f(x)=x++x2﹣2ex﹣m+1,F′(x)=1﹣+2x﹣2e=(x﹣e)(+2);故当x∈(0,e)时,F′(x)<0,x∈(e,+∞)时,F′(x)>0;故F(x)在(0,e)上是减函数,在(e,+∞)上是增函数,故只需使F(e)<0,即e+e+e2﹣2e2﹣m+1<0;故m>2e﹣e2+1.【点评】本题考查了基本不等式的应用及导数的综合应用,同时考查了函数零点的判断与应用,属于中档题.19.已知函数f(x)=log a(x+1)(a>1),若函数y=g(x)的图象上任意一点P关于原点的对称点Q的轨迹恰好是函数f(x)的图象.(1)写出函数g(x)的解析式;(2)当x∈[0,1)时,总有f(x)+g(x)≥m成立,求m的取值X围.【考点】求对数函数解析式;函数解析式的求解及常用方法;函数最值的应用.【专题】计算题;转化思想.【分析】(1)由已知条件可知函数g(x)的图象上的任意一点P(x,y)关于原点对称的点Q (﹣x,﹣y)在函数f(x)图象上,把Q(﹣x,﹣y)代入f(x),整理可得g(x)(2)由(1)可令h(x)=f(x)+g(x),先判断函数h(x)在[0,1)的单调性,进而求得函数的最小值h(x)min,使得m≤h(x)min【解答】解:(1)设点P(x,y)是g(x)的图象上的任意一点,则Q(﹣x,﹣y)在函数f (x)的图象上,即﹣y=log a(﹣x+1),则∴(2)f(x)+g(x)≥m 即,也就是在[0,1)上恒成立.设,则由函数的单调性易知,h(x)在[0,1)上递增,若使f(x)+g(x)≥m在[0,1)上恒成立,只需h(x)min≥m在[0,1)上成立,即m≤0.m的取值X围是(﹣∞,0]【点评】本题(1)主要考查了函数的中心对称问题:若函数y=f(x)与y=g(x)关于点M (a,b)对称,则y=f(x)上的任意一点(x,y)关于M(a,b)对称的点(2a﹣x,2b﹣y)在函数y=g(x)的图象上.(2)主要考查了函数的恒成立问题,往往转化为求最值问题:m≥h(x)恒成立,则m≥h(x)m≤h(x)恒成立,max则m≤h(x)min20.某机床厂今年初用98万元购进一台数控机床,并立即投入使用,计划第一年维修、保养费用12万元,从第二年开始,每年的维修、保养修费用比上一年增加4万元,该机床使用后,每年的总收入为50万元,设使用x年后数控机床的盈利总额y元.(1)写出y与x之间的函数关系式;(2)从第几年开始,该机床开始盈利?(3)使用若干年后,对机床的处理有两种方案:①当年平均盈利额达到最大值时,以30万元价格处理该机床;②当盈利额达到最大值时,以12万元价格处理该机床.问哪种方案处理较为合理?请说明理由.【考点】基本不等式在最值问题中的应用.【专题】计算题.【分析】(1)赢利总额y元即x年中的收入50x减去购进机床的成本与这x年中维修、保养的费用,维修、保养的费用历年成等差数增长,,(2)由(1)的结论解出结果进行判断得出何年开始赢利.(3)算出每一种方案的总盈利,比较大小选择方案.【解答】解:(1)y=﹣2x2+40x﹣98,x∈N*.(2)由﹣2x2+40x﹣98>0解得,,且x∈N*,所以x=3,4,,17,故从第三年开始盈利.(3)由,当且仅当x=7时“=”号成立,所以按第一方案处理总利润为﹣2×72+40×7﹣98+30=114(万元).由y=﹣2x2+40x﹣98=﹣2(x﹣10)2+102≤102,所以按第二方案处理总利润为102+12=114(万元).∴由于第一方案使用时间短,则选第一方案较合理.【点评】考查审题及将题中关系转化为数学符号的能力,其中第二问中考查了一元二次不等式的解法,第三问中考查到了基本不等式求最值,本题是一个函数基本不等式相结合的题.属应用题中盈利最大化的问题.21.已知函数f(x)=+xlnx,g(x)=x3﹣x2﹣3.(1)讨论函数h(x)=的单调性;(2)如果对任意的s,t∈[,2],都有f(s)≥g(t)成立,某某数a的取值X围.【考点】利用导数求闭区间上函数的最值;利用导数研究函数的单调性.【专题】综合题;导数的综合应用.【分析】(1)求导数,利用导数的正负,即可讨论函数h(x)=的单调性;(2)求出g(x)max=g(2)=1,当x∈[,2]时,f(x)=+xlnx恒成立,等价于a≥x﹣x2lnx 恒成立,然后利用导数求函数u(x)=x﹣x2lnx在区间[,2]上取得最大值,则实数a的取值X围可求.【解答】解:(1)h(x)==+lnx,h′(x)=,①a≤0,h′(x)≥0,函数h(x)在(0,+∞)上单调递增②a>0时,h'(x)>0,则x∈(,+∞),函数h(x)的单调递增区间为(,+∞),h'(x)<0,则x∈(0,),函数h(x)的单调递减区间为(0,),.(2)g(x)=x3﹣x2﹣3,g′(x)=3x(x﹣),x 2g′(x)0 ﹣0 +g(x)﹣递减极小值递增 13由上表可知,g(x)在x=2处取得最大值,即g(x)max=g(2)=1所以当x∈[,2]时,f(x)=+xlnx≥1恒成立,等价于a≥x﹣x 2lnx恒成立,记u(x)=x﹣x2lnx,所以a≥u(x)max,u′(x)=1﹣x﹣2xlnx,可知u′(1)=0,当x∈(,1)时,1﹣x>0,2xlnx<0,则u′(x)>0,∴u(x)在x∈(,2)上单调递增;当x∈(1,2)时,1﹣x<0,2xlnx>0,则u′(x)<0,∴u(x)在(1,2)上单调递减;故当x=1时,函数u(x)在区间[,2],上取得最大值u(1)=1,所以a≥1,故实数a的取值X围是[1,+∞).【点评】本题考查了利用导数研究函数的单调性,考查了导数在最大值、最小值问题中的应用,考查了数学转化思想方法和函数构造法,训练了利用分离变量法求参数的取值X围,属于中档题.四、选做题:请考生在第22、23题中任选一题作答,如果多做,则按所做的第一题记分.22.已知曲线C1的参数方程是(θ为参数)以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线C2的极坐标方程是ρ=﹣4cosθ.(1)求曲线C1与C2交点的极坐标;(2)A、B两点分别在曲线C1与C2上,当|AB|最大时,求△OAB的面积(O为坐标原点).【考点】参数的意义;简单曲线的极坐标方程.【专题】选作题;转化思想;综合法;坐标系和参数方程.【分析】(1)把参数方程和极坐标方程化为直角坐标方程,联立方程组求出交点的坐标,再把交点的直角坐标化为极坐标;(2)画出图象,由平面几何知识可知,A,C1,C2,B依次排列且共线时|AB|最大.【解答】解:(1)由(θ为参数),消去参数得:x2+(y﹣2)2=4,即x2+y2﹣4y=0;由ρ=﹣4cosθ,得ρ2=﹣4ρcosθ,即x2+y2=﹣4x.两式作差得:x+y=0,代入C1得交点为(0,0),(﹣2,2).其极坐标为(0,0),(2,);(2)如图,由平面几何知识可知,A,C1,C2,B依次排列且共线时|AB|最大.此时|AB|=2+4,O到AB的距离为.∴△OAB的面积为S=×(2+4)×=2+2.【点评】本题考查了极坐标方程化为直角坐标方程、参数方程化为普通方程,考查了推理能力与计算能力,属于基础题.23.已知不等式|2x+2|﹣|x﹣1|>a.(1)当a=0时,求不等式的解集(2)若不等式在区间[﹣4,2]内无解.某某数a的取值X围.【考点】绝对值不等式的解法.【专题】不等式的解法及应用.【分析】(1)把要解的不等式等价转化为与之等价的三个不等式组,求出每个不等式组的解集,再取并集,即得所求.(2)求得f(x)=|2x+2|﹣|x﹣1|=在区间[﹣4,2]内的值域,结合|2x+2|﹣|x﹣1|>a无解,求得a的X围.【解答】解:(1)当a=0时,不等式即|2x+2|﹣|x﹣1|>0,可得①,或②,或③.解①求得 x<﹣3,解②求得﹣<x<1,解③求得x≥1.综上可得,原不等式的解集为{x|x<﹣3,或x>﹣}.(2)当x∈[﹣4,2],f(x)=|2x+2|﹣|x﹣1|=的值域为[﹣2,3],而不等式|2x+2|﹣|x﹣1|>a无解,故有a≤3.【点评】本题主要考查绝对值不等式的解法,体现了转化、分类讨论的数学思想;还考查了分段函数的应用,求函数的值域,属于中档题.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
河北定州中学届高三上学期第二次月考数学文试题一、选择题:本大题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的.1、设集合{})23lg(x y x A -==,集合{}x y y B -==1,则AB = ( )A . (]1,∞-B. )23,(-∞ C .)23,0[ D .),23(+∞ 2、sin160sin10cos 20cos10︒︒︒︒-的值是( )A .3-B .12-C .12D .33、已知a 为实数,若复数2(1)(1)z a a i =-++为纯虚数,则20151a i i++的值为( )A .1B .-1C .iD .i -4、直线:1l y kx =+与圆221x y +=相交于A ,B 两点,则“△OAB 的面积为43”是“3=k ”的( )A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件5、设y x ,满足约束条件⎪⎩⎪⎨⎧≤-≥+≤+1011y x x y x ,则目标函数2-=x y z 的取值范围为( )A .[]3,3-B .[]2,2-C .[]1,1-D .⎥⎦⎤⎢⎣⎡-32,326、定义在R 上的偶函数)(x f 满足:对任意的1212,(,0)()x x x x ∈-∞≠,都有1212()()0f x f x x x -<-.则下列结论正确的是 ( )A .)5(log )2()3.0(23.02f f f << B .)3.0()2()5(log 23.02f f f <<C .)2()3.0()5(log 3.022f f f << D .)2()5(log )3.0(3.022f f f <<7、当输入的实数[]2,30x ∈时,执行如图所示的程序框图,则输出的x 不小于103的概率是 ( )A .528B .629C .914D .1929正视图侧视图俯视图5343(10题图)8、函数()sin()(,0,0,)2f x A x x R A πωϕωϕ=+∈>><的部分图象如图所示, 如果1x 、2(,)63x ππ∈-,且12()()f x f x =,则 12()f x x +等于( )A .12B .22C .32D .19、设正项等比数列{}n a 的前n 项之积为n T ,且14128T =,则7811a a +的最小值是 ( ) A 2B 3 C .2D .2310、若某几何体的三视图(单位:cm )如右图所示,则该几何体的 体积等于( )A .310cm B .320cm C .330cm D .340cm 11、定义12nnp p p +++为n 个正数n p p p ,,,21 的“均倒数”.若已知数列{}n a 的前n 项的“均倒数”为123n +,又12n n a b +=,则1223910111+b b b b b b ++…=( ) A .17 B .1069 C .14 D .103912、已知双曲线22221(0,0)x y a b a b-=>>的左、右焦点分别为1(,0)F c -,2(,0)F c ,若双曲线上存在点P ,使1221sin sin 0c PF F a PF F ∠=∠≠,则该双曲线离心率的取值范围为( )A .(2,B .(2, C .(2+1⎤⎦, D .()2+1, 二、填空题(本大题共4小题,每小题5分,共20分.)13、设向量,a b 是两个不共线的向量,若3-a b 与λ+a b 共线,则实数λ= . 14、设函数2()ln f x a x bx =+,若函数()f x 在1x =处与直线12y =-相切,则实数a b +=15、已知ABC ∆的三个顶点在同一个球面上,6AB =,8BC =,10AC =.若球心O 到平面ABC 的距离为5,则该球的表面积为 .16、若函数对定义域的每一个值,在其定义域内都存在唯一的,使成立,则称该函数为“依赖函数”.给出以下命题:①是“依赖函数”;②是“依赖函数”;③是“依赖函数”;④是“依赖函数”;⑤,都是“依赖函数”,且定义域相同,则是“依赖函数”.其中所有真命题的序号是_____.三、解答题(本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.) 17、(本小题满分12分)已知函数)0(21cos cos sin 3)(2>+-=ωωωωx x x x f 经化简后利用x ① π32 π35 )(x f1-1(Ⅰ)请直接写出①处应填的值,并求函数()f x 在区间,23⎡⎤-⎢⎥⎣⎦上的值域; (Ⅱ)∆ABC 的内角,,A B C 所对的边分别为c b a ,,,已知()1,3f A π+=4+=b c ,7a =,求ABC ∆的面积.18、(本小题满分12分)2015年“五一节”期间,高速公路车辆较多,交警部门通过路面监控装置抽样调查某一山区路段汽车行驶速度,采用的方法是:按到达监控点先后顺序,每隔50辆抽取一辆,总共抽取120辆,分别记下其行车速度,将行车速度(km/h )分成七段[60,65),[65,70),[70,75),[75,80),[80,85),[85,90),[90,95)后得到如图所示的频率分布直方图,据图解答下列问题: (Ⅰ)求a 的值,并说明交警部门采用的是什么抽样方法? (Ⅱ)求这120辆车行驶速度的众数和中位数的估计值(精确到0.1);(Ⅲ)若该路段的车速达到或超过90km/h 即视为超速行驶,试根据样本估计该路段车辆超速行驶的概率.19、(本小题满分12分)如图,三棱柱111ABC A B C -中,侧面11BCC B 是矩形,截面1A BC 是等边三角形.(Ⅰ) 求证:AB AC =;(Ⅱ)若AB AC ⊥,三棱柱的高为1,求点1C 到截面1A BC 的距离.()y f x =1x 2x 12()()1f x f x =y x =1y x=2xy =ln y x =()y f x =()y g x =()()y f x g x =⋅20、(本小题满分12分)已知函数()()2+1ln f x a x ax =-,21()2g x x x =-. (I )若函数()f x 在定义域内为单调函数,求实数a 的取值范围; (II )证明:若17a -<<,则对于任意1212,(1,),,x x x x ∈+∞≠有1212()()1()()f x f xg x g x ->--.21、(本小题满分12分)设椭圆2222:1(0)x y C a b a b +=>>的离心率12e =,右焦点到直线1=+b y a x 的距离721=d ,O 为坐标原点. (I )求椭圆C 的方程;(II )过点O 作两条互相垂直的射线,与椭圆C 分别交于A 、B 两点,证明点O 到直线AB 的距离为定值,并求弦AB 长度的最小值.请考生在第22、23、24题中任选一题作答,如果多做,则按所做的第一题计分,作答时请写清题号.22、(本小题满分10分)如图,设AB 为⊙O 的任一条不与直线l 垂直的直径,P 是⊙O 与l 的公共点,AC⊥l ,BD⊥l ,垂足分别为C ,D ,且PC=PD . (Ⅰ)求证:l 是⊙O 的切线;(Ⅱ)若⊙O 的半径OA=5,AC=4,求CD 的长.23、(本小题满分10分)已知直线l 的参数方程是22242x t y t ⎧=⎪⎪⎨⎪=+⎪⎩(t 为参数),⊙C 的极坐标方程为22cos()4πρθ=+.(Ⅰ)求圆心C 的直角坐标;(Ⅱ)试判断直线l 与⊙C 的位置关系.24、(本小题满分10分)已知函数()2123f x x x =-++. (Ⅰ)求不等式()6f x ≤的解集;(Ⅱ)若关于x 的不等式()1f x a <-的解集非空,求实数a 的取值范围.河北定州中学2016届高三上学期第二次月考数学文试题一、选择题:(1)--(6) CADBDA (7)--(12) CCABAD 二、填空题:(13) 13-(14)12(15) 200π (16) ②③ 三、解答题:(17)(本小题满分12分) (Ⅰ)①处应填入6π.………1 分1cos 21()222x f x x ωω+=-+12cos 2sin(2)226x x x πωωω=-=-.………3分 因为T=522()233πππ-=,所以222ππω=,12ω=,即()sin()6f x x π=-.………4分因为,23x ππ⎡⎤∈-⎢⎥⎣⎦,所以2366x πππ-≤-≤,所以11sin()62x π-≤-≤,故)(x f 的值域为11,2⎡⎤-⎢⎥⎣⎦…6分(Ⅱ)()sin()136f A A ππ+=+=,又0,A π<<∴ 7666A πππ<+<,得62A ππ+=,3A π=…8分由余弦定理得2222cos a b c bc A =+-2()2cos 3b c bc bc π=+--2()3b c bc =+-,即2243bc =-,所以3bc =.………10分所以ABC ∆的面积11sin 322S bc A ==⨯=. ………12 分(18)(本小题满分12分) (I )由图知:(a +0.05+0.04+0.02+0.02+0.005+0.005)×5=1,∴a =0.06,该抽样方法是系统抽样; …4分(II )根据众数是最高矩形底边中点的横坐标,∴众数为77.5;∵前三个小矩形的面积和为0.005×5+0.020×5+0.040×5=0.325,第四个小矩形的面积为0.06×5=0.3,∴中位数在第四组,设中位数为75+x ,则0.325+0.06×x=0.5⇒x ≈2.9, ∴数据的中位数为77.9; …8分(III )样本中车速在[90,95)有0.005×5×120=3(辆),∴估计该路段车辆超速的概率P=3112040=. …12分(19)(本小题满分12分)(Ⅰ)证明:取BC 中点O ,连OA ,OA 1.因为侧面BCC 1B 1是矩形,所以BC ⊥BB 1,BC ⊥AA 1, 因为截面A 1BC 是等边三角形,所以BC ⊥OA 1,所以BC ⊥平面A 1OA ,BC ⊥OA ,因此,AB =AC . …5分(Ⅱ)设点A 到截面A 1BC 的距离为d ,由V A -A 1BC =V A 1-ABC 得S △A 1BC ×d =S △ABC ×1,得BC ×OA 1×d =BC ×OA ×1,得d =OAOA 1.由AB ⊥AC ,AB =AC 得OA = 1 2BC ,又OA 1=32BC ,故d. 因为点A 与点C 1到截面A 1BC 的距离相等,所以点C 1到截面A 1BC 的距离为33.…12分(20)(本小题满分12分)(I )解析:函数()()2+1ln f x a x ax =-的定义域为(0,)+∞()()2+12+1()a ax a f x a x x-+'=-=令()()2+1m x ax a =-+,因为函数()y f x =在定义域内为单调函数,说明()0f x '≥或()0f x '≤恒成立,……………2分即()()2+1m x ax a =-+的符号大于等于零或小于等于零恒成立,当0a =时,()20m x =>,()0f x '>,()y f x =在定义域内为单调增函数; 当0a >时,()()2+1m x ax a =-+为减函数, 只需()(0)2+10m a =≤,即1a ≤-,不符合要求; 当0a <时,()()2+1m x ax a =-+为增函数,只需()(0)2+10m a =≥即可,即1a ≥-,解得10a -≤<, 此时()y f x =在定义域内为单调增函数;……………4分 综上所述[1,0]a ∈-………………5分 (II )22111()(1)222g x x x x =-=--在区间(1,)+∞单调递增, 不妨设121x x >>,则12()()g x g x >,则1212()()1()()f x f xg x g x ->--等价于1212()()(()())f x f x g x g x ->--等价于1122()()()+()f x g x f x g x +>………………7分 设()21()()+()2+1ln (1)2n x f x g x x a x a x ==+-+,解法一:则22(1)()(1)(1)2a n x x a a x +'=+-+≥+=-,由于17a -<<,故()0n x '>,即()n x 在(1,)+∞上单调增加,……………10分 从而当211x x <<时,有1122()()()+()f x g x f x g x +>成立,命题得证!………………12分解法二:则22(1)(1)2(1)()(1)=a x a x a n x x a x x+-+++'=+-+ 令2()(1)2(1)p x x a x a =-+++22(1)8(1)67(7)(1)0a a a a a a ∆=+-+=--=-+<即2()(1)2(1)0p x x a x a =-+++>在17a -<<恒成立 说明()0n x '>,即()n x 在(1,)+∞上单调增加,………………10分从而当211x x <<时,有1122()()()+()f x g x f x g x +>成立,命题得证!………………12分(21)(本小题满分12分) (I )由题意得12c e a ==,∴2a c =,∴b ==………………….1分 由题意得椭圆的右焦点(,0)c 到直线1x ya b+=即0bx ay ab +-=的距离为77d c ====,∴1c =………….…….……...3分∴2a =,b =∴椭圆C 的方程为22143x y +=……..…….…….…….…….…….4分(II )(i)当直线AB 斜率不存在时,直线AB 方程为7212=x , 此时原点与直线AB 的距离7212=d …..……..…….…….…….…….…….…….… 5分(ii)当直线AB 斜率存在时,设直线AB 的方程为y kx m =+1122(,),(,)A x y B x y ,直线AB 的方程与椭圆C 的方程联立得22143y kx m x y =+⎧⎪⎨+=⎪⎩, 消去得222(34)84120k x kmx m +++-=,122834kmx x k ∴+=-+,212241234m x x k -=+…….6分OA OB ⊥,12120x x y y ∴+=由1212()2y y k x x m +=++,22121212()y y k x x km x x m =+++, ∴221212(1)()0k x x km x x m ++++=整理得22712(1)m k =+,∴212(1)7k m +=, 故O 到直线AB 的距离22212(1)7122217711k m d k k +====++ 综上:O 到直线AB 的距离定值2217……………………………………………………9分OA OB ⊥,2222AB OA OB OA OB ∴=+≥⋅,当且仅当OA OB =时取“=”号.∴22AB OA OB ⋅≤, 又由等面积法知d AB OA OB ⋅=⋅,∴22AB d AB ⋅≤,有42127AB d ≥=即弦AB 的长度的最小值是4217………………..12分(22)(本小题满分10分)(Ⅰ)证明:连接OP ,因为AC ⊥l ,BD ⊥l ,所以AC ∥BD . 又OA=OB ,PC=PD ,所以OP ∥BD ,从而OP ⊥l .因为P 在⊙O 上,所以l 是⊙O 的切线.…………..5分 (Ⅱ)解:由上知OP=(AC+BD ),所以BD=2OP ﹣AC=6,过点A 作AE ⊥BD ,垂足为E ,则BE=BD ﹣AC=6﹣4=2, 在Rt △ABE 中,AE==4,∴CD=4.………………………………………….10分(23)(本小题满分10分)(I )由⊙C 的极坐标方程为22cos()4πρθ=+,展开化为2cos()2(cos sin )4πρθρθθ=+=-, 即2222x y x y +=-,化为22(1)(1)2x y -++=∴圆心C (1,1)-.……………………………..5分(II )由直线l 的参数方程(t 是参数),消去参数t 可得x ﹣y-4=0,∴圆心C 到直线的距离4d ==>l 与圆相离.…………….10分(24)(本小题满分10分)(Ⅰ)由()21236f x x x =-++≤得13322x x -++≤解得12≤≤-x ∴不等式的解集为[2,1]-.………………………………….4分(Ⅱ)∵()212321(23)4f x x x x x =-++≥--+=即)(x f 的最小值等于4,….6分由题可知|a ﹣1|>4,解此不等式得a <﹣3或a >5.故实数a 的取值范围为(﹣∞,﹣3)∪(5,+∞).…………………………………10分。
