2021届吉林省长春市东北师大附中高三年级上学期第三次摸底数学(理)试题
吉林省实验中学2021届高三上学期第三次质量检测数学(理)试题 Word版含解析

吉林省试验中学2021届高三上学期第三次质量检测数学(理)试题(解析版)本试卷是高三理科试卷,以基础学问和基本技能为为主导,在留意考查运算力量和分析问题解决问题的力量,学问考查留意基础、留意常规、留意主干学问,兼顾掩盖面.试题重点考查:不等式、复数、导数、圆锥曲线、数列、函数的性质及图象、三角函数的性质、三角恒等变换与解三角形、立体几何,数列,参数方程,几何证明等;考查同学解决实际问题的综合力量,是份较好的试卷.【题文】一.选择题:本大题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合要求的。
【题文】1.已知集合U={1,2,3,4},集合A={1,2},B={2,3},则()U C A B ⋃=( ) A.{1,3,4} B{3,4} C.{3} D{4} 【学问点】集合及其运算A1【答案解析】D 由A={1,2},B={2,3}则A B ⋃={1,2,3}所以()U C A B ⋃={4}故选D 。
【思路点拨】先求出A B ⋃再求出结果。
【题文】2.已知i 是虚数单位,则31ii+=-( )A.1-2iB.2-iC.2+iD. 1+2i 【学问点】复数的基本概念与运算L4 【答案解析】D 由31i i +=-242i+=1+2i 故选D 。
【思路点拨】先化简求出结果【题文】3.若条件:12p x +>,条件:q x a >,且p q ⌝⌝是的充分不必要条件,则a 的取值范围围是 A .1a ≥ B .1a ≤ C .3a ≥- D .3a ≤-【学问点】充分条件、必要条件A2【答案解析】A ∵p :|x+1|>2,∴p={x|x >1或x <-3},若¬p 是¬q 的充分不必要条件则q 是p 的充分不必要条件,则q ⊊p ,∴a ≥1,故答案为:A .【思路点拨】先求出,p={x|x >1或x <-3},再依据¬p 是¬q 的充分不必要条件,得到q 是p 的充分不必要条件,即q ⊊p ,从而得出答案.明显面积的最大值为10故答案为:C【思路点拨】三视图复原的几何体是一个三棱锥,依据三视图的图形特征,推断三棱锥的外形,三视图的数据,求出四周体四个面的面积中,最大的值 【题文】5.若02πθ-<<,且sin 3P θ=,()3sin Q θ=,()13sin R θ=,则,,P Q R 大小关系为A. R Q P <<B. Q R P <<C. P Q R <<D. R P Q << 【学问点】指数与指数函数对数与幂函数B6 【答案解析】A 0<sin 3θ<13,由于1sin 0θ-<<,则Q>R,所以R Q P <<故选A. 【思路点拨】先依据指数函数幂函数性质确定大小【题文】6.已知函数()2sin ,(),(),()f x x g x x x m f x g x ===直线与的图象分别交,M N 两点,则MN 的最大值为A. 3B. 4C. D .2 【学问点】三角函数的图象与性质C3【思路点拨】依题意可设M (x 0,2sinx 0),N (x 0 ,0),|MN|=|2sinx 0- 0|,利用帮助角公式即可.【题文】7.设m n ,是两条不同的直线, αβ,是两个不同的平面,下列命题中正确的是 A .若αβ⊥,,m n αβ⊂⊂,则m n ⊥ B .若α∥β,,m n αβ⊂⊂,则n ∥m C .若m n ⊥,,m n αβ⊂⊂,则αβ⊥D .若m α⊥,n ∥m ,n ∥β,则αβ⊥【学问点】空间中的平行关系 空间中的垂直关系G4 G5【答案解析】D 选项A ,若α⊥β,m ⊂α,n ⊂β,则可能m ⊥n ,m ∥n ,或m ,n 异面,故A 错误;选项B ,若α∥β,m ⊂α,n ⊂β,则m ∥n ,或m ,n 异面,故B 错误;选项C ,若m ⊥n ,m ⊂α,n ⊂β,则α与β可能相交,也可能平行,故C 错误; 选项D ,若m ⊥α,m ∥n ,则n ⊥α,再由n ∥β可得α⊥β,故D 正确.故选D【思路点拨】由α⊥β,m ⊂α,n ⊂β,可推得m ⊥n ,m ∥n ,或m ,n 异面;由α∥β,m ⊂α,n ⊂β,可得m ∥n ,或m ,n 异面;由m ⊥n ,m ⊂α,n ⊂β,可得α与β可能相交或平行;由m ⊥α,m ∥n ,则n ⊥α,再由n ∥β可得α⊥β.【题文】8.已知函数()()log 1a f x x =+,1a >,对于定义域内的12,x x 有1201x x <<<,给出下列结论:①()()()21210x x f x f x --<⎡⎤⎣⎦; ②()()2112x f x x f x <;1xyO •③()()2112f x f x x x ->-;④()()121222f x f x x x f ++⎛⎫< ⎪⎝⎭.其中正确结论的序号是 A. ①② B. ①③ C. ②④ D ③④ 【学问点】对数与对数函数B7【答案解析】D 由于1a >所以为增函数①错误,()()2112x f x x f x <没有必定联系所以②错误③()()2112f x f x x x ->-;④()()121222f x f x x x f ++⎛⎫< ⎪⎝⎭正确。
吉林省长春市普通高中2021届高三数学质量监测(三模)试题(三)理.doc
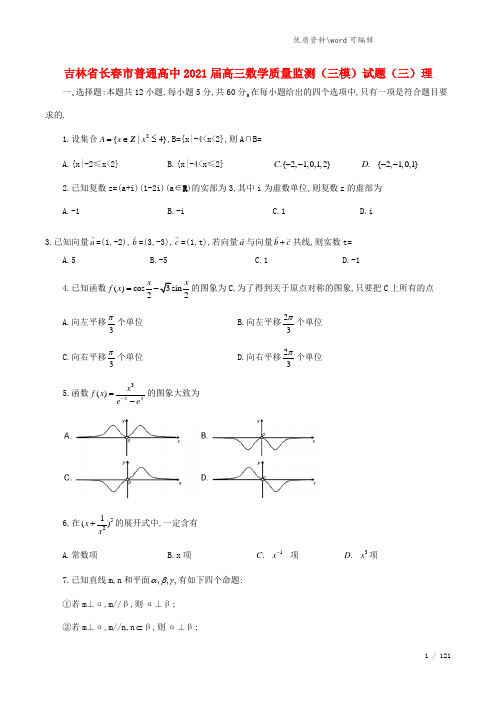
吉林省长春市普通高中2021届高三数学质量监测(三模)试题(三)理一、选择题:本题共12小题,每小题5分,共60分。在每小题给出的四个选项中,只有一项是符合题目要求的.1.设集合2{|4}A x x =∈≤Z ,B={x|-4<x<2},则A∩B= A.{x|-2≤x<2}B.{x|-4<x≤2}.{2,1,0,1,2}C --.{2,1,0,1}D --2.已知复数z=(a+i)(1-2i)(a ∈R )的实部为3,其中i 为虚数单位,则复数z 的虚部为 A.-1B.-iC.1D.i3.已知向量a =(1,-2),b =(3,-3),c =(1,t),若向量a 与向量b c +共线,则实数t=A.5B.-5C.1D.-14.已知函数()cos 3sin 22x xf x =-的图象为C,为了得到关于原点对称的图象,只要把C 上所有的点A.向左平移3π个单位 B.向左平移23π个单位 C.向右平移3π个单位 D.向右平移23π个单位 5.函数3()x xx f x e e -=-的图象大致为6.在521()x x +的展开式中,一定含有 A.常数项B.x 项1.C x - 项3.D x 项7.已知直线m,n 和平面,,,αβγ有如下四个命题: ①若m ⊥α,m//β,则α⊥β; ②若m ⊥α,m//n,n ⊂β,则α⊥β;③若n ⊥α,n⊥β,m⊥α,则m ⊥β; ④若m ⊥α,m⊥n,则n//α. 其中真命题的个数是 A.1B.2C.3D.48.风雨桥是侗族最具特色的建筑之一,风雨桥由桥、塔、亭组成,其塔俯视图通常是正方形、正六边形和正八边形.右下图是风雨桥中塔的俯视图。该塔共5层,若01122334000.5,8.B B B B B B B B m A B m =====这五层正六边形的周长总和为A.35mB.45mC.210mD.270m9.已知圆E 的圆心在y 轴上,且与圆C:2220x y x +-=的公共弦所在直线的方程为30,x y -=则圆E 的方程为22.(3)2A x y +-= 22.(3)2B x y ++= 22.(3)3C x y +-=22.(3)3D x y ++=10.某项针对我国《义务教育数学课程标准》的研究中,列出各个学段每个主题所包含的条目数(如下表),下右图是将统计表的条目数转化为百分比,按各学段绘制的等高条形图,由图表分析得出以下四个结论,其中错误的是A.除了“综合与实践”外,其它三个领域的条目数都随着学段的升高而增加,尤其“图形与几何”在第三学段增加较多,约是第二学段的3.5倍。B.所有主题中,三个学段的总和“图形与几何”条目数最多,占50%,综合与实践最少,约占4%C.第一、二学段“数与代数”条目数最多,第三学段“图形与几何”条目数最多.D.“数与代数”条目数虽然随着学段的增长而增长,而其百分比却一直在减少.“图形与几何”条目数,百分比都随学段的增长而增长.11.已知数列{}n a 的各项均为正数,其前n 项和n S 满足2*42,()n nn S a a n =+∈N ,设1(1),n n n n b a a +=-⋅T n 为数列{}n b 的前n 项和,则20T =A.110B.220C.440D.88012.设椭圆的左右焦点为12,,F F 焦距为2c,过点1F 的直线与椭圆C 交于点P,Q,若2||2,PF c =且114||||3PF QF =,则椭圆C 的离心率为 1.2A3.4B 5.7C 2.3D 二、填空题:本题共4小题,每小题5分,共20分。13.一名信息员维护甲、乙两公司的5G 网络,一天内甲公司需要维护和乙公司需要维护的概率分别为0.4和0.3,则至少有一个公司不需要维护的概率为___.14.等差数列{}n a 中,11,a =公差d ∈[1,2],且391515,a a a λ++=则实数λ的最大值为___.15.若12,x x 是函数2()74f x x x lnx =-+的两个极值点,则12x x =__;12()()f x f x +=___.(本题第一空2分,第二空3分)16.现有一批大小不同的球体原材料,某工厂要加工出一个四棱锥零件,要求零件底面ABCD 为正方形,AB=2,侧面△PAD 为等边三角形,线段BC 的中点为E,若PE=1.则所需球体原材料的最小体积为____.三、解答题:共70分,解答应写出文字说明、证明过程或演算步骤。第17~21题为必考题,每个试题考生都必须作答。第22~23题为选考题,考生根据要求作答。(一)必考题:共60分。 17.(12分)笔、墨、纸、砚是中国独有的文书工具,即“文房四宝”.笔、墨、纸、砚之名,起源于南北朝时期,其中的“纸”指的是宣纸,宣纸“始于唐代,产于泾县”,而唐代泾县隶属于宣州府管辖,故因地而得名“宣纸”,宣纸按质量等级,可分为正牌和副牌(优等品和合格品),某公司年产宣纸10000刀(每刀100张),公司按照某种质量标准值x给宣纸确定质量等级,如下表所示:x (48,52] (44,48]∪(52,56] (0,44]∪(56,100]质量等级正牌副牌废品,已知每张正牌纸的利润是10元,副牌纸的利润是5元,废品亏损10元.(1)估计该公司生产宣纸的年利润(单位:万元);(II)该公司预备购买一种售价为100万元的机器改进生产工艺,这种机器的使用寿命是一年,只能提高宣纸的质量,不影响产量,这种机器生产的宣纸的质量标准值x的频率,如下表所示:其中x为改进工艺前质量标准值x的平均值,改进工艺后,每张正牌和副牌宣纸的利润都下降2元,请判断该公司是否应该购买这种机器,并说明理由.18.(12分)在△ABC中,角A,B,C所对的边分别为a,b,c,且a=4ccosB.(1)求证:sinBcosC=3sinCcosB;(II)求B-C的最大值.19.(12分)四棱锥P-ABCD中,ABCD为直角梯形,BC//AD,AD⊥DC,BC=CD=1,AD=2,PA=PD,E为PC中点,平面PAD⊥平面ABCD,F为AD上一点,PA//平面BEF.(1)求证:平面BEF⊥平面PAD;(II)若PC与底面ABCD所成的角为60°.求二面角E-BF-A的余弦值.20.(12分)已知点A(0,1),点B在y轴负半轴上,以AB为边做菱形ABCD,且菱形ABCD对角线的交点在x轴上,设点D的轨迹为曲线E.(1)求曲线E的方程;(II)过点M(m,0),其中1<m<4,作曲线E的切线,设切点为N,求△AMN面积的取值范围.21.(12分)已知函数1()ln ,()(0)x f x m x g x x x-==>. (1)讨论函数F(x)=f(x)-g(x)在(0,+∞)上的单调性;(II)是否存在正实数m,使y=f(x)与y=g(x)的图象有唯一一条公切线,若存在,求出m 的值,若不存在,请说明理由.(二)选考题:共10分,请考生在22-23题中任选一题作答,如果多做则按所做的第一题计分. 22.[选修4-4坐标系与参数方程](10分)以直角坐标系的原点为极点,x 轴的非负半轴为极轴建立极坐标系,曲线C 的极坐标方程为2212([0,])23sin πρθθ=∈+,直线1的参数方程为23x y ⎧=-⎪⎪⎨⎪=+⎪⎩(t 为参数). (1)求曲线C 的参数方程与直线l 的普通方程;(II)设点P 为曲线C 上的动点,点M 和点N 为直线l 上的点,且满足△PMN 为等边三角形,求△PMN 边长的取值范围.23.[选修4-5不等式选讲](10分)已知函数()()2, , 3f x m x m g x x =--∈=+R .(1)当x∈R时,有f(x)≤g(x),求实数m的取值范围;(II)若不等式f(x)≥0的解集为[1,3],正数a,b满足ab-2a-b=3m-1,求a+b的最小值.。
【精准解析】吉林省长春市东北师大附中2020届高三上学期第三次摸底考试数学(理)试题

根据an 是等比数列,由 S6 2S3 2 ,即 S6 S3 S3 2 可得 S3, S6 S3, S9 S6 也是等比
数列,结合基本不等式的性质即可求出 a7 a8 a9 的最小值.
【详解】an 是等比数列, S6 2S3 2 ,即 S6 S3 S3 2 ,
-5-
S3, S6 S3, S9 S6 也是等比数列,且 S9 S6 a7 a8 a9 ,
S6 S3 2 S3 S9 S6 ,
可得: S9
S6
S3 22
S3
S32
4S3 S3
4
S3
4 S3
4
2
S3
4 S3
4
8
,当且仅当
S3
2
时取等号,
a7 a8 a9 的最小值为 8 .
故选:B
【点睛】本题考查了等比数列的前 n 项和性质以及基本不等式求和的最小值,熟记等比数列的 前 n 项和性质是关键,属于基础题.
由
y
2x
4
为增函数,则 23
2
23
20 ,所以 b
4
23
c
1 2
2 3
2
23
1,
综上可得 b c a .
故选:B
【点睛】本题考查了指数函数、对数函数的单调性比较指数式、对数式的大小,属于基础题.
x y 0
6.若
x,
y
满足
y
1
0
,则 x - y 的最大值为
y 2x 6
A. 4
B. 2
2019-2020 学年高三年级上学期第三次摸底考试理科数学
一、选择题
1
1.
2i
(
1 2i
吉林省东北师范大学附属中学2021届第一学期高三第三次摸底考数学文试题及答案

第Ⅰ卷一、选择题(本题共12小题,每小题5分, 共60分,在每小题给出的四个选项中,只有一项是符合题目要求的.) 1.已知集合{}|02A x x =≤≤,集合{}|lg 0B x x =>,则A B =A .(](),12,-∞+∞ B .()(),01,2-∞ C .[)1,2 D .(]1,22.已知复数iiz -=3,则||z = A .4 B .10 C .5 D .2 3.下列说法正确的是A .若p q ∨为真命题,则p q ∧为真命题B .命题“若cos cos x y ≠,则x y ≠”的否命题是“若cos cos x y =,则x y ≠”C .“0x <”是“20x x ->”的充要条件D .若p :x ∀∈R ,2320x x --<,则p ⌝:0x ∃∈R ,200320x x --.4.设12log 3a =,0.913b ⎛⎫= ⎪⎝⎭,182c =,则A .a b c <<B .b c a <<C .c a b <<D .b a c <<5.某四棱锥的三视图如图所示,则 此四棱锥的体积为A .2B .3C .4D .66.等差数列}{n a 前n 项和为n S ,281112a a a ++=,则13S =A.32B.42C .52D. 627.为了得到函数2sin 3y x =的图象,可以将函数sin 3cos3y x x =+的图象A .向右平移4π个单位 B .向左平移4π个单位切磋砥砺足千日 紫电龙光助鹰扬东北师大附中2021届高三年级第三次摸底考试(数学文)学科试题C .向右平移12π个单位 D .向左平移12π个单位 8.设双曲线22221x y a b-=的渐近线与抛物线21y x =+相切,则该双曲线的离心率ABC .5D .29.正四棱锥的顶点都在同一球面上,若该棱锥的高为4,底面边长为2,则该球的表面积为A .812π B .814πC .815πD .817π10.已知()f x 是R 上的偶函数,对任意∈x R , 都有(6)()(3)f x f x f +=+,且(1)2f =,则(2021)f 的值为A .0B .2-C .2D .6 11.在钝角ABC ∆中,2AB =,sin 2B =,且ABC ∆面积是2,则=AC A .B .2 CD12.已知()f x 是定义在R 上的奇函数,()f x '是函数()f x 的导函数且在[)0,+∞上()1f x '<, 若(2020)()20202f m f m m --≥-,则实数m 的取值范围为 A .[]1010,1010- B .[)1010,+∞ C .(],1010-∞-D .(][),10101010,-∞-+∞第Ⅱ卷二、填空题(本题共4小题,每小题5分, 共20分.)13. 已知向量(1,1)a =,(2,)b x =,若a b +与b a -平行,则实数x 的值为 .14. 设直线l 过点(0,),a 倾斜角为︒45,且与圆222220x y x y +---=相切,则a 的值为 .15. 若y x ,满足约束条件⎪⎩⎪⎨⎧≥-+≤--≥+-0101022y x y x y x ,则y x z -=2的取值范围为 .16. 设()f x 与()g x 是定义在同一区间[],a b 上的两个函数,若函数()()()=-h x f x g x 在[],a b 上有两个不同的零点,则称()f x 与()g x 在[],a b 上是“关联函数”.若()=f x 234-+x x 与()2=+g x x m 在[03],上是“关联函数”,则实数m 的取值范围是.三.解答题:解答应写出文字说明,证明过程或演算步骤. 17. (本小题满分12分)已知等差数列{}n a 的公差为d ,前n 项和为n S ,且4228S S =+. (1)求公差d 的值; (2)若11,n a T =是数列11n n a a +⎧⎫⎨⎬⎩⎭的前n 项和,求使不等式511nT ≥成立的n 的最小值.18. (本小题满分12分)在四棱锥P ABCD -中,PD ⊥平面ABCD ,底面四边形ABCD 是边长为1的 正方形,侧棱PA 与底面成的角是︒45,,M N 分别是,AB PC 的中点. (1)求证:MN ∥平面PAD ; (2)求三棱锥M PBC -的体积.19.(本小题满分12分)东北师大附中数学科技节知识竞赛活动圆满结束,现从参加知识竞赛活动的学生中随机抽取了100名学生,将他们的比赛成绩(满分为100分)分为6组:[40,50),[50,60),[60,70),[70,80),[80,90),[90,100],得到如图所示的频率分布直方图.(1)求a 的值并估计这100名学生的平均成绩(同一组中的数据用该组区间的中点值为代表); (2)在抽取的100名学生中,规定:比赛成绩低于50分为困难生,已知甲乙两人是困难生,为了解困难生具体情况,从选取的困难生随机抽取两人,求甲乙两人中至少有一人被抽到的概率?20(本小题满分12分) 已知函数()ln 1f x ax x =++. (1)若1a =-,求函数()f x 的最大值;(2)对任意的0x >,不等式()xf x e ≤恒成立,求实数a 的取值范围.21. (本小题满分12分)如图,已知椭圆)0(1:2222>>=+b a by a x C 上一点)2,0(A ,右焦点为)0,(c F ,直线AF交椭圆于B 点,且满足||2||FB AF =, 233||=AB . (1)求椭圆C 的方程;(2)若直线)0(>=k kx y 与椭圆相交于D C ,两点,求四边形ACBD 面积的最大值.请考生在(22)、(23)两题中任选一题作答,如果多答,则按做的第一题记分.作答时用2B 铅笔在答题卡上把所选题目对应题号右侧的方框涂黑.22.(本小题满分10分)【选修4-4:坐标系与参数方程】在直角坐标系xOy 中,以坐标原点为极点,x 轴正半轴为极轴建立极坐标系,曲线1C 的极坐标方程为01)4cos(2=+-πθρ,曲线2C 的参数方程为⎩⎨⎧==ααsin 3cos 2y x (α为参数). (1)写出曲线1C 的直角坐标方程和曲线2C 的普通方程;(2)已知点)1,0(-P ,曲线1C 与曲线2C 相交于A ,B 两点,求PA PB +.23.(本小题满分10分)【选修4-5:不等式选讲】已知函数|1||2|)(-++=x x x f (1)解不等式5)(≤x f ;(2)若关于x 的不等式2()2f x a a ≤-有解,求实数a 的取值范围.一、选择题 DBDAD CCCBC CB 二、填空题高三年级第三次摸底考试(数学文)学科试题(参考答案)13. 2 14 22± 15. ]5,1[- 16. 9,24⎛⎤-- ⎥⎝⎦三.解答题17. 解:(1)由4228S S =+,即()1146228a d a d +=++,化简得:48d =,解得2d =; (2)由11,2a d ==,得21n a n =-, 所以()()111111212122121n n a a n n n n +⎛⎫==- ⎪-+-+⎝⎭, 所以12231111111111123352121n n n T a a a a a a n n +⎛⎫=+++=-+-++- ⎪-+⎝⎭11122121nn n ⎛⎫=-= ⎪++⎝⎭,由511n T ≥解得5n ≥,所以n 的最小值为5. 18. 证明:(1)取PD 的中点Q ,连结QN 、AQ ,N 是PC 的中点QN ∴//CD ,且QN =12CD ,底面四边形ABCD 是边长是1的正方形,又M 是AB 的中点,AM ∴//CD ,且AM ∴=12CD ,QN ∴//AM ,且QN =AM ,AMNQ ∴四边形是平行四边形,//MN AQ ∴,又AQ PAD ⊂平面,MN ∴∥平面PAD .(2)PD ⊥平面ABCD ,PAD ∴∠是侧棱PA 与底面成的角,即PAD ∴∠=045,PAD ∆∴是等腰直角三角形,则1PD AD ==, 11331111113412M PBC P MBC MBC V V S PD AB BC PD--∴==⋅=⋅⋅=⨯⨯⨯⨯=19 .解:(1)由题可得()0.0050.0100.0200.0300.010101a +++++⨯= ,解得0.025a =. ,平均成绩为:450.05550.1650.2750.3850.25950.1⨯+⨯+⨯+⨯+⨯+⨯74= (2)困难生共5人,设另外三人a,b,c,甲乙为1,2,所有情况:ab,ac,a1,a2,bc,b1,b2,c1,c2,12710P =20解:(1)当1a =-时,()ln 1f x x x =-++,定义域为()0,∞+,()111xf x x x'-=-+=. 令()0f x '>,得01x <<;令()0f x '<,得1x >.因此,函数()y f x =的单调递增区间为()0,1,单调递减区间为()1,+∞; 所以()()max 10==f x f(2)不等式ln 1xax x e ++≤恒成立,等价于ln 1x e x a x--≤在()0,∞+恒成立,令()ln 1x e x g x x --=,0x >,故只需()min a g x ≤即可,()()21ln x x e x g x x'-+=, 令()()1ln xh x x e x =-+,0x >,则()10xh x xe x=+>', 所以()y h x =在()0,∞+单调递增,而()10h =,所以()0,1x ∈时,()0h x <,即()0g x '<,()y g x =在()0,1单调递减;()1,x ∈+∞时,()0h x >,即()0g x '>,()y g x =在()1,+∞单调递增,所以在1x =处()y g x =取得最小值()11g e =-, 所以1a e -≤,即实数a 的取值范围是{}1a a e ≤-.21.解:(1)由题意, ||2||FB AF =,由233||=AB 知3||=AF , 右焦点为)0,(cF ||2AF a b ∴===又.椭圆C 的标准方程是12322=+y x . (2)由(Ⅰ)知)0,1(F ,)2,0(A ,∴直线AF 的方程为022=-+y x ,联立⎪⎩⎪⎨⎧=-+=+02212322y x y x 得0)3(26422=-=-x x x x ,得23,021==x x .∴)22,23(-B 设点)2,0(A ,)22,23(-B 到直线)0(>=k kx y 的距离为1d 和2d , 1221+=k d ,122322++=k k d , 直线)0(>=k kx y 与椭圆相交于D C ,两点,∴联立⎪⎩⎪⎨⎧==+kxy y x 12322,得6)23(22=+x k ,得236,2362423+=+-=k x k x . 23162||1||22432++=-+=∴k k x x k CD .∴设四边形ACBD 面积为S ,则12)2(32316)(||2122221++⋅++=+=k k k k d d CD S )0(2322632>++⋅=k k k .设),2(2+∞∈+=k t ,则2-=t k ,)2(2)2(32632>+-⋅=∴t t t S .2218126312638263263tt t t t S ⋅+⋅-⋅=+-⋅=2343)8231(812632≤+-⋅=t 8231=t ,即2324238+===k t ,即32=k 时,四边形ACBD 面积有最大值23.(以||AB 为底边,点C 点D 到线段AB 的距离为高计算四边形ACBD 面积也可以) 22解:(1)01sin cos ,sin ,cos =++∴==θρθρθρθρy x ,1C 的普通方程为01=++y x , 2C 的普通方程为13422=+y x . (2)1C 的参数方程为⎪⎪⎩⎪⎪⎨⎧-=-=12222t y t x (t 为参数),将曲线1C 的参数方程代入2C 的普通方程, 整理得0162872=--t t ,令1PA t =,2PB t =,由韦达定理⎪⎪⎩⎪⎪⎨⎧-==+7167282121t t t t , 则有7244)(||||||||||212212121=-+=-=+=+t t t t t t t t PB PA . 23.解:(1)|1||2|)(-++=x x x f①当2-≤x 时,512)1(2)(≤--=----=x x x x f ,3-≥∴x ,,2-≤x ∴23-≤≤-x ; ②当12<<-x 时,53)1(2)(≤=--+=x x x f 恒成立, 12<<-∴x 符合题意; ③当1≥x 时,512)1(2)(≤+=-++=x x x x f ,2≤∴x ,又21,1≤≤∴≥x x ; 综上知不等式5)(≤x f 的解集为]2,3[-.(2)由(Ⅰ)知,⎪⎩⎪⎨⎧≥+<<--≤--=1,1212,32,12)(x x x x x x f ,所以3)(min =x f , 2232,2331a a a a a a ≤--≥≥≤-即,,所以或。
东北师范大学附属中学2019学年高三年级第三次摸底考试 数学理

东北师范大学附属中学2019学年高三年级第三次摸底考试数 学 试 题(理)说明:本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,总分150分;考试时间120分钟. 注意事项:1.答第Ⅰ卷前,考生务必将自己姓名、考号、考试科目用2B 铅笔涂写在答题卡上. 2.每小题选出答案后,用铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其它答案.3.将第Ⅰ卷选择题的答案涂在答题卡上,第Ⅱ卷每题的答案写在答题纸的指定位置. 4.考试结束,将答题纸和答题卡一并交回,答案写在试卷上视为无效答案.第Ⅰ卷(选择题 共60分)一、选择题(本题共有12小题,每小题5分, 共60分,在每小题给出的四个选项中,只有一项是符合题目要求的.) 1.已知集合=A }{32<≤-x x ,)}1lg({-==x y x B ,那么集合B A ⋂等于 ( ) A .{}31<<-x x B .{}31>-≤x x x 或 C .{}12-<≤-x xD .}31{<<x x2.已知命题R x p ∈∀:,210x x -+≤,则( )A .R x p ∈∃⌝:,210x x -+≥B .R x p ∈∀⌝:,210x x -+≥C .R x p ∈∃⌝:,210x x -+>D .R x p ∈∀⌝:,210x x -+> 3.已知等差数列{}n a 的前5项和525S =,且137=a ,则=2a ( )A .2B .3C .4D .54.经过点)2,1(-P 且与直线0:=+y x l 垂直的直线方程为 ( ) A .30x y -+=B .30x y --=C .10x y +-=D .30x y ++=5.已知直线m 、n 、l ,平面α、β,下列命题正确的是 ( )A .若ββ⊂⊂n m ,,α//m ,α//n ,则βα//;B .若ββ⊂⊂n m ,,n l m l ⊥⊥,,则β⊥l ;C .若n m m //,α⊥,则α⊥n ;D .若βαβα⊂⊂⊥n m ,,,则n m ⊥. 6.已知))4sin(),4(cos(ππ--=x x a ))4sin(),4(cos(ππ---=x x b ,则函数b a x f ⋅=)(是( )A .最小正周期为π的偶函数B .最小正周期为π的奇函数C .最小正周期为2π的偶函数D .最小正周期为2π的奇函数7.已知函数()[0,3]f x x =∈,则函数()f x 的最小值为 ( )A .4B .3-C .0D .4- 8.在底面为正方形的四棱锥V ABCD -中,侧棱VA 垂直于底面,且VA AB =.点M 为VA 的中点,则直线VC 与平面MBC 所成角的正弦值是 ( )A.6B.5C .23D.159)1<x的图象的大致形状是( )A .B .C .D .10.已知圆C 与直线340x y ++=及360x y +-=都相切,且圆心在直线290x y --=上,则圆C 的方程为( )A .225(4)(1)2x y -++=B .225(4)(1)2x y ++-=C .10)4()1(22=++-y x D .10)4()1(22=-++y x 11.一个几何体的三视图如图,其中正视图是腰长为2的等腰三角形,俯视图是半径为1的半圆,则该几何体的体积是 ( ) A.3 B .12π C.3 D.6 12.已知函数()y f x =的定义域为R ,当0<x 时,()1f x >,且对任意的,x y ∈R ,等式()()()f x f y f x y =+成立.若数列{}n a 满足1(0)a f =,且11()(2)n n f a f a +=--)(*∈N n ,则2009a 的值为( )A .4016B .4017C .4018D .4019第Ⅱ卷(非选择题 共90分)二、填空题(本题共4小题, 每小题5分, 共20分)13.定义在R 上的函数()f x 满足()(2)0f x f x +-=,当1x >,2()log (1)f x x =+,则(1)f -= .14.若实数x 、y 满足约束条件10310110x y x y x y -+≤⎧⎪--≥⎨⎪+-≤⎩,则22(1)(1)z x y =-++的最小值为 .15.已知方程()()22220x mx x nx -+-+=的四个根组成一个首项为12的等比数列,则||m n -= .16.如图,正方体1AC 的棱长为1,过点A 作平面1A BD 的垂线,垂足为点H .有下列四个命题,① 点H 是1A BD △的垂心; ② AH 垂直平面11CB D ;③ 二面角111C B D C --④ 点H 到平面1111A B C D 的距离为34.其中真命题的代号是 .(写出所有真命题的代号) 三、解答题(本题共6小题, 共70分, 解答应写出文字说明、证明过程或演算步骤)111B17.(本题满分10分)AB 是底部B 不能到达的烟囱,A 是烟囱的最高点,选择一条水平基线HG ,使得H 、G 、B 三点在同一条直线上,在相距为d 的G 、H 两点用测角仪测得A 的仰角分别为α、β,已知测角仪器高m h 5.1=,试完成如下《实验报告》(要求:1.计算两次测量值的平均值,填入表格;2.利用α、β、d 的平均值,求AB 的值,写出详细计算过程;3.把计算结果填入表格) 相关数据:.7.13,4.12≈≈18.(本题满分12分)直三棱柱111ABC A B C -中,E 是C A 1的中点,ED A C ⊥1且交AC 于D ,A A AB BC 122==. (Ⅰ)证明:B C 11//平面A BC 1; (Ⅱ)证明:A C 1⊥平面EDB .DEA 1CBAC 1B 119.(本题满分12分)已知圆C :222610x y x y ++-+=内一定点(1,2)A , P 、Q 为圆上的动点.(Ⅰ)若P 、Q 两点关于过定点A 的直线l 对称,求直线l 的方程; (Ⅱ)若0AP AQ ⋅=,求线段PQ 中点M 的轨迹方程.20.(本题满分12分)如图,四棱锥P ABCD -中,PA ⊥底面ABCD ,底面ABCD 为梯形,//AB DC ,︒=∠=∠90CAD ABC ,且PA AB BC ==,点E 是棱PB 上的动点. (Ⅰ)当PD ∥平面EAC 时,确定点E 在棱PB 上的位置; (Ⅱ)在(Ⅰ)的条件下,求二面角A CE P --余弦值.21.(本题满分12分)已知函数)1(222)(),0(1)(x b x g x x b ax x f +=≥++=,且2)0(=g ,32)3(-=f .(Ⅰ)求)(x g 的值域;(Ⅱ)指出函数)(x f 的单调性(不需证明),并求解关于实数m 的不等式)43()(2-<-m f m m f ;(Ⅲ)定义在R 上的函数)(x h 满足)()(),()2(x h x h x h x h -=--=+,且当10≤≤x 时)],([log 21)()(2x f x h x g -=求方程21)(-=x h 在区间]2009,0[上的解的个数.22.(本题满分12分)已知),1(10)(,1)(2+=-=x x g x x f 各项均为正数的数列}{n a 满足21=a ,0)()()(1=+⋅-+n n n n a f a g a a , )1)(2(109-+=n n a n b . (Ⅰ)求证:数列}1{-n a 是等比数列;(Ⅱ)当n 取何值时,n b 取最大值,并求出最大值;(Ⅲ)若11++<m m m m b t b t 对任意*N m ∈恒成立,求实数t 的取值范围.参考答案一、选择题(本题共有12小题,每小题5分, 共60分)1. D 2.C 3.B 4. A 5.C 6. B 7. B 8. D 9.D 10. A 11. D 12.B 二、填空题(本题共4小题, 每小题5分, 共20分) 13. 2- 14.9 15.2316.①②③ 三、解答题(本题共6小题, 共70分, 解答应写出文字说明、证明过程或演算步骤) 17mAB m AE 425.15.40.5.40)31(15,462)4530sin(75sin ≈+=∴≈+=∴+=+=︒︒︒而18.证明:(Ⅰ)证: 三棱柱ABC A B C -111中B C BC 11//,又BC ⊂平面A BC 1,且B C 11⊂/平面A BC 1,∴B C 11//平面A BC 1 (Ⅱ)证: 三棱柱ABC A B C -111中A A AB 1⊥,∴Rt A AB ∆1中,AB A B =221,∴=∴BC A B A BC 11,∆是等腰三角形. E 是等腰∆A BC 1底边A C 1的中点,BEC A ⊥∴1 ①又依条件知 EDC A ⊥1 ②且EBE ED = ③由①,②,③得A C 1⊥平面EDB .19.解:(Ⅰ)圆C 方程可化为22(1)(3)9x y ++-=,∴圆心C (-1,3),半径为3R =.∵点P 、Q 在圆上且关于直线l 对称, ∴圆心C (-1,3)在直线l 上. 又直线l 过点(1,2)A ,由两点式得2132(1)1y x --=--- 即直线l 的方程为250x y +-=18题图DEA 1C BAC 1B 1(Ⅱ)设PQ 的中点为(,)M x y ,∵0AP AQ ⋅=,∴AP AQ ⊥∴在Rt PAQ ∆中,||||PM AM =, 连结CM ,则CM PQ ⊥, 所以222222||||||||||CM PM CM AM CP R +=+==, 所以2222(1)(3)(1)(2)9x y x y ++-+-+-= 故线段PQ 中点M 的轨迹方程为22530x y y +-+=.20.解:(Ⅰ)在梯形ABCD 中,由A B B C ⊥,AB BC =,得4BAC π∠=,∴4DCA BACπ∠=∠=.又ACAD ⊥,故DAC ∆为等腰直角三角形.∴)2DC AB ===.连接BD ,交AC 于点M ,则2.DM DCMB AB== PD ∥平面EAC ,又平面 EACPDB =平面∴//PD EM 在BPD ∆中,2PE DM EB MB==,即2PE EB =时,PD ∥平面EAC(Ⅱ)方法一:在等腰直角PAB ∆中,取PB 中点N ,连结AN ,则AN PB ⊥.∵平面PAB ⊥平面PCB ,且平面PAB 平面PCB =PB , ∴AN ⊥平面PBC .在平面PBC 内,过N 作NH ⊥直线CE 于H ,连结AH ,由AN CE ⊥、NH CE ⊥,得CE ⊥平面ANH ,故AH CE ⊥.∴AHN ∠就是二面角A CE P --的平面角.在Rt PBC ∆中,设CB a =,则PB ==,13BE PB ==,16NE PB ==,CE==,由NH CE⊥,EB CB⊥可知:NEH∆∽CEB∆,∴NH CBNE CE=,代入解得:NH=.在Rt AHN∆中,AN=,∴tanANAHNNH∠==,cos6AHN∠==.∴二面角A CE P--的余弦值为6.方法二:以A为原点,,AB AP所在直线分别为y轴、z轴,如图建立空间直角坐标系.设PA AB BC a===,则()0,0,0A,()0,,0B a,(),,0C a a,()0,0,P a,20,,33a aE⎛⎫⎪⎝⎭.设)1,,(1yxn=,为平面EAC的一个法向量,则⊥1n AC,⊥1n AE,∴0,20.33ax ayay a+=⎧⎪⎨+=⎪⎩,解得11,22x y==-,∴)1,21,21(1-=n.设)1,,(''2yxn=为平面PBC的一个法向量,则⊥2n BC,⊥2n BP,又(),0,0BC a=,(0,,)BP a a=-,∴''0,0,axay a=⎧⎨-+=⎩,解得'0,'1x y==,∴)1,1,0(2=n..63||||,cos212121=⋅>=<∴nnnn∴二面角A CE P --21.解:(Ⅰ)由2)0(,32)3(=-=g f 得22,3223=-=+b b a , 解得,1,1=-=b a .x x x f -+=∴21)(,212)(x x g +=22,11,112122≥∴≥+∴≥++x x x)(x g ∴的值域为),2[+∞; (Ⅱ)函数)(x f 在[)0,+∞是减函数,所以,0432≥->-m m m , 解得,2,34≠≥m m , 所以,不等式的解集为),2()2,34[+∞⋃;(Ⅲ)当10≤≤x 时,x x h 21)(=,∴当01≤≤-x 时, x x h x h 21)()(=--=, 11,21)(≤≤-=∴x x x h 当31<<x 时,121<-<-x ,)2(21)2()(--=--=∴x x h x h 故⎪⎪⎩⎪⎪⎨⎧<<--≤≤-=.31),2(21,11,21)(x x x x x h 由,21)(-=x h 得1-=x∵),()2(x h x h -=+)()]([)2()4(x h x h x h x h =--=+-=+∴,∴)(x h 是以4为周期的周期函数,故21)(-=x h 的所有解是41()x n n Z =-∈, 令0412009n ≤-≤,则1100542n ≤≤ 而,n Z ∈∴1502()n n Z ≤≤∈,∴21)(-=x h 在[]0,2009上共有502个解.22.解:(I )∵1()()()0n n n n a a g a f a +-+=,2()1n n f a a =-,()10(1)n n g a a =+,∴21()10(1)(1)0n n n n a a a a +-++-=. 即1(1)(1091)0n n n a a a ++--=.又*,01N n a n ∈>+,所以1911010n n a a +=+. ∵19111910101110n n n n a a a a ++--==--, ∴{1}n a -是以111a -=为首项,公比为109的等比数列. (II )由(I )可知191()10n n a --= (*N n ∈). ∴n n n 99(2)(1)(2)()1010b n a n =+-=+. n 1n 1n n 9(3)()9110(1)9102(2)()10n b b n n +++==+++. 当n =7时,871b b =,87b b =; 当n <7时,n 1n1b b +>,n 1n b b +>; 当n >7时,n 1n 1b b +<,n 1n b b +<. ∴ >>>=<<<1098721b b b b b b∴当n =7或n =8时,n b 取最大值,最大值为8787910b b ==. (III )由m m 1m m 1t t b b ++<,得m 110[]029(3)t t m m -<++ (*) 依题意(*)式对任意*N m ∈恒成立,当t =0时,(*)式显然不成立,因此t =0不合题意.②当t <0时,由110029(3)t m m ->++,可知m 0t <(*N m ∈). 而当m 是偶数时m 0t >,因此t <0不合题意.③当t >0时,由m 0t >(*N m ∈), ∴110<029(3)t m m -++ ∴9(3)10(2)m t m +>+. (*N m ∈) 设9(3)()10(2)m h m m +=+ (*N m ∈) ∵9(4)9(3)(1)()10(3)10(2)m m h m h m m m +++-=-++ =91010(2)(3)m m -⋅<++, ∴(1)(2)(1)()h h h m h m >>>->>.∴()h m 的最大值为6(1)5h =. 所以实数t 的取值范围是65t >.。
东北三省三校(哈师大附中)2021届高三第三次模拟考试 (三模)数学(理) 含答案

哈师大附中三模(理科)数学答案一、选择题:DDDBD DAABA AC二、填空题:13.-3;14.216;15.20;16.(-∞,-2),(-2,+∞),[-1,2]17.选择条件是:;△ABC(1分)解:由已知:2sinA+π()6=2 ∴sinA+π()6=1(4分)∵A+π6∈π6,7π()6 ∴A+π6=π2 ∴A=π3(7分)选①:由S△ABC=12bcsinA=槡34bc槡=3 ∴bc=4(8分)由余弦定理:4=b2+c2-bc(10分)解得:b=2,c=2(12分)选②:由已知:b+c槡=23由余弦定理得:4=b2+c2-bc(10分)解得:a=槡433,b=槡233或a=槡233,b=槡433(12分)选③:由→ AB·→ AC=3得:bc=6(8分)由余弦定理:4=b2+c2-bc≥2bc-bc ∴bc≤4矛盾∴△ABC不存在(12分)18.解:(1)由已知得:小明中奖概率为23,小红中奖的概率为25.且两人中奖与否互不影响.(1分)设“这两人的累计得分X≤3”为事件A,则A的对立事件为“X=5”∵P(X=5)=23×25=415(4分)∴P(A)=1-P(X=5)=1115(6分)(2)设小明、小红都选择方案甲,抽奖中奖次数为X1,都选择乙方案抽奖,中奖次数为X2,则这两人选择甲方案抽奖,累计得分的期望为E(2X1),选择乙方案抽奖累计得分期望为E(3X2)(8分)由已知:X1~B2,()23;X2~B2,()25(10分)∴E(X1)=2×23=43,E(X2)=2×25=45∴E(2X1)=2E(X1)=83,E(3X2)=3×45=125∵E(2X1)>E(3X2)∴他们选择甲方案抽奖时,累计得分的期望较大(12分)—1—∴PD⊥AD,PD⊥CD 在矩形ABCD中,AD⊥CD∴DA、DC、DP三条线两两垂直(1分)如图,分别以DA、DC、DP所在直线为x轴、y轴、z轴建立空间直角坐标系则:A(2,0,0),B(2,4,0),C(0,4,0),P(0,0,4)(2分)∵→ PE=3→ EC ∴E(0,3,1);∵→ PF=2→ FB ∴→ PF=23→ PB=43,83,()83∴→ AF=→ AP+→ PF=(-2,0,4)+43,83,-()83=-23,83,()43设→ n=(x,y,z)为平面BDE的一个法向量由→ n·→ DE=0→ n·→ DB{=0 得:2x+4y=03y+z{=0 取→ n=(-2,1,-3)(4分)∵→ AF·→ n=43+83-4=0∴→ AF⊥→ n又∵AF 平面BDE ∴AF∥平面BDE(7分)(2)假设存在M满足→ AM=λ→ AP(0≤λ≤1),使CM⊥平面BDE→ CM=→ CA+→ AM=(2,-4,0)+λ(-2,0,4)=(2-2λ,-4,4λ)(8分)若CM⊥平面BDE,则→ CM∥→ n∴2-2λ-2=-41=4λ-3(10分)即:2-2λ=812=4{λ ∴λ∈故不存在满足条件的点M(12分)20.解:(1)由已知:C2(4,0);C1的准线为:x=-14.(2分)∴圆心C2到C1准线距离为4--()14=174(3分)(2)设P(y20,y0),A(y21,y1)·B(y22,y2)切线PA:x-y20=m1(y-y0)由x=m1y+y20-m1y0y2={x 得:y2-m1y-y20+m1y0=0由y0+y1=m1 得:y1=m1-y0切线PB:x-y20=m2(y-y0)同理可得:y2=m2-y0依题意:C2(4,0)到PA:x-m1y-y20+m1y0=0距离 |4-y20+m1y0|m21槡+1=1—2—同理: (y20-1)m22+(8y0-2y30)m2+y40-8y20+15=0∴ m1+m2=2y30-8y0y20-1 (y20≠1)(9分)∵ k1=y0y20-4,k2=y1-y2y21-y22=1y1+y2=1m1+m2-2y0=y20-1-6y0∴ k1k2=y0y20-4·y20-1-6y0=-524.解得:y=±4故所求P点坐标为(16,4)或(16,-4)(12分)21.解:(1)由已知:f′(x)=a+1+lnx(1分)依题意:f(e)=3e-3e=0=ae+elnx+bf′(e)=a+1+lne=a{+2=3解得:a=1,b=-2e(4分)(2)由(1)知:f(x)=x+xlnx-2ef(x)+2ex-1>n 即:x+xlnxx-1>n设:g(x)=x+xlnxx-1,(x>1) 原问题转化为g(x)min>n(5分)g′(x)=(1+1+lnx)(x-1)-(x+xlnx)(x-1)2=x-lnx-2(x-1)2令h(x)=x-lnx-2,(x>1)∵h′(x)=1-1x=x-1x>0∴h(x)在(1,+∞)上递增.又∵h(3)=1ln3<0 h(4)=2-2ln2>0∴h(x)存在唯一零点,设为x0,x0∈(3,4) h(x)>0 x>x0, h(x)<0 |<x<x0∴g′(x)>0 x>x0, g′(x)<0 |<x<x0∴g(x)在(1,x0)递减,(x0,+∞)上递增∴g(x)min=g(x0)=x0+x0lnx0x0-1(9分)∵g′(x0)=0 ∴x0-lnx0-2=0 ∴lnx0=x0-2∴g(x)min=x0+x0(x0-2)x0-1=x0∈(3,4) ∴x0>n(11分)∴n的最大值为3(12分)—3—22.解:(1)消参得l的普通方程为:y=1-x(2分)∵ρ2=123cos2θ+4sin2θ ∴3ρ2cos2θ+4ρ2sin2θ=12∵ρcosθ=xρsinθ={y ∴3x2+4y2=12 ∴x24+y23=1∴C的直角坐标方程为:x24+y23=1.(5分)(2)设A、B对应参数为t1,t2,则M对应参数为t1+t22由t的几何意义知:|PM|=|t1+t2|2将x=-槡22ty=1+槡22 t 代入3x2+4y2-12=0 得:3x12t2+4t22槡+2t()+1-12=0 ∴7t2槡+82t-16=0 Δ>0∴t1+t2=-槡827 ∴|PM|=|t1+t2|2=槡427(10分)23.(1)解:当x<-1时,f(x)=1-2x-2x-2=-4x-1≥4 ∴x≤-54 ∴x≤-54当-1≤x≤12时,f(x)=1-2x+2x+2=3≥4 ∴x∈当x>12时,f(x)=2x-1+2x+2=4x+1≥4 ∴x≥34 ∴x≥34∴不等式解集为:-∞,-(]54∪34,+[)∞(5分)(2)f(x)=|2x-1|+|2x+2|=|1-2x|+|2x+2|≥|(1-2x)+(2x+2)|=3当且仅当(1-2x)(2x+2)≥0,即:-1≤x≤12时,f(x)min=3 ∴m=3(7分)∴a+2b+3c=3由柯西不等式可得:(a2+b2+c2)(12+22+32)≥(a+2b+3c)2∴a2+b2+c2≥3212+22+32=914当且仅当a1=b2=c3即:a=314,b=614,c=914时:a2+b2+c2最小值为914(10分)—4—。
吉林省东北师大附中2021届上学期高三年级第三次摸底考试物理试卷
吉林省东北师大附中2021届上学期高三年级第三次摸底考试物理试卷本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,满分100分,时间100分钟。
第Ⅰ卷(选择题,共52分)一、选择题(本大题共13小题,每小题4分,共计52分。
其中1-8小题为单选题,9-13小题为多选题。
全部选对得4分,选对但不全的得2分,有错的得0分。
9小题为选修3-3、3-4,选其中任一个小题作答。
)1.物理教材中有很多经典的插图能够形象的表现出物理实验、物理现象及物理规律,下列四幅图涉及到不同的物理知识,其中说法正确的是A.甲图中,卢瑟福通过分析粒子散射实验结果,发现了质子和中子B.乙图中,在光的颜色保持不变的情况下,入射光越强,饱和光电流越大C.丙图中,射线甲由电子组成,射线乙为电磁波,射线丙由粒子组成D.丁图中,链式反应属于轻核聚变方式2.“竹蜻蜓”是民间的儿童玩具,如图所示,双手用力搓柄可使“竹蜻蜓”上升。
在某次实验中,“竹蜻蜓”离开手后沿直线上升到最高点。
在上升过程中,下列说法正确的是A.“竹蜻蜓”叶片上A、B两点的速度大小相等B.“竹蜻蜓”的重力势能一直增加C.“竹蜻蜓”的动能先增加后减小D.“竹蜻蜓”的机械能先减小后增大3.2020年11月17~20日长春遭遇了一轮冻雨暴雪天气,致使多条供电线路停运,电力部门持续进行抢修除冰作业。
针对高压输电线融冰有一种电流发热融冰法,就是增大高压电线内通入的电流使电线发热,利用电线自身的发热量使其外部冰层由内向外融化,达到融冰除冰的目的。
为了监测高压线路融冰进展情况,技术人员通过如图所示的装置检测融冰线路。
图中T1、T2是监测交流高压输电参数的互感器(均视为理想变压器),T1的原、副线圈匝数比为1:1000,a、b是交流电压表或交流电流表,其中交流电压表两端的电压为10V,高压线路输送的电功率是2200W、电压是22V,则A.a是交流电压表B.T2的原、副线圈匝数比为1000:1C.通过交流电流表的电流为D.绕制T1副线圈的导线应比原线圈的粗4.2020年11月24日4时30分,我国在文昌航天发射场,用长征五号遥五运载火箭成功发射探月工程“嫦娥五号”探测器。
吉林省东北师大附中2021届高三第三次摸底考试 地理答案
高三年级第三次摸底考试(地理)学科参考答案(1)整体海拔较高;地势南北高、中部低,起伏较小;北部是东西走向的阴山山脉,中部是河套平原,南部是鄂尔多斯高原。
(4分)(2)有利:库布齐沙漠降水少,晴天多,日照时间长,太阳辐射强;海拔较高,大气透明度高,太阳能资源丰富;地广人稀,土地资源丰富,地价低廉。
(4分)不利:与消费市场距离远;风沙大,遮蔽太阳能电池板,降低发电效率;基础设施不完善,建设成本高。
(4分)(3)植被覆盖率增加;气温日较差减小,空气湿度增大,沙尘天气减少;土壤含水量增大,土壤肥力提高;河流含沙量减少;生物多样性增多。
(气候、土壤、河流、生物等自然因素,任答三个角度,得6分)32.(16分)(1)特征:降水总量稀少,冬季稍多;成因:该地大多数时间受副热带高压控制;且该地受加那利寒流影响,降温减湿;冬季受西风带影响,有少量降水。
(6分)(2)纬度低,热量充足;降水量较少,光照充足;晴天多,昼夜温差大,有利于糖分积累;土壤(火山土)中有丰富的矿物质。
(6分)(3)石墙开口朝向上坡向,有利于收集坡面径流(或深坑利于收集雨水);石墙散热快,夜晚利于形成和收集冷凝水(露水);石墙起到削减风速、减少蒸发和避免植株倒伏的作用。
(答出两点得4分)33.(16分)(1)河流水位季节变化大;汛期流域内径流流速快,侵蚀和搬运能力强,携带大量泥沙汇入;河谷平坦开阔,流速慢,泥沙在河床中大量沉积,形成水下堆积体;枯水期,水位下降,沙洲裸露;河道多分叉,形成辫状水系。
(8分)(2)冬季河流封冻,河面光滑,摩擦力小,加上谷地的狭管效应,风力增大;冬春季河流水位低,沙洲裸露,易受风力侵蚀、搬运。
(4分)(3)4—10月份沱沱河地区气候温暖湿润;浅滩沙洲广布,水源和食物丰富;浅滩水系阻挡了大量的天敌。
(答出两点得4分)1。
吉林省长春市东北师范大学附属中学2021-2022学年高三上学期第三次摸底考试数学(理)试题
东北师大附中 2019 级高三年级 (6)已知角α 的终边与单位圆交于点P⎛ 6 , - 3 ⎫ ,则sin⎛ π -α ⎫ + cos (π - 2α ) = 3 3 ⎪ 2 ⎪ 第三次摸底考试(数学)科(理)试卷注意:本试卷满分 150 分,考试时间 120 分钟。
A . - 33⎝ ⎭B .6+1 3⎝ ⎭C.3 3D .6 -1 3一、选择题(本大题共 12 小题,每小题 5 分,在每小题给出的四个选项中,只有一项是符合题目要求的)(1)已知集合 A = {x x 2 ≥ 1},集合 B = {x 1 < x < 2} ,则 A (7)在直三棱柱 ABC - A 1B 1C 1 中,点M 是侧棱CC 1 中点,BC ⊥ BA ,BC = BA = AA 1 = 2 ,则异面直线 BM 与 A 1C 所成角的余弦值为A. {x x < 2}B. {x 1 < x < 2}C. {x 1 ≤ x < 2}D. {x x ≥ 1或x ≤ -1}A. -(2)命题“ ∀x ∈(0, +∞) , x ≥ 1 ”的否定是x(8)关于圆周率π ,数学发展史上出现过许多很有创意的求法,如著名的蒲丰实验和查理斯 A .∀x ∈(0, +∞) , x ≤ 1xC . ∃x ∈(0, +∞) ,x < 1xB .∃x ∈(0, +∞) , x ≥ 1xD .∃x ∈(-∞, 0], x < 1x 实验.受其启发,我们也可以通过设计下面的实验来估计π 的值:先请 200 名同学,每人随机写下一个都小于 1 的正实数对( x ,y ) ,再统计 x 、y 两数能与 1 构成钝角三角形时的数对( x ,y ) 的个数m ,最后再根据m 来估计π 的值.假如统计结果是m = 60 ,那么π ≈(3)若 a = 2 , b = 4 , (a +b )⊥ a ,则a 与b 的夹角为A. πB. πC. 2πD. 4πA. 16B. 6C. 78D. 1425 5 25 456 3 3 3(9)函数 f ( x )( x ∈ R )满足 f ( x + 6) + f ( x ) = 2 f (3) ,函数 y = f ( x -1) 的图象关于点(4)已知函数 f (x ) = lg (a x -b x )( a , b 为常数,a > 1 > b > 0),当 x ∈[2,+∞ ) 时, f ( x ) > 0 恒成立,则(1, 0) 对称,则 f (2022) =A . a 2 - b 2 > 1B . a 2 - b 2 ≥ 1C . a 2 - b 2 < 1D . a 2 - b 2 ≤ 1A . -16B.-8C.-4D .0(5)函数 f ( x ) = x 2- cos x - x sin x +1的图象大致为AB C D(10) 我国古代数学家刘徽在其《海岛算经》中给出了著名的望海岛问题及二次测望方法:今有望海岛,立两表,齐高三丈,前后相去千步,令后表与前表三相直.从前表却行一百二十三步,人目着地取望岛峰,与表末三合.从后表却行一百二十七步,人目着地取望岛峰,亦与表末三合.问岛高及去表各几何?这一方法领先印度 500 多年,领先欧洲 1300 多年.其大意为:测量望海岛 PQ 的高度及海岛离岸距离,在海岸边立两根等高标B= 10 B. 15 C. 30 D. 1010 15 12 12PBD QAE CF( ) n nn杆 AB , CD ( P Q , AB , C D 共面,均垂直于地面),使目测点 E 与P 、B 共线, 目测点 F 与 P 、D 共线,测出 AE 、CF 、AC , 即可求出岛高 PQ 和 EQ 的距离(如图).若 AB = CD = r , AE = a ,CF = b , EF = d ,则 PQ =二.填空题(本大题共 4 小题,每小题 5 分)(13) 若 (ax -1)5的展开式中 x 3 的系数是 −80, 则实数a 的值是.(14) 某学校社会实践小组共有5 名成员,该小组计划前往该地区三个红色教育基地进行“学党史,颂党恩,跟党走”的主题宣讲志愿服务.若每名成员只去一个基地,每个基地至少有一名成员前往,且甲、乙两名成员前往同一基地,则不同的分配方案共有种.(15)已知函数 f (x ) =1(sin ωx -1) + cos 2ω x(ω > 0) ,若 f (x ) 在(2π, 3π) 内无零点,则ω 的dr A .b - adr B . b +adr C .a - bd - a r D .b +a22取值范围是.(11) 已知数列{a } 满足: a = 1, a= 1, a = a + a (n ≥ 3, n ∈ N * ) ,若将数列{a } 的(16) 在四棱锥S - ABCD 中,已知SA ⊥ 底面 ABCD , AB ∥ CD , AB ⊥ AD ,AB = 2n12nn -1n -2n每一项按照下图方法放进格子里,每一小格子的边长为 1,记前n 项所占的格子的面积之 CD = AD = 4 . M 是平面SAD 内的动点,且满足∠CMD = ∠BMA .则当四棱锥 和为S n ,每段螺旋线与其所在的正方形所围成的扇形面积为c n . 现有如下命题:M - ABCD 的体积最大时,三棱锥M - ACD 外接球的表面积为.p 1 : S n +1 2 n +1 + a n +1 ⋅ a n ;三、解答题(共 70 分.解答应写出文字说明、证明过程或演算步骤.第 17~21 题为必考题,每个试题考生都必须作答,第 22、23 题为选考题,考生根据要求作答.)p 2 : a 1 + a 3 + + a 2n -1 = a 2n -1;p 3 : ∑a i= a n +2 -1;i =1(一)必考题:每题 12 分,共 60 分.(17)已知数列{a }前 n 项和为 S ,且2S= n (n +1) ,记b n = (-1)n 2a n +1 .p 4 : 4(c n - c n -1) = πa n +1 ⋅ a n -2 .nnna 2 + a则下列选项正确的是A . p 1 ∧ p 2B . p 1 ∧ p 3C . ⌝p 2 ∧ ⌝p 3D . p 2 ∨ ⌝p 4(Ⅰ)求数列{a n }的通项公式;(Ⅱ)设数列{b n } 的前n 项和为T n ,求T 2021 .(12)已知函数 f (x ) =x - 2m (m < 0), g (x ) =2 ln(-x ) ,设方程 f (g (x )) + 1= 0 的 3 个实根3x 2xm分别为 x 1, x 2 , x 3 ,且 x 1 < x 2 < x 3 ,则 g (x 1) + 2g (x 2 ) + 3g (x 3 ) 的值可能为A . -2 B . 2ee C . -3 D . 3ee2= a5(18) 某物流公司专营从长春市到吉林市的货运业务,现统计了最近 100 天内每天可配送的货物量,按照可配送货物量 T (单位:箱)分成了以下几组:[40, 50) ,[50,60) ,[60,70) ,[70,80) ,[80,90) ,[90,100],并绘制了如图所示的频率分布直方图(同一组中的数据用该区间的中点值为代表,视频率为概率 ).(Ⅰ)求该公司平均每天的配货量是多少箱?(Ⅱ)为了调动公司员工的积极性,特制定了以下奖励方案:利用抽奖的方式获得奖金,每次抽奖的结果相互独立.其中每 天的可配送货物量不低于80 箱时有两次抽奖机会;每天的可 配送货物量低于80 箱时只有一次抽奖机会.每次抽奖获得的 奖金及对应的概率分别为:(19) 如图, AE ⊥ 平面 ABCD ,CF ∥ AE , AD ∥ BC , AD ⊥ AB , AB =AD =1, AE = BC = 2 .(Ⅰ)求证: DE // 平面 BCF ;(Ⅱ)若二面角 E - BD - F 的余弦值为 1,求直线 FB 与平面 ABCD 所成角的正切值.3x 2 y 2(20) 椭圆C : a 2 + b2= 1(a > b > 0) 的左、右焦点分别为 F 1 ,F 2 ,过点 F 2 的直线l 交椭圆于 A ,若小张是该公司一名员工,他每天所获奖金为 X 元,请写出 X 的分布列并求出数学期望E ( X ) .B 两点. 当直线l ⊥ x 轴时, AF 1 (Ⅰ)求椭圆的离心率;= 3AF 2 .(Ⅱ)若椭圆C 上存在点M ,使得四边形 AF 1BM 是平行四边形,求此时直线l 的斜率.EFDCAB奖金(元) 50 100概率231 3PN+(21) 已知函数 f (x ) =x ln a + a sin x (a > 0) e x, f '(x ) 为 f (x ) 的导数.(二)选考题:共 10 分.请考生在第 22、23 题中任选一题作答.如果多做,则按所做的第一题计分.(22) 【选修 4—4:坐标系与参数方程】(Ⅰ)若 x = 0 为 f '(x ) 的零点,试讨论 f (x ) 在区间[0, π]的零点的个数;f (x )⎧⎪x = 曲线C 的参数方程为⎨ y = 3 cos α (α 为参数,α ∈ R ). 以坐标原点为极点, x 轴正半2 sin α(Ⅱ)当a = 1时,2 + cos x< mx (x > 0),求实数m 的取值范围.⎪⎩轴为极轴建立极坐标系,点 A 的极坐标为⎛2 2,π ⎫,直线l 的极坐标方程为 ρ cos⎛θ - π ⎫ = m ,4 ⎪ 4 ⎪ ⎝⎭⎝ ⎭且直线l 经过点 A .(Ⅰ)写出曲线C 的普通方程和直线l 的直角坐标方程;(Ⅱ)过点 P (1,0) 的直线l ' 交曲线C 于M 、 N 两点,且l ' ⊥ l ,求+ 1 的值.(23) 【选修 4—5:不等式选讲】已知函数 f (x ) = x +1 + 2x -1 . (Ⅰ)求不等式 f ( x ) > 2 的解集;(Ⅱ)已知函数 f ( x ) 的最小值为t ,正实数a , b , c 满足a + c = 4t - 2b .1 12证明:≥ . a + b b + c 3PM 1高三年级第三次摸底 数学(理)试卷参考答案二、填空题(本大题共4小题,每小题5分,共计20分)(13) 2- (14) 36 (15)137711(0,][,][,]4812812(16) 160π 三、解答题(共70分)(17)(本小题满分12分)解:(Ⅰ)()112n S n n =+,当1n =时,111212S =⨯⨯=; 当2n ≥,n N *∈时,()1112n S n n -=-,()()1111122n n n a S S n n n n n -=-=+--=.当1n =时也符合, ()n a n n N *∴=∈.(Ⅱ)()()()()()()221212*********nn n n n n n n n n a n b a a n n n n n n ++++⎛⎫=-=-=-=-+ ⎪++++⎝⎭202111111111...12233420212022T ⎛⎫⎛⎫⎛⎫⎛⎫∴=-+++-++-+ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭111111112023=1 (1223342021202220222022)--++--+--=--=-.(18)(本小题满分12分)解: (Ⅰ)根据频率分布直方图,该公司平均每天的配货量为:450.05550.2650.3750.3850.1950.0568.5⨯+⨯+⨯+⨯+⨯+⨯=(箱)(Ⅱ)每天的可配送货物量不低于80箱的概率为30.10.050.1520+==,每天的可配送货物量低于80箱的概率为31712020-=. X 的所有可能取值为50,100,150,200.则()172175020330P X ==⨯=, ()1713227100203203320P X ==⨯+⨯⨯=, ()31211502203315P X ==⨯⨯⨯=, ()3111200203360P X ==⨯⨯=. 所以X 的分布列为:所以()1771123050100150200302015603E X =⨯+⨯+⨯+⨯=(元).(19)(本小题满分12分)解:依题意,可以建立以A 为原点,分别以AB AD AE ,,的方向为x 轴,y 轴,z 轴正方向的空间直角坐标系(如图),可得(0,0,0),(1,0,0),(1,2,0),(0,1,0)A B C D ,(0,0,2)E .设(0)CF h h =>,则()1,2,F h .CF AE ∥,CF ∴⊥平面ABCD ,CF AB ∴⊥,又AB BC ∴⊥,BC CF C =,AB ∴⊥平面(Ⅰ)法一:证明:依题意,AE ⊥平面ABCD ,BCF ,(1,0,0)AB ∴=是平面BCF 的法向量,又(0,1,2)DE =-,可得0AB DE ⋅=,又因为直线DE ⊄平面BCF ,所以DE ∥平面BCF .ADE ,//CF ∴平面ADE .同理//BC 平面ADE ,CF BC C =,∴平面BCF //平面ADE ,又法二:CF AE ∥,CF ⊄平面ADE ,AE ⊂平面DE ⊂平面ADE , 所以DE ∥平面BCF .00BD m BF m ⎧⋅=⎪⎨⋅=⎪⎩即0,20,x y y hz -+=⎧⎨+=⎩ (Ⅱ)解:设(),,x y m z =为平面BDF 的法向量,则不妨令1y =,可得21,1,m h ⎛⎫=-⎪⎝⎭.同理可得平面BDE 的一个法向量为(2,2,1)n =由题意,有4||1cos ,3||||32m n m n m n ⋅〈〉===,解得87h =. 87CF ∴=. CF ⊥平面ABCD ,FBC ∴∠为直线FB 与平面ABCD 所成角,4tan .7CF FBC BC ∴∠==(20)(本小题满分12分) 解:(Ⅰ)法一:l 过()2,0F c ,且l x ⊥,设(),A c y ,不妨设A 为第一象限点,则0y >.则222221,,c y b A c a b a ⎛⎫+=∴ ⎪⎝⎭,22b AF a ∴=,2153b AF a ∴=⋅,2221258233b b b AF AF a a a a∴+=+⋅==.()2222223444a b a c a c ∴==-∴=,12e =.法二: 1211225245334AF AF a AF a AF AF AF a⎧⎧+==⎪⎪⎪∴∴⎨⎨=⎪⎪=⎩⎪⎩,2222253144442a a c a c e ⎛⎫⎛⎫∴-=∴=∴= ⎪ ⎪⎝⎭⎝⎭. (Ⅱ)由(Ⅰ)知,可设椭圆2222:143x y C c c +=, ()()1122,,,A x y B x y ,线段AB 的中点()00,N x y ,由题意可以判断直线l 的斜率存在,设():l y k x c =-()2222143x y c c y k x c ⎧+=⎪∴⎨⎪=-⎩,()2222223484120k x ck x c k c ∴+-+-=,2122834ck x x k∴+=+, 212024234x x ck x k +∴==+ ()002334cky k x c k-∴=-=+ ① 四边形1AF BM 是平行四边形,N ∴是1F M 的中点,()002,2M x c y ∴+,M 在椭圆上,()()22200324212x c y c ∴++= ②①代入②得,222222123634123434ck c ck c k k ⎛⎫+-⎛⎫∴+= ⎪ ⎪++⎝⎭⎝⎭, 整理得428024270k k +-=,解得2920k =或234k =-(舍去),k ∴=所以直线l的斜率为.(21)(本小题满分12分) 解:(Ⅰ)ln (1)()cos exa x f x a x -'=+,因为0x =为()f x '的零点,所以(0)0f '=, 即ln 0a a +=,从而(1)()cos [cos (1)e ]ex xa x f x a x a x x ---'=+=--. ①因为(0)0f =,所以0是()f x 的零点. ②当(0,π]x ∈时,设()cos (1)exg x x x -=--,则()(2)esin xg x x x -'=--.(ⅰ)若π(0,]2x ∈,令()()(2)esin xh x g x x x -'==--,则()(3)e cos 0x h x x x -'=--<,所以()h x 在π(0,]2单调递减,因为π2ππ(0)20,()(2)e 1022h h -=>=--<,所以存在唯一的0π(0,)2x ∈,使得0()0h x =.当0(0,)x x ∈时,()()0h x g x '=>,()g x 在0(0,)x 上单调递增;当0π(,)2x x ∈时,()()0h x g x '=<,()g x 在0π(,)2x 上单调递减;(ⅱ)若π(,2]2x ∈,令()(2)e xx x ϕ-=-,则()(3)e 0x x x ϕ-'=-<,故()x ϕ在π(,2]2上单调递减,所以π2ππ1()()(2)22e x e ϕϕ-<=-<.又π1sin sin 2sin(π2)sin 62x ≥=->=,所以()(2)e sin 0,()xg x x x g x -'=--<在π(,2]2上单调递减;(ⅲ)若(2,π]x ∈,则()(2)e sin 0,()xg x x x g x -'=--<在(2,π]上单调递减.由(ⅰ)(ⅱ)(ⅲ)可得,()g x 在0(0,)x 上单调递增,在0(,π]x 上单调递减,因为π0()(0)0,(π)(π1)e 10g x g g ->==--<,所以存在唯一10(,π)x x ∈使得1()0g x =.当1(0,)x x ∈时,()()0f x ag x '=>,()f x 在1(0,)x 上单调递增,()(0)0f x f >=, 当1(,π]x x ∈时,()()0f x ag x '=<,()f x 在1(,π]x 上单调递减, 因为1()(0)0,(π)0f x f f >=<,所以()f x 在1(,π]x 上有且只有一个零点. 综上,()f x 在[]0,π上有两个零点.(Ⅱ)当1a =时,()sin f x x =,则不等式化为sin 2cos x mx x <+,即为sin 02cos xmx x->+.法一: 令sin ()2cos xG x mx x =-+则()()2222cos +123111()=+=32cos 2cos 332cos 2cos x G x m m m x x x x ⎛⎫'=---+- ⎪++⎝⎭++ 当13m ≥时,()0G x '>,()G x 在()0+∞,单调递增,且(0)=0G ,故13m ≥时满足题意; 当103m <<时,令()sin 3H x x mx =-,则()cos 3H x x m '=-在()0+∞,有无数零点 ∴存在最小的一个()00,x x ∈,使()0H x '>,则()H x 在()0+∞,单调递增,()(0)0H x H >=∴sin 3x mx >()00,x x ∴∃∈,使sin sin 2cos 3x xmx x >>+∴sin 02cos x mx x -<+,故103m <<不满足题意,舍去.当0m ≤时,0,0x mx >∴≤,令()sin 2cos x n x x =+,πsinπ12=0π222cos 2n ⎛⎫=> ⎪⎝⎭+,不满足题意,舍去.综上,13m ≥. 法二: 令sin ()2cos x F x mx x =-+,则(0)0F =,22cos 1()(2cos )x F x m x +'=-+,1(0)3F m '=-.当13m ≥时,sin 1()2cos 3x F x x x ≤-+,令sin 1()2cos 3x G x x x =-+,则 22(1cos )()03(2cos )x G x x -'=-≤+,于是()G x 在(0,)+∞上单调递减,所以()(0)0G x G <=,故()0F x <.当13m <时,考虑π(0,)2x ∈,此时311()sin ()336x F x x mx x mx >->--2(618)18m x x --=⋅.记}2t π=,于是当0x t <<时,()0F x >,不符合题意.综上所述,实数m 的取值范围是1[,)3+∞.(22)(本小题满分10分)解:(Ⅰ)22cos 3cos :1322sin x x y C y αααα=⎧=⎪∴∴+=⎨=⎪⎩=. π4A ⎛⎫ ⎪⎝⎭在πcos 4m ρθ⎛⎫-= ⎪⎝⎭上,ππ22cos 44m m ⎛⎫-=∴= ⎪⎝⎭πcos sin 422ρθρθθ⎛⎫⎛⎫∴-=∴+= ⎪ ⎪ ⎪⎝⎭⎝⎭:40l x y ∴+-=.(Ⅱ)1l l l k ''⊥∴=,∴l '的倾斜角为π4,12x l y ⎧=+⎪⎪∴⎨⎪=⎪⎩的参数方程为(t 为参数) 代入22:132x y C +=得2580t +-=,121285t t t t ∴+==-.12121211115t t PM PN t t t t -+=+====.(23)(本小题满分10分) 解:(Ⅰ)由题设,()311=2,1213,.2x x f x x x x x ⎧⎪-≤-⎪⎪--<≤⎨⎪⎪>⎪⎩,;; ∴要使()2f x >,由132x x ≤-⎧⎨->⎩得1x ≤-;由11222x x ⎧-<≤⎪⎨⎪->⎩得10x -<<;由1232x x ⎧>⎪⎨⎪>⎩得23x >; 综上,()2f x >的解集为203x x x ⎧⎫<>⎨⎬⎩⎭或. (Ⅱ)由(Ⅰ)知:()f x 的最小值为32,即32t =.数学(理)试题 第 11 页 ,共 4 页 ∵42a c t b +=- ∴+26a c b += ∴()()()()1126a b c a b b c a b b c a b b c +++==++++++, ∵,,a b c 为正实数,()()2662=322a b b c a b c ∴≥++++⎛⎫ ⎪⎝⎭当且仅当=3a b b c +=+时等号成立, ∴1123a b b c +≥++得证.。
吉林省长春市东北师范大学附属中学2021届高三数学上学期一摸试题 理(含解析).doc
吉林省长春市东北师范大学附属中学2021届高三数学上学期一摸试题 理(含解析)一、选择题1.若i 是虚数单位,在复平面内复数21ii-+表示的点在( ) A. 第一象限 B. 第二象限C. 第三象限D. 第四象限【答案】D 【解析】 【分析】运用复数除法的运算法则,化简复数21ii-+,最后选出正确答案. 【详解】因为2(2)(1)131(1)(1)22i i i i i i i --⋅-==-++⋅-,所以复平面内复数21ii-+表示的点的坐标为13(,)22-,该点在第四象限. 故选:D【点睛】本题考查了复数除法的运算法则.考查了复数在复平面表示点的位置问题. 2.若全集{}*2560U x N x x =∈--≤,集合{}2,3A =,{}0,1,5B =,则()UB A ⋂( )A. {}0,1,5B. {}1,5C. ∅D.{}0,1,4,5,6【答案】B 【解析】 【分析】解一元二次不等式,并求出正整数解集,化简全集的表示,根据补集、交集的定义,求出()U B A ⋂.【详解】{}{}{}*2*560161,2,3,4,5,6U x N x x x N x =∈--≤=∈-≤≤=.因为{}2,3A =,所以{}1,4,5,6UA =,因此(){}1,5UB A ⋂=.故选:B【点睛】本题考查了集合的补集运算、并集运算,考查了解一元二次不等式,考查了数学运算能力.3.下列函数中,既是偶函数,又在()0,∞+上单调递增的函数是( ) A. 32y x =B. xy e-=C. 21lg y x =-D.6y x =+【答案】D 【解析】 【分析】对选项中的四个函数,先求定义域,再判断是不是偶函数,当()0,x ∈+∞时,化简函数的解析式,再判断单调性即可选出正确答案.【详解】选项A :函数32y x =的定义域为全体非负实数集,故该函数不具有奇偶性,不符合题意; 选项B :函数()xy f x e-==的定义域为全体实数集. ()()xxf x eef x ----===,所以该函数是偶函数, 当()0,x ∈+∞时, 1()()xx x f x e e e --===,因为101e<<,所以该函数此时是减函数,不符合题意;选项C :函数2()1lg y f x x ==-的定义域为非零的全体实体集,22()1lg()1lg ()y f x x x f x =-=--=-=,所以该函数是偶函数,当()0,x ∈+∞时, 2()1lg 12lg f x x x =-=-,根据单调性的性质可知:该函数此时单调递减,不符合题意;选项D :函数()6y f x x ==+的定义域为全体实数集, ()66()f x x x f x -=-+=+=,所以该函数是偶函数, 当()0,x ∈+∞时, ()6y f x x ==+,符合题意. 故选:D【点睛】本题考查了函数的奇偶性、单调性,属于基础题.4.设50.3a =,0.35b =,0.3log 5c =,则,,a b c 的大小关系是( ) A. a b c >>B. a c b >>C. c a b >>D.b ac >>【解析】 【分析】根据对数函数、指数函数的单调性,运用中间值比较法,可以比较出,,a b c 的大小关系. 【详解】因为函数0.3xy =是全体实数集上的减函数,所以有5000.30.31<<=; 因为函数5xy =是全体实数集上的增函数,所以有0.30551>=;因为函数0.3log y x =是正实数集上的减函数,所以有0.30.3log 5log 10<=,因此有b a c >>. 故选:D【点睛】本题考查了对数式、指数式的比较,运用对数函数、指数函数的单调性,运用中间值比较法是解题的关键.5.素数也叫质数,部分素数可写成“21n -”的形式(n 是素数),法国数学家马丁•梅森就是研究素数的数学家中成就很高的一位,因此后人将“21n -”形式(n 是素数)的素数称为梅森素数.2021年底发现的第51个梅森素数是8258993321P =-,它是目前最大的梅森素数.已知第8个梅森素数为3121P =-,第9个梅森素数为6121Q =-,则QP约等于(参考数据:lg 20.3≈)( )A. 710B. 810C. 910D. 1010【答案】C 【解析】 【分析】根据,P Q 两数远远大于1, Q P 的值约等于613122,设613122k =,运用指数运算法则,把指数式转化对数式,最后求出k 的值.【详解】因为,P Q 两数远远大于1,所以Q P 的值约等于613122,设6130303122lg 2lg 2k k k =⇒=⇒=, 因此有930lg 2lg lg 910k k k =⇒=⇒=.【点睛】本题考查了数学估算能力,考查了指数运算性质、指数式转化为对数式,属于基础题. 6.函数y =2x 2–e |x |在[–2,2]的图像大致为( )A. B. C. D.【答案】D 【解析】试题分析:函数f (x )=2x 2–e |x|在[–2,2]上是偶函数,其图象关于y 轴对称,因为22(2)8,081f e e =-<-<,所以排除,A B 选项;当[]0,2x ∈时,4x y x e '=-有一零点,设为0x ,当0(0,)x x ∈时,()f x 为减函数,当0(,2)x x ∈时,()f x 为增函数.故选D7.“22a -≤≤”是“关于x 的不等式210ax ax a-+≥的解集为R ”的( ) A. 充分不必要条件 B. 必要不充分条件 C. 充要条件 D. 既不充分也不必要条件【答案】B 【解析】 【分析】先判断不等式210ax ax a-+≥的解集为R 成立的条件,然后根据充分性、 必要性的定义选 出正确答案.【详解】因为关于x 的不等式210ax ax a-+≥的解集为R ,所以有:0a >且21()40a a a--⋅≤, 所以有02a <≤,显然由22a -≤≤不一定能推出02a <≤,但由02a <≤一定能推出22a -≤≤,故“22a -≤≤”是“关于x 的不等式210ax ax a-+≥的解集为R ”的必要不故选:B【点睛】本题考查了必要不充分条件的判断,解决不等式恒成立问题是解题的关键.8.已知函数()3211,0log ,0x x f x x x ⎧+-≤=⎨>⎩,若()1f a ≤,则实数a 的取值范围是( )A. [)3,3,2⎛⎤-∞-+∞⎥⎝⎦B. 3,32⎡⎤-⎢⎥⎣⎦C. (]3,00,32⎡⎫-⎪⎢⎣⎭D. []4,2-【答案】B 【解析】 【分析】根据分段函数的解析式,分类讨论解不等式,最后求出实数a 的取值范围. 【详解】当0a ≤时, ()311211122f a a a ≤⇒+-≤⇒-≤≤,而0a ≤,所以 302a -≤≤; 当0a >时, ()31log 13f a a a ≤⇒≤⇒≤,而0a >,所以03a <≤,综上所述:实数a 的取值范围是3,32⎡⎤-⎢⎥⎣⎦. 故选:B【点睛】本题考查了分段函数不等式的解法,正确求解对数不等式、绝对值不等式是解题的关键.9.二次函数2y ax bx c =++和2y cx bx a =++(0ac ≠,a c ≠)的值域分别为M 和N ,命题:p MN ,命题:q M N ≠∅,则下列命题中真命题的是( )A. p q ∧B. ()p q ∨⌝C. ()()p q ⌝∧⌝D.()p q ⌝∧【答案】D 【解析】根据两个二次函数最高次项系数的正负性可以通过举例说明命题p 的真假,根据两个二次函数最高次项系数的正负性进行分类讨论,可以判断出命题q 的真假,最后根据且命题、或命题的真假判断方法选出正确答案.【详解】(1)当0a >,0c <时, 二次函数2y ax bx c =++的值域为:244ac b M y y a ⎧⎫-⎪⎪=≥⎨⎬⎪⎪⎩⎭,二次函数2y cx bx a =++的值域为:244ac b N y y c ⎧⎫-⎪⎪=≤⎨⎬⎪⎪⎩⎭,此时显然:p MN是假命题,而244ac b a -是负的, 244ac b c -是正的,故命题:p MN 是假命题,命题:q MN ≠∅是真命题;(2)当0a >,0c >时, 二次函数2y ax bx c =++的值域为:244ac b M y y a ⎧⎫-⎪⎪=≥⎨⎬⎪⎪⎩⎭,二次函数2y cx bx a =++的值域为:244ac b N y y c ⎧⎫-⎪⎪=≥⎨⎬⎪⎪⎩⎭,此时244ac b a -、 244ac b c-是同号,故命题:q M N ≠∅是真命题;(3)当0a <,0c <时, 二次函数2y ax bx c =++的值域为:244ac b M y y a ⎧⎫-⎪⎪=≤⎨⎬⎪⎪⎩⎭,二次函数2y cx bx a =++的值域为:244ac b N y y c ⎧⎫-⎪⎪=≤⎨⎬⎪⎪⎩⎭,此时244ac b a -、 244ac b c-是同号,故命题:q M N ≠∅是真命题;(4)当0a <,0c >时, 二次函数2y ax bx c =++的值域为:244ac b M y y a ⎧⎫-⎪⎪=≤⎨⎬⎪⎪⎩⎭,二次函数2y cx bx a =++的值域为:244ac b N y y c ⎧⎫-⎪⎪=≥⎨⎬⎪⎪⎩⎭,此时244ac b a-是正数、 244ac b c-是负数,故命题:q MN ≠∅是真命题;综上所述:p 是假命题, q 是真命题.选项A: 因为p 是假命题, q 是真命题,p q ∧是假命题;选项B: 因为p 是假命题, q 是真命题,所以q ⌝是假命题,因此()p q ∨⌝是假命题; 选项C: 因为p 是假命题, q 是真命题,所以p ⌝是真命题,q ⌝是假命题,因此()()p q ⌝∧⌝是假命题;选项D: 因为p 是假命题, q 是真命题,所以p ⌝是真命题, ()p q ⌝∧是真命题. 故选:D【点睛】本题考查了命题的真假判断,考查了二次函数的值域,考查了集合之间的关系、运算问题,分类讨论是解题的关键.10.若函数(),0231,0x e x a x f x ax a x ⎧-+>=⎨+-≤⎩在(),-∞+∞上是单调函数,且()f x 存在负的零点,则a 的取值范围是( )A. 10,3⎛⎤ ⎥⎝⎦B. (]0,1C. 1,13⎛⎤ ⎥⎝⎦D.1,3⎛+∞⎫ ⎪⎝⎭【答案】C 【解析】 【分析】利用导数,判断出函数在0x >时的单调性,进而可以判断整个函数的单调性,这样利用分段函数的单调性的性质和()f x 存在负的零点,这样可以选出正确答案. 【详解】当0x >时, ()()'10xx f x e x a fx e =-+-⇒>=,所以函数在0x >时单调递增,由题意可知整个函数在全体实数集上也是单调递增,因此有:2001311a a a a >⎧⇒<≤⎨-≤+⎩,又因为()f x 存在负的零点,因此有13103a a ->⇒>,综上所述:a 的取值范围是1,13⎛⎤ ⎥⎝⎦.故选:C【点睛】本题考查了已知分段函数的单调性和零点求参数问题,考查了数学运算能力. 11.已知()f x 是定义在()(),00,-∞⋃+∞上的奇函数,且()26f =,若对任意两个不相等的正数12,x x ,都有()()2112120x f x x f x x x -<-,则()30f x x->的解集为( )A. ()(),20,2-∞-B. ()()2,02,-+∞C. ()()2,00,2-D. ()(),22,-∞-+∞【答案】C 【解析】 【分析】根据所求不等式的形式构造新函数,根据()()2112120x f x x f x x x -<-,可以判断出函数()f x 的单调性,最后利用函数的单调性和偶函数数的性质,求出()30f x x->的解集. 【详解】由题意可知:120,0x x >>,因此有()()()()21121221121212121212()()000x f x x f x f x f x x f x x f x x x x x x x x x x x ---⋅<⇒<⇒<---, 设()()f x g x x=,因此函数()g x 在0x >时是单调递减函数, 因为()26f =, 所以(2)3g =,而()f x 是定义在()(),00,-∞⋃+∞上的奇函数,所以有()()()()()f x f x f x g x g x x x x---====--,因此函数()g x 是()(),00,-∞⋃+∞上的偶函数. 由偶函数的性质可知:当0x <时, 函数()g x 是单调递增的.所以当0x >时,()30()(2)02f x g x g x x->⇒>⇒<<; 当0x <时,()30()(2)0220f x g x g x x x->⇒>-⇒>>-⇒-<<,综上所述:()30f x x->的解集是()()2,00,2-.故选:C【点睛】本题考查了通过构造函数求解不等式解集问题,对已知的不等式进行数学变形,利用函数的单调性和偶函数的性质是解题的关键.12.若关于x 的方程10x x xx em e x e+++=+有三个不等的实数解123,,x x x ,且1230x x x <<<,其中m R ∈, 2.71828e =为自然对数的底数,则3122312x x x x x x m m m e e e ⎛⎫⎛⎫⎛⎫+++ ⎪ ⎪⎪⎝⎭⎝⎭⎝⎭的值为( ) A. eB. 2eC. ()42m m +D.()41m m +【答案】B 【解析】 【分析】根据所给的方程的特征,令x x t e=进行换元,方程转化为2(1)0t m t m e ++++=,画出函数 ()xxg x e =的图象,利用函数的图象和所求的代数式特征,求出所求代数式的值. 【详解】令x x t e =,所以由10x x xx e m e x e+++=+可得2(1)0t m t m e ++++=, 设()x x g x e =,1()xx g x e'-=,当1x >时, '()0g x <,所以函数()x x g x e =单调递减, 当1x <时, '()0g x >,所以函数()x x g x e =单调递增,而1(0)0,(1)g e==,显然当0x >时,()0>g x ,当0x <时, ()0<g x 因此函数()x xg x e=的图象如下图所示:要想关于x 的方程10x x xx em e x e+++=+有三个不等的实数解123,,x x x ,且1230x x x <<<, 结合函数图象可知,只需关于t 的方程2(1)0t m t m e ++++=有两个不相等的实数根12,t t ,且12312123,x x x x x x t t e e e ===, ()()3122231212x x x x x x m m m t m t m e e e ⎛⎫⎛⎫⎛⎫⎡⎤∴+++=++ ⎪ ⎪⎪⎣⎦⎝⎭⎝⎭⎝⎭, ()()()22121212()(1)t m t m t t m t t m e m m m m e ++=+++=+-++=,31222312111x x x x x x e e e e ⎛⎫⎛⎫⎛⎫+++= ⎪ ⎪⎪⎝⎭⎝⎭⎝⎭. 故选:B【点睛】本题考查了函数与方程思想,考查了数形结合思想,属于中档题. 二、填空题13.已知函数()()1,0,0f x x f x x x ⎧-≥⎪=⎨-<⎪⎩,那么74f ⎛⎫⎪⎝⎭的值为__________. 【答案】12- 【解析】 【分析】 求74f ⎛⎫⎪⎝⎭的值,根据分段函数的解析式,就要求34f ⎛⎫⎪⎝⎭的值, 要求34f ⎛⎫⎪⎝⎭的值,根据分段函数的解析式,就要求14f ⎛⎫-⎪⎝⎭的值,而14f ⎛⎫- ⎪⎝⎭的值直接代入即可求出.【详解】7733111(1)()(1)()()4444442f f f f f ⎛⎫=-==-=-=---=- ⎪⎝⎭. 故答案为:12-【点睛】本题考查了已知分段函数的解析式求函数值问题,考查了数学运算能力.14.函数()()212log 6f x x x =-+的单调递增区间为__________. 【答案】()3,6 【解析】 【分析】先求出函数()f x 的定义域,再根据复合函数的单调性的性质,可以求出函数()f x 的单调递增区间. 【详解】函数()f x 的定义域为:{}06x x <<,()()221122log 6log [(3)9]f x x x x =-+=--+,所以函数()f x 的单调递增区间为()3,6. 故答案为:()3,6【点睛】本题考查了复合函数的单调区间,本题易忘记求函数的定义域.15.如图,将边长为1的正方形ABCD 沿x 轴正向滚动,先以A 为中心顺时针旋转,当B 落在x 轴时,又以B 为中心顺时针旋转,如此下去,设顶点C 滚动时的曲线为()y f x =,则()5f =__________;当23x <≤时,()f x =__________.【答案】2243x x -+-【解析】 【分析】根据题意分别求出0,1,2,3,4,x =时对应的函数值,结合正方形运动的轨迹图象求出当23x <≤时,函数的解析式即可.【详解】边长为1的正方形ABCD 的对角线长为2,当0x =时, C 点的坐标为:(0,1),即(0)1f =; 当1x =时, C 点的坐标为:2),即(1)2f =当2x =时, C 点的坐标为:(2,1),即(2)1f =; 当3x =时, C 点的坐标为:(3,0),即(3)0f =; 当4x =时, C 点的坐标为:(4,1),即(4)1f =; 当5x =时, C 点的坐标为:2),即(5)2f =当23x <≤时, 顶点C 的轨迹是以(2,0)为圆心,半径为1的14圆,其方程为: 222(2)143x y y x x -+=⇒=-+-所以2()43f x x x =-+-.2243x x -+-【点睛】本题考查了函数值的计算,考查了函数的解析式和性质,考查了数学阅读能力. 16.已知函数()22ln f x ax x x =-+有两个不同的极值点12,x x ,且不等式()()1212f x f x x x t +<++恒成立,则t 的取值范围是__________.【答案】[)5,-+∞ 【解析】 【分析】根据函数()22ln f x ax x x =-+有两个不同的极值点12,x x ,通过求导,可以求出a 的取值范围,求出 ()()1212f x f x x x +--的表达式,最后利用导数,通过构造函数,求出新构造函数的单调性,最后求出t 的取值范围.【详解】2221()(0)ax x f x x x'-+=>,因为函数()22ln f x ax x x =-+有两个不同的极值点12,x x ,所以方程22210ax x -+=有两个不相等的正实数根,于是有:121248010102a x x a x x a ⎧⎪∆=->⎪⎪+=>⎨⎪⎪=>⎪⎩,解得102a <<. ()()221112221212122ln 2ln f x f x x x x ax x x ax x x x +--+--++=--()()212121212()23ln a x x x x x x x x ⎡⎤=+--++⎣⎦21ln 2a a=---,设21()1ln 2,02h a a a a ⎛⎫=---<< ⎪⎝⎭, 22()0a h a a '-=>,故()h a 在102a <<上单调递增,故1()52h a h ⎛⎫<=- ⎪⎝⎭,所以5t ≥-.因此 t 的取值范围是[)5,-+∞故答案为:[)5,-+∞【点睛】本题考查了已知函数极值情况求参数取值范围问题,考查了不等式恒成立问题,构造新函数,利用导数是解题的关键. 三、解答题17.在ABC △中,角,,A B C 所对的边分别为,,a b c ,且222cos cos sin sin sin C B A A C -=-.(1)求角B 的值;(2)若ABC △的面积为b =,求ac +的值.【答案】(1)3π;(2)9 【解析】(1)利用同角的三角函数关系式中的平方和关系,把等式中的余弦变形为正弦形式,由正弦定理,变形为边之间的关系,再由余弦定理可以求出角B 的值;(2)根据面积公式、余弦定理可以得到,a c 之间的关系式,最后求出a c +的值. 【详解】(1)由222cos cos sin sin sin C B A A C -=-, 得222sin sin sin sin sin B C A A C -=-.由正弦定理,得222b c a ac -=-,即222a c b ac +-=,所以222cos 2a c b B ac+-==122ac ac =. 因为0B π<<,所以3B π=.(2)由(1)知3B π=,又b =,2222cos b a c ac B ∴=+-2221a c ac =+-=,①又1sin 2S ac B ==20ac ∴=,②由①②得,2241a c +=,所以()222a c a c +=++281ac =, 所以9a c.【点睛】本题考查了同角三角函数的平方和关系,考查了正弦定理、余弦定理、面积公式,考查了数学运算能力.18.已知函数()22ln f x x a x =-,()222ln 2g x x x =-+-.(1)讨论函数()f x 的单调性;(2)当1a =时,判断()()g x f x -的零点个数. 【答案】(1)见解析;(2)2 【解析】(1)对函数()f x 进行求导,利用分类讨论法求出函数()f x 的单调性;(2)设()()()F x g x f x =-,求导,让导函数等于零,然后判断出函数的单调性,最后确定函数零点个数.【详解】(1)()22a f x x x '=-()22x ax-=, 故当0a ≤时,()0f x '≥,所以函数()f x 在()0,∞+上单调递增,当0a >时,令()0f x '>,得x所以函数()f x 在)+∞上单调递增,令()0f x '<,得x <所以函数()f x 在(上单调递减,综上,当0a ≤时,函数()f x 在()0,∞+上单调递增,当0a >时,函数()f x 在)+∞上单调递增,在(上单调递减.(2)设()()()F x g x f x =-=2ln 22ln 2x x -+-, 则()21F x x'=-,令()0F x '=, 解得2x =,当()0,2x ∈时,()0F x '>; 当()2,x ∈+∞时,()0F x '<; 故()F x 最大值为()20F=,所以()()g x f x -有且只有一个零点2.【点睛】本题考查了利用导数研究函数的单调性、零点,考查了分类讨论思想,考查了数学运算能力.19.将边长为2的正方形ABCD 沿对角线BD 折叠,使得平面ABD ⊥平面CBD ,AE ⊥平面ABD ,F 是BD 的中点,且2AE =.(1)求证:DE AC ⊥;(2)求二面角B EC F --的大小. 【答案】(1)见解析;(2)45︒ 【解析】 【分析】(1) 以A 为坐标原点,,,AB AD AE 所在的直线分别为x 轴、y 轴、z 轴建立空间直角坐标系, 求出点,,E B D 三点的坐标,通过F 是BD 的中点,可得CF BD ⊥,利用面面垂直的性质定理可得CF ⊥平面BDA ,进而可以求出点C 的坐标,最后利用向量法可以证明出DE AC ⊥; (2)分别求出平面BCE 、平面FCE 的法向量,最后利用空间向量夹角公式求出二面角B EC F --的大小.【详解】(1)证明:以A 为坐标原点,,,AB AD AE 所在的直线分别为x 轴、y 轴、z 轴建立空间直角坐标系,如图所示,则()0,0,2E ,()2,0,0B ,()0,2,0D取BD 的中点F 并连接,CF AF . 由题意得,CF BD ⊥ 又平面BDA ⊥平面BDC ,CF ∴⊥平面BDA ,(C ∴,(0,DE ∴=-,(AC =, (0,DE AC ⋅=-⋅(0=,DE AC ∴⊥.(2)解:设平面BCE 的法向量为()111,,n x y z =,则(2,0,EB =,(BC =-,DE n CB n ⎧⋅=⇒⎨⋅=⎩1111120x x y ⎧-=⎪⎨--=⎪⎩ 令()1,1,n =-.平面FCE 的法向量为()222,,m x y z =,()1,1,0F 所以()1,1,0EC =,(FC =,由2220000x y EC m z FC m +=⎧⎧⋅=⇒⎨⎨=⋅=⎩⎩得()1,1,0m =-.设二面角B EC F --为θ, 则2cos cos ,n m θ==所以二面角B EC F --的大小为45︒.【点睛】本题考查了用空间向量的知识解决线线垂直、二面角的问题,正确求出相关点的坐标是解题的关键.20.已知12,F F 是椭圆()222210x y a b a b +=>>的两个焦点,O 为坐标原点,,点()在椭圆上.(1)求椭圆的标准方程;(2),,D E F 为椭圆上三个动点,D 在第二象限,,E F 关于原点对称,且DE DF =,判断tan DE DF EDF ⋅∠是否存在最小值,若存在,求出该最小值,并求出此时点D 的坐标,若不存在,说明理由.【答案】(1)22162x y +=;(2)存在,最小值为6,,22D ⎛⎫- ⎪ ⎪⎝⎭【解析】 【分析】(1)把点的坐标代入椭圆方程中,再求出离心率的表达式,最后根据,,a b c 三者之间的关系,可以求出,a b 的值,最后写出椭圆的标准方程;(2)利用平面向量数量积的定义,化简tan DE DF EDF ⋅∠的表达式,可以发现只需判断EDF 面积是否有最小值,设出直线EF 的方程,与椭圆的方程联立,利用一元二次方程的根与系数的关系,求出EF 的表达式,同理求出OD 的表达式,最后确定EDF 面积的表达式,利用基本不等式可以求出EDF 面积的最小值,最后求出点D 的坐标.【详解】(1)点()在椭圆上,则22311a b+=, 又c a =222a b c =+, 解得26a =,22b =,∴椭圆的方程为22162x y +=;(2)tan DE DF EDF DE⋅∠=sin 2DEF DFEDF S ∠=△, 只需判断EDF 面积是否有最小值. 设直线EF 的方程为()0y kx k =>, 设()11,E x y ,()22,F x y ,联立22162y kxx y =⎧⎪⎨+=⎪⎩,得22631x k =+, 所以1EF x ==因为1ODk k=-,同理可知OD ==,1122EDF S EF OD ==⋅△261k +=()()()2226133132k k k +≥=++,此时22313k k +=+,因为0k >即1k =时,tan DE DF EDF ⋅∠最小值为6, 易知直线OD 的方程为y x =-,联立22162y x x y =-⎧⎪⎨+=⎪⎩,解得2x y ⎧=-⎪⎪⎨⎪=⎪⎩,即D ⎛ ⎝⎭. 【点睛】本题考查了求椭圆的标准方程,考查了直线与椭圆的位置关系,考查了求三角形面积最小值问题,考查了基本不等式的应用,考查了数学运算能力. 21.已知函数()()ln 1f x x =+,()()202xg x a x a=>+,设()()()F x f x g x =-. (1)如果曲线()y f x =与曲线()y g x =在1x =处的切线平行,求实数a 的值; (2)若对()0,x ∀∈+∞,都有()0F x >成立,求实数a 的取值范围;(3)已知()F x 存在极大值与极小值,请比较()F x 的极大值与极小值的大小,并说明理由.【答案】(1)12;(2)1a ≥;(3) 当112a <<时,()F x 极大值大于极小值;当102a <<时,()F x 极大值小于极小值. 【解析】 【分析】(1)分别求出两个函数的导数,把1x =代入两个导函数中,根据线线平行斜率的关系,可以求出实数a 的值;(2)对函数()F x 求导,分类讨论函数的单调性,最后求出实数a 的取值范围;(3)令()F x 的导函数等于零,求题意确定实数a 的取值范围,分类讨论,根据函数的单调性确定极大值与极小值之间的大小关系即可.【详解】(1)因为()11f x x '=+,()()242a g x x a '=+, 所以()112f '=,()()24112ag a '=+,由()()11f g ''=,得12a =(2)()()()F x f x g x =-=()()2ln 102xx x x a+->+, 易知()00F =,()()21412a F x x x a '=-++()()()224112x a a x x a +-=++ ①当()4100a a a ⎧-≥⎨>⎩,即1a ≥时,有()0F x '>,所以()F x 在()0,∞+上是增函数, 所以()()00F x F >=,满足题意.②当()4100a a a ⎧-<⎨>⎩,即01a <<时,()0F x '=,得1x =-,2x =因为()20,x x ∈,()0F x '<, 所以()F x 在()20,x 上是减函数,()()00F x F <=,不符合题意.综上,1a ≥. (3)()()()()2241012x a a F x x x a +-'==++,即()2410x a a +-=有两个不相等实数根1x =-2x =因为()101a a ⎧->⎪⎨-≠-⎪⎩,所以01a <<且12a ≠,①当21a -<-时,即112a <<时, ()F x 在()11,x -上是增函数,在()12,x x 上是减函数,在()2,x +∞上是增函数,故()F x 极大值为()1F x ,极小值为()2F x ,且()()12F x F x >.②当120a -<-<时,即102a <<时, ()F x 在()11,x -上是增函数,在()1,2x a -上是减函数,在()22,a x -上是减函数,在()2,x +∞上是增函数,故()F x 极大值为()1F x ,极小值为()2F x .()()()121ln 1F x F x x -=+-()1221222ln 122x x x x a x a-++++ ()()()21121241ln 122a x x x x x a x a -⎛⎫+=+ ⎪+++⎝⎭, 因为210x x ->,220x a +>,120x a +<,所以()()12F x F x <. 综上,当112a <<时,()F x 极大值大于极小值; 当102a <<时,()F x 极大值小于极小值. 【点睛】本题考查了导数的几何意义,考查了利用导数证明不等式恒成立问题,考查了函数的极大值与极小值之间的大小关系问题,考查了数学运算能力.22.在直角坐标系xOy 中,直线l 的参数方程为32x t y t =--⎧⎨=+⎩(t 为参数).以坐标原点O 为极点,x 轴的非负半轴建立极坐标系,点P的极坐标54π⎛⎫ ⎪⎝⎭,曲线C的极坐标方程为4πρθ⎛⎫=+ ⎪⎝⎭. (1)求直线l 的普通方程和曲线C 的直角坐标方程;(2)若Q 为曲线C 上的动点,求PQ 中点M 到直线l 的距离最小值.【答案】(1)10x y ++=,()()22112x y -++=;【解析】【分析】 (1)利用加减消元法消参可以求出直线l 的普通方程.利用极坐标与直角坐标之间的转化公式可以求出曲线C 的直角坐标方程;(2)求出P 的直角坐标,利用曲线C 的参数方程设出点Q 的坐标,利用中点坐标公式,求出M 的坐标,利用点到直线距离公式求出M 到直线l 的距离,利用辅助角公式,根据正弦型函数的单调性可以求出PQ 中点M 到直线l 的距离最小值.【详解】(1)直线l 的普通方程10x y ++=,由4πρθ⎛⎫=+= ⎪⎝⎭cos sin 22θθ⎫⋅-⋅⎪⎪⎭2cos 2sin θθ=-, 22cos 2sin ρρθρθ∴=-,即2222x y x y +=-, ∴曲线C 的直角坐标方程为()()22112x y -++=;(2)易知P 的直角坐标()3,3--,设()1,1Q αα-+, 则PQ的中点24,22M αα⎛⎫--+ ⎪ ⎪⎝⎭, 设M 到直线l 的距离为d ,则d==当sin 14πα⎛⎫+= ⎪⎝⎭时,min 2d =. 【点睛】本题考查了参数方程化为普通方程、极坐标方程化为直角坐标方程,考查了中点坐标公式,考查了点到直线距离公式,考查了圆的参数方程的应用,考查了数学运算能力.23.已知函数()12f x x x =+-.(1)求不等式()2f x ≥-的解集;(2)若关于x 的不等式()235f x a a -≥-在2,13⎡⎤-⎢⎥⎣⎦上有解,求实数a 的取值范围. 【答案】(1){}13x x -≤≤;a ≤≤【解析】【分析】 (1)利用零点法分类讨论求出不等式()2f x ≥-的解集;(2)根据题意本问题题可以转化为()2max 35f x a a -≥-⎡⎤⎣⎦成立,求出()f x 的最大值,最后求出实数a 的取值范围.【详解】(1)不等式化为0122x x x ≥⎧⎨+-≥-⎩或10122x x x -≤<⎧⎨++≥-⎩或1122x x x <-⎧⎨--+≥-⎩, 解得03x ≤≤或10x -≤<或∅故不等式()2f x ≥-的解集为{}13x x -≤≤;(2)由题意知,只需()2max 35f x a a -≥-⎡⎤⎣⎦成立, 因为()1,03231,03x x f x x x -+≤≤⎧⎪=⎨+-≤<⎪⎩, 在2,03⎡⎤-⎢⎥⎣⎦上单调递增,在[]0,3上单调递减, 所以()()max 01f x f ==,所以2520a a -+≤,解得5522a +≤≤. 【点睛】本题考查了利用零点法分类讨论求解绝对值问题,考查了不等式在闭区间上有解问题,考查了解一元二次不等式,考查了数学运算能力.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2020届吉林省长春市东北师大附中高三年级上学期第三次摸底数学(理)试题学校:___________姓名:___________班级:___________考号:___________一、单选题1.12i 12i+=- A .43i 55-- B .43i 55-+ C .34i 55-- D .34i 55-+ 2.已知集合{}2230A x N x x =∈--≤,{}1B x Z x =∈≤,则AB =( ) A .{}1,0,1- B .{}0,1C .{}11x x -≤≤D .{}13x x -≤≤ 3.角θ的终边与单位圆O交于点13P ⎫-⎪⎪⎝⎭,则cos2θ=( )A .79B .89C .79-D .89- 4.已知向量()1,3a =,()0,3a b +=,设a 与b 的夹角为θ,则θ=( ) A .6π B .3π C .23π D .56π 5.设3log 2a =,432b =,2312c -⎛⎫= ⎪⎝⎭,则,,a b c 的大小关系为( ) A .a b c >> B .b c a >> C .c a b >> D .a c b >>6.若,x y 满足01026x y y y x +≥⎧⎪+≤⎨⎪≥-⎩,则x y -的最大值为A .4B .2C .1D .0 7.函数()cos x x x f x e e-=-的图像大致是( ) A . B . C . D .8.设R θ∈,则“66ππθ-<”是“1cos θ2”的( ) A .充分而不必要条件 B .必要而不充分条件 C .充要条件D .既不充分也不必要条件9.已知正项等比数列{}n a 的前n 项和为n S ,且6322S S -=,则789a a a ++的最小值为( )A .9B .8C .6D .410.已知函数()()sin f x A x =+ωϕ0,,2A N πωϕ⎛⎫>∈< ⎪⎝⎭的部分图象如图所示,则()f x 的单调递增区间为( )A .2,,63k k k Z ππππ⎡⎤++∈⎢⎥⎣⎦ B .22,2,63k k k Z ππππ⎡⎤++∈⎢⎥⎣⎦ C .,,36k k k Z ππππ⎡⎤-+∈⎢⎥⎣⎦D .2,2,36k k k Z ππππ⎡⎤-+∈⎢⎥⎣⎦ 11.设函数()f x 的定义域为R ,满足()()12f x f x +=,且当()0,1x ∈时,()sin f x x π=.记当[)0,x ∈+∞时,函数()f x 的极大值点从小到大依次记为123,,,...,,...n a a a a 并记相应的极大值为123,,,...,,...n b b b b ,则()101k k k a b =+=∑( )A .561B .611C .1073D .209712.已知O 为锐角ABC ∆的外心,且三边,,a b c 与面积S 满足2224b c a S +-=,若AO AB AC λμ=+(其中,λμ是实数),则λμ的最大值是( )A.22- B.22+C.32+ D.32-二、填空题13.曲线cos y x x =+在点(0,1)处的切线方程为__________.14.如图,正六边形ABCDEF 的边长为1,记AB a =,从点A 、B 、C 、D 、E 、F 这六点中任取两点为向量b 的起点和终点,则a b ⋅的最大值为______.15.公元前6世纪,古希腊的毕达哥拉斯学派研究过正五边形和正十边形的作图方法,发现了黄金分割,其比值为方程210x x +-=的正根10.6182≈,这一数值也可以表示为2sin18,则sin54sin18-=______. 16.已知函数()2,0,1,0,x e x x f x ax x ⎧->=⎨-<⎩若存在实数0x ,使得()()00f x f x -=-成立,则实数a 的取值范围是______.三、解答题17.已知数列{}n a 的前n 项和为n S ,且满足12a =,12n n S a +=-.(Ⅰ)求数列{}n a 的通项公式;(Ⅱ)数列{}n b 满足22log 1n n b a =+,记数列{}n b 的前n 项和为n T ,求证111334n k k T =≤<∑. 18.如图,在ABC ∆中,内角,,A B C 的对边分别为,,a b c ,已知()cos 2cos c B a b C =-,点D 在边BC 上.(Ⅰ)求角C ;(Ⅱ)若5b =,11cos 14B =,且ABD ∆的面积与ADC ∆的面积之比为3:1,求AD . 19.如图,三棱柱111ABC A B C -的侧面11AC CA 是正方形,平面11AC CA ⊥平面11BCC B ,11BC C C ⊥,11BC C C =,点E 在AC 上,3AC EC =,F 是11A B 的中点.(Ⅰ)求证:1//AC 平面1FBC ; (Ⅱ)判断平面1FBC 与平面1ABC 是否垂直,直接写出结论,不必说明理由; (Ⅲ)求二面角1C BF E --的余弦值.20.已知ABC ∆的两个顶点,A B 的坐标分别为()2,0-,()2,0,且,CA CB 所在直线的斜率之积等于34-,记顶点C 的轨迹为Γ. (Ⅰ)求顶点C 的轨迹Γ的方程;(Ⅱ)若直线:l y kx m =+与曲线Γ交于,M N 两点,点P 在曲线Γ上,且O 为PMN ∆的重心(O 为坐标原点),求证:PMN ∆的面积为定值,并求出该定值. 21.已知函数()()21ln 12f x ax a x x =-+-,()1xg x e x =--. (Ⅰ)若0x =为函数()f x 的极小值点,求a 的取值范围,并求()f x 的单调区间; (Ⅱ)若0x ∀≥,()()212g x f x x ≥+,求a 的取值范围. 22.在直角坐标系xOy 中,以坐标原点为极点,x 轴正半轴为极轴建立极坐标系,已知直线l 的极坐标方程为sin 23πρθ⎛⎫-= ⎪⎝⎭,曲线C 的参数方程为cos ,2sin x m y αα=⎧⎨=⎩(α为参数,0m >). (Ⅰ)当2m =时,判断直线l 与曲线C 的位置关系;(Ⅱ)设直线l 与y 轴的交点为P ,且与曲线C 交于,M N 两点,且15PM PN ⋅=,求m 的值.23.设0a >,0b >,0c >.(Ⅰ)若1a b c ++=,求111a b c++的最小值;(Ⅱ)若1abc =111a b c≤++.参考答案1.D【解析】分析:根据复数除法法则化简复数,即得结果. 详解:212(12)341255i i i i ++-+==∴-选D. 点睛:本题考查复数除法法则,考查学生基本运算能力.2.B【分析】求出集合,A B ,利用集合的交运算即可求解.【详解】{}{}{}2230130,1,2,3A x N x x x N x =∈--≤=∈-≤≤=,{}{}{}1111,0,1B x Z x x Z x =∈≤=∈-≤≤=-, {}0,1A B ∴⋂=.故选:B【点睛】本题考查了集合的交运算,同时考查了一元二次不等式的解法以及绝对值不等式的解法,属于基础题.3.A【分析】利用三角函数的定义可得cos θ=cos2θ 【详解】由题意可得cos 3θ=, 所以287cos22cos 12199θθ=-=⨯-=. 故选:A【点睛】本题考查了三角函数的定义以及二倍角公式,需熟记公式,掌握三角函数的定义是关键,属于基础题.4.C【分析】根据向量的坐标运算求出向量b ,再利用向量数量积的坐标运算即可求解.【详解】设(),b x y =,由()1,3a =,()0,3a b +=,可得()(()0,31,0b =-=-,设a 与b 的夹角为θ,且[]0,θπ∈ 则21cos 21a b a b θ⋅===-+,所以θ=23π. 故选:C【点睛】本题考查了向量坐标表示、向量数量积的坐标运算,属于基础题.5.B【分析】利用指数函数、对数函数的单调性即可求解.【详解】由3log y x =单调递增,所以333log 1log 2log 3<<,即01a <<. 由2x y =为增函数,则42033222>>,所以24233312212b c -⎛⎫=>==> ⎪⎝⎭, 综上可得b c a >>.故选:B【点睛】本题考查了指数函数、对数函数的单调性比较指数式、对数式的大小,属于基础题. 6.A【解析】【分析】先作出不等式组对应的可行域,再利用线性规划求最值得解. 【详解】当x≥y时,设z=x-y,由题得1026 x yyy xx y⎧⎪+≥⎪⎪+≤⎨⎪≥-⎪≥⎪⎩,不等式组对应的可行域如图所示,当直线z=x-y经过点B(2,-2)时,直线的纵截距-z最小,z最大,此时z取最大值2-(-2)=4.当x<y时,设z=y-x,由题得1026x yyy xx y⎧⎪+≥⎪⎪+≤⎨⎪≥-⎪<⎪⎩,不等式组没有可行域,所以该情况不存在.故选:A【点睛】本题主要考查线性规划求最值,意在考查学生对这些知识的理解掌握水平和分析推理能力. 7.A【解析】因为()()f x f x -=- ,所以去掉B,D;当π(0,)2x ∈ 时,()0f x > 所以去掉C,选A. 8.A【分析】运用绝对值不等式的解法和余弦函数的图象和性质,化简两已知不等式,结合充分必要条件的定义,即可得到结论.【详解】 ∵0666663ππππππθθθ-<⇔-<-<⇔<<,1cos 22,233k k k Z ππθπθπ>⇔-+<<+∈, 则0,2,2,333k k k Z πππππ⎛⎫⎛⎫⊆-++∈ ⎪ ⎪⎝⎭⎝⎭, 可得“66ππθ-<”是“1cos 2θ>”的充分不必要条件,故选A. 【点睛】本题考查充分必要条件的判断,同时考查余弦函数的图象和性质,运用定义法和正确解不等式是解题的关键,属于基础题.9.B【分析】根据{}n a 是等比数列,由6322S S -=,即6332S S S -=+可得36396,,S S S S S --也是等比数列,结合基本不等式的性质即可求出789a a a ++的最小值.【详解】 {}n a 是等比数列,6322S S -=,即6332S S S -=+,∴36396,,S S S S S --也是等比数列,且96789S S a a a -=++,()()263396S S S S S ∴-=⋅-,可得:()2233396333324444S S S S S S S S S +++-===++48≥=,当且仅当32S =时取等号, ∴789a a a ++的最小值为8.故选:B 【点睛】本题考查了等比数列的前n 项和性质以及基本不等式求和的最小值,熟记等比数列的前n 项和性质是关键,属于基础题. 10.C 【分析】由图可知函数的周期T π=,进而根据周期公式求出ω,利用对称轴以及ϕ的范围可求出ϕ,再由正弦函数的单调递增区间整体代入即可求解. 【详解】 由图可知22362T πππ=-=,解得T π=,所以22πωπ==, 又()2262k k Z ππϕπ⨯+=+∈,解得()26k k Z πϕπ=+∈.2πϕ<,所以6π=ϕ,所以()sin 26f x A x π⎛⎫=+ ⎪⎝⎭,0A > 由()222262k x k k ππππ-≤+≤π+∈Z , 解得()36k x k k πππ-≤≤π+∈Z ,所以()f x 的单调递增区间为,,36k k k Z ππππ⎡⎤-+∈⎢⎥⎣⎦. 故选:C 【点睛】本题考查了由图像求三角函数的解析式以及整体代入法求函数的单调区间,属于基础题. 11.C 【分析】根据()()12f x f x +=以及极值点与极值的定义求出123,,,a a a 123,,,b b b 判断{}{},n n a b 分别为等差数列与等比数列,利用等差数列与等比数列的求和公式即可求解. 【详解】由()()12f x f x +=,即()()21=-f x f x ,当()0,1x ∈时,()sin f x x π=, 由题意可知112a =,11b =, 当12x <<时,则011x <-<,()()()212sin 1f x f x x π=-=- 则232a =,22b =, 当23x <<时,则021x <-<,()()()414sin 2f x f x x π=-=-, 则352a =,34b =,所以{}n a 是以12为首项,1为公差的等差数列, {}n b 是以1为首项,2为公比的等比数列,所以()()()101212101kk n k ab a a a b b b =+=+++++++∑()1011121091105010231073212a ⨯-⨯⨯=++=+=-.故选:C 【点睛】本题考查了三角函数的性质、极值点以及极值的定义、等差数列、等比数列的前n 项和公式,需熟记定义与公式,属于中档题. 12.D 【分析】利用余弦定理以及三角形的面积公式求出cos A =BC 边所在的直线为x 轴,BC 边的垂直平分线为y 轴建立直角坐标系(D 为BC 边的中点),由外接圆的性质可得BOD COD BAC ∠=∠=∠,由cos A =2R =,则2OA OB OC ===,可得,,B C O 的坐标,设(),A m n ,则ABC ∆的外接圆的方程为:(224x y +-=,利用向量的坐标运算可得())m m mn n nλμλμ⎧-=+⎪=--,从而求出,m n ,代入外接圆方程可得()221λμλμ+=+,再利用基本不等式即可求解. 【详解】由2224b c a S +-=,可知12cos 4sin 2bc A bc A =⨯, 解得tan 1A =,所以cos A =如图所示,以BC 边所在的直线为x 轴,BC 边的垂直平分线为y 轴建立直角坐标系 (D 为BC 边的中点)由外接圆的性质可得BOD COD BAC ∠=∠=∠,由cos A =2R =, 则2OA OB OC ===,cos OD COD OC ∠==OD DC ∴===,())((),,,,B O CO A m n ∴,则ABC ∆的外接圆的方程为:(224x y +-=,AO AB AC λμ=+,()()),,m n m n m n λμ∴-=-+-,())m m mn n nλμλμ⎧-=+⎪∴=-- ,1λμ+≠,否则,,C O B 三点共线,由图可知不可能的.∴可化为)1m n μλλμ⎧-=⎪+-⎪⎨⎪=⎪⎩,代入ABC ∆的外接圆的方程可得()()2222411μλλμλμ⎛-+= +-+-⎝, 化为()221λμλμ+=+, 化为()2122λμλμ+=+≥⨯12+12≤-, 又01λμ<<,所以302λμ-<≤, 所以λμ的最大值为32-. 故选:D 【点睛】本题考查了余弦定理、三角形的面积公式、向量的坐标运算以及基本不等式求最值,综合性比较强,属于难题. 13.10x y -+= 【分析】由题可判断出点在曲线上,所以通过求导求出切线的斜率,把斜率和点代入点斜式方程即可. 【详解】∵点(0,1)在曲线上,又由题意,1sin y x '=-,∴斜率k =0101x y ==-=',∴所求方程为:10y x -=-,即y =x +1.故答案为:10x y -+=. 【点睛】本题考查导数的几何意义的应用,属于基础题. 14.2 【分析】向量的数量积最大,需要两个向量的模以及两个向量的夹角的余弦函数值的乘积取得最大值即可. 【详解】由题意可知:则cos ,cos ,a b a b a b b a b ⋅==,由图可知2,cos ,1b a b b FC ≤<>≤∴=时,所以cos ,2a b b a b ⋅==, 故a b ⋅的最大值为2. 故答案为:2 【点睛】本题考查了向量数量积的定义,掌握向量数量积的定义是关键,属于基础题. 15.12【分析】利用诱导公式以及二倍角的余弦公式即可求解. 【详解】2sin54sin18cos36sin1812sin 18sin18-=-=--()()1112sin181sin18111242⎛⎫⎛⎫-=--+=---= ⎪⎪ ⎪⎪⎝⎭⎝⎭.故答案为:12【点睛】本题考查了诱导公式以及二倍角的余弦公式,需熟记公式,属于基础题. 16.[)2,e -+∞ 【分析】由已知条件令00x >可得02001x ax e x +=-,分离参数可得00001x e a x x x =--,令 ()000001x e g x x x x =--,求出()0g x 的值域即可求解.【详解】()2,0,1,0,x e x x f x ax x ⎧->=⎨-<⎩,且()()00f x f x -=-令00x >,∴()02001xax e x --=--,即02001x ax e x +=-,从而可得00001x e a x x x =--, 令()000001x e g x x x x =--, 则()()()0000002220001111x x x x e x e x e g x x x x ---⋅-'=-+=, 令()0001xh x e x =--,则()001xh x e '=-,因为00x >,所以()0010xh x e '=->,即()0h x 在()0,∞+上为增函数,所以()()00h x h >,即()00010xh x e x =-->,所以()()()00002011xx e x g x x ---'=,当01x>时,()00g x '>,当001x <<时,()00g x '<,所以()0g x 在()0,1上单调递减,在[)1,+∞上单调递增,所以()()012g x g e ≥=-, 所以2a e ≥-,实数a 的取值范围是[)2,e -+∞. 故答案为:[)2,e -+∞ 【点睛】本题考查了导数在求函数最值中的应用,考查了分离参数法求参数的取值范围,属于难题.17.(Ⅰ)2nn a =(Ⅱ)证明见解析【分析】(Ⅰ)根据n S 与n a 的关系,可得12n n a a +=,从而判断{}n a 为等比数列,利用等比数列的通项公式即可求解.(Ⅱ)由(Ⅰ)得,22log 121n n b a n =+=+,利用等差数列的求和公式可得()2n T n n =+,再利用裂项求和法可求出11nk kT =∑,令()31114212f n n n ⎛⎫=-+ ⎪++⎝⎭,易知()f n 单调递增,借助函数的单调性即可求解. 【详解】(Ⅰ)因为12n n S a +=-,① 当2n ≥时,12n n S a -=-,②由①-②得1n n n a a a +=-,即12n n a a +=, 当1n =时,2124a a =+=,21422a a ==, 所以数列{}n a 为等比数列,其首项为12a =,公比为2,所以112n nn a a q -==;(Ⅱ)由(Ⅰ)得,22log 121n n b a n =+=+,所以()2n T n n =+,所以()11111222k T k k k k ⎛⎫==- ⎪++⎝⎭, 所以11111111111...2324112nk k T n n n n =⎡⎤⎛⎫⎛⎫⎛⎫⎛⎫=-+-++-+- ⎪ ⎪ ⎪ ⎪⎢⎥-++⎝⎭⎝⎭⎝⎭⎝⎭⎣⎦∑31114212n n ⎛⎫=-+ ⎪++⎝⎭令()31114212f n n n ⎛⎫=-+ ⎪++⎝⎭,易知()f n 单调递增, 所以()()314f f n ≤<,即()1334f n ≤<, 所以111334n k k T =≤<∑. 【点睛】本题考查了n S 与n a 的关系、等比数列的通项公式、等差数列的前n 项和公式、裂项求和法以及函数的单调性求值域,综合性比较强,属于中档题. 18.(Ⅰ)3C π=(Ⅱ)AD =【分析】(Ⅰ)利用正弦定理边化角可得2sin cos sin cos sin cos A C C B B C =+,再利用两角和的正弦公式的逆应用即可求解.(Ⅱ)在ABC ∆中,0B π<<,11cos 14B =,从而可得sin B =进而求出sin BAC ∠,在ABC ∆中,由正弦定理可得BC ,根据ABD ∆的面积与ADC ∆的面积之比为3:1,可得2DC =,在ADC ∆中,利用余弦定理即可求解.【详解】(Ⅰ)由题意,∵()2cos cos a b C c B -=,由正弦定理可得()2sin sin cos sin cos A B C C B -=, 即2sin cos sin cos sin cos A C C B B C =+, ∴()()2sin cos sin sin sin A C B C A A π=+=-=, 在ABC ∆中,0A π<<,∴sin 0A ≠. ∴cos 12C =,又在ABC ∆中,0C π<<, ∴3C π=.(Ⅱ)在ABC ∆中,0B π<<,11cos 14B =,∴sin B ==由(Ⅰ)可知3C π=,∴()111sin sin sin cos cos sin 214BAC B C B C B C ∠=+=+=+=, 在ABC ∆中,由正弦定理可得5sin 8sin b BACBC B∠===,∵ABD ∆的面积与ADC ∆的面积之比为3:1, ∴3BD DC =,∴2DC =. 在ADC ∆中,由余弦定理可得2222212cos 52252192AD AC DC AC DC C =+-⋅⋅=+-⨯⨯⨯=,∴AD =【点睛】本题考查了正弦定理、余弦定理解三角形,需熟记定理,属于中档题.19.(Ⅰ)证明见解析(Ⅱ)平面1FBC ⊥平面1ABC ( 【分析】(Ⅰ)连结1B C 交1BC 于D ,因为F 为中点,所以1//FD A C ,利用线面平行的判定定理即可证出(Ⅱ)首先利用面面垂直的判定定理即可得出结论.(Ⅲ)建立空间直角建立坐标系,分别求出平面1FB C 的一个法向量、平面EBF 的一个法向量,利用空间向量的数量积即可求解. 【详解】(Ⅰ)如图所示,连结1B C 交1BC 于D ,因为F 为中点,所以1//FD A C ,又因为FD ⊂平面1FBC , 1AC ⊄平面1FBC , 所以1//A C 平面1FBC .(Ⅱ)平面1FBC ⊥平面1ABC .(Ⅲ)如图建立坐标系,设1CC a =,()1,0,0C B a =,1,,222a a a C F ⎛⎫=-⎪⎝⎭, 设平面1FB C 的一个法向量为(),,n x y z =,则1100n C B n C F ⎧⋅=⎪⎨⋅=⎪⎩,00222ax a a ax y z =⎧⎪⎨++=⎪⎩, 令1y =,则()0,1,1n =,同理可得平面EBF 的一个法向量为()2,1,3k =,所以()2cos ,7n k n k n k⋅===+, 因为二面角为锐二面角,所以求二面角1C BF E --.【点睛】本题考查了线面平行的判定定理、面面垂直的判定定理以及空间向量法求二面角,考查了推理能力以及空间想象能力,属于中档题.20.(Ⅰ)()221243x y x +=≠±(Ⅱ)证明见解析,定值为92.【分析】(Ⅰ)设(),C x y ,根据题意列方程即可求解.(Ⅱ)设()11,M x y ,()22,N x y ,()33,P x y ,由O 为PMN ∆的重心,可得0OP MO NO ++=,从而1230x x x ++=,1230y y y ++=,将直线与椭圆方程联立整理利用韦达定理求出点P 坐标,代入椭圆方程可得22443m k =+,再利用弦长公式以及三角形的面积公式即可求解.【详解】(Ⅰ)设(),C x y ,因为点A 的坐标为()2,0-,所以直线AC 的斜率为()22AC y k x x =≠-+ 同理,直线BC 的斜率为()22BC y k x x =≠- 由题设条件可得,()32224y y x x x ⋅=-≠±+-. 化简整理得,顶点C 的轨迹Γ的方程为:()221243x y x +=≠±. (Ⅱ)设()11,M x y ,()22,N x y ,()33,P x y ,因为O 为PMN ∆的重心,所以0OP MO NO ++=,所以1230x x x ++=,1230y y y ++=, 由22143y kx m x y =+⎧⎪⎨+=⎪⎩得()2224384120k x kmx m +++-=,()()()2222264443412484320k m k m k m ∆=-+-=+->122843km x x k -+=+,()121226243m y y k x x m k +=++=+, 32843km x k =+,32643m y k =-+,∴2286,4343km m P k k ⎛⎫- ⎪++⎝⎭, 又点P 在椭圆上,所以()()2222222161214343k m m k k +=++,∴22443m k =+,因为O 为PMN ∆的重心,所以PMN ∆是OMN ∆的3倍,21MN x=-=,原点O到直线MN的距离为d=12OMNS MN d∆=⋅=32==.所以932PMN OMNS S∆∆==,所以,PMN∆的面积为定值,该定值为92.【点睛】本题考查了直接法求曲线的轨迹方程、直线与椭圆的位置关系,考查了学生的计算能力,属于中档题.21.(Ⅰ)1a>,()f x的递减区间()1,0-和()1,a-+∞,递增区间为()0,1a-,(Ⅱ)1a≤【分析】(Ⅰ)首先求出函数()f x导数,分类讨论10a-≤或10a->,判断()f x'的正负即可求解.(Ⅱ)令()()()()()()21ln11102xF x g x f x x e a x a x x=--=++-+-≥,且()00F=,求出()()()1111xF x e x axx⎡⎤'=-+-⎣⎦+,令()()()()110xg x e x ax x=-+-≥,且()00g=,求出()g x'在[)0,+∞上单调递增,进而分类讨论10a-≥或10a-<,求出()g x的单调区间,即可求出()F x的单调区间,判断()F x的正负即可求解.【详解】(Ⅰ)由题意知:()1,x∈-+∞,且()()11x x aaf x a xa x x---⎡⎤⎣⎦'=--=-+,若10a-≤,即1a≤时,当0x>,()0f x'<,所以0x=不可能为()f x的极小值点;若10a ->,即1a >时,令()001f x x a '>⇒<<-;令()010f x x '<⇒-<<或1x a <-,所以()f x 的递减区间()1,0-和()1,a -+∞,递增区间为()0,1a -,所以0x =为函数()f x 的极小值点,综上:1a >,()f x 的递减区间()1,0-和()1,a -+∞,递增区间为()0,1a -.(Ⅱ)令()()()()()()21ln 11102x F x g x f x x e a x a x x =--=++-+-≥, 则()00F =, ()()()11111111x x x a x F x e a e a e x ax x x x ⎡⎤'=+--=--=-+-⎣⎦+++, 令()()()()110x g x e x ax x =-+-≥,则()00g =, 因为()()()21xg x x e a '=+-+,令()()()0h x g x x '=≥, 则()()30xh x x e '=+>,()0x ≥, 所以()g x '在[)0,+∞上单调递增,所以()()01g x g a ''≥=-,(1)当10a -≥,即1a ≤时,()0g x '≥,0x ≥,所以()g x 在[)0,+∞上单调递增,所以()0g x ≥对0x ≥恒成立.所以()()101F x g x x '=≥+恒成立,所以()F x 在[)0,+∞上单调递增,所以()()00F x F ≥=,0x ≥,符合题意;(2)当10a -<,即1a >时,因为()010g a '=-<,又10a ->且()()()()1111110a g a a e a a a -'-=+-+>+-+=,又()g x '在[)0,+∞上连续且单调递增,所以存在00x >,使得()00g x '=,此时,当()00,x x ∈时,()0g x '<,所以()g x 单调递减,所以()()00g x g <=,所以()()101F x g x x '=<+,所以()F x 在()00,x x ∈单调递减, 所以()()00F x F <=,()00,x x ∈,矛盾,舍去.综上:1a ≤.【点睛】本题考查了导数在研究函数单调性以及导数在研究不等式恒成立中的应用,考查了转化与化归的思想、分析问题与解决问题的能力,属于难题.22.(Ⅰ)直线l 与曲线C 相切(Ⅱ)【分析】(Ⅰ)将极坐标方程以及参数方程化为普通方程,再利用点到直线的距离公式即可判断.(Ⅱ)由(Ⅰ)知,P 点坐标为()0,4,且直线的斜率为k =l 的倾斜角为3π,将直线l 的参数方程与曲线C 的普通方程联立,利用参数t 的几何意义即可求解.【详解】(Ⅰ)当2m =时,曲线C 的参数方程为2cos 2sin x a y a=⎧⎨=⎩, ∴曲线C 的普通方程为224x y +=,表示以原点O 为圆心,2为半径的圆, ∵sin 23πρθ⎛⎫-= ⎪⎝⎭,∴1sin cos 22ρθρθ=,∴直线l 的直角坐标方程为122y x =,40y -+=,∵O 到直线l 的距离为2d ==,∴直线l 与曲线C 相切;(Ⅱ)由(Ⅰ)知,P 点坐标为()0,4,且直线的斜率为k =∴直线l 的倾斜角为3π,∴直线l的参数方程为1242x t y t ⎧=⎪⎪⎨⎪=+⎪⎩(t 为参数), 曲线C 的普通方程为222244x m y m +=,将直线l 的参数方程代入曲线C 的普通方程,整理,得()222243480m t t m +++=,∵直线l 与曲线C 交于,M N 两点,设,M N 两点对应的参数分别为1t ,2t ,∴()()()2222224484319240m m m m ∆=-⨯⨯+=->, 且21224843m t t m =+, ∵121215PM PN t t t t ⋅===, ∴22481543m m =+,解得m >0∆),∴m的值为【点睛】本题考查了参数方程、极坐标方程与普通方程的互化,考查了参数方程中参数的几何意义,属于基础题.23.(Ⅰ)9(Ⅱ)证明见解析【分析】(Ⅰ)将1用a b c ++替换,利用基本不等式即可求解.(Ⅱ)根据1111111111122a b c a b c a b c ⎛⎛⎫++=+++++≥ ⎪ ⎝⎭⎝,由1abc =代入即可证出.【详解】(Ⅰ)因为111a b c a b c a b c a b c a b c++++++++=++111b c a c a b a a b b c c =++++++++339b c a c a b a a b b c c =++++++≥≥, (当a b c ==时,等号成立) 所以111a b c++的最小值为9;(Ⅱ)证明:因为1111111111122a b c a b c a b c ⎛⎛⎫++=+++++≥ ⎪ ⎝⎭⎝, 又因为1abc =,所以1c ab =,1b ac =,1a bc =,∴()111a b c ++≥, 当a b c ==时等号成立,即原不等式成立.【点睛】本题考查了基本不等式证明不等式,注意验证等号成立的条件,属于基础题.。
