最大值、最小值问题
最大值最小值问题

作业布置
课本P69第2题,P71第2题 第 题 课本 第 题
3.给定函数 = f ( x) x∈[a, b]如何求取最值? y 如何求取最值? ,
y
y = f ( x)
a
x1
o
X2
X3
b
x
4.函数 = f ( x)的最值与极值的联系 y 与区别? 与区别?
值可能有多个,而最大( (1). 函数的极大(小)值可能有多个,而最大(小)值只 ) 函数的极大( 有唯一的一个 (2)极大值不一定比极小值大,但是最大值一定比最小值大 )极大值不一定比极小值大, (3)极值只能在区间的内部取得,不能在端点处取得,而函 )极值只能在区间的内部取得,不能在端点处取得, 数的最值可以在端点处取得 (4)函数的最值在函数在整个定义域内的整体性质,极 )函数的最值在函数在整个定义域内的整体性质, 值只是函数在某一点附近的局部性质
最大值与最小值问题(一 最大值与最小值问题 一)
导数与函数的最值问题
情境引入
如图,在边长为60cm的正方形铁片的四角上切去 如图,在边长为 的正方形铁片的四角上切去 相等的正方形,再把它的边沿虚线折起, 相等的正方形,再把它的边沿虚线折起,做成一个无 盖的方底箱子,要求箱子的高度不小于5cm且不大于 不小于5cm 盖的方底箱子,要求箱子的高度不小于5cm且不大于 问当箱子的高度为多少时,容积最大? 20cm,问当箱子的高度为多少时,容积最大?最大容 积是多少? 积是多少?
3
y
6
x ∈ [−2,0] −
5
4
y = f ( x)
x ∈ [0,2]
2
x ∈ [−2,2] −
-2 -1
1 0 1 2
x
§2 2.2 最大值、最小值问题

一、预习教材·问题导入 1.问题:如何确定你班哪位同学最高? 提示:方法很多,可首先确定每个学习小组中最高的同学, 再比较每组的最高的同学,便可确定班中最高的同学.
2.如图为 y=f(x),x∈[a,b]的图像.
问题 1:试说明 y=f(x)的极值. 提示:f(x1),f(x3)为函数的极大值,f(x2),f(x4)为函数的极 小值. 问题 2:你能说出 y=f(x),x∈[a,b]的最值吗? 提示:函数的最小值是 f(a),f(x2),f(x4)中最小的,函数的 最大值是 f(b),f(x1),f(x3)中最大的. 问题 3:根据问题 2 回答函数 y=f(x),x∈[a,b]的最值可能 在哪些点取得. 提示:在极值点或端点中.
令 f′(x)=0,解得 x=59或 x=3(舍去). 当 0<x<59时,f′(x)>0,当59<x<1 时,f′(x)<0, 所以 x=59时,f(x)有最大值 f59=20 000. 所以当 x=59时,本年度的年利润最大,最大年利润为 20 000 万元.
[类题通法] 利用导数解决优化问题的一般步骤 (1)抽象出实际问题的数学模型,列出函数关系式 y=f(x). (2)求函数 f(x)的导数 f′(x),并解方程 f′(x)=0,即求函数 可能的极值点. (3)比较函数 f(x)在区间端点的函数值和可能极值点的函数 值的大小,得出函数 f(x)的最大值或最小值. (4)根据实际问题的意义给出答案.
二、归纳总结·核心必记 1.最值点 (1)最大值点:函数 y=f(x)在区间[a,b]上的最大值点 x0 指 的是:函数在这个区间上所有点的函数值都 不超过 f(x0). (2)最小值点:函数 y=f(x)在区间[a,b]上的最小值点 x0 指 的是:函数在这个区间上所有点的函数值都 不小于 f(x0). 2.最值 函数的 最大值 与 最小值 统称为最值.
高等数学3.6 最大值、最小值问题

最大值和最小值的求法:
设f(x)在(a,b)内的驻点和不可导点(它们是可能的极值)为
x1,x2, ···,xn,则比较 f(a),f(x 1), f(x 2), ···,f(x n),f(b) 的大小,其中最大的便是函数f(x)在[a,b]上的最大值,最小的 便是函数f(x)在[a,b]上的最小值. 求最大值和最小值的步骤: (1)求出f(x)在(a,b)内的所有驻点和不可导点;
1 1 W b(d 2b 2) 在(0,d)内只有一个驻点, 所以当b d 时, (0<b<d). 6 3
W的值最大.这时, h
2 d . 于是有 d :h :b 3 : 2 :1. 3
(2)求出函数在上述点处和区间端点处的函数值;
(3)比较上述函数值,找出最大的和最小的.
例1 求函数y2x33x212x14在[3, 4]上的最大值与最小值. 解 f(x) 2x 33x 212x 14,
f (x)6x 26x126(x2)(x1),
解方程f (x)0,得一 x12,x21,由于 f(3) 2(3)33(3) 212(3) 1423; f(2) 2(2)33(2) 212(2) 1434; f(1)2312147; f(4)2· 33· 2 12· 4 4 414142, 比较可得f(x)在 x4取得它在[3,4]上的最大值f(4)142 ,在
D
100km
B
C
解 设ADx (km),则 DB100x ,
CD 20 2 x 2 400 x 2 .
设从B点到C点需要的总运费为y,那么
y5k· CD3k· (k是某个正数), DB
y5k 400 x 2 3k(100x) (0x100). 5x 3 , 先求y对x的导数: y k 400 x 2 解方程y0,得x15(km).
最大值最小值问题
bx o a
bx o a
bx
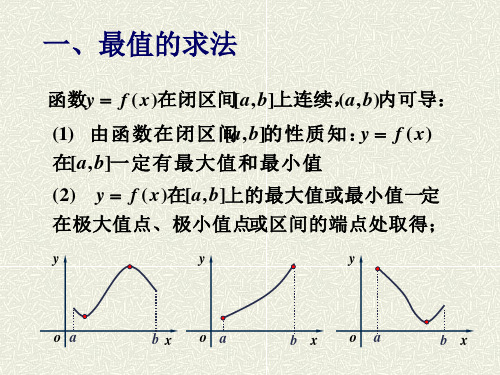
(3) y f ( x)的最大值、最小值一定在 f ' ( x) 0或f ' ( x)不存在的点及区间的端 点取得;
(4) 极大值、极小值是局部的概念,而 最大值、最小值是全局的概念。
步骤:
1.求驻点和不可导点;
2.求区间端点及驻点和不可导点的函数值,比 较大小,那个大那个就是最大值,那个小那个就 是最小值;
0.5公里
s(t ) A
B 4公里
解 (1)建立敌我相距函数关系
设 t 为我军从B处发起 追击至射击的时间(分).
0.5公里
s(t ) A
敌我相距函数 s(t)
B
s(t) (0.5 t)2 (4 2t)2
4公里
(2) 求s s(t)的最小值点.
s(t)
5t 7.5 .
(0.5 t)2 (4 2t)2
令s(t) 0,
得唯一驻点 t 1.5. 故得我军从B处发起追击后 1.5 分钟射击最好.
实际问题求最值应注意:
(1)建立目标函数; (2)求最值;
若目标函数只有唯一驻点,则该点的 函数值即为所求的最大(或最小)值.
例3 某房地产公司有50套公寓要出租,当租金定 为每月180元时,公寓会全部租出去.当租 金每月增加10元时,就有一套公寓租不出去, 而租出去的房子每月需花费20元的整修维护 费.试问房租定为多少可获得最大收入?
f (2) 34;
f (1) 7;
f (4) 142;
y 2x3 3x2 12x 14
比较得 最大值 f (4) 142,最小值 f (1) 7.
例2 敌人乘汽车从河的北岸A处以1千米/分钟 的速度向正北逃窜,同时我军摩托车从河的 南岸B处向正东追击,速度为2千米/分钟.问 我军摩托车何时射击最好(相距最近射击最 好)?
第四章 §2 2.2 最大值、最小值问题

面积、体积(容积)的最值问题
[例 3] 某地政府为科技兴市,欲将如图所示的 一块不规则的非农业用地规划建成一个矩形的高科 技工业园.已知 AB⊥BC,OA∥BC,且|AB|=|BC| =4 km,|AO|=2 km,曲线段 OC 是以点 O 为顶点 且开口向上的抛物线的一段.如果要使矩形的两边分别落在 AB,BC 上,且一个顶点落在曲线段 OC 上,应如何规划才能使矩形工业园 的用地面积最大?并求出最大的用地面积(精确到 0.1 km2).
(2)当 x∈[-1,2]时,f(x)<m 恒成立,只需使 f(x)在[-1,2]上的 最大值小于 m 即可.
由(1)知 f(x)极大值=f(-23)=5+2227, f(x)极小值=f(1)=72. 又 f(-1)=121,f(2)7. 所以 m>7,即 m 的取值范围为(7,+∞).
求函数的最值 [例 1] 求下列函数的最值. (1)f(x)=4x3+3x2-36x+5,x∈[-2,+∞); (2)f(x)=12x+sin x,x∈[0,2π] [思路点拨] 先求函数在给定区间的极值,然后再与端点 值比较,即可确定函数的最值.
[精解详析] (1)f′(x)=12x2+6x-36,
元,则总造价的最小值为
()
A.400 元
B.1 200 元
C.1 600 元
D.2 800 元
解析:设总造价为 y 元,池底的一边长 x 米,池底的面积为 8÷2 =4(平方米),池底的另一边长为4x米,池壁的面积为 4x+4x平 方米,故有 y=4×300+4x+4x×100=400x+4x+1 200(x> 0).y′=4001-x42, 令 y′=0 得 x=2,由 y′ >0 得 x >2,由 y′<0 得 0<x<2, 即 y 在(0,2)上是减少的,在(2,+∞)上是增加的,所以当 x=2 时,y 取得最小值,且 ymin=2 800. 答案:D
第2章 2.4 最大值与最小值问题,优化的数学模型

第2章 2.4 最大值与最小值问题,优化的数学模型2.4 最大值与最小值问题,优化的数学模型1.理解最值概念,并能应用柯西不等式、平均值不等式求函数的最值.2.能利用不等式解决有关的实际问题.[基础·初探]教材整理 最值问题,优化的数学模型 1.最值设D 为f (x )的定义域,如果存在x 0∈D ,使得f (x )≤f (x 0)(f (x )≥f (x 0)),x ∈D ,则称f (x 0)为f (x )在D 上的最大(小)值,x 0称为f (x )在D 上的最大(小)值点.寻求函数的最大(小)值及最大(小)值问题统称为最值问题,它属于更一般的问题——极值问题的一个特别的情况.2.分离常数法分离常数法就是在分子中凑出与分母相同的项,然后约分.这在求含有分式的最值问题时经常用到.这种类型的最值问题也可以用去分母的方法转化成关于x 的二次方程,然后利用判别式求最值.用平均值不等式来解此类问题时,特别要注意等号成立的条件.1.已知0<x <1,则x (1-x )取最大值时x 的值为( ) A.13 B.12 C.14 D.23 【解析】 ∵0<x <1, ∴x (1-x )≤⎣⎢⎡⎦⎥⎤x +(1-x )22=14, 当且仅当x =12时取等号.【答案】 B2.已知t >0,则函数y =t 2-4t +1t 的最小值为________. 【解析】 ∵t >0,∴y =t 2-4t +1t =t +1t -4≥2-4=-2.[再练一题]2.设x ,y ,z ∈R ,且(x -1)216+(y +2)25+(z -3)24=1.求x +y +z 的最大值和最小值.【解】 根据柯西不等式,知[42+(5)2+22]·⎣⎢⎡⎦⎥⎤⎝⎛⎭⎪⎫x -142+⎝ ⎛⎭⎪⎫y +252+⎝ ⎛⎭⎪⎫z -322≥⎣⎢⎡⎦⎥⎤4·x -14+5·y +25+2·z -322,当且仅当x -116=y +25=z -34,即x =215,y =-1,z =195或x =-115,y =-3,z =115时等号成立.∴25×1≥(x +y +z -2)2. ∴|x +y +z -2|≤5, ∴-3≤x +y +z ≤7,即x +y +z 的最大值为7,最小值为-3.利用二次函数求最值某地区地理环境偏僻,严重制约着经济发展,某种土特产品只能在本地销售,该地区政府每投资x 万元,所获利润为P =-1160(x -40)2+10万元,为顺应开发大西北的宏伟决策,该地区政府在制订经济发展十年规划时,拟开发此种土特产品,而开发前后用于该项目投资的专项财政拨款每年都是60万元,若开发该产品,必须在前5年中,每年从60万元专款中拿出30万元投资修建一条公路,且5年可以修通,公路修通后该土特产品在异地销售,每投资x 万元,可获利润Q =-159160(60-x )2+1192(60-x )万元.问:从10年的总利润来看,该项目有无开发价值?【精彩点拨】 分别求出开发前、后该项目10年利润的最大值,比较大小即可.【自主解答】 若按原来投资环境不变,由题设知,每年只需从60万元中拿出40万元投资,可获最大利润10万元.这样10年总利润最大值为W =10×10=100(万元).若对该产品开发,则前5年中,当x =30时,P max =758,前5年总利润为W 1=758×5=3758(万元);设后5年中,x 万元用于本地销售投资,60-x 万元用于异地销售投资,则总利润W 2=⎣⎢⎡⎦⎥⎤-1160(x -40)2+10×5+⎝ ⎛⎭⎪⎫-159160x 2+1192x ×5=-5(x -30)2+4 500, 当x =30时,(W 2)max =4 500. ∴10年总利润最大值为3758+4 500(万元). 因3758+4 500>100,故该项目具有极大的开发价值.1.本题实际上是两个二次函数的叠加问题,叠加后的二次函数最值要比叠加前的二次函数最值大,从而得解.本题的现实意义也很大.2.解不等式应用题的步骤(1)认真审题,抓住问题中的关键词,找准不等关系; (2)引入数学符号,用不等式表示不等关系,使其数学化; (3)求解不等式; (4)还原实际问题. [再练一题]2.某农贸公司按每担200元收购某农产品,并按每100元纳税10元(又称征税率为10个百分点),计划可收购a 万担,政府为了鼓励收购公司多收购这种农产品,决定将征税率降低x (x ≠0)个百分点,预测收购量可增加2x 个百分点.(1)写出税收y (万元)与x 的函数关系式;(2)要使此项税收在税率调节后,不少于原计划税收的83.2%,试确定x 的取值范围.【解】(1)降低税率后的税率为(10-x)%,农产品的收购量为a(1+2x%)万担,收购总金额为200a(1+2x%)万元.依题意:y=200a(1+2x%)(10-x)%=150a(100+2x)(10-x)(0<x<10).(2)原计划税收为200a·10%=20a(万元).依题意得:150a(100+2x)(10-x)≥20a×83.2%,化简得,x2+40x-84≤0,∴-42≤x≤2.又∵0<x<10,∴0<x≤2,∴x的取值范围是0<x≤2.[探究共研型]利用不等式解决实际问题探究利用不等式解决实际问题的步骤是什么?【提示】利用不等式解决实际应用问题,一般可分四个步骤:(1)阅读理解材料,弄清问题背景.(2)建立合理的数学模型,将实际问题转化为数学问题.(3)运用不等式的知识、手段讨论不等式关系.(4)做出结论.然后利用柯西不等式、均值不等式或二次函数等方法来求最值.如图2-4-1所示,把一块边长是a的正方形铁片的各角切去大小相同的小正方形,再把它的边沿着虚线翻折成一个无盖方底的盒子,问切去的正方形边长是多少时,才能使盒子的容积最大?图2-4-1【精彩点拨】 设切去的小正方形的边长为x ,由题意可知,折成的盒子的底面边长为a -2x ,高为x ,这时盒子的容积为V =(a -2x )2x ,再利用三个正数的算术-几何平均值不等式,变形为xyz ≤⎝⎛⎭⎪⎫x +y +z 33求解即可. 【自主解答】 设切去的小正方形的边长为x ⎝ ⎛⎭⎪⎫x <a 2,无盖方底盒子的容积为V ,则V =(a -2x )2x =14(a -2x )·(a -2x )×4x ≤14⎣⎢⎡⎦⎥⎤(a -2x )+(a -2x )+4x 33=2a 327. 当且仅当a -2x =a -2x =4x ,即当x =a6时,不等式取等号,此时V 取最大值2a 327,即当切去的小正方形边长是原来正方形边长的16时,折成的盒子容积最大. 在解决实际问题时,阅读理解题意,建立数学模型是关键,在求解数学模型时,平均值不等式是常用的手段之一.[再练一题]3.用一块钢锭浇铸一个厚度均匀且全面积为2平方米的正四棱锥形有盖容器(如图2-4-2),设容器的高为h 米,盖子边长为a 米.图2-4-2(1)求a 关于h 的函数解析式;(2)设容器的容积为V 立方米,则当h 为何值时,V 最大?求出V 的最大值. (求解本题时,不计容器的厚度) 【解】 (1)设h ′为正四棱锥的斜高, 由已知⎩⎪⎨⎪⎧a 2+4·12h ′a =2,h 2+14a 2=h ′2,解得a =1h 2+1(h >0).(2)由V =13ha 2=h 3(h 2+1)(h >0),易得V =13⎝ ⎛⎭⎪⎫h +1h .∵h +1h ≥2h ·1h =2,∴V ≤16. 等号当且仅当h =1h ,即h =1时取得.故当h =1米时,V 有最大值,V 的最大值为16立方米.[构建·体系]最值问题—⎪⎪⎪⎪⎪⎪—最大值、最小值——分离常数法——应用1.已知x >1,y >1,且lg x +lg y =4,那么lg x ·lg y 的最大值是( ) A.2 B.12 C.14D.4【解析】 ∵4=lg x +lg y ≥2lg x ·lg y , ∴lg x ·lg y ≤4. 【答案】 D2.已知a ,b 为正数,且a +b =1,则(4a +1+4b +1)2的最大值是( )【导学号:38000046】A.2 6B. 6C.6D.12【解析】 (4a +1+4b +1)2 =(1×4a +1+1×4b +1)2≤(12+12)(4a +1+4b +1)=2[4(a +b )+2]=2×(4×1+2)=12, 当且仅当4b +1=4a +1,即a =b =12时等号成立.【答案】 D3.数列{a n }的通项公式a n =nn 2+90,则数列{a n }中的最大项是( ) A.第9项 B.第8项和第9项 C.第10项D.第9项和第10项 【解析】 a n =n n 2+90=1n +90n ≤12n ×90n =1610, 当且仅当n =90n ,即n =310时等号成立. 又n 为正整数,检验可知选D. 【答案】 D4.函数y =5x -1+10-2x 的最大值为________. 【解析】 因为函数的定义域为[1,5],且y >0,则 y =5x -1+2·5-x ≤52+(2)2×(x -1)2+(5-x )2=27×4=6 3.当且仅当2·x -1=5·5-x 时,等号成立, 即x =12727时,函数取最大值6 3. 【答案】 6 35.(1)求函数y =x 2+5x 2+4的最小值;(2)求函数y =cos 2x (1+sin x )的最大值; (3)设x >1,求函数y =log 2x +log x 4的最小值. 【解】 (1)设l =x 2+4,则l ≥2,于是y =x 2+4+1x 2+4=l +1l .∵y ′=1-1l 2=l 2-1l2,∴当l ∈[2,+∞)时,y ′>0,即在[2,+∞)上函数单调递增,∴当l =2,即x =0时,y 取得最小值,最小值为y =2+12=52.(2)y =(1-sin 2x )(1+sin x ) =(1-sin x )(1+sin x )(1+sin x ) =4(1-sin x )·1+sin x 2·1+sin x2≤4⎝ ⎛⎭⎪⎫1-sin x +1+sin x 2+1+sin x 233=4×827=3227. 等号成立⇔1-sin x =1+sin x 2⇔sin x =13,方程sin x =13有解,于是函数y=cos 2x (1+sin x )有最大值3227. (3)当x >1时,log 2x >0,log x 4>0,于是 y =log 2x +log x 4=log 2x +2log 2x≥2 2.等号成立⇔log 2x =2log 2x ⇔log 2x =2(log 2x =-2舍去)⇔x =22,于是y min=2 2.我还有这些不足:(1) (2) 我的课下提升方案:(1) (2)。
最大值与最小值问题
函数的最大值与最小值我们常常遇到求最大值和最小值的问题,在许多情况下可以归结为求函数的最大值与最小值.这类问题涉及的知识面广,综合性强,解法灵活,因而对于培养学生的数学能力具有重要作用.本讲从四个方面来讨论如何求解函数的最大值与最小值问题.1.一次函数的最大值与最小值一次函数y=kx+b在其定义域(全体实数)内是没有最大值和最小值的,但是,如果对自变量x的取值范围有所限制时,一次函数就可能有最大值和最小值了.例1 设a是大于零的常数,且a≠1,求y的最大值与最小值.大值a.例2 已知x,y,z是非负实数,且满足条件 x+y+z=30,3x+y-z=50.求u=5x+4y+2z的最大值和最小值.分析题设条件给出两个方程,三个未知数x,y,z,当然,x,y,z的具体数值是不能求出的.但是,我们固定其中一个,不妨固定x,那么y,z都可以用x来表示,于是u便是x的函数了.解从已知条件可解得 y=40-2x,z=x-10.所以u=5x+4y+2z=5x+4(40-2x)+2(x-10)=-x+140.又y,z均为非负实数,所以解得10≤x≤20.由于函数u=-x+140是随着x的增加而减小的,所以当x=10时,u有最大值130;当x= 20时,u有最小值120.2.二次函数的最大值与最小值例3 已知x1,x2是方程 x2-(k-2)x+(k2+3k+5)=0解由于二次方程有实根,所以△=[-(k-2)]2-4(k2+3k+5)≥0,3k2+16k+16≤0,例4 已知函数有最大值-3,求实数a的值.解因为的范围内分三种情况讨论.-a2+4a-1=-3例5 已知边长为4的正方形截去一个角后成为五边形ABCDE(如图3-12),其中AF=2,BF=1.试在AB上求一点P,使矩形PNDM有最大面积.解设矩形PNDM的边DN=x,NP=y,于是矩形PNDM的面积 S=xy,2≤X≤4.易知CN=4-x,EM=4-y,且有二次函数S=f(x)的图像开口向下,对称轴为x=5,故当x≤5时,函数值是随x的增加而增加,所以,对满足2≤x≤4的S来说,当x=4时有最大值例6 设p>0,x=p时,二次函数f(x)有最大值5,二次函数g(x)的最小值为-2,且g(p)=25,f(x)+g(x)=x2+1 6x+13.求g(x)的解析式和p的值.解由题设知f(p)=5,g(p)=25,f(p)+g(p)=p2+16p+13,所以 p2+16p+13=30, p=1(p=-17舍去).由于f(x)在x=1时有最大值5,故设 f(x)=a(x-1)2+5,a<0,所以g(x)=x2+16x+13-f(x)=(1-a)x2+2(a+8)x+8-a.由于g(x)的最小值是-2,于是解得a=-2,从而g(x)=3x2+12x+10.3.分式函数的最大值与最小值法是去分母后,化为关于x的二次方程,然后用判别式△≥0,得出y的取值范围,进而定出y的最大值和最小值.解去分母、整理得(2y-1)x2+2(y+1)x+(y+3)=0.△≥0,即△=[2(y+1)]2-4(2y-1)(y+3)≥0,解得-4≤y≤1.时,取最小值-4,当x=-2时,y取最大值1.说明本题求最值的方法叫作判别法,这也是一种常用的方法.但在用判别法求最值时,应特别注意这个最值能否取到,即是否有与最值相应的x值.解将原函数去分母,并整理得yx2-ax+(y-b)=0.因x是实数,故△=(-a)2-4?y?(y-b)≥0,由题设知,y的最大值为4,最小值为-1,所以(y+1)(y-4)≤0,即y2-3y-4≤0.②由①,②得所以a=±4,b=3.4.其他函数的最大值与最小值处理一般函数的最大值与最小值,我们常常用不等式来估计上界或下界,进而构造例子来说明能取到这个上界或下界.解先估计y的下界.又当x=1时,y=1,所以,y的最小值为1.说明在求最小(大)值,估计了下(上)界后,一定要举例说明这个界是能取到的,才能说这就是最小(大)值,否则就不一定对了.例如,本题我们也可以这样估计:但无论x取什么值时,y取不到-3,即-3不能作为y的最小值.例10 设x,y是实数,求u=x2+xy+y2-x-2y的最小值.分析先将u看作是x的二次函数(把y看作常数),进行配方后,再把余下的关于y的代数式写成y的二次函数,再配方后,便可估计出下界来.又当x=0,y=1时,u=-1,所以,u的最小值为-1.例11 求函数的最大值,并求此时的x值,其中[a]表示不超过a的最大整数.练习1.填空:(1)函数y=x2+2x-3(0≤x≤3)的最小值是_____,最大值是_______.(3)已知函数y=x2+2ax+1(-1≤x≤2)的最大值是4,则a=_____.是_______.(5)设函数y=-x2-2kx-3k2-4k-5的最大值是M,为使M最大,k=_____.2.设f(x)=kx+1是x的函数,以m(k)表示函数f(x)=kx+1在-1≤x≤3条件下的最大值,求函数m(k)的解析式和其最小值.3.x,y,z是非负实数,且满足x+3y+2z=3,3x+3y+z=4.求u=3x-2y+4z的最大值与最小值.4.已知x2+2y2=1,求2x+5y2的最大值和最小值.交点间的距离的平方最小,求m的值.6.已知二次函数y=x2+2(a+3)x+2a+4的图像与x轴的两个交点的横坐标分别为α,β,当实数a变动时,求(α-1)2+(β-1)2的最小值.。
九年级数学最大值、最小值问题
一、最大值、最小值的求法 二、应用
一、最值的求法
若函数 f ( x ) 在 [a , b] 上连续,除个别点外处 处 可导,并且至多有有限 个导数为零的点,则 f ( x ) 在 [a , b]上的最大值与最小值存 在.
y
y
y
o a
bx
o a
b x
o
a
b x
步骤:
1.求驻点和不可导点; 2.求区间端点及驻点和不可导点的函数值,比较大 小,其中最大的就是函数在所求区间的最大值,最 小的就是函数在所求区间的最小值; 注意:如果函数在区间内只有一个极值,则这个 极值就是最大值或最小值.
R( x ) 0 x 350
(唯一驻点)
故每月每套租金为350元时收入最高. 最大收入为
350 R( 350) ( 350 20) 68 10
10890 ( 元).
例4
由直线 y 0,x 8 及抛物线 y x 2 围
成一个曲边三角形,在 曲边 y x 2 上求一点,使 曲线在该点处的切线与 直线 y 0 及 x 8 所围成 的三角形面积最大.
;/ 试管婴儿 子宫肌瘤 不孕不育 ;
星辰海之行,会很有意思!" 白重炙默默の想到,难怪海边の府域都会让年轻の子弟,去星辰海历练.在这样の地方历练,很容易锻造一批批精英子弟の.只有经历过血与火の考验,才会成长,在生死之间也是最容易突破の,宝物不少,至强者死前の洞府,也容易遇到大机缘… "好了,多谢店主为俺解惑, 麻烦你呀给俺备上三份星辰海需要の物品,俺们大概有一百多人,你呀看着办吧!" 事情了解の差不多了,白重炙也就不再墨迹了,直接对着店主说道. "三份!一百多人!" 胖子店主,一听见顿时笑脸
九年级数学最大值、最小值问题
f (1) 7; f (4) 142. 比较得 最大值 f (4) 142, 最小值 f (1) 7.
; 流量卡代理
;
够抵御的风险毕竟有限,世上无法预计的灾难却是无限的。战胜灾难靠的更多的是临门一脚,先前的惴惴不安帮不上忙。 当风暴的尾巴终于远去,我们守住零乱的家园。气还没有喘匀,新的提醒又智慧地响起来,我们又开始对未来充满恐惧的期待。 人生总是有灾难。其实大多 数人早已练就了对灾难的从容,我们只是还没有学会灾难间隙的快活。我们太多注重了自己警觉苦难,我们太忽视提醒幸福。请从此注意幸福!幸福也需要提醒吗? 提醒注意跌倒……提醒注意路滑……提醒受骗上当……提醒荣辱不惊……先哲们提醒了我们一万零一次,却不提醒我 们幸福。 也许他们认为幸福不提醒也跑不了的。也许他们以为好的东西你自会珍惜,犯不上谆谆告诫。也许他们太崇尚血与火,觉得幸福无足挂齿。他们总是站在危崖上,指点我们逃离未来的苦难。但避去苦难之后的时间是什么? 那就是幸福啊! 享受幸福是需要学习的, 当幸福即将来临的时刻需要提醒。人可以自然而然地学会感官的享乐,人却无法天生地掌握幸福的韵律。灵魂的快意同器官的舒适像一对孪生兄弟,时而相傍相依,时而南辕北辙。 幸福是一种心灵的振颤。它像会倾听音乐的耳朵一样,需要不断地训练。 简言之,幸福就是没有 痛苦的时刻。它出现的频率并不像我们想象的那样少。 人们常常只是在幸福的金马车已经驶过去很远,捡起地上的金鬃毛说,原来我见过它。 人们喜爱回味幸福的标本,却忽略幸福披着露水散发清香的时刻。那时候我们往往步履匆匆,瞻前顾后不知在忙着什么。 世上有 预报台风的,有预报蝗虫的,有预报瘟疫的,有预报地震的。没有人预报幸福。其实幸福和世界万物一样,有它的征兆。 幸福常常是朦胧的,很有节制地向我们喷洒甘霖。你不要总希冀轰轰烈烈的幸福,它多半只是悄悄地扑面而来。你也不要企图把水龙头拧得更大,使幸福很快地 流失。而需静静地以平和之心,体验幸福的真谛。 幸福绝大多数是朴素的。它不会像信号弹似的,在很高的天际闪烁红色的光芒。它披着本色外衣,亲切温暖地包裹起我们。 幸福不喜欢喧嚣浮华,常常在暗淡中降临。贫困中相濡以沫的一块糕饼,患难中心心相印的一个眼神, 父亲一次粗糙的抚摸,女友一个温馨的字条……这都是千金难买的幸福啊。像一粒粒缀在旧绸子上的红宝石,在凄凉中愈发熠熠夺目。 幸福有时会同我们开一个玩笑,乔装打扮而来。机遇、友情、成功、团圆…… 它们都酷似幸福,但它们并不等同于幸福。幸福会借了它们的衣 裙,袅袅婷婷而来,走得近了,揭去帏幔,才发觉它有钢铁般的内核。幸福有时会很短暂,不像苦难似的笼罩天空。如果把人生的苦难和幸福分置天平两端,苦难体积庞大,幸福可能只是一块小小的矿石。但指针一定要向幸福这一侧倾斜,因为它有生命的黄金。 幸福有梯形的切面, 它可以扩大也可以缩小,就看你是否珍惜。 我们要提高对于幸福的警惕,当它到来的时刻,激情地享受每一分钟。据科学家研究,有意注意的结果比无意要好得多。 当春天来临的时候,我们要对自己说,这是春天啦!心里就会泛起茸茸的绿意。 幸福的时候,我们要对自 己说,请记住这一刻!幸福就会长久地伴随我们。那我们岂不是拥有了更多的幸福! 所以,丰收的季节,先不要去想可能的灾年,我们还有漫长的冬季来得及考虑这件事。我们要和朋友们跳舞唱歌,渲染喜悦。既然种子已经回报了汗水,我们就有权沉浸幸福。不要管以后的风霜雨 雪,让我们先把麦子磨成面粉,烘一个香喷喷的面包。 所以,当我们从天涯海角相聚在一起的时候,请不要踌躇片刻后的别离。在今后漫长的岁月里,有无数孤寂的夜晚可以独自品尝愁绪。现在的每一分钟,都让它像纯净的酒精,燃烧成幸福的淡蓝色火焰,不留一丝渣滓。让我们 一起举杯,说:我们幸福。 所以,当我们守候在年迈的父母膝下时,哪怕他们鬓发苍苍,哪怕他们垂垂老矣,你都要有勇气对自己说:我很幸福。因为天地无常,总有一天你会失去他们,会无限追悔此刻的时光。 幸福并不与财富地位声望婚姻同步,这只是你心灵的感觉。 所以,当我们一无所有的时候,我们也能够说:我很幸福。因为我们还有健康的身体。当我们不再享有健康的时候,那些最勇敢的人可以依然微笑着说:我很幸福。因为我还有一颗健康的心。甚至当我们连心也不再存在的时候,那些人类最优秀的分子仍旧可以对宇宙大声说:我很幸福。 因为我曾经生活过。 常常提醒自己注意幸福,就像在寒冷的日子里经常看看太阳,心就不知不觉暖洋洋亮光光。 造心 蜜蜂会造蜂巢。蚂蚁会造蚁穴。人会造房屋,机器,造美丽的艺术品和动听的歌。但是,对于我们最重要最宝贵的东西──自己的心,谁是它的建造者? 孔 雀绚丽的羽毛,是大自然物竞天择造出。白杨笔直刺向碧宇,是密集的群体和高远的阳光造出。清香的花草和缤纷的落英,是植物吸引异性繁衍后代的本能造出。卓尔不群坚韧顽强的性格,是秉赋的优异和生活的历练造出。 我们的心,是长久地不知不觉地以自己的双手,塑造而成。 造心先得有材料。有的心是用钢铁造的,沉黑无比。有的心是用冰雪造的,高洁酷寒。有的心是用丝绸造的,柔滑飘逸。有的心是用玻璃造的,晶莹脆薄。有的心是用竹子造的,锋利多刺。有的心是用木头造的,安稳麻木。有的心是用红土造的,粗糙朴素。有的心是用黄连造的,苦楚不 堪。有的心是用垃圾造的,面目可憎。有的心是用谎言造的,百孔千疮。有的心是用尸骸造的,腐恶熏天。有的心是用眼镜蛇唾液造的,剧毒凶残。 造心要有手艺。一只灵巧的心,缝制得如同金丝荷包。一罐古朴的心,淳厚得好似百年老酒。一枚机敏的心,感应快捷电光石火。一 颗潦草的心,门可罗雀疏可走马。一滩胡乱堆就的心,乏善可陈杂乱无章。一片编织荆棘的心,暗设机关处处陷井。一道半是细腻半是马虎的心,好似白蚁蛀咬的断堤。一朵绣花枕头内里虚空的心,是假冒伪劣心界的水货。 造心需要时间。少则一分一秒,多则一世一生。片刻而成 的大智大勇之心,未必就不玲珑。久拖不绝的谨小慎微之心,未必就很精致。有的人,小小年纪,就竣工一颗完整坚实之心。有的人,须发皆白,还在心的地基挖土打桩。有的人,半途而废不了了之,把半成品的心扔在荒野。有的人,成百里半九十,丢下不曾结尾的工程。有的人,精雕 细刻一辈子,临终还在打磨心的剔透。有的人,粗制滥造一辈子,人未远行,心已灶冷坑灰。 心的边疆,可以造的很大很大。像延展性最好的金箔,铺设整个宇宙,把日月包涵。没有一片乌云,可以覆盖心灵辽阔的疆域。没有哪次地震火山,可以彻底颠覆心灵的宏伟建筑。没有任 何风暴,可以冻结心灵深处喷涌的温泉。没有某种天灾人祸,可以在秋天,让心的田野颗粒无收。 心的规模,也可能缩得很小很小,只能容纳一个家,一个人,一粒芝麻,一滴病毒。一丝雨,就把它淹没了。一缕风,就把它粉碎了。一句流言,就让它痛不欲生。一个阴谋,就置它 万劫不复。 心可以很硬,超过人世间已知的任何一款金属。心可以很软,如泣如诉如绢如帛。心可以很韧,千百次的折损委屈,依旧平整如初。心可以很脆,一个不小心,顿时香消玉碎。 造心的时候,可以有很多讲究和设计。 比如预埋下一处心灵的生长点,像一株植物, 具有自动修复,自我养护的神奇功能。心受了创伤,它会挺身而出,引导心的休养生息,在最短的时间内,使心整旧如新。 比如高高竖起心灵的避雷针,以便在危急时刻,将毁灭性的灾难导入地下,耐心等待雨过天晴。 比如添加防震防爆的性能,在心灵遭受短时间高强度的残 酷打击下,举重若轻,镇定地维持蓬勃稳定。 比如…… 优等的心,不必华丽,但必须坚固。因为人生有太多的压榨和当头一击,会与独行的心灵,在暗夜狭路相逢。如果没有精心的特别设计,简陋的心,很易横遭伤害一蹶不振,也许从此破罐破摔,再无生机。没有自我康复本 领的心灵,是不设防的大门。一汪小伤,便漏尽全身膏血。一星火药,烧毁绵延的城堡。 心为血之海,那里汇聚着每个人的品格智慧精力情操,心的质量就是人的质量。有一颗仁慈之心,会爱世界爱人爱生活,爱自身也爱大家。有一颗自强之心,会勤学苦练百折不挠,宠辱不惊大 智若愚。有一颗尊严之心,会珍惜自然善待万物。有一颗流量充沛羽翼丰满的心,会乘上幻想的航天飞机,抚摸月亮的肩膀。 造心是一项艰难漫长的工程,工期也许耗时一生。通常是母亲的手,在最初心灵的模型上,留下永不消退的指纹。所以普天下为人父母者,要珍视这一份特 别庄重的义务与责任。 当以我手塑我心的时候,一定要找好样板,郑重设计,万不可草率行事。造心当然免不了失败,也很可能会推倒重来。不必气馁,但也不可过于大意。因为心灵的本质,是一种缓慢而精细的物体,太多的揉搓,会破坏它的灵性与感动。 造好的心,如同造 好的船。当它下水远航时,蓝天在头上飘荡,海鸥在前面飞翔,那是一个神圣的时刻。会有台风,会有巨涛。但一颗美好的心,即使巨轮沉没,它的颗粒也会在海浪中,无畏而快乐地燃烧。 读书使人优美 优美在字典上的意思是:美好。 ? 做一个美好的人,我相信是绝大多数人的心愿。 谁不愿意美好啊?除了心灵的美好,外表也需美好。为了这份美好,人们使出了万千手段。比如刀兵相见的整容,比如涂脂抹粉的化妆。为了抚平脸上的皱纹,竟然发明了用肉毒杆菌的毒素在眉眼间注射,让面部微小神经麻痹,换来皮肤的暂时平滑……让我这个曾经当过医生的人胆战心 惊。 其实,有一个最简单的美容之法,却被人们忽视,那就是读书! 读书的时候,人是专注的。因为你在聆听一些高贵的灵魂自言自语,就会不由自主地谦逊和聚精会神。即使是读闲书,看到妙处,也会忍不住拍案叫绝……长久的读书可以使人养成恭敬的习惯,知道这个世界上可以 为师的人太多了,在生活中也会沿袭洗耳倾听的姿态。而倾听,是让人神采倍添的绝好方式。所有的人都渴望被重视,而每一个生命也都不应被忽视。你重视了他人,魅力就降临在你双眸。 ? 读书的时候,常常会会心一笑。那些智慧和精彩,那些英明与穿透,让我们在惊叹的同时拈页 展颜。微笑是最好的敷粉和装点,微笑可以传达比所有语言更丰富的善意与温暖。有
九年级数学最大值、最小值问题
f (1) 7; f (4) 142. 比较得 最大值 f (4) 142, 最小值 f (1) 7.
;温州乐清包船捕鱼 温州乐清包船捕鱼 ;
材的多样化,非要把闲情雅致、风花雪月从散文主题上驱逐出去不可,而是指一个“比例”问题。我和散文家刘烨园先生在谈话中,他提出一个“比例”说,问题点得很到位:评价一种事物和现象,关键看它所包含的各项的比例。纠正一个偏颇,其实即对一种比例作调整,而非彻底颠覆或灭杀 什么。现在的情况是:散文中赋闲成分太大,精神比例过小。对我们这样一个远不轻松的时代更是如此。除了过去所赋予散文的那些品质以外,散文应融入更多的思想和良知的品质,除了生命美学和感性元素,更应融入理性揭批功能,应在问题上更贴近当代生存,应放扩关怀力,让更多更严峻 的事物进入视野……尤其眼下是这样一个“问题”和“隐患”威胁到人类生存的时代,散文应适度地选择承担,选择发言,而非冷漠与旁观。 过去有一句话:“民族的,就是世界的。”套用一下,也可以说:“当代的,就是永恒的”,如果对当代最重大和最急峻的现实命题都回避,如果连 当代生活都不感兴趣的话,那所谓“藏之名山”的想法无疑是可笑的,一种虚妄的幻觉与自欺罢了。其实,西方的优秀作家和作品,本质上无时无刻不是在为当代人而作,也是为未来而作——因为未来者对先人生存历史和精神困境的了解,无不是通过这些作品实现的。 当代叙事的不足,也 表现在所谓的“文化大散文”上,它们更多地扮演了一种“棕子”,一种“裹脚”的叙事角色,更多的停滞在对史事片段的重复叙述和揣摩上(我一点不否定它的价值,只是觉得它应该而且能够承担更多的东西)。文化不应只是“过去时”的,更应有“现在时”和“进行时”,应把精神触角延 伸至当下的国民生态,应在时间过渡的表面下,找到“根”和“枝叶”的血脉递承与母子关系,否则,文化散文就成了彻头彻尾的“历史散文”。说到底,这取决于作者的内里和品格,尤其在中国,这甚至不是才华、能力和技术问题,而是一个写作信仰问题,是对作家生命关怀力的考验,对其 精神诉求和承担能力的考验! 所以我觉得,其实有一个比“写得好坏”更重大的问题我们没解决好:“为什么写作?”在这样一个职业选择日益多样化的时代,是什么样的绝对理由和终极信仰使一个人选择了孤独的写作生涯而没有去干别的?这个问题在西方作家身上可以说是一个永恒的终 身命题,从他开始写作的那天起,就要面对,就要选择,就要确立一种生存立场和写作姿势,就要为自己一生的作品命名,一直到死。但在很多中国作家这儿,你很可能找不到这样一个“基因”,或者未曾遇到,或者根本不当回事。也就是说,我们的文学深处,很有可能缺乏一个结实的“奠 基”,缺乏一种“根”。 最后,我还想说明的一点是:当前散文的“热闹”很大程度上是由杂文、思想或文化随笔——由作者队伍的结构和角色改变所带来的,散文从业人员的成分复杂和丰富了,它不再是传统文学作者的专利,诗人、人文学者、自然科学家、批评型知识分子、小说家的 “另类散文”都给人耳目一新的感觉。虽然表面上看,涉及社会民生、历史文化、自然生态的文本如今比任何一个时期显得都多,但实际质量不容乐观,除了刚才提到的“文化散文”的缺陷外,还要警惕一点:在给散文松绑、融入理性品质的同时,要防止文学美质和艺术性的流失!我注意到很 多理性散文和思想性随笔在文本上的机械、粗糙与僵硬,其美学含量是严重不足的——不仅仅反映在语言表层,更多还体现于思维、思路的粗糙和欠精准上。 总之,散文现在面临的不再是它能承载什么——允许什么进入的问题?而关键看我们能够赋予散文什么?散文应从传统的那种松垮、 慵散、懈怠的过于休闲状态中解脱出来,应该更多针承担人文精神与良知功能,应该有更多对社会和当代的思考……在生命诚实、精神关怀力社会良知和道义承担上下工夫!应该端正身子,以直视生命的态度写散文,而非懒洋洋地画散文,描散文。 散文不该沦为文学的剩饭、闲饭、馊饭。 而文学,更不应被稀释成一个时代的胃酸和呕吐物。 向一个人的死因致敬 王开岭 一 一个人精神毁容了,被自己或别人的硫酸,如何是好,如何是好…… 面皮移植?铸一铁面具?归隐山泉与雀兽为伴? 卢武铉先是对观众说了声对不起,然后散步,迎着日出,迎着故里的崖。 山脚下的小村子 很美,无论地理还是气质,卢武铉回忆得也很美,说那是个“连乌鸦都会因找不到食物哭着飞走”的地方,他的话深情而充满感恩。在乌鸦身上,他用了个哭字。 想当年,他就是因找不到食物而哭着飞走的。去了大田,去了汉城,去了青瓦台。 每次出发,他都空空荡荡,除了一个贫民之子的 誓言、一个清卷书生的豪气,别无行李。 坑坑洼洼的故乡,那些含辛茹苦、蓬蓬勃勃的野草,似乎给了他最生动的精神注脚,也预支了最有力的人格担保。 怎么看,此人的变节风险都是最小的。他有着淳朴的起点和奋斗史。 坎坷身世、卑微学历、民权斗士、草根总统……卢武铉像一个童话。 全世界,包括我这个外国人都对这个童话喜爱不已,也觉得和自己隐隐有关。 这世界需要童话,需要一次童话的胜利,就像需要一场雪。 最近一场雪是奥巴马带来的,他的肤色照亮了星条旗,也鼓舞了地球仪。只是他离得远了点,不如卢武铉这般近,像亲戚。 有时,我觉得卢武铉酷似中国史 书上的那些前辈,很儒家,很士林。你看他说过的—— 大选获胜后,他用噙泪的语调承诺:“我知道大家对我的期望是什么,那是一个没有腐败、没有特权、没有违规的社会,一个用自己双手生活的诚实的社会。” 面对反腐的重重险碍,他说:“没有一个农民,会因土地贫瘠而放弃劳作。” 住青瓦台后,他与友人私下谈心,称执政关键有三:一将改革进行到底,二让总统府远离金钱,三管好自己亲属。 凡此种种,都让我想起先人那句话:“富贵不能淫,贫贱不能移,威武不能屈。” 做好这几条,孟子说,你就是大丈夫了。其实,也就是最好的公仆。 还有啊,论面相,卢武铉的 东方脸孔上有一种让人特放心的东西,温绵、敦厚、亲蔼,处处散发着安全感,完全符合中国人推崇的“方正”。 然而,童话终究是童话。事实明,贫穷和廉洁并无直接关系,监督权力和坐拥权力是截然不同的两份差事。 当他和故乡不再为食物发愁的时候,其家人被怀疑偷拿了别人的东西。 终于,一名英勇的律师站在了审判席上,一位历史的原告变成了现实的被告。某种意义上,卢武铉成了自己信仰的敌人。至少客观上,他互换了位置。 二 为什么会这样,怎么会这样呢? 对此我不感兴趣,我只留意到了那天,他最后一次攀登。 他选择了故乡的崖。崖,本身就意味着高度,是 尊严的象征,是清高者的去处。 可以想象,这曾是他少年立志和理想出发的地方。 清晨的草木,带露水,很干净。 一个人在做自由落体前,心真的会安宁吗? 世间很美,他远远看见山脚下活动的人影。同胞的生活又开始了,接下来,将是忙碌而幸福的一天。 对他来说,今天只意味着一个早 晨。 这一天,卢武铉将成为全世界的新闻头条。他料到了,但他已从看客中划掉了自己。 这是个脸皮薄的男人。性情如铅笔,直、细、脆,又爱哭鼻子。有人说,流泪是孱弱的表现,他不具职业政治家应有的坚韧。何谓坚韧呢?我不太懂。稍后,似乎也懂了,就是脸皮厚实且富弹性吧。 不错, 论政治体格,此人是弱了点,可谓弱不禁风。和城府深沉、世故圆滑的同行相比,他似乎太嫩,像书生,不像政客,甚至还有孩子的茸毛。 “我已丧失了再讲民主、进步与正义的资格……各位不能和我一起陷入这个泥淖,请大家舍弃我卢武铉吧。” 他没有狡辩,他说他无颜家乡父老,无颜全 体国民。其歉意之巨大,甚至连肇事的家人,他都表示了歉意。他觉得是自己,让最爱的人不幸沾染了权力,是自己的事业把亲属带到了危险地带。 非得纵身一跳?别无选择吗? 世间那么多毁容者,不都活得好好的? 这大概和一个人的精神体质有关。该体质决定了一个人的生命意义和存在依 据,决定了他遇事妥协的程度、忍受之底限。比如逆境之下的抉择,“好死不如赖活着”是一种,“留得青山在”是一种,“宁玉碎不瓦全”是一种,“万念俱灰唯死一途”是一种…… 卢武铉属哪种呢?我说不太清。 但有一点能确认:他死于面子,死于廉耻和羞愧,死于精神毁容后的照镜子。 “我现在没有脸正对你们的眼睛……我现在完全可以被抛弃了,现在我完全不足代表任何道德进步。” 这是个爱照镜子的政治家,是一个道德自尊心极强、自珍甚至自恋的人。他并非死于惊恐和畏惧,而是死于意境的破灭,死于内心的狂风,死于肖像的被毁,死于一个理想主义者和完美主义者 的失败感。还有,就是对清静、安宁和独处的渴望。 这种死因,包括死法,确不像现代政客所为。对许许多多政客来说,精神毁容、身败名裂,不过是轻若稻草的一件事,审判席上,磕头捣蒜乞饶求生者多如蝼蚁,贪生即怕死。但于一个自我器重惯了、把尊严和仪容视若性命之人,这事故就如 泰山压顶,漆黑一片。 所以,当有人说他死于一根道德稻草时,我不同意,我说他死于泰山。 不是说他死得重于泰山。 三 这种死因,多少让我想起了古人,想起了士林之风。我觉得精神气质上,卢武铉很有点前辈风度,像从竹林里走出来的,士大夫的腰板,昂首挺胸,纤尘不染。 古人是把 “知耻”当头等大事的,礼义廉耻被看作国之四维。 “无羞恶之心,非人也”“羞耻之心,义之端也”“五刑不如一耻”“士皆知有耻,则国家无耻矣”。 如果说古代士子是吃“素”的,一日三省谋求肺腑洁净,衣冠楚楚力图众口皆碑;那现代政客则少然,他们更崇尚丛林法则和蔽人耳目, 内心多“荤腥”之物。逻辑和尺度变了,精神体质也就变了,政治品格也就变了。丑事当前,拼命遮挡;铁如山,又死乞白赖。 古人惜名,今人惜命。古人自责,今人诿责。 谁脸上没个疮?在今人看来,卢武铉在道德反应上显然过度了,但古时候,这绝对算一个正常的“均值”,算一个合理 的脸皮厚度。 由此我涌生敬意。我向一个人的死因致敬。向他骨子里的那份“古意”致敬。 古意,让生命葱茏如竹。 我还想起了另一位自杀者,一个小得不能再小的小人物。三年前,南方一家小煤矿爆出档新闻,纸媒标题是,《倔犟矿工打赌嫖娼后服毒自杀“谢罪”》。事情大致如此:端午 节,矿上发了点酒,歇工后,矿友们围一起打牙祭,不能喝酒的张某很快有了醉意,后和人打起了赌,对方说如果你敢去“耍小姐”
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
【提升总结பைடு நூலகம்】 函数f(x)在区间[a,b]上最值的取值规律:
函数的最值或者在极值点取得,或者在区间的
端点取得.因此,要想求函数的最值,应首先求出函
数的极值,然后所有的极值点与区间端点的函数值
进行比较,其中最大的值即为函数的最大值,最小
的值即为最小值.
例题解析
例1.求函数y=f(x)=x3-2x2 +5在区间[-2,2]上的 最大值和最小值. 2 3 2 f '( x ) 3 x 4x 解由f(x)=x -2x +5,得 4 2 由 f '( x) 3 x 4 x 0 ,得x=0,x= 3 列表如下:
f '( x) 6 x2 6(2 a 2 ) x 6(1 a 2 ) 由题意知 f '( x) 6 x2 6(2 a2 ) x 6(1 a2 ) 0 恒成立 2 2 2 36 ( 2+ a ) 144(1 a ) 0 ,得 a 4 0 则
解:(1)首先写出V关于x的函数解析式.根据
题意可得V=f(x)=(48-2x)2x 由实际情况可知函数的定义域为{x︳0<x<24}. 根据导数公式表及求导法则,可得
f (x) 4x(48 2x) (48 2x) 2 (48 2x)(6x 48) 12(x 24)(x 8) 解方程V(x) 0, 得x1 8, x 2 24.
y 5t CD 3t BD 5t 400 x 2 3t (100 x )(0 x 100)
令 y t (
5x
唯一解x=15,比较后可得在x=15处取得最大值。 所以,当x=15 km,即D点选在距A点15 km时, 总运费最省.
400 x 2
3) 0,在 0 x 100 的范围内有
2 2 f (2) 16 12(2 a ) 12(1 a )1 5 由于
所以 3 3a 2 5
解得 6 a 6 3 3 所以a的取值范围为 ( 6 , 6 ) 3 3
1.下列说法正确的是( D ) A.函数的极大值就是函数的最大值 B.函数的极小值就是函数的最小值 C.函数的最值一定是极值 D.若函数的最值在区间内部取得,则一定是极值
(1)试写出该企业获得的生产利润w(单位:万元)
与产量x之间的函数关系式;
(2)当产量为多少时,该企业可获得最大利润?最大
利润为多少?
解:(1)因为总利润=总收入-总成本,即w=z-y, 所以,由w=w(x)=18x-(x3-24x2+63x+10), (2)求w=w(x)的导函数
w(x) 3x 2 48x 45.由w(x) 0, 得x1 1, x 2 15.
【提升总结】
求函数最值的四个步骤
第一步 求函数的定义域.
第二步 求 f'(x) ,解方程f'(x)=0 . 第三步 列出关于x,f'(x) ,f(x)的变化表. 第四步 求极值、端点值,确定最值.
探究点3
生活中的最值问题
利用导数解决生活中的最值问题 的基本思路:
生活中的最值 问题 用函数表示的数学问题 解决数 学模型 作答 生活中的最值问题 的答案 用导数解决数学问题
根据x1=8,x2=24列表,分析导函数的符号得
到函数的单调性与极值点
x f′(x) V=f(x)
(0,8) +
8 0 极大值
(8,24) -
x=8是函数的极大值点,相应极大值为 V=f(8)=(48-16)2×8=8 192(cm3). 根据对函数变化规律的讨论可知: 当0<x≤8时,函数V=f(x)是增加的;当8≤x< 24时,V=f(x)是减少的. (2)区间(0,24)上任意点的函数值都不超过 f(8),因此x=8是函数的最大值点.此时V=8192cm3
x
-2
f′(x) 20
(2,0) +
0
0
极大值
4 (0, ) 3
4 3
4 ( , 2) 3
2
4
-
0
极小值
+
f(x) -11
4 f(0)=5,f( 3
5
f(-2)=-11,f(2)=5 y=x3-2x2+5在区间[-2,2]上的最大值是5,最小值是-11
103 )= 27 ,
【举一反三 】4-2x2+5在区间[-2,2]上的最大值与最小 求函数y=x
典型例题
例4.已知函数 f ( x) tx 2t x t 1(t 0) (1)求f(x)的最小值h(t). (2)若h(t)<-2t+m对t (0, 2)恒成立,求实数 m的取值范围。
2 2
3 f ( x ) t x t t t 1(t 0) 解:(1) 2
变式训练
函数 f ( x) 2 x3 3(2 a2 ) x2 6(1 a2 ) x 1 (1)若f(x)在R上单调,求实数a的值。 (2)f(x)在 [0, 2] 的最大值为5,求实数a的取值范围.
3 2 2 2 解:(1)由 f ( x) 2 x 3(2 a ) x 6(1 a ) x 1 ,得
即当截去的小正方形的边长为8cm时,得到的容 器容积最大,最大容积为8 192 cm3.
例3
产量与利润
对于企业来说,生产成本、销售收
入和利润之间的关系是个重要的问题.对一家药品生产 企业的研究表明,该企业的生产成本y(单位:万元)和 生产收入z(单位:万元)都是产量x(单位:t)的函数,
分别为y=x3-24x2+63x+10, z=18x.
回顾本节课你有什么收获?
1.函数f(x)在[a,b]上的最值的步骤: (1)求f(x)在(a,b)内的极值. (2)将f(x)的各极值与f(a)、f(b)比较,其中最
列表如下
x (0,1) - 1 0 极小值 (1,15 ) + 15 0 极大值 (15,+ ∞) -
w'(x)
w(x)
w(0)=-10,w(15)=1 340,故函数w=w(x)的最大值为 w(15)=1340,即该企业的产量为15t时,可获得最大 利润,最大利润为1340万元。
【变式练习 】
如图,铁路线上AB段长
所以a=0
2 2 2 2 f '( x ) 6 x 6(2 a ) x 6(1 a ) 6( x 1 a )( x 1) (2)由 且1 1 a 2 知f(x)在(0,1)上增,在[1,1 a 2 ] 上减
在[1 a2 , ) 上增 所以f(x)的最大值为f(1)或f(2)
b 4a 5, b 3,
所以a=2.
5.已知函数f(x)=2x3-12x.求函数f(x)的
单调递增区间,并求函数f(x)在[-1,3]上
的最大值和最小值.
解析: f(x)=2x3-12x, f′(x)=6x2-12=6(x+ 2)(x- 2). 令 f′(x)=0,得 x=- 2或 x= 2.
3
典型例题
t g′(t) g(t) (0,1) + 1 0 极大值 (1,2) -
所以,g(t)在(0,2)内有最大值g(1)=1-m 由h(t)<-2t+m对t (0, 2) 恒成立,得 1-m<0,即m>1 所以m的取值范围为(1, ) 点评:把恒成立问题转化为求函数最值问题。 注意端点处能否取得,本题中函数有最大 值,因而端点处不能取。
当 x 变化时,f′(x)与 f(x)的变化情况如下表:
X
f′(x)
, 2
+
2
0
2, 2
2
0
2,
-
+
f(x)
极大值
极小值
所以函数 f(x)的单调递增区间为 (-∞,- 2,( 2,+∞ ). 因为 f(-1)= 10,f(3)= 1,f( 2)=- 8 2, 所以当 x= 2时 ,f(x)取得最小值为-8 2; 当 x= 3 时,f(x)取得最大值为 18.
1 4 1 3 1 2 2.函数y= x x x ,在[-1,1]上 4 3 2 的最小值为( A )
A.0
B.-2
C.-1
13 D. 12
76
,最小值为 -5 .
3.函数 y = x³ + 3 x²-9x在 [-4 , 4 ]上
的最大值为
4.函数f(x)=ax4-4ax2+b(a>0,1≤x≤2)的最大值
100km,工厂C到铁路的
距离CA=20km.现在要
C
在AB上某一处D,向C修
一条公路.已知铁路每吨
B
D
A
千米与公路每吨千米的运费之比为3:5.为了使原料 从供应站B运到工厂C的运费最省,D应修在何处?
【变式练习答案 】 解析 :设DA=xkm,那么DB=(100-x)km,
2 km). CD= 202 x 2 400 x( 又设铁路上每吨千米的运费为3t元,则公路上每吨 千米的运费为5t元.这样,每吨原料从供应站B运到 工厂C的总运费为
不小于 函数在这个区间上所有点的函数值都________f(x 0).
最值 函数的最大值和最小值统称为______.
练一练
观察右边一个定义
y
在区间[a,b]上的函数
y=f(x)的图像,你能找
出函数y=f(x)在区间
[a,b]上的最大值、最 小值吗? f(x2) 是极大 f(x1)、f(x3) 是极小值,_________ 发现图中____________ 值,在区间上的函数的最大值是______ f(b) ,最小值是 f(x3) _______.
