最大值最小值问题
最大值最小值问题

作业布置
课本P69第2题,P71第2题 第 题 课本 第 题
3.给定函数 = f ( x) x∈[a, b]如何求取最值? y 如何求取最值? ,
y
y = f ( x)
a
x1
o
X2
X3
b
x
4.函数 = f ( x)的最值与极值的联系 y 与区别? 与区别?
值可能有多个,而最大( (1). 函数的极大(小)值可能有多个,而最大(小)值只 ) 函数的极大( 有唯一的一个 (2)极大值不一定比极小值大,但是最大值一定比最小值大 )极大值不一定比极小值大, (3)极值只能在区间的内部取得,不能在端点处取得,而函 )极值只能在区间的内部取得,不能在端点处取得, 数的最值可以在端点处取得 (4)函数的最值在函数在整个定义域内的整体性质,极 )函数的最值在函数在整个定义域内的整体性质, 值只是函数在某一点附近的局部性质
最大值与最小值问题(一 最大值与最小值问题 一)
导数与函数的最值问题
情境引入
如图,在边长为60cm的正方形铁片的四角上切去 如图,在边长为 的正方形铁片的四角上切去 相等的正方形,再把它的边沿虚线折起, 相等的正方形,再把它的边沿虚线折起,做成一个无 盖的方底箱子,要求箱子的高度不小于5cm且不大于 不小于5cm 盖的方底箱子,要求箱子的高度不小于5cm且不大于 问当箱子的高度为多少时,容积最大? 20cm,问当箱子的高度为多少时,容积最大?最大容 积是多少? 积是多少?
3
y
6
x ∈ [−2,0] −
5
4
y = f ( x)
x ∈ [0,2]
2
x ∈ [−2,2] −
-2 -1
1 0 1 2
x
高中数学最值问题12种

高中数学最值问题12种高中数学最值问题是指在一定条件下,找出某个函数的最大值和最小值的问题。
这些问题需要通过一定的方法来求解,涉及到导数、不等式、二次函数、三角函数等数学知识。
下面我们将介绍12种高中数学最值问题的解法和相关概念。
1.函数的最大值和最小值:函数的最大值和最小值是指函数的各个值中最大和最小的值。
一元函数的最大值和最小值通常可以通过求解导数为0的点来获得。
多元函数的最大值和最小值可能需要使用拉格朗日乘数法等方法。
2.二次函数的最值:二次函数的最值可以通过求解顶点坐标来获得。
二次函数的最大值发生在开口向下的情况下,最小值发生在开口向上的情况下。
3.三角函数的最值:三角函数的最值可以通过研究函数的周期性和对称性来获得。
一般情况下,三角函数的最值为1和-1。
4.不等式的最值:不等式的最值是指不等式的解集中最大和最小的值。
不等式的最值可以通过求解方程来获得。
需要注意确定不等式边界的方式。
5.绝对值函数的最值:绝对值函数的最值可以通过研究函数的分段性质来获得。
需要考虑绝对值函数的参数取值范围。
6.对数函数的最值:对数函数的最值可以通过研究函数的定义域和值域来获得。
对数函数的最大值和最小值通常发生在底数小于1的情况下。
7.指数函数的最值:指数函数的最值可以通过研究函数的定义域和值域来获得。
指数函数的最大值和最小值通常发生在指数大于1的情况下。
8.等式的最值:等式的最值是指满足等式的变量的最大和最小的值。
等式的最值通常可以通过求解方程组来获得,在求解过程中需要注意排除无解的情况。
9.不定积分的最值:不定积分的最值可以通过求导和临界点的方式来获得。
需要注意确定积分的上下界。
10.定积分的最值:定积分的最值可以通过函数在积分区间上的最值来获得。
需要注意确定积分的上下界和积分变量的取值范围。
11.矩形面积的最值:矩形面积的最值可以通过求解矩形的边长和面积关系来获得。
需要注意确定矩形的条件和限制条件。
12.三角形面积的最值:三角形面积的最值可以通过求解三角形的边长和高的关系来获得。
高等数学3.6 最大值、最小值问题

最大值和最小值的求法:
设f(x)在(a,b)内的驻点和不可导点(它们是可能的极值)为
x1,x2, ···,xn,则比较 f(a),f(x 1), f(x 2), ···,f(x n),f(b) 的大小,其中最大的便是函数f(x)在[a,b]上的最大值,最小的 便是函数f(x)在[a,b]上的最小值. 求最大值和最小值的步骤: (1)求出f(x)在(a,b)内的所有驻点和不可导点;
1 1 W b(d 2b 2) 在(0,d)内只有一个驻点, 所以当b d 时, (0<b<d). 6 3
W的值最大.这时, h
2 d . 于是有 d :h :b 3 : 2 :1. 3
(2)求出函数在上述点处和区间端点处的函数值;
(3)比较上述函数值,找出最大的和最小的.
例1 求函数y2x33x212x14在[3, 4]上的最大值与最小值. 解 f(x) 2x 33x 212x 14,
f (x)6x 26x126(x2)(x1),
解方程f (x)0,得一 x12,x21,由于 f(3) 2(3)33(3) 212(3) 1423; f(2) 2(2)33(2) 212(2) 1434; f(1)2312147; f(4)2· 33· 2 12· 4 4 414142, 比较可得f(x)在 x4取得它在[3,4]上的最大值f(4)142 ,在
D
100km
B
C
解 设ADx (km),则 DB100x ,
CD 20 2 x 2 400 x 2 .
设从B点到C点需要的总运费为y,那么
y5k· CD3k· (k是某个正数), DB
y5k 400 x 2 3k(100x) (0x100). 5x 3 , 先求y对x的导数: y k 400 x 2 解方程y0,得x15(km).
最大值最小值问题
bx o a
bx o a
bx
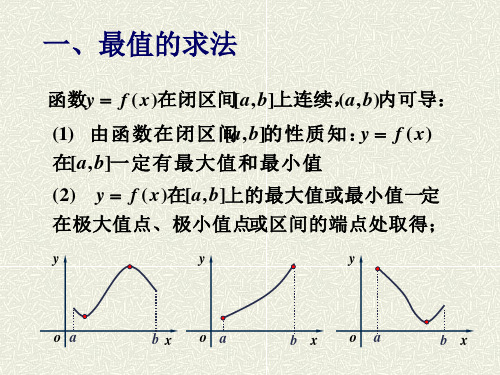
(3) y f ( x)的最大值、最小值一定在 f ' ( x) 0或f ' ( x)不存在的点及区间的端 点取得;
(4) 极大值、极小值是局部的概念,而 最大值、最小值是全局的概念。
步骤:
1.求驻点和不可导点;
2.求区间端点及驻点和不可导点的函数值,比 较大小,那个大那个就是最大值,那个小那个就 是最小值;
0.5公里
s(t ) A
B 4公里
解 (1)建立敌我相距函数关系
设 t 为我军从B处发起 追击至射击的时间(分).
0.5公里
s(t ) A
敌我相距函数 s(t)
B
s(t) (0.5 t)2 (4 2t)2
4公里
(2) 求s s(t)的最小值点.
s(t)
5t 7.5 .
(0.5 t)2 (4 2t)2
令s(t) 0,
得唯一驻点 t 1.5. 故得我军从B处发起追击后 1.5 分钟射击最好.
实际问题求最值应注意:
(1)建立目标函数; (2)求最值;
若目标函数只有唯一驻点,则该点的 函数值即为所求的最大(或最小)值.
例3 某房地产公司有50套公寓要出租,当租金定 为每月180元时,公寓会全部租出去.当租 金每月增加10元时,就有一套公寓租不出去, 而租出去的房子每月需花费20元的整修维护 费.试问房租定为多少可获得最大收入?
f (2) 34;
f (1) 7;
f (4) 142;
y 2x3 3x2 12x 14
比较得 最大值 f (4) 142,最小值 f (1) 7.
例2 敌人乘汽车从河的北岸A处以1千米/分钟 的速度向正北逃窜,同时我军摩托车从河的 南岸B处向正东追击,速度为2千米/分钟.问 我军摩托车何时射击最好(相距最近射击最 好)?
最大值和最小值问题

最⼤值和最⼩值问题最⼤值和最⼩值问题3.2.2 最⼤值、最⼩值问题教学过程:⼀、复习引⼊: 1.极⼤值:⼀般地,设函数f(x)在点x0附近有定义,如果对x0附近的所有的点,都有f(x)<f(x0),就说f(x0)是函数f(x)的⼀个极⼤值,记作y极⼤值=f(x0),x0是极⼤值点 2.极⼩值:⼀般地,设函数f(x)在x0附近有定义,如果对x0附近的所有的点,都有f(x)>f(x0).就说f(x0)是函数f(x)的⼀个极⼩值,记作y极⼩值=f(x0),x0是极⼩值点 3.极⼤值与极⼩值统称为极值注意以下⼏点:(?。
┘?值是⼀个局部概念由定义,极值只是某个点的函数值与它附近点的函数值⽐较是最⼤或最⼩并不意味着它在函数的整个的定义域内最⼤或最⼩(??)函数的极值不是唯⼀的即⼀个函数在某区间上或定义域内极⼤值或极⼩值可以不⽌⼀个(?#┘?⼤值与极⼩值之间⽆确定的⼤⼩关系即⼀个函数的极⼤值未必⼤于极⼩值,如下图所⽰,是极⼤值点,是极⼩值点,⽽ > (?ぃ┖?数的极值点⼀定出现在区间的内部,区间的端点不能成为极值点⽽使函数取得最⼤值、最⼩值的点可能在区间的内部,也可能在区间的端点⼆、讲解新课: 1.函数的最⼤值和最⼩值观察图中⼀个定义在闭区间上的函数的图象.图中与是极⼩值,是极⼤值.函数在上的最⼤值是,最⼩值是.⼀般地,在闭区间上连续的函数在上必有最⼤值与最⼩值.说明:⑴在开区间内连续的函数不⼀定有最⼤值与最⼩值.如函数在内连续,但没有最⼤值与最⼩值;⑵函数的最值是⽐较整个定义域内的函数值得出的;函数的极值是⽐较极值点附近函数值得出的.⑶函数在闭区间上连续,是在闭区间上有最⼤值与最⼩值的充分条件⽽⾮必要条件. (4)函数在其定义区间上的最⼤值、最⼩值最多各有⼀个,⽽函数的极值可能不⽌⼀个,也可能没有⼀个⒉利⽤导数求函数的最值步骤: 由上⾯函数的图象可以看出,只要把连续函数所有的极值与定义区间端点的函数值进⾏⽐较,就可以得出函数的最值了.设函数在上连续,在内可导,则求在上的最⼤值与最⼩值的步骤如下:⑴求在内的极值;⑵将的各极值与、⽐较得出函数在上的最值三、讲解范例:例1求函数在区间上的最⼤值与最⼩值例2已知x,y为正实数,且满⾜,求的取值范围例3.设 ,函数的最⼤值为1,最⼩值为 ,求常数a,b 例4已知 ,∈(0,+∞).是否存在实数 ,使同时满⾜下列两个条件:(1) )在(0,1)上是减函数,在[1,+∞)上是增函数;(2)的最⼩值是1,若存在,求出,若不存在,说明理由. 四、课堂练习: 1.下列说法正确的是( ) A.函数的极⼤值就是函数的最⼤值 B.函数的极⼩值就是函数的最⼩值 C.函数的最值⼀定是极值 D.在闭区间上的连续函数⼀定存在最值 2.函数y=f(x)在区间[a,b]上的最⼤值是M,最⼩值是m,若M=m,则f′(x) ( ) A.等于0 B.⼤于0 C.⼩于0 D.以上都有可能 3.函数y= ,在[-1,1]上的最⼩值为( ) A.0 B.-2 C.-1 D. 4.函数y= 的最⼤值为( )。
第四章 §2 2.2 最大值、最小值问题

面积、体积(容积)的最值问题
[例 3] 某地政府为科技兴市,欲将如图所示的 一块不规则的非农业用地规划建成一个矩形的高科 技工业园.已知 AB⊥BC,OA∥BC,且|AB|=|BC| =4 km,|AO|=2 km,曲线段 OC 是以点 O 为顶点 且开口向上的抛物线的一段.如果要使矩形的两边分别落在 AB,BC 上,且一个顶点落在曲线段 OC 上,应如何规划才能使矩形工业园 的用地面积最大?并求出最大的用地面积(精确到 0.1 km2).
(2)当 x∈[-1,2]时,f(x)<m 恒成立,只需使 f(x)在[-1,2]上的 最大值小于 m 即可.
由(1)知 f(x)极大值=f(-23)=5+2227, f(x)极小值=f(1)=72. 又 f(-1)=121,f(2)7. 所以 m>7,即 m 的取值范围为(7,+∞).
求函数的最值 [例 1] 求下列函数的最值. (1)f(x)=4x3+3x2-36x+5,x∈[-2,+∞); (2)f(x)=12x+sin x,x∈[0,2π] [思路点拨] 先求函数在给定区间的极值,然后再与端点 值比较,即可确定函数的最值.
[精解详析] (1)f′(x)=12x2+6x-36,
元,则总造价的最小值为
()
A.400 元
B.1 200 元
C.1 600 元
D.2 800 元
解析:设总造价为 y 元,池底的一边长 x 米,池底的面积为 8÷2 =4(平方米),池底的另一边长为4x米,池壁的面积为 4x+4x平 方米,故有 y=4×300+4x+4x×100=400x+4x+1 200(x> 0).y′=4001-x42, 令 y′=0 得 x=2,由 y′ >0 得 x >2,由 y′<0 得 0<x<2, 即 y 在(0,2)上是减少的,在(2,+∞)上是增加的,所以当 x=2 时,y 取得最小值,且 ymin=2 800. 答案:D
初中几何最值问题类型

初中几何最值问题类型
初中几何中的最值问题类型有以下几种:
1.最大值最小值问题:
求某个几何图形的最大面积或最小周长,如矩形、三角形等。
求抛物线的最高点或最低点,即顶点的坐标。
2.极值问题:
求函数图像与坐标轴的交点。
求函数在某个区间内的最大值或最小值,如求二次函数的最
值等。
3.最优化问题:
求物体从一个点到另一个点的路径问题,如两点之间的最短
路径、最快速度等。
4.最长边最短边问题:
求三角形的最长边或最短边,如用三根木棍构成三角形,求
最长边的长度。
5.相等问题:
求两个几何形状中的某个参数,使得它们的某个关系成立,
如求两个相似三角形的边长比、两个等腰三角形的底角角度等。
这些问题类型都需要通过合理的分析和运用相关的几何定理
来解决。
对于初中学生来说,熟练掌握基本的几何概念和定理,灵活运用数学思维和方法,可以较好地解决这些最值问题。
通
过多做练习和思考,培养几何思维和解决问题的能力。
初中八年级(初二)数学课件 最大值、最小值问题

实际问题求最值应注意: (1)建立目标函数; (2)求最大值或最小值; 若目标函数只有唯一驻点,则该点处的函数值 即为所求的最大值或最小值.
例2 某房地产公司有50套公寓要出租,当租 金定为每月180元时,公寓会全部租出去.当租金 每月增加10元时,就有一套公寓租不出去,而租出 去的房子每月需花费20元的整修维护费.试问房租 定为多少可获得最大收入?
注意:如果函数在区间内只有一个极值,则这个 极值就是最大值或最小值.
二、应用
例1 求函数 y 2x3 3x2 12x 14 的在 [3,4]
上的最大值与最小值.
解 f ( x) 6( x 2)( x 1)
解方程 f ( x) 0,得 x1 2, x2 1.
计算 f (3) 23; f (2) 34;
R(350)
(350
20)
6831500 108 Nhomakorabea0 (元).
例4 由直线 y 0,x 8 及抛物线 y x2 围
成一个曲边三角形,在曲边 y x2 上求一点,使 曲线在该点处的切线与直线 y 0 及 x 8 所围成 的三角形面积最大.
解 如图,
设所求切点为P( x0 , y0 ),
x0 16 (舍去).
P
oA
T B
Cx
S(16) 8 0. S(16) 4096 为极大值 .
3
3 217
故 S(16) 4096为所有三角形中面积的最大者. 3 27
则切线 PT 为 y y0 2x0( x x0 ),
y
P
oA
T B
Cx
y0 x02 ,
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
解 设房租为每月x元,
租出去的房子有
50
x
180 10
套,
每月总收入为
R(
x)
(
x
20)
50
x
180 10
R(
x)
(
x
20)
68
x 10
R( x)
68
x 10
(x
20)
1 10
70
x 5
R( x) 0 x 350 (唯一驻点)
故每月每套租金为350元时收入最高。
f (2) 34;
f (1) 7;
f (4) 142;
y 2x3 3x2 12x 14
比较得 最大值 f (4) 142,最小值 f (1) 7.
例2 敌人乘汽车从河的北岸A处以1千米/分钟 的速度向正北逃窜,同时我军摩托车从河的 南岸B处向正东追击,速度为2千米/分钟.问 我军摩托车何时射击最好(相距最近射击最 好)?
注意:如果区间内只有一个极值,则这个极值就 是最值.(最大值或最小值)
二、应用举例
例1 求函数 y 2x3 3x2 12x 14 的在[3,4] 上的最大值与最小值.
解 f ( x) 6( x 2)(x 1)
解方程 f ( x) 0,得 x1 2, x2 1.
计算 f (3) 23;
0.5公里
s(t )
A
B 4公里
解 (1)建立敌我相距函数关系
设 t 为我军从B处发起 追击至射击的时间(分).
0.5公里
s(t ) A
敌我相距函数 s(t)
B
s(t) (0.5 t)2 (4 2t)2
4公里
(2) 求s s(t)的最小值点.
s(t)
5t 7.5 .
(0.5 t)2 (4 2t)2
x0 16 (舍去).
s(16) 8 0. s(16) 4096 为极大值.
3
3 217
故 s(16) 4096为所有三角形中面积的最大者. 3 27
三、小结
注意最值与极值的区别. 最值是整体概念而极值是局部概念. 实际问题求最值的步骤.
思考题
若 f (a) 是 f ( x) 在[a, b] 上的最大值或最 小值,且 f (a)存在,是否一定有 f (a) 0 ?
y
y
y
oa
bx o a
bx o a
bx
(3) y f ( x)的最大值、最小值一定在 f ' ( x) 0或f ' ( x)不存在的点及区间的端 点取得;
(4) 极大值、极小值是局部的概念,而 最大值、最小值是全局的概念。
步骤:
1.求驻点和不可导点;
2.求区间端点及驻点和不可导点的函数值,比 较大小,那个大那个就是最大值,那个小那个就 是最小值;
思考题解答
结论不成立. 因为最值点不一定是内点.
例 y f ( x) x x [0,1] 在 x 0 有最小值,但 f (0) 1 0
返
P
则切线PT为
y y0 2 x0( x x0 ),
oA
T B
Cx
y0 x02 ,
A(
1 2
x0
,
0),
C(8, 0),
B(8, 16x0 x02 )
SABC
1(8 2
1 2
x0 )(16x0
x02 )
(0 x0 8)
令
S
1 4
(3 x02
64 x0
16
16)
0,
解得
x0
16 , 3
令s(t) 0,
得唯一驻点 t 1.5. 故得我军从B处发起追击后 1.5 分钟射击最好.
实际问题求最值应注意:
(1)建立目标函数; (2)求最值;
若目标函数只有唯一驻点,则该点的 函数值即为所求的最大(或最小)值.
例3 某房地产公司有50套公寓要出租,当租金定 为每月180元时,公寓会全部租出去.当租 金每月增加10元时,就有一套公寓租不出去, 而租出去的房子每月需花费20元的整修维护 费.试问房租定为多少可获得最大收入?
3.4 最大值、最小值问题
最值的求法 应用举例
返
一、最值的求法
函数y f ( x)在闭区间[a, b]上连续,(a, b)内可导:
(1) 由函数在闭区间[a, b]的性质知:y f ( x) 在[a, b]一定有最大值和最小值; (2) y f ( x)在[a, b]上的最大值或最小值一定 在极大值点、极小值点或区间的端点处取得;
最大收入为R(
x)
(350
20)
68
350 10
10890 (元)
例4 由直线 y 0,x 8 及抛物线 y x2 围
成一个曲边三角形,在曲边 y x2 上求一点,
使曲线在该点 处的切线与直 线 y0及 x8 所围成的三角 形面积最大.
y
P
oAห้องสมุดไป่ตู้
T B
Cx
解 如图,
y
设所求切点为P( x0 , y0 ),
