第五章聚类分析..
多元统计分析 第5章 聚类分析
余弦相似性 Cosine Similarity
A document can be represented by thousands of attributes,
p (such as each recording the frequency of a particular word keywords) or phrase in the document. xi yi
feature mapping, ... Cosine measure: If d1 and d2 are two vectors (e.g., termfrequency vectors), then cos(d1, d2) = (d1 d2) /||d1|| ||d2|| ,
where indicates vector dot product, ||d||: the length of vector d
d1 = (5, 0, 3, 0, 2, 0, 0, 2, 0, 0) d2 = (3, 0, 2, 0, 1, 1, 0, 1, 0, 1) d1 d2 = 5*3+0*0+3*2+0*0+2*1+0*1+0*1+2*1+0*0+0*1 = 25 ||d1||= (5*5+0*0+3*3+0*0+2*2+0*0+0*0+2*2+0*0+0*0)0.5=(42)0.5 = 6.481 ||d2||= (3*3+0*0+2*2+0*0+1*1+1*1+0*0+1*1+0*0+1*1)0.5=(17)0.5 = 4.12 cos(d1, d2 ) = 0.94
聚类分析步骤
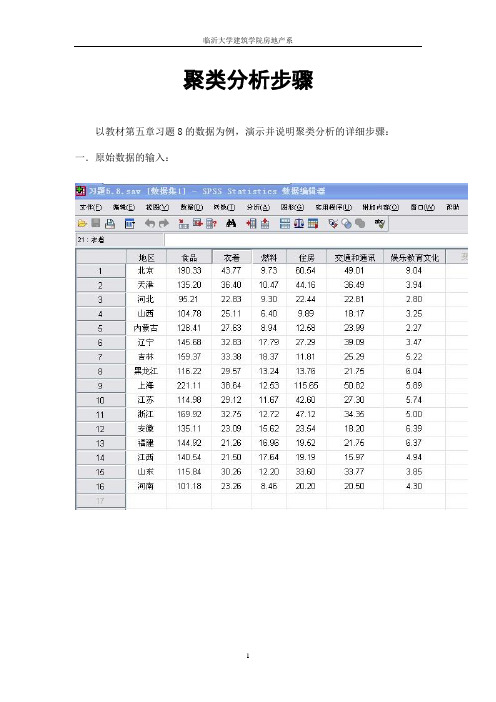
聚类分析步骤以教材第五章习题8的数据为例，演示并说明聚类分析的详细步骤：一．原始数据的输入：二．选项操作：1. 打开SPSS的“分析”→“分类”→“系统聚类”，打开“系统聚类”对话框。
把“食品”、“衣着”等6变量输入待分析变量框；把“地区”输入“标注个案”；“分群”选中“个案”；“输出”选中“统计量”和“图”。
（如下图）相关说明：（1）系统聚类法是最常用的方法，其他的方法较少使用。
（2）“标注个案”里输入“地区”，在输出结果的距离方阵和聚类树状图里会显示出“北京”、“天津”等，否则SPSS自动用“1”、“2”等代替。
（3）“分群”选中“个案”，也就是对北京等16个样本进行分类，而不是对食品等6个变量分类。
（4）必须选中“输出”中的“统计量”和“图”。
在该例中会输出16个地区的欧氏距离方阵和聚类树状图。
2. 设置分析的统计量打开最右上角的“统计量”对话框，选中“合并进程表”和“相似性矩阵”，“聚类成员”选中“无”。
然后点击“继续”。
打开第二个“绘制”对话框，必须选中“树状图”，其他的默认即可。
打开第三个对话框“方法”：聚类方法选中“最邻近元素”；“度量标准”选中“区间”的“欧氏距离”；“转换值”选中“标准化”的“Z得分”，并且是“按照变量”。
打开第四个对话框“保存”，“聚类成员”选默认的“无”即可。
三．分析结果的解读：按照SPSS输出结果的先后顺序逐个介绍：1.欧氏距离矩阵：是16个地区两两之间欧氏距离大小的方阵，该方阵是应用各种聚类方法进行聚类的基础。
52.合并进程表：主要看前四列，现在以前三个步骤为例说明合并过程：第一步，样本12和样本13合并，此时系数为0.650；第二步，样本3和样本16合并，此时系数为0.960；第三步，样本3（实际上是第二步样本3和16组成的新类）和样本4合并，此时系数为0.989；以此类推。
3. 冰柱：左侧是分组数目，上侧是被分组的样本，样本之间由等距的间隔分开，间隔被填充的，说明相邻两样本合并为一组，没有被填充就不被合并。
多元统计分析课件第五章_聚类分析
止。如果某一步距离最小的元素不止一个，则对应ቤተ መጻሕፍቲ ባይዱ些
最小元素的类可以同时合并。
【例5.1】设有六个样品，每个只测量一个指标，分别是1， 2，5，7，9，10，试用最短距离法将它们分类。
（1）样品采用绝对值距离，计算样品间的距离阵D（0） ，见 表5.1
一、系统聚类的基本思想
系统聚类的基本思想是：距离相近的样品（或变量）先聚成 类，距离相远的后聚成类，过程一直进行下去，每个样品 （或变量）总能聚到合适的类中。系统聚类过程是：假设总 共有n个样品（或变量），第一步将每个样品（或变量）独 自聚成一类，共有n类；第二步根据所确定的样品（或变量） “距离”公式，把距离较近的两个样品（或变量）聚合为一 类，其它的样品（或变量）仍各自聚为一类，共聚成n 1类； 第三步将“距离”最近的两个类进一步聚成一类，共聚成n 2类；……，以上步骤一直进行下去，最后将所有的样品 （或变量）全聚成一类。为了直观地反映以上的系统聚类过 程，可以把整个分类系统画成一张谱系图。所以有时系统聚 类也称为谱系分析。除系统聚类法外，还有有序聚类法、动 态聚类法、图论聚类法、模糊聚类法等，限于篇幅，我们只 介绍系统聚类方法。
在生物、经济、社会、人口等领域的研究中，存在着大量量 化分类研究。例如：在生物学中，为了研究生物的演变，生 物学家需要根据各种生物不同的特征对生物进行分类。在经 济研究中，为了研究不同地区城镇居民生活中的收入和消费 情况，往往需要划分不同的类型去研究。在地质学中，为了 研究矿物勘探，需要根据各种矿石的化学和物理性质和所含 化学成分把它们归于不同的矿石类。在人口学研究中，需要 构造人口生育分类模式、人口死亡分类状况，以此来研究人 口的生育和死亡规律。
《Python数据分析与应用》教学课件第5章聚类分析
图 5<16 运行结果
553 算法实例
运行结果如图5-16所示。 由图5-16可以看出 ，300个数据点被 分成三类 ，聚类中心分别为（ 3,3 ）、
（ -3 ,-3 ）和（ 3 ,-3 ） ,符合原始数
据的分布趋势 ，说明sklearn库中的近 邻传播算法 AffinityPropagation能够
按预期完成聚类功能。
5.1基本概NTENTS
DBSCAN聚类算法
5.4 谱聚类算法
5.5 近邻传播算法
学习目标
( 1 )了解聚类分析的定义 ，并了解几种聚类分析方法。
(2 )了解簇的定义及不同的簇类型。
( 3 )学习K means聚类算法、DBSCAN聚类算法、谱聚类 ( spectral clustering )算法和近邻传播( affinity propagation )算法。 ( 4 )通过算法的示例进一步理解算法的过程。 ( 5 )了解聚类分析的现状与前景。
5.5.3 算法实例
23. plt.plot(cluster_center [ 0 ] ,cluster_center [ 1 ] , o ,
markerfacecolor=col, \
24.
markeredgecolor= k , markersize=14)
25. for x in X [ class_members ] :
26.
plt.plot( [ cluster_center [ 0 ] , x [ 0 ] ] , [ cluster_center
[l],x[l] ] , col)
27.plt.title( Estimated number of clusters: %d % n_clustersJ
数据挖掘原理、 算法及应用第5章 聚类方法
第5章 聚类方法
5.1 概述 5.2 划分聚类方法 5.3 层次聚类方法 5.4 密度聚类方法 5.5 基于网格聚类方法 5.6 神经网络聚类方法：SOM 5.7 异常检测
第5章 聚类方法
5.1 概 述
聚类分析源于许多研究领域，包括数据挖掘、统计学、 机器学习、模式识别等。它是数据挖掘中的一个功能，但也 能作为一个独立的工具来获得数据分布的情况，概括出每个 簇的特点，或者集中注意力对特定的某些簇作进一步的分析。 此外，聚类分析也可以作为其他分析算法 (如关联规则、分 类等)的预处理步骤，这些算法在生成的簇上进行处理。
凝聚的方法也称为自底向上的方法，一开始就将每个对 象作为单独的一个簇，然后相继地合并相近的对象或簇，直 到所有的簇合并为一个，或者达到终止条件。如AGNES算法 属于此类。
第5章 聚类方法
(3) 基于密度的算法(Density based Methods)。 基于密度的算法与其他方法的一个根本区别是： 它不是 用各式各样的距离作为分类统计量，而是看数据对象是否属 于相连的密度域，属于相连密度域的数据对象归为一类。如 DBSCAN (4) 基于网格的算法(Grid based Methods)。 基于网格的算法首先将数据空间划分成为有限个单元 (Cell)的网格结构，所有的处理都是以单个单元为对象的。这 样处理的一个突出优点是处理速度快，通常与目标数据库中 记录的个数无关，只与划分数据空间的单元数有关。但此算 法处理方法较粗放，往往影响聚类质量。代表算法有STING、 CLIQUE、WaveCluster、DBCLASD、OptiGrid算法。
(3) 许多数据挖掘算法试图使孤立点影响最小化，或者排除 它们。然而孤立点本身可能是非常有用的，如在欺诈探测中， 孤立点可能预示着欺诈行为的存在。
多元统计期末复习题
多元数据分析练习题第二章多元正态的参数估计一. 判断题（1）若∑∑=),,(~),,,(21μp T p N X X X X 是对角矩阵，则p X X X ,,,21 相互独立。
（ ）（2）多元正态分布的任何边缘分布为正态分布，反之也成立。
（ ）（3）对任意的随机向量T p X X X X ),,,(21 =来说，其协方差矩阵∑是对称矩阵，并且总是半正定的。
（ ）（4）对标准化的随机向量来说，它的协方差矩阵与原来变量的相关系数阵相同。
（ ） （5）若),,(~),,,(21∑=μp T p N X X X X S X ,分别为样本均值和样本协差阵，则S nX 1,分别为∑,μ的无偏估计。
（ ） 二.计算题1. 假设随机向量TX X X X ),,(321=的协方差矩阵为⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---=∑9232443416，试求相关系数矩阵R 。
⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎣⎡----=131413112141211R 2. 假设随机向量Tx x x ),(21=的协方差矩阵为⎥⎦⎤⎢⎣⎡=∑20119，令212211,2x x y x x y -=+=，试求T y y y ),(21=的协方差矩阵。
⎥⎦⎤⎢⎣⎡--=∑2733603.假设⎥⎦⎤⎢⎣⎡---=∑5.005.05.015.0),,(~3A N X μ，其中T)1,2,1(-=μ，⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--=∑411121112，试求Ax y =的分布。
)2224,02(2⎪⎪⎭⎫ ⎝⎛--⎪⎪⎭⎫ ⎝⎛-N 三.证明题1.设)()2()1(,,,n X X X 是来自),(∑μp N 的随机样本，X 为样本均值。
试证明：μ=)(X E ，∑=nX D 1)(。
2.设)()2()1(,,,n X X X 是来自),(∑μp N 的随机样本，S n 11-为样本协差阵。
试证明：∑=-)11(S n E 。
3．证明：若p 维正态随机向量),,,(21'=p X X X X 的协差阵为对角矩阵，则X 的各分量是相互独立的随机变量。
市场研究——聚类分析法
市场研究——聚类分析法
聚类分析法在市场研究中有着广泛的应用。
通过对市场中消费者、产品、品牌等进行聚类分析，可以帮助市场研究人员更好地理解市场细分和
目标受众，并制定针对不同群体的市场营销策略。
下面将详细介绍聚类分
析法的原理、应用和步骤。
聚类分析的原理是将数据样本划分为不同的类别或群组，使得同类之
间的差异最小，而不同类之间的差异最大。
输入聚类分析的数据通常是多
维的，每个维度代表一个变量。
聚类分析的目标是找到一个最优的聚类方案，使得相同类别内的样本相似度最高，而不同类别的样本相似度最低。
聚类分析法的应用非常广泛。
在市场研究中，它可以用于客户细分、
产品定位、市场定位等方面。
通过对消费者进行聚类，可以发现隐藏在市
场中的不同消费者群体，并确定他们的特征、需求和偏好。
对产品和品牌
进行聚类分析，则可以帮助确定产品和品牌的差异化定位和市场竞争策略。
需要注意的是，聚类分析法只是一种分析工具，通过聚类分析得到的
结果并不一定代表真实的市场现象，仅供市场研究人员参考和决策。
在市场研究中，聚类分析法的应用是非常重要的。
它能够帮助市场研
究人员更好地理解市场细分和目标受众，并制定针对不同群体的市场营销
策略。
随着数据量的不断增加和分析技术的不断发展，聚类分析法在市场
研究中的应用前景将更加广阔。
聚类分析方法
聚类分析方法聚类分析是一种常用的数据分析方法，它可以帮助我们将数据集中的对象按照它们的相似性进行分组。
通过聚类分析，我们可以发现数据中的内在结构和规律，从而更好地理解数据。
在本文中，我们将介绍聚类分析的基本概念、常见的聚类方法以及聚类分析的应用场景。
首先，让我们来了解一下聚类分析的基本概念。
聚类分析是一种无监督学习方法，它不需要预先标记的训练数据，而是根据数据对象之间的相似性来进行分组。
在聚类分析中，我们通常会使用距离或相似度作为衡量对象之间关系的指标。
常见的距离指标包括欧氏距离、曼哈顿距离和余弦相似度等。
通过计算对象之间的距离或相似度，我们可以将它们划分到不同的类别中，从而实现数据的聚类。
接下来，让我们来介绍一些常见的聚类方法。
最常用的聚类方法包括层次聚类、K均值聚类和密度聚类。
层次聚类是一种基于对象之间相似性构建层次结构的方法，它可以分为凝聚式层次聚类和分裂式层次聚类。
K均值聚类是一种迭代的聚类方法，它将数据对象划分为K个类别，并通过迭代优化来找到最优的聚类中心。
密度聚类是一种基于数据密度的聚类方法，它可以发现任意形状的聚类簇，并对噪声数据具有较强的鲁棒性。
最后，让我们来看一些聚类分析的应用场景。
聚类分析可以应用于各个领域，例如市场营销、生物信息学、社交网络分析等。
在市场营销中，我们可以利用聚类分析来识别不同的消费群体，并针对不同群体制定个性化的营销策略。
在生物信息学中，聚类分析可以帮助我们发现基因表达数据中的基因模式，并识别相关的生物过程。
在社交网络分析中，我们可以利用聚类分析来发现社交网络中的社区结构，并识别影响力较大的节点。
总之，聚类分析是一种非常有用的数据分析方法，它可以帮助我们发现数据中的内在结构和规律。
通过本文的介绍，相信大家对聚类分析有了更深入的了解，希望能够在实际应用中发挥其价值，为各行各业的发展提供有力支持。
多元统计分析聚类分析
[ ( xi xi ) ][ ( xj x j ) ]
2 2
n
n
1
1
相似矩阵
第三节 八种系统聚类方法
（hierarchical clustering method）
系统聚类法是诸聚类分析方法中使用最多 的一种，按下列步骤进行：
将n个样品各作为一类
计算n个样品两两之间的距离，构成距离矩阵 合并距离最近的两类为一新类 计算新类与当前各类的距离。再合并、计算 ，直至只有一类为止
如果在某一步将类Gp与Gq类合并为Gr，任一类Gk和新 Gr的距离公式为：
当
时，由初等几何知就是上面三角形的中线。
D2（0）
G1={X1}
G1
0
G2
G3
G4
G5
G2={X2}
G3={X3} G4={X4} G5={X5}
1
6.25 36 64
0
2.25 25 49 0 12.25 30.25 0 4 0
（2）相似系数
研究样品间的关系常用距离，研究指标（ 变量）间的关系常用相似系数。 相似系数常用的有：夹角余弦与相关系数
2、对指标（变量）分类（R型）
相似系数的定义
夹角余弦（Cosine）
相似矩阵
变量间相似矩阵
相关系数
ij
( x x )( x x )
1 i i j j n
64
49
30.25
4
0
D2（1）
G6
G3 0
G4
G5
G6={X1, X2}
G3={X3}
0
4
={X4}
G5={X5}
30.25
56.25
聚类分析步骤
聚类分析步骤以教材第五章习题8的数据为例，演示并说明聚类分析的详细步骤:原始数据的输入:丈件（D 霸甸〔口锻国（蜀散惭直I 转快（D 分折（幻圈解〔⑤ 密坏賤序〔史Mt加内容（Q）SUM 帮肋S暗事？* ™ S?鮒*ffl ft韶亟蔚粤箱「专.选项操作:1. 打开SPSS的“分析”-“分类”-“系统聚类”,打开“系统聚类”对话框。
把“食品”、“衣着”等6变量输入待分析变量框；把“地区”输入“标注个案”；“分群”选中“个案”；“输出”选中“统计量”和“图”。
(如下图)相关说明:(1) 系统聚类法是最常用的方法，其他的方法较少使用。
(2) “标注个案”里输入“地区”，在输出结果的距离方阵和聚类树状图里会显示出“北京”、“天津”等，否则SPSS自动用“ 1”、“2”等代替。
(3) “分群”选中“个案”，也就是对北京等16个样本进行分类，而不是对食品等6个变量分类。
(4) 必须选中“输出”中的“统计量”和“图”。
在该例中会输出16个地区的欧氏距离方阵和聚类树状图。
密Ife鸟駝£臭* I必炮区H-qI 1E曲前 -------------输出v熨计養y岡2. 设置分析的统计量打开最右上角的“统计量”对话框，选中“合并进程表”和“相似性矩阵” “聚类成员”选中“无”。
然后点击“继续”。
打开第二个“绘制”对话框，必须选中“树状图”，其他的默认即可打开第三个对话框“方法”：聚类方法选中“最邻近元素”；“度量标准” 选中“区间”的“欧氏距离”；“转换值”选中“标准化”的“ Z 得分”，并且是“按照变量”。
+区町（LD ： E uclidean 肚屈7" T计徹D ； 卡方度豪▼二鼻細^?TEuclicteeri■|i |g |打开第四个对话框“保存”，“聚类成员”选默认的“无”即可 三•分析结果的解读：按照SPSS 俞出结果的先后顺序逐个介绍：1. 欧氏距离矩阵：是16个地区两两之间欧氏距离大小的方阵， 该方阵是应用各 种聚类方法进行聚类的基础。
聚类分析原理
聚类分析原理聚类分析是一种常用的数据分析方法，它可以将数据集中的个体按照相似性进行分组，从而揭示数据内在的结构和规律。
在实际应用中，聚类分析被广泛应用于市场细分、社交网络分析、生物信息学、图像处理等领域。
本文将介绍聚类分析的原理及其常见的方法。
首先，聚类分析的原理是基于样本之间的相似性进行分组。
相似的样本被归为同一类别，而不相似的样本则被划分到不同的类别中。
在进行聚类分析时，我们需要选择合适的相似性度量方法，常见的相似性度量包括欧氏距离、曼哈顿距离、余弦相似度等。
通过计算样本之间的相似性，我们可以构建出样本之间的相似性矩阵，从而为后续的聚类分析提供依据。
其次，聚类分析的方法包括层次聚类和非层次聚类两种。
层次聚类是一种自下而上或自上而下的聚类方法，它通过计算样本之间的相似性来构建聚类树，从而实现对样本的分层聚类。
非层次聚类则是一种直接将样本划分为不同类别的方法，常见的非层次聚类方法包括K均值聚类、DBSCAN聚类等。
不同的聚类方法适用于不同的数据特点和分析目的，选择合适的聚类方法对于获得准确的聚类结果至关重要。
此外，聚类分析还需要考虑到聚类数目的确定。
在进行聚类分析时，我们需要事先确定聚类的数目，这也是聚类分析的一个重要参数。
常见的确定聚类数目的方法包括肘部法则、轮廓系数法等。
通过选择合适的聚类数目，我们可以获得更加准确和有意义的聚类结果。
总之，聚类分析是一种重要的数据分析方法，它可以帮助我们揭示数据内在的结构和规律。
在进行聚类分析时，我们需要选择合适的相似性度量方法、聚类方法和确定聚类数目的方法，以获得准确和有意义的聚类结果。
希望本文能够帮助读者更好地理解聚类分析的原理和方法，从而更好地应用聚类分析于实际问题中。
Python中的数据分析和统计方法
Python中的数据分析和统计方法Python是一门功能强大的编程语言，广泛应用于数据分析和统计方法。
本文将详细介绍Python中常用的数据分析和统计方法，并按类进行章节划分，深入探讨每个章节的具体内容。
第一章：数据预处理在进行数据分析之前，通常需要对原始数据进行清洗和预处理。
Python提供了很多用于数据预处理的库和方法。
其中，pandas是最常用的库之一。
pandas可以用于数据的读取、清洗、转换和合并等操作。
另外，NumPy库也提供了许多用于数组操作和数值运算的函数，可用于数据预处理过程中的一些计算。
第二章：数据可视化数据可视化是数据分析的重要环节，它可以使得数据更加直观和易于理解。
Python中有多个可视化库可以使用，如Matplotlib、Seaborn和Plotly等。
这些库可以生成各种类型的图表，如线图、散点图、柱状图和饼图等。
通过合理选择和使用可视化方法，可以更好地展示数据的分布和趋势。
第三章：统计描述统计描述是对数据进行摘要和概括的过程。
在Python中，可以使用pandas库的describe()函数来计算数据的基本统计量，如均值、标准差、最大值和最小值等。
此外，还可以使用scipy库中的一些函数来计算概率分布、置信区间和假设检验等统计指标。
第四章：回归分析回归分析是数据分析中常用的一种方法，用于探究变量之间的关系和预测未来趋势。
Python中的statsmodels库提供了许多回归分析的方法，如线性回归、逻辑回归和多元回归等。
通过回归分析，可以得到模型的参数估计和拟合优度等指标，进而对未知数据进行预测和推测。
第五章：聚类分析聚类分析是将数据按照相似性进行分组的一种方法。
在Python 中，可以使用scikit-learn库中的KMeans算法来进行聚类分析。
KMeans算法通过迭代计算将数据划分为K个簇，使得同一簇内的数据相似度最高，不同簇之间的相似度最低。
聚类分析可以帮助我们发现数据中潜在的模式和规律。
数据挖掘概念与技术课后答案第二版
数据挖掘概念与技术课后答案第二版第一章：数据挖掘概论1.什么是数据挖掘？数据挖掘是一种通过从大量数据中发现隐藏模式、关系和知识的方法。
它将统计学、机器学习和数据库技术结合起来，用于分析海量的数据，并从中提取出有用的信息。
2.数据挖掘的主要任务有哪些？数据挖掘的主要任务包括分类、回归、聚类、关联规则挖掘和异常检测等。
3.数据挖掘的流程有哪些步骤？数据挖掘的典型流程包括问题定义、数据收集、数据预处理、特征选择、模型构建、模型评估和模型应用等步骤。
4.数据挖掘的应用领域有哪些？数据挖掘的应用领域非常广泛，包括市场营销、金融分析、生物医学、社交网络分析等。
5.数据挖掘的风险和挑战有哪些？数据挖掘的风险和挑战包括隐私保护、数据质量、误差纠正、过拟合和模型解释等。
第二章：数据预处理1.数据预处理的主要任务有哪些？数据预处理的主要任务包括数据清洗、数据集成、数据转换和数据规约等。
2.数据清洗的方法有哪些？数据清洗的方法包括缺失值填补、噪声数据过滤、异常值检测和重复数据处理等。
3.数据集成的方法有哪些？数据集成的方法包括实体识别、属性冲突解决和数据转换等。
4.数据转换的方法有哪些？数据转换的方法包括属性构造、属性选择、规范化和离散化等。
5.数据规约的方法有哪些？数据规约的方法包括维度规约和数值规约等。
第三章：特征选择与数据降维1.什么是特征选择？特征选择是从原始特征集中选择出最具有代表性和区分性的特征子集的过程。
2.特征选择的方法有哪些？特征选择的方法包括过滤式特征选择、包裹式特征选择和嵌入式特征选择等。
3.什么是数据降维？数据降维是将高维数据映射到低维空间的过程，同时保留原始数据的主要信息。
4.数据降维的方法有哪些？数据降维的方法包括主成分分析、线性判别分析和非负矩阵分解等。
5.特征选择和数据降维的目的是什么？特征选择和数据降维的目的是减少数据维度、提高模型训练效果、降低计算复杂度和防止过拟合等。
第四章：分类与预测1.什么是分类？分类是通过训练数据集建立一个分类模型，并将未知数据对象分配到其中的某个类别的过程。
使用R语言进行聚类分析的步骤
使用R语言进行聚类分析的步骤第一章：简介聚类分析是一种将数据集合划分为具有相似特征的组的统计方法。
在许多领域中，聚类分析被广泛应用，包括数据挖掘、生物信息学和市场研究等。
R语言是一种开源的统计分析软件，提供了丰富的聚类分析工具和函数库，使得聚类分析的实施变得简单和高效。
第二章：数据准备在进行聚类分析之前，首先需要准备好数据。
通常，数据以矩阵的形式表示，其中每一行代表一个样本，每一列代表一个特征。
如果存在缺失值或离群值，可以根据具体情况进行处理，例如使用插补方法填充缺失值或删除离群值。
第三章：选择合适的聚类算法R语言提供了多种聚类算法，常用的包括K均值聚类、层次聚类和密度聚类等。
在选择聚类算法时，要考虑数据的特点和分析目标。
例如，如果数据的特征较多且样本数较大，可以选择K均值聚类算法；如果数据具有层次结构，可以使用层次聚类算法。
第四章：确定聚类数目聚类数目的确定是聚类分析的关键步骤之一。
在选择合适的聚类数目时，可以尝试使用手肘法、轮廓系数或树状图等方法。
手肘法通过绘制误差平方和与聚类数目的关系图，找到误差平方和急剧下降的拐点作为聚类数目的估计值。
轮廓系数衡量了聚类的紧密度和分离度，取值范围从-1到1，越接近1表示聚类效果越好。
树状图可以帮助判断合适的聚类数目，通过观察树状图中的层次结构，选取适当的聚类数目。
第五章：聚类分析的实施在R语言中，可以使用各种聚类函数实施聚类分析。
以K均值聚类为例，可以使用kmeans()函数进行分析。
此函数需要输入数据矩阵和聚类数目，然后根据指定的聚类数目将样本分为不同的簇。
聚类结果可以通过打印或绘图等方式进行展示。
第六章：聚类结果评估聚类结果的评估对于判断聚类分析的有效性和准确性非常重要。
常用的评估指标包括轮廓系数、Davies-Bouldin指标和Calinski-Harabasz指数等。
这些指标可以帮助评估聚类结果的质量，并提供一种比较不同聚类算法和聚类数目的方式。
第应用多元统计五章实验题答案
第五章聚类分析
班级：姓名：学号：
5.8 下表是15个上市公司2001年的一些主要财务指标，使用系统聚类法和K
类，所做结果如下：
2）K均值法：在SPSS4类，所做结果如下：
公司分为3类时，分类相同。
5.9 下表是某年我国16个地区农民支出情况的抽样调差数据，每个地区调查了反应每个人平局生活消费支出情况的六个经济指标，试通过统计分析软件用不同
择了以下四个方法，进行系统聚类分析，将16个地区分为4类： 1）组间连接法：
3）最近距离法：
4）最远距离法：
类，但是结果不同。
5.10 根据上题数据通过SPSS 统计分析软件进行快速聚类运算，并与系统聚类分析结果进行比较。
解：K 均值法：在SPSS 中根据K 均值法法，对16个城市为4类，所做结果如下：
出水平较接近，天津、辽宁、吉林等城市农民支出水平较接近。
5.11 表是2003年我国省会城市和计价单列市的主要经济指标：人均GDPX1（元）、人均工业产值X2（元）、客运总量X3(万人)、货运总量X4(万吨)、地方财政预算内收入X5（亿元）、固定资产投资总额X6（亿元）、在岗职工占总人口的比例X7（%）、在岗职工人均收入X8（元）、城乡居民年底储蓄余额X9(亿元)。
试通统计分析软件进行系统聚类分析，并比较何种方法与人们观察到得实际情况较接
37个城市分为3类：
1）组间连接法：
由上可以看出，将37个城市根据农民支出聚为3类时，可见下表
由上可以看出，应用组间连接法将37个城市根据农民支出聚为3类时，可见
由上可以看出，应用组内连接法将16个城市根据农民支出聚为3类时，可见
解：。
论文写作中的实证数据分析工具
论文写作中的实证数据分析工具引言：在当今科技发达的时代，数据已经成为了我们生活和工作中不可分割的一部分。
在学术界，研究人员经常需要进行实证数据分析来验证他们的假设和理论。
本文将讨论在论文写作中常用的实证数据分析工具，并探讨它们在研究中的应用。
第一章：描述统计描述统计是一种最基本的数据分析方法，它用于总结和描述收集的数据。
通过描述统计，研究人员可以计算出数据的均值、中位数、标准差等指标来揭示数据的分布和趋势。
在论文写作中，描述统计提供了基础的数据分析结果，可以帮助读者快速了解研究的基本情况。
第二章：回归分析回归分析是一种用于探索变量之间关系的数据分析方法。
它通过建立数学模型来预测一个或多个自变量对因变量的影响。
在论文写作中，回归分析通常用于验证研究假设，找出变量之间的相关性。
通过回归分析，研究人员可以得出结论并解释变量之间的因果关系。
第三章：方差分析方差分析是一种用于比较不同组之间差异的数据分析方法。
它通过比较组内和组间的变异性来判断不同组别或处理的均值是否有显著性差异。
在论文写作中，方差分析通常用于实验研究或样本比较，用于检验不同条件下的差异，并找出影响结果的因素。
第四章：因子分析因子分析是一种用于揭示变量之间潜在关系的数据分析方法。
它通过将多个变量综合为几个潜在因子来简化数据集。
在论文写作中，因子分析可以帮助研究人员减少变量的复杂性并提取主要因素，从而更好地理解变量之间的关系。
第五章：聚类分析聚类分析是一种用于将相似对象归类的数据分析方法。
它通过测量对象之间的相似性来将它们分组并形成簇。
在论文写作中，聚类分析可以用于分类研究对象、发现群组之间的异同以及分析潜在的关联和模式。
结论：实证数据分析工具在论文写作中起着至关重要的作用。
既可以帮助研究人员总结和描述数据分布的描述统计，也可以验证假设和揭示变量之间的关系的回归分析。
此外，方差分析、因子分析和聚类分析也为研究人员提供了更深入的数据分析工具。
因此，在进行实证研究时，研究人员应该根据自己的研究目的和需求选择合适的数据分析工具，并合理运用它们，以便更好地解答研究问题和推进学术领域的发展。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
4. Lance和Williams 距离
对标准化变量：
xik x jk 1 d ij p k 1 xik x jk
p
5. 配合距离
前几类距离多用于定距和定比尺度数据 ，对于定类和定序变量：
X 1 (V , Q, S , T , K ) X 2 (V , M , S , F , K ) m2 配合数 d12 不配合数 2 2 d12 m 1 m2 不配合数 配合数 2 2 ＝ ＝ 23 5
点A到μ的欧氏距离 12 12 2 , 点B到μ的欧氏距离 12 12 2
点A到μ的马氏距离
1 0.9 1 1 1 1 点B到μ的马氏距离 1.05 0 . 9 1 1 0.19
欧式等距离线
欧氏距离、标准化变量的欧式距 离与马氏距离的比较
μ 0 , Σ 0.9 1
A
B
分别求点A=(1,1)’, 和点B=(1,-1)到均值 的欧式距离和马氏距离
马氏等距离线
Σ 1 1 1 0.9 0.19 0.9 1 1 0.9 1 1 1 1 10 0.19 0.9 1 1
x2 x12 ① x22- x12
d 21 ( x21 x11 ) 2 ( x22 x12 ) 2
k 1 p
x22 x11
x21- x11 ② x21 x1
2. 明氏（Minkowski ）距离
dij [ xik x jk ]
k 1 p 1 q q
q=2
q=1 q=∞
不配合数 配合数 23 5
配合距离例
4种品牌的软饮料在4个方面的特性：是否可乐口味？是 否含有咖啡因？是否节食饮料？是否可口可乐公司产？
可乐味 咖啡因 节食 可口可乐
Coke Pepsi Diet Coke Caffeine-free Diet Coke
距离矩阵
Coke Pepsi Diet Caf free
3. 马氏(Mahalanobis) 距离
明氏距离没有考虑数据中的协方差模式，马 氏距离则考虑了协方差，且不受指标测量单 位的影响：
2 dij ( Xi X j ) ' 1 ( Xi X j )
其中为p维随机向量的协方差矩 阵
Mahalanobis 距离例
已知二维正态总体G的分布为：G～N（,）,其 中 0.9 0 1
变量聚类
一、概述
聚类的实质
根据样本（变量）间的亲疏关系将样本（变量）分 为类，相近的归为一类，差别较大的归为另一类。 所获得的分类应有一定的意义。
聚类分析的关键
亲疏关系的判别：相似性与距离（不相似性） 分类数的确定：分多少类合适
聚类分析的应用
不同地区城镇居民收入和消费状况的分类研究。 区域经济及社会发展水平的分析及全国区域经 济综合评价 产品市场细分：按照消费者的需求特征分成不 同的细分市场
快速聚类(k-means clustering)
模糊聚类
聚类分析数据格式
k
二、距离与相似系数
样本间的亲疏关系通常用距离描述，变 量间的亲疏关系通常用相似系数或相关 系数描述
不同测量尺度的数据，其距离的计算方 法不同
（一）、距离：样本间的亲疏关系
距离的定义：
假设每个样品由p个变量描述，则每个样品 都可以看成p维空间中的一个点，n个样品就 是p维空间中的n个点，则第i样品与第j样品 之间的距离记为dij
dij满足下列条件
dij≥0
dii =0
dij = dji dij ≤ dik + dkj
1. 欧式（Euclidian ）距离
d ij ( xi1 x j1 ) 2 ( xi 2 x j 2 ) 2 ( xip x jp ) 2 [ ( xik x jk ) 2 ]1 2
在儿童生长发育研究中，把以形态学为主的指 标归于一类，以机能为主的指标归于另一类
聚类分析的类型
根据分类的对象
Q型聚类（即样本聚类clustering for individuals） R型聚类（变量聚类clustering for variables)
根据分类的方法：
系统聚类(hierarchical clustering )
x
k 1 n k 1
ki kj n
x
2 2 12 [( xki )( xkj )] k 1
当q=1， dij (1) xik x jk 为绝对值距离，SPSS称为block
p
当q=2，即为欧式距离
当q=∞，有 dij () max xik x jk 1 k p （Chebychev）距离 , 称为切比雪夫
k 1
实例计算
品
距离矩阵
绝对值距离
品
dij (1) xik x jk
1 1 1 1
1 1 1 0
0 0 1 1
1 0 1 1
Coke Pepsi Diet Caf free 1/4 1/4 2/4 2/4 3/4 1/4
（二）相似系数：变量间的亲疏关系
1. 夹角余弦（Cosine）
受相似形的启发而来，AB和CD尽管 长度不一，但形状相似 A C B D
n
Cij
k 1 p
Euclidian距离的平方
2
Euclidian距离
明氏距离的缺点
各指标同等对待（权数相同），不能反 映各指标变异程度上的差异 距离的大小与各指标的观测单位有关， 有时会出现不合理结果
没有考虑指标之间的相关性
当各指标的测量值相差悬殊时，可以先 对数据标准化，然后用标准化后的数据 计算距离
第五章
概述
聚类分析cluster analysis
聚类分析是多元分析的 主要方法之一，主要用 来对大量的样品或变量 进行分类，是初步数据 分析的重要工具之一。
距离与相似系数
系统聚类法
(hierarchical clustering )
快速聚类法
(k-means clustering)