电路分析第三章第一节练习题
电子电路第三章习题及参考答案
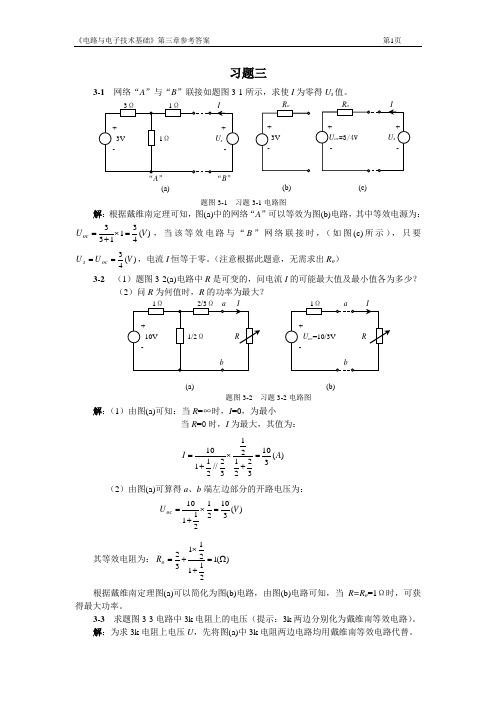
习题三3-1 网络“A ”与“B ”联接如题图3-1所示,求使I 为零得U s 值。
解:根据戴维南定理可知,图(a)中的网络“A ”可以等效为图(b)电路,其中等效电源为:)(431133V U oc =⨯+=,当该等效电路与“B ”网络联接时,(如图(c)所示),只要)(43V U U oc s ==,电流I 恒等于零。
(注意根据此题意,无需求出R o ) 3-2 (1)题图3-2(a)电路中R 是可变的,问电流I 的可能最大值及最小值各为多少? (2)问R 为何值时,R 的功率为最大?解:(1)由图(a)可知:当R =∞时,I =0,为最小当R =0时,I 为最大,其值为: )(31032212132//21110A I =+⨯+=(2)由图(a)可算得a 、b 端左边部分的开路电压为: )(3102121110V U oc =⨯+=其等效电阻为:)(121121132Ω=+⨯+=o R根据戴维南定理图(a)可以简化为图(b)电路,由图(b)电路可知,当R=R o =1Ω时,可获得最大功率。
3-3 求题图3-3电路中3k 电阻上的电压(提示:3k 两边分别化为戴维南等效电路)。
解:为求3k 电阻上电压U ,先将图(a)中3k 电阻两边电路均用戴维南等效电路代替。
“A ” “B ” (a)(b)(c)题图3-1 习题3-1电路图(a)(b)题图3-2 习题3-2电路图对于左边电路由弥尔曼定理有:)(1060//30//20)(20301601201302402012011Ω==-=++-=k R V U o oc对于右边电路由弥尔曼定理有:)(712040//60//60)(7240401601601402406048022Ω===++-=k R V U o oc 所以图(a)可以简化为图(b)电路,由图(b)很容易求得: )(4.5211338037120103207240V U ≈⨯=⨯+++=3-4 试求题图3-4所示的桥式电路中,流过5Ω电阻的电流。
电路分析基础第三章作业答案
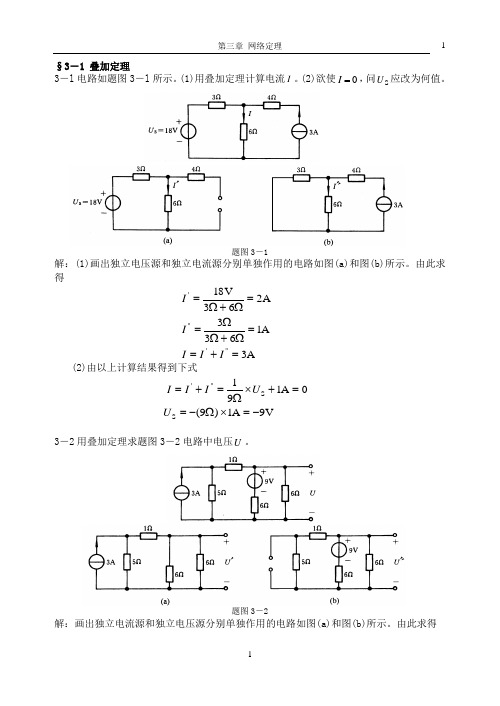
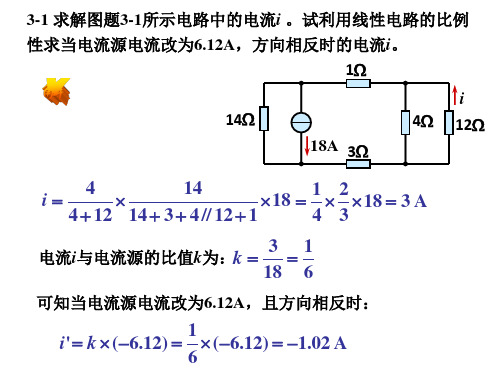
§3-1 叠加定理3-l 电路如题图3-l 所示。
(1)用叠加定理计算电流I 。
(2)欲使0=I,问S U 应改为何值。
题图3-1解:(1)画出独立电压源和独立电流源分别单独作用的电路如图(a)和图(b)所示。
由此求得A3 A1633 A 263V 18"'"'=+==Ω+ΩΩ==Ω+Ω=I I I I I(2)由以上计算结果得到下式V 9A 1)9(0A 191 S S "'-=⨯Ω-==+⨯Ω=+=U U I I I3-2用叠加定理求题图3-2电路中电压U 。
题图3-2解:画出独立电流源和独立电压源分别单独作用的电路如图(a)和图(b)所示。
由此求得V8V 3V 5 V3V 9)363V 53A 3)31(55 "'"'=+=+==⨯Ω+ΩΩ==Ω⨯⨯Ω+Ω+ΩΩ=U U U U U3-3用叠加定理求题图4-3电路中电流i 和电压u 。
题图3-3解:画出独立电压源和独立电流源分别单独作用的电路如图(a)和图(b)所示。
由此求得V )3cos 104( A )3cos 52( V3cos 10)2(A 3cos 53cos 1232332321554V V 8636326363 A 263632V8 "'"'"""''t u u u t i i i t i u t t i u i +=+=-=+==Ω-=-=⨯+-⨯+⨯++==⨯Ω+⨯+ΩΩ+⨯==Ω+⨯+Ω=3-4用叠加定理求题图3-4电路中的电流i 和电压u 。
题图3-4解:画出独立电压源和独立电流源分别单独作用的电路如图(a)和图(b)所示。
由此求得V 3V 6V 3 A 3A 2A 1V 6)-A 4(3A 26V 12 1 0A)4(321 KVL )b (V33A 16V 6 1 0V 62)31( KVL )a ("'"'"""""1""1"'''''1'1'=+-=+==+=+==⨯Ω==Ω=⨯Ω==-⨯Ω++⨯Ω-=⨯Ω-==Ω=⨯Ω==-+Ω+Ωu u u i i i i ui i u i u i i u i i u u i 最后得到得到代入方程电路列出图得到代入方程电路列出图3-6用叠加定理求题图3-6电路中电流i 。
电路分析第三章习题解答
+
10Ω
u1
30Ω
+ uo
78Ω
50V
39Ω
4
图题 3-11 解:选节点 4 为参考节点,列出节点方程为
u n1 = 50V − 1 1⎞ ⎛ 1 ' u n1 + ⎜ + ⎟u n 2 = −i x 10 ⎝ 30 10 ⎠
(1)
(2)
1 ⎞ ⎛ 1 ' ⎜ + ⎟u n3 = i x 39 78 ⎝ ⎠
50Ω
30Ω
i1 5A
15Ω
30Ω
10Ω
5i 1
图题 3-12 解: (1)原电路等效为下面电路
1
50Ω
2
30Ω
i1 5A
15Ω
30Ω
10Ω
5i1 30
3
选节点 3 作为参考节点,列出节点方程
1 ⎞ 1 ⎛1 u n1 ⎜ + ⎟ − u n 2 = 5 A ⎝ 15 50 ⎠ 50 −
(1)
1 1 1 1 ⎞ 1 ⎛ 1 u n1 + ⎜ + + + ⎟u n 2 = − i1 (2) 50 6 ⎝ 50 30 10 30 ⎠
u n1 = 5i
(1)
1 1 ⎛1 1 1⎞ − u n1 + ⎜ + + ⎟u n 2 − u n3 = 0 (2) 3 6 ⎝3 4 6⎠ 1 30 ⎛1 1⎞ − u n 2 + ⎜ + ⎟u n3 = − ix 6 8 ⎝6 8⎠ u n3 − u n1 = 24
辅助方程: i = (1) (2) (3) (4) (5)联立得: (3)
电路分析第三章答案
uS1 I1R1 I 2 R2 uS 2 uS 2 I 4 R4 I 3 R3 I 2 R2 I 3 R3 I 5 R5 ri3
附加方程:
I 3 iS
3-4 电路如图,列写支路电流方程 设电流I1、I2、I3、I4、I5、I6、U5 uS2 R + 列写节点①②③的KCL方程 I2 2 3 I1 I 2 I 5 I 5 I 6 I 4 ① I5 R5 ② iS5 + uS4
p1 4i 2W 8V电压源的功率: p2 8I1 28W
4V电压源的功率:
受控源的功率: p2 U n3 2i1 4W
3-16 用节点分析法,求图 示电路中的电压U1和电流I 解:(1)给节点编号, 以节点④为参考节点,列 写节点方程。
U n1 0.5U1 U n1 U n 2 (1 2) 0.5I 2U n1 U n3 (1 2) 0.5I 2
R3 R 3
3-13 列写图示电路的节点电压方程 解:给节点编号,以节点 4A ③为参考节点,列写节点 ① 方程。 + 1Ω
10V 2A
② + 3V 1Ω
+ 5V ③
2Ω
U n1 (1 0.5) U n 2
Un2 5
10 24 2
3-14 列写图示电路的节点电压方程 解:给节点编号,以节点 4Ω ③为参考节点,列写节点 ① 2Ω ② 方程。 + 2A +
I6
I 2 I3 I6
列写回路1、2、3的 KVL方程
I1 + + U5 − R1 U1 R42 − I4 1 + + uS1 βU1
教科版九年级上册物理 第三章 第一节 电现象

2019-2019学年教科版九年级上册物理第三章第一节电现象一、单选题(共8题;共16分)1.有甲、乙两个不带电的验电器||,现将一根与丝绸摩擦过的玻璃棒与验电器甲接触后||,发现验电器甲上的金属箔张开||,另取带绝缘柄的金属杆将两个验电器的金属球接触||,则()A. 自由电子由甲到乙B. 自由电子由乙到甲C. 摩擦过的丝绸不带电D. 电流方向由乙到甲2.如图所示||,打开水龙头||,放出一股细细的水流||,用在干燥的头发上梳过的塑料梳子靠近水流||,将发生的现象及原因是()A. 水流远离梳子||,因为梳子摩擦后具有磁性排斥水流B. 水流靠近梳子||,因为梳子摩擦后具有磁性吸引水流C. 水流远离梳子||,因为梳子摩擦带电后排斥水流D. 水流靠近梳子||,因为梳子摩擦带电后吸引水流3.如图所示||,小杜同学用与丝绸摩擦过的玻璃棒接触验电器的金属球||,看到验电器的金属箔张开||,在这个过程中()A. 玻璃棒和验电器都带负电荷B. 玻璃棒带正电荷||,验电器带负电荷C. 用丝绸摩擦过的玻璃棒产生了电荷D. 金属箔张开是因为同种电荷相排斥4.如图所示||,已知甲乙两个相同的验电器||,甲带负电||,乙不带电||,拿一根有绝缘柄的金属杆把两个验电器连接起来.下列说法正确的是()A. 甲验电器的金属箔张角变大B. 金属杆中有持续的电流通过C. 乙验电器最终带上正电D. 连接的瞬间||,有电流从乙流向甲5.有两个相同的验电器A和B||,A带负电||,B不带电||,当用金属棒连接A和B的金属球时||,A的金属箔张角变小||,B的金属箔明显张开||,如图所示.则下列说法正确的是()A. 金属棒一定带正电B. 验电器B带上了负电C. 瞬间电流从验电器A流到验电器BD. 金属箔张开是因为金属箔带了异种电荷相互排斥6.如图所示||,是闪电产生的电流通过避雷针的示意图(已知云层带正电).则下列说法中正确的是()A. 产生闪电时||,创造了电荷B. 产生闪电时||,云层失去了原子核C. 云层带正电||,是因为云层得到了电子D. 图中的电流方向是从云层到避雷针7.关于电流、电压和电阻||,下列说法正确的是()A. 电荷的移动就形成了电流B. 导体的电阻越大||,它两端的电压就越高C. 电路中通过的电流越大||,导体的电阻就越小D. 自由电子定向移动的方向与电流的方向相反8.如图所示||,小杜同学用与丝绸摩擦过的玻璃棒接触验电器的金属球||,看到验电器的金属箔张开||,在这个过程中()A. 玻璃棒和验电器都带负电荷B. 玻璃棒带正电荷||,验电器带负电荷C. 用丝绸摩擦过的玻璃棒产生了电荷D. 金属箔张开是因为同种电荷相排斥二、多选题(共1题;共3分)9.关于电流的方向||,下列说法中不正确的是()A. 正电荷的运动方向就是电流方向B. 自由电子的定向移动方向都是电流的方向C. 金属导体中的电流方向跟自由电子的实际移动方向相反D. 在酸碱盐的水溶液中有自由的正负离子||,所以电流方向不能确定三、填空题(共4题;共7分)10.工厂里经常使用静电除尘技术||,用一块带电的金属板||,把浮尘吸附在金属板上||,静电除尘的原理是________ ||。
电路分析基础第3章习题答案
3-16 电路如图题3-16所示,其中g=1/2S。(1)试用叠加方法求 电压u;(2)求电压源、电流源和受控源对电路提供的功率。
-6V+
5A
+
5A
+
2 u 4
-
gu
2 u1 4
-
gu1
(1) (a)5A电流源单独作用时
11 ( 2 4)u1 5 gu1
uab2
4 //
4 // 6
6 4 //
6
uS
1 2
uS
(3)根据叠加定理
uab
uab1 uab2
4
uS 2
0
则可得 uS 8 V
3-8 电路如图题3-8所示,试填写下表:
根据线性电路的叠加定理的特点,可设 i k1uS1 k2uS2
由表中的第一行数据,可得
0.8 mA
(3)6mA电流源单独作用 i3
(2 5) 6103 253
4.2 mA
(4)根据叠加定理 i i1 i2 i3 0.4 0.8 4.2 3 mA
则3k电阻的功率为 P Ri2 3103 (3103 )2 27mW
3
3
+4V- 1
+
+ 2 u
2A μu -
-
i
+
2 u -
1 + 2A μu
i2 -
(2)2A电流源单独作用
3i2 u 2(i2 2) 0
u 2(i2 2)
5i2 16 得 i2 3.2 A
(3)根据叠加定理 i i1 i2 0.8 3.2 4 A
电工技术第3章李中发版课后习题及详细解答
电工技术第3章(李中发版)课后习题及详细解答第3章单相正弦电路分析3.1 已知正弦电压(V)、(V),则u1与u2的相位差为,是否正确?为什么?分析讨论相位差问题时应当注意,只有同频率正弦量才能对相位进行比较。
这是因为只有同频率正弦量在任意时刻的相位差是恒定的,能够确定超前、滞后的关系,而不同频率正弦量的相位差是随时间变化的,无法确定超前、滞后的关系,因此不能进行相位的比较。
解不正确。
因为u1的角频率为ω,而u2的角频率为2ω,两者的频率不同,相位差随时间变化,无法确定超前、滞后的关系,因此不能进行相位的比较。
3.2 已知某正弦电流的有效值为10 A,频率为50 Hz,初相为45°。
(1)写出该电流的正弦函数表达式,并画出波形图;(2)求该正弦电流在s时的相位和瞬时值。
解(1)由题设已知正弦电流的有效值A,频率Hz,初相。
由频率f可得角频率ω为:(rad/s)所以,该电流的正弦函数表达式为:(A)波形图如图3.7所示。
(2)s时的相位为:(rad)瞬时值为:(A)3.3 已知正弦电流(A)、(A),试求i1与i2的振幅、频率、初相、有效值和相位差,并画出其波形图。
解i1与i2的振幅分别为:(A)(A)频率分别为:(Hz)初相分别为:有效值分别为:(A)(A)i1与i2的相位差为:说明i 1超前i2。
波形图如图3.8所示。
图3.7 习题3.2解答用图图3.8 习题3.3解答用图3.4 设,,试计算、、AB、。
分析复数可用复平面上的有向线段、代数型、三角函数型和指数型(极坐标型)等形式表示。
复数的加减运算就是将实部和虚部分别进行加减,因而采用代数型比较方便。
复数的乘法运算就是将模相乘而辐角相加,复数的除法运算就是将模相除而辐角相减,因而采用指数型(极坐标型)比较方便。
解3.5 写出下列各正弦量所对应的相量,并画出其相量图。
(1)(mA)(2)(A)(3)(V)(4)(V)分析用相量来表示正弦量,就是用一个复数来反映正弦量的振幅(或有效值)和初相,即用相量的模来代表正弦量的振幅(或有效值),用相量的辐角来代表正弦量的初相。
《电路分析基础(史健芳)》第三章习题详细解答
P15A 70 15 1050W
图 3-10b
U 20V
计算题 10( b)解用图
P1 10 10 100W P2 10 20 200W P3 20 60 1200W P10V PU P15A P1 P2 P3
4
( b)解: 16I 6 10 U 3U 15
25 U 10I 3U 15
得到: U 30V , I 4A P3U 12 90 1080W P6A 6 80 480W P1 10 10 100W P2 8 4 32W P3 12 4 48W P10 6 60 360W P15 2 30 60W P3 U P6A P1 P2 P3 P10 P15
制量的补充方程 D.若采用回路电流法, 对列写的方程进行化简, 在最终的表达式中互阻始终是相等的,
即: Rij =R ji
3.2 填空题
1. 对于具有 n 个结点 b 条支路的电路,可列出
n-1
个独立的 KCL 方程,可
列出 b-n+1
个独立的 KVL方程。
2. 具有两个引出端钮的电路称为
二端(单口) 网络,其内部包含电源的称为
5.对于回路电流法中的电流源,下列叙述中, ( D )是错误的。 A .对于有伴电流源,可利用电源等效变换转化为电压源后,再列写回路电流方程
B.对于无伴电流源,可选择合适的回路,使只有一个回路电流流过该无伴电流源,则 该回路电流为已知,可少列一个方程
C.对于无伴电流源,可添加该无伴电流源两端电压这一新的未知量,只需多列一个无 伴电流源电流与回路电流之间关系的辅助方程即可
11. 电路如图 x3.11 所示,设法分别只用一个方程求得
解: (6 2) U A 2 6 20 6
电路分析基础习题第三章答案
选择题可利用电源等效变换转化为电流源后,再列写结点电压方程 可选择该无伴电压源的负极性端为参考结点,则该无伴电压源正极性端对应的结点 电压为已知,可少列一个方程 C.可添加流过该无伴电压源电流这一新的未知量,只需多列一个该无伴电压源电压与 结点电压之间关系的辅助方程即可D.无伴受控电压源可先当作独立电压源处理,列写结点电压方程,再添加用结点电压 表示控制量的补充方程A.对于有伴电流源,可利用电源等效变换转化为电压源后,再列写回路电流方程B.对于无伴电流源,可选择合适的回路,使只有一个回路电流流过该无伴电流源,则 该回路电流为已知,可少列一个方程C 对于无伴电流源,可添加该无伴电流源两端电压这一新的未知量,只需多列一个无 伴电流源电流与回路电流之间关系的辅助方程即可对于含有受控源的电路,下列叙述中, ( D )是错误的。
在结点电压法中,当受控源的控制量不是结点电压时,需要添加用结点电压表示控 制量的补充方程 C 在回路电流法中,当受控源的控制量不是回路电流时,需要添加用回路电流表示控第3章A . 受控源可先当作独立电源处理,列写电路方程1.必须设立电路参考点后才能求解电路的方法是( )。
A . 支路电流法B.回路电流法C 节点电压法D .2b 法2. 对于一个具有 n 个结点、b 条支路的电路,他的 KVL 独立方程数为( B )个。
A . n-1B . b-n+1C . b-nD . b-n-13. 对于一个具有 n 个结点、b 条支路的电路列写结点电压方程,需要列写( )。
A . (n-1 )个KVL 方程B .( b-n+1 )个 KCL 方程C . (n-1 )个KCL 方程D .( b-n-1 )个 KCL 方程4. 对于结点电压法中的无伴电压源,下列叙述中,)是错误的。
A .B .5.对于回路电流法中的电流源,下列叙述中,D )是错误的。
D . 电流源两端的电压通常为零6. B .制量的补充方程列出 b-n+1个独立的KVL 方程。
电路分析试题与答案(第三章)
相量图形:1、下图中,R i=6Q, L=0.3H, R2=6.25Q, C=0.012F,u(t)= 1^2cos(10t),求稳态电流i 1、i 2和i 3,并画出电路的相量图。
R1 i1 L解:U 10 00VR2和C 的并联阻抗Z仁R2〃 (1/j C) =(4-j3) Q,输入阻抗Z = R+j L+Z1 =10Q,贝U: I1U 10 0 1 00AZ 1012丛0.8 36.87° AR213j CU20.6 53.130 A所以:112cos(10t)A120.8、2cos(10t 36.87 )Ai2 0.6.2cos(10t 53.13 )A相量图见上右图2、下图所示电路,A、B间的阻抗模值Z为5kQ,电源角频率3 =1000rad/s , 为使U1超前U2300,求R和C的值。
B联列(1)、(2)两式得 R=2.5kQ, C=0.231 卩 F3、测量阻抗Z 的电路如下图所示。
已知 R=20Q,巳=6.5 Q,在工频(f =50Hz) 下,当调节触点c 使 志=5Q 时,电压表的读数最小,其值为30V,此时电源电压 为100V 。
试求Z 及其组成的元件的参数值。
(注意:调节触点C ,只能改变U cd 的实部,电压表读数最小,也就是使实部为零,U cd 为纯虚数,即U cd =±j30V)解:U cdR acUR^UR R 2 Z调节触点C ,只能改变U cd 的实部,其值最小,也就是使实部为零,U cd 为纯虚数,即U cd =± j30V , 因此上式可表示为:± j 30=-25+(100 6.5)/(6.5+ Z) 解得:Z=(4.15 ± j 12.79) Q 故:艮=4.15QL=40.7mH C=249 卩 F4、电路如下图所示,已知f=1kHz , U=10V , U 1=4V , U 2=8V 。
求 R 和 L 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
例4
电流i 计算电压u电流 。 电流
i (1) = 2A
10V电源作用: 电源作用: 电源作用
+ 10V -
i
2Ω Ω
5A + 1Ω Ω + 2i - u -
i (1) = (10 − 2i(1) ) /(2 +1)
( 2)
u(1) = 1× i (1) + 2i (1) = 3i (1) = 6V
10V电源作用: 电源作用: 电源作用
3 2 - u = ( − ) ×10 = 2V 5 5 2×3 (2) × 2× 2 = 4.8V 2A电源作用:u = 电源作用: 电源作用 2+3
u = 6.8 V
P = 6.8×2 =13.6W
+
3Ω Ω
画出分 电路图 10V -
+
2Ω + Ω
) U(1) - 3Ω Ω
5A电源作用: 2i 电源作用: 电源作用
+1×(5 + i ) + 2i
( 2)
( 2)
=0
i (2) = −1A
受控源始 终保留
u = −2i
( 2)
( 2)
= −2×(−1Байду номын сангаас = 2V
i = 2 + (−1) = 1A
1Ω Ω ) u(1) + (1) 2i - - +
u = 6+ 2 = 8 V
iS
无源 线性 网络
i
研 究 激 励 和 响 应 关 系 的 实
3 求 uS = - V , iS = 5A 时, 响应 i =?
解
根据叠加定理, 根据叠加定理,有: 代入实验数据,得: 代入实验数据,
k1 + k2 = 2 2k1 − k2 = 1
i = k1iS + k2uS
k1 = 1 k2 = 1
解
则
采用倒推法: 采用倒推法:设i'=1A。 。
i us = ' i' us
us 51 即 i = ' i' = ×1 = 1.5A us 34
齐性原理
线性电路中,所有激励(独立源)都增大(或减小) 线性电路中,所有激励(独立源)都增大(或减小)同样 的倍数,则电路中响应(电压或电流)也增大(或减小) 的倍数,则电路中响应(电压或电流)也增大(或减小)同样 的倍数。 的倍数。 当激励只有一个时,则响应与激励成正比。 当激励只有一个时,则响应与激励成正比。
) i(1) + 画出分 电路图 10V
2Ω Ω
+
i (2)
2Ω Ω
-
5A + 1Ω Ω u(2) + (2) 2i - -
例5
封装好的电路如图, 封装好的电路如图,已知下 + 列实验数据: 列实验数据:
uS
-
V 当 uS = 1 , iS = 1A 时, 响应 i = 2A V 当 uS = −1 , iS = 2A 时, 响应 i = 1A
画出分 电路图
8Ω Ω – 12V + 2Ω Ω
6Ω Ω 3Ω Ω
+
+ U(1) -
8Ω Ω 2Ω Ω
3A
6Ω Ω + ) U(2) 3Ω Ω -
例2
求电流源的电压和发出 的功率
(1)
+ 10V
2Ω + 2A Ω u 3Ω Ω 2Ω Ω 为两个简 单电路 2Ω + 2A Ω ) U(2) 3Ω Ω 2Ω Ω - 3Ω Ω - 3Ω Ω
( 2)
u = u(1) + u(2) = 9 + 8 = 17V
i
(2) ) u (2)
画出分 电路图 6Ω Ω
+ (1) - u ) 1Ω Ω 3Ω Ω
3A
+
6Ω Ω - 6V +
3Ω + - Ω 1Ω Ω + 12V 2A -
说明:叠加方式是任意的,可以一次一个独立源单独作用, 说明:叠加方式是任意的,可以一次一个独立源单独作用, 也可以一次几个独立源同时作用,取决于使分析计算简便。 也可以一次几个独立源同时作用,取决于使分析计算简便。
2Ω Ω
例3
(1)
计算电压u。 6Ω Ω - 6V + 3Ω Ω
u + - 3A + 12V - 1Ω Ω 2A
3A电流源作用: 电流源作用: 电流源作用
u = (6 // 3+1) ×3 = 9V
其余电源作用: 其余电源作用:
i = (6 +12) /(6 + 3) = 2A u(2) = 6i (2) − 6 + 2×1 = 8V
i = uS + iS = −3+ 5 = 2A
齐性原理的应用 2. 齐性原理的应用 例6. RL=2Ω R1=1 Ω R2=1 Ω us=51V 求电流 i 。 Ω
R1 21A R1 8A R1 3A + 3V – + 21V– + 8V – + + R2 us 13A R2 5A R2 – –us'=34V i i '=1A 2 RL A + 2V –
1. 叠加定理的应用 例1 解
(1)
求电压U. 求电压
8Ω Ω – 12V + 2Ω Ω
3A
6Ω Ω + 3Ω U Ω -
12 V 12V电源作用: U = − ×3 = −4 电源作用: 电源作用 9 3A电源作用: U(2) = (6 // 3) ×3 = 6 电源作用: 电源作用 V
U = −4 + 6 = 2V
