一元线性回归模型案例分析
一元线性回归案例
S=963.191+18.501R
例9. CEO薪水与股本回报率
OLS回归线为 S=963.191+18.501R N=209, R^2=0.0132
企业股本回报率只能解释薪水变异中的 1.3%.
例2. 一个简单的工资方程
美国研究者以1976年的526名美国工人为样 本，OLS回归方程为：
W=-0.90 +0.54 E 这里W单位为美元/小时，E单位为年. E平均工资计算为5.90美元/小时. 根据消费者价格指数，这一数值相当于2003
年的19.06美元.
例2. 一个简单的工资方程
对同样的数据，但是把log(w)作为因变量， 得到的回归方程为：
Log(invpc)=-0.550+1.24log(price) (0.043) (0.382)
N=42 R^2=0.208 显著性检验不明显,事实上这一关系也是错误的,未
来我们将加上时间序列分析中特有的趋势分析说 名这个问题.
例8. 集装箱吞吐量与外贸额
2001-2006年中国集装箱吞吐量增长与外贸 额增长的弹性分析.以Y表示集装箱吞吐量( 百万标准箱),X表示外贸额(百亿美元).
出勤率无关，但这几乎不可能.
例5. 学校的数学成绩与学校午餐项目
以math10表示高中十年级学生在一次标准化 数学考试中通过的百分比.lnchprg表示有资 格接受午餐计划的学生的百分比.
若其他条件不变,若学生太贫穷不能保证正常 饮食,可以有资格接受学校午餐项目的资助, 他的成绩应有所提高.
例5. 学校的数学成绩与学校午餐项目
1992-1993学年美国密歇根州408所高中的 数据的OLS回归方程:
一元线性回归模型典型例题分析
第二章 一元线性回归模型典型例题分析例1、令kids 表示一名妇女生育孩子的数目，educ 表示该妇女接受过教育的年数。
生育率对教育年数的简单回归模型为μββ++=educ kids 10（1）随机扰动项μ包含什么样的因素？它们可能与教育水平相关吗？（2）上述简单回归分析能够揭示教育对生育率在其他条件不变下的影响吗？请解释。
例2．已知回归模型μβα++=N E ，式中E 为某类公司一名新员工的起始薪金（元），N 为所受教育水平（年）。
随机扰动项μ的分布未知，其他所有假设都满足。
如果被解释变量新员工起始薪金的计量单位由元改为100元，估计的截距项与斜率项有无变化？如果解释变量所受教育水平的度量单位由年改为月，估计的截距项与斜率项有无变化？例3．对于人均存款与人均收入之间的关系式t t t Y S μβα++=使用美国36年的年度数据得如下估计模型，括号内为标准差：)011.0()105.151(067.0105.384ˆtt Y S +=＝0.538 023.199ˆ=σ （1）β的经济解释是什么？（2）α和β的符号是什么？为什么？实际的符号与你的直觉一致吗？如果有冲突的话，你可以给出可能的原因吗？（3）对于拟合优度你有什么看法吗？ （4）检验统计值？例4．下列方程哪些是正确的？哪些是错误的？为什么？⑴ y xt n t t=+=αβ12,,, ⑵ yx t n t tt=++=αβμ12,,, ⑶ y x t n t t t=++= ,,,αβμ12⑷ ,,,y x t n t t t =++=αβμ12 ⑸ y x t n t t =+= ,,,αβ12 ⑹ ,,,y x t n t t=+=αβ12 ⑺ y x t n t t t =++= ,,,αβμ12 ⑻ ,,,y x t n t t t=++=αβμ12 其中带“＾”者表示“估计值”。
例5．对于过原点回归模型i i i u X Y +=1β ，试证明∑=∧221)(iu X Var σβ例6、对没有截距项的一元回归模型i i i X Y μβ+=1称之为过原点回归（regression through the origin ）。
一元线性回归案例
例8. 集装箱吞吐量与外贸额
2001-2006年中国集装箱吞吐量增长与外贸 额增长的弹性分析.以Y表示集装箱吞吐量 (百万标准箱),X表示外贸额(百亿美元). OLS回归方程为 Y=3.7667+0.509X (2.06) (31.78) t (5)=2.776 n=6 R^2=0.996
0.1
例8. 集装箱吞吐量与外贸额
例8. 集装箱吞吐量与外贸额
2001-2007年中国集装箱吞吐量增长与外贸 额增长的弹性分析.以Y表示集装箱吞吐量 增长率(%),X表示外贸额增长率(%). OLS回归方程为 Y=18.449+0.3155X (2.3982) (1.078) t (5)=2.015 n=7 R^2=0.1887
0.1
例4. 考试分数与出勤率
假如期末考试的分数(score)取决于出勤率 (attend)和影响考试成绩的其他无法观测因素 （如学生能力等）： score= β1+β2 attend+u 许多不加分析的回归发现： 这一回归中β2 〈0，即分数与出勤率负相关. 这一模型在什么情况下满足均值独立条件？ 除非学生学习能力、学习攻击、年龄及其他因素与 出勤率无关，但这几乎不可能.
例3. 静态菲利普斯曲线
时间序列数据 令inf(t)表示年通货膨胀率,unem(t)表示事业率, 下 列菲利普斯曲线假定了一个不变的自然失业率和 固定的通货膨胀率预期. Inf(t)=β1+β2 unem(t)+u 依据1948-1996年美国经济数据, OLS回归方程为 Inf(t)=1.42+0.468 unem(t) (1.72) (0.289) n=49 R^2=0.053
例5. 学校的数学成绩与学校午餐项目
一元线性回归案例spss
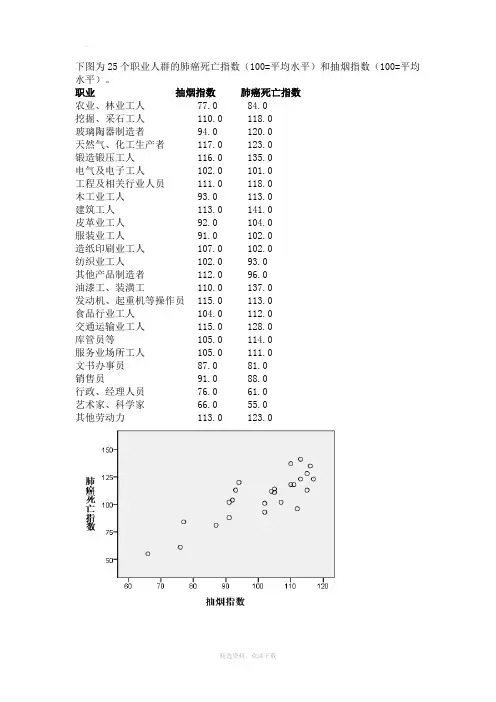
下图为25个职业人群的肺癌死亡指数（100=平均水平）和抽烟指数（100=平均水平）。
职业抽烟指数肺癌死亡指数农业、林业工人77.0 84.0挖掘、采石工人110.0 118.0玻璃陶器制造者94.0 120.0天然气、化工生产者117.0 123.0锻造锻压工人116.0 135.0电气及电子工人102.0 101.0工程及相关行业人员111.0 118.0木工业工人93.0 113.0建筑工人113.0 141.0皮革业工人92.0 104.0服装业工人91.0 102.0造纸印刷业工人107.0 102.0纺织业工人102.0 93.0其他产品制造者112.0 96.0油漆工、装潢工110.0 137.0发动机、起重机等操作员115.0 113.0食品行业工人104.0 112.0交通运输业工人115.0 128.0库管员等105.0 114.0服务业场所工人105.0 111.0文书办事员87.0 81.0销售员91.0 88.0行政、经理人员76.0 61.0艺术家、科学家66.0 55.0其他劳动力113.0 123.0散点图呈线性关系令Y=肺癌死亡指数，X=抽烟指数，做线性回归分析如下：表2中R=0.839 表示两变量高度相关R方=0.703 表示拟合较好，散点相对集中于回归线表3中sig.<0.05 则自变量与因变量具有显著的线性关系，即可以用回归模型表示表4中自变量sig.<0.05 则自变量对因变量的线性影响是显著的由此得到抽烟指数及肺癌死亡指数的一元回归方程：Y=-24.421+1.301X即抽烟指数每变动一个单位则肺癌死亡指数平均变动1.301个单位Welcome !!! 欢迎您的下载，资料仅供参考！。
一元线性回归分析案例
求根据一名女大学生的身高预报她的体重的回归方程，并预报一名身高为 172cm的女大学生的体重。
解：1、选取身高为自变量x，体重为因变量y，作散点图：
2、由散点图知道身高和体重有比较好的线性相 关关系，因此可以用线性回归方程刻画它们之间 的关系。
第17页/共39页
课题：选修2-3 8.5 回归分析案例
分析：由于问题中要求根 据身高预报体重，因此选 取身高为自变量，体重为 因变量．
再冷的石头，坐上三年也会暖 !
1. 散点图；
2.回归方程： yˆ 0.849x 85.172 身高172cm女大学生体重 yˆ = 0.849×172 - 85.712 = 60.316(kg)
本例中, r=0.798>0.75．这表明体重与身高有很强的线性相关关系，从而也表明我们 建立的回归模型是有意义的。
xi2
2
nx
,......(2)
i 1
i 1
其中x
1 n
n i 1
xi ,
y
1 n
n i 1
yi .
(x, y) 称为样本点的中心。
第8页/共39页
课题：选修2-3 8.5 回归分析案例
再冷的石头，坐上三年也会暖 !
1、回归直线方程
1、所求直线方程叫做回归直线方程；
相应的直线叫做回归直线。
2、对两个变量进行的线性分析叫做线性回归分析。
然后，我们可以通过残差 e1, e2 , , en 来判断模型拟合的效果，
判断原始数据中是否存在可疑数据，这方面的分析工作称为残差分析。
表3-2列出了女大学生身高和体重的原始数据以及相应的残差数据。
编号 1
2
3
4
5
一元回归案例数据
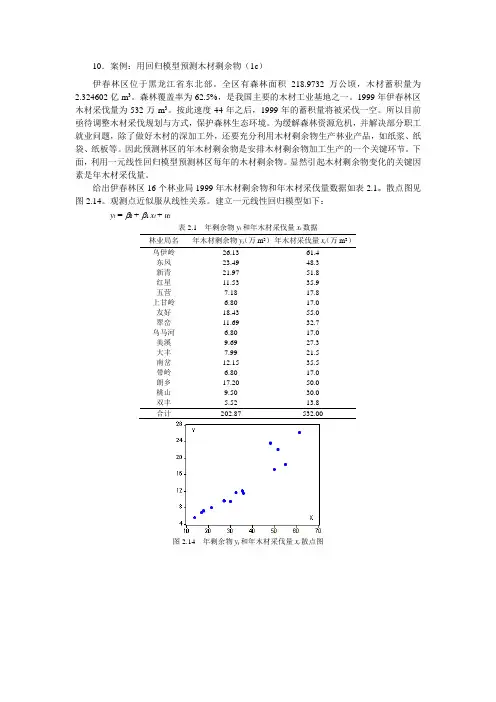
10．案例：用回归模型预测木材剩余物（1c）伊春林区位于黑龙江省东北部。
全区有森林面积218.9732万公顷，木材蓄积量为2.324602亿m3。
森林覆盖率为62.5%，是我国主要的木材工业基地之一。
1999年伊春林区木材采伐量为532万m3。
按此速度44年之后，1999年的蓄积量将被采伐一空。
所以目前亟待调整木材采伐规划与方式，保护森林生态环境。
为缓解森林资源危机，并解决部分职工就业问题，除了做好木材的深加工外，还要充分利用木材剩余物生产林业产品，如纸浆、纸袋、纸板等。
因此预测林区的年木材剩余物是安排木材剩余物加工生产的一个关键环节。
下面，利用一元线性回归模型预测林区每年的木材剩余物。
显然引起木材剩余物变化的关键因素是年木材采伐量。
给出伊春林区16个林业局1999年木材剩余物和年木材采伐量数据如表2.1。
散点图见图2.14。
观测点近似服从线性关系。
建立一元线性回归模型如下：y t = β0 + β1 x t + u t表2.1 年剩余物y t和年木材采伐量x t数据林业局名年木材剩余物y t（万m3）年木材采伐量x t（万m3）乌伊岭26.13 61.4东风23.49 48.3新青21.97 51.8红星11.53 35.9五营7.18 17.8上甘岭 6.80 17.0友好18.43 55.0翠峦11.69 32.7乌马河 6.80 17.0美溪9.69 27.3大丰7.99 21.5南岔12.15 35.5带岭 6.80 17.0朗乡17.20 50.0桃山9.50 30.0双丰 5.52 13.8合计202.87 532.00图2.14 年剩余物y t和年木材采伐量x t散点图图2.15 EViews 输出结果EViews 估计结果见图2.15。
建立EViews 数据文件的方法见附录1。
在已建立Eviews 数据文件的基础上，进行OLS 估计的操作步骤如下：打开工作文件，从主菜单上点击Quick 键，选Estimate Equation 功能。
一元线性回归案例
8.5一元线性回归案例一、教学内容与教学对象分析学生将在必修课程学习统计的基础上，通过对典型案例的讨论，了解和使用一些常用的统计方法，进一步体会运用统计方法解决实际问题的基本思想，认识统计方法在决策中的作用。
二、学习目标1、知识与技能通过本节的学习，了解回归分析的基本思想，会对两个变量进行回归分析，明确建立回归模型的基本步骤，并对具体问题进行回归分析，解决实际应用问题。
2、过程与方法 本节的学习，应该让学生通过实际问题去理解回归分析的必要性，明确回归分析的基本思想，从散点图中点的分布上我们发现直接求回归直线方程存在明显的不足，从中引导学生去发现解决问题的新思路—进行回归分析，进而介绍残差分析的方法和利用R 的平方来表示解释变量对于预报变量变化的贡献率，从中选择较为合理的回归方程，最后是建立回归模型基本步骤。
3、情感、态度与价值观 通过本节课的学习，首先让显示了解回归分析的必要性和回归分析的基本思想，明确回归分析的基本方法和基本步骤，培养我们利用整体的观点和互相联系的观点，来分析问题，进一步加强数学的应用意识，培养学生学好数学、用好数学的信心。
加强与现实生活的联系，以科学的态度评价两个变量的相关系。
教学中适当地增加学生合作与交流的机会，多从实际生活中找出例子，使学生在学习的同时。
体会与他人合作的重要性，理解处理问题的方法与结论的联系，形成实事求是的严谨的治学态度和锲而不舍的求学精神。
培养学生运用所学知识，解决实际问题的能力。
三、教学重点、难点教学重点：熟练掌握回归分析的步骤；各相关指数、建立回归模型的步骤；通过探究使学生体会有些非线性模型通过变换可以转化为线性回归模型，了解在解决实际问题的过程中寻找更好的模型的方法。
教学难点：求回归系数 a , b ；相关指数的计算、残差分析；了解常用函数的图象特点，选择不同的模型建模，并通过比较相关指数对不同的模型进行比较。
四、教学策略： 教学方法：诱思探究教学法学习方法：自主探究、观察发现、合作交流、归纳总结。
8.2.1一元线性回归模型
确定儿子身高Y 吗？
e 不能，因为随机误差 不可事先设定.
四、模型理解
• 当父亲身高为 xi ，对应的儿子身高 yi 不是唯一
确定的,而是有很多可能的取值，记作
yi bxi a e
它们的均值为：
E( yi ) E(bxi a e) bE(xi ) E(a) E(e) bxi a 0 bxi a.
（2）销售量与广告费用之间的关系能否用一元线性回归模
型 Y bx a e,
来刻画？
E(e) 0, D(e) 2.
（3）请说明模型中 bx a与e分别表示什么？本题中 e 的具
体含义是什么？
1 2 3 4 5 6 7 8 9 10 11 12 13 14 174 170 173 169 182 172 180 172 168 166 182 173 164 180 176 176 170 170 185 176 178 174 170 168 178 172 165 182
儿子身高 父亲身高
176 176 170 170 185 176 178 174 170 168 178 172 165 182
问题1 由这组样本数据能否推断儿子的身高
与父亲的身高有关系？关系的相关程度如 何？是函数关系还是线性相关关系？为什 么？
（1）散点图
（2）相关系数 r 0.886
选择性必修三8.2.1 ggb文件.ggb (命令行)
问题8 • 一元线性回归模型有何作用？
当父亲身高为 xi 时可以通过
E( yi ) bxi a
了解儿子身高的总体情况，从而预测儿子的 身高.
问题9
• 产生随机误差的原因有哪些？ • （1）除父亲身高外其他可能影响儿子身高
一元线性回归模型案例
一元线性回归模型案例一元线性回归模型是统计学中最基本、应用最广泛的一种回归分析方法，可以用来探究自变量与因变量之间的线性关系。
一元线性回归模型的数学公式为：y = β0 + β1x，其中y表示因变量，x表示自变量，β0和β1分别为截距和斜率。
下面以一个实际案例来说明一元线性回归模型的应用。
假设我们有一组数据，其中x表示一个房屋的面积，y表示该房屋的售价，我们想利用一元线性回归模型来预测房屋的售价。
首先，我们需要收集一组已知数据，包括房屋的面积和售价。
假设我们收集了10个不同房屋的面积和售价数据，如下所示：房屋面积（x）（平方米）售价（y）（万元）80 12090 130100 140110 150120 160130 170140 180150 190160 200170 210我们可以根据这组数据绘制散点图，横坐标表示房屋面积x，纵坐标表示售价y，如下所示：（插入散点图）接下来，我们可以利用最小二乘法来拟合一条直线，使其能够最好地拟合这些散点。
最小二乘法是一种最小化误差平方和的方法，可以得到最优的拟合直线。
根据一元线性回归模型的公式，可以通过计算拟合直线的斜率β1和截距β0来实现最小二乘法。
其中，斜率β1可以通过下式计算得到：β1 = n∑(xiyi) - (∑xi)(∑yi)n∑(xi^2) - (∑xi)^2截距β0可以通过下式计算得到：β0 = (1/n)∑yi - β1(1/n)∑xi通过带入已知数据，我们可以计算得到斜率β1和截距β0的具体值。
在本例中，计算结果如下：β1 ≈ 1.0667β0 ≈ 108.6667最后，利用得到的斜率β1和截距β0，我们可以得到一元线性回归模型的具体公式为：y ≈ 108.6667 + 1.0667x我们可以利用这个回归模型进行预测。
例如，如果有一个房屋的面积为130平方米，那么根据回归模型，可以预测该房屋的售价为170 + 108.6667 ≈ 278.6667万元。
一元线性规划及先关分析案例
3
层次分析法和德尔菲法
哈尔滨城市综合承载力评价指标体系构建
城市综合承载力的评价实质上就是判定该城市现有的承载力能否支撑目前
的人口规模及人类各种经济社会活动的规模和强度。衡量城市综合承载力需
要考虑以下几个方面： 1)环境承载力2)资源承载力3)基础设施承载力4)生态系统承载力5)安全承载 力6)公共服务承载力7)科学技术承载力8)社会文化承载力 通过德尔菲法和参考已有的研究成果等初步确立了1个一级指标，8个二级 指标，49个三级指标，本次参与德尔菲法的专家组由15位专家组成，包括住 建部城市建设司人员3人、城乡规划司人员2人、哈尔滨城乡规划局人员4人 、哈尔滨市政府人员2人、哈尔滨社会研究所人员4人，所有专家都具有多年 的工作经历和丰富的实践经验，充分了解城市发展历程和城市发展动力所在 。应用sPss软件对城市综合承载力评价指标进行相关性检验等一系列优化处
5.采用时间尺度分析的方法，提取交通流的时间一尺度耦合特征考虑到每个网格站点的负载量，得到时间一尺 度耦合元线性回归
基于一元线性回归分析的公路工程企业定额消耗量 推算方法研究
在公路工程施工过程中影响人工消耗量的因素很多，大致可以分为生产条件方面、技术条件方面、组织条件方面三类。而 这些影响条件根据其影响因素变化规律的不同又可分为连续性因素和间断性因素。连续性影响因素的特点是影响因素对于人 工消耗的影响变化是呈连续性渐变的。对于此类问题而言，一元线性回归分析方法是一种很好的分析影响因素带来影响大小 的方法。
3.在上述网络模型分析的基础上，采用 Small—World模型模拟交通拥堵在复杂 路网中的动态演进过程，如图。
1
线性回归
基于线性规划的城市交通流优化调度模型
4.在上述交通路网模型构建的基础上，进行交通流信息特征提取， 信息特征提取之前，采用线性规划方案，对交通网络路网结构进行 线性分割，分割结果，如图
8.2 一元线性回归模型及其应用(精讲)(解析版)
8.2 一元线性回归模型及其应用（精讲）考点一 样本中心解小题【例1】（2021·江西赣州市）某产品在某零售摊位上的零售价x （元）与每天的销售量y （个）统计如下表：据上表可得回归直线方程为 6.4151y x =-+，则上表中的m 的值为（ ） A ．38B ．39C ．40D ．41【答案】D 【解析】由题意1617181917.54x +++==，50343111544m my ++++==，所以115 6.417.51514m+=-⨯+，解得41m =．故选：D ． 【一隅三反】1．（2021·江西景德镇市·景德镇一中）随机变量x 与y 的数据如表中所列，其中缺少了一个数值，已知y关于x 的线性回归方程为ˆ0.93yx =+，则缺少的数值为（ ）A ．6B ．6.6C ．7.5D ．8【答案】A【解析】设缺少的数值为m ，由于回归方程为ˆ0.93yx =+过样本中心点(),x y ， 且2345645x ++++==，代入0.943 6.6y =⨯+=，所以5679 6.65my ++++==，解得6m =.故选：A.2．（2021·河南信阳市）根据如下样本数据：得到的回归方程为y bx a =+，则（ ） A ．0a >，0b > B ．0a >，ˆ0b < C ．0a <，0b > D ．0a <，ˆ0b< 【答案】B【解析】由图表中的数据可得，变量y 随着x 的增大而减小，则ˆ0b<， 2345645x ++++==，4 2.50.5230.25y +---==，又回归方程y bx a =+经过点(4,0.2)，可得0a >，故选：B ．3．（2021·安徽六安市·六安一中）蟋蟀鸣叫可以说是大自然优美、和谐的音乐，殊不知蟋蟀鸣叫的频率x（每分钟鸣叫的次数）与气温y （单位：C ）存在着较强的线性相关关系．某地观测人员根据下表的观测数据，建立了y 关于x 的线性回归方程0.25y x k =+.则当蟋蟀每分钟鸣叫62次时，该地当时的气温预报值为（ ） A ．33C B ．34CC ．35CD ．35.5C【答案】D【解析】由表格中的数据可得2030405060405x ++++==，2527.52932.536305y ++++==，由于回归直线过样本中心点(),x y ，可得300.2540k =⨯+，解得20k =.所以，回归直线方程为0.2520y x =+.在回归直线方程中，令62x =，可得0.25622035.5y =⨯+=.故选：D.考点二一元线性方程【例2】（2021·兴义市第二高级中学）在2010年春节期间，某市物价部门，对本市五个商场销售的某商品一天的销售量及其价格进行调查，五个商场的售价x 元和销售量y 件之间的一组数据如下表所示： 通过分析，发现销售量y 对商品的价格x 具有线性相关关系，求 （1）销售量y 对商品的价格x 的回归直线方程； （2）若使销售量为12，则价格应定为多少.附：在回归直线ˆˆy bxa =+中1221ˆni ii nii x y nxyb xnx ==-=-∑∑，ˆˆay bx =- 【答案】（1） 3.240y x =-+ （2） 8.75 【解析】（1）由题意知10x =，8y =，∴999580635551083.28190.25100110.25121ˆ5100b++++-⨯⨯==-++++-⨯，8(3.2)1040a =--⨯=，∴线性回归方程是 3.240y x =-+；（2）令 3.24012y x =-+=，可得8.75x =，∴预测销售量为12件时的售价是8.75元．【一隅三反】1．（2020·河南开封市）配速是马拉松运动中常使用的一个概念，是速度的一种，是指每公里所需要的时间，相比配速，把心率控制在一个合理水平是安全理性跑马拉松的一个重要策略.图1是一个马拉松跑者的心率y （单位：次/分钟）和配速x （单位：分钟/公里）的散点图，图2是一次马拉松比赛（全程约42公里）前3000名跑者成绩（单位：分钟）的频率分布直方图.（1）由散点图看出，可用线性回归模型拟合y 与x 的关系，求y 与x 的线性回归方程；（2）该跑者如果参加本次比赛，将心率控制在160左右跑完全程，估计他跑完全程花费的时间，并估计他能获得的名次.参考公式：线性回归方程ˆˆˆybx a =+中，12()()ˆ()nii i nixx y y b xx =--=-∑∑，ˆˆay bx =- 参考数据：135y =.【答案】（1）25285x y ∧=-+；（2）210分钟，192名． 【解析】（1）由散点图中数据和参考数据得 4.55677.565x ++++==，1001091301651711355y ++++==，()()()51522222211.536(1)300(5)1(26) 1.5(35)25( 1.5)(1)01 1.5ˆiii i i x x y y bx x ==---⨯+-⨯+⨯-+⨯-+⨯-===--+-+++-∑∑，135(25)62ˆ85ˆay bx =-=--⨯=， 所以y 与x 的线性回归方程为25285x y ∧=-+. （2）将160y =代入回归方程得5x =，所以该跑者跑完马拉松全程所花的时间为425210⨯=分钟. 从马拉松比赛的频率分布直方图可知成绩好于210分钟的累积频率为()0.0008500.00242102000.064⨯+⨯-=，有6.4%的跑者成绩超过该跑者，则该跑者在本次比赛获得的名次大约是0.0643000192⨯=名.2．（2020·云南红河哈尼族彝族自治州）随着电商事业的快速发展，网络购物交易额也快速提升，特别是每年的“双十一”，天猫的交易额数目惊人.2020年天猫公司的工作人员为了迎接天猫“双十一”年度购物狂欢节，加班加点做了大量准备活动，截止2020年11月11日24时，2020年的天猫“双十一”交易额定格在3700多亿元，天猫总公司所有员工对于新的战绩皆大欢喜，同时又对2021年充满了憧憬，因此公司工作人员反思从2014年至2020年每年“双十一”总交易额(取近似值)，进行分析统计如下表：（1）通过分析，发现可用线性回归模型拟合总交易额y 与年份代码t 的关系，请用相关系数加以说明； （2）利用最小二乘法建立y 关于t 的回归方程(系数精确到0.1)，预测2021年天猫“双十一”的总交易额. 参考数据：71()()138.5ii i tt y y =--=∑26.7= 2.646≈；参考公式：相关系数()()niit t y y r --=∑；回归方程y bt a ∧∧∧=+中，斜率和截距的最小二乘估计公式分别为：()()()711722211niii ii i niii i tty y t y nx yb tttnx∧====---==--∑∑∑∑，=a y bt ∧∧-.【答案】（1）答案见解析；（2）回归方程为ˆ 4.9 1.2yt =-，预测2021年天猫“双十一”的总交易额约为38百亿.【解析】（1）4t =，721()28ii tt =-=∑，17()()138.5i ii t t yy =--=∑26.7=所以()()138.50.982 2.64626.7niit t y y r --=≈≈⨯⨯∑因为总交易额y 与年份代码t 的相关系数近似为0.98， 说明总交易额y 与年份代码t 的线性相关性很强，从而可用线性回归模型拟合总交易额y 与年份代码t 的关系. （2）因为18.4y =，721()28ii tt =-=∑，所以()()71271()138.5ˆ 4.928i ii i i t t yy bt t ==--==≈-∑∑， ˆˆay b =-，18.4 4.94 1.2b ≈-⨯=- 所以y 关于t 的回归方程为ˆ 4.9 1.2yt =- 又将2021年对应的8t =代入回归方程得：ˆ 4.98 1.238y=⨯-=. 所以预测2021年天猫“双十一”的总交易额约为38百亿.3．（2021·湖北省武昌实验中学高二期末）根据统计，某蔬菜基地西红柿亩产量的增加量y （百千克）与某种液体肥料每亩使用量x（千克）之间的对应数据的散点图，如图所示．（1）依据数据的散点图可以看出，可用线性回归模型拟合y与x的关系，请计算相关系数r并加以说明（若0.75r>，则线性相关程度很高，可用线性回归模型拟合）；（2）求y关于x的回归方程，并预测当液体肥料每亩使用量为12千克时，西红柿亩产量的增加量约为多少？附：相关系数公式()()n ni i i ix x y y x y nx y r---==∑∑0.55≈0.95≈．回归方程y bx a=+中斜率和截距的最小二乘估计公式分别为()()()1122211n ni i i ii in ni ii ix x y y x y nx ybx x x nx====---==--∑∑∑∑，a y xb=-．【答案】（1）0.95；答案见解析；（2）0.3 2.5y x=+；610千克.【解析】（1）由已知数据可得2456855x++++==，3444545y++++==，所以()()()()()5131100010316i iix x y y=--=-⨯-+-⨯+⨯+⨯+⨯=∑，====所以相关系数()()50.95iix x y y r --===≈∑．因为0.75r >，所以可用线性回归模型拟合y 与x 的关系．（2）()()()5152160.320iii ii x x y y b x x ==--===-∑∑，450.3 2.5a =-⨯=， 所以回归方程为0.3 2.5y x =+． 当12x =时，0.312 2.5 6.1y =⨯+=，即当液体肥料每亩使用量为12千克时，西红柿亩产量的增加量约为610千克．考点三 非一元线性方程【例3】（2020·全国高二课时练习）在一次抽样调查中测得5个样本点，得到下表及散点图．（1）根据散点图判断y a bx =+与1y c k x -=+⋅哪一个适宜作为y 关于x 的回归方程；（给出判断即可，不必说明理由）（2）根据（1）的判断结果试建立y 与x 的回归方程；（计算结果保留整数） （3）在（2）的条件下，设=+z y x 且[)4,x ∈+∞，试求z 的最小值．参考公式：回归方程ˆˆˆybx a =+中，()()()1122211ˆn niii ii i nniii i x x y y x y nx yb x x xnx====---==--∑∑∑∑，a y bx =-.【答案】（1）1y c k x -=+⋅；（2）41y x=+；（3）6. 【解析】（1）由题中散点图可以判断，1y c k x -=+⋅适宜作为y 关于x 的回归方程； （2）令1t x -=，则y c kt =+，原数据变为由表可知y 与t 近似具有线性相关关系，计算得4210.50.251.555t ++++==，16125217.25y ++++==，222222416212150.520.2515 1.557.238.4544210.50.255 1.559.3k ⨯+⨯+⨯+⨯+⨯-⨯⨯==≈++++-⨯，所以，7.24 1.551c y kt =-=-⨯=，则41y t =+． 所以y 关于x 的回归方程是41y x=+． （3）由（2）得41z y x x x=+=++，[)4,x ∈+∞， 任取1x 、24x ≥，且12x x >，即124x x >≥，可得()()()21121212121212124444411x x z z x x x x x x x x x x x x -⎛⎫⎛⎫⎛⎫-=++-++=-+-=-+ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭()()1212124x x x x x x --=，因为124x x >≥，则120x x ->，1216>x x ，所以，12z z >，所以，函数41z x x =++在区间[)4,+∞上单调递增，则min 44164z =++=. 【一隅三反】1．（2020·江苏省如皋中学高二月考）某种新产品投放市场一段时间后，经过调研获得了时间x （天数）与销售单价y （元）的一组数据，且做了一定的数据处理（如表），并作出了散点图（如图）.表中10111,10i i i i w w w x ===∑.（1）根据散点图判断y a bx =+，与dy c x=+哪一个更适合作价格y 关于时间x 的回归方程类型？（不必说明理由）（2）根据判断结果和表中数据，建立y 关于x 的回归方程. （3）若该产品的日销售量()g x （件）与时间x 的函数关系为()()100120g x x N x-=+∈，求该产品投放市场第几天的销售额最高？最高为多少元？附：对于一组数据()()()()112233,,,,,,...,,n n u v u v u v u v ，其回归直线vuαβ=+的斜率和截距的最小二乘法估计分别为121()(),()nii i nii vv u u v u u u βαβ==--==--∑∑.【答案】（1）dy c x =+更适合作价格y 关于时间x 的回归方程；（2）120(1)y x=+；（3）第10天，最高销售额为2420元；【解析】（1）根据散点图知dy c x=+更适合作价格y 关于时间x 的回归方程类型； （2）令1w x=，则y c dw =+， 而1011021()()18.4200.92()iii ii w w yy d w w ==--===-∑∑， 37.8200.8920c y dw =-=-⨯=，即有120(1)y x=+；（3）由题意结合（2）知：日销售额为1100()()20(1)(120)f x y g x x x=⋅=+-， ∴2110015()20(1)(120)400(6)f x x x x x=+-=+-， 若1t x =，令221121()655()1020h t t t t =+-=--+， ∴110t =时，max 1121()()1020h t h ==，即10x =天，max 121()(10)400242020f x f ==⨯=元, 所以该产品投放市场第10天的销售额最高，最高销售额为2420元.2．（2021·江苏苏州市）我国为全面建设社会主义现代化国家，制定了从2021年到2025年的“十四五”规划.某企业为响应国家号召，汇聚科研力量，加强科技创新，准备增加研发资金.现该企业为了了解年研发资金投入额x （单位：亿元）对年盈利额y （单位：亿元）的影响，研究了“十二五”和“十三五”规划发展期间近10年年研发资金投入额i x 和年盈利额i y 的数据.通过对比分析，建立了两个函数模型：①2y x αβ=+，②x t y e λ+=，其中α，β，λ，t 均为常数，e 为自然对数的底数．令2i i u x >，()ln 1,2,,10i i v y i ==⋅⋅⋅，经计算得如下数据：（1）请从相关系数的角度，分析哪一个模型拟合程度更好?（2）（ⅰ）根据（1）的选择及表中数据，建立y 关于x 的回归方程;（系数精确到0.01）（ⅱ）若希望2021年盈利额y 为250亿元，请预测2021年的研发资金投入额x 为多少亿元？（结果精确到0.01）附：①相关系数()()niix x y y r --=∑，回归直线ˆˆˆya bx =+中：121()()ˆ()niii nii x x yy b x x ==--=-∑∑，ˆˆay bx =- ②参考数据：ln 20.693≈，ln5 1.609≈． 【答案】（1）模型x ty eλ+=的拟合程度更好；（2）（ⅰ）0.180.56ˆx ye +=；（ⅱ）27.56.【解析】（1）设{}i u 和{}i y 的相关系数为1r ，{}i x 和{}i v 的相关系数为2r ，由题意，()()101130.8715iiu u y y r --===≈∑，()()102120.9213iix x v v r --===≈∑，则12r r <，因此从相关系数的角度，模型x ty e λ+=的拟合程度更好．（2）（ⅰ）先建立v 关于x 的线性回归方程， 由x ty eλ+=，得ln y t x λ=+，即v t x λ=+，()()()101102112ˆ65iii ii x x v v x x λ==--==-∑∑， 12ˆˆ 5.36260.5665tv x λ=-=-⨯=， 所以v 关于x 的线性回归方程为ˆ0.180.56vx =+， 所以ˆln 0.180.56yx =+，则0.180.56ˆx y e +=．（ⅱ）2021年盈利额250y =（亿元）， 所以0.180.56250x e +=，则0.180.56ln 250x +=， 因为ln 2503ln5ln 23 1.6090.693 5.52=+≈⨯+=， 所以 5.520.5627.560.18x -≈≈．所以2021年的研发资金投入量约为27.56亿元．。
一元线性回归模型案例
⼀元线性回归模型案例第⼆章⼀元线性回归模型案例⼀、中国居民⼈均消费模型从总体上考察中国居民收⼊与消费⽀出的关系。
表2.1给出了1990年不变价格测算的中国⼈均国内⽣产总值（GDPP）与以居民消费价格指数（1990年为100）所见的⼈均居民消费⽀出（CONSP）两组数据。
1) 建⽴模型，并分析结果。
输出结果为：对应的模型表达式为：201.1070.3862CONSP GDPP =+(13.51) (53.47) 20.9927,2859.23,0.55R F DW ===从回归估计的结果可以看出，拟合度较好，截距项和斜率项系数均通过了t 检验。
中国⼈均消费增加10000元，GDP 增加3862元。
⼆、线性回归模型估计表2.2给出⿊龙江省伊春林区1999年16个林业局的年⽊材采伐量和相应伐⽊剩余物数据。
利⽤该数据（1）画散点图；（2）进⾏OLS 回归；（3）预测。
表2.2 年剩余物y 和年⽊材采伐量x 数据（1）画散点图先输⼊横轴变量名，再输⼊纵轴变量名得散点图（2）OLS估计弹出⽅程设定对话框得到输出结果如图：由输出结果可以看出，对应的回归表达式为：0.76290.4043t t yx =-+ (-0.625) (12.11)20.9129,146.7166, 1.48R F DW === （3）x=20条件下模型的样本外预测⽅法⾸先修改⼯作⽂件范围将⼯作⽂件范围从1—16改为1—17确定后将⼯作⽂件的范围改为包括17个观测值，然后修改样本范围将样本范围从1—16改为1—17打开x的数据⽂件，利⽤Edit+/-给x的第17个观测值赋值为20将Forecast sample选择区把预测范围从1—17改为17—17，即只预测x=20时的y的值。
由上图可以知道，当x=20时，y的预测值是7.32，yf的分布标准差是2.145。
三、表2.3列出了中国1978—2000年的参政收⼊Y和国内⽣产总值GDP的统计资料。
案例：一元线性回归模型实现
一元线性回归模型：案例分析下面用一个实例对本章内容作一简单回顾。
我们将收集中国财政收入和国内生产总值在1978~2006年间的历史数据，然后建立两者的一元线性回归模型，并用最小二乘法对其中的参数进行估计，最后对模型进行一些必要的检验。
一、中国财政收入和国内生产总值的历史数据由经济学等相关学科的理论我们知道，国内生产总值是财政收入的来源，因此财政收入在很大程度上由国内生产总值来决定。
为了考察中国财政收入和国内生产总值之间的关系，我们收集了中国财政收入和国内生产总值在1978~2005年间的历史数据，如表 2.4.1所示。
表2.4.1中国财政收入和国内生产总值数据表单位：亿元年份财政收入(Y) 国内生产总值(X) 年份财政收入(Y) 国内生产总值(X)1978 1132 3624 1992 3483 266521979 1146 4038 1993 4349 345611980 1160 4518 1994 5218 466701981 1176 4860 1995 6242 607941982 1212 5302 1996 7408 711771983 1367 5957 1997 8651 789731984 1643 7207 1998 9876 844021985 2005 8989 1999 11444 896771986 2122 10201 2000 13395 992151987 2199 11955 2001 16386 1096551988 2357 14922 2002 18904 1203331989 2665 16918 2003 21715 1358231990 2937 18598 2004 26396 1598781991 3149 21663 2005 31628 183868我们以X为横轴，Y为纵轴将这些数据的描绘在二维坐标图上，得到如下的散点图(图2.4.1 )。
简单线性相关(一元线性回归分析)
第十三讲简单线性相关（一元线性回归分析）对于两个或更多变量之间的关系，相关分析考虑的只是变量之间是否相关、相关的程度，而回归分析关心的问题是：变量之间的因果关系如何。
回归分析是处理一个或多个自变量与因变量间线性因果关系的统计方法。
如婚姻状况与子女生育数量，相关分析可以求出两者的相关强度以及是否具有统计学意义，但不对谁决定谁作出预设，即可以相互解释，回归分析则必须预先假定谁是因谁是果，谁明确谁为因与谁为果的前提下展开进一步的分析。
一、一元线性回归模型及其对变量的要求（一）一元线性回归模型1、一元线性回归模型示例两个变量之间的真实关系一般可以用以下方程来表示：Y=A+BX+方程中的 A 、B 是待定的常数，称为模型系数，是残差，是以X预测Y 产生的误差。
两个变量之间拟合的直线是：y a bxy 是y的拟合值或预测值，它是在X 条件下 Y 条件均值的估计a 、b 是回归直线的系数，是总体真实直线距，当自变量的值为0 时，因变量的值。
A、B 的估计值， a 即 constant 是截b 称为回归系数，指在其他所有的因素不变时，每一单位自变量的变化引起的因变量的变化。
可以对回归方程进行标准化，得到标准回归方程：y x为标准回归系数，表示其他变量不变时，自变量变化一个标准差单位（ Z XjXj），因变量 Y 的标准差的平均变化。
S j由于标准化消除了原来自变量不同的测量单位，标准回归系数之间是可以比较的，绝对值的大小代表了对因变量作用的大小，反映自变量对Y 的重要性。
（二）对变量的要求：回归分析的假定条件回归分析对变量的要求是：自变量可以是随机变量，也可以是非随机变量。
自变量 X 值的测量可以认为是没有误差的，或者说误差可以忽略不计。
回归分析对于因变量有较多的要求，这些要求与其它的因素一起，构成了回归分析的基本条件：独立、线性、正态、等方差。
（三）数据要求模型中要求一个因变量，一个或多个自变量（一元时为 1 个自变量）。
一元线性回归模型案例
一元线性回归模型案例一元线性回归是统计学中常用的一种回归分析方法，用于研究一个自变量和一个因变量之间的线性关系。
在本文中，我们将通过一个实际案例来介绍一元线性回归模型的应用和分析过程。
案例背景：假设我们是某家电商平台的数据分析师，我们希望通过用户的年龄来预测其在平台上的消费金额。
我们收集了100位用户的年龄和其在平台上的消费金额的数据，现在我们希望利用一元线性回归模型来分析这些数据，以便更好地了解用户消费行为。
数据分析：首先，我们需要对收集到的数据进行初步的分析。
我们可以使用散点图来观察年龄和消费金额之间的关系。
通过观察散点图，我们可以初步判断年龄和消费金额之间是否存在线性关系，以及线性关系的方向和强度。
模型建立：在确认了年龄和消费金额之间存在线性关系后，我们可以建立一元线性回归模型。
模型的基本形式为，Y = β0 + β1X + ε，其中Y表示因变量（消费金额），X表示自变量（年龄），β0和β1分别表示截距和斜率，ε表示误差项。
我们需要通过最小二乘法来估计β0和β1的值，从而建立回归方程。
模型评价：建立回归模型后，我们需要对模型进行评价。
我们可以通过计算回归方程的拟合优度R^2来评价模型的拟合程度，R^2的取值范围为0到1，值越接近1表示模型拟合得越好。
此外，我们还可以利用残差分析来检验模型的假设是否成立，以及检验模型的稳健性和可靠性。
预测分析：最后，我们可以利用建立的回归模型进行预测分析。
通过输入不同年龄的值，我们可以利用回归方程来预测用户在平台上的消费金额。
预测分析可以帮助电商平台更好地了解不同年龄段用户的消费特点，从而制定针对性的营销策略和服务方案。
结论：通过以上一元线性回归模型的应用分析，我们可以得出结论，用户的年龄和在平台上的消费金额之间存在一定的线性关系，通过建立回归模型，我们可以对用户的消费金额进行预测和分析。
这对于电商平台来说具有重要的参考价值，可以帮助平台更好地了解用户消费行为，从而提升用户体验和增加销售额。
一元线性回归模型案例分析
一元线性回归模型案例分析一、研究的目的要求居民消费在社会经济的持续发展中有着重要的作用。
居民合理的消费模式和居民适度的消费规模有利于经济持续健康的增长，而且这也是人民生活水平的具体体现。
改革开放以来随着中国经济的快速发展，人民生活水平不断提高，居民的消费水平也不断增长。
但是在看到这个整体趋势的同时，还应看到全国各地区经济发展速度不同，居民消费水平也有明显差异。
例如，2002年全国城市居民家庭平均每人每年消费支出为6029.88元, 最低的黑龙江省仅为人均4462.08元，最高的上海市达人均10464元，上海是黑龙江的2.35倍。
为了研究全国居民消费水平及其变动的原因，需要作具体的分析。
影响各地区居民消费支出有明显差异的因素可能很多，例如，居民的收入水平、就业状况、零售物价指数、利率、居民财产、购物环境等等都可能对居民消费有影响。
为了分析什么是影响各地区居民消费支出有明显差异的最主要因素，并分析影响因素与消费水平的数量关系，可以建立相应的计量经济模型去研究。
二、模型设定我们研究的对象是各地区居民消费的差异。
居民消费可分为城市居民消费和农村居民消费，由于各地区的城市与农村人口比例及经济结构有较大差异，最具有直接对比可比性的是城市居民消费。
而且，由于各地区人口和经济总量不同，只能用“城市居民每人每年的平均消费支出”来比较，而这正是可从统计年鉴中获得数据的变量。
所以模型的被解释变量Y 选定为“城市居民每人每年的平均消费支出”。
因为研究的目的是各地区城市居民消费的差异，并不是城市居民消费在不同时间的变动，所以应选择同一时期各地区城市居民的消费支出来建立模型。
因此建立的是2002年截面数据模型。
影响各地区城市居民人均消费支出有明显差异的因素有多种，但从理论和经验分析，最主要的影响因素应是居民收入，其他因素虽然对居民消费也有影响，但有的不易取得数据，如“居民财产”和“购物环境”；有的与居民收入可能高度相关，如“就业状况”、“居民财产”；还有的因素在运用截面数据时在地区间的差异并不大，如“零售物价指数”、“利率”。
案例13 一元线性回归
案例13 一元线性回归（一）一元线性回归介绍(1)相关关系是一种不确定性关系；(2)对具有相关关系的两个变量进行统计分析，给出其统计规律性的方法叫回归分析.两个变量之间相关程度的分析应用十分广泛。
如：家庭收入与家庭消费支出之间关系是否相关;商品销售价格与商品销售额之间关系是否相关;客户满意度与商业企业综合竞争力之间关系是否相关; 广告投入和销售额之间关系是否相关.（二）回归模型和参数估计11(,)(,),...,(,)n n x Y x Y x Y 从总体中抽取的一个样本()012201,1,2,...,,~0,,(,i i i i Y x i n N ββεεσββσ=++=⎧⎪⎨⎪⎩一元线性回归模型：，且相互独立，回归系数）未知.01011ˆˆ,,ˆ/.xy xx y x s s βββββ⎧=-⎪⎨=⎪⎩的最小二乘估计： ()()()()2211,,,,.i i xx i i i ixy i i yy i iiy y x x s x x n n s x x y y s y y ===-=--=-∑∑∑∑∑其中：（三）建立工业总产值与能源消耗量的回归方程工业总产值是工业企业在一定时期内生产的以货币形式表现的工业最终产品或提供工业性劳务活动的总价值量。
它反映一定时间内工业生产的总规模和总水平。
能源消费总量指一定时期内，全国各行业和居民生活消费的各种能源的总和。
而能源消耗除了用于工业外，还用于农业，建筑业，交通运输和邮电通信业，生活消费等。
本案例研究能源消耗对工业总产值的贡献。
由相关分析知，工业总产值与能源消耗量之间存在高度的正相关关系。
经计算两者为高相关，相关系数为0.986。
y: 工业总产值(亿元）x: 能源消耗量（万吨标准煤）年份工业总产值（Y）工业能源消耗（X）1994 70176 87853.4 1995 91894 96191.3 1996 99595 100322 1997 113733 100080 1998 66737 94409 1999 72707 90797 2000 85673 89634 2001 95449 92347 2002 110777 102181 2003 142271 119627 2004 202217 143244 2005 251619 158058 2006 316589 175137 2007 405177 190167 2008 507448 209302 2009 548311 219197正态QQ的残差图发现，数据正态性并不很好，（若残差是来自正态总体分布的样本，则QQ图中的点应该在一条直线上）。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
一元线性回归模型案例分析
一元线性回归是最基本的回归分析方法，它的主要目的是寻找一个函数能够描述因变
量对于自变量的依赖关系。
在一元线性回归中，我们假定存在满足线性关系的自变量与因变量之间的函数关系，
即因变量y与单个自变量x之间存在着线性关系，可表达为：y=β0+ β1x (1)
其中，β0和β1分别为常量，也称为回归系数，它们是要由样本数据来拟合出来的。
因此，一元线性回归的主要任务就是求出最优回归系数和平方和最小平方根函数，从而评
价模型的合理性。
下面我们来介绍如何使用一元线性回归模型进行案例分析。
数据收集：首先，研究者
需要收集自变量和因变量之间关系的相关数据。
这些数据应该有足够多的样本观测值，以
使统计分析结果具有足够的统计力量，表示研究者所研究的关系的强度。
此外，这些数据
的收集方法也需要正确严格，以避免因相关数据缺乏准确性而影响到结果的准确性。
模型构建：其次，研究者需要利用所收集的数据来构建一元线性回归模型。
即建立公
式（1），求出最优回归系数β0和β1，即最小二乘法拟合出模型方程式。
模型验证：接下来，研究者需要对所构建的一元线性回归模型进行验证，以确定模型
精度及其包含的统计意义。
可以使用F检验和t检验，以检验回归系数β0和β1是否具
有统计显著性。
另外，研究者还可以利用R2等有效的拟合检验统计指标来衡量模型精度，从而对模型的拟合水平进行评价，从而使研究者能够准确无误地判断其研究的相关系数的
统计显著性及包含的统计意义。
另外，研究者还可以利用偏回归方差分析（PRF），这是一种多元线性回归分析技术，用于计算每一个自变量对相应因变量的贡献率，使研究者能够对拟合模型中每一个自变量
的影响程度进行详细的分析。
模型应用：最后，研究者可以利用一元线性回归模型进行应用，以实现实际问题的求
解以及数据挖掘等功能。
例如我们可以使用这一模型来预测某一物品价格及销量、研究公
司收益及投资、检测影响某一地区经济发展的因素等。
综上所述，一元线性回归是一种利用单变量因变量之间存在着线性关系来拟合出回归
系数的回归分析方法，它可以应用于许多不同的问题，是一种非常实用的有效的统计分析
方法。