gold序列自相关函数
移动通信实验指导书CDMA部分.docx

CDMA系统一.概述CDMA (Code Division Multiple Access)称作码分多址。
在CDMA通信系统中,不同用户传输信息所用的信号不是靠频率不同或时隙不同来区分的,而是用各不相同的编码序列来区分的。
或说是靠信号的不同形来区分的。
从频域或时域观察,多个CDMA信号是互相重叠的。
码分多址是以扩频技术为妹础,所谓扩频是把信息的频谱扩展到宽带中进行传输的技术。
CDMA信号的产生包括调制和扩频两个步骤,可以先用待传送的信息比特刈•载波进行调制,再用伪随机系列(PN)扩展信号的频谱,也可以先用伪随机系列为待传送的信息比特相乘, 把信息的频谱扩展后,再对载波进行调制。
这两种方式是等效的。
适用于CDMA系统的扩频技术是直接序列扩频(DS),这巾CDMA系统称作直接序列扩频CDMA 系统(DS-CDMA)o在直接序列扩频CDMA系统中,所有用户(或称信道)工作在相同的中心频率上,用户信息信号与高速率的伪随机码序列(PN序列或称码字)相乘得到宽带信号。
不同的川户使用不同PN序列。
这些PN序列相互正交,利用PN序列来区分不同的用户,如图0—1所示。
得到的宽带信号再去调制载波信号的某个参量。
▲玛字图0—1 DS—CDMA示意图接收端要从收到的扩频信号中恢复出它携带的信息,必须经过解扩和解调两个步骤。
解扩就是接收端以与发送端相同的PN序列与接收到的扩频信号相乘,恢复出原频带信号;解扩后的信号再经过常规的解调,即可恢复出其中传送的信息。
二.DS-CDMA移动通信原理图0-2为DS-CDMA移动通信系统原理框图。
系统中采用包含N个正交的PN序列CI, C2,…,6作为地址码,分别与信码dl,d2,…,dn相乘或模2加实现扩频调制。
信码速率fb (单位:b/s,比特/秒)、丿謹月Tb=l/fb;地址码速率fp (单位:c/s,子码/秒或码片/秒)、翩Tp=l/fp, 地址码序列每周期包含p个子码元,序列周期T = pT p.通常设置(0-1)(0-2)式中,K为正整数。
Gold序列产生及特性分析实验

2、在测试点TP201测试输出的时钟,在测试点TP202、TP203、TP204测试用于产生Gold序列的周期为31的m序列优选对。
实验二、Gold序列产生及特性分析实验
1、实验目的
1、了解Gold序列的性质和特点。
2、熟悉Gold序列的产生方法。
2、实验内容
1、熟悉Gold序列的产生方法。
2、测试Gold序列的波形。
3、实验原理
m序列虽然性能优良,但同样长度的m序列个数不多,且m序列之间的互相关函数并不理想(为多值函数)。1967年,R.Gold提出和讨论了一种新的序列,即Gold序列。这种序列有较为优良的自相关和互相关特性,构造简单,产生的序列数多,因而得到广泛的应用。
TP202测试点输出的m序列为:1 1 0 0 1 1 0 1 1 0 1 1.......
TP203测试点输出的m序列为:1 0 1 0 0 0 1 1 0 1 1 1.......
经验证符合实验结果。
1.m序列优选对
m序列优选对是指在m序列集中,其互相关函数最大值的绝对值满足下式的两条n介m序列:
2.Gold序列的产生方法
Gold序列是m序列的组合序列,由同步时钟控制的两个码元不同的m序列优选对逐位模2加得到。这两个序列发生器的周期相同,速率相同,因而两者保持一定的相位关系,这样产生的组合序列与这两个自序列的周期也相同。当改变两个序列的相对位移,会得到一个新的Gold序列。Gold序列具有以下性质:
(1)两个m序列优选对经不同移位相加产生的新序列都是Gold序列,两个n级移位寄存器可以产生 个Gold序列,周期均为 。
gold序列的生成与相关特性仿真

Gold序列生成与相关性仿真1.1 references[1] 基于Matlab的Gold码序列的仿真与实现.[2] Code Selection for CDMA Systems.1.2 m序列的生成原理1.2.1生成本原多项式利用Matlab编程环境求解本原多项式,其运行结果如表1所示.选择n=7,采用7级移位寄存器,产生的序列周期是127,其程序如下所示.N=7; %以7级寄存器为例,并组其中的一组优选对:211,,217connections=gfprimfd(N,'all');表(1)n=7 本原多项式上面的多项式中,仅有9个是独立的.因为第一行和第十行,第二行和四行,第三行和第十六行,第五行和第八行,第六行和第十四行,第七行和第十三行,第九行和第十八行,第十一行和第十二行,第十五行和第十七行是两两对称的.用八进制数表示时,所选择的本原多项式为211、217、235、367、277、325、203、313和345共9条.在这9条本原多项式中,选择一个基准本原多项式,再按要求选择另一本原多项式与之配对,构成m序列优选对,对7级m序列优选对如下表:表(2)n=7 m序列所以优选对1.2.2构成移位寄存器根据产生Gold码序列的方法,从上述本原多项式中选择一对m序列优选对,以211作为基准本原多项式,217作为配对本原多项式,通过并联结构形式来产生Gold序列,生成gold 序列的结构如图(6)所示:图(6)Gold序列生成结构1.3 自相关函数仿真参数及初始值设定如下:N=7; %以7级寄存器为例,并组其中的一组优选对:211,,217connections=gfprimfd(N,'all');f1=connections(4,:); %取一组本原多项式序列,211f2=connections(16,:); %取另一组本原多项式序列,217registers1=[1 0 0 0 0 0 0];%给定寄存器的初始状态registers2=[1 0 0 0 0 0 0];%取相同的初始状态生成的gold 序列自相关函数如图(7)、(8)所示图(7) Gold 序列周期自相关函数结论:自相关函数取值集合{127,15,-1,-17}图(8)Gold 序列非周期自相关函数020406080100120140gold 序列周期自相关函数020406080100120140-40-2020406080100120140gold 序列非周期自相关函数1.4 互相关函数仿真时改变m序列寄存器初始状态,从而生成两个gold序列,求得互相关函数如图(9)(10)所示。
扩频编码M序列和gold序列
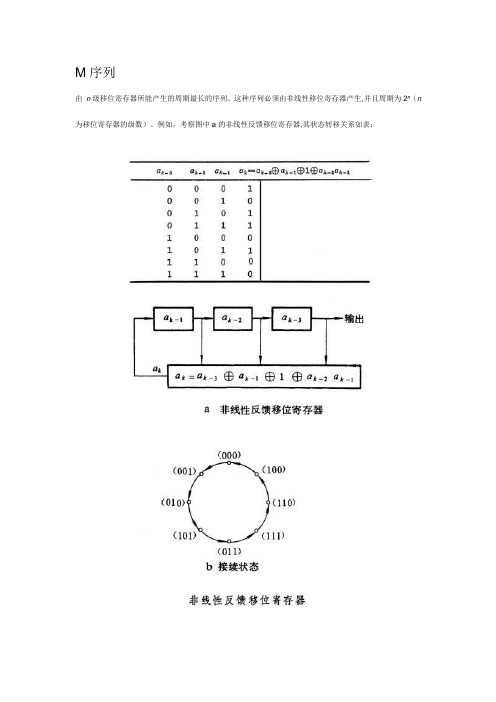
M序列由n级移位寄存器所能产生的周期最长的序列。
这种序列必须由非线性移位寄存器产生,并且周期为2n(n 为移位寄存器的级数)。
例如,考察图中a的非线性反馈移位寄存器,其状态转移关系如表:状态(a k-3,a k-2,a k-1)的接续状态是(a k-2,a k-1,a k),其中a k=a k-3嘰a k-1嘰1嘰a k-2a k-1是一种非线性逻辑。
从任一状态出发,例如从(000)出发,其接续状态恰好构成一个完全循环(图b),由此产生一个周期为23=8的3级序列。
M序列最早是用抽象的数学方法构造的。
它出现于组合数学的一些数学游戏中,例如L.欧拉关于哥尼斯堡的七桥问题等。
后来发现这种序列具有某些良好的伪随机特性。
例如,M序列在一个周期中,0与1的个数各占一半。
同时,同样长度的0游程与1游程也各占一半。
所有这些性质在数据通信、自动控制、光学技术和密码学诸领域中均有重要应用。
隐蔽通信内容的通信方式。
为了使非法的截收者不能理解通信内容的含义,信息在传输前必须先进行各种形式的变化,成为加密信息,在收信端进行相应的逆变化以恢复原信息。
电报通信、电话通信、图像通信和数据通信,都有相应的保密技术问题。
另一方面,为了从保密通信中获得军事、政治、经济、技术等机密信息,破译技术也在发展。
保密技术和破译技术是在相互对立中发展起来的。
1881年世界上出现了第一个电话保密专利。
电话保密开始是采用模拟保密或置乱的方法,即把话音的频谱或时间分段打乱。
置乱后的信号仍保持连续变化的性质。
在第二次世界大战期间,频域和时域的置乱器在技术上已基本成熟。
70年代以来,由于采用集成电路,电话保密通信得到进一步完善。
但置乱器仍是有线载波和短波单边带电话保密通信的主要手段。
模拟保密还可以采用加噪声掩盖、人工混响或逆向混响等方法,但因恢复后话音的质量大幅度下降或保密效果差,这些方法没有得到推广应用。
数字保密是由文字密码发展起来的。
数字信号(包括由模拟信号转换成的数字信号),由相同速率的密码序列加密,成为数字保密信号;保密信号传输到收信端后由同一密码序列去密,恢复原数字信号。
Gold序列与m序列仿真应用

1. 绪论m序列具有优良的双值自相关特性,但互相关特性不是很好。
作为CDMA通信地址码时,由于互相关特性不理想,使得系统内多址干扰影响增大,且可用地址码数量较少。
在某些应用场合,利用狭义伪随机序列复合而成复合序列更为有利。
这是因为通过适当方法构造的复合序列具有某些特殊性质。
Gold序列就是一种复合序列,而且具有良好的自相关与互相关特性,地址码数量远大于m序列,且易于实现、结构简单,在工程上得到广泛应用。
表1是m序列和Gold序列的主要性能比较,表中为m序列的自相关峰值,为自相关主峰;为Gold序列的互相关峰值,为其自相关主峰。
从表1中可以看出:当级数n一定时,Gold序列中可用序列个数明显多于m序列数,且Gold序列的互相关峰值和主瓣与旁瓣之比都比m序列小得多,这一特性在实现码分多址时非常有用。
表1. m序列和Gold序列性能比较在引入Gold序列概念之前先介绍一下m序列优选对。
m序列优选对,是指在m序列集中,其互相关函数绝对值的最大值(称为峰值互相关函数)最接近或达到互相关值下限(最小值)的一对m序列。
设{ai}是对应于r次本原多项式F1(x)所产生的m序列, {bi} 是另一r次本原多项式F2(x)产生的m序列,峰值互相关函数满足(1)则m序列{ai}与{bi}构成m序列优选对。
例如:的本原多项式与所产生的m序列与,其峰值互相关函数。
满足式(1),故与构成m序列优选对。
而本原多项式所产生的m序列,与m序列的峰值互相关函数,不满足上式,故与不是m序列优选对。
2. Gold序列1967年,R·Gold指出:“给定移位寄存器级数r时,总可找到一对互相关函数值是最小的码序列,采用移位相加方法构成新码组,其互相关旁瓣都很小,且自相关函数和互相关函数均有界”。
这样生成的序列称为Gold码(Gold序列)。
Gold序列是m序列的复合序列,由两个码长相等、码时钟速率相同的m序列优选对的模2和序列构成。
m序列和Gold序列特性研究要点上课讲义

m序列和G o l d序列特性研究要点Harbin Institute of Technology扩频通信实验报告课程名称:扩频通信实验题目:Gold码特性研究院系:电信学院班级:通信一班姓名:学号:指导教师:迟永钢时间: 2012年5月8日哈尔滨工业大学第1章实验要求1.以r=5 1 45E为基础,抽取出其他的m序列,请详细说明抽取过程;2.画出r=5的全部m序列移位寄存器结构,并明确哪些序列彼此是互反多项式;3.在生成的m序列集中,寻找出m序列优选对,请确定优选对的数量,并画出它们的自相关和互相关函数图形;4.依据所选取的m序列优选对生成所有Gold序列族,确定产生Gold序列族的数量,标出每个Gold序列族中的所有序列,并实例验证族内序列彼此的自相关和互相关特性;5.在生成的每个Gold序列族内,明确标出平衡序列和非平衡序列,并验证其分布关系。
6.完整的作业提交包括:纸质打印版和电子版两部分,要求两部分内容统一,且在作业后面附上源程序,并加必要注释。
7.要求统一采用Matlab软件中的M文件实现。
第2章 实验原理2.1 m 序列二元m 序列是一种伪随机序列,有优良的自相关函数,是狭义伪随机序列。
m 序列易于产生于复制,在扩频技术中得到了广泛应用。
2.1.1 m 序列的定义r 级非退化的移位寄存器的组成如图1所示,移位时钟源的频率为c R 。
r 级线性移位寄存器的反馈逻辑可用二元域GF(2)上的r 次多项式表示2012() {0,1}r r i f x c c x c x c x c =++++∈L (1)图 2-1 r 级线性移位寄存器式(1)称为线性移位寄存器的特征多项式,其给出的表示反馈网络的而逻辑关系式是现行的。
因此成为线性移位寄存器。
否则称为,非线性移位寄存器。
对于动态线性移位寄存器,其反馈逻辑也可以用线性移位寄存器的递归关系式来表示112233 {0,1}i i i i r i r i a c a c a c a c a c ----=++++∈L (2) 特征多项式(1)与递归多项式(2)是r 级线性移位寄存器反馈逻辑的两种不同种表示法,因其应用的场合不同而采用不同的表示方法。
信号相关分析原理自相关函数互相关函数

信号相关分析原理自相关函数互相关函数1. 自相关函数(Autocorrelation Function):自相关函数用于衡量信号与其自身之间的相似性和相关性。
自相关函数是信号的一个函数,描述了信号与其自身在不同时间延迟下的相似程度。
自相关函数的计算公式为:R_xx(tau) = E[x(t)x(t+tau)]其中,R_xx(tau)表示在时间延迟tau下信号x(t)与自身的相关程度,E表示期望值运算。
自相关函数的值越大,表示信号在不同时间延迟下的相似性越高。
自相关函数在信号处理中有广泛的应用,例如:-信号周期性分析:自相关函数可以用于检测信号是否具有周期性,通过寻找自相关函数的周期性峰值,可以判断信号的周期。
-信号估计:通过自相关函数的峰值位置可以估计信号的延迟时间。
2. 互相关函数(Cross-correlation Function):互相关函数用于衡量两个信号之间的相似性和相关性。
互相关函数描述了两个信号在不同时间延迟下的相似程度。
互相关函数的计算公式为:R_xy(tau) = E[x(t)y(t+tau)]其中,R_xy(tau)表示信号x(t)与信号y(t)在时间延迟tau下的相关程度。
互相关函数的值越大,表示信号之间的相关性越高。
互相关函数在信号处理中也有广泛的应用,例如:-图像配准:互相关函数可以用于图像配准,通过计算两幅图像之间的互相关函数找到最大峰值,可以确定两幅图像的平移和旋转关系。
-信号相似性检测:在音频、图像和视频等领域中,可以通过互相关函数比较两段信号之间的相似性,例如音频中的语音识别和音乐识别。
总结起来,自相关函数和互相关函数是信号相关分析中常用的方法,可以用来描述信号之间的相似性、周期性和相关程度。
通过计算自相关函数和互相关函数可以在信号处理、图像处理和音频处理等领域中得到广泛的应用。
GOLD序列的相关性

谢谢!
追求人生的美好!
我们的共同目标!
gold序列是用一对周期和速率均相同但码字不同的n级m序列发生器时钟n级m序列发生器gold码序列gold码发生器的原理结构图
GOLD序列的相关性
主要内容
• m序列 • Gold序列 • Gold序列的相关特性
m序列
m序列是目前CDMA系统中采用的最基本 的PN序列。它是最长线性反馈移位寄存器 序列的简称。若移位寄存器为n级, 则其周 期P=2n-1 。
• 如果有两个m序列, 它们的互相关函数的绝
对值有界, 且满足2 n1
1,
2 2 1,
n为奇数 n为偶数(不是4的倍数)
则我们称这一对m序列为优选对。
n级m序列发生器 时钟
n级m序列发生器
模2加
Gold码序列
(a)
1
2
3
4
5
12345 (b)
图2 Gold (a) Gold码发生器的原理结构图; (b) 5级m序列优选对构成的Gold码发生器
• 随着级数n的增加,Gold码序列的数量远远 超过同级数的m序列的数量,便于扩频多址 应用。
Gold序列的相关性
• 自相关性:Gold 证明了Gold 码序列的自 相关函数的所有非最高峰的取值是三值。
• 互相关性:Gold 码序列的互相关函数值的 最大值不超过其m 序列优选对的互相关值, 具有三值互相关函数 。
图1 反馈移位寄存器原理框图
Gold序列
• m序列虽然性能优良(具有尖锐而无旁瓣 的自相关函数), 但同样长度的m序列个数 不多,且序列之间的互相关性不够好。 R·Gold提出了一种基于m序列的PN码序 列, 称为Gold码序列。
• Gold序列是用一对周期和速率均相同,但 码字不同的m序列优选对模2加后得到的。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
gold序列自相关函数
就是金序列自相关函数,首先是解释它的定义——金序列自相关函数(GSCF)是一个关于序列间滞后关系的统计概念。
它的定义是描述两个序列之间的滞后关系的参数,同样地,它也可以用于描述一个单独的序列内部的滞后关系。
GSCF能够衡量一段时间序列(以向量形式表示)之间存在的线性或者因果关系。
GSCF自相关函数采用传统的距离函数来测量时间序列之间的差异,包括最小二乘法、贝叶斯方法等。
它的计算方法可以用来比较两个序列的相关性,进而确定它们之间的关系。
实际应用中,GSCF自相关函数可以用来判断某一系统的稳定性;通过判断两个序列之间的相似性,GSCF可以提高数据分析的准确性。
例如:市场走势、风险管理等,都可以以GSCF自相关函数来反映。
此外,GSCF自相关函数也可以用于指标建模,数据可视化,以及序列模式检测,GSCF自相关函数可以被用于更广泛的应用,例如指标的选择,优化序列的性能,提高分析的准确度等。
GSCF自相关函数也可以应用于大数据中,以及机器学习,使用GSCF可以帮助用户提高数据分析的准确性,更有效地进行数据处理。
总之,GSCF自相关函数是一门统计概念,用于描述序列间的滞后关系,它可以用于评估序列行为的稳定性,以及检测其相似性,它也可以用于大数据的处理,通过分析不同的时间序列间的相关性,从而更好地分析数据,并找出隐藏的有价值的信息。
GSCF也有助于提高预测的准确性,在后续的分析中能够有效地获取更好的结果。
