2.1双光束干涉讲解
合集下载
双光束干涉PPT课件
从一个条纹过渡到另一个条纹，平板的厚度均改变
/ (2n)。
L h sin
h 2n
46
(2)劈尖的等厚干涉条纹
L2nsin (33)
劈角 小，条纹间距大；反之，劈角 大，条纹
间距小。因此，当劈尖上表面绕棱线旋转时, 随着
的增大, 条纹间距变小, 条纹将向棱线方向移动。
47
(2)劈尖的等厚干涉条纹
49
(2)劈尖的等厚干涉条纹 应用:
Δh
b
b'
50
（3）牛顿环 在一块平面玻璃上放置一曲率半径 R 很大的平凸透 镜，在透镜凸表面和玻璃板的平面之间便形成一厚 度由零逐渐增大的空气薄层。
S
R
r
o
h
51
（3）牛顿环 当以单色光垂直照射时，在空气层上会形成一组以 接触点 O 为中心的中央硫、边缘密的圆环条纹，称 为牛顿环。
II12 00..906016 V0.0814
所以，在平行板表面反射率较低的情况下，通常应
用的是反射光的等倾干涉。
35
2）楔形平板产生的干涉——等厚干涉 扩展光源中的某点 S0 发出一束光，经楔形板两表面 反射的两支光相交于 P 点，产生干涉，其光程差为
n ( A B B C ) n 0 ( A P A C )
23
②等倾亮圆环的半径
一般情况下，1N 和 2N 都很小，近似有 nn01N/ 2N
1 c o s2 N 2 2 N /2 n 0 21 2 N /2 n 2 ，因而由上式可得
1Nn10
n N1
h
(23)
2 n h ( 1 c o s2 N ) ( N 1 ） ]
1 c o s2 N 2 2 N /2 n 0 21 2 N /2 n 2
/ (2n)。
L h sin
h 2n
46
(2)劈尖的等厚干涉条纹
L2nsin (33)
劈角 小，条纹间距大；反之，劈角 大，条纹
间距小。因此，当劈尖上表面绕棱线旋转时, 随着
的增大, 条纹间距变小, 条纹将向棱线方向移动。
47
(2)劈尖的等厚干涉条纹
49
(2)劈尖的等厚干涉条纹 应用:
Δh
b
b'
50
（3）牛顿环 在一块平面玻璃上放置一曲率半径 R 很大的平凸透 镜，在透镜凸表面和玻璃板的平面之间便形成一厚 度由零逐渐增大的空气薄层。
S
R
r
o
h
51
（3）牛顿环 当以单色光垂直照射时，在空气层上会形成一组以 接触点 O 为中心的中央硫、边缘密的圆环条纹，称 为牛顿环。
II12 00..906016 V0.0814
所以，在平行板表面反射率较低的情况下，通常应
用的是反射光的等倾干涉。
35
2）楔形平板产生的干涉——等厚干涉 扩展光源中的某点 S0 发出一束光，经楔形板两表面 反射的两支光相交于 P 点，产生干涉，其光程差为
n ( A B B C ) n 0 ( A P A C )
23
②等倾亮圆环的半径
一般情况下，1N 和 2N 都很小，近似有 nn01N/ 2N
1 c o s2 N 2 2 N /2 n 0 21 2 N /2 n 2 ，因而由上式可得
1Nn10
n N1
h
(23)
2 n h ( 1 c o s2 N ) ( N 1 ） ]
1 c o s2 N 2 2 N /2 n 0 21 2 N /2 n 2
《双光束干涉》课件
扩展光源
对于某些实验需求，可以使用扩 展光源代替激光器，以模拟自然 光或实现更大的干涉条纹可见度 。
分束器
半透半反镜
将一束光分成两束相同的光，一束反 射，一束透射，是常用的分束器。
分束棱镜
利用棱镜的折射特性将一束光分成两 束不同角度的光，常用于产生不同路 径长度的干涉。
反射镜和干涉仪
反射镜
用于改变光路，使两束光在空间上交叠，形成干涉。
干涉条纹的移动与变化
当一束光波的波长或相位发生变化时，干涉条纹的位置 和形状也会随之改变。
当两束光波的振幅（强度）发生变化时，干涉条纹的可 见度和强度也会受到影响。
当一束光波在空间中传播时，遇到不均匀介质或受到外 界扰动时，干涉条纹的位置和形状也会发生变化。
干涉条纹的可见度与强度
01
干涉条纹的可见度与两束光波的 相位差和振幅有关。相位差越小 ，可见度越高；振幅越大，可见 度越高。
双光束干涉的原理
光程差
01
两束光在相遇点产生的光程差会导致相位发生变化，进而影响
干涉结果。
干涉加强
02
当两束光的光程差为半波长的偶数倍时，光强增强，形成明条
纹。
干涉减弱
03
当两束光的光程差为半波长的奇数倍时，光强减弱，形成暗条
纹。
02
双光束干涉实验装置
Chapter
光源
激光器
作为相干性好的光源，激光器能 够产生单色性好的光束，是双光 束干涉实验中的理想选择。
激光器稳定性误差
激光器的输出功率和波长可能会随时间变化，导 致干涉条纹的移动和变化。
探测器响应误差
探测器的响应速度和精度会影响对干涉条纹的记 录和分析。
THANKS
对于某些实验需求，可以使用扩 展光源代替激光器，以模拟自然 光或实现更大的干涉条纹可见度 。
分束器
半透半反镜
将一束光分成两束相同的光，一束反 射，一束透射，是常用的分束器。
分束棱镜
利用棱镜的折射特性将一束光分成两 束不同角度的光，常用于产生不同路 径长度的干涉。
反射镜和干涉仪
反射镜
用于改变光路，使两束光在空间上交叠，形成干涉。
干涉条纹的移动与变化
当一束光波的波长或相位发生变化时，干涉条纹的位置 和形状也会随之改变。
当两束光波的振幅（强度）发生变化时，干涉条纹的可 见度和强度也会受到影响。
当一束光波在空间中传播时，遇到不均匀介质或受到外 界扰动时，干涉条纹的位置和形状也会发生变化。
干涉条纹的可见度与强度
01
干涉条纹的可见度与两束光波的 相位差和振幅有关。相位差越小 ，可见度越高；振幅越大，可见 度越高。
双光束干涉的原理
光程差
01
两束光在相遇点产生的光程差会导致相位发生变化，进而影响
干涉结果。
干涉加强
02
当两束光的光程差为半波长的偶数倍时，光强增强，形成明条
纹。
干涉减弱
03
当两束光的光程差为半波长的奇数倍时，光强减弱，形成暗条
纹。
02
双光束干涉实验装置
Chapter
光源
激光器
作为相干性好的光源，激光器能 够产生单色性好的光束，是双光 束干涉实验中的理想选择。
激光器稳定性误差
激光器的输出功率和波长可能会随时间变化，导 致干涉条纹的移动和变化。
探测器响应误差
探测器的响应速度和精度会影响对干涉条纹的记 录和分析。
THANKS
双光束干涉实验的实施与分析
光的偏振与干涉效应
偏振性质研 究
对实验结果的影 响
偏振实验展 示
拓展干涉应用领 域
干涉效应分 析
光的偏振行为认 识
偏振片调整
观察到的效应
惠更斯原理在干涉实验中的应 用
惠更斯原理是描述波动现象的重要原理，可以应 用于解释干涉实验中的一些现象。结合惠更斯原 理，可以更深入地理解干涉现象的成因和干涉条 纹的形成规律。
激光干涉仪的精密测量
高精度测量
激光干涉仪能够 实现高精度的长 度、位移等参数
测量
原理优化
利用双光束干涉 实验的原理，可 以改进激光干涉
仪的性能
测量精度提 高
优化激光干涉仪， 可以提高测量的
精度和准确性
广泛应用
激光干涉仪在科 学研究、工业制 造等领域都有重
要应用
光栅测量与光学信号处理
01 精密测量
实验结果的统计与分析
多次实验数据统计
对多次实验数据进行统计 分析，可以得到更加准确 的结果和结论。
误差排除
利用统计方法对实验数据 进行处理，可以排除误差 影响，提高实验结果的可 靠性。
● 04
第四章 双光束干涉实验的进 一步研究
光的相干性与干 涉结果
光的相干性是影响干 涉结果的重要因素， 对光源的相干性进行 研究有助于理解干涉 现象的本质。通过改 变光源的相干性，可 以观察到干涉条纹的 变化，从而探究相干 性对干涉实验的影响。
校准精度
仪器校准是确保测量准确 性的重要环节 利用双光束干涉实验，可 以提高校准的精度，保证 测量结果的可信度
性能稳定
校准后的光学仪器性能更 为稳定，能够长时间保持 高精度工作 为各种应用提供可靠的测 量支持
可靠性提升
双光束干涉1.
因此干涉图样可见度变低。
I = I1 I2 2 I1I2 cos
P = IM Im = 4 =1 IM Im 4
使一个狭缝加宽一倍，振幅变为原来的 2 倍，光强 变为原来的 4 倍，相干度为
I = I1 4I1 2 4I1I1 cos = 5I1 4I1 cos
P = IM Im = 8 = 0.8 IM Im 10
3.1.2 双光束干涉 (Two-beam interference) 1．分波面法双光束干涉 在实验室中为了演示分波面法的双光束干涉，最常 采用的是图所示的双缝干涉实验。
分波面法
p S*
激
S1*
光
S2 *
x
k=+2
k=+1
k= 0
I
k=-1
k=-2
1．分波面法双光束干涉
Sl 和 S2 双缝从来自狭缝 S 的光波波面上分割出很小的 两部分作为相干光源，它们发出的两列光波在观察屏 上叠加，形成干涉条纹。
1．分波面法双光束干涉 对应 = (2m+1)π (m=0, 1, 2 ) 的空间点
y = (m 1 ) Dl (12)
2d
为光强极小，呈现干涉暗条纹。
1．分波面法双光束干涉
相邻两亮（暗）条纹间的距离是条纹间距为，且
= Dy = Dl = l (13) d
其中 = d/D 叫光束会聚角。在实验中，可以通过 测量 D、d 和 ，计算求得光波长 l。
于是，零级条纹（因而所有条纹）应当上移。
(2) 考察屏幕上的一个固定点移动一个条纹，表明光 程差相差一个波长，因此
(n n)l = 20l n = n 20l
进而可得
I = I1 I2 2 I1I2 cos
P = IM Im = 4 =1 IM Im 4
使一个狭缝加宽一倍，振幅变为原来的 2 倍，光强 变为原来的 4 倍，相干度为
I = I1 4I1 2 4I1I1 cos = 5I1 4I1 cos
P = IM Im = 8 = 0.8 IM Im 10
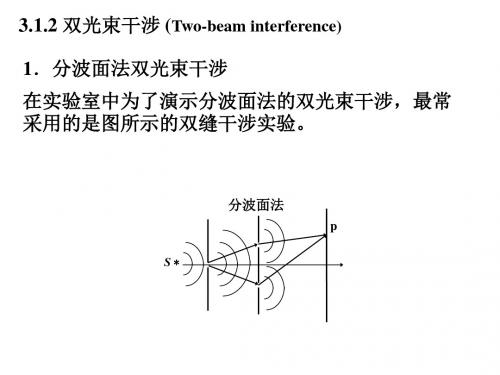
3.1.2 双光束干涉 (Two-beam interference) 1．分波面法双光束干涉 在实验室中为了演示分波面法的双光束干涉，最常 采用的是图所示的双缝干涉实验。
分波面法
p S*
激
S1*
光
S2 *
x
k=+2
k=+1
k= 0
I
k=-1
k=-2
1．分波面法双光束干涉
Sl 和 S2 双缝从来自狭缝 S 的光波波面上分割出很小的 两部分作为相干光源，它们发出的两列光波在观察屏 上叠加，形成干涉条纹。
1．分波面法双光束干涉 对应 = (2m+1)π (m=0, 1, 2 ) 的空间点
y = (m 1 ) Dl (12)
2d
为光强极小，呈现干涉暗条纹。
1．分波面法双光束干涉
相邻两亮（暗）条纹间的距离是条纹间距为，且
= Dy = Dl = l (13) d
其中 = d/D 叫光束会聚角。在实验中，可以通过 测量 D、d 和 ，计算求得光波长 l。
于是，零级条纹（因而所有条纹）应当上移。
(2) 考察屏幕上的一个固定点移动一个条纹，表明光 程差相差一个波长，因此
(n n)l = 20l n = n 20l
进而可得
2.1 双光束干涉
当干涉光强的极小值Imin=0时，V=1，二光束
完全相干，条纹最清晰；
当Imax=Imin时，V=0，二光束完全不相干，无
干涉条纹；
当Imax≠Imin≠0时，0＜V＜1，二光束部分相
干，条纹清晰度介于上面两种情况之间。
4/2/2021
5
2）产生干涉的条件
双光束叠加在P点处的光强分布为
I I1 I2 2 I1I2 cos cos
0
2nh
2
m0
m0
0
2nh
1 2
通常，m0不一定是整数，即中心未必是最亮点，故经
常把m0写成 m0 m1
其中，m1是靠中心最近的亮条纹的级数(整数)， 0＜ε＜1。
4/2/2021
29
等倾干涉条纹的特性②
② 等倾亮圆环的半径
由中心向外计算，第N个亮环的干涉级数为[m1-(N1)]，该亮环的张角为θ1N，它可由
稳定：用肉眼或记录仪器能观察到
或记录到条纹分布，即在一定时间 内存在着相对稳定的条纹分布。
讨论，图2-1所示的两列单色
线偏振光的叠加
E1
E01
c os (1t
k1
r
01 )
E2 E02 cos(2t k2 r 02 )
波函数
4/2/2021
2
在P点相遇，E1与E2振动方向间的夹角为θ，则在P点
肉眼或探测仪器就将观察不到稳定的条纹分布。 因此，为了产生干涉现象，要求两叠加光束的频率尽量相等。
4/2/2021
6
(2) 对叠加光束振动方向的要求
当两光束光强相等，则条纹可见度为V=cosθ
若θ=0，两光束的振动方向相同时，V=1，干涉条
2.1 双光束干涉解析
1 2 I12 I1I 2 cos cos
10/7/2018
涉现象； 2.若随时间变化(即 随时间变化)太快，也 看不到干涉现象。
3
在能观察到稳定的光强分布的情况下
1.出现光强极大的条件
2m , m 0,1,2...
光强极大值Imax为 I max I1 I 2 2 I1 I 2 cos
10/7/2018
波函数
2
在 P 点相遇， E1 与 E2 振动方向间的夹角为 θ ，则在 P 点
处的总光强为
I I1 I 2 2 I1 I 2 cos cos I1 I 2 2 I12
式中，I1、I2是二光束的光强，I12为干涉项； 是二光束 的相位差，且有 注意：对干涉项I12 1.若太小，看不到干 k2 r k1 r 01 02 t
2.1 双光束干涉
2.1.1 产生干涉的基本条件
1.两束光的干涉现象 2.产生干涉的条件 3.实现光束干涉的基本方法
2.1.2 双光束干涉
1.分波面法双光束干涉 2.分振幅双光束干涉
10/7/2018
1
1.两束光的干涉现象
光的干涉：指两束或多束光在 空间相遇时， 在重叠区内形成 稳定的强弱强度分布的现象。
10/7/2018
4
2.产生干涉的条件
讨论：
1）干涉条纹可见度 定义
I max I min V I max I min
当干涉光强的极小值Imin=0时，V=1，二光束 完全相干，条纹最清晰； 当Imax=Imin时，V=0，二光束完全不相干，无 干涉条纹； 当Imax≠Imin≠0时，0＜V＜1，二光束部分相 干，条纹清晰度介于上面两种情况之间。
《双光束干涉》课件
在双光束干涉实验中，测量仪器通常 包括显微镜、测微器和光电探测器等。
03
双光束干涉的实验操作
实验准备
01
02
03
实验器材
包括分束器、反射镜、光 屏、激光器、测量尺等。
实验环境
确保实验室环境安静、无 风，避免外界因素干扰实 验结果。
安全措施
确保实验人员佩戴护目镜， 避免激光直接照射眼睛。
实验步骤
安装调试
按照实验要求，正确安 装和调试实验器材，确
保光路正确。
开启激光器
调整激光器输出功率， 使光束稳定。
观察干涉现象
观察双光束在光屏上的 干涉现象，记录干涉条
纹。
改变实验条件
可改变光束角度、光束 间距等条件，观察干涉
现象的变化。
数据处理与分析
数据记录
详细记录不同实验条件下 干涉条纹的数量、宽度和 分布。
改进方法一
使用更稳定的光源，如激光， 以减小光波相位差的不稳定性
。
改进方法二
使用高精度测量设备，确保双 缝宽度和间距的准确性。
THANKS
感谢观看
干涉现象
干涉现象是指两束或多束相干波在空 间某些区域相遇时，相互叠加而形成 的稳定强度分布现象。
干涉现象是波动性的重要特征之一， 是双光束干涉的基础。
双光束干涉的形成原理
双光束干涉是指两束相干光在空间相遇并相互叠加，形成稳 定的干涉现象。
双光束干涉的形成原理基于光的波动性和相干性，当两束相 干光波的相位差恒定时，它们在空间某些区域形成稳定的干 涉图案。
数据处理
对记录的数据进行计算和 处理，求出干涉条纹的间 距和角度。
结果分析
根据数据处理结果，分析 双光束干涉的规律和特点， 得出结论。
分波前双光束干涉实验
分波前双光束干涉实验观察双光束干涉现象，通常的办法是将同一波列分解为二，使他们经过不同的途径后重新相遇。
由于这样得到的两个波列是由同一波列分解而来，他们频率相同，相位差稳定，震动方向也可作到基本上平行，从而可以产生稳定的干涉场。
分解波列的方法通常有分波前和和分振幅两种方法，其中分波前方法是通过光具将光源波前分成两部分，使之分别通过两个光具组，经衍射、反射或折射后交叠起来，在一定区域内产生干涉场，经典的杨氏双缝实验就属于这类分波前干涉装置，分波前干涉装置有多种类型，其中利用切开的透镜可以组成多种对切透镜装置观察双光束干涉，此外劳埃德镜装置和菲涅耳双棱镜也是典型的分波前干涉装置。
在本实验中我们主要讨论典型的分波前干涉装置包括比列(Billet)对切透镜和梅斯林(Maslin)对切透镜两种利用对切透镜实现双光束干涉的实验装置，此外还有利用劳埃德镜装置和菲涅耳双棱镜实现双光束干涉。
1.待研究问题：(1)比列对切透镜双光束干涉现象有什么特点，如何观察。
(2)梅斯林对切透镜干涉现象有什么特点，如何观察。
(3)如何利用劳埃德镜装置观察双光束干涉现象。
(4)如何利用菲涅耳双棱镜装置观察双光束干涉现象。
2实验原理2.1比列(Billet)对切透镜实验比列对切透镜一般是将焦距为f的透镜中间宽度为a的部分切去，如图1所示将余下的两部分粘和后所构成。
图1 比列对切透镜组成粘合的比列对切透镜分波前双光束干涉可分为会聚光的干涉和发散光的干涉两种情形进行分析。
如图2所示，点光源S 位于透镜物方焦点以外的粘合透镜中心线上距离中心o 点距离为L ，根据透镜成像基本原理，该点光源将在透镜像方成实像,且由于上下两部分光心错开，因此点光源s 经过该粘合透镜将如图2所示得到两个实像S 1和S 2。
这样点光源发出的球面波将会由该粘合透镜分成两束光分别会聚与S 1与S 2。
在透镜后方如图2所示阴影区内则可以观察到两光束干涉现象。
根据图1所示粘合透镜的结构可知，粘合透镜上半部分的光心是在粘合透镜中心点O 下方a/2处的O 2，同理下半部分的光心是O 点上方a/2处的O 1，若原透镜焦距为f ，则可以通过透镜成像原理计算得到实像S 1S 2距离d 满足：f L aL-=d (1)根据两点光源的干涉原理，和粘合透镜成像情况，在阴影区域内光屏上的干涉条纹应为双曲线型，在傍轴情况下近似为平行直条纹，若光屏距离透镜距离为D 则根据(1)式及两点光源干涉基本原理可得条纹间距为：λ⋅+-=∆aLDf DL fL x (2)图2 比列对切透镜会聚球面波干涉比列对切粘合透镜干涉情况的典型光路是在对切透镜的中心线上物方焦平面上放置一点光源S ，如图3所示，由S 点发出的球面波经透镜上下两部分分割，分波前折射后变成夹角为θ的两束平行光，他们叠加后在斜线所示的区域内将产生干涉。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
10/23/2018
5
2）产生干涉的条件
双光束叠加在P点处的光强分布为
I I1 I 2 2 I1 I 2 cos cos
影响光强条纹稳定分布的主要因素是：1）两光束频率； 2）两光束振动方向夹角和3）两光束的相位差。 (1) 对叠加光束的频率要求
当两光束频率相等，Δ ω =0时，干涉光强不随时间变化，可以 得到稳定的干涉条纹分布。 当两光束的频率不相等，Δ ω ≠0时，干涉条纹将随着时间产生 移动，且Δ ω 愈大，条纹移动速度愈快，当Δ ω 大到一定程度时， 肉眼或探测仪器就将观察不到稳定的条纹分布。 因此，为了产生干涉现象，要求两叠加光束的频率尽量相等。
2.1 双光束干涉
2.1.1 产生干涉的基本条件
1.两束光的干涉现象 2.产生干涉的条件 3.实现光束干涉的基本方法
2.1.2 双光束干涉
1.分波面法双光束干涉 2.分振幅双光束干涉
10/23/2018
1
1.两束光的干涉现象
光的干涉：指两束或多束光在 空间相遇时， 在重叠区内形成 稳定的强弱强度分布的现象。
1 2 I12 I1I 2 cos cos
10/23/2018
涉现象； 2.若随时间变化(即 随时间变化)太快，也 看不到干涉现象。
3
在能观察到稳定的光强分布的情况下
1.出现光强极大的条件
2m , m 0,1,2...
光强极大值Imax为 I max I1 I 2 2 I1 I 2 cos
稳定：用肉眼或记录仪器能观察到
或记录到条纹分布，即在一定时间 内存在着相对稳定的条纹分布。
讨论，图2-1所示的两列单色 线偏振光的叠加
E1 E01 cos(1t k1 r 01 ) E2 E02 cos(2t k 2 r 02 )
2
① 如果S1、S2到S的距离相等，Δ R=0，则
对应=2mπ(m=0,±1,±2,…)的空间点
D 为光强极大，呈现干涉亮条纹； ym d
对应 =(2m+1)π的空间 点 1 D y m 为光强极小，呈现干涉暗条纹。
2 d
10/23/2018
12
干涉条纹形状（以强度为特征的空间分布）
光屏上是与y轴垂直、明暗相间的直条纹。相邻两亮 (暗)条纹间的距离是条纹间距ε，且
• 条纹间距与会聚角成反比 , 与波长 成正比; • 在实验中，可以通过测量D、d和ε， 其中w=d/D叫光束会聚 计算光波长λ。
D y d w
6
10/23/2018
(2) 对叠加光束振动方向的要求
当两光束光强相等，则条纹可见度为V=cosθ
若θ =0，两光束的振动方向相同时，V=1，干涉条 纹最清晰； 若θ =π/2，两光束正交振动时，V=0，不发生干涉； 当0＜θ ＜π/2时，0＜V＜1，干涉条纹清晰度介于上 面两种情况之间。
为了产生明显的干涉现象，要求两叠加光束的 振动方向相同。
10/23/2018
7
(3) 对叠加光束相位差的要求
为了获得稳定的干涉图形，两叠加光束的相位 差必须固定不变，即要求两等频单色光波的初 相位差恒定。 实际上，考虑到光源的发光特点，这是最关键 的要求。 结论：要获得稳定的干涉条纹，要求：
①两束光波的频率相同； ②两束光波在相遇处的振动方向相同； ③两束光波在相遇处应有固定不变的相位差。
这三个条件就是两束光波发生干涉的必要条件， 通常称为相干条件。
10/23/2018
8
3.实现光束干涉的基本方法
原子的发光特点
获得相干光的方法
普通光源：自发辐射- -非相干光源 时间：持续时间有限(10-8s)- -波列； 相位：彼此无关- -同一原子不同时刻，不同原子同 一时刻。 激光：受激辐射 - -相干光源
狭缝S和双缝S1、S2都很窄，均可视为次级线光源。 从线光源S发出的光波经SS1P和SS2P两条不同路径， 在观察屏P点上相交，其光程差为
Δ =(R2-R1)+(r2-r1)=Δ R+Δ r
10/23/2018
11
近轴远场条件下：d« D,且y在很小范围内
两光束的相位差为
讨论
2 yd R D
两独立光源不可能相干；将一波列的光分成两束或多 束，然后再令其重叠，在相遇区域有可能发生干涉。 分波面法- -杨氏干涉 分振幅法- -薄膜干涉(迈克尔逊干涉) 分振动面- -偏振光干涉
9
10/23/2018
1.分波面法双光束干涉
10/23/2018
10
杨氏双缝干涉实验
实验原理图
S1、S2从来自S 的光波波面上分 割出很小的两部 分作为相干光源， 它们发出的光相 遇形成干涉条纹。
10/23/2018
波函数
2
在 P 点相遇， E1 与 E2 振动方向间的夹角为 θ ，则在 P 点
处的总光强为
I I1 I 2 2 I1 I 2 cos cos I1 I 2 2 I12
式中，I1、I2是二光束的光强，I12为干涉项； 是二光束 的相位差，且有 注意：对干涉项I12 1.若太小，看不到干 k2 r k1 r 01 02 t
10/23/2018
4
2.产生干涉的条件
讨论：
1）干涉条纹可见度 定义源自I max I min V I max I min
当干涉光强的极小值Imin=0时，V=1，二光束 完全相干，条纹最清晰； 当Imax=Imin时，V=0，二光束完全不相干，无 干涉条纹； 当Imax≠Imin≠0时，0＜V＜1，二光束部分相 干，条纹清晰度介于上面两种情况之间。
2.出现光强极小的条件
光强极小值Imin为
(2m 1) , m 0,1,2...
I min I1 I 2 2 I1 I 2 cos
当两束光强相等，I1=I2=I0，相应的极大值和极小值 分别为 Imax=2I0(1+cosθ ) Imin=2I0(1-cosθ )