最新21双光束干涉
2.1双光束干涉讲解

10/23/2018
5
2)产生干涉的条件
双光束叠加在P点处的光强分布为
I I1 I 2 2 I1 I 2 cos cos
影响光强条纹稳定分布的主要因素是:1)两光束频率; 2)两光束振动方向夹角和3)两光束的相位差。 (1) 对叠加光束的频率要求
当两光束频率相等,Δ ω =0时,干涉光强不随时间变化,可以 得到稳定的干涉条纹分布。 当两光束的频率不相等,Δ ω ≠0时,干涉条纹将随着时间产生 移动,且Δ ω 愈大,条纹移动速度愈快,当Δ ω 大到一定程度时, 肉眼或探测仪器就将观察不到稳定的条纹分布。 因此,为了产生干涉现象,要求两叠加光束的频率尽量相等。
2.1 双光束干涉
2.1.1 产生干涉的基本条件
1.两束光的干涉现象 2.产生干涉的条件 3.实现光束干涉的基本方法
2.1.2 双光束干涉
1.分波面法双光束干涉 2.分振幅双光束干涉
10/23/2018
1
1.两束光的干涉现象
光的干涉:指两束或多束光在 空间相遇时, 在重叠区内形成 稳定的强弱强度分布的现象。
1 2 I12 I1I 2 cos cos
10/23/2018
涉现象; 2.若随时间变化(即 随时间变化)太快,也 看不到干涉现象。
3
在能观察到稳定的光强分布的情况下
1.出现光强极大的条件
2m , m 0,1,2...
光强极大值Imax为 I max I1 I 2 2 I1 I 2 cos
稳定:用肉眼或记录仪器能观察到
或记录到条纹分布,即在一定时间 内存在着相对稳定的条纹分布。
讨论,图2-1所示的两列单色 线偏振光的叠加
双光束干涉PPT课件

/ (2n)。
L h sin
h 2n
46
(2)劈尖的等厚干涉条纹
L2nsin (33)
劈角 小,条纹间距大;反之,劈角 大,条纹
间距小。因此,当劈尖上表面绕棱线旋转时, 随着
的增大, 条纹间距变小, 条纹将向棱线方向移动。
47
(2)劈尖的等厚干涉条纹
49
(2)劈尖的等厚干涉条纹 应用:
Δh
b
b'
50
(3)牛顿环 在一块平面玻璃上放置一曲率半径 R 很大的平凸透 镜,在透镜凸表面和玻璃板的平面之间便形成一厚 度由零逐渐增大的空气薄层。
S
R
r
o
h
51
(3)牛顿环 当以单色光垂直照射时,在空气层上会形成一组以 接触点 O 为中心的中央硫、边缘密的圆环条纹,称 为牛顿环。
II12 00..906016 V0.0814
所以,在平行板表面反射率较低的情况下,通常应
用的是反射光的等倾干涉。
35
2)楔形平板产生的干涉——等厚干涉 扩展光源中的某点 S0 发出一束光,经楔形板两表面 反射的两支光相交于 P 点,产生干涉,其光程差为
n ( A B B C ) n 0 ( A P A C )
23
②等倾亮圆环的半径
一般情况下,1N 和 2N 都很小,近似有 nn01N/ 2N
1 c o s2 N 2 2 N /2 n 0 21 2 N /2 n 2 ,因而由上式可得
1Nn10
n N1
h
(23)
2 n h ( 1 c o s2 N ) ( N 1 ) ]
1 c o s2 N 2 2 N /2 n 0 21 2 N /2 n 2
《双光束干涉》课件

对于某些实验需求,可以使用扩 展光源代替激光器,以模拟自然 光或实现更大的干涉条纹可见度 。
分束器
半透半反镜
将一束光分成两束相同的光,一束反 射,一束透射,是常用的分束器。
分束棱镜
利用棱镜的折射特性将一束光分成两 束不同角度的光,常用于产生不同路 径长度的干涉。
反射镜和干涉仪
反射镜
用于改变光路,使两束光在空间上交叠,形成干涉。
干涉条纹的移动与变化
当一束光波的波长或相位发生变化时,干涉条纹的位置 和形状也会随之改变。
当两束光波的振幅(强度)发生变化时,干涉条纹的可 见度和强度也会受到影响。
当一束光波在空间中传播时,遇到不均匀介质或受到外 界扰动时,干涉条纹的位置和形状也会发生变化。
干涉条纹的可见度与强度
01
干涉条纹的可见度与两束光波的 相位差和振幅有关。相位差越小 ,可见度越高;振幅越大,可见 度越高。
双光束干涉的原理
光程差
01
两束光在相遇点产生的光程差会导致相位发生变化,进而影响
干涉结果。
干涉加强
02
当两束光的光程差为半波长的偶数倍时,光强增强,形成明条
纹。
干涉减弱
03
当两束光的光程差为半波长的奇数倍时,光强减弱,形成暗条
纹。
02
双光束干涉实验装置
Chapter
光源
激光器
作为相干性好的光源,激光器能 够产生单色性好的光束,是双光 束干涉实验中的理想选择。
激光器稳定性误差
激光器的输出功率和波长可能会随时间变化,导 致干涉条纹的移动和变化。
探测器响应误差
探测器的响应速度和精度会影响对干涉条纹的记 录和分析。
THANKS
光的干涉与双缝干涉实验

光的干涉与双缝干涉实验光的干涉是光学中的一个重要现象,它展示了光波的波动性质。
其中,双缝干涉实验是最经典的实验之一。
本文将介绍光的干涉以及双缝干涉实验,并探讨其原理和应用。
一、光的干涉干涉是两个或多个光波相遇形成干涉图案的现象。
在光的干涉中,光波叠加后会出现明暗相间的干涉条纹。
这是由于光波的相位差引起的,相位差决定了光波的相互叠加情况。
光的干涉有两种类型,一种是构造干涉,一种是破坏干涉。
构造干涉是指两个光波相遇时,相位差为整数倍的情况,此时光波会相互加强,形成明亮的条纹。
而破坏干涉则是指相位差为半整数倍的情况,此时光波会相互抵消,形成暗淡的条纹。
二、双缝干涉实验双缝干涉实验是一种经典的验证光的干涉现象的实验。
它是由英国物理学家托马斯·杨于1801年首次进行的。
实验的装置比较简单,只需要一个光源、两个狭缝和一个屏幕即可。
实验的原理是,当光通过两个狭缝后,会形成两个新的光源,并在屏幕上形成干涉条纹。
这是因为通过两个狭缝后的光波具有不同的相位差。
当相位差为整数倍时,两个光波相互加强,形成明亮的条纹;当相位差为半整数倍时,两个光波相互抵消,形成暗淡的条纹。
双缝干涉实验的结果是令人惊讶的,它证实了光既具有粒子性又具有波动性。
在实验中,当光波通过狭缝时,每个狭缝都像是发射了一个光子,这就产生了干涉条纹。
这一实验结果深刻地影响了人们对光的理解。
三、双缝干涉实验的应用双缝干涉实验不仅仅是一种观察光波性质的实验,还有一些实际的应用。
首先,双缝干涉实验可以用于测量光的波长。
根据双缝干涉实验的原理,通过测量干涉条纹的间距和距离等参数,可以推导出光的波长。
这对于确定光的性质以及进行一些光学测量非常重要。
其次,双缝干涉实验也可以用于制作光栅。
光栅是一种具有周期性结构的光学元件,可以根据不同波长的光波进行分光。
通过将许多狭缝排列在一起,形成光栅,再利用干涉的原理,可以实现对光波的分光,广泛应用于光学领域。
此外,双缝干涉实验还可以用于光学显微镜的分辨率改善。
物理光学 双光束干涉(1)

D = S2Q2 (n n)l
零级条纹出现条件是
D = ml = 0
即
D = S2Q2 (n n)l = 0 S 2Q2 = (n n)l
考虑到
n n S 2Q2 0
于是,零级条纹(因而所有条纹)应当上移。
(2) 考察屏幕上的一个固定点移动一个条纹,表明光 程差相差一个波长,因此
因此干涉图样可见度变低。
洛埃镜
S
d
S’
M
D 洛 埃 镜 的 干 涉
1.分波面法双光束干涉 这些实验的共同点是: ①在两束光的叠加区内,到处都可以观察到干涉条 纹,只是不同地方条纹的间距、形状不同而已。这 种在整个光波叠加区内随处可见干涉条纹的干涉, 称为非定域干涉。 ②在这些干涉装置中,都有限制光束的狭缝或小孔, 因而干涉条纹的强度很弱,以致于在实际上难以应 用。
2π 2π
Dr dy / D
2π yd = D = (Dr DR) ( DR) ( 10 ) l l l D
1.分波面法双光束干涉
①如果 S1、S2 到 S 的距离相等,DR=0, 则对应 = 2mπ (m=0, 1, 2) 的空间点
Dl y=m d (11)
为光强极大,呈现干涉亮条纹;
I = I1 I 2 2 I1I 2 cosq cos = I1 I 2 +2 I12 (3)
1.分波面法双光束干涉
对应 = (2m+1)π (m=0, 1, 2) 的空间点
1 Dl y = (m ) 2 d
(12)
为光强极小,呈现干涉暗条纹。
1.分波面法双光束干涉
1 l y = (m ) = (m ) 2 d 2
双光束干涉的基本条件

双光束干涉的基本条件《双光束干涉的基本条件》有一次啊,我和我的实验室小伙伴在做光学实验,那场景简直是“鸡飞狗跳”。
小伙伴大喊着:“这双光束干涉到底需要啥条件啊,怎么就是出不来效果呢?”这就引出了我们今天要好好讨论的双光束干涉的基本条件。
那到底啥是双光束干涉呢?简单来说,就是两束光相互叠加后产生的一种光学现象,有的地方加强了,有的地方减弱了。
这就像是两个人在拔河,如果力都往一块儿使就加强了,如果方向相反那就相互抵消减弱了,不过光可比这拔河复杂多了。
首先啊,光源得是相干光源。
啥叫相干光源呢?就好比两个双胞胎,得非常相似。
光是一种电磁波,相干光源发出的光它的频率得相同,要是频率不一样,就像两个人唱歌不在一个调上,肯定没法很好地产生干涉现象。
比如说,我们常见的普通灯泡发出的光就不是相干光,因为里面各种频率的光都有混在一起,乱哄哄的。
但是像激光就很容易满足这个条件,激光的频率那是相当单一的,就像训练有素的士兵一样整齐。
而且啊,相干光源的相位差还得保持恒定。
这相位就像是两个人出发的起始位置,定好了就不能乱变,如果一会儿超前一会儿落后,那也没法玩干涉了。
其次呢,这两束光还得满足振动方向相同或者有平行的振动分量。
这就好比两个人跳舞,得朝向一个方向扭,要是一个横着扭一个竖着扭,那肯定乱套了,光也同理。
如果振动方向完全垂直,那是不可能形成干涉现象的。
不过要是有平行的分量,那至少还能部分地干涉一下。
再就是两束光在相遇的区域里,它们的光程差还得在相干长度之内。
啥叫光程差呢?就是两束光走过的路程不一样产生的差值。
比如说一束光抄近道了,另一束光绕路了。
但是这个差值得在一个合理的范围内,要是超出了相干长度,就像两个人走散得太远了,那也就没法干涉了。
打个比方啊,你和朋友约好了在一个广场碰面一起做点啥,但是他离得太远,你们的“波”(就类比着资源或者联系之类的东西)完全到不了一起,那还咋相互作用呢。
从实际操作来说啊,我觉得对于那些想做好双光束干涉实验的人,在选择光源的时候就要特别小心了。
双光束干涉1.
I = I1 I2 2 I1I2 cos
P = IM Im = 4 =1 IM Im 4
使一个狭缝加宽一倍,振幅变为原来的 2 倍,光强 变为原来的 4 倍,相干度为
I = I1 4I1 2 4I1I1 cos = 5I1 4I1 cos
P = IM Im = 8 = 0.8 IM Im 10
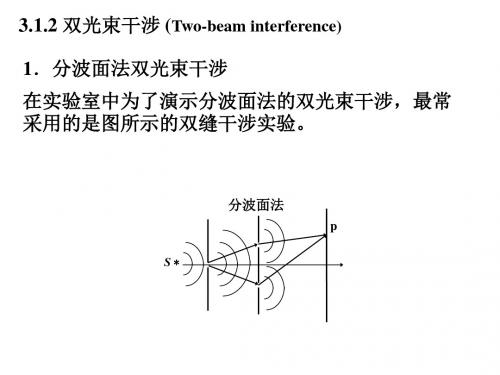
3.1.2 双光束干涉 (Two-beam interference) 1.分波面法双光束干涉 在实验室中为了演示分波面法的双光束干涉,最常 采用的是图所示的双缝干涉实验。
分波面法
p S*
激
S1*
光
S2 *
x
k=+2
k=+1
k= 0
I
k=-1
k=-2
1.分波面法双光束干涉
Sl 和 S2 双缝从来自狭缝 S 的光波波面上分割出很小的 两部分作为相干光源,它们发出的两列光波在观察屏 上叠加,形成干涉条纹。
1.分波面法双光束干涉 对应 = (2m+1)π (m=0, 1, 2 ) 的空间点
y = (m 1 ) Dl (12)
2d
为光强极小,呈现干涉暗条纹。
1.分波面法双光束干涉
相邻两亮(暗)条纹间的距离是条纹间距为,且
= Dy = Dl = l (13) d
其中 = d/D 叫光束会聚角。在实验中,可以通过 测量 D、d 和 ,计算求得光波长 l。
于是,零级条纹(因而所有条纹)应当上移。
(2) 考察屏幕上的一个固定点移动一个条纹,表明光 程差相差一个波长,因此
(n n)l = 20l n = n 20l
进而可得
双缝干涉原理

双缝干涉原理
双缝干涉原理是一种经典的实验现象,将一束单色光通过两个非常接近并且很窄的缝隙形成一个单色光源。
当这束光照射到一个屏幕上时,光波会通过两个缝隙同时传播到屏幕上。
由于光波是波动性质的,它们会相互干涉,形成一系列的明暗条纹,即干涉条纹。
当两束光波传播过程中相遇时,它们会发生干涉。
根据波的性质,光的干涉可以是增强或者抵消。
在干涉条纹中,亮条纹表示增强,暗条纹表示抵消。
这种干涉现象可以通过计算光波的相位差来解释。
在双缝干涉实验中,当两个缝隙之间的距离很小,且与光的波长相当时,干涉现象更加显著。
当两束光波同时到达屏幕上的某一点时,它们的相位差会决定干涉的结果。
具体来说,如果两束光波的相位差为整数倍的波长,它们会相互增强,产生亮条纹。
如果相位差为半波长,它们会相互抵消,产生暗条纹。
通过计算相位差,可以预测出明暗条纹的位置和形态。
双缝干涉原理是波动性质的光学实验之一,它证明了光同时具有粒子和波动性质。
这一原理在实验室中得到广泛应用,用于研究光的性质和解释其他干涉现象。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
当两束光强相等,I1=I2=I0,相应的极大值和极小值
分别为
Imax=2I0(1+cosθ) Imin=2I0(1-cosθ)
10/10/2020
3
2.产生干涉的条件
1)干涉条纹可见度 定义
讨论:
V Imax Imin Imax Imin
10/10/2020
10
近轴远场条件下:d«D,且y在很小范围内
两光束的相位差为
讨论
22yDdR
① 如果S1、S2到S的距离相等,ΔR=0,则
对应=2mπ(m=0,±1,±2,…)的空间点
y m D 为光强极大,呈现干涉亮条纹;
d
对应 =(2m+1)π的空间
点 ym1D 为光强极小,呈现干涉暗条纹。
面两种情况之间。
为了产生明显的干涉现象,要求两叠加光束的 振动方向相同。
10/10/2020
6
(3) 对叠加光束相位差的要求
为了获得稳定的干涉图形,两叠加光束的相位 差必须固定不变,即要求两等频单色光波的初 相位差恒定。
实际上,考虑到光源的发光特点,这是最关键 的要求。
结论:要获得稳定的干涉条纹,要求:
①两束光波的频率相同;
②两束光波在相遇处的振动方向相同;
③两束光波在相遇处应有固定不变的相位差。
这三个条件就是两束光波发生干涉的必要条件,
通常称为相干条件。
10/10/2020
7
3.实现光束干涉的基本方法
原子的发光特点
普通光源:自发辐射- -非相干光源 时间:持续时间有限(10-8s)- -波列; 相位:彼此无关- -同一原子不同时刻,不同原子同
肉眼或探测仪器就将观察不到稳定的条纹分布。 因此,为了产生干涉现象,要求两叠加光束的频率尽量相等。
10/10/2020
5
(2) 对叠加光束振动方向的要求
当两光束光强相等,则条纹可见度为V=cosθ
若θ=0,两光束的振动方向相同时,V=1,干涉条
纹最清晰; 若θ=π/2,两光束正交振动时,V=0,不发生干涉; 当0<θ<π/2时,0<V<1,干涉条纹清晰度介于上
21双光束干涉
在P点相遇,E1与E2振动方向间的夹角为θ,则在P点
处的总光强为(??解释)
I I1I22 I1I2coscos
I1I22I12
式中,I1、I2是二光束的光强,I12为干涉项;是二光束
的相位差,且有
注意:对干涉项I12
k2rk1r0102t 1.若太小,看不到干
12
涉现象;
2.若随时间变化(即
一时刻。 激光:受激辐射 - -相干光源
获得相干光的方法
两独立光源不可能相干;将一波列的光分成两束或多 束,然后再令其重叠,在相遇区域有可能发生干涉。
分波面法- -杨氏干涉
分振幅法- -薄膜干涉(迈克尔逊干涉)
分振动面- -偏振光干涉
10/10/2020
8
1.分波面法双光束干涉
10/10/2020
入射角i1接近90o-掠射,可使很小。
12
对波长一定的单色光,间距的y大小与 D成正比,而与d(缝间距)成反比;
y D
d
10/10/2020 返回
13
当D(d’)、d一定时,间距y的大小与光 的波长成正比
y D
d
10/10/2020
14
用白光作为光源时,出现彩色条纹
由 ymmD d,m0,1,2......
可知
m=0的中央明纹为白色; m≠0的各级明纹均为彩色; 当m较大时,不同级数的各色
影响光强条纹稳定分布的主要因素是:1)两光束频率;
2)两光束振动方向夹角和3)两光束的相位差。
(1) 对叠加光束的频率要求
当两光束频率相等,Δω=0时,干涉光强不随时间变化,可以
得到稳定的干涉条纹分布。
当两光束的频率不相等,Δω≠0时,干涉条纹将随着时间产生 移动,且Δω愈大,条纹移动速度愈快,当Δω大到一定程度时,
条纹,因相互重叠而得到均匀 的强度; 示意图如右图所示。
10/10/2020
m=2 m=1 m=0 m=-1 m=-2
15
讨论:②如果S1、S2到S的距离不相等,ΔR 0
亮条纹的空间位置 暗条纹的空间位置
y mR
w
y(m1/2)R
w
即干涉图样相对于ΔR=0的情况,沿着y方向发生
了平移。
• 除杨氏干涉实验外,菲涅耳双棱镜、菲涅耳双面 镜和洛埃镜都属于分波面法双光束干涉。
I12 I1I2coscos
随时间变化)太快,也
看不到干涉现象。
10/10/2020
2
在能观察到稳定的光强分布的情况下
1.出现光强极大的条件 2 m ,m 0 , 1 , 2 ...
光强极大值Imax为 Ima xI1I22I1I2cos
2.出现光强极小的条件 (2 m 1 ),m 0 , 1 , 2 ...
2 d
10/10/2020
11
干涉条纹形状(以强度为特征的空间分布)
光屏上是与y轴垂直、明暗相间的直条纹。相邻两亮 (暗)条纹间的距离是条纹间距ε,且
yD
dwΒιβλιοθήκη • 条纹间距与会聚角成反比,与波长 成正比;
• 在实验中,可以通过测量D、d和ε,
其中w=d/D叫光束会聚 计算光波长λ。
角
10/10/2020
当干涉光强的极小值Imin=0时,V=1,二光束
完全相干,条纹最清晰;
当Imax=Imin时,V=0,二光束完全不相干,无
干涉条纹;
当Imax≠Imin≠0时,0<V<1,二光束部分相
干,条纹清晰度介于上面两种情况之间。
10/10/2020
4
2)产生干涉的条件
双光束叠加在P点处的光强分布为
II1I22I1I2co cso s
• 这些实验的共同点
10/10/2020
16
菲涅耳双棱镜装置示意图
10/10/2020 返回
17
菲涅耳双面镜装置示意图
P
s
P1
M1
L
s1
d
s2
C
M2
P2
r0
10/10/2020 返回
18
劳埃德镜示意图
P'
P
s1
d
ML
P0
s2
d'
狭缝S1被强单色光照射,作为单色线状光源;
S1经M所成的虚像S2与S1构成相干光源;
9
杨氏双缝干涉实验
实验原理图
S1、S2从来自S 的光波波面上分 割出很小的两部 分作为相干光源, 它们发出的光相 遇形成干涉条纹。
狭缝S和双缝S1、S2都很窄,均可视为次级线光源。 从线光源S发出的光波经SS1P和SS2P两条不同路径,
在观察屏P点上相交,其光程差为
Δ=(R2-R1)+(r2-r1)=ΔR+Δr
