七年级数学下册第一章平行线综合卷浙教版
(完整word)浙教版七年级下册第一章平行线单元测试卷

浙教版七年级下第一章平行线单元测试卷题号一二三总分得分第Ⅰ卷(选择题)评卷人得分一.选择题(共10小题,3*10=30)1. 下列结论正确的是()A.过一点有且只有一条直线与已知直线垂直B.过一点有且只有一条直线与已知直线平行C.在同一平面内,不相交的两条射线是平行线D.如果两条直线都与第三条直线平行,那么这两条直线互相平行2. 如图,直线l1,l2被直线l3所截,且l1∥l2,则α的度数是()A.41°B.49°C.51°D.59°3. 已知∠AOB,P是任一点,过点P画一条直线与OA平行,则这样的直线()A.有且仅有一条B.有两条C.不存在D.有一条或不存在4. 如图,直线a与直线b交于点A,与直线c交于点B,∠1=120°,∠2=45°,若要使直线b与直线c平行,则可将直线b绕点A逆时针旋转()A.15°B.30°C.45°D.60°5. 已知:如图,AB∥CD,BC平分∠ABD,且∠C=40°,则∠D的度数是() A.40°B.80°C.90°D.100°6. 如图,点D,E,F分别在AB,BC,AC上,且EF∥AB,要使DF∥BC,只需添加条件()A.∠1=∠2 B.∠1=∠DFEC.∠1=∠AFD D.∠2=∠AFD7. 如图,AB∥CD,直线EF交AB于点E,交CD于点F,EG平分∠BEF交CD于点G,∠1=50°,则∠2等于()A.50°B.60°C.65°D.90°8. 如图,将三角形ABC平移到三角形EFG的位置,则图中共有平行线()A.3对B.5对C.6对D.7对9. 如图,把长方形ABCD沿EF对折后使两部分重合,若∠1=50°,则∠AEF等于() A.100°B.115°C.120°D.130°10.如图,AB∥CD,∠1=100°,∠2=120°,则∠α等于()A.100°B.80°C.60°D.40°第Ⅱ卷(非选择题)评卷人得分二.填空题(共6小题,3*6=18)11. 如图,若∠1+∠2=180°,∠3=110°,则∠4=_______.12. 在一块长为a,宽为b的长方形草地上,有一条弯曲的柏油小路(小路任何地方的水平宽度都是1个单位长度),则草地的面积为________.13. 如图,为了把△ABC平移得到△A′B′C′,可以先将△ABC向右平移______格,再向上平移______格.14. 如图,直线l1∥l2∥l3,点A,B,C分别在直线l1,l2,l3上,若∠1=70°,∠2=50°,则∠ABC=________.15. 如图,AB∥CD,则∠α,∠β,∠γ之间的关系是__∠α+∠β-∠γ=_______.16. 如图,边长为8 cm的正方形ABCD先向上平移4 cm,再向右平移2 cm,得到正方形A′B′C′D′,此时阴影部分的面积为_________.评卷人得分三.解答题(共7小题,52分)17. (6分) 如图,按要求完成作图.(1)过点P作AB的平行线EF;(2)过点P作CD的平行线MN;(3)过点P作AB的垂线段,垂足为G.18. (6分)如图,直线AB,CD相交于点O,∠AOD=70°,OE平分∠BOC,求∠DOE的度数.19. (6分)如图,E点为DF上的点,B为AC上的点,∠1=∠2,∠C=∠D.试说明:AC∥DF.20. (8分)如图,已知AB∥CD,∠B=40°,点E在DC的延长线上,CN 是∠BCE的平分线,CM⊥CN,求∠BCM的度数.21. (8分)如图,∠1+∠2=180°,∠A=∠C,DA平分∠BDF.(1)AE与FC会平行吗?说明理由;(2)AD与BC的位置关系如何?为什么?(3)BC平分∠DBE吗?为什么?22. (8分)如图,已知EF⊥AC,垂足为点F,DM⊥AC,垂足为点M,DN的延长线交AB 于点A,且∠1=∠C,点N在AD上,且∠2=∠3,证明AB∥MN.22. (8分)如图①,在三角形ABC中,点E,F分别为线段AB,AC上任意两点,EG交BC 于点G,交AC的延长线于点H,∠1+∠AFE=180°.(1)证明:BC∥EF;(2)如图②,若∠2=∠3,∠BEG=∠EDF,证明:DF平分∠AFE.参考答案1-5 DBAAD 6-10 BCCBD11. 110°12. b(a-1) 13. 5 , 3 14. 120°15. 180°16. 24cm217. 解:图略18. 解:∵∠AOD=70°,∴∠BOC=∠AOD=70°.∵OE平分∠BOC,∴∠COE=12∠BOC=12×70°=35°.∴∠DOE=180°-∠COE=180°-35°=145°.19. 解:∵∠1=∠2,∠1=∠3,∴∠2=∠3,∴DB∥EC,∴∠C=∠ABD,又∵∠C=∠D,∴∠D=∠ABD,∴AC∥DF20. 解:∵AB∥CD,∴∠B+∠BCE=180°,∴∠BCE=180°-40°=140°.∵CN平分∠BCE,∴∠BCN=70°.∵∠NCM=90°,∴∠BCM=90°-70°=20°.21. 解:(1)AE∥FC,理由:∵∠2+∠CDB=180°,又∠1+∠2=180°,∴∠1=∠CDB,∴AE∥FC.(2)AD∥BC,理由:由(1)得AE∥FC,∴∠A+∠ADC=180°.又∠A=∠C,∴∠C+∠ADC =180°,∴AD∥BC.(3)BC平分∠DBE,理由:∵AB∥CF,∴∠EBC=∠C.∵AD∥BC,得∠DBC=∠ADB,而∠C=∠ADF,∠ADF=∠ADB,∴∠EBC=∠DBC,∴BC平分∠DBE.22. 证明:∵EF⊥AC,DM⊥AC,∴EF∥DM,∴∠3=∠CDM,∵∠3=∠2,∴∠2=∠CDM,∴MN∥CD,∴∠AMN=∠C,∵∠1=∠C,∴∠1=∠AMN,∴AB∥MN23. 证明:(1)∵∠1+∠AFE=180°,∠CFE+∠AFE=180°,∴∠1=∠CFE,∴BC∥EF (2)∵∠BEG=∠EDF,∴DF∥EH,∴∠DFE=∠GEF,由(1)知BC∥EF,∴∠GEF=∠2,∴∠DFE=∠2,∵∠2=∠3,∴∠DFE=∠3,∴DF平分∠AFE∴∠ABC=30°,∠DEF=30°,或∠ABC=110°,∠DEF=70°.。
浙教版七年级下《第1章平行线》检测卷(有答案)

第1章平行线检测卷3.如图,/ 1 = / 2,则下列结论一定成立的是()A. AB //CDB. AD //BC4.如图是小敏作“过已知直线外一点画这条直线的平行线”①两直线平行,同位角相等②两直线平行,内错角相等两直线平行一、选择题(每小题3分,共30分)1.如图,A、B、C、D四个图案中可以由左下图平移得到的是(O第I理圏)D.2.下列所示的四个图形中,/ 1和/ 2不是同位角的是(I)A .①② B.②③ C.③④ D.①④5.如图, AB //CD ,/ D=42。
,/ CBA=64 ° ,则/ CBD 的度数是(42°A.B.D .106°,从图中可知,小敏画平行线的依据是()③同位角相等,两直线平行④内错角相等,6.如图,AB // CD , DB 丄BC,/ 1=40°,则/ 2 的度数是( )B. 50°C. 60°D. 1407. 如图所示,下列判断错误的是(A.若/ 1 = / 3, AD // BC,贝U BD 是/ ABC 的平分线B. 若 AD // BC ,则/ 1= / 2= / 3C. 若/ 3+ / 4+ / C=180。
,贝U AD // BCD. 若/ 2= / 3,贝U AD // BC8. 如图,有一块含45°角的直角三角板的两个顶点放在直尺的对边上.如果/ 2 = 60°,则/ 1=……( )A . 10 ° B.15 ° C.20° D. 25 °9. 如图,一条公路修到湖边时,需拐弯绕湖而过,如果第一次拐的角/ A 是120°,第二次拐的角/ B 是150°,第三次拐的角是/ C ,这时的道路恰好和第一次拐弯之前的道路平行,则/C 的大小是( ) A .150 ° B . 130° D . 120°已知村庄A 和B 分别在一条河的两岸,现要在河上造一座桥 岸互相垂直),下列示意图中,桥的建造位置能使从村庄10. MN (假定河的两岸彼此平行,且桥与河 A 经桥过河到村庄斗:垂査于亦 A. 12.如图,把一块含/ CEF 的度数是—) b11.如图所示,直线则二、填空题(每小题13. 如图,C 岛在A 岛的北偏东60°方向,在B 岛的北偏西45°方向,则从 C 岛看A 、B 两岛的视角/ACB = _____________ °14. 如图,直线 11 // 12 // 13,点 A ,B ,C 分别在直线 11 ,12,13 上,若/ 1=70°,/ 2=50 °,则/ ABC= _____ .15. 如图,有下列条件:①/ 1 = / 2;②/ 3= / 4;③/ B= / 5;④/ B+ / BAD=180 ° .其中能得到 AB // CD 的是 __________ (填写编号) .20. (6分)如图,已知 CD 丄DA , DA 丄AB , / 1= / 2•试说明DF // AE.请你完成下列填空,把解答过 程补充完整.解:••• CD 丄 DA , DA 丄 AB , A / CDA=90 °,/ DAB=90 ° ().•••/ CDA= / DAB (等量代换).又/ 1 = / 2,从而/ CDA- /仁/ DAB- ____________ (等式的性质).即/ 3= _________ .• DF // AE ( ).16. 如果一个角的两边分别与另一个角的两边平行,若其中一个角为17. 有一条直的宽纸带,按如图所示的方式折叠时,纸带重叠部分中的/40°,则另一个角为 _____________ 18. 一副三角板按如图放置,下列结论:①/1= / 3;②若BC // AD ,则/ 4= / 3;③若/ 2=15°,必有/ 4=2/ D ;④若/ 2=30°,则有 AC // DE.其中正确的有 ______________三、解答题(共46分)19. (6分)如图,在正方形网格中有一个△ ABC ,按要求进行下列作图(只借助于网格,需写出结论)(1) 过点A 画出BC 的平行线;(2) 画出先将厶ABC 向右平移5格,再向上平移 3格后的△ DEF .嬴IX 題團1)(6分)如图,AB // CD , BF // CE ,则/ B 与/ C 有什么关系?请说明理由22. (8分)如图,11 // 12,/ a 是/ B 的2倍,求/ a 的度数.23. ( 8 分)如图所示,/ A+ / D=180。
浙教版七年级下册数学第一章 平行线含答案

浙教版七年级下册数学第一章平行线含答案一、单选题(共15题,共计45分)1、如图,下列推理错误的是()A.∵,B.∵C.D.∵2、如图,在△ABC中AB=AC,D,E两点分别在AC,BC上,BD是∠ABC的平分线,DE∥AB,若BE=5cm,CE=3cm,则△CDE的周长是()A.13cmB.11cmC.9cmD.7cm3、如图,将直角三角形ABC沿着点B到点C的方向平移3cm得到三角形DEF,且DE交AC于点H,AB=6cm.BC=9cm.DH=2cm.那么图中阴影部分的面积为()A.9 cm 2B.10 cm 2C.15 cm 2D.30 cm 24、如图:直线a,b都与直线c相交,给出下列条件:①∠1=∠2,②∠3=∠6,③∠4+∠7=180°,④∠5+∠8=180°,其中能判断a∥b的条件有()个A.1B.2C.3D.45、将一副三角板()按如图所示方式摆放,使得,则等于()A. B. C. D.6、如图,在中,,在同一平面内,将绕点A旋转到的位置,连接.若,则的度数为()A. B. C. D.7、如图,直线AB是⊙O的切线,C为切点,OD∥AB交⊙O于点D,点E在⊙O 上连接OC,EC,ED,则∠CED 的度数为( )A.30°B.35°C.15°D.45°8、如图,直线都与直线相交,其中不能判定的条件是().A.∠1=∠2B.∠3=∠6C.∠1=∠4D.∠5+∠8=180°9、如图,△ABC沿着由点B到点E的方向,平移到△DEF,已知BC=5.EC=3,那么平移的距离为()A.2B.3C.5D.710、如图.已知直线a,b被直线c所截,且a∥b,∠1=48°,那么∠2的度数为()A.42°B.48°C.52°D.132°11、如图,直线,,,则的度数是()A. B. C. D.12、在长为20m,宽为16m的长方形空地上,沿平行于长方形各边的方向割出三个完全相同的小长方形花圃,其示意图如图所示,则花圃的面积是()A.64m 2B.32m 2C.128m 2D.96m 213、如图,AB∥CD,∠ABE=60°,∠D=50°,则∠E的度数为()A.30°B.20°C.10°D.40°14、如图所示,∠B与∠3是一对()A.同位角B.内错角C.同旁内角D.对顶角15、下列四个图形中,不能推出∠2与∠1相等的是()A. B. C. D.二、填空题(共10题,共计30分)16、如图,∠1与∠2是直线________和________被直线________所截的一对________角.17、如图,将纸片 ABCD 沿 PR 翻折得到三角形 PC′R,恰好 C′P∥AB,C′R ∥AD.若∠B=120°,∠D=50°,则∠C=________°.18、将一个含的三角尺和一把直尺按如图所示摆放,若,则________ .19、如图,在△ABC中,∠BAC=35°,延长AB到点D,∠CBD=65°,过顶点A 作AE∥BC,则∠CAE=________°.20、将一直角三角板与一直尺如图放置。
2022-2023学年浙教版七年级数学下册第1章平行线 单元综合达标测试题 (含解析)

2022-2023学年浙教版七年级数学下册《第1章平行线》单元综合达标测试题(附答案)一.选择题(共7小题,满分28分)1.如图,下列说法正确的是()A.∠1与∠2是同位角B.∠1与∠2是内错角C.∠1与∠3是同位角D.∠2与∠3是同旁内角2.如图,四边形ABCD中,∠1=∠3,AD∥BC,则下列等式不成立的是()A.∠1=∠2B.∠3=∠4C.∠2=∠3D.∠1+∠2+∠B=180°3.如图,有一块含有30°角的直角三角板的两个顶点放在直尺的对边上,如果∠2=42°,那么∠1的度数是()A.18°B.17°C.16°D.15°4.如图,在弯形管道ABCD中,若AB∥CD,拐角∠ABC=122°,则∠BCD的大小为()A.58°B.68°C.78°D.122°5.直线BD∥EF,两个直角三角板如图摆放,若∠CBD=10°,则∠1=()A.75°B.80°C.85°D.95°6.如图,△ABC沿BC方向平移得到△DEF,已知BC=5,EC=2,则平移的距离是()A.1B.2C.3D.47.如图,直线a∥b,点A在直线a上,点C、D在直线b上,且AB⊥BC,BD平分∠ABC,若∠1=32°,则∠2的度数是()A.13°B.15°C.14°D.16°二.填空题(共7小题,满分28分)8.如图,已知AB∥CD,∠1=55°,则∠2的度数为.9.如图,DE∥BC,CD平分∠ACB,∠ACB=58°,则∠EDC=.10.如图所示,要在竖直高AC为2米,水平宽BC为8米的楼梯表面铺地毯,地毯的长度至少需要米.11.∠1与∠2的两边分别平行,且∠2的度数比∠1的度数的3倍少40°,那么∠2的度数为.12.如图,AB∥CD∥EF,若∠ABC=125°,∠CEF=105°,则∠BCE的度数为.13.如图,AB∥CD,AD与BC相交于点F,BE平分∠ABC,DE平分∠ADC,∠AFB=96°,则∠BED的度数为度.14.太阳灶、卫星信号接收锅、探照灯以及其他很多灯具都与抛物线有关.如图,从点O 照射到抛物线上的光线OB,OC等反射以后沿着与POQ平行的方向射出.图中如果∠BOP=45°,∠QOC=68°,则∠ABO=,∠DCO=.三.解答题(共6小题,满分64分)15.如图,点D、E、F分别是三角形ABC的边BC、CA、AB上的点,且∠B+∠BDE=180°,∠A=∠FDE.求证:DF∥AC.16.如图,FG∥AC,∠1=∠2,DE与FC平行吗?为什么?17.如图,已知DE∥BC,∠3=∠B,则∠1+∠2=180°.下面是小王同学的说明过程,请你在括号内填上理由、依据或内容,请你帮助小王同学完成说明过程:∵DE∥BC(已知),∴∠3=∠EHC(),∵∠3=∠B(),∴∠B=∠EHC(等量代换),∴AB∥EH(),∴∠2+∠4=180°(),又∵∠1=∠4 (),∴∠1+∠2=180°().18.如图,点F在线段AB上,点E,G在线段CD上,FG∥AE,∠1=∠2.(1)求证:AB∥CD;(2)若BC平分∠ABD,∠D=112°,求∠C的度数.19.如图,点E在AB上,点F在CD上,CE、BF分别交AD于点G、H,已知∠A=∠AGE,∠D=∠DGC.(1)AB与CD平行吗?请说明理由;(2)若∠2+∠1=180°,且3∠B=∠BEC+20°,求∠C的度数.20.【提出问题】若两个角的两边分别平行,则这两个角有怎样的数量关系?【解决问题】分两种情况进行探究,请结合如图探究这两个角的数量关系.(1)如图1,AB∥EF,BC∥DE,试证:∠1=∠2;(2)如图2,AB∥EF,BC∥DE,试证:∠1+∠2=180°;【得出结论】由(1)(2)我们可以得到结论:若两个角的两边分别平行,则这两个角的数量关系为;【拓展应用】(3)若两个角的两边分别平行,其中一个角比另一个角的2倍少60°,求这两个角的度数.(4)同一平面内,若两个角的两边分别垂直,则这两个角的数量关系为.参考答案一.选择题(共7小题,满分28分)1.解:A、∠1和∠2不是同位角,故本选项不符合题意;B、∠1和∠2不是内错角,故本选项不符合题意;C、∠1和∠3是内错角,不是同位角,故本选项不符合题意;D、∠2和∠3是同旁内角,故本选项符合题意;故选:D.2.解:∵AD∥BC,∴∠2=∠3,∠1+∠2+∠B=180°,∵∠1=∠3,∴∠1=∠2,故A、C、D成立,不符合题意,根据题意不能判定∠3=∠4,故B不成立,符合题意,故选:B.3.解:如图,∵∠2+∠3=60°,∴∠3=60°﹣∠2=60°﹣42°=18°,根据平行线的性质可得,∠1=∠3=18°.故选:A.4.解:∵AB∥CD,∴∠ABC+∠BCD=180°,∵∠ABC=122°,∴∠BCD=180°﹣122°=58°,故选:A.5.解:∵∠ABC=30°,∠CBD=10°,∴∠ABD=∠ABC+∠CBD=30°+10°=40°,∵BD∥EF,∴∠BAF=∠ABD=40°,∵∠EFD=45°,∴∠1=180°﹣∠BAF﹣∠EFD=180°﹣40°﹣45°=95°.故选:D.6.解:点B平移后对应点是点E.∴线段BE就是平移距离,∵已知BC=5,EC=2,∴BE=BC﹣EC=5﹣2=3.故选:C.7.解:延长CB交直线a于点E,如图,∵AB⊥BC,∠1=32°,∴∠ABC=90°,∴∠AEC=90°﹣∠1=58°,∵a∥b,∴∠ECF=∠AEC=58°,∵BD平分∠ABC,∴∠CBD=∠ABC=45°,∵∠ECF是△BCD的外角,∴∠2=∠ECF﹣∠CBD=13°.故选:A.二.填空题(共7小题,满分28分)8.解:∵AB∥CD,∠1=55°,∴∠3=∠1=55°,∴∠2=180°﹣∠3=125°,故答案为:125°.9.解:∵CD平分∠ACB,∠ACB=58°,∴∠ECD=∠ACB=29°,∵DE∥BC,∴∠EDC=∠ECD=29°.故答案为:29°.10.解:由题意可知,地毯的水平长度与BC的长度相等,垂直长度与AC的长度相等,所以地毯的长度至少需要8+2=10(米).故答案为:10.11.解:如图1所示:①当∠1=∠2时,∵∠2=3∠1﹣40°,∴∠1=3∠1﹣40°,解得∠1=20°,∴∠2=20°;如图2:②当∠1+∠2=180°时,∵∠2=3∠1﹣40°,∴∠1+3∠1﹣40°=180°,解得∠1=55°,∴∠2=125°;故答案为:20°或125°.12.解:∵AB∥CD∥EF,∠ABC=125°,∠CEF=105°,∴∠BCD=∠ABC=125°,∠DCE=180°﹣∠CEF=75°,∴∠BCE=∠BCD﹣∠DCE=50°.故答案为:50°.13.解:如图,过点E作EP∥AB,∵AB∥CD,∴AB∥CD∥EP,∴∠ABE=∠BEP,∠CDE=∠DEP,∠ABC=∠BCD,∵∠ABC+∠BAD+∠AFB=180°,∴∠ABC+∠BAD=180°﹣∠AFB=84°,∵BE平分∠ABC,DE平分∠ADC,∴∠ABE=∠ABC,∠CDE=∠ADC,∴∠ABE+∠CDE=(∠ABC+∠BAD)=42°,∴∠BED=∠BEP+∠DEP=∠ABE+∠CDE)=42°,故答案为:42.14.解:∵AB∥PQ,∴∠ABO=∠BOP=45°,∵CD∥PQ,∴∠DCO+∠QOC=180°,即∠DCO+68°=180°,解得∠DCO=112°.故答案为:45°;112°.三.解答题(共6小题,满分64分)15.证明:∵∠B+∠BDE=180°,∴AB∥DE,∴∠BFD=∠FDE,∵∠A=∠FDE,∴∠BFD=∠A,∴DF∥AC.16.解:DE∥FC,理由如下:∵FG∥AC,∴∠1=∠ACF,∵∠1=∠2,∴∠ACF=∠2,∴DE∥FC.17.解:∵DE∥BC(已知),∴∠3=∠EHC(两直线平行,内错角相等),∵∠3=∠B(已知),∴∠B=∠EHC(等量代换),∴AB∥EH(同位角相等,两直线平行),∴∠2+∠4=180°(两直线平行,同旁内角互补),∵∠1=∠4(对顶角相等),∴∠1+∠2=180°(等量代换).18.解:(1)证明:∵FG∥AE,∴∠FGC=∠2,∵∠1=∠2,∴∠1=∠FGC,∴AB∥CD;(2)∵AB∥CD,∴∠ABD+∠D=180°,∴∠ABD=180°﹣112°=68°,∵BC平分∠ABD,∴∠ABC=ABD=34°,∵AB∥CD,∴∠C=∠ABC=34°.所以∠C的度数为34°.19.解:(1)AB∥CD,理由如下:∵∠A=∠AGE,∠D=∠DGC,∠AGE=∠DGC,∴∠A=∠D,∴AB∥CD;(2)∵∠2+∠1=180°,∠CGD+∠2=180°,∴∠1=∠CGD,∴CE∥BF,∴∠C=∠BFD,∠BEC+∠B=180°,∵∠BEC=3∠B+20°,∴∠B=40°,∵AB∥CD,∴∠B=∠BFD,∴∠C=∠B=40°.20.【提出问题】(1)证明:如图1,∵AB∥EF,∴∠1=∠3,又∵BC∥DE,∴∠2=∠3,∴∠1=∠2;(2)证明:如图2,∵AB∥EF,∴∠1=∠4,∴∠2+∠4=180°,∴∠1+∠2=180°;【得出结论】解:由(1)(2)我们可以得到的结论是:若两个角的两边分别平行,则这两个角的数量关系是相等或互补,故答案为:相等或互补;【拓展应用】(3)解:设其中一个角为x,则另一角为2x﹣60°,当x=2x﹣60°时,解得x=60°,此时两个角为60°,60°;当x+2x﹣60°=180°,解得x=80°,则2x﹣60=100°,此时两个角为80°,100°;∴这两个角分别是60°,60°或80°,100°.(4)解:如图,这两个角之间的数量关系是:相等或互补.故答案为:相等或互补.。
七年级数学下册第1章平行线综合测试含答案(新版)浙教版

“平行线”综合测试题满分120分,时间100分钟一、选择题(每题2分,满分20分)1. 如图,∠1和∠2是同位角的是()A.B.C.D.2.在同一平面内,两条直线可能的位置关系是()A.平行 B.相交 C.相交或平行 D.垂直3.下列说法正确的是()A.在同一平面内,a,b,c是直线,且a∥b,b∥c,则a∥cB.在同一平面内,a,b,c是直线,且a⊥b,b⊥c,则a⊥cC.在同一平面内,a,b,c是直线,且a∥b,b⊥c,则a∥cD.在同一平面内,a,b,c是直线,且a∥b,b∥c,则a⊥c4.若∠1与∠2是内错角,∠1=40°,则()A.∠2=40° B.∠2=140°C.∠2=40°或∠2=140° D.∠2的大小不确定5.如图,在△ABC中,BC=5,∠A=70°,∠B=75°,把△ABC沿直线BC的方向平移到△DEF 的位置,若CF=3,则下列结论中错误的是()A.BE=3 B.∠F=35°C.DF=5 D.AB∥DE6. 下列图形中,不能通过其中一个四边形平移得到的是()A.B.C.D.7. 如图,B C⊥AE于点C,CD∥AB,∠B=55°,则∠1等于()A.55° B.45° C.35° D.25°8. 如图,将一块直角三角板的直角顶点放在直尺的一边上.如果∠1=50°,那么∠2的度数是()A.30°B.40°C.50°D.60°9. 如图,AB∥CD,CB平分∠ABD,若∠C=40°,则∠D的度数为()A.90° B.100° C.110° D.120°10. 如图,AB、CD、EF、MN均为直线,∠2=∠3=70°,∠GPC=80°,GH平分∠MGB,则∠1=()A.35°B.40°C.45°D.50°二、填空题(每题4分,满分24分)11.如图,写出图中∠A所有的内错角:.12.如图,直线l1∥l2,∠1=62°,则∠2的度数为.13.如图,请你添加一个条件,使AB∥CD,这个条件是,你的依据是.14.如图,直线a∥b,∠1=125°,则∠2的度数为°.15.如图,直角三角形AOB的周长为100,在其内部有n个小直角三角形,则这n个小直角三角形的周长之和为.16.如图,直线l1∥l2,∠α=∠β,∠1=40°,则∠2=°.三、解答题(满分56分)17. (10分)已知:如图,∠AOB和OB上的一点P.(1)求作直线MN,使直线MN过点P且MN∥OA.(2)写出一对相等的同位角和一对互补的同旁内角.AO BP18. (10分)如图,将三角形ABC沿直线l向右平移2cm.''',将图中相等的线段找出来.(1)平移后所得的为三角形A B C(2)连接AA',BB',CC',这三条直线之间存在着什么关系?19. (12分)已知:如图,AB∥CD,∠1=∠2,试说明:∠B=∠D.20. (12分)如图,直线AB∥CD,BC平分∠ABD,165∠的度数.∠=︒,求221. (12分)(1)把①号图向上平移4个格.(2)把②号图向左平移4个格,再向下平移1个格.(3)把③号图向右平移2个格,再向下平移2个格.(4)移一移,画一画,涂上你喜欢的颜色,看一看像什么?参考答案“平行线”综合测试题一、选择题1.D2.C3.A4.D5.C6.D7.C8.B9.B提示:∵AB∥CD,∴∠C=∠ABC=40°.∵BC是∠ABD的平分线,∴∠ABC=∠DBC=40°.∴∠ABD=80°.又∵AB∥CD,∴∠ABD+∠D=180°.∴∠D=100°.10.D提示:∵∠2=∠3=70°,∴AB∥CD,∴∠BGP=∠GPC,∵∠GPC=80°,∴∠BGP=80°,∴∠BGM=180°-∠BGP=100°,∵GH平分∠MGB,∴∠1=1 2 ∠BGM=50°,故选D.二、填空题(每题4分,满分24分)11. ∠ACD,∠ACE12.62°13.答案不唯一,如:∠CDA=∠DAB;内错角相等,两直线平行14.5515.100提示:如图所示:过小直角三角形的直角定点作AO,BO的平行线,所得四边形都是矩形.则小直角三角形的与AO平行的边的和等于AO,与BO平行的边的和等于BO.因此小直角三角形的周长等于直角△ABC的周长.故这n个小直角三角形的周长为100.16. 140提示:延长AB与直线l2相交于点C,∵直线l1∥l2,∴∠3=∠1=40°,∵∠α=∠β,∴AC∥DE,∴∠3+∠2=180°,∴∠2=140°,故答案为140° .三、解答题(满分56分)17.(1)如图所示:A OBP M N(2)一对相等的同位角:O BPN ∠=∠,一对互补的同旁内角:O OPN ∠=∠.18.解:(1)图中相等的线段有,AB A B ''=,BC B C ''=,AC A C ''=,AA BB CC '''==.(2)直线AA ',BB ',CC '的关系是////AA BB CC '''.19.解:∵∠1=∠2,∴AD ∥BC.∴∠BAD +∠B =180°.又∵AB ∥CD ,∴∠D +∠BAD =180º,∴∠B =∠D .20.∵AB ∥CD ,∴165ABC ∠=∠=︒,180ABD BDC ∠+∠=︒.∵BC ABD ∠平分,∴2130ABD ABC ∠=∠=︒,∴18050BDC ABD ∠=︒-∠=︒,∴250BDC ∠=∠=︒.21. 解:(1)把①号图向上平移4个格(下图).(2)把②号图向左平移4个格,再向下平移1个格(下图).(3)把③号图向右平移2个格,再向下平移2个格(下图).(4)涂上我喜欢的颜色如下(下图),像一棵小松树.。
浙教版七年级下数学第一章平行线单元测试及答案(共7张)

浙教版七年级下第一章平行线单元测试卷注意事项:1.答题前填写好自己的姓名、班级、考号等信息2.请将答案正确填写在答题卡上第Ⅰ卷(选择题)请点击修改第I卷的文字说明一.选择题(共10小题,3*10=30)1.若∠α与∠β同旁内角,且∠α=50°时,则∠β的度数为()A.50°B.130°C.50°或130°D.无法确定2.已知∠AOB,P是任一点,过点P画一条直线与OA平行,则这样的直线()A.有且仅有一条B.有两条C.不存在D.有一条或不存在3.下列说法不正确的是()A.过任意一点可作已知直线的一条平行线B.同一平面内两条不相交的直线是平行线C.在同一平面内,过直线外一点只能画一条直线与已知直线垂直D.平行于同一直线的两直线平行4.如图是用一张长方形纸片折成的,如果∠1=100°,那么∠2的度数是()A.50°B.60°C.70°D.80°5.如图所示,AB∥CD,OE平分∠AOD,OF⊥OE,∠D=50°,则∠BOF为()A.35°B.30°C.25°D.20°6.如图,AB∥CD,MP∥AB,MN平分∠AMD,∠A=40°,∠D=30°,则∠NMP等于()A.10°B.15°C.5°D.7.5°7.将一副三角板按如图放置,则下列结论①∠1=∠3;②如果∠2=30°则有AC∥DE;③如果∠2=30°,则有BC∥AD;④如果∠2=30°,必有∠4=∠C,其中正确的有()A.①②③B.①②④C.③④D.①②③④8.如图,多边形ABCDEFGHIJ的相邻两边互相垂直,要求出它的周长,至少需要知道()条边的边长.A.3 B.4 C.5 D.69.如果两个角的两边分别平行,而其中一个角比另一个角的4倍少30°,那么这两个角是()A.42°、138°B.都是10°C.42°、138°或42°、10°D.以上都不对10.如图,已知AB∥DE,那么下列结论正确的是()A.∠1+∠2+∠3=180°B.∠1+∠2﹣∠3=180°C.∠1=∠2+∠3 D.∠1﹣∠2+∠3=180°第Ⅱ卷(非选择题)请点击修改第Ⅱ卷的文字说明二.填空题(共6小题,3*6=18)11.在同一平面内有三条直线,如果其中有两条且只有两条相互平行,那么它们有个交点.12.如图,与∠1构成同位角的是,与∠2构成同旁内角的是.13.经过直线外一点,一条直线与这条直线平行.14.如图,将一副三角板按如图放置,则下列结论①∠1=∠3;②如果∠2=30°,则有AC∥DE;③如果∠2=30°,则有BC∥AD;④如果∠2=30°,必有∠4=∠C.其中正确的有.(填序号)15.如图a是长方形纸带,∠DEF=26°,将纸带沿EF折叠成图b,则∠FGD的度数是度,再沿BF折叠成图c,则图c中的∠DHF的度数是.16.把一张长方形纸片ABCD沿EF折叠后ED与BC的交点为G,D、C分别在MN的位置上,若∠EFG=55°,则∠2=.三.解答题(共7小题,52分)17.(6分)按要求完成作图,并回答问题;如图在△ABC中:(1)过点A画BC的垂线,垂足为E;(2)画∠ABC的平分线,交AC于F;(3)过E画AB的平行线,交AC于点G;(4)过点C画AB所在的直线的垂线段,垂足为H.18.(6分)如图,有四条互相不平行的直线L1、L2、L3、L4所截出的八个角.请你任意选择其中的三个角(不可选择未标注的角),尝试找到它们的关系,并选择其中一组予以证明.19.(6分)如图,已知∠1=∠2,∠B=∠C,可推得AB∥CD.理由如下:∵∠1=∠2(已知),且∠1=∠CGD()∴∠2=∠CGD(等量代换)∴CE∥BF()∴∠=∠BFD()又∵∠B=∠C(已知)∴∠BFD=∠B(等量代换)∴AB∥CD()20.(8分)(1)如图1,已知直线l1∥l2,且l3和l1,l2分别交于A,B两点,点P在线段AB上,则∠1,∠2,∠3之间的等量关系是;如图2,点A在B处北偏东40°方向,在C处的北偏西45°方向,则∠BAC=°.(2)如图3,∠ABD和∠BDC的平分线交于E,BE交CD于点F,∠1+∠2=90°,试说明:AB∥CD;并探究∠2与∠3的数量关系.21.(8分)如图,已知AB∥CD,现将一直角三角形PMN放入图中,其中∠P=90°,PM 交AB于点E,PN交CD于点F(1)当△PMN所放位置如图①所示时,则∠PFD与∠AEM的数量关系为;(2)当△PMN所放位置如图②所示时,求证:∠PFD﹣∠AEM=90°;(3)在(2)的条件下,若MN与CD交于点O,且∠DON=30°,∠PEB=15°,求∠N 的度数.22.(8分)若在方格(每小格正方形边长为1m)上沿着网格线平移,规定:沿水平方向平移的数量为a(向右为正,向左为负,平移|a|个单位),沿竖直方向平移的数量为b(向上为正,向下为负,平移|b|个单位),则把有序数对{a,b}叫做这一平移的“平移量”.例如:点A按“平移量”{1,4}可平移至点B.(1)从点C按“平移量”{,}可平移到点B;(2)若点B依次按“平移量”{4,﹣3}、{﹣2,1}平移至点D,①请在图中标出点D;(用黑色水笔在答题卡上作出点D)②如果每平移1m需要2.5秒,那么按此方法从点B移动至点D需要多少秒?③观察点D的位置,其实点B也可按“平移量”{,}直接平移至点D;观察这两种平移的“平移量”,猜想:点E依次按“平移量”{2a,3b}、{﹣5a,b}、{a,﹣5b}平移至点F,则相当于点E按“平移量”{,}直接平移至点F.23.(10分)如图1所示,已知BC∥OA,∠B=∠A=120°(1)说明OB∥AC成立的理由.(2)如图2所示,若点E,F在BC上,且∠FOC=∠AOC,OE平分∠BOF,求∠EOC的度数.(3)在(2)的条件下,若左右平移AC,如图3所示,那么∠OCB:∠OFB的比值是否随之发生变化?若变化,请说明理由;若不变,请求出这个比值.(4)在(3)的条件下,当∠OEB=∠OCA时,求∠OCA的度数.参考答案与试题解析一.选择题(共10小题)1.D2.D 3.A 4.A 5.C 6.C 7.B 8.A 9.D 10.B 二.填空题(共6小题)11.2 12.∠B,∠1 13.有且只有.14.①②④15.52,78°16.110°三.解答题(共7小题)17.解:(1)作法利用量角器测得∠AEC=90°,AE即为所求;(2)作法:①以点B为圆心,以任意长为半径画弧,两弧交∠ABC两边于点M,N.②分别以点M,N为圆心,以大于MN的长度为半径画弧,两弧交于点P③作射线BP,则射线BP为角ABC的角平分线;④射线BP交AC于点F;(3)作法:用量角器测得∠ABC=∠GEC,EG即为所求;(4)作法:利用量角器测得∠BHC=90°,CH即为所求.18.解:如∠2+∠4+∠6=360°,∠1+∠5+∠7=180°,∠2=∠5+∠7,∠3=∠1+∠8,已知如图:有四条互相不平行的直线L1、L2、L3、L4所截出的八个角,求证:∠1+∠5+∠7=180°,证明:∵∠DAC+∠7+∠5=180°,又∵∠1=∠DAC,∴∠1+∠5+∠7=180°.19.解:∵∠1=∠2(已知),且∠1=∠CGD(对顶角相等),∴∠2=∠CGD(等量代换),∴CE∥BF(同位角相等,两直线平行),∴∠C=∠BFD(两直线平行,同位角相等),又∵∠B=∠C(已知),∴∠BFD=∠B(等量代换),∴AB∥CD(内错角相等,两直线平行).故答案为:(对顶角相等),(同位角相等,两直线平行),C,(两直线平行,同位角相等),(内错角相等,两直线平行).20.解:(1)如图1中,作PM∥AC,∵AC∥BD,∴PM∥BD,∴∠1=∠CPM,∠2=∠MPD,∴∠1+∠2=∠CPM+∠MPD=∠CPD=∠3.由题可知:∠BAC=∠B+∠C,∵∠B=40°,∠C=45°,∴∠BAC=40°+45°=85°.故答案为:∠1+∠2=∠3,85°.(2)证明:∵BE、DE平分∠ABD、∠BDC,∴∠1=∠ABD,∠2=∠BDC;∵∠1+∠2=90°,∴∠ABD+∠BDC=180°;∴AB∥CD;(同旁内角互补,两直线平行)∵DE平分∠BDC,∴∠2=∠FDE;∵∠1+∠2=90°,∴∠BED=∠DEF=90°;∴∠3+∠FDE=90°;∴∠2+∠3=90°.21.解:(1)作PG∥AB,如图①所示:则PG∥CD,∴∠PFD=∠1,∠2=∠AEM,∵∠1+∠2=∠P=90°,∴∠PFD+∠AEM=∠1+∠2=90°,故答案为:∠PFD+∠AEM=90°;(2)证明:如图②所示:∵AB∥CD,∴∠PFD+∠BHF=180°,∵∠P=90°,∴∠BHF+∠2=90°,∵∠2=∠AEM,∴∠BHF=∠PHE=90°﹣∠AEM,∴∠PFD+90°﹣∠AEM=180°,∴∠PFD﹣∠AEM=90°;(3)如图③所示:∵∠P=90°,∴∠PHE=90°﹣∠FEB=90°﹣15°=75°,∵AB∥CD,∴∠PFC=∠PHE=75°,∵∠PFC=∠N+∠DON,∴∠N=75°﹣30°=45°.22.解:(1)从C到B,向左2个单位,向下1个单位,所以,平移量为{﹣2,﹣1};(2)①点B依次按“平移量”{4,﹣3}、{﹣2,1}平移至点D如图所示;②(4+3+2+1)×2.5=10×2.5=25秒;③由图可知,点B到点D,向右2个单位,向下2个单位,所以,平移量为{2,﹣2},∵2a﹣5a+a=﹣2a,3b+b﹣5b=﹣b,∴点E到F的平移量为{﹣2a,﹣b}.故答案为:(1)﹣2,﹣1;(2)③2,﹣2;﹣2a,﹣b.23.【解答】解:(1)∵BC∥OA,∴∠B+∠O=180°,∴∠O=180°﹣∠B=60°,而∠A=120°,∴∠A+∠O=180°,∴OB∥AC;(2)∵OE平分∠BOF,∴∠BOE=∠FOE,而∠FOC=∠AOC,∴∠EOF+∠COF=∠AOB=×60°=30°,即∠EOC=30°;(3)比值不改变.∵BC∥OA,∴∠OCB=∠AOC,∠OFB=∠AOF,∵∠FOC=∠AOC,∴∠AOF=2∠AOC,∴∠OFB=2∠OCB,即∠OCB:∠OFB的值为1:2;(4)设∠AOC的度数为x,则∠OFB=2x,∵∠OEB=∠AOE,∴∠OEB=∠EOC+∠AOC=30°+x,而∠OCA=180°﹣∠AOC﹣∠A=180°﹣x﹣120°=60°﹣x,∵∠OEB=∠OCA,∴30°+x=60°﹣x,解得x=15°,∴∠OCA=60°﹣x=60°﹣15°=45°.浙教版七年级下第一章平行线单元检测卷姓名:__________班级:__________考号:__________一 、选择题(本大题共10小题,每小题3分,共30分。
浙教版七年级下册第1章“平行线”综合测试题
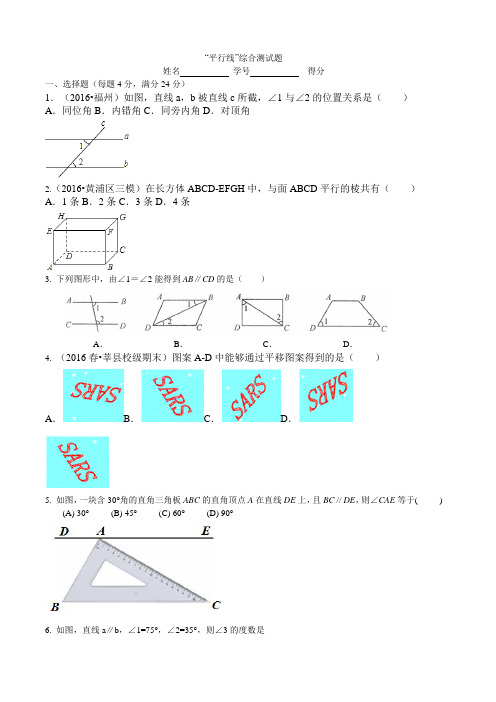
“平行线”综合测试题姓名学号得分一、选择题(每题4分,满分24分)1.(2016•福州)如图,直线a,b被直线c所截,∠1与∠2的位置关系是()A.同位角B.内错角C.同旁内角D.对顶角2.(2016•黄浦区三模)在长方体ABCD-EFGH中,与面ABCD平行的棱共有()A.1条B.2条C.3条D.4条3. 下列图形中,由∠1=∠2能得到AB∥CD的是()A.B.C.D.4. (2016春•莘县校级期末)图案A-D中能够通过平移图案得到的是()A.B.C.D.5. 如图,一块含30°角的直角三角板ABC的直角顶点A在直线DE上,且BC // DE,则∠CAE等于( )(A) 30°(B) 45°(C) 60°(D) 90°6. 如图,直线a∥b,∠1=75°,∠2=35°,则∠3的度数是A.75°B.55°C.40°D.35°7. 如图,直线a∥b,直角三角形ABC的顶点B在直线b上,∠C=90°,∠β=55°,则∠α的度数为()A. 15°B.25°C. 35°D.55°B8. 如图,将矩形纸带ABC D,沿EF折叠后,C、D两点分别落在C′、D′的位置,经测量得∠EFB=65°,则∠AED′的度数是A.65°B.55°C.50°D.25°二、填空题(每题6分,满分24分)9. 在同一平面内,若a⊥b,b⊥c,则a与c的位置关系是..10.(2016•漳州)如图,若a∥b,∠1=60°,则∠2的度数为11.(2016 •浦东新区期末)如图,∠2的同旁内角是.12. 下列说法中:(1)不相交的两条直线叫做平行线;(2)经过一点,有且只有一条直线与已知直线平行;(3)垂直于同一条直线的两直线平行;(4)直线a∥b,b∥c,则a∥c;(5)两条直线被第三条直线所截,同位角相等.其中正确的是.13.(2016 •成安县期中)如图∠1=82°,∠2=98°,∠3=80°,则∠4= 度.14. (2016•泰州)如图,△ABC中,BC=5cm,将△ABC沿BC方向平移至△A′B′C′的对应位置时,A′B′恰好经过AC的中点O,则△ABC平移的距离为cm.15. 如图,已知直线AB∥CD,直线EF与AB、CD相交于N、M两点,MG平分∠EMD,若∠BNE=30°,则∠EMG等于.16.(2016 •长春校级期末)某小区有一块长方形的草地(如图),长18米,宽10米,空白m.部分为两条宽度均为2米的小路,则草地的实际面积2三、解答题(满分52分)(本题共5小题,第11~14题,每题10分,第15题12分)17.如图,已知AD⊥BC,EF⊥BC,∠3=∠C,试说明:∠1=∠2.18.已知,如图∠1和∠D互余,CF⊥DF,问AB与CD平行吗?为什么?19.如图所示,BC为固定的木条,且BC=a,AB,AC为可伸缩的橡皮筋.当点A在与BC平行的轨道MN 上滑动时(MN与BC的距离为b),你能说明△ABC的面积将如何变化吗?请说明你的理由.20.如图,已知E、A、B三点在同一直线上,AD是∠EAC的平分线,AD∥BC,∠B=50°,求∠EAD,∠DAC,∠C的度数.21.如图,电讯公司在由西向东埋设通讯电缆线,他们从点A埋设到点B时突然发现碰到了一个具有研究价值的古墓,不得不改变方向绕开古墓,结果改为沿南偏东40°方向埋设到点O,再沿古墓边缘埋设到点C处,测∠BOC=60°.现要恢复原来的正东方向CD,则∠OCD应等于多少度?参考答案1.B2.D3.B4.B5.A6.C7.C8.C9.平行10.120 11.∠4 12. (2)(4)13.80 14.2.5 15. 15° 16.12817.解:∵AD⊥BC,EF⊥BC(已知),∴AD∥EF(垂直于同一条直线的两直线平行),∴∠1=∠4(两直线平行,同位角相等),又∵∠3=∠C(已知),∴AC∥DG(同位角相等,两直线平行),∴∠2=∠4(两直线平行,内错角相等),∴∠1=∠2(等量代换).18.解:∵CF⊥DF,∴∠CFD=90°.∵∠1+∠CFD+∠2=180°,∴∠1+∠2=90.∵∠1与∠D互余,∴∠1+∠D=90°,∴∠2=∠D,∴AB∥CD(内错角相等,两直线平行).19.解:设△ABC的边BC上的高为b.∵轨道与BC平行,即MN∥BC,而两平行线间的距离处处相等,∴MN与BC之间的距离不变,即△ABC中BC边上的高b不变.根据S△ABC= 12ab可知,△ABC的面积保持不变.20.解:∵AD∥BC,∴∠EAD=∠B=50°,又AD是∠EAC的平分线,∴∠DAC=∠EAD=50°,又AD∥BC,∴∠C=∠DAC=50°.21.解:过点O作OE∥BM,过点C作CF∥BM,则BM∥EO∥CF,由沿南偏东40°方向埋设到点O可知,∠MBO=40°,∵BM∥EO∥CF,∴∠BOE=∠MBO=40°,又∵∠BOC=60°,∴∠EOC=∠OCF=20°,∴∠OCD=∠OCF+∠DCF=110°.。
七年级数学下册 第一章平行线单元综合测试 (新版)浙教版

第一章平行线单元测试一.单项选择题〔共10题;共30分〕1.如图,能使BF∥DG的条件是〔〕A. ∠1=∠3 B. ∠2=∠4 C. ∠2=∠3 D. ∠1=∠4 2.如图,在△ABC中,点D、E、F分别是三条边上的点,EF∥AC,DF∥AB,∠B=45°,∠C=60°.那么∠EFD=〔〕A. 80°B. 75°C. 70°D. 65°3.如图,∠1和∠2是一对〔〕A. 同位角B. 内错角C. 同旁内角D. 对顶角4.如下列图的图案中,不能由根本图形通过平移方法得到的图案是〔〕A. B. C. D.5.以下条件不能够证明a∥b的是〔〕A. ∠2+∠3=180°B. ∠1=∠4 C. ∠2+∠4=180° D. ∠2=∠36.如图,在△ABC中,D、E、F分别在AB、BC、AC上,且EF∥AB,要使DF∥BC,只需满足以下条件中的〔〕A. ∠1=∠2B. ∠2=∠AFDC. ∠1=∠AFDD. ∠1=∠DFE7.如图,直线a∥b,∠1=120°,那么∠2的度数是〔〕A. 120°B. 80°C. 60°D. 50°8.如图,以下能判定AB∥CD的条件有〔〕个.①∠B+∠BCD=180°;②∠1=∠2;③∠3=∠4;④∠B=∠5.A. 1B. 2C. 3D. 49.,如图AB∥CD,∠1=∠2,EP⊥FP,那么以下错误的选项是〔〕A. ∠3=∠4B. ∠2+∠4=90°C. ∠1与∠3互余D. ∠1=∠310.如图,点E在BC的延长线上,由以下条件能得到AD∥BC的是〔〕A. ∠1=∠ 2B. ∠3=∠4 C. ∠B=∠DCE D. ∠D+∠DAB=180°二.填空题〔共8题;共28分〕11.如图,按角的位置关系填空:∠A与∠1是________ ;∠A与∠3是________ ;∠2与∠3是________ .12.如图把三角板的直角顶点放在直线b上,假设∠1=40°,那么当∠2=________ 度时,a ∥b.13.如图,四边形ABCD中,AB∥CD,∠B=60°,当∠D=________°时,AD∥BC.14.完成下面推理过程:如图,DE∥BC,DF、BE分别平分∠ADE、∠ABC,可推得∠FDE=∠DEB的理由:∵DE∥BC〔〕∴∠ADE=________〔________〕∵DF、BE分别平分∠ADE、∠ABC,∴∠ADF= ________〔________〕∠ABE= ________〔________〕∴∠ADF=∠ABE∴________∥________〔________〕∴∠FDE=∠DEB.〔________ 〕15.如图,直线a,b与直线c,d相交,∠1=∠2,∠3=110°,那么∠4的度数为________.16.如图,∠1=∠2,∠2=∠C,那么图中互相平行的直线有________17.如图,超市里的购物车,扶手AB与车底CD平行,∠2比∠3大10°,∠1是∠2的倍,∠2的度数是________.18.如图是一块电脑主板的示意图〔单位:mm〕,其中每个角都是直角,那么这块主板的周长是________mm.三.解答题〔共6题;共40分〕19.如下列图,∠1与∠2,∠3与∠4之间各是哪两条直线被哪一条直线所截而形成的什么角?20.如下列图,AB∥CD,∠1=36°,∠1:∠4=1:2.〔1〕求∠3的度数;〔2〕求证:AB平分∠EBG.21.如图,∠1和∠2是哪两条直线被哪一条直线所截形成的?它们是什么角?∠1和∠3是哪两条直线被哪一条直线所截形成的?它们是什么角?22.如图,直线AB∥CD,BC平分∠ABD,∠1=65°,求∠2的度数.23.如图,∠1=∠2,∠B=∠C.求证:(1)AB∥CD(2)∠AEC=∠3.24.如图,AB∥CD,AE平分∠BAD,CD与AE相交于F,∠CFE=∠E.求证:AD∥BC.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
A
B C
D
1
23
4
七下第1章平行线综合卷
班级组名姓名
一、选择题(30分)
()1.如图,由∠3=∠4,得出结论AB∥CD,其根据是
A. 同位角相等,两直线平行
B. 内错角相等两直线平行
C. 同旁内角互补,两直线平行
D. 在同一平面内垂直于同一条直线的两条直线平行
()2. 下列图形中,∠1与∠2不是同位角的是()
A. B. C. D.
()3.如图,如果∠D=∠EFC,那么
A.AD∥BC
B.EF∥BC
C.AB∥DC
D.AD∥EF
()4. 将图1所示的图案通过平移后可以得到的图案是()
()5.下列现象中,不属于平移的是
A.滑雪运动员在平坦的雪地上滑行
B.大楼上上下下地迎送来客的电梯
C.钟摆的运动
D.火车在笔直的铁轨上飞驰而过
()6.如图,下列推理不正确
...的是()
A.∵AB∥CD,∴∠ABC+∠C=180°
B.∵∠1=∠2,∴AD∥BC
C.∵AD∥BC,∴∠3=∠4
D.∵∠A+∠ADC=180°,∴AB∥CD
()7.在同一平面内有三条直线,则它们的交点个数有
A.1或3
B.0或1
C.0,1,3
D.0,1,2,3
()8. 若直线a∥b,a⊥c,b∥d,c⊥e,则下列结论错误的是()
A. a∥d
B. a∥e
C. b⊥c
D. a⊥e
()9.下列说法正确的是
A.两条直线被第三条所截,同位角相等
B.不相交的两条直线互相平行
C.垂直于同一条直线的两条直线互相平行
D.平行于同一条直线的两条直线互相平行()10. 一束光线垂直照射在水平地面,在地面上放一个平面镜,欲使这束光线经过平面镜反射后成水平光线,则平面镜与地面所成锐角的度数为()
A. 45º
B. 60º
C. 75º
D. 80º
二、填空题(30分)
11.如图,直线AD,BC被AB所截,则∠B的同旁内角是________.
2
1
2
1
2
1
2
1
F
E
D
C
B
A
12.已知:如图,由∠2=∠3得AB∥CD的理由是;
由AB∥CD得∠2+∠4=180°的理由是 .
2
3
14
D
C
B
A
第12题图第13题图第14题图第16
题图
13. 如图,一个弯形管道ABCD的拐角∠ABC=110º,要使AB∥CD,那么另一个拐角∠BCD应
弯成_______度.
14. 在上图方格纸中,△ABC向右平移_______格后得到△A1B1C1.
15.如图,给出了过直线外一点画已知直线的平行线的方法,其依据是
16. 如图所示,请写出能判定CE∥AB的一个条件.
17. 如图,a∥b,∠1=(2x+10)°,∠4=(3x+20)°,则∠3= 度.
18.一辆汽车在笔直的公路上行驶,两次拐弯后,仍在原来的方向上平行前进.
如果第一次向右拐40º,那么第二次向拐(填“左”可“右”)
º .
19. 如图,将边长为2个单位的等边三角形ABC沿边BC向右平移1个单
位得到三角形DEF,则四边形ABFD的周长为 .
20. 如图是我们生活中经常接触的小刀,刀柄外形是一个直角梯形(下底
挖去一小半圆),刀片上、下是平行的,转动刀片时会形成∠1、
∠2,则∠1+∠2=度.
三、解答题(40分)
21.(8分)如图,在方格纸中平移三角形ABC,使点A与点D重
合,并请描述这个平移过程.
C
A B
D
E
a b
135
24
F
E
D
C
B
A
G
D
C
A
22.(8分)如图,按要求解答以下各题: (1)过D 作DE ∥AB ,交AC 于E ;
(2)过D 作DF ∥AC ,且F 点在D 点的右侧; (3)请判断∠A 与∠EDF 的关系,并说明理由.
23.(8分)如图,已知AB ∥CD ,BE 平分∠ABC ,∠CDE =150°,求∠ABC 的度数. 24.(8分)如图,点E 在直线AB 上,EF ⊥EH 交CD 于G . 若
∠AEF =30°,∠DGH =60°.请判断AB 与CD 的位置关系,
并说明理由.
25.(8分)如图,DB ∥FG ∥EC ,∠ABD =70°,∠ACE =40°,若AH 平分∠BAC ,求∠GAH 的度数.
D
C
B
A A
B
C
D
E
H
G F E
D
C
B
A
四、附加题(如果前面试题估计不足60分的同学可试做A 组题,但满分最多60分;对于其他同学,请直接做B 组题)
A 组(10分)
1.(4分)如图,在所标识的角中,∠1的内错角是 ,如果AB ∥CD ,∠1=50°,则∠4= 度.
2.(3分)第1题图中下列条件不能判定AB ∥CD 的是( ) A.∠1=∠3 B.∠2=∠ C.∠1=∠54 D.∠1+∠2=180°
3.(3分)平移改变的是图形的( )
A.位置
B.形状
C.大小
D.位置、形状、大小
B 组(20分)
1.(4分)如图,直线a ∥b ,AB ⊥a ,∠ABC =138º,则∠1= 度.
1
C
A
b a
B
E
D
A B C
第1题图 第2题图 第3题图 2.(4分)如图,AB ∥DC ,则θ的值可用含α,β,γ的式子表示为( )
A.αγβ+-
B.βγα+-
C.180γαβ+--o
D.180αβγ++-o 3.(4分)如图,AB ∥CD ,∠E =37°,∠C =62°,求∠EAB 的度数.
4.(8分)一副三角尺按如图所示叠放在一起,若固定△AOB ,改变△ACD 的位置(其中点A 位置始终不变),使△ACD 的一边与△AOB 的某一边平行. 请画出相应的草图,并直接写出∠BAD 的度数. 此题我们在《导学新作业B 》中做过,共有8个答案,请画图并写出答案.
∠BAD= ∠BAD= ∠BAD= ∠BAD= A O
B A O
B
A B
A O
B A O B A O B A O B A O B B (D )
C O
A。
