【全国校级联考】四川省宜宾市第四中学2018届高三高考适应性考试数学(文)试题
四川省宜宾市第四中学最新通用版届高三12月月考数学(文)试题(详解版)

2018年秋四川省宜宾市四中高三12月考试数学(文科)试题说明:本试卷分为第Ⅰ、Ⅱ卷两部分,请将第Ⅰ卷选择题的答案填在机读卡上 第Ⅱ卷可在各题后直接作答。
全卷共150分,考试时间120分钟.第I 卷(选择题共60分)一.选择题(本大题共12题,每小题5分,共60分)1.设全集为R ,函数()22f x x =-M ,则R C M 为 ( ) A. (-∞,1) B. (1,+∞) C. (-∞,1] D. [1,+∞) 【答案】A 【解析】 【分析】求出函数f (x )的定义域M ,再写出它的补集即可. 【详解】全集为R ,函数()22f x x - M ={x |22x -?0}={x |x ³1}, 则∁R M ={x |x<1}=(-∞,1). 故选:A .【点睛】本题考查了补集的定义与应用问题,是基础题目. 2.已知复数2z i =+ ,则zz 的值为 ( ) A. 3355【答案】C 【解析】 【分析】由z 求出z ,然后直接利用复数代数形式的乘法运算求解. 【详解】由z =2i +,得z •z =(2﹣i )(2+i )=4﹣i 2=5. 故选:C .【点睛】本题考查了复数代数形式的乘法运算,是基础的计算题. 3.“1<x <2”是“x<2”成立的 ( )A. 充分必要条件B. 充分不必要条件C. 必要不充分条件D. 既不充分也不必要条件 【答案】A 【解析】试题分析:若12x <<成立,则2x <成立;反之,若2x <成立,则12x <<不一定成立,因此“12x <<”是“2x <”成立的充分不必要条件; 考点:充分必要条件; 4.已知1sin 64x p 骣琪+=琪桫,则2cos 3x p骣琪-琪桫值为( ) A.14 B. 34 C. 1516 D. 116【答案】D 【解析】分析:由题意结合诱导公式求得cos 3x p骣琪-琪桫的值,然后求解其平方即可.详解:由诱导公式可得:1cos cos sin 32664x x x p ppp 轾骣骣骣犏琪琪琪-=-+=+=琪琪琪犏桫桫桫臌, 则2211cos 3416x p 骣骣琪琪-==琪琪桫桫. 本题选择D 选项.点睛:本题主要考查诱导公式及其应用,意在考查学生的转化能力和计算求解能力. 5.函数()sin ln f x x x =?的图象大致是( )【答案】A 【解析】试题分析:因为()()()sin lnsin ln f x x x x xf x -=-?=-?-,所以函数()sin ln f x x x =?为奇函数,图像关于原点对称,故排除BC,当(),2x p p Î时,()0f x <,故排除D .故A 正确. 考点:函数图像.6.已知,a b 为两个平面,l 为直线,若,l a b a b^?,则下面结论正确的是( )A. 垂直于平面b 的平面一定平行于平面aB. 垂直于平面l 的平面一定平行于平面aC. 垂直于平面b 的平面一定平行于直线lD. 垂直于直线l 的平面一定与平面,a b 都垂直 【答案】D 【解析】因为,a b 相交不一定垂直,所以垂直于b 的平面可能与平面a 相交,A 不正确; 垂直于直线l 的直线可能在平面a 内,B 不正确;如图可知,垂直于b 的平面g 与l 垂直,C 不正确; 设l g ^,而,l l a b 烫,由面面垂直判定可得,a g b g ^^,D 正确,故选D7.设不等式组0101x y ì#ïí#ïî表示的平面区域为D ,在区域D内随机取一个点,则此点到坐标原点的距离大于1的概率是( ) A.4p B. 22p - C. 6p D. 44p- 【答案】A 【解析】试题分析:由表示的平面区域为D ,为一个边长为1的正方形,而在D 内随机取一个点,则此点到点(1,1)的距离大于1,可转而找出到点(1,1)的距离小于等于1的点为;以(1,1)为圆心,半径为1的圆,落在D 内的面积为14p ,而距离大于1的面积为:114p -,由几何概型,化为面积比得:14144P p p -=-=. 考点:几何概型的算法.8.已知11a =,1()n n n a n a a +=-(*n N Î),则数列{}n a 的通项公式是 ( ) A. 21n - B. 11()n n n-+ C. n D. 2n 【答案】C 【解析】由()1n n n a n a a +=-,得:()11n n n n a a ++=,11n na a n n+=+ ∴n a n禳镲睚镲铪为常数列,即111n a a n ==,故n a n = 故选:C9.若函数2()2f x x ax =-+与()1ag x x =+在区间[1,2]上都是减函数,则a 的取值范围 ( )A. (1,0)(0,1)-?B. (1,0)(0,1]-?C. (0,1)D. (0,1] 【答案】C 【解析】 略10.若f (x )=x 2-2x -4ln x ,则f ′(x )>0的解集为( )A. (0,+∞)B. (-1,0)∪(2,+∞)C. (-1,0)D. (2,+∞) 【答案】C 【解析】试题分析:函数的定义域为()0,+?,所以()224224220x x f x x x x --¢=--=>,解得(2,)x ??.考点:导数与不等式.11.正项等比数列{}n a 中,2018201620142a a a =+,若214m n a a a =, 则11m n+的最小值等( ) A. 1 B. 45 C. 23 D. 35【答案】C 【解析】 【分析】由等比数列的性质,结合已知条件可求q ,结合通项公式可求m +n ,代入所求式子,利用基本不等式即可求.【详解】∵正项等比数列{a n }中,a 2018=a 2016+2a 2014, a 2014q 4=a 2014q 2+2a 2014, ∵a 2014>0, ∴q 4=q 2+2, 解可得,q 2=2, ∴2q = ∵214m n a a a =,221n m a q +-?421aq m +n ﹣2=4, ∴m +n =6, 则1116m n +=(11m n+)(m +n )12263n m m n 骣琪=++?琪桫, 当且仅当n mm n=且m +n =6即m =n =3时取等号. 故选:C .【点睛】本题主要考查了等比数列的 性质及基本不等式的简单应用,求解最值的关键是进行1的代换.12.已知直线l 的倾斜角为45o,直线l 与双曲线2222x y :-=1a>0,b>0)a bC ( 的左、右两支分别交于M 、N 两点,且12,MF NF 都垂直于x 轴(其中12,F F 分别为双曲线C 的左、右焦点),则该双曲线的离心率为( )355-1 D. 5+12【答案】D 【解析】 【分析】根据题意设点(,)M c y -,(,)N c y -,则12MF NF y ==,又由直线l 的倾斜角为45°,得12=MF NF y c==,结合点在双曲线上,即可求出离心率. 【详解】Q 直线l 与双曲线的左、右两支分别交于M 、N 两点,且1 M F 、2NF 都垂直于x 轴,\根据双曲线的对称性,设点(,)M c y -,(,)N c y -,则22221c y a b -=,即22=c a y a-,且12MF NF y ==, 又Q 直线l 的倾斜角为45°,\直线l 过坐标原点,=y c ,\22=c a c a-,整理得22=0c ac a --,即21=0e e --,解方程得5+1e 5-1e (舍) 故选D.【点睛】本题考查双曲线的几何性质、直线与双曲线的位置关系及双曲线离心率的求法,考查化简整理的运算能力和转化思想,属于中档题. 圆锥曲线离心率的计算,常采用两种方法: 1、通过已知条件构建关于a c 、的齐次方程,解出e .根据题设条件(主要用到:方程思想,余弦定理,平面几何相似,直角三角形性质等)借助a b c 、、之间的关系,得到关于e 的一元方程,从而解得离心率. 2、通过已知条件确定圆锥曲线上某点坐标,代入方程中,解出e .根据题设条件,借助a b c 、、表示曲线某点坐标,代入曲线方程转化成关于e 的一元方程,从而解得离心率.第Ⅱ卷(非选择题90分)二.填空题(本大题共4个小题,每小题5分,共20分)13.已知函数f (x )=3x +ax+1的图象在点(1,f (1))处的切线过点(-1,1),则a=_______. 【答案】-5 【解析】 【分析】求出函数的导数f′(x )=3x 2+a ,f′(1)=3+a ,而f (1)=a+2,根据点斜式得到程,利用切线的方程经过的点求解即可.【详解】函数f (x )=x 3+ax+1的导数为:f′(x )=3x 2+a ,f′(1)=3+a ,而f (1)=a+2, 切线方程为:y ﹣a ﹣2=(3+a )(x ﹣1),因为切线方程经过(-1,1), 所以1﹣a ﹣2=(3+a )(-1﹣1), 解得a=-5. 故答案为:-5.【点睛】这个题目考查了利用导数求函数在某一点处的切线方程;步骤一般为:一,对函数求导,代入已知点得到在这一点处的斜率;二,求出这个点的横纵坐标;三,利用点斜式写出直线方程.14.“斐波那契”数列由十三世纪意大利数学家斐波那契发现.数列中的一系列数字常被人们称之为神奇数.具体数列为1,1,2,3,5,8¼,即从该数列的第三项数字开始,每个数字等于前两个相邻数字之和.已知数列{}n a 为“斐波那契”数列,n S 为数列{}n a 的前项和,若2020a =M 则2018=S __________.(用M 表示) 【答案】1M - 【解析】分析:由“斐波那契”数列定义找n S 与2n a +的关系。
四川省宜宾四中2018届高三高考适应性(最后一模)考试语文试卷

四川省宜宾市第四中学2018年高考适应性考试语文试题注意事项:1.答题前填写好自己的姓名、班级、考号等信息2.请将答案正确填写在答题卡上第I卷(阅读题 70分)一、现代文阅读(35分)(一)论述类文本阅读(本题共3小题,9分)阅读下面的文字,完成下列小题。
很多人认为社交网络的实时性加速了谣言的传播,这似乎是有道理的,但先于社交网络存在的BBS、“论坛”和“社区”等交流平台也有实时性;很多研究复杂网络的分析则认为,社交网络的复杂结构更易于传播谣言,复杂网络的结构特性确实会加速谣言的传播,但事实上社交网络的复杂结构特性在人际社会中同样具备,因此这不能解释两者的区别。
实时性所带来的信息成本降低因素不是决定性的,网络结构因素又不能完全说明问题,真正造成社交网络谣言传播加剧的根源是信息反馈机制的失效。
在传统的人际社会中,谣言传播是在一对一或者一对多的人际圈子中,首先由“谣言感染者“发起谣言,接着倾听者们会逐一表示自己的态度:认同、反对或沉默。
“认同”会增加圈子中的个体进一步将谣言带入另一个交际圈的兴趣;相反,“反对”会减弱圈子里的个休对于谣言的兴趣。
如果反对者的态度足够强烈且理由充分,圈子中的其他人也会成为“谣言免疲者”甚至“谣言粉碎者”——当其在别的圈子中再次听到该谣言时,也会加以反对。
在虚拟的社交网络中,由于信息发布的单向性和局城广播性,谣言的传播机制通常是:谣言发布——推送给交际圈中的每一个个体——个体转发——再次推送给新的圈子,而反馈并不在再次推送的内容中。
在整个传播机制中,一方面,个体对谣言的反馈无法与谣言的传播同步,谣言的单向发布使得信息并不需要获得反馈就可以传播,这样导致反馈远远滞后;另一方面,社交网络的反馈只针对谣言发起者,并不具有等同的局域广播性,这使得反馈变得异常微弱。
严重滞后和微弱到不起眼的音量,使得人际社会的反馈机制在社交网络中根本无法发挥作用——这就是为什么社交网络中“智者”的声音会为谣言所淹没。
四川省宜宾市第四中学2018届高三高考适应性(最后一模)考试理综-化学试题+Word版含答案

7.能用来区别甲烷和乙烯的是A. 水B. 酒精C. 酸性高锰酸钾溶液D. NaOH溶液8.设N A表示阿伏加德罗常数的值。
下列说法正确的是A. 0.5mol雄黄(As4S4),结构如右图,含有N A个S-S键B. 将1mol NH4NO3溶于适量稀氨水中,所得溶液呈中性,则溶液中NH4+的数目为N AC. 标准状况下,33.6 L二氯甲烷中含有氯原子的数目为3N AD. 高温下,16.8 g Fe 与足量水蒸气完全反应,转移的电子数为0.6N A9.向四支试管中分别加入少量不同的无色溶液进行如下操作,其中结论正确的是()A. AB. BC. CD. D10.常温下,下列各组离子在指定溶液中一定能大量共存的是A.常温下加水稀释时c(H+)/c(OH-)明显增大的溶液:CH3COO-、Ba2+、NO3-、Br-B.pH=1的溶液中:Na+、Fe2+、NO3-、SO42-C.由水电离的c(OH-)=10-13mol·L-1的溶液中:Na+、Cl-、CO32-、NO3-D.能使淀粉碘化钾试纸显蓝色的溶液:K+、SO42-、S2-、SO32-11.设N A表示阿伏加德罗常数的数值,下列叙述中正确的是A. 1 mol NH3所含有的原子数为N AB. 将100 mL 0.1 mol·L-1的FeCl3溶液滴入沸水中可制得Fe(OH)3胶粒的数目为0.01N AC. 常温常压下,48gO2和O3的混和物中所含氧原子数为3N AD. 1L 0.1 mol·L-1 NaCl溶液中所含的Na+为N A12.质子交换膜燃料电池(简称:PEMFC),又称固体高分子电解质燃料电池,是一种以含氢燃料与空气作用产生电力与热力的燃料电池,膜极组和集电板串联组合成一个燃料电池堆。
目前,尤以氢燃料电池倍受电源研究开发人员的注目。
它的结构紧凑,工作温度低(只有80℃),启动迅速,功率密度高,工作寿命长。
四川省2018届高三高考适应性考试数学(文)试题

2018年四川省高考适应性考试数学(文科)本试题卷共6页,23题(含选考题)。
全卷满分150分。
考试用时120分钟。
★祝考试顺利★注意事项:1、答题前,先将自己的姓名、准考证号填写在试题卷和答题卡上,并将准考证号条形码粘贴在答题卡上的指定位置。
用2B 铅笔将答题卡上试卷类型A 后的方框涂黑。
2、选择题的作答:每小题选出答案后,用2B 铅笔把答题卡上对应题目的答案标号涂黑。
写在试题卷、草稿纸和答题卡上的非答题区域均无效。
3、填空题和解答题的作答:用签字笔直接答在答题卡上对应的答题区域内。
写在试题卷、草稿纸和答题卡上的非答题区域均无效。
4、选考题的作答:先把所选题目的题号在答题卡上指定的位置用2B 铅笔涂黑。
答案写在答题卡上对应的答题区域内,写在试题卷、草稿纸和答题卡上的非答题区域均无效。
5、考试结束后,请将本试题卷和答题卡一并上交。
第I 卷(选择题 60分)一.选择题(本大题共12个小题,每小题5分,共60分) 1.复数)1)(31(i i z -+-=在复平面内对应的点位于( ) A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限2.已知全集为R ,集合{}2log 2<=x x A ,{}0322>--=x x x B ,则=B A C R )(( ) A. [)+∞,1 B. [)+∞,4 C.),3()1,(+∞--∞ D. [)+∞--∞,4)1,( 3.若对于变量x 的取值为3,4,5,6,7时,变量y 对应的值依次分别为4.0,2.5,-0.5,-1,-2;若对于变量u 的取值为1,2,3,4时,变量v 对应的值依次分别为2,3,4,6,则变量x 和y ,变量u 和v 的相关关系是( )A .变量x 和y 是正相关,变量u 和v 是正相关B .变量x 和y 是正相关,变量u 和v 是负相关C .变量x 和y 是负相关,变量u 和v 是负相关D .变量x 和y 是负相关,变量u 和v 是正相关4.若双曲线19222=-x a y (0>a )的一条渐近线与直线x y 31=垂直,则此双曲线的实轴长为( )A.2B.4C. 18D.36 5.已知为实数,则“2b ab >”是“0>>b a ”的( )A. 充分不必要条件B. 必要不充分条件C. 充要条件D. 既不充分也不必要条件6.已知y x ,满足不等式组⎪⎩⎪⎨⎧≤-≤-+≥-+0010230532y x y x y x ,则y x 2-的最大值为( )A.6B.2C.1-D. 2-7.某几何体的三视图如图所示,则该几何体的体积是( ) A.342+π B.322+π C.34+π D.32+π 8.已知函数)(x f 为偶函数,且函数)(x f 与)(x g 的图象关于直线x y =对称,3)2(=g ,则=-)3(f ( )A.2-B.2C.3-D.39.设21,F F 分别为双曲线)0(12222>>=-b a by a x 的左、右焦点,过1F 作一条渐近线的垂线,垂足为M ,延长M F 1与双曲线的右支相交于点N ,若M F 13=,此双曲线的离心率为( ) A.35 B.34 C.213 D.362 10.已知函数)0)(2sin()(<<-+=ϕπϕx x f .将)(x f 的图象向左平移3π个单位长度后所得的函数图象关于y 轴对称,则关于函数)(x f ,下列命题正确的是( ) A. 函数)(x f 在区间)3,6(ππ-上有最小值 B. 函数的一条对称轴为12π=xC.函数)(x f 在区间)3,6(ππ-上单调递增 D. 函数)(x f 的一个对称点为)0,3(π11.在ABC ∆中,060B =,AC =AC 边上的高为2,则ABC ∆的内切圆半径r =( )A ..1)1 D .1)12.设实数0>m ,若对任意的e x ≥,不等式0ln 2≥-xm me x x 恒成立,则m 的最大值是( ) A. e 1 B. 3eC.e 2D.e第II 卷(非选择题 90分)试题答案用0.5毫米黑色签字笔答在答题卡上,答在试卷上概不给分. 二.填空题(本大题共4个小题,每小题5分,共20分)13.已知向量b a ,的夹角为060,2=a ,))(sin ,(cos R b ∈=ααα ,则=+b a 2 . 14.函数2()ln f x x x =+在(1,1)处的切线方程为 . 15.已知3sin()45πα-=,(,)42ππα∈,则tan α= . 15.在三棱锥ABC D -中,1====DC DB BC AB ,当三棱锥体积最大时,其外接球的表面积为_______.三.解答题(解答题需要有计算和相应的文字推理过程) 17.(本大题满分12分)在ABC ∆中,内角A 、B 、C 的对边分别为a 、b 、c ,且c A b B a =+sin cos . (Ⅰ)求角A 的大小; (Ⅱ)若2=a ,ABC ∆的面积为212-,求c b +的值.18.(本大题满分12分)如图,D 是AC 的中点,四边形BDEF 是菱形,平面BDEF ⊥平面ABC ,60FBD ∠=,AB BC ⊥,AB BC ==(Ⅰ)若点M 是线段BF 的中点,证明:BF ⊥平面AMC ;(Ⅱ)求六面体ABCEF 的体积.19.(本大题满分12分)甲、乙两家销售公司拟各招聘一名产品推销员,日工资方案如下: 甲公司规定底薪80元,每销售一件产品提成1元; 乙公司规定底薪120元,日销售量不超过45件没有提成,超过45件的部分每件提成8元.(I)请将两家公司各一名推销员的日工资y (单位: 元) 分别表示为日销售件数n 的函数关系式;(II)从两家公司各随机选取一名推销员,对他们过去100天的销售情况进行统计,得到如下条形图。
2018年四川省宜宾市高考数学三诊试卷(文科)

20.已知抛物线 的焦点在 轴上,顶点在原点且过点 ,过点 的直线 交抛物线 于 , 两点, 是线段 的中点,过点 作 轴的垂线交 于点 .
(1)求抛物线 的方程;
(2)是否存在直线 ,使得以 为直径的圆 经过点 ?若存在,求出直线 的方程;若不存在,说明理由.
(1)根据面面垂直的性质可得 平面 ,故而平面 平面 ;
【解析】
可得 , ,又 , ,则 .
【解答】
∵ 是偶函数,且 ,∴ ,
又 , ,则 .
15.
【答案】
【考点】
球的体积和表面积
球内接多面体
【解析】
由题意,底面 是边长为 的等边三角形, , 平面 ,把三棱锥 放到正方体中,可得 是正方体的三个平面对角线.即可求解外接球半径;
【解答】
由题意,底面 是边长为 的等边三角形, , 平面 ,
二、填空题:本大题共4个小题,每小题5分,共20分.
13.
【答案】
【考点】
等比数列的通项公式
【解析】
设出等比数列的首项,公比 ,结合已知列式求得首项,代入等比数列的通项公式得答案.
【解答】
设等比数列 的首项为 ,公比 , ,
可得 , ,
解得 , ,
则该数列的通项公式 .
14.
【答案】
【考点】
函数奇偶性的性质
2018年四川省宜宾市高考数学三诊试卷(文科)
一、选择题:本题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.已知集合 , ,则
A. B. C. D.
2.若 为虚数单位,则复数 在复平面上对应的点位于( )
四川省宜宾四中2018届高三高考适应性(最后一模)考试文科综合试卷
2018年四川省宜宾市四中高考适应性考试文科综合试题一.选择题:本卷共35个小题,每小题4分,共140分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
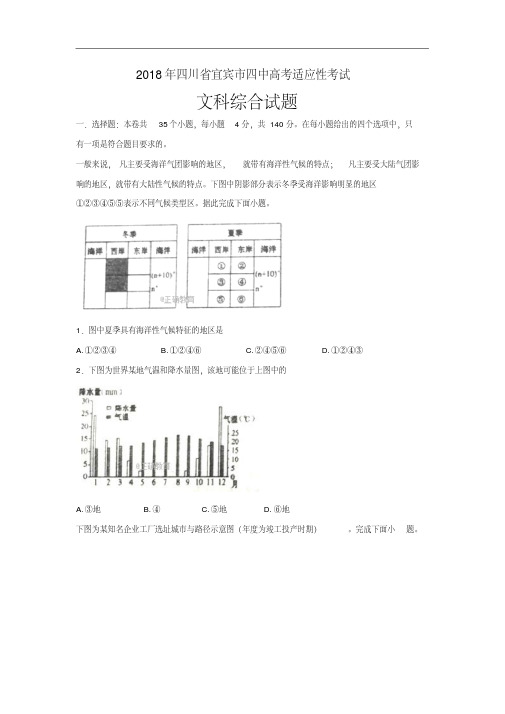
一般来说,凡主要受海洋气团影响的地区,就带有海洋性气候的特点;凡主要受大陆气团影响的地区,就带有大陆性气候的特点。
下图中阴影部分表示冬季受海洋影响明显的地区①②③④⑤⑤表示不同气候类型区。
据此完成下面小题。
1.图中夏季具有海洋性气候特征的地区是A. ①②③④B. ①②④⑥C. ②④⑤⑥D. ①②④③2.下图为世界某地气温和降水量图,该地可能位于上图中的A. ③地B. ④C. ⑤地D. ⑥地下图为某知名企业工厂选址城市与路径示意图(年度为竣工投产时期)。
完成下面小题。
3.影响该企业选址最主要的因素是A. 节省运输费用B. 减少工人数量C. 降低生产成本D. 靠近原料产地4.该企业对工厂所在城市的主要影响有①缓解交通拥堵②优化空间结构③引发人口集聚④提高城市化水平A. ①②B. ②③C. ①④D. ③④吐鲁番盆地低于海平面的面积有4050平方千米,盆地内生长着一种多年生植物--刺山柑(又名老鼠瓜),其主根入土很深,水平根极少。
地上部分为放射状的平卧株丛,叶片为肥厚肉质卵圆形,花朵呈白色或淡绿色。
读图,完成下面小题。
5.关于刺山柑,下列说法正确的是①主根深是为吸收深埋的地下水②平卧株丛有利于吸收地表径流③肥厚肉质叶片利于水分的保存④花朵颜色可以减弱强光的照射A. ①②③B. ①②④C. ②③④D. ①③④6.关于该地区,下列说法正确的是A. 吐鲁番盆地是风力作用下形成B. 吐鲁番盆地是流水作用下形成C. 盆地内部外力以风力作用为主D. 盆地内部外力以冰川作用为主“晒晒太阳就能发电,电动汽车跑在上面就能充电,下雪后还能自行感知、融化路面积。
四川省宜宾市第四中学2018届高三高考适应性最后一模考试文综-历史试题 含答案 精品

24.有学者指出,在先秦诸子百家中,儒法两家尖锐对立。
秦朝尊崇法家,厉行法治,遭到儒家批评。
秦朝灭亡后,取代法家的是道家。
文景以后,道家淡出政治舞台,儒家取而代之,登上正统学说的宝座。
这表明秦汉时期A. 根据统治需要选择治国思想B. 延续了百家争鸣的思想局面C. 对待思想流派态度变换不定D. 逐渐认识到法、道思想的弊端25.古代中国有数量丰富的各类文学作品,其中被誉为“中国文学现实主义传统的基础”的是A. 《诗经》B. 《离骚》C. 《上林赋》D. “三吏”26.明末淸初,金圣叹择取历史上各体文学之精粹,选出“六才子书”,即“一庄子、二离骚、三史记、四杜甫、五水浒、六西厢”。
李贽也有“宇宙间有五大部文章”之说,与上述吻合的有史记、杜甫、水浒。
造成这一现象的原因是A. 这些著作真实地记录了历史B. 文人们有强烈的社会批判意识C. 世俗文学登上大雅之堂D. 商品经济下文学观念逐渐开放27.斯塔夫里阿诺斯在《全球通史》中写道:三次灾难性的战争使中国受到了巨大的刺激,第一次是1840~1842年同英国的战争,第二次是1856~1860年同英法的战争,第三次是1894~1895年同日本的战争。
这三次战争的共同之处是A. 使中国逐步卷入资本主义世界市场B. 使清政府中央机构完全半殖民地化C. 中国开放的通商口岸由内地向沿海扩展D. 列强侵略以资本输出为主28.晚清民间教科书关于近代政治知识的介绍日见增多。
商务印书馆1910年初版陆费逵的《修身讲义》中有:“立法、行政、司法三权,由一机关行之者,曰专制政体;三权各有独立之机关者,曰立宪政体”。
对此解读最为合理的是A.民主思想推动教育内容的更新 B.清朝的教育体制发生了巨变C.三权分立学说率先影响了教育 D.教育引发了辛亥革命的爆发29.上海作为中国近代思想文化的发源地之一,在某一时期成为现代新儒家、自由主义、权威主义、新民主主义、和平主义、社会主义等各种思想文化论战的阵地。
四川省宜宾市第四中学校2023届高考适应性考试文科数学试题
四川省宜宾市第四中学校2023届高考适应性考试文科数学试题学校:___________姓名:___________班级:___________考号:___________二、填空题13.为了迎接春节,小王买了红黄紫三种颜色的花各一盆,准备并排摆放在自家阳、、(2)已知2020年全国居民人均可支配收入为32189元,若从2020年开始,以后每年全国居民人均可支配收入均以6%的速度增长,预计哪一年全国居民每百户家用汽车拥有量可以达到50辆.参考数据:17.(1)2n n a =;(2)22122nnn n T ++=-.【分析】(1)设{}n a 的公比为(2)写出n b ,由分组求和法求【详解】(1)设{}n a 的公比为因为12a =,且2a ,32a +,4a 所以2432(2)a a a +=+,即2q +所以2n n a =;(2)利用等体积法求解点到平面的距离.【详解】(1)延长CD至点F ,且DF =CD ,延长11C D 至点H ,使得111D H C D =,连接FH ,1C F 交1DD 于点Q ,因为四棱柱1111ABCD A B C D -中,底面ABCD 是等腰梯形,24AB CD ==,所以四棱柱111ABCF A B C H -为长方体,11//AB FC ,且Q 为1DD 的中点,取1CC 的中点E ,连接ED ,则1//ED FC ,所以1//AB ED ,故棱1CC 与平面1ADB 的交点E 的位置为1CC 的中点;(2)取AB 的中点M ,连接DM ,因为24AB CD ==,060BAD Ð=,故△ADM 为等边三角形,所以2AM AD ==,因为侧棱1DD ⊥底面ABCD 且112BB DD DC ===,AB Ì平面ABCD ,所以1BB AB ^,。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
【全国校级联考】四川省宜宾市第四中学2018届高三高考适应性考试数学(文)试题
学校_________ 班级__________ 姓名__________ 学号__________
一、单选题
1. 已知集合或,则( ) A.B.或C.D.或
2. 复数().
A.B.C.D.
3. 已知双曲线的焦距为,且双曲线的一条渐近线与直线平行,则双曲线的方程为()
A.B.C.D.
4. 设,,则“”是“”的()
A.充要条件B.充分而不必要条
件
C.必要而不充分条
件
D.既不充分也不必
要条件
5. 已知圆截直线所得线段的长度是,
则圆与圆的位置关系是()
A.内切B.相交C.外切D.相离
6. 中,角A,B,C的对边分别是a,b,c,已知,则A=
A.B.C.D.
7. 如图是由圆柱与圆锥组合而成的几何体的三视图,则该几何体的表面积为()
A.B.C.D.
8. 某路口人行横道的信号灯为红灯和绿灯交替出现,红灯持续时间为40秒,若一名行人来到该路口遇到红灯,则至少需要等待15秒才出现绿灯的概率为()
A.B.C.D.
9. 平面过正方体ABCD—A 1B1C1D1的顶点A,
,,则m,n所成角的正切值为()
D.
A.B.
C.
10. 若函数在上单调递增,则的取值范围是( )
A.
B.C.D.
11. 已知函数满足,若函数与
图象的交点为,则( ) A.B.C.D.
12. 已知正三角形的边长为,平面内的动点满足,
,则的最大值是( )
A.B.C.D.
二、填空题
13. 已知向量,若,则__________.
14. 已知,则__________.
15. 若满足约束条件,则,都有
成立;则的取值范围是__________.
16. 已知函数在R上单调递减,且关于x的方程恰有两个不相等的实数解,则a的取值范围是
___________.
三、解答题
17. 已知是公差为3的等差数列,数列满足
.
(Ⅰ)求的通项公式;(Ⅱ)求的前n项和.
18. 省环保厅对、、三个城市同时进行了多天的空气质量监测,测得三个城市空气质量为优或良的数据共有180个,三城市各自空气质量为优或良的数据个数如下表所示:
城城城
优(个)28
良(个)32 30
已知在这180个数据中随机抽取一个,恰好抽到记录城市空气质量为优的数据的概率为0.2.
(I)现按城市用分层抽样的方法,从上述180个数据中抽取30个进行后续分析,求在城中应抽取的数据的个数;
(II)已知,,求在城中空气质量为优的天数大于空气质量为良的天数的概率.
19. 如图,菱形的对角线与交于点,点分别在
上,交于点,将沿折起到的位置.
(Ⅰ)证明:;
(Ⅱ)若,求五棱锥的体积.
20. 设椭圆的右焦点为,右顶点为,已知
,其中为原点,为椭圆的离心率.
(1)求椭圆的方程;
(2)设过点的直线与椭圆交于点(不在轴上),垂直于的直线与交于点,与轴交于点,若,且,求直线的斜率的取值范围.
21. 函数.
(I)求的单调区间;
(II)若,求证:.
22. 已知直线l的参数方程为(t为参数),以原点为极点,x轴
的正半轴为极轴建立极坐标系,圆C的极坐标方程为.
(Ⅰ)求圆C的直角坐标方程;
(Ⅱ)若是直线l与圆面的公共点,求的取值范围.
23. 已知函数
(Ⅰ)若,求实数的取值范围;
(Ⅱ)若,判断与的大小关系并证明.。
